A Study on the Non-Linear Murray Equation Through the Bernoulli Wavelet Approach

Abstract

In this paper, we developed the operational matrices of integration based on the Bernoulli wavelets and proposed the novel technique known as the Bernoulli wavelet collocation method (BWCM) for extended boundary conditions of the non-linear Murray equation. Abiding by this method, given equations are converted into a system of algebraic equations. On solving these algebraic equations that yield desired approximate solution. The obtained outcome is compared with the exact and other numerical solutions in the literature through tables and graphs. The accuracy of the extended boundary conditioned problem of the Murray equation is better than the Haar wavelet method. The convergence analysis is discussed through theorems.

Introduction

Partial differential equations (PDEs) are used to formulate real-world problems in terms of solving mathematical equations, and thus help to obtain the solution of physical and other problems having functions of several variables, such as the fluid flow, propagation of heat or sound, elasticity, electrodynamics, electrostatics, etc. The thorough study of physical models is one of the fundamental concerns of PDE development to the present day. PDEs play a vital role in several areas of mathematics. There are possibly better applications that have frequently ended up being very progressive for PDEs as an instrument in the advancement of different areas of mathematics. Many types of PDEs exist in which Reaction–diffusion (RD) equations are one type of class. RD equations express the way of behaving of an enormous scope of substance frameworks where the dispersion of material rivals the creation of that material by some types of chemical reactions. RD equations emerge normally in frameworks comprising numerous synthetic responses, and connecting parts, and are broadly used to describe design development peculiarities in an assortment of physical, compound, and organic frameworks. In most recent years, non-linear RD [1, 2] equations have been broadly examined and applied in engineering and biological sciences such as the advance wave equations in genes [3], heat-and-mass transfer equations in Tokamak plasma [4], etc. This study helps us with the mathematical solutions of non-linear RD modeling the periodic moving elements of dispersion and non-linear propagation for a populace. for insane, A constructive method for construction of new exact solutions of nonlinear evolution equations [5], the constructive method for construction of non-Lie solutions of nonlinear evolution equations[6], Nonlinear Diffusion in Population Genetics Combustion and Never Pulse Propagation [7, 8], Soliton solutions for the Fitzhugh-Nagumo equation with the Homotopy analysis method [9]. The related non-linear RD equation was started by Fisher [3] to portray the engendering conduct of a virile freak. The non-linear RD equations portray a populace of diploid people [1, 3].

Let us consider non-linear RD equations with convection terms of the form,

$$ U_{t} = L\left( { U} \right)U_{xx} + M\left( { U} \right) U_{x} + N\left( { U} \right) $$

(1.1)

Here, $U=U (x,t)$ is an unknown function, $L( U)$, $M\left( U\right)$, and $N\left( U\right)$ are erratic smooth functions. $x$ and $t$ are independent variables. Equation (1.1) can be derived into a number of the popular non-linear second-order evolution equations depicting different portrayals in biological science [1, 2, 10]. The classical Burgers equation can be generalized from the Eq. (1.1) is given below.

$${U}_{t}= {U}_{xx}+{\lambda }_{0}U{U}_{x}$$

(1.2)

and the renowned Fisher equation is also derived from (1.1) equation [4],

$${U}_{t}= {U}_{xx}+{\lambda }_{1}U-{\lambda }_{2}{U}^{2}$$

(1.3)

where, ${\lambda }_{0}$, ${\lambda }_{1}$, and ${\lambda }_{2}\in {\varvec{R}}$.

The particular case of Eq. (1.1) i.e., $L\left(U\right)=1$, $M\left(U\right)={\lambda }_{0}U$, $N\left(U\right)={\lambda }_{1}U-{\lambda }_{2}{U}^{2}$ is the Murray equation that represents as;

$${U}_{t}={U}_{xx}+{\lambda }_{0}U{U}_{x}+{\lambda }_{1}U-{\lambda }_{2}{U}^{2}$$

(1.4)

The Eq. (1.4) is considered as a speculation of the Fisher and Burgers equations.

The exact solution for Eq. (1.4) is given by [19]

$$U\left(x,t\right)=\frac{{\lambda }_{1}+{c}_{1}{e}^{({\gamma }^{2}t+\gamma x)}}{{\lambda }_{2}+{c}_{0}{e}^{(-{\lambda }_{1}t)}}$$

(1.5)

where $\gamma =\frac{{\lambda }_{2}}{{\lambda }_{0}}$ and ${\lambda }_{0}\ne 0$, ${c}_{0}$ is constant such that ${\lambda }_{2}+{c}_{0}{e}^{-({\lambda }_{1}t)}\ne 0$ and ${c}_{1}$ is an arbitrary constant.

Wavelet analysis is a recent and arising region in applied and computational numerical exploration. Wavelets are the mathematical functions that help to cut up the information into different recurrence parts and which prompt the investigation of every part of information with a goal matched to its scale. Wavelets lead over the regular Fourier strategies in dissecting physical circumstances where the sign contains discontinuities and sharp spikes. The wavelet transform is an emerging mathematical scheme that can decompose a signal into multiple lower resolution levels by controlling a single wavelet function's scaling and shifting factors. Bernoulli wavelets have come to be a rising famous tool in the applied and computational sciences. They have had several applications in a broad range of areas such as data compression, signal analysis, and many others. Some types of mathematical problems tackled by the wavelet method are listed as follows; Anomalous infiltration and diffusion modeling by nonlinear fractional differential equations with variable order [11], neutral delay differential equations [12], fractional partial differential equations with Dirichlet boundary condition [13], fractional delay differential equations [14], Nonlinear Singular Lane–Emden Type Equations [15], singular Volterra integro-differential equations [16], Caputo fractional delay differential equations [17], Numerical solution of the Jeffery–Hamel flow through the wavelet technique [20], A novel approach for multi-dimensional fractional coupled Navier–Stokes equation [21], A new coupled wavelet-based method applied to the nonlinear reaction–diffusion equation [22], An effective numerical simulation for solving a class of Fokker–Planck equations using Laguerre wavelet method [23], On pulse propagation of soliton wave solutions related to the perturbed Chen-Lee-Liu equation in an optical fiber [24], On the conformable nonlinear Schrödinger equation with second-order spatiotemporal and group velocity dispersion coefficients [25], Application of Hermite Wavelet Method and Differential Transformation Method for Nonlinear Temperature Distribution in a Rectangular Moving Porous Fin [26], On the Complex Simulations with Dark–Bright to the Hirota-Maccari System [27, 28].

Bernoulli Wavelet and its Functional Matrix of Integration

Bernoulli Wavelets

Bernoulli wavelets ${U}_{n,m}\left( t\right)=U \left( k,\widehat{n }, m, t\right)$ have four parameters; $\widehat{n}=n-1, n=1, 2, 3,\dots ,{2}^{k-1}, k$ is a + ve integer, $m$ be the degree of the Bernoulli polynomials, and $t$ be the normalized time. Bernoulli wavelets are well-defined on the interval $[\mathrm{0,1})$ as [18],

$$ U_{{n,m}} \left( t \right) = \left\{ \begin{gathered} 2^{{\frac{{k - 1}}{2}}} \widetilde{{b_{m} }}\left( {2^{{k - 1}} t - \hat{n}} \right),\quad \frac{{\hat{n}}}{{2^{{k - 1}} }} \le t < \frac{{\hat{n} + 1}}{{2^{{k - 1}} }} \hfill \\ 0,\quad \quad\quad \quad \quad \quad \quad \quad \quad Otherwise \hfill \\ \end{gathered} \right. $$

with

$$ \widetilde{{b_{m} }}\left( t \right) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \quad \quad \quad \quad\; \quad \quad m = 0 \hfill \\ \frac{1}{{\sqrt {\frac{{\left( { - 1} \right)^{{m - 1}} \left( {m!} \right)^{2} }}{{\left( {2m} \right)!}}a_{{2m}} } }}b_{m} \left( t \right),\quad m > 0 \hfill \\ \end{gathered} \right. $$

where $m=0, 1, 2, \dots , M -1, n =1, 2, \dots , {2}^{k-1}$. The coefficient $\frac{1}{\sqrt{\frac{{\left(-1 \right)}^{m-1}{\left( m!\right)}^{2}}{\left(2 m\right)!}{a}_{2m}}}$ is for normality, $p={2}^{-(k-1)}$ is the dilation-parameter and $q=\widehat{n}{2}^{-(k-1)}$ is the translation parameter. Here, ${b}_{m}\left(t\right)$ are the renowned Bernoulli polynomials of order $m$ which can be well-defined by;

$${b}_{m}\left(t\right)=\sum_{i=0}^{m}\left(\genfrac{}{}{0pt}{}{m}{i}\right){a}_{m-i}{t}^{i},$$

where ${a}_{i}, i= 0, 1, \dots ,m$ are the Bernoulli numbers. Now, we fairly accurate the function $y(x)$ under Bernoulli wavelet space is as follows:

$$y(x)={\sum }_{n=1}^{\infty }{\sum }_{m=0}^{\infty }{C}_{n,m}{U}_{n,m}\left(x\right)$$

(2.1)

where ${U}_{n,m}\left(x\right)$ is the Bernoulli wavelet. We approximate $y(x)$ by truncating the series as follows;

$$y(x)\approx {\sum }_{n=1}^{{2}^{k-1}}{\sum }_{m=0}^{M-1}{C}_{n,m}{U}_{n,m}(x)={A}^{T}U\left(x\right)$$

(2.2)

where $A$ and $U(x)$ are ${2}^{k-1}M\times 1$ matrix,

$${A}^{T}=[{C}_{\mathrm{1,0}},\dots ,{C}_{1, M -1},{C}_{\mathrm{2,0}},\dots ,{C}_{2,M -1},\dots ,{C}_{{2}^{k-1}, 0},\dots {C}_{{2}^{k-1}, M -1}],$$

$$U(x)=[{U}_{\mathrm{1,0}},\dots ,{U}_{1,M-1},{U}_{\mathrm{2,0}},\dots {U}_{2,M-1},\dots {U}_{{2}^{k-1},0},\dots {U}_{{2}^{k-1},M-1}{]}^{T}.$$

Let $\left\{{U}_{i,j}\right\}$ be the sequence of Bernoulli wavelets, ${i }= 0, 1, \dots ,$ and ${j}=1, 2, \dots$ For every fixed j, there is a Bernoulli space spanned by the elements of the sequence$\left\{{U}_{i,j}\right\}$. That is, $L\left(\left\{{U}_{i,j}\right\}\right)={L}^{2}[\mathrm{0,1})$ is Banach space.

Functional Matrix of Integration

Here, we simplified some basis of the Bernoulli wavelets at $k=1$ as follows:

$${U}_{\mathrm{1,0}}\left(t\right)=1,$$

$${U}_{\mathrm{1,1}}\left(t\right)=\sqrt{3}\left(-1+2t\right),$$

$${U}_{\mathrm{1,2}}\left(t\right)=\sqrt{5}\left(1-6t+6{t}^{2}\right),$$

$${U}_{\mathrm{1,3}}\left(t\right)=\sqrt{210}\left(t-3{t}^{2}+2{t}^{3}\right),$$

$${U}_{\mathrm{1,4}}\left(t\right)=10\sqrt{21}\left(-\frac{1}{30}+{t}^{2}-2{t}^{3}+{t}^{4}\right),$$

$${U}_{\mathrm{1,5}}\left(t\right)=\sqrt{\frac{462}{5}} \left(-t+10{t}^{3}-15{t}^{4}+6{t}^{5}\right),$$

$${U}_{\mathrm{1,6}}\left(t\right)=\sqrt{\frac{1430}{691}} \left(1-21{t}^{2}+105{t}^{4}-126{t}^{5}+42{t}^{6}\right),$$

$${U}_{\mathrm{1,7}}\left(t\right)=2\sqrt{\frac{143}{7}} \left(t-7{t}^{3}+21{t}^{5}-21{t}^{6}+6{t}^{7}\right),$$

$${U}_{\mathrm{1,8}}\left(t\right)=\sqrt{\frac{7293}{3617}} \left(-1+20{t}^{2}-70{t}^{4}+140{t}^{6}-120{t}^{7}+30{t}^{8}\right),$$

$${U}_{\mathrm{1,9}}\left(t\right)=\sqrt{\frac{1939938}{219335}} \left(-3t+20{t}^{3}-42{t}^{5}+60{t}^{7}-45{t}^{8}+10{t}^{9}\right),$$

$${U}_{\mathrm{1,10}}\left(t\right)=22\sqrt{\frac{125970}{174611}} \left(\frac{5}{66}-\frac{3{t}^{2}}{2}+5{t}^{4}-7{t}^{6}+\frac{15{t}^{8}}{2}-5{t}^{9}+{t}^{10}\right),$$

$${U}_{\mathrm{1,11}}\left(t\right)=2\sqrt{\frac{676039}{854513}} \left(5t-33{t}^{3}+66{t}^{5}-66{t}^{7}+55{t}^{9}-33{t}^{10}+6{t}^{11}\right).$$

where $U_{{10}} \left( t \right) = \left[ {U_{{1,0}} \left( t \right),U_{{1,1}} \left( t \right),U_{{1,2}} \left( t \right),U_{{,3}} \left( t \right),U_{{1,4}} \left( t \right),U_{{1,5}} \left( t \right),U_{{1,6}} \left( t \right),U_{{1,7}} \left( t \right),U_{{1,8}} \left( t \right),U_{{1,9}} \left( t \right)} \right]^{T} .$

Now integrate the above basis elements concerning $t$ limit from $0$ to $t$, then express as a linear combination of Bernoulli wavelet basis as;

$$\underset{0}{\overset{t}{\int }}{U}_{1, 0}\left(t \right)dt=\left[\begin{array}{cccccccccc}\frac{1}{2}& \frac{1}{2\sqrt{3}}& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,1}}\left(t\right)dt=\left[\begin{array}{cccccccccc}-\frac{1}{2\sqrt{3}}& 0& \frac{1}{2\sqrt{15}}& 0& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,2}}\left(t\right)dt=\left[\begin{array}{cccccccccc}0& 0& 0& \frac{1}{\sqrt{42}}& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,3}}\left(t\right)dt=\left[\begin{array}{cccccccccc}\frac{\sqrt{7}}{2\sqrt{30}}& 0& 0& 0& \frac{1}{2\sqrt{10}}& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,4}}\left(t\right)dt=\left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& \frac{\sqrt{5}}{3\sqrt{22}}& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,5}}\left(t\right)dt=\left[\begin{array}{cccccccccc}-\sqrt{\frac{11}{210}} & 0& 0& 0& 0& 0& \frac{\sqrt{691}}{10\sqrt{273}}& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,6}}\left(t\right)dt=\left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& 0& 0& \sqrt{\frac{35}{1382}} & 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,7}}\left(t\right)dt=\left[\begin{array}{cccccccccc}\frac{\sqrt{143}}{20\sqrt{7}}& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{3617}}{20\sqrt{357}}& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,8}}\left(t\right)dt=\left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{219335}}{3\sqrt{962122}}\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,9}}\left(t\right)dt=\left[\begin{array}{cccccccccc}-\sqrt{\frac{146965}{2895222}} & 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right)+\frac{\sqrt{1222277}}{10\sqrt{482537}}{U}_{\mathrm{1,10}}\left(t\right).$$

Hence,

$$\underset{0}{\overset{t}{\int }}U\left(t\right)dt={B}_{10\times 10}{U}_{10}\left(t\right)+\overline{{U }_{10}\left(t\right).}$$

where

${B}_{10\times 10}=\left[\begin{array}{cccccccccc}\frac{1}{2}& \frac{1}{2\sqrt{3}}& 0& 0& 0& 0& 0& 0& 0& 0\\ -\frac{1}{2\sqrt{3}}& 0& \frac{1}{2\sqrt{15}}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{1}{\sqrt{42}}& 0& 0& 0& 0& 0& 0\\ \frac{\sqrt{7}}{2\sqrt{30}}& 0& 0& 0& \frac{1}{2\sqrt{10}}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \frac{\sqrt{5}}{3\sqrt{22}}& 0& 0& 0& 0\\ -\sqrt{\frac{11}{210}} & 0& 0& 0& 0& 0& \frac{\sqrt{691}}{10\sqrt{273}}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& \sqrt{\frac{35}{1382}} & 0& 0\\ \frac{\sqrt{143}}{20\sqrt{7}}& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{3617}}{20\sqrt{357}}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{219335}}{3\sqrt{962122}}\\ -\sqrt{\frac{146965}{2895222}} & 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right],$

$$\overline{{U }_{10}\left(t\right)}=\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \frac{\sqrt{1222277}}{10\sqrt{482537}}{U}_{\mathrm{1,10}}\left(t\right)\end{array}\end{array}\right]$$

Next, twice integration of basis, we get;

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,0}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}\frac{1}{6}& \frac{1}{4\sqrt{3}}& \frac{1}{12\sqrt{5}}& 0& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,1}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}-\frac{1}{4\sqrt{3}}& -\frac{1}{12}& 0& \frac{1}{6\sqrt{70}}& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,2}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}\frac{1}{12\sqrt{5}}& 0& 0& 0& \frac{1}{4\sqrt{105}}& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,3}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}\frac{\sqrt{7}}{4\sqrt{30}}& \frac{\sqrt{7}}{12\sqrt{10}}& 0& 0& 0& \frac{1}{12\sqrt{11}}& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,4}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}-\frac{1}{6\sqrt{21}}& 0& 0& 0& 0& 0& \frac{\sqrt{691}}{6\sqrt{30030}}& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,5}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}-\frac{\sqrt{11}}{2\sqrt{210}}& -\frac{\sqrt{11}}{6\sqrt{70}}& 0& 0& 0& 0& 0& \frac{1}{2\sqrt{390}}& 0& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,6}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}\frac{\sqrt{143}}{4\sqrt{6910}}& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{3617}}{4\sqrt{352410}}& 0\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,7}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}\frac{\sqrt{143}}{40\sqrt{7}}& \frac{\sqrt{143}}{40\sqrt{21}}& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{43867}}{84\sqrt{9690}}\end{array}\right]{U}_{10}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,8}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}-\frac{5\sqrt{221}}{6\sqrt{119361}}& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right)+\frac{\sqrt{174611}}{6\sqrt{7559530}}{U}_{\mathrm{1,10}}\left(t\right),$$

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}{U}_{\mathrm{1,9}}\left(t\right)dtdt=\left[\begin{array}{cccccccccc}-\frac{\sqrt{146965}}{2\sqrt{2895222}}& -\frac{\sqrt{146965}}{6\sqrt{965074}}& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]{U}_{10}\left(t\right)+\frac{\sqrt{77683}}{2\sqrt{30268230}}{U}_{\mathrm{1,11}}\left(t\right).$$

Hence,

$$\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}U\left(t\right)dtdt={B}_{10\times 10}^{^{\prime}}{U}_{10}\left(t\right)+{\overline{{U }_{10}\left(t\right)}}^{^{\prime}},$$

where

$${B}_{10\times 10}^{^{\prime}}=\left[\begin{array}{cccccccccc}\frac{1}{6}& \frac{1}{4\sqrt{3}}& \frac{1}{12\sqrt{5}}& 0& 0& 0& 0& 0& 0& 0\\ -\frac{1}{4\sqrt{3}}& -\frac{1}{12}& 0& \frac{1}{6\sqrt{70}}& 0& 0& 0& 0& 0& 0\\ \frac{1}{12\sqrt{5}}& 0& 0& 0& \frac{1}{4\sqrt{105}}& 0& 0& 0& 0& 0\\ \frac{\sqrt{7}}{4\sqrt{30}}& \frac{\sqrt{7}}{12\sqrt{10}}& 0& 0& 0& \frac{1}{12\sqrt{11}}& 0& 0& 0& 0\\ -\frac{1}{6\sqrt{21}}& 0& 0& 0& 0& 0& \frac{\sqrt{691}}{6\sqrt{30030}}& 0& 0& 0\\ -\frac{\sqrt{11}}{2\sqrt{210}}& -\frac{\sqrt{11}}{6\sqrt{70}}& 0& 0& 0& 0& 0& \frac{1}{2\sqrt{390}}& 0& 0\\ \frac{\sqrt{143}}{4\sqrt{6910}}& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{3617}}{4\sqrt{352410}}& 0\\ \frac{\sqrt{143}}{40\sqrt{7}}& \frac{\sqrt{143}}{40\sqrt{21}}& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{43867}}{84\sqrt{9690}}\\ -\frac{5\sqrt{221}}{6\sqrt{119361}}& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -\frac{\sqrt{146965}}{2\sqrt{2895222}}& -\frac{\sqrt{146965}}{6\sqrt{965074}}& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right],$$

$${\overline{{U }_{10}\left(t\right)}}^{^{\prime}}=\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \frac{\sqrt{174611}}{6\sqrt{7559530}}{U}_{\mathrm{1,10}}\left(t\right)\\ \frac{\sqrt{77683}}{2\sqrt{30268230}}{U}_{\mathrm{1,11}}\left(t\right)\end{array}\end{array}\right]$$

In the same way, we can generate matrices of different sizes for our requirements.

Some Theorems on Convergence Analysis and the Bernoulli Wavelet

The Space of Functions ${{\varvec{L}}}^{2}({\mathbb{R}})$

The set of all functions $f$ for which ${\left|f(x)\right|}^{2}$ is integrable on the region ${\mathbb{R}}$.

Continuous Functions in ${{\varvec{L}}}_{2}({\mathbb{R}})$

Let $U(x,t)\in {L}_{2}({\mathbb{R}})$ with$t\;\in [a,b]$. Then $U(x,t)$ is continuous in ${L}_{2}({\mathbb{R}})$ in the variable $t$ on $[a,b]$ if $U ( x , {t}^{^{\prime}})\to U( x ,t)$ in ${L}^{2}({\mathbb{R}})$ whenever ${t}^{^{\prime}} \to t \forall t\in [a,b]$.

The above definition says that if the function $U(x ,t )$ is continuous in $t$ on$[a,b]$, then the $\Vert U \left(x ,t\right)\Vert$ is continuous in $t$ on$[ a,b]$.

Riesz Fischer Theorem

If a sequence of functions ${\{{f}_{k}\}}_{k=1}^{\infty }$ in ${L}_{2}({\mathbb{R}})$ converges itself in ${L}^{2}({\mathbb{R}})$ then there is a function $f\in {L}_{2}({\mathbb{R}})$ such that $\Vert {f}_{k}-f\Vert \to 0$ as $k\to \infty$.

Theorem 1

Let $U(x,t)$ in ${L}^{2}({\mathbb{R}}\times {\mathbb{R}})$ be a continuous bounded function defined on $\left[0, 1\right) \times [ 0, 1)$ , then Bernoulli wavelet expansion of $U(x,t)$ is uniformly converges to it.

Proof

Let $U(x,t)$ in ${L}^{2}({\mathbb{R}}\times {\mathbb{R}})$ be a continuous function defined on $\left[0, 1\right) \times [ 0, 1)$ and bound by a real number$\mu$. The approximation of $U( x ,t)$ is;

$$U\left(x ,t \right)=\sum_{ i=1}^{\infty } \sum_{j=0}^{\mathrm{ \infty }}{a}_{i,j}{U}_{i,j} \left( x\right) {U}_{ i, j}( t),$$

where ${a}_{ i, j}=\langle U\left(x,t \right),{U}_{ i, j}( x){U}_{i,j}( t)\rangle$, and $\langle ,\rangle$ represents inner product. Since ${U }_{i, j} ( x){ U}_{ i, j}( t)$ are orthogonal functions on$\left[\mathrm{0,1}\right)$. Then,

$${a}_{ i, j} = \underset{0}{\overset{1}{\int }} \underset{0}{\overset{1}{\int }} U\left( x, t \right){U}_{i,j} (x){U}_{i,j }( t)dxdt,$$

$${a}_{i, j}=\underset{0}{\overset{1 }{\int }}\underset{I}{{\int }}U\left( x,t\right)\frac{{2}^{\left(\frac{k -1}{2}\right)}}{\sqrt{\frac{{\left(- 1 \right)}^{ m-1}{\left(m !\right)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}{b}_{m}\left({2}^{k-1}x-n+1\right) {U}_{i,j}( t)dxdt,$$

where $I=\left[\frac{n-1}{{2}^{k-1}},\frac{n}{{2}^{k-1}}\right]$, Put ${2}^{k-1}x-n+1 =r$ then,

$${a}_{ i, j }=\frac{{2}^{\frac{ k -1}{2}}}{\sqrt{\frac{{(- 1 )}^{ m-1}{(m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}U\left(\frac{r -1 +n}{{2 }^{ k -1}}, t\right){b}_{m}\left(r\right)\frac{dr}{{2 }^{k -1}} {U}_{i,j}( t)dt,$$

$${a}_{i,j} =\frac{{2}^{ - \frac{k -1}{2}}}{\sqrt{\frac{{(- 1)}^{m-1}{(m !)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}\underset{0}{\overset{1}{\int }} \left[ \underset{0}{\overset{1}{\int }} U\left(\frac{r -1+n}{{2}^{k-1}}, t\right){b}_{m}\left(r\right)dr\right]{U}_{i,j}\left( t\right)dt,$$

By generalized mean value theorem for integrals,

$${a}_{i,j}=\frac{{2}^{-\left[-\frac{k -1}{2}\right]}}{\sqrt{\frac{{(-1)}^{ m -1}{ ( m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}\underset{0}{\overset{1}{\int }}U\left(\frac{ r -1+ n}{{2}^{k-1}} , t\right){U}_{i,j}( t)dt\left[\underset{0}{\overset{1}{\int }}{b}_{m}\left( r \right)dr\right],$$

where $\xi \in (\mathrm{0,1})$ and choose $\int_{{ - 1}}^{1} {b_{m} \left( r \right)dr = A}$,

$${a}_{i,j}=\frac{A{2}^{- \left[- \frac{k - 1}{2}\right]}}{\sqrt{\frac{{(-1)}^{m-1}{ ( m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}} \underset{\frac{n-1}{{2}^{k-1}}}{\overset{\frac{n}{{2}^{k-1}}}{\int }}U\left(\frac{\xi -1+n}{{2}^{k-1}},t\right)\frac{{2}^{\frac{k -1}{2}}}{\sqrt{\frac{{(-1)}^{m-1}{(m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}{b}_{m}({2}^{k-1}t-n+1)dt,$$

$${a}_{i,j}= \frac{A}{\left(\frac{{(-1)}^{ m -1}{( m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}\right)} \underset{\frac{n-1}{{2}^{k-1}}}{\overset{\frac{n}{{2}^{k-1}}}{\int }}U\left(\frac{\xi -1 + n}{{2}^{k- 1}}, t\right){b}_{m}\left({2 }^{k-1}t-n+ 1\right)dt,$$

Put ${2}^{k-1}t-n+1=\mathcalligra{s}$ then,

$${a}_{ i, j}= \frac{ A}{\left(\frac{{(-1 )}^{ m-1}{(m !)}^{2}{\alpha }_{2m}}{\left(2 m\right)!}\right)} \underset{0}{\overset{1}{\int }}U\left(\frac{\xi -1+ n}{{2}^{k-1}},\frac{\mathcalligra{s}-1+ n}{{2}^{k-1}}\right){b}_{m}(\mathcalligra{s})\frac{d\mathcalligra{s}}{{2}^{k-1}},$$

$${a}_{ i, j}=\frac{A{2}^{-k+1}}{\left(\frac{{(-1 )}^{ m-1}{(m !)}^{2}{\alpha }_{2m}}{\left(2 m\right)!}\right)} \underset{0}{\overset{1}{\int }} U\left(\frac{\xi -1 + n}{{2 }^{ k -1}},\frac{\mathcalligra{s}- 1+ n}{{2 }^{ k -1}}\right){b}_{m}\left(\mathcalligra{s}\right)d\mathcalligra{s},$$

By generalized mean value theorem for integrals,

$${a}_{ i, j}=\frac{A{2}^{-k+1}}{\left(\frac{{(-1 )}^{ m-1}{(m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}\right)} U\left(\frac{\xi -1+ n}{{2}^{k-1}},\frac{{\xi }_{1}-1+ n}{{2}^{k-1}}\right)\underset{0}{\overset{1}{\int }}{b}_{m}\left(\mathcalligra{s}\right)d\mathcalligra{s},$$

where, ${\xi }_{1}\in (\mathrm{0,1})$ and $\underset{0}{\overset{1}{\int }}{b}_{m}(\mathcalligra{s})d\mathcalligra{s}=B$ then,

$${a}_{i,j}=\frac{AB{2}^{-k+1}}{\left(\frac{{(-1)}^{m-1}{(m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}\right)} U\left(\frac{\xi -1+n}{{2}^{k-1}},\frac{{\xi }_{1}-1+n}{{2}^{k-1}}\right),\;\forall \xi ,{\xi }_{1}\in (\mathrm{0,1}),$$

Therefore,

$$\left|{a}_{i,j}\right|=\left|\frac{AB{2}^{-k+1}}{\left(\frac{{(-1 )}^{ m-1}{(m !)}^{2}{\alpha }_{2m}}{\left(2m \right)!}\right)}\right|\left|U\left(\frac{\xi -1 + n}{{2}^{k-1}},\frac{{\xi }_{1}-1 + n}{{2}^{k-1}}\right)\right|.$$

Since $U$ is bounded by $\mu$,

$$\left|{a}_{i,j}\right|=\frac{\left|A\right|\left|B\right| {2}^{ -k+1}\mu }{\left|\frac{{(-1)}^{m -1}{( m!)}^{2}{\alpha }_{2m}}{\left(2m\right)!}\right|} .$$

Therefore $\sum_{i =1}^{\infty } \sum_{ j=0}^{ \infty }{a}_{i,j}$ is convergent. Consequently, the Bernoulli wavelet expansion of $U(x,t)$ converges uniformly.

Theorem 2

Let the Bernoulli wavelet sequence ${\{{U}_{n,m}^{k}(x,t)\}}_{k=1}^{\infty }$ which are continuous functions defined in ${L}^{2}({\mathbb{R}})$ in $t$ on $[a,b]$ converges to the function $U(x,t)$ in ${L}^{2}({\mathbb{R}})$ uniformly in $t$ on $[a,b]$ . Then $U(x,t)$ is continuous in ${L}^{2}({\mathbb{R}})$ in $t$ on $[a,b]$ .

Proof

Since, the Bernoulli wavelet sequence ${\{{U}_{n,m}^{k}(x,t)\}}_{k=1}^{\infty }$ is uniformly converges to $U(x,t)$ in ${L}^{2}({\mathbb{R}})$. Therefore, for every $\varepsilon >0$, there exists a number $k={k}_{\varepsilon }$ such that,

$$\Vert {U}_{n,m}^{k}\left(x,t\right)-U\left(x,t\right)\Vert <\frac{\varepsilon }{3} , \forall t\in \left[ a,b\right]$$

(3.1)

Also, $\{{U}_{n,m}^{k}\left(x,t\right)\}$ is continuous in ${L}_{2}({\mathbb{R}})$ in $t\in \left[a,b\right]$. Then there exists a number $\delta ={\delta }_{\varepsilon }$ such that,

$$\Vert {U}_{n,m}^{k}\left(x , t\mathrm{^{\prime}} \right)- {U}_{ n, m}^{ k}\left(x ,t\right)\Vert <\frac{\varepsilon }{3} ,\mathrm{whenever }\Vert t\mathrm{^{\prime}}- t\Vert <\delta \forall t\mathrm{^{\prime}} , t\in \left[ a ,b\right]$$

(3.2)

$$ \left\| {U\left( {x,t^{\prime } } \right) - U\left( {x,t} \right)} \right\| = \left\| {U\left( {x,t^{\prime } } \right) - U_{{n,m}}^{k} \left( {x,t^{\prime } } \right) + U_{{n,m}}^{k} \left( {x,t^{\prime } } \right) - U_{{n,m}}^{k} \left( {x,t} \right) + U_{{n,m}}^{k} \left( {x,t} \right) - U\left( {x,t} \right)} \right\|, $$

$$ \le \left\| {U\left( {x,t^{\prime } } \right) - U_{{n,m}}^{k} \left( {x,t^{\prime } } \right)} \right\| + \left\| {U_{{n,m}}^{k} \left( {x,t^{\prime } } \right) - U_{{n,m}}^{k} \left( {x,t} \right)} \right\| + \left\| {U_{{n,m}}^{k} \left( {x,t} \right) - U\left( {x,t} \right)} \right\|, $$

$<\frac{\varepsilon }{3}+\frac{\varepsilon }{3}+\frac{\varepsilon }{3}=\varepsilon$,

$\left\| {U\left( {x,t^{\prime } } \right) - U\left( {x,t} \right)} \right\|{\text{ }} < \varepsilon$, $\forall \left\| {t - t^{\prime } {\text{ }}} \right\| < \delta$ with $t,t^{\prime } \in \left[ {a ,b} \right]$. Hence $U\left( {x,t} \right)$ is continuous in ${L}^{2}({\mathbb{R}})$ in $t$ on$\left[a,b\right]$.

Theorem 3

Let the Bernoulli wavelet sequence ${\{{U}_{n,m}^{k}(x,t)\}}_{k=1}^{\infty }$ converges itself in ${L}_{2}({\mathbb{R}})$ uniformly in $t$ on $\left[a,b\right]$ . Then there is a function $U(x , t)$ is continuous in ${L}_{2}({\mathbb{R}})$ in $t$ on $\left[a,b\right]$ and $\underset{k\to \infty }{\mathit{lim}}{U }_{n, m}^{k}\left(x ,t\right)={U}_{n,m}\left(x , t\right) \forall t\in \left[a,b\right]$ .

Proof

By Riesz Fischer theorem, for each $t\in \left[a,b\right]$ there is a function $U(x , t)$ in ${L}^{2}({\mathbb{R}})$ such that.

$$\underset{k\to \infty }{\mathrm{lim}}{U}_{n,m}^{k}\left(x ,t\right)=U\left(x ,t\right)$$

(3.3)

Consider the subsequence ${\{{U}_{n,m}^{{k}_{i}}(x , t)\}}_{i=1}^{\infty }$ such that,

$$\Vert {U}_{n,m}^{{k}_{i+1}}(x , t)-{U}_{n,m}^{{k}_{i}}(x , t)\Vert <\frac{1}{{2}^{i}}, \forall t \in \left[a,b\right]$$

(3.4)

from (3.3)

$$U\left(x,t\right)=\underset{p\to \infty }{\mathrm{lim}}{U}_{n,m}^{{k}_{p}}={U}_{n,m}^{{k}_{i}}+ \left({U }_{n, m}^{{k}_{i+1}}-{U }_{n, m}^{{k}_{i}}\right)+\left({U}_{n, m}^{{k}_{i+2}}-{U}_{n, m}^{{k}_{i+1}}\right)+,\dots ,$$

from (3.4)

$$\Vert {U\left(x,t\right)-U}_{n,m}^{{k}_{i}}\Vert \le \Vert {U}_{n,m}^{{k}_{i+1}}-{U}_{n,m}^{{k}_{i}}\Vert +\Vert {U}_{n,m}^{{k}_{i+2}}-{U}_{n,m}^{{k}_{i+1}}\Vert +,\dots ,$$

$$\le \frac{1}{{2}^{i}}+\frac{1}{{2}^{i+1}}+,\dots ,=\frac{1}{{2}^{i-1}} , i=\mathrm{1,2},3,\dots ,$$

This shows that the subsequence $\left\{{U}_{n,m}^{{k}_{i}}\left(x,t\right)\right\}$ converges to $U\left(x,t\right)$ in ${L}^{2}({\mathbb{R}})$ uniformly in $t$ on $\left[a,b\right]$. By theorem 2 the function $U\left(x,t\right)$ is continuous in ${L}_{2}({\mathbb{R}})$ in $t$ on $\left[a,b\right]$.

Bernoulli Wavelets Method

Consider the nonlinear PDE is of the form:

$${U}_{t}={U}_{xx}+{\lambda }_{0}U{U}_{x}+{\lambda }_{1}U-{\lambda }_{2}{U}^{2}$$

(4.1)

where $x$ and $t$ are the independent variables, $U$ is the dependent variable with the following physical conditions.

$$U\left( x , 0\right)={H}_{1}\left(x \right), U \left( 0,t\right)={H}_{2}\left(t\right), U\left(l,t\right)={H}_{3}\left(t\right)$$

(4.2)

where, ${\lambda }_{0},{\lambda }_{1},{\lambda }_{2}$ and $l$ be any constant, ${H}_{1}\left(x\right), {H}_{2}\left(t\right), {H}_{3}\left(t\right)$ are continuous real functions. suppose that,

$$\frac{{\partial }^{3}U\left(x,t\right)}{{\partial x}^{2}\partial t}\approx {U}^{T}\left(x\right)KU\left(t\right)$$

(4.3)

where, ${U}^{T}\left(x\right)=\left[{U}_{\mathrm{1,0}} \left( x\right),\dots ,{U}_{1, M -1}\left( x\right),\dots ,{U}_{{2}^{k- 1}, 0}( x),\dots ,{U}_{{2}^{k-1}, M- 1}( x)\right],$

$K=\left[{a}_{i,j}\right]$ be ${2}^{k-1}M\times {2}^{k-1}M$ unknown matrix such that $i=1,\dots ,{2}^{k-1}, j=0,\dots ,M-1$.

$$U\left( t\right)={\left[{U}_{\mathrm{1,0}}\left( t\right),\dots ,{U}_{1, M- 1}\left( t\right),\dots ,{U}_{{2}^{k-1},0}(t),\dots ,{U}_{{2}^{k-1},M-1}(t)\right]}^{T},$$

Integrate (4.3) concerning $t$ from limit 0 to $t$.

$$\frac{{\partial ^{2} U\left( {x,t} \right)}}{{\partial x^{2} }} = \frac{{\partial ^{2} U\left( {x,0} \right)}}{{\partial x^{2} }} + U^{T} \left( x \right)K\left[ {BU\left( t \right) + \overline{{U\left( t \right)}} } \right]$$

(4.4)

Now integrate (4.4) twice concerning $x$ from 0 to $x$.

$$ \frac{{\partial U\left( {x,t} \right)}}{{\partial x}} = \frac{{\partial U\left( {0,t} \right)}}{{\partial x}} + \frac{{\partial U\left( {x,0} \right)}}{{\partial x}} - \frac{{\partial U\left( {0,0} \right)}}{{\partial x}} + \left[ {BU\left( x \right) + \overline{{U\left( x \right)}} } \right]^{T} K\left[ {BU\left( t \right) + \overline{{U\left( t \right)}} } \right]$$

(4.5)

$$U\left( x , t\right)=U\left( 0 , t \right)+U\left( x , 0\right)-U \left( 0 , 0\right)+x\left[\frac{\partial U \left(0,t\right)}{\partial x}-\frac{\partial U \left( 0 , 0\right)}{\partial x}\right]+{\left[{B}^{^{\prime}} U\left( x\right)+{\overline{{U\left(x \right)}}}^{\boldsymbol{^{\prime}}}\right]}^{T}K\left[BU\left(t \right)+ \stackrel{-}{U\left( t\right)}\right]$$

(4.6)

Put $x=l$ on (4.6) along with physical conditions given in (4.2). We get,

$${H}_{3}\left(t\right)={H}_{2}\left(t\right)+{H}_{1}\left(l\right)-{H}_{1}\left(0 \right)+ l\left[\frac{\partial U\left( 0 , t\right)}{\partial x}-\frac{\partial U\left(\mathrm{0,0}\right)}{\partial x}\right]+\underset{x\to l}{\mathrm{lim}}{\left[{B}^{^{\prime}}U \left( x\right)+{\overline{{U\left(x \right)}}}^{\boldsymbol{^{\prime}}}\right]}^{T}K\left[BU\left(t\right)+\stackrel{-}{U\left(t \right)}\right].$$

$$\left[\frac{\partial U \left(0,t\right)}{\partial x}-\frac{\partial U\left(\mathrm{0,0}\right)}{\partial x}\right]=\frac{1}{l}\left[{H}_{3}\left(t\right)-{H}_{2}\left(t\right)-{H}_{1}\left(l\right)+{H}_{1}\left(0\right)-\underset{x\to l}{\mathrm{lim}}{\left[{B}^{^{\prime}}U\left(x\right)+{\overline{{U\left( {x} \right)}}}^{\boldsymbol{^{\prime}}}\right]}^{T}K\left[BU\left(t\right)+\overline{{U\left( t \right)}}\right]\right]$$

(4.7)

Substitute (4.7) in (4.5) and (4.6)

$$\begin{aligned}\frac{\partial U\left(x,t\right)}{\partial x}=&\frac{\partial {H}_{1}\left(x\right)}{\partial x}+\frac{1}{l}\left[{H}_{3}\left(t\right)-{H}_{2}\left(t\right)-{H}_{1}\left(l\right)\right.\\&\left.+{H}_{1}\left(0\right)-\underset{x\to l}{\mathrm{lim}}{[{B}^{^{\prime}}U \left( x\right)+{\overline{{U\left( {x} \right)}}}^{\boldsymbol{^{\prime}}}]}^{T}K[BU\left(t\right)+\overline{{U\left( t \right)}}]\right]\\&+{[BU\left(x\right)+\stackrel{-}{U\left(x\right)}]}^{T}K\left[BU\left(t\right)+\overline{{U\left( t \right)}}\right]\end{aligned}$$

(4.8)

$$\begin{aligned}U\left( x ,t\right)=&{H}_{2}\left(t\right)+{H}_{1}\left(x\right)-{H}_{1}\left(0\right)+{\left[{B}^{^{\prime}}U\left(x \right) +{\stackrel{-}{U \left(x\right)}}^{\boldsymbol{^{\prime}}}\right]}^{T}K\left[BU\left(t \right)+\overline{{U\left( t \right)}}\right]\\&+\frac{x}{l}\left[{H}_{3}\left(t\right)-{H}_{2}\left(t\right)-{H}_{1}\left(l\right)+{H}_{1}\left(0\right)-\underset{x\to l}{\mathrm{lim}}{\left[{B}^{^{\prime}}U\left( x \right)+{\stackrel{-}{U \left(x\right)}}^{\boldsymbol{^{\prime}}}\right]}^{T}\right.\\&\left.K\left[BU\left(t\right)+\overline{{U\left( t \right)}}\right]\right]\end{aligned}$$

(4.9)

Now, differentiate $U\left(x,t\right)$ concerning $t$ twice. We get,

$$\begin{aligned}\frac{\partial U\left(x,t\right)}{\partial t}=&{{H}_{2}}^{^{\prime}}\left(t\right)+\frac{x}{l}\frac{d}{dt}\left[{H}_{3}\left(t\right)-{H}_{2}\left(t\right)-{H}_{1}\left(l\right)+{H}_{1}\left(0\right)-\underset{x\to l}{\mathrm{lim}}{[{B}^{^{\prime}}U\left( x \right)+ {\overline{{U\left(x \right)}}}^{\boldsymbol{^{\prime}}}]}^{T}K[BU \left(t\right)+\overline{{U\left( t \right)}}]\right]\\&+\frac{d}{dt}\left[{[{B}^{^{\prime}}U\left(x\right)+{\overline{{U\left( {x} \right)}}}^{\boldsymbol{^{\prime}}}]}^{T}K[BU\left(t\right)+\overline{{U\left( t \right)}}]\right]\end{aligned}$$

(4.10)

$$ \begin{aligned}\frac{{\partial^{2} U\left( {x,t}\right)}}{{\partial t^{2} }} = & H_{2}^{\prime \prime } \left( t \right) + \frac{x}{l}\frac{{d^{2} }}{{dt^{2} }}\left[ {H_{3} \left(t \right) - H_{2} \left( t \right) - H_{1} \left( l \right) + H_{1}\left( 0 \right) - \mathop {\lim }\limits_{x \to l} \left[{B^{\prime } U \left( { x } \right) + \overline{{U \left( { x}\right)}}^{\prime } } \right]^{T} K\left[ {BU\left( t \right) +\overline{U \left( t \right)} } \right]} \right] \\&+ \frac{{d^{2}}}{{dt^{2} }}\left[ {\left[ {B^{\prime} U\left( { x } \right) +\overline{{U\left( { x } \right)}}^{\prime } } \right]^{T} K\left[{BU\left( t \right) + \overline{U\left( t \right)} } \right]}\right]\end{aligned} $$

(4.11)

Now, fit $U,{U}_{t},{U}_{tt},{U}_{x},{U}_{xx}$ in (4.1) and discretize by following discrete points,

$${x }_{i}={t}_{i}=\frac{2i-1}{2{[{2 }^{k-1}M]}^{2}} , i =\mathrm{1,2},\dots ,{[{2}^{k-1}M]}^{2}$$

To extract the values of unknown coefficients, we use the Newton Raphson method. Finally, substitute obtained values of unknown coefficients in (4.9) yield the Bernoulli wavelet numerical solution of the given PDE.

Applications of the Proposed Method

Consider three different types of error norms for calculating the errors given,

${{\varvec{L}}}^{2}error=\sqrt{\sum_{i=1}^{n}{Y}_{i}^{2}}$, ${{\varvec{L}}}^{\boldsymbol{\infty }}error=Max\left({Y}_{i}\right), 1\le i\le n-1$, ${\varvec{R}}{\varvec{M}}{\varvec{S}}\boldsymbol{ }error=\sqrt{\sum_{i=1}^{n}\frac{{Y}_{i}^{2}}{n}}$ where, ${Y}_{i}={U}_{i}\left(exact \,solution\right)-{U}_{i}\left(approximate\, solution\right).$

Example 1

Consider the non-linear Murray equation [19]

$$\frac{\partial U}{\partial t}=\frac{{\partial }^{2}U}{\partial {x}^{2}}+U\frac{\partial U}{\partial x}+U-{U}^{2}, 0\le x \le 1, 0\le t\le 1$$

(5.1)

with initial condition

$$U\left( x,0\right)=\frac{{\lambda }_{1}+{c}_{1}{e}^{(\gamma x)}}{{\lambda }_{2}+{c}_{0}},$$

and boundary conditions

$$U\left(0,t\right)=\frac{{\lambda }_{1}+{c}_{1}{e}^{({\gamma }^{2}t)}}{{\lambda }_{2}+{c}_{0}{e}^{(-{\lambda }_{1}t)}},$$

$$U\left(1,t\right)=\frac{{\lambda }_{1}+{c}_{1}{e}^{({\gamma }^{2}t+\gamma )}}{{\lambda }_{2}+{c}_{0}{e}^{(-{\lambda }_{1}t)}},$$

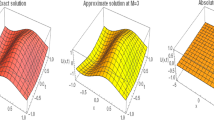
with ${c}_{0}=1$, ${c}_{1}=1$ and$\gamma =1$. The literal solution of the Eq. (5.1) is $\left(x , t\right)=\frac{1+{e}^{(t+x)}}{1+{e}^{(-t)}}$. The above non-linear equation is solved by the proposed method. From Fig. 1, we observe the time–space graph which shows the proposed BWCM graphical compared with the exact solution and its error analysis at $M=2$. Table 1 and Table 2 show the comparison between the BWCM solution and the accurate solution at different values of $t$ and$x$. Table 3 compares the mathematical solutions obtained from the proposed method and the Haar wavelet method (HWM) from the literature [19] with the accurate solution and mentioned the absolute errors. Figures 2 and 3 narrate the graphical comparison of the BWCM solution with the accurate solution at different values of $t$ and $x$. Table 4 explains the error norms of the present method.

Fig. 1

Graphical illustration of BWCM and Literal solution along with the absolute error, for example, 1

Table 1 Comparison of Numerical solution with the literal solution at different values of $t$ and $M=2$

Table 2 Comparison of Numerical solution with an accurate solution at different values of $x$ and $M=2$

Table 3 Numerical comparison between the proposed method and Haar wavelet method with an exact solution at $M=2$

Fig. 2

Graphical judgment between the proposed technique and accurate solution at different values of $t,$ for example, 1

Fig. 3

Graphical comparison of the present method solution along with the accurate solution at different values of $x,$ for example, 1

Table 4 Error norms comparison between the BWCM and other methods in the literature

The approximate polynomial solution of the BWCM at $M=2$ is given by,

$$\begin{aligned}U\left(x,t\right)=&-\frac{1}{2}+\frac{{e}^{x}}{2}+\frac{1}{1+{e}^{-t}}+\frac{{e}^{t}}{1+{e}^{-t}}+\frac{x}{2}-\frac{ex}{2}-\frac{{e}^{t}x}{1+{e}^{-t}}+\frac{{e}^{1+t}x}{1+{e}^{-t}}\\&-0.5970tx-0.2727{t}^{2}x+0.3864t{x}^{2}-0.1212{t}^{2}{x}^{2}+0.2106t{x}^{3}+0.3939{t}^{2}{x}^{3}.\end{aligned}$$

Conclusion

In this article, the Bernoulli wavelet collocation technique has been efficiently implemented for the numerical approximation of the non-linear Murray equation, which arises in Reaction–diffusion equations. We present a new functional matrix of integration by using Bernoulli wavelets for solving the non-linear Murray equation. The collocation scheme based on Bernoulli wavelets has been carried out to get a system of non-linear algebraic equations that can be solved by the Newton–Raphson method. From Tables 1, 2 and 4, we can see the efficiency of the proposed method. The comparison of the obtained results with the Haar wavelet collocation scheme has been demonstrated in Table 3. Figures 1, 2 and 3 show that the BWCM solution is very close to the exact solution. The precision and accuracy of the proposed scheme have been checked by enumerating the ${L}^{2}$, ${L}^{\infty }$ and the RMS errors of a numerical problem. From the tables, we have seen that the efficiency of the Bernoulli wavelet collocation scheme is good, even on account of only a few collocation points.