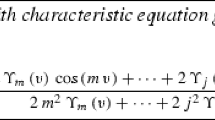Abstract
In this article, we establish exact solutions for the generalised third-order nonlinear Schrödinger equation. The elliptic function expansion and He’s semi-inverse techniques are employed to establish exact solutions for this equation. These solutions are so important and vital for mathematicians and physicists to prescribe some complex physical phenomena. Using Matlab 18, we plot 2D and 3D graphs of acquired solutions for certain values of the parameters. The proposed techniques are direct, sturdy and efficient tools to solve different types of nonlinear partial differential equations arising in engineering and physics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Nonlinear wave is one of the main area of focus for researchers and scientists doing research in applied science, such as biology, engineering, electromagnetic theory, optics, chemical physics, fluid mechanics, ecology, deep water, plasma physics, elastic media, [1,2,3,4,5,6,7,8,9,10]. Nonlinear complex features in plasma physics, quantum mechanics, optoelectronics hydrodynamics, semiconductors and bimolecular dynamical modes can be formulated in the form of the nonlinear Schrödinger equations (NLSEs). These equations are the nonlinear partial differential equations (NLPDEs), which have been studied in various areas of applied science [11,12,13]. Studying of their soliton solutions is so important in explaining various interesting physical phenomena in nature, and this branch turns into one of the most vital area of scientific research [14,15,16,17,18,19,20].
Because of the complexity structure of the nonlinear wave equations, there is no unified technique to extract all solutions of these equations. Different analytical and numerical methods are used to find solutions of these equations, such as tanh-sech method [21], sine-cosine method [22], Jacobi elliptic function method [23], \((\frac{G^{'}}{G})-\) expansion method [24], F-expansion method [25], exp-function method [26], extended tanh-method [27], homogeneous balance method [28] and Riccati-Bernoulli sub-ODE technique [29, 30]. Recently, there are a great development in analytical and numerical techniques for extracting solutions for NLPDEs, see for example [31,32,33,34,35,36,37,38,39,40,41,42].
The generalised third-order nonlinear NLSE given as follows [43]
where \(\alpha _1,\alpha _2,\alpha _3\), are real-valued parameters and \(\psi \) is a complex-valued function. Eq. (1) has been utilized to prescribe the propagation of ultra-short pulses in nonlinear optical fibres. The present work is motivated to find new and more general solutions to (1). Namely, the main interest is to introduce some new exact solution of the generalised third-order nonlinear Schrödinger equation, using extended Jacobian elliptic function expansion method (JEFEM) and He’s variational principle. To the best of our knowledge, no previous article has been done utilizing the techniques in this paper for solving this equation.
This paper is arranged as follows. In Sect. 2, some new exact solutions for the generalised third-order nonlinear Schrödinger equation are presented. Indeed, some 2D and 3D graphs of acquired solutions are illustrated. The conclusions are reported in Sect. 3.
Soliton Solutions of the Generalised Third-Order NLSE
k, p, w and \(\mu \) are constants and \(\epsilon \) is the phase constant.
Superseding (2) into Eq. (1) yields:
Integrating Eq. (4) and taking the integration constant as zero, we have
Eqs. (3) and (5) are the same under the constraint conditions
In the sequel we use the extended JEFEM and He’s principle for solving Eq. (1).
The Extended JEFEM
According to the extended JEFEM [24, 44,45,46], the solution of Eq. (1) is
Eq. (7) yields
Superseding Eqs. (7)-(9) into Eq. (3) and putting the coefficients of \(sn^{3}\), \(sn^{2} { cn}\), \(sn^{2}\), \(sn { cn}\), sn, cn, \(sn^{0}\) with zero, gives
Solving these algebraic equations, gives:
Family 1.
The first family of solutions is
When \(m \rightarrow 1\), Eq. (17) becomes
Real and imaginary travelling wave solutions for Eq. (18) are illustrated: real solutions in (a), imaginary solutions in (b). c presents 2D real and imaginary solutions for Eq. (18). The parameter values are given by \(\alpha _2=2.1,\,\alpha _3=1.2,\,p=1.5,\,k=0.1,\,\epsilon =2.2.\) \(x\in [-5,\,5]\) and \(t=0\rightarrow 6.\) The values of \(\alpha _1\) and \(\mu \) are taken by Eq. (6). c plotted at \(t=6.\)
Family 2.
The second family of solutions is
When \(m \rightarrow 1\), Eq. (19) becomes
3D real and imaginary travelling wave solutions for Eq. (20) are plotted: real solutions in (a), imaginary solution in (b). 2D real and imaginary solutions are presented in (c) at \(t=6.\) The parameter values are taken by \(\alpha _2=2.1,\,\alpha _3=1.2,\,p=1.5,\,k=0.1,\,\epsilon =2.2.\) \(x\in [-5,\,5]\) and \(t=0\rightarrow 6.\) The values of \(\alpha _1\) and \(\mu \) are taken by Eq. (6)
Family 3.
The third family of solutions is
When \(m \rightarrow 1\), Eq. (21) becomes
3D real and imaginary travelling wave solutions for Eq. (22) are depicted: real travelling wave solutions in (a), imaginary travelling wave solutions in (b). c 2D graph for the real and imaginary solutions of Eq. (22) at \(t=6.\). The considered parameters are given by the values \(\alpha _2=2.1,\,\alpha _3=1.2,\,p=1.5,\,k=0.1,\,\epsilon =2.2.\) \(x\in [-5,\,5]\) and \(t=0\rightarrow 6.\) The values of \(\alpha _1\) and \(\mu \) are taken by Eq. (6)
Family 4.
The fourth family of solutions is
When \(m \rightarrow 1\), Eq. (23) becomes
a, b show the real and imaginary travelling wave solutions for Eq. (24), respectively. 2D graph for the real and imaginary travelling wave solutions of Eq. (24) are demonstrated in (c) at \(t=6.\) The parameter values are given by \(\alpha _2=2.1,\,\alpha _3=1.2,\,p=1.5,\,k=0.1,\,\epsilon =2.2.\) \(x\in [-5,\,5]\) and \(t=0\rightarrow 6.\) The values of \(\alpha _1\) and \(\mu \) are taken by Eq. (6)
The He’s Semi-inverse Technique
Based on the He’s semi-inverse technique [47,48,49], the variational formulation corresponding to Eq. (3) is
By Ritz-like method, we search for the following solitary wave solution
superseding Eq. (26) into Eq. (25), gives
For getting stationary with respect to A and B results in
Solving Eqs. (27) and (28), we can easily obtain the following relations:
The solitary wave solution is, therefore, given as follows
Shortly, it has been investigated that the exact solutions of the generalised third-order nonlinear NLSE were obtained in the explicit form. The behavior of solutions for this equation being solitons, rouge, periodic, breather or shock, is a significance for the values of the physical parameters of the generalised third-order NLSE. Moreover, the obtained solutions may be interpreted the telecommunications experiments, nuclear physics, chaotic pulses laser, capillary profiles and transistor [50,51,52,53,54,55]. Finally, the gained solutions is so vital in the developments of quantum mechanics, namely in quantum hall effect, entire computer industry and nuclear medicine.
3D real and imaginary travelling wave solutions for Eq. (30) are illustrated in (a, b), respectively. c depicts 2D travelling wave solutions for Eq. (30) at \(t=6.\) The used parameters are given by the values \(\alpha _2=2.1,\,\alpha _3=1.2,\,p=1.5,\,k=0.1,\,\epsilon =2.2.\) \(x\in [-5,\,5]\) and \(t=0\rightarrow 6.\) The values of \(\alpha _1\) and \(\mu \) are taken by Eq. (6)
Conclusions
In this work, we have developed a new type of solution for the generalised third-order nonlinear Schrödinger equation, utilizing the extended Jacobian elliptic function expansion and variational principle techniques. These solutions are very vital for explaining some complex physical phenomena. All gained solutions have been plotted in 2D and 3D surfaces, using Matlab 18, for appropriate values of the parameters. The proposed techniques in this study are efficient for establishing vital solutions for other NPDEs, which are involved in physics and engineering.
References
Abdelrahman, M.A.E., Kunik, M.: The ultra-relativistic Euler equations. Math. Meth. Appl. Sci. 38, 1247–1264 (2015)
Abdelrahman, M.A.E.: Global solutions for the ultra-relativistic Euler equations. Nonlinear Anal. 155, 140–162 (2017)
Abdelrahman, M.A.E.: On the shallow water equations, Z. Naturforsch., 72(9)a , 873-879 (2017)
Abdelrahman, M.A.E., Sohaly, M.A.: On the new wave solutions to the MCH equation. Indian J. Phys. 93, 903–911 (2019)
Abdelrahman, M.A.E.: Conserved schemes with high pressure ratio, high particle density ratio and self-similar method. Eur. Phys. J. Plus 133, 304 (2018)
Hassan, S.Z., Abdelrahman, M.A.E.: Solitary wave solutions for some nonlinear time fractional partial differential equations. Pramana-J. Phys. 91, 67 (2018)
Abdelrahman, M.A.E., Hassan, S.Z., and Inc, M.: The coupled nonlinear Schrödinger-type equations. Mod. Phys. Lett. B, 2050078. https://doi.org/10.1142/s0217984920500785 (2020)
Razborova, P., Ahmed, B., Biswas, A.: Solitons, shock waves and conservation laws of Rosenau-KdV-RLW equation with power law nonlinearity. Appl. Math. Inf. Sci. 8(2), 485–491 (2014)
Younis, M., Ali, S., Mahmood, S.A.: Solitons for compound KdV Burgers equation with variable coefficients and power law nonlinearity. Nonlinear Dyn. 81, 1191–1196 (2015)
Bhrawy, A.H.: An efficient Jacobi pseudospectral approximation for nonlinear complex generalized Zakharov system. Appl. Math. Comput. 247, 30–46 (2014)
Hosseini, K., Kumar, D., Kaplan, M., Bejarbaneh, E.Y.: New exact traveling wave solutions of the unstable nonlinear Schrödinger equations. Commun. Theor. Phys. 68, 761–767 (2017c)
Tala-Tebue, E., Djoufack, Z.I., Fendzi-Donfack, E., Kenfack-Jiotsa, A., Kofane, T.C.: Exact solutions of the unstable nonlinear Schrödinger equation with the new Jacobi elliptic function rational expansion method and the exponential rational function method. Optik 127, 11124–11130 (2016)
Hosseini, K., Zabihi, A., Samadani, F., Ansari, R.: New explicit exact solutions of the unstable nonlinear Schrödinger’s equation using the expa and hyperbolic function methods. Opt. Quant. Electron. 50, 82 (2018)
Sulem, C., Sulem, P.L.: The Nonlinear Schrödinger Equation Self-focusing and Wave Collapse. Springer, New-York (1999)
Liu, C.: Exact solutions for the higher-order nonlinear Schrödinger equation in nonlinear optical fibres. Chaos Solit. Fract. 23, 949–955 (2005)
Mora, C.M., Rebolledo, R.: Basic properties of nonlinear stochastic Schrödinger equations driven by Brownian motions. Ann. Appl. Probab. 18(2), 591–619 (2008)
Eslami, M.: Exact traveling wave solutions to the fractional coupled nonlinear Shrödinger equations. Appl. Math. Comput. 285, 141–148 (2016)
Abdelrahman, M.A.E., Sohaly, M.A.: Solitary waves for the nonlinear Schrödinger problem with the probability distribution function in stochastic input case. Eur. Phys. J. Plus. 132, 339 (2017)
Hassan, S.Z., Abdelrahman, M.A.E.: A RiccatiBernoulli sub-ODE method for some nonlinear evolution equations. Int. J. Nonlinear Sci. Numer. Simul. 20, 303–313 (2019)
Hassan, S.Z., Alyamani, N.A., Abdelrahman, M.A.E.: A construction of new traveling wave solutions for the 2D GinzburgLandau equation. Eur. Phys. J. Plus 134, 425 (2019)
Wazwaz, A.M.: The tanh method for travelling wave solutions of nonlinear equations. Appl. Math. Comput. 154, 714–723 (2004)
Wazwaz, A.M.: Exact solutions to the double sinh-Gordon equation by the tanh method and a variable separated ODE. method. Comput. Math. Appl. 50, 1685–1696 (2005)
Dai, C.Q., Zhang, J.F.: Jacobian elliptic function method for nonlinear differential difference equations. Chaos Solut. Fract. 27, 1042–1049 (2006)
Dai, C.Q., Zhang, J.F.: Jacobian elliptic function method for nonlinear differential-difference equations. Chaos Solut. Fract. 27, 1042–1049 (2006)
Zhang, J.L., Wang, M.L., Wang, Y.M., Fang, Z.D.: The improved F-expansion method and its applications. Phys. Lett. A 350, 103–109 (2006)
Aminikhad, H., Moosaei, H., Hajipour, M.: Exact solutions for nonlinear partial differential equations via Exp-function method. Numer. Methods Partial Differ. Equ. 26, 1427–1433 (2009)
Wazwaz, A.M.: The extended tanh method for abundant solitary wave solutions of nonlinear wave equations. Appl. Math. Comput. 187, 1131–1142 (2007)
Fan, E., Zhang, H.: A note on the homogeneous balance method. Phys. Lett. A 246, 403–406 (1998)
Abdelrahman, M.A.E., Sohaly, M.A.: The development of the deterministic nonlinear PDEs in particle physics to stochastic case. Results Phys. 9, 344–350 (2018)
Yang, X.F., Deng, Z.C., Wei, Y.: A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equ. 1, 117–133 (2015)
Golam Hafez, Md, Iqbal, S.A., Akther, S., Uddin, M.F.: Oblique plane waves with bifurcation behaviors and chaotic motion for resonant nonlinear Schrödinger equations having fractional temporal evolution. Results Phys. 15, 102778 (2019)
Akther, S., Golam Hafez, Md, Ferdous, F.: Oblique resonance wave phenomena for nonlinear coupled evolution equations with fractional temporal evolution. Eur. Phys. J. Plus 134, 473 (2019)
Akther, S., Golam Hafez, Md, Rezazadeh, H.: Resonance nonlinear wave phenomena with obliqueness and fractional time evolution via the novel auxiliary ordinary differential equation method. SN Appl. Sci. 1, 567 (2019)
Hafez, M.G., Talukder, M.R., Ali, M.H.: New analytical solutions for propagation of small but finite amplitude ion-acoustic waves in a dense plasma. Waves Rand. Complex Media 26(1), 68 (2016)
Ferdous, F., Golam Hafez, Md, Biswas, A., Ekici, M., Zhou, Q., Alfiras, M., Moshokoa, S., Belic, M.: Oblique resonant optical solitons with Kerr and parabolic law nonlinearities and fractional temporal evolution by generalized exp(\(-\phi ( )\))-expansion. Optik 178, 439–449 (2019)
Ferdous, F., Golam Hafez, Md: Nonlinear time fractional Korteweg-de Vries equations for interaction of wave phenomena in fluid-filled elastic tubes. Eur. Phys. J. Plus 133, 384 (2018)
Ferdous, F., Golam Hafez, Md: Oblique closed form solutions of some important fractional evolution equations via the modified Kudryashov method arising in physical problems. J. Ocean Eng. Sci. 3, 244–252 (2018)
Alharbi, A.R., Almatrafi, M.B., Abdelrahman, M.A.E.: Analytical and numerical investigation for KadomtsevPetviashvili equation arising in plasma physics. Phys. Scripta 95, 4 (2020)
Alharbi, A.R., Abdelrahman, M.A.E., Almatrafi, M.B.: Analytical and numerical investigation for the DMBBM equation. Comput. Model. Eng. Sci. 122(2), 743–756 (2020)
Abdelrahman, M.A.E., Almatrafi, M.B., Alharbi, A.R.: Fundamental solutions for the coupled KdV system and its stability. Symmetry 12, 429 (2020)
Li, T., Pintus, N., Viglialoro, G.: Properties of solutions to porous medium problems with different sources and boundary conditions. Z. Angew. Math. Phys. 70, 1–18 (2019)
Viglialoro, G., Woolley, T.E.: Boundedness in a parabolic-elliptic chemotaxis system with nonlinear diffusion and sensitivity and logistic source. Math. Methods Appl. Sci. 41, 1809–1824 (2018)
Pelinovsky, D.E., Yang, J.: Stability analysis of embedded solitons in the generalized third-order nonlinear Schrödinger equation. Chaos 15, 037115 (2005)
Liu, S., Fu, Z., Liu, S., Zhao, Q.: Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 289, 69–74 (2001)
Zhao, X.Q., Zhi, H.Y., Zhang, H.Q.: Improved Jacobi-function method with symbolic computation to construct new double-periodic solutions for the generalized Ito system. Chaos Solit. Fract. 28, 112–126 (2006)
Wanga, Q., Chen, Y., Zhang, H.: An extended Jacobi elliptic function rational expansion method and its application to (2+1)-dimensional dispersive long wave equation. Phys. Lett. A 289, 411–426 (2005)
He, J.H.: Semi-inverse method of establishing generalized variational principles for fluid mechanics with emphasis on turbomachinery aerodynamics. Int. J. Turbo Jet Eng. 14(1), 23–28 (1997)
He, J.: Variational principles for some nonlinear partial dikerential equations with variable coencients. Chaos Solit. Fract. 19(4), 847–851 (2004)
He, J.H.: Some asymptotic methods for strongly nonlinear equations. Internat. J. Mod. Phys. B 20, 1141–1199 (2006)
Taylor, J.R.: Optical Solitons: Theory and Experiment. Cambridge University Press, Cambridge (1992)
Bloch, V.: Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 52, 555–600 (1929)
Bailung, H., Sharma, S.K., Nakamura, Y.: Observation of Peregrine Solitons in a Multicomponent Plasma with Negative Ions. Phys. Rev. Lett. 107, 255005 (2011)
Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.M.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6, 790–795 (2010)
Chabchoub, A., Hoffmann, N.P., Akhmediev, N.: Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106, 204502 (2011)
Pathak, P., Sharma, S.K., Akamura, Y.N., Bailung, H.: Observation of ion acoustic multi-Peregrine solitons in multicomponent plasma with negative ions. Phys. Lett. A 381, 4011–4018 (2017)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Abdelrahman, M.A.E., Alharbi, A. & Almatrafi, M.B. Fundamental Solutions for the Generalised Third-Order Nonlinear Schrödinger Equation. Int. J. Appl. Comput. Math 6, 160 (2020). https://doi.org/10.1007/s40819-020-00906-2
Accepted:
Published:
DOI: https://doi.org/10.1007/s40819-020-00906-2
Keywords
- Elliptic functions
- Variational principle
- Solitons
- Physical phenomena
- Generalised third-order nonlinear Schrödinger equation