Introduction

Image de-noising has been a well-studied problem in image processing and computer version fields. It is a typical inverse problem, which approximates the original image describing a real scene from the observed image of the same scene [7]. In many real world practices, images are often degraded with noise, either because of the image acquiring process or because of naturally occurring phenomena. Therefore, the process of approximating the unknown image of interest from the given noisy image, known as image restoration, plays an important role in various fields. Applications that require a restoration step range from astronomy, astrophysics, biology, chemistry, arts, geophysics, physics, hydrology, remote sensing and other areas involving imaging techniques [8]. In many image formulated models, the additive noise (AN) model is commonly found in acquiring images via digital devices. Most of the literature deal with this type of image restoration models: given an original image u, it is assumed to be corrupted by the additive noise \(\eta _1\). The goal is then to recover ‘u’ from the data

$$\begin{aligned} f=u+\eta _{1} \end{aligned}$$
(1)

There are many effective methods to tackle this problem. Among the most famous ones are wavelets approaches, stochastic approaches, principal component analysis-based approaches, and variational approaches, introduced by ROF [22]. It became evident that variational approaches to the image de-noising problem have attracted much attention by directly approximating the reflectance of the underlying scene and yield often excellent results. Due to the edge-preserving and noise removing properties, total variation approach has been widely utilized in the noise removal task. However, it has two main disadvantages: (a) In ROF model, the structure of image is modeled as a function belonging to the bounded variation space and therefore it favors a piecewise constant function in bounded variation space which often causes the staircase effect, (b) The ROF method cannot preserve finer details such as textures well. According to [28], the \(L^{2}\)-norm cannot separate different oscillatory components with different frequencies such as textures and noise, and therefore the textures are filtered out with noise in the process of restoration. The interested reader is referred to [2, 8, 14, 22, 28] for more details.

In practice, there exist different types of noise as well such as multiplicative noise. It can also degrade an image. Multiplicative noise (also known as speckle) is a signal independent, non-Gaussian and spatially dependent, i.e. variance is a function of signal amplitude. In the case of multiplicative noise variance of the noise is higher when an amplitude of the signal is higher. In other words, noise in bright regions have higher variations and could be interpreted as features in the original image. Due to this degraded mechanism, mostly all the information of the original image may be lost when it is corrupted by multiplicative noise. The problem of removing multiplicative noise occurs in many practices such as images generated by coherent imaging modalities. For example, synthetic aperture radar, ultrasound, and laser imaging, inevitably come with speckle (multiplicative noise), due to the coherent nature of the scattering phenomena which prevents us from analyzing valuable information of images such as edges, textures, point target and other image details [9]. Hence, the removal of multiplicative noise is a very challenging task compared with additive Gaussian noise. In the multiplicative noise model, the assumption is that the original image ‘u’ has been corrupted by some multiplicative noise \(\eta _{2}\), the goal is then to recover ‘u’ from the data which can be formulated uniformly as follows

$$\begin{aligned} f=u\eta _{2} \end{aligned}$$
(2)

Which obeys a Gamma law with mean one and its probability density function is given by

$$\begin{aligned} G_{\eta _2}^\upsilon =\frac{L^{L}}{\Gamma (L)}\eta _2^{L-1} e^{(-L\eta _2 )} \end{aligned}$$
(3)

where ‘L’ is the number of looks (in general, an integer coefficient) and \(\Gamma (\cdot )\) is a Gamma function. To the best of our knowledge, there exist several variational approaches devoted to multiplicative noise removal problem. We refer the reader to the literature [2, 3, 8, 10, 13, 14, 22, 23, 26] and references included herein for an overview of the subject. In this paper, we deal with the combined additive and multiplicative noise removal problem.

Image de-noising through classical algorithms do not approximate images containing edges well. To overcome this, a technique based on the minimization of the total variation norm is proposed in [22], which is also known as ROF-model. This technique has been proved to be able to achieve a good trade-off between edge preservation and noise removal but the images resulting from the application of this method in the presence of noise tends to produce the so-called staircase (blocky) effects on the images because it favors a piecewise constant solution in bounded variation space. Thus, the image features in the original image may not be recovered satisfactorily and ramps will give piecewise constant regions (staircase effect). To deal with blocky effects, the improved methods of total variation (TV) are divided into two kinds; the high order derivative and the fractional order derivative. In this paper, we focus on the fractional-order total variation (FOTV) based method.

As a compromise between the first-order total variational regularized models and high-order derivative based models, some fractional-order derivative based models have been introduced in for additive and multiplicative noise removal and subsequently used for image restoration and super resolution [4–7, 27, 28]. They can ease the conflict between blocky-effect elimination and edge preservation by choosing the order of derivative properly. Moreover, the fractional-order derivative operator has a non-local behavior because the fractional-order derivative at a point depends on the characteristics of the entire function and not just the values in the vicinity of the point, which is beneficial to improve the performance of texture preservation [28].

The experimental results in the literature [4, 20, 21, 27, 28] have demonstrated that the fractional-order derivative performs well for eliminating staircase effect and preserving textures. It has been proved in [20] that the fractional-order derivative satisfies the lateral inhibition principle of the biological visual system better than the integer-order derivative. In Pu et al. [21] have discussed the kinetic physical meaning of the fractional-order derivative and proposed fractional inspection methods for images texture details.

In this section, we present the numerical experiment below, to illustrate the efficiency and feasibility of fractional-order total variational filter for reducing staircase effect. Consider a one-dimension sine signal \(\Phi (x)=4sin(2\pi x)+8sin(3\pi x)\) which is degraded by Gaussian noise with SD = 0.6. The contaminated signal is shown in Fig. 1. The difference between the integer-order TV and fractional-order TV is obvious and one can see that the restoration result of FOTV based algorithm looks more natural and does not produce false edges whereas the integer order TV-denoising algorithm approximates the observed signal with a step signal. From the PSNR results, it is concluded that the fractional order TV algorithm can reduce blocky effect effectively comparing with the traditional integer-order TV algorithm.

Fig. 1
figure 1

One-dimension signal processed by Fractional Order-TV with \(\alpha =1.0,1.5\)

Full size image

Recently, the newly developed Fields of Expert (FoE) image prior model has been proved to be the more effective variational model than TV and TGV-based models. The variational model based on a FoE prior have demonstrated state of the art performance for image restoration problems such as the FoE image prior model for de-speckling which involve an expressive image prior Model-FoE and a highly efficient non-convex optimization algorithm-iPiano, show competitive de-speckling performance with respect to the state of the art method SAR-BM3D [9]. In a subsequent work, iPiano-algorithm has been applied to a forward-backward splitting algorithm, for solving a sub-part of our minimization problem. It can be seen as a non-smooth split version of the heavy-ball method from Polyak [16].

Motivated by these works, in order to restore the observed images degraded by mixed additive noise and multiplicative noise, a new variational model based on FOTV-norm combined with the FoE-image prior is proposed. A fast alternating minimization algorithm is applied to solve our minimization problem. We report some numerical experiments which show that the proposed method achieves the state of the art restoration results, both visually and quantitatively and substantially improves the PSNR of images, preserve textures and avoid the staircase effect comparing to corresponding restoring methods.

The outline of this paper is as follows. A review of the previous work is presented in Sect. 2. In Sect. 3 our new model for addressing the problem is introduced.Alternating minimization algorithm (AMA) is described for solving the minimizer of the proposed energy functional efficiently in Sect. 4. In order to demonstrate the performance of the proposed method and discuss parameter sensitivity analysis,computational analysis, and some restoration results are provided in Sect. 5. Section 6 concludes the paper.

Previous Work

In this section, the following variational models for the additive noise (AN) and multiplicative noise (MN) removal problems are reviewed, from which our new model was developed. As can be seen, each model able to offer high quality of restored images.

FOTV Based Additive Noise Removal Model

Total variation functional TV (u) is being used on large scale since it was introduced by Rudin et al. [22].

TV(u) is defined as \(\hbox {TV}(u)=\int _\Omega | Du|=\sup \limits _{p\in C_0^1,\parallel |p|\parallel _\infty } \int _\Omega u\,divp\;d\Omega \)

This leads for \(L^{1}(\Omega )\) functions with weak first derivatives in \(L^{1}(\Omega )\) as

$$\begin{aligned} \hbox {TV}(u)=\int _\Omega | \nabla u\,|d\Omega . \end{aligned}$$

Using property of total variational filter as edge preserver, ROF [22] proposed the following variational method for the mentioned problem

$$\begin{aligned} \hat{{u}}=\mathop {\arg \min }\limits _{u\in BV(\Omega )} \left\{ E(u)=\int _\Omega | \nabla u\,|d\Omega +\frac{\zeta }{2}\parallel u-f\parallel _2^2 \right\} \end{aligned}$$
(4)

where \(BV(\Omega )\) denotes the bounded variation space and \(\zeta >0\) is the regularization parameter which controls the quantity of noise to be removed. In this paper, we focus on the fractional-order total variational (FOTV) filter based denoising model which is described by

$$\begin{aligned} \hat{{u}}=\mathop {\arg \min }\limits _{u\in BV(\Omega )} \left\{ E(u)=\int _\Omega \zeta |\nabla ^{\alpha }u|d\Omega +\frac{1}{2}\parallel u-f\parallel _2^2 \right\} \end{aligned}$$
(5)

where \(\nabla ^{\alpha }u=(\partial _x^\alpha u,\partial _y^\alpha u)^{T}\) and \(|\nabla ^{\alpha }u|=|\partial _x^\alpha u|+|\partial _y^\alpha u|.\)The parameter \(\zeta >0\) is a trade-off parameter. So the fractional-order total variation model can be seen as the generalization of the typical integer-order total variation model.

FOTV Based Multiplicative Noise Removal Model

The fractional order total variation (FOTV) based multiplicative noise removal models have been studied recently. However, we consider two fractional order TV based models for multiplicative noise removal as follows:

  1. (a.)

    The fractional order AA model [1]

    $$\begin{aligned} \mathop {\min }\limits _u \left\{ E(u)=\int _\Omega | \nabla ^{\alpha }u|d\Omega +\lambda \int _\Omega \left( log( u)+\frac{f}{u} \right) dxdy \right\} ;\quad 1\le \alpha \le 2 \end{aligned}$$
    (6)
  2. (b.)

    The fractional order I-divergence model [26]

    $$\begin{aligned} \mathop {\min }\limits _u \left\{ E(u)=\int _\Omega | \nabla ^{\alpha }u|d\Omega +\lambda \int _\Omega {(u-f\;logu)} dxdy\right\} ;\quad 1\le \alpha \le 2 \end{aligned}$$
    (7)

    where the first term is the FOTV based regularization term, \(\lambda >0\) is the regularized parameter and the second term is the data fidelity term. When \(\alpha =1\) the first term is the TV regularized term as usual. In recent times, Huang et al. [15] applied the logarithmic transformation \(\omega =logu\) with the fitting term of AA model and thus obtained the following fractional-order restoration model for the mentioned problem

    $$\begin{aligned} \mathop {\min }\limits _w \left\{ E(u)=\int _\Omega | \nabla ^{\alpha }e^{w}|d\Omega +\lambda \int _\Omega {(\omega +f\;e^{-w})} dxdy\right\} ;\quad 1\le \alpha \le 2 \end{aligned}$$
    (8)

Which reduces the non-convex data term to a convex function via commonly used logarithmic transformation or exponential transformation.

Y. Chen Model for Multiplicative Noise Removal

Chen et al. [9] proposed a novel variational model for speckle removal which involves an expressive image prior Model-FoE and a highly efficient iPiano algorithm which gives state of the art performance, can be written uniformly as follows:

$$\begin{aligned} \mathop {\arg \min }\limits _u E_{{ FoE}} (u,f)=\left[ \sum \limits _{i=0}^{N_f} \theta _i \rho (k_i *u)+\lambda \;G(u,f)\right] \end{aligned}$$
(9)

where the first term is the FoE-image prior, the second term is the data fidelity term, \(\lambda >0\) is the regularized parameter and u is the underlying unknown image.

K. Hirakawa TLS Image Approximation Model (M1)

Hirakawa et al. [12] proposed a method for restoring images corrupted with additive, multiplicative and mixed noise, in the total least squares (TLS) sense, taking into account the stochastic nature of the noise and allowing small perturbations in the system. Furthermore, a de-noising algorithm was employed that, while effective in removing additive white Gaussian noise, removes the signal-dependent noise (multiplicative noise) as well. They proposed the following deterministic image approximation model

$$\begin{aligned} \widetilde{S_0 }+e_0 =(\hat{{X}}+E)\alpha \end{aligned}$$
(10)

where ‘S’ is an ideal clean image, ‘x’ is its noise corrupted version and \(S_0 \in R^{m}\) be an image patch from ‘S’. \(\widetilde{S_0 }=S_0 -\overline{S_0 } \in R^{m},\tilde{x}=x_i -\overline{x_i } \in R^{m}(i{th}\,\hbox {column of }\tilde{X})\,and\,\overline{S_0 },\overline{x_i } \in R\) are the average values of elements in \(S_0 \) and \(x_i \) respectively. The interested reader is referred to [12] for a more thorough discussion.

N. Chumchob Model (M2)

Chumchob et al. [8] proposed a new variational model for removing noise from digital images corrupted with additive, multiplicative and mixed noise and employed a fast non-linear multi-grid algorithm via a robust fixed-point smoother for its numerical solution. They proposed the following variational model

$$\begin{aligned} \mathop {\min }\limits _u \left\{ E(u)=\int _\Omega | \nabla u|d\Omega +\frac{\gamma _1 }{2}\int _\Omega {(u-f)^{2}} d\Omega +\gamma _2 \int _\Omega {(u+fe^{-u})\,} d\Omega \right\} \end{aligned}$$
(11)

where \(\gamma _1,\gamma _2 >0\) are the regularization parameters used to balance between the additive and multiplicative noise fidelity terms. In the next section, we give a description of our proposed model.

The Proposed Image Restoration Variational Model (M3)

In this section, our aim is to propose a novel variational model for restoring images contaminated with additive (AN), multiplicative (MN) and mixed noise, with the assumption that AN and MN are both independent or not related to each other. This type of situation is likely to occur in many real-world applications when they come from different channels. For example, synthetic aperture radar (SAR) images are usually corrupted by the multiplicative noise as a consequence of image formation under coherent radiation and the additive noise due to thermal vibrations in the electronic components of the image capture instruments. The following suitable image formulation model is proposed for this case is as follows

$$\begin{aligned} f=u+\chi _0 \nu _1 +\chi _1 u\nu _2 \end{aligned}$$
(12)

Where \(\chi _0,\chi _1 \) are constants \(\nu _1,\nu _2 \) are AN and MN components respectively [8].

In this paper, a novel noise removal model based on the variational method and a filter based higher-order Markov Random fields (MRF) which explicitly characterizes the statistics properties of natural images is proposed. It combines a fractional-order total variational filter with an expressive FoE image prior filter. The combined algorithm takes the advantage of both filters since it is able to preserve textures, sharp edges while avoiding the staircase effect in smooth regions. Given an observation image, ‘f’ contaminated by additive and multiplicative noise, the following image restoration model to remove both AN and MN is proposed for minimization

$$\begin{aligned} \hat{{u}}=\mathop {\arg \min }\limits _u E(u,f)=\left[ J_{FOTV}^{\;\alpha } (u)+\mu J_{FoE} (u)+H_{DFT} (f,u)\right] \end{aligned}$$
(13)

where ‘u’ is the noiseless image, \(J_{FOTV}^{\;\alpha } (u)\hbox { and }J_{FoE} (u)\) are regularization terms, the third term \(H_{DFT} (f,u)\) is the data fidelity term and \(\mu \in [0,1]\) is the weight parameter.

FOTV-Based Filter Used in Our Variational Model (M3)

The fractional-order total variational (FOTV) filter [4, 5] for an image ‘u’ is formulated as

$$\begin{aligned} J_{FOTV}^{\;\alpha } (u)=\int _\Omega | \nabla ^{\alpha }u|dxdy\approx \sum _{i,j} {\left\{ |\nabla _x^\alpha u_{i,j} |+|\nabla _y^\alpha u_{i,j} |\right\} } \end{aligned}$$
(14)

From \(Gr\ddot{u}\hbox {nwald-Letnikov}\) fractional derivative definition, the finite fractional difference can be defined by

$$\begin{aligned} \nabla _x^\alpha u_{i,j} = \sum \limits _{k=0}^{K-1} C_k^{(\alpha )} u_{i-k,j} ;\quad \nabla _y^\alpha u_{i,j} =\mathop \sum \limits _{k=0}^{K-1} C_k^{(\alpha )} u_{i,j-k} \end{aligned}$$
(15)

where \(C_k^{(\alpha )} =(-1)^{k}C_k^{(\alpha )},C_k^{(\alpha )} =\frac{\Gamma (\alpha +1)}{\Gamma (k+1)\Gamma (\alpha -k+1)}\) denotes the generalized binomial coefficient and \(\Gamma (x)\) is the Gamma function. The coefficients \(C_k^{(\alpha )} \) can also be obtained recursively from \(C_0^{(\alpha )} =1, \quad C_k^{(\alpha )} =(1-\frac{\alpha +1}{k})C_{k-1}^{(\alpha )},k=1,2,3 \ldots K-1.\) When \(\alpha =1,C_k^1 =0\) for \(k>1.\) Equation (14) becomes the TV of ‘u’ as usual and therefore FOTV can be cast as an extension of the traditional total variation [4–7].

The FoE Image Prior Utilized in Our Variational Model (M3)

The FoE image prior model is based on a set of learned/linear filters. According to [9], the student-t distribution based FoE image prior model for an image ‘u’ is defined as

$$\begin{aligned} J_{FoE} =\sum \limits _{i=0}^{N_f} \theta _i \rho (k_i *u) \end{aligned}$$
(16)

where \(\rho (k_i *u)=\sum \nolimits _{p=1}^N \rho ((k_i *u))_p\), ‘N’ is the number of pixels in image ‘u’, \(N_f \) is the number of linear filters, \(k_i \) is the set of learned filters with the corresponding weights \(\theta _i >0,k_i *u\) denotes the convolution of the filter \(k_i \) with a two-dimensional image ‘u’ and \(\rho (.)\) denotes the non-convex potential function and their associated derivatives are given by

$$\begin{aligned} \begin{array}{l} \rho (q)=log(1+q^{2})\hbox { and }\dot{\rho }(q)=\frac{2q}{1+q^{2}};\quad \rho (q)=\sqrt{q^{2}+\varepsilon ^{2}}\hbox { and }\dot{\rho }(q)=\frac{q}{\sqrt{q^{2}+\varepsilon ^{2}}} \\ \rho (q)=log(1-\varepsilon +\sqrt{q^{2}+\varepsilon ^{2}})\;\,\hbox {and }\dot{\rho }(q)=\frac{q}{(\sqrt{q^{2}+\varepsilon ^{2}})(1-\varepsilon +\sqrt{q^{2}+\varepsilon ^{2})}} \\ \end{array} \end{aligned}$$
(17)

Here we used \(\rho (q)=log(1+q^{2})\hbox { as a penality function}\) which is derived from the student-t distribution. In this paper, we make use of the learned filters of a previous work [9] which is shown in Fig. 2.

Fig. 2
figure 2

48 learned filters of size \(7\times 7\) exploited in our model. The first number in the bracket is the norm of the filter and the second one is the weight \(\theta _i \) [9]

Full size image

Modeling of the Data Fidelity Terms

In this subsection, modeling of the data fidelity terms for both AN and MN is discussed. In case of Gaussian noise, the data fidelity term [22] can be formulated as

$$\begin{aligned} H_{{ DFT1}} (f,u)=\int _\Omega {\parallel u-f\parallel _2^2 } dxdy \end{aligned}$$
(18)

Now the MAP-based multiplicative noise modeling from the statistical point of view by using Bayesian formulation is considered. Let ‘f’ be the given noisy image which follows a Nakagami distribution depending on the underlying restored image amplitude ‘u’, the square root of the reflectivity [8, 11, 14, 15, 23].

$$\begin{aligned} P(f/u)=\frac{L^{L}}{\Gamma (L)u^{L}}f^{L-1}exp\left( \frac{-Lf}{u}\right) \end{aligned}$$
(19)

where ‘L’ is the number of looks of the image and \(\Gamma (.)\) is the Gamma function. Using the MAP frameworks, according to the Gibbs prior, this likelihood leads to the following energy term via E = −log P(f/u).

$$\begin{aligned} H_{DFT2} (f,u)=\int _\Omega \left( logu+\frac{f}{u}\right) dxdy \end{aligned}$$
(20)

Note that the data term is not convex w.r.t ‘\(\hbox {u}>0\)’, which generally will make the corresponding problem difficult to solve. Following previous works of modeling the MN image intensity, the I-divergence based data term for the amplitude model is given by

$$\begin{aligned} H_{DFT3} (f,u)=\int _\Omega {(u^{2}-2f^{2}logu)} dxdy \end{aligned}$$
(21)

Which is strictly convex with respect to ‘\(\hbox {u}>0\)’. The non-convex data term in (20) can be converted to a convex function via commonly used logarithmic transformation i.e \(\omega =logu\Leftrightarrow u=e^{\omega }.\) As a result, our novel variational model for both AN and MN incorporating these three data terms comes out as follows

$$\begin{aligned} \hat{{u}}= & {} arg\;\mathop {min}\limits _u \,\left[ E(u,f)=\int _\Omega | \nabla ^{\alpha }u|dxdy+\mu \sum \limits _{i=0}^{N_f } \theta _i \rho (k_i *u)+\frac{\alpha _1 }{2}\int _\Omega {\parallel u-f \parallel _2^2 } dxdy \right. \nonumber \\&\left. +\frac{\alpha _2 }{2}\int _\Omega \left( logu+\frac{f}{u}\right) dxdy+\frac{\alpha _3 }{2}\int _\Omega {(u^{2}-2f^{2}logu)} dxdy\right] \end{aligned}$$
(22)

Under the logarithmic transformation, i.e \(\omega =logu\Leftrightarrow u=e^{\omega }\), (22) can be rewritten as follows

$$\begin{aligned}&arg\;\mathop {min}\limits _\omega \left[ E(e^{\omega },f)=\int _\Omega | \nabla ^{\alpha }e^{\omega }|dxdy+\mu \sum \limits _{i=0}^{N_f } \theta _i \rho (k_i *e^{\omega })+\frac{\alpha _1 }{2}\int _\Omega {\parallel e^{\omega }-f \parallel _2^2 } dxdy \right. \nonumber \\&\quad \left. +\frac{\alpha _2 }{2}\int _\Omega \left( \omega +fe^{-\omega }\right) dxdy+\frac{\alpha _3 }{2}\int _\Omega {(e^{2\omega }-2f^{2}\omega )} dxdy\right] \,\hbox {with }u=e^{\omega }. \end{aligned}$$
(23)

where \(\alpha _1,\alpha _2 \,\hbox {and }\alpha _3 \) are the regularization parameters used to keep a balance between the additive and multiplicative noise fitting terms. The existence and uniqueness of the solution of the energy functional (23) and convergence of iPiano-algorithm, can be proved along similar lines to Refs. [8, 9, 16, 24]. In the next section, we give description of the numerical method for the solution of the arisen equation.

Numerical Methods

In this work, alternate minimization algorithm (AMA) is employed to solve (23), with the simultaneous operations of Newton method, explicit time marching scheme and a recently published non-convex optimization algorithm-iPiano [9].

iPiano Algorithm:

The iPiano algorithm composed of a smooth (non-convex) function say ‘F’ and a convex (possibly non-smooth) function ‘G’, is designed for a structured non-smooth/ non-convex optimization problem which can be formulated as follows

$$\begin{aligned} arg\;\mathop {min}\limits _u \;H(u)=\mathop {F(u)}\limits _{\mathrm{Regularizer \, Term}} +\mathop {G(u)}\limits _{\mathrm{Data \, Fidelity \, term}} \end{aligned}$$
(24)

Comparing (23) with (24), we have

$$\begin{aligned} F(\omega )= & {} \int _\Omega | \nabla ^{\alpha }e^{\omega }|dxdy+\mu \sum \limits _{i=0}^{N_f} \theta _i \rho (k_i *e^{\omega })\hbox { and} \end{aligned}$$
(25)
$$\begin{aligned} G(\omega )= & {} \frac{\alpha _1 }{2}\int _\Omega {\parallel e^{\omega }-f\parallel _2^2 } dxdy+\frac{\alpha _2 }{2}\int _\Omega {(\omega +fe^{-\omega }} )dxdy \nonumber \\&+\frac{\alpha _3 }{2}\int _\Omega {(e^{2\omega }-2f^{2}\omega )} dxdy \end{aligned}$$
(26)

To use the iPiano algorithm, we need to calculate the gradient of ‘F’ and the proximal map w.r.t ‘G’ which can be calculated as follows

$$\begin{aligned} \nabla _\omega F=(-1)^{\alpha }\nabla ^{\alpha }\cdot \left( \frac{\nabla ^{\alpha }e^{\omega }}{\sqrt{|\nabla ^{\alpha }e^{\omega }|^{2}+\varepsilon }}\right) +\mu \sum \limits _{i=0}^{N_f } \theta _i WK_i^T \dot{\rho }(K_i *e^{\omega }) \end{aligned}$$
(27)

where \(K_i \) is \(N\times N\) highly sparse matrix implemented as 2D convolution of the image ‘u’ with filter kernel \(k_i \,i.e\,K_i u\Leftrightarrow k_i *u\), \(\dot{\rho }(K_i u)=(\dot{\rho }(K_i u)_1 ),\ldots ,\dot{\rho }(K_i u)_N ))^{T}\in R^{N}\hbox { with }\dot{\rho }(q)=\frac{2q}{1+q^{2}}\) and \(W=diag(e^{\omega })\).

Proximal Maps w.r.t \(G(u,\omega )\)

The proximal map with respect to ‘G’ is simply point wise operations. For the case \(H_{{ DFT1}}\), it is given by

$$\begin{aligned} 1.\;u=(I+\delta _1 \partial G)^{-1}(\hat{{u}})\Leftrightarrow u_p =\frac{\hat{u}_p+\delta _1 \alpha _1 u_p^0 }{1+\delta _1 \alpha _1 },\ p=1,2,\ldots ,N. \end{aligned}$$
(28)

The proximal map w.r.t \(H_{DFT2}\) is given as the following minimization problem

$$\begin{aligned} 2.\;(I+\beta _1 \partial G)^{-1}(\hat{{\omega }})=arg\;\mathop {min}\limits _\omega \frac{|\omega -\hat{{\omega }}|_2^2 }{2}+\frac{\beta _1 \alpha _2 }{2}\langle \omega +fe^{-\omega },1\rangle . \end{aligned}$$
(29)

and the proximal map w.r.t \(H_{DFT3} \) is given by the following point-wise calculation

$$\begin{aligned} 3.\;(I+\tau \partial G)^{-1}(\hat{{u}})\Leftrightarrow u_p =\frac{\hat{u}_p+\sqrt{\hat{u}_p^2+4(1+\tau \alpha _3 )\tau \alpha _3 f_p^2 }}{2(1+\tau \alpha _3 )} \end{aligned}$$
(30)

Note the proximal map w.r.t G is solved by using Newton’s method as this scheme has a quite fast convergence about less than 10-iterations [9, 25].

iPiano-algorithm is a forward-backward splitting algorithm incorporating an inertial force. In the forward step, \(\beta _1 \) decides the step size in the direction of the gradient of the differentiable function ‘F’, which aggregated with the inertial force from the previous iteration, weighted by \(\beta _2\). Then the backward step is the result of the proximity operator for the function ‘G’ with the weight \(\beta _1\). According to [9], a iPiano is an inertial force enhanced forward-backward splitting algorithm with the following basic update rule

$$\begin{aligned} u^{(n+1)}=(I+\beta _1 \partial G)^{-1}(u^{(n)}-\beta _1 \nabla F(u^{(n)})+\beta _2 (u^{(n)}-u^{(n-1)})) \end{aligned}$$
(31)

where \(\beta _1 \,\hbox {and }\beta _2 \) are the step size parameters. To conclude, the algorithm is done in the following steps

Algorithm-1

Inertial Proximal Algorithm for non-convex Optimization (iPiano) [16]

1.

Procedure

Initialization: Choose a starting point \(u^{(0)}\in \hbox {dom H}\) and set \(u^{(-1)}=u^{(0)}\) Moreover, define sequences of step size parameters

2.

Iterations \(n\ge 0\):update

\(u^{(n+1)}=(I+\beta _1 \partial G)^{-1}(u^{(n)}-\beta _1 \nabla F(u^{(n)})+\beta _2 (u^{(n)}-u^{(n-1)})) \qquad \quad (32)\)

Where \(\beta _1 \,\hbox {and }\beta _2 \) are the step size parameters

3.

End Procedure

Note the step size parameters should be selected appropriately in order to make the algorithm specific and convergent.

The Alternating Minimization Algorithm

Alternating minimization algorithm is developed to find the minimizer of the objective functional efficiently. For this purpose, the energy functional (23) can be re-written as follows

$$\begin{aligned}&\mathop {arg\;min}\limits _\omega \left[ E(\omega ,f)=\int _\Omega | \nabla ^{\alpha }e^{\omega }|dxdy+\mu \sum \limits _{i=0}^{N_f } \theta _i \rho (k_i *e^{\omega })+\frac{\alpha _1 }{2}\int _\Omega {\parallel e^{\omega }-f\parallel _2^2 } dxdy \right. \nonumber \\&\quad \left. +\frac{\alpha _2 }{2}\int _\Omega {(\omega +fe^{-\omega }} )dxdy+\frac{\alpha _3 }{2}\int _\Omega {(e^{2\omega }-2f^{2}\omega )} dxdy\right] \end{aligned}$$
(33)

where \(\alpha _1,\alpha _2,\alpha _3 >0\) are the regularization parameters used to balance between the additive noise and multiplicative noise fitting terms. To solve (33), we need to consider the following three minimization subproblems.

  1. 1.

    Determine the solution of

$$\begin{aligned} \mathop {argmin}\limits _\omega \left\{ \frac{|\omega -\hat{{\omega }}|_2^2 }{2}+\beta _1 G(\omega )\right\} \,\hbox {with }u=e^{\omega } \end{aligned}$$
(34)

We utilized Newton’s method to solve (34).

  1. 2.

    Apply iPiono algorithm (Algorithm-1) to obtain the restored image \(\omega ^{{*}}.\)

  2. 3.

    Then evaluate \(\omega ^{(n+1)}\) as

    $$\begin{aligned} \omega _{i,j}^{(n+1)}= & {} (\omega _{i,j}^{*} )^{(n)}+\Delta t\left[ G((\omega _{i,j}^{*} )^{(n)})+(-1)^{\alpha }\nabla ^{\alpha }\cdot \left( \frac{\nabla ^{\alpha }((\omega {*})_{i,j}^{(n)} )}{\sqrt{\left| \nabla ^{\alpha }\left( (\omega ^{{*}})_{i,j}^{(n)}\right) \right| ^{2}+\varepsilon }}\right) \right] \nonumber \\&\hbox {Output }u=e^{(\omega ^{(n+1)})} \end{aligned}$$
    (35)

where \(\Delta t\) is the step size, \(\varepsilon >0\) is introduced to avoid singularity and \(\alpha \in [1,2].\) There is an issue of choosing the optimal step size \(\Delta t\) which can ensure fast convergence. Due to the non-linearity of the equation however such an optimal step size is difficult to obtain theoretically and expensive computationally. Instead we took an experimental approach and noted that a good step size is 0.03.

To summarize, the numerical algorithm is performed in the following steps.

Algorithm-2

Alternating Minimization Algorithm (AMA)

1.

Procedure

Input: choose an initial guess \(\omega ^{(0)}=f,\alpha _1,\alpha _2,\alpha _3,\beta _1,\beta _2>0,\alpha \in [1,2],\mu >0\)

2.

Apply the Newton’s iterative method to compute

\(\mathop {argmin}\limits _\omega \left\{ \frac{|\omega -\hat{{\omega }}|_2^2 }{2}+\beta _1 G(\omega )\right\} \qquad (36)\)

3.

Use the iPiono-algorithm (Algorithm-1) to compute \(\omega ^{{*}}\)

4

Then evaluate \(\omega ^{(n+1)}\) as

\(\omega _{i,j}^{(n+1)} =\left( \omega _{i,j}^{*}\right) ^{(n)}+\triangle t\left[ G\left( (\omega _{i,j}^{*} )^{(n)}\right) +(-1)^{\alpha }\nabla ^{\alpha }\cdot \left( \frac{\nabla ^{\alpha }((\omega {*})_{i,j}^{(n)} )}{\sqrt{|\nabla ^{\alpha }\left( (\omega ^{{*}})_{i,j}^{(n)} \right) |^{2}+\varepsilon }}\right) \right] \qquad (37)\)

\(\hbox {Output }u=e^{(\omega ^{(n+1)})}\)

Where \(\Delta t\) is the step size, \(\varepsilon >0\) is introduced to avoid singularity and \(\alpha \in [1,2]\)

5

Check the stopping criteria. If a stopping criterion is satisfied, then exit with the restored image u; otherwise let n=n+1 and go to step (2)

6

Output \(u=e^{(\omega ^{(n+1)})}\)

End procedure

Experimental Results

In this section, some numerical experiments are presented to demonstrate the performance of our proposed model M3. The results are compared with M1 and M2 methods, which are introduced by Hirakawa et al. [12] and Chumchob et al. [8]. In the experiments, the noise levels are determined by different values of \(\chi _0 \,and\,\chi _1\). The AMA-algorithm is tested on different images (real and synthetic) of size \((256^{2}-1024^{2})\). In this paper, the peak signal to noise ratio (PSNR) and structural similarity index (SSIM) are used to measure the image quality. These measures are given by

$$\begin{aligned} PSNR= & {} 10^{*} log_{10} \left[ \frac{N^{2}m_1 m_2 }{\sum \limits _{i=1}^{m_1 } {\sum \limits _{i=1}^{m_2 } {\hat{{u}}(i,j)-u(} } i,j))^{2}}\right] \end{aligned}$$
(38)
$$\begin{aligned} SSIM= & {} \frac{(2\mu _{\hat{{u}}} +a_1 )(2\sigma _{\hat{{u}}u} +a_2 )}{(\sigma _{\hat{{u}}}^2 +\sigma _u^2 +a_1 )(\sigma _{\hat{{u}}}^2 +\sigma _u^2 +a_2 )} \end{aligned}$$
(39)

where ‘N’ is the maximal gray level of the image, ‘u’ is the original image, \(\hat{{u}}\) is the restored image, \(\mu _{\hat{{u}}} ,\mu _u, \sigma _{\hat{{u}}}^2, \sigma _u^2, \sigma _{\hat{{u}}u}, a_1 , a_2 \) are the average values of \(\hat{{u}},u\), variance of \(\hat{{u}},u\) covariance of \(\hat{{u}}, u\) and two small positive constants respectively. Note,that all numerical algorithms are implemented in MATLAB-R2013a and all tests were carried out on Intel(R) Core(TM) i3-4160 CPU @360GHz 3.60 GHz, 8.00 Gb of RAM and 64-bit operating system.

Comparison of Our Proposed Method M3 with M1 in [12] and M2 in [8]

First in Table 1, we give the details of ten experimental setups likewise; the problems; the noise levels determined by \((\chi _0 ,\chi _1 )\); the PSNR results reported in [12] for M1; the PSNR values showed in [8] for M2; the PSNR results obtained from the proposed restoration method M3 and SSIM values for M3. Algorithm-2 was run with the parameters, \(\alpha =1.5,\alpha _1 =0.005,\alpha _2 =325,\alpha _3 =0.003,\beta _1 =1e^{-5},\beta _2 =0.75,\Delta t=0.03\) and number of iterations equal to 600. As shown in the third, fourth and fifth columns of Table 1, the proposed image restoration model M3 performs a clear improvement over the existing methods M1, M2, when images are corrupted by an increased level of noise.

Table 1 Images (Peppers and boats) with size 512 \(^{2}\) corrupted by combination of different values of \((\chi _0,\chi _1 )\), the third, fourth and fifth columns show the PSNR values obtained from M1, M2, and M3
Full size table

Qualitative Results

Secondly, we present the numerical results on different noisy images (synthetic and real) of size \(1024^{2}\) pixels below, to illustrate the efficiency and feasibility of our novel method. The results are compared with M2-method. For this purpose, three images (natural and synthetic) namely Problem1, Problem2, Problem3 are considered for tests.

In the first experiment, the Problem1 is contaminated by combination of both multiplicative and additive noise and recorded its PSNR equal to 14.30. We tune the following empirical choice for the parameters \(\alpha _1 =0.003, \alpha _2 =190, \alpha _3 =0.006, \alpha =1.3\), number of iterations equal to 620. For iPiano algorithm the optimal values of the step size parameters are adjusted and noted\(\beta _1 =1e^{-5}\,\hbox {or }1e^{-4}\), \(\beta _2 =0.75\, \quad or\,\beta _2 =0.85\). The results in Fig. 3 and Table 2 demonstrate that our proposed method can improve the visual quality of the images and PSNR better than M2-method.

In the second test, the Problem2 is corrupted by both multiplicative and additive noise showed in Fig. 4 with PSNR equal to 12.32. For this experiment, the parameters values are tuned as \(\alpha _1 =0.004\), \(\alpha _2 =220\), \(\alpha _3 =0.05\), \(\alpha =1.5\), number of iterations equal to 600. From Fig. 4f and Table 2, it can be observed that our proposed method improves the PSNR of the image better than M2-method.

In the third experiment, in order to further show the efficiency of our proposed model in combined multiplicative and additive noise removal, it was extended to a synthetic image such as Problem3.For this test, the parameter values are chosen as \(\alpha _1 =0.003\), \(\alpha _2 =450, \quad \alpha _3 =0.005,\alpha =1.5\), number of iterations equal to 600. The restored result of our method is optimal, which is shown in Fig. 5. Therefore, from the PSNR and SSIM values showed in Table 2 and Figs. 3, 4 and 5 restoration results, it is reasonable to conclude that our proposed model is best in the sense that it has piecewise smooth intensities, sharp edges and avoiding the staircase effect better than M2-method.

Fig. 3
figure 3

a, d Original image of size \(1024^{2}\); b, e Problem1; c De-noised image by M2 with \(\alpha _1 =6.0,\alpha _2 =0.01,\beta =1e^{-4}, w=1.25\), number of cycles \(=\) 9; f Restored image by M3

Full size image
Table 2 Images with size \(1024^{2}\) corrupted by both additive and multiplicative noise
Full size table
Fig. 4
figure 4

a, d Original image of size \(1024^{2}\); b, e Problem2; c De-noised image by M2 with \(\alpha _1 =10.0,\alpha _2 =0.02,\beta =1e^{-4},w=1.25\), number of cycles = 7; f Restored image by M3

Full size image
Fig. 5
figure 5

a, d Original image of size \(1024^{2}\); b, e Problem3; c De-noised image by M2 with \(\alpha _1 =6.0,\alpha _2 =0.03,\beta =1e^{-4},w=1.25\), number of cycles \(=\) 9; f restored image by M3

Full size image

Computational Analysis

Here, the effect of variation in size of the image, noise level and step size parameters \(\beta _1,\beta _2 \) on the performance of our model and algorithm is analyzed. The values of the other parameters are kept fixed. For this purpose, the Problem1 of size \(128^{2}-1024^{2}\)is used as a test image.

Size-Dependence Test

In Table 3, the size dependence of our method is demonstrated. It implies performance variations with respect to different sizes of the image (Problem1). Our algorithm was run with parameters \(\alpha =1.5,\alpha _1 =0.003\), \(\alpha _2 =405,\alpha _3 =0.005\), number of iterations equal to 100, noise level equal to (25, 0.1) and \(\beta _1 =1e^{-5},\beta _2 =0.75,\Delta t=0.03\) for all tests. Obviously the performance of our algorithm gets better as the size of the image increases in term of PSNR and SSIM values. Although CPU time increase when the size of the image increases. For more details, see Table 3.

Table 3 Problem1 with size \(128^{2}-1024^{2}\) corrupted by both additive and multiplicative noise
Full size table

Noise Level Test

In Table 4, the performance of our algorithm is presented for different noise levels. Our algorithm was run with the parameters \(\alpha =1.5\), \(\alpha _1 =0.003,\alpha _2 =405\), \(\alpha _3 =0.005\), \(\beta _1 =1e^{-5}\), \(\beta _2 =0.75,\Delta t=0.03\) and number of iterations=100 and size equal to \(256^{2}\) for all tests. It can be seen that PSNR and SSIM values get decrease with the increase noise level. Note that optimal number of iterations should be selected with the varying noise levels to get better PSNR and SSIM results. For more details, see Table 4.

\(\beta _1 \)-Dependent Test

Here our aim for this experiment is to observe how the proposed variational method and our algorithm (mainly iPiano) are affected by changes in values of \(\beta _1\) i.e from \(\,1e^{-1}\) to \(1e^{-5}\). Our algorithm was run with the parameters, \(\alpha =1.5,\alpha _1 =0.003,\alpha _2 =405,\alpha _3 =0.005\),number of iteration=100, \(\beta _2 =0.75\), noise level equal to (25, 0.1), \(\Delta t=0.03\) and size equal to \(256^{2}\) for all tests. Theoretically \(\beta _1\) may be selected to be small as possible. As clearly given in Table 5, \(\beta _1 =1e^{-5}\hbox {or }\beta _1 =1e^{-4}\) is the optimal value to remove this type of noise with the good PSNR and SSIM values if we select well-adjusted iteration steps. For more details, see Table 5.

Table 4 Problem1 with size \(256^{2}\) corrupted by both additive and multiplicative noise
Full size table
Table 5 Problem1 with size \(256^{2}\) corrupted by both additive and multiplicative noise
Full size table

\(\beta _2\)-Dependent Test

Here our aim for this experiment is to observe how our variational method and algorithm (mainly iPiano) are affected by varying the values of \(\beta _2 \in [0.3,0.85]\). Our algorithm was run with the parameters, \(\alpha =1.5,\alpha _1 =0.003,\alpha _2 =405,\alpha _3 =0.005,\beta _1 =1e^{-5}\hbox {or}\beta _1 =1e^{-4}\), noise level equal to (25, 0.1), \(\Delta t=0.03\), the number of iteration equal to 100 and size equal to \(256^{2}\) for all tests. As clearly shown in Table 6, \(\beta _2 =0.75\hbox { or }\beta _2 =0.85\) is the optimal value to remove this type of noise with the good PSNR and SSIM values. For more details, see Table 6.

Table 6 Problem1 with size \(256^{2}\) corrupted by both additive and multiplicative noise
Full size table

\(\Delta t\)-Dependent Test

Here our aim for this experiment is to demonstrate how the proposed variational method and our algorithm are performed by changes in values of \(\Delta t\).Our algorithm was run with the parameters, \(\alpha =1.5\), \(\alpha _1 =0.003\), \(\alpha _2 =405\), \(\alpha _3 =0.005\), number of iterations equal to \(100\beta _1 =1e^{-5}\), noise level equal to (25, 0.1), \(\beta _2 =0.75\) and size equal to \(256^{2}\) for all tests. Theoretically \(\Delta t\) may be selected to be small as possible. As clearly given in Table 7, \(\Delta t=0.03\) is the optimal value to remove this type of noise with the good PSNR value. For more details, see Table 7.

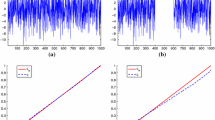
Table 7 Problem1 with size \(512^{2}\) corrupted by multiplicative noise
Full size table

Convergence Result for Algorithm-2

In the following Fig. 6 convergence of Algorithm-2 is demonstrated. For this purpose, the Problem1 of size \(256^{2}\)with noise level (50, 0.1) is used as a test image. Algorithm-2 was run with the parameters, \(\alpha =1.7,\alpha _1 =0.003, \alpha _2 =425,\alpha _3 =0.004\), \(\beta _1 =1e^{-5}\), \(\beta _2 =0.75\) and \(\Delta t=0.03.\) In the Fig. 6, the x-axis is the number of iterations and y-axis is the relative error between the restored image and the original image. It can be seen that the relative error of the proposed algorithm is small and the speed of convergence is optimal.

Fig. 6
figure 6

Relative error curve for Algorithm-2

Full size image

Sensitivity Analysis of Regularization Parameters

Changing the values of regularization parameters may lead towards different restoration results. In image processing selection of parameters is a challenging task, in this regards sensitivity is playing a vital role. Here, we discuss sensitivity of our model with respect to parameters \(\alpha _1,\alpha _2,\alpha _{3}\). It is worth noting that sometimes a small deviation from the optimal parameter or selecting a wrong parameter may lead to significantly wrong/poor results.

To obtain acceptable restoration results, it requires to choose dozens of hand-tuned parameters and it seems a great benefit to use sensitivity analysis to identify those parameters that have a strong influence on the result. It identifies the importance of parameters, the parameters with the strongest influence on the result, and parameter ranges where the result is sensitive to small variations of these parameters [17, 18, 21, 28].

Table 8 PSNR and SSIM values of the restored image with optimal values of \(\alpha _1,\alpha _2 \,\hbox {and }\alpha _3 \) equal to 26.69 and 0.7932
Full size table

To demonstrate the sensitivity analysis of our proposed model (M3), a test image (Problem1) of size \(256\times 256\), which is corrupted by both AN and MN with noise level = (25, 0.1) is utilized. Our algorithm was run with the optimal values of parameters, \(\alpha = 1.5, \alpha _1 =0.003, \alpha _2 =405, \alpha _3 =0.005\), fixed number of iterations = 100, \(\beta _1 = 1e^{-5}\) or \(\beta _1 = 1e^{-4}\) and \(\beta _2 = 0.75\hbox { or }\beta _2 = 0.85\) with time step \(\Delta t=0.03\) according to the image size \(256^{2}\). The values of \(\alpha _1 ,\alpha _2\) and \(\alpha _3 \) are increased and decreased by \((50, 75, 100/99\,\% )\) around its optimal values and noted its PSNR results for the recovered image.

To briefly comment on the choice of the various regularization parameters used in the algorithm described above, it must be noted that according to our experience, the three parameters \(\alpha _1 ,\alpha _2\) and \(\alpha _3\) are more complicated to choose. However, its optimal values are adjusted and tuned according to the noise variance and so on. It was observed that the allowable ranges of values are \(\alpha \in [1.2,1.7],\alpha _1 \in [0.001,0.009]\), \(\alpha _2 \in [50,980]\) and \(\alpha _3 \in [0.004,0.009]\) while the number of iterations are considered to be in the range [100, 800] for natural and synthetic images according to the noise variance. Using these ranges better restoration results could be obtained with improved PSNR and SSIM. Results are presented in Tables 8 and  9.

For the sake of brevity, the following notations are utilized in Tables 8 and  9.

  1. 1.

    \((\cdot )\,\%\) increase-\(\uparrow \), and \((\cdot )\,\%\) decrease-\(\downarrow \)

  2. 2.

    For example \((0.45)\downarrow \) stands for \(0.45\,\%\) decrease in PSNR

  3. 3.

    \((0.25)\uparrow \) Stands for \(0.25\,\%\) increase in PSNR

Table 9 PSNR and SSIM values of the restored image with optimal values of \(\alpha _1, \alpha _2 \,\hbox {and }\alpha _3\) equal to 26.69 and 0.7932
Full size table

Tables 8 and  9 indicate that parameters \(\alpha _1,\alpha _2 \) and \(\alpha _3 \) are important for improving restoration performance. It is noteworthy that the value of \(\alpha \) and \(\alpha _2 \) should not be greater than 1.9 and 1000 and should not be less than 1.2 and 50, while the value of \(\alpha _1\) and \(\alpha _3\) should not be less than 0.001 and 0.004. Hence the availability of information about the uncertainty of the de-noising results with respect to the user-chosen parameters is helpful to avoid incorrect decisions.

Conclusion

In this paper, a novel variational model was proposed using fractional-order total variational filter combined with FOE-image prior for restoration of images corrupted at one time by independent AN and MN. Alternating minimization algorithm (AMA) was exploited for solving non-linear PDE arisen from minimization of the proposed functional. Experimental results demonstrate that the proposed model improves PSNR better than M1 and M2 method. Parameters dependence was also discussed. Developing fast algorithms for solving partial differential equations arisen from model minimization might be considered in future research.