An Inventory Model for Weibull Deterioration with Stock and Price Dependent Demand

Abstract

Customer purchasing needs are generally affected by factors such as selling price and inventory level and not only by demand. Demand is considered either to be a constant or a function of a single variable in most of the cases, which is not always feasible. Consequently, in the present study, demand rate as a function of stock level and selling price. The deterioration rate has been considered here to be Weibull two parameters, shortages are partially backlogged. The major objective is to determine the optimal selling price, the optimal replenishment schedule and the optimal order quantity simultaneously such that, the total profit is maximized. In this model, first show that for any given selling price, optimal replenishment schedule exists and unique. Then, the total profit is a concave function of price with respect to time. Next, present a simple algorithm to find the optimal solution. Finally, in this paper solve a numerical example to illustrate the solution procedure and the algorithm.

Introduction

In the classical inventory models, the demand rate is generally assumed to be either constant or time dependent, but in general independent of the stock levels and selling price. However, it is observed that practically an increase in shelf space for an item induces more consumers to buy it. This occurs owing to its visibility, which attracts customers, popularity of the product, etc. Conversely, low stocks of certain foods might raise the perception that they are not fresh and/or popular. Therefore, it is observed that the demand rate may be influenced by the stock levels for some types of items. In years, marketing researchers and practitioners have recognized the phenomenon that the demand for some items could be based on the inventory level on the display. Gupta and Vrat [9] were the first to develop models for stock dependent consumption rate. Baker and Urban [1] established an economic order quantity model for a power form inventory level dependent demand pattern. Mandal and Phaujdar [15] developed an economic production quantity model for deteriorating items with constant production rate and linearly stock dependent demand. Researchers such as [3, 7, 21, 24, 29] and many others have worked in related fields. Soni and Shah [27] discussed the optimal ordering policy for an inventory model with stock-dependent demand. Wu et al. [32] first developed an inventory model for non-instantaneous deteriorating items with stock dependent demand. Chang et al. [2] developed an optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand. Recently, among others, Mishra and Tripathy [19] proposed an inventory model for time dependent Weibull deterioration with partial backlogging, Mishra [16] proposed a new inventory model a waiting time deterministic inventory model for perishable items in stock and time dependent demand, Mishra and Tripathy [20] proposed an inventory model for Weibull deteriorating items with salvage value, Roy and Chaudhuri [26] developed an EOQ model for perishable items with stock-dependent demand, and Gupta et al. [10] developed an optimal ordering policy for stock-dependent demand, inventory model with non instantaneous deteriorating items.

In classical inventory models, the constant demand rate has generally been considered. But in reality, demand is not usually constant, but tends to depend on time, stock, price, etc. Selling price often plays an important role while deciding the demand pattern. You [33] developed an inventory model with a price and time-dependent demand. In most of the models, holding cost is taken to be constant which is not so always true due to the devaluation of the currency (money), the holding-contract price, changing administrative cost, etc. Hence, in generalization of EOQ models, various functions describing holding cost were considered by several researchers like [8, 30] and [11, 18, 25], etc.

Maintaining of deteriorating inventories is a major issue for almost all business organizations. Most of the goods decay over time. Some products deteriorate in a certain fixed period of storage like seasonal goods, fruits, vegetables, etc., but certain goods lose their potency when the time passes, such as electronic items, radioactive substances, etc. Certain inventories like highly volatile liquids as ethanol, gasoline, etc., undergo depletion due to evaporation, so that deterioration is one of the most influential factors that affect the decision related to inventory management. Each business organization considers it quite seriously. With regard to all these issues, deterioration function is of various types that may be constant and time dependent. Weibull distribution is one of the most reliable deterioration functions because it presents a perfect view of the deteriorating inventory level. Covert and Philip [5] established an inventory model for deteriorating items having variable rate of deterioration. In their model, they use two-parameter Weibull deterioration. Wu [31] presented an EOQ inventory model for items with Weibull distribution deterioration, ramp type demand rate, and partial backlogging. Lee and Wu [13] formulate an EOQ model for items with Weibull distributed deterioration, shortages, and power demand pattern. Roy and Chaudhuri [26] scheduled a production inventory model under stock dependent demand, Weibull distribution deterioration, and shortage. Konstantaras and Skouri [12] dealt a note on a production inventory model under stock dependent demand, Weibull distribution deterioration, and shortage. Many researchers consider this as a realistic assumption, such as [16, 17, 19], etc.

The work of the researchers who used different demand function and various forms of deterioration with shortages (allowed/not allowed), for developing the economic order quantity (EOQ) models are summarized below.

Table 1 Author’s contributions

Table 1 shows that all the researchers developed EOQ models by taking different demand, deterioration (Constant/Linear/Weibull distribution) and shortages allowed or not allowed. In the above mentioned references, most researchers assumed that shortages are completely backlogging. In practice, some customers would like to wait for backlogging during the shortage period, but the other would not. Consequently, the opportunity cost due to lost sales should be considered in the model. The motivation behind developing an inventory model in the present article is to prepare a more general inventory model, which includes; (a) demand rate as a function of stock level and selling price, (b) Weibull deterioration, (c) shortages are allowed and are partially backlogged; (d) and holding costs as time dependent. Holding cost may not be constant over time, as there is a change in time value of money and change in the price index. In real markets, it is observed that because of the goodwill of the retailer, customers are willing to wait till arrival of new stocks, but as the waiting time increases, some of them may opt to go elsewhere, which is a case of partial backlogging. Many inventory models have been developed using backlogging rate to be an exponential function of waiting time of the customers, but in real practice, backlogging rate never varies as high as exponential. Therefore, in the present paper considering the backlogging rate to be $\frac{1}{1+\delta x},\delta >0$, where x is the waiting time of the customers for receiving their goods which seems to be better. Therefore, it is necessary to consider as part backlogging while developing the inventory model. Generally in most of the cases the entrepreneurs try to sell as much as they can and try to fulfill the demand in full. So, for the trader the replenishment rate becomes infinite. Models for deteriorating inventory can be broadly categorized according to the lifetime of products and characteristics of demand. Three categories are distinguished based on shelf life characteristics: (1) fixed lifetime, i.e. predetermined deterministic lifetime of e.g. two days or one season. (2) Age dependent deterioration rate (which implies a probabilistic distributed lifetime, e.g. Weibull). (3) Time or inventory (but not age) dependent deterioration rate. Both models with a constant deterioration rate per stocked item (and so inventory, but not age dependent) belong to class 3. In the present article the inventory dependent deterioration rate has been considered. Therefore, the deterioration rate has been considered as Weibull deterioration here.

In this paper, a new economic order quantity (EOQ) models for the demand rate to be stocked and price dependent with Weibull two parameter deterioration rate to develop a deterministic inventory model. In this model shortages are allowed and are partially backlogged. Also replenishment rate is considered to be is instantaneous and lead time is considered to be zero or negligible. The holding cost considered to be a function of time. The main objective of this paper was to find the optimal replenishment and price investments strategies while maximize the total profit cost per unit time. The notations of the model are introduced in “Assumptions and notations” section. In “Mathematical formulation” section, a mathematical model is established and solution procedure is discussed for maximizing the total profit cost. Numerical examples are provided to illustrate the proposed model in “Numerical example” section. The model proved that the total cost function is concave in “Graphical proof for the concavity of the total profit function” section. Sensitivity analysis of the optimal solution with respect to major parameters of the system is carried out, and their results are discussed in “Sensitivity analysis” section. The article ends with some concluding remarks and scope of future research.

Assumptions and Notations

The following assumptions and notations required to develop the mathematical model.

Assumptions

• (a) The demand rate is a function of stock and selling price considered as;

  $$\begin{aligned} f(t)=\left\{ {\begin{array}{ll} a+\gamma Q(t)-p,&{}\quad Q(t)\ge 0 \\ a-p, &{}\quad Q(t)<0 \\ \end{array}} \right. , \end{aligned}$$

  where $a>0, 0<\gamma \ll 1, a>p$ and p is selling price.

• (b) Holding cost is h(t) per item per time unit is time dependent and is assumed to be $h(t)=h+\delta t$, where $h>0$ and $\delta >0$.

• (c) $\theta (t)=\alpha \beta t^{\beta -1}:$ Deterioration rate which follows a two parameter Weibull distribution, where $0<\alpha <1$ is the scale parameter, $\beta >0$ is the shape parameter.

• (d) Replenishment rate is instantaneous.

• (e) Lead time is zero.

• (f) The planning horizon is infinite.

• (g) During the stock out period, the unsatisfied demand is backlogged; the rate of backlogging is variable and is dependent on the length of the waiting time for the next replenishment. For the negative inventory the backlogging rate is; $B(t)=\frac{1}{1+\eta (T-t)} ;\eta >0$ denotes the backlogging parameter and $t_1 \le t\le T.$

• (h) During time $0\le t<t_1$, inventory is depleted due to deterioration and demand of the item. At time $t_1$ the inventory becomes zero and backlogging of demand starts due to shortages.

Notations

• (i) A :  Ordering cost per order, $/per order.

• (ii) $c_1 :$ Purchase cost per unit, $/per unit/per unit time.

• (iii) $c_2 :$ Backordered cost per unit short per time unit, $/per unit/per unit time.

• (iv) $c_3 :$ Cost of lost sales per unit, $/per unit/per unit time.

• (v) T :  The length of the cycle time.

• (vi) ${ IM}:$ Maximum inventory level during $\left[ {0,T} \right]$.

• (vii) ${ IB}:$ Maximum backordered units during stock out period.

• (viii) $Q={ IM}+{ IB}:$ Order quantity during a cycle of length T.

• (ix) $Q_1 (t):$ Level of positive inventory at time $t,0\le t\le t_1.$

• (x) $Q_2 (t):$ Level of negative inventory at time $t, t_1 \le t\le T.$

• (xi) P(T, p) :  Total profit per unit time, $/per unit/per unit time.

Mathematical Formulation

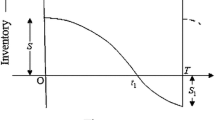
Under above assumption, the on hand inventory level at any instant of time is exhibited in Fig. 1.

Fig. 1

Representation of inventory system

During the period $[0, t_1 ]$, the inventory is depleted as a result of cumulative effects of demand and deterioration. Thus, the inventory level at any instant of time t during $[0,t_1 ]$ is described by the differential equation;

$$\begin{aligned} \frac{dQ_1 (t)}{dt}+(\theta (t)+\gamma ) Q_1 (t)=-\left( {a-p} \right) ,\quad 0\le t\le t_1. \end{aligned}$$

(1)

The boundary condition $Q_1 (t_1 )=0$.

Solving Eq. (1) and neglecting second and higher powers of $\alpha$ and $\gamma$, we have;

$$\begin{aligned} Q_1 (t)= & {} (a-p)\left[ t_1 +\frac{\alpha t_1 ^{\beta +1}}{\beta +1}+\frac{\gamma t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +2}-\alpha \gamma t_1 t^{\beta }-\frac{\alpha \gamma t_1 ^{2}t^{\beta }}{2}-\gamma t_1 t\right. \nonumber \\&\left. -\frac{\alpha \gamma tt_1 ^{\beta +1}}{\beta +1}-t -\frac{\alpha t^{\beta +1}}{\beta +1}+\frac{\gamma t^{2}}{2}+\alpha t^{\beta +1}+\frac{\alpha \gamma t^{\beta +2}}{2}+\frac{\alpha \gamma t^{\beta +2}}{\beta +1}\right] ,\quad 0\le t\le t_1.\nonumber \\ \end{aligned}$$

(2)

Inventory level reaches to zero at time $t_1$, there after shortages occur. During the interval $[t_1, T]$, the unsatisfied demand is partially backlogged. The state of inventory during $[t_1 , T]$ can be represented by the differential equation;

$$\begin{aligned} \frac{dQ_2 (t)}{dt}=-\frac{a-p}{1+\eta (T-t)},\quad t_1 \le t\le T. \end{aligned}$$

(3)

Using the boundary condition $Q_1 (t_1 )=0$ and $Q_2 (t_1 )=0$, the solution of differential equation is;

$$\begin{aligned} Q_2 (t)=\frac{(a-p)}{\eta }\left( {\ln (1+\eta (T-t))- \ln (1+\eta (T-t_1)) } \right) ,\quad t_1 \le t\le T. \end{aligned}$$

(4)

The maximum positive inventory is;

$$\begin{aligned} { IM}=Q_1 (0)=(a-p)\left[ t_1 +\frac{\alpha t_1 ^{\beta +1}}{\beta +1}+\frac{\gamma t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +2}\right] ,\quad 0\le t\le t_1. \end{aligned}$$

(5)

The maximum backordered units are;

$$\begin{aligned} { IB}=-Q_2 (T)=\frac{(a-p)}{\eta }\ln (1+\eta (T-t_1)). \end{aligned}$$

(6)

Hence, the order size during $\left[ {0,T} \right]$ is;

$$\begin{aligned} Q= & {} { IM}+{ IB}.\nonumber \\\Rightarrow & {} Q=(a-p)\left[ t_1 +\frac{\alpha t_1 ^{\beta +1}}{\beta +1}+\frac{\gamma t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +2}+\frac{1}{\eta }\ln (1+\eta (T-t_1))\right] . \end{aligned}$$

(7)

The total profit per cycle consists of following cost components;

• (i) Ordering cost per cycle; ${ { OC}}=A.$

• (ii) Inventory holding cost per cycle is;

  $$\begin{aligned} { IHC}= & {} {\mathop {\int }\limits _0^{t_1 }} {(h+\delta t)Q_1 (t) dt}.\\\Rightarrow & {} { IHC}=h(a-p)\left[ \frac{t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +3}-\frac{\alpha \gamma t_1 ^{\beta +3}}{\beta +1}-\frac{\alpha t_1 ^{\beta +2}}{(\beta +1)(\beta +2)}+\frac{\gamma t_1 ^{3}}{6}+\frac{\alpha t_1 ^{\beta +2}}{\beta +2}\right. \\&\left. +\,\frac{\alpha \gamma t_1 ^{\beta +3}}{2(\beta +3)} +\frac{\alpha \gamma t_1 ^{\beta +3}}{(\beta +1)(\beta +3)}\right] +\delta (a-p)\left[ \frac{t_1 ^{3}}{6}+\frac{\alpha t_1 ^{\beta +3}}{2(\beta +1)}+\frac{\gamma t_1 ^{4}}{24}-\alpha \gamma t_1 ^{\beta +4}\right. \\&\left. -\,\alpha t_1 ^{\beta +3} -\frac{\alpha \gamma t_1 ^{\beta +4}}{2(\beta +2)}-\frac{\alpha \gamma t_1 ^{\beta +4}}{3(\beta +1)}-\frac{\alpha t_1 ^{\beta +3}}{(\beta +3)(\beta +1)}+\frac{\alpha t_1 ^{\beta +3}}{\beta +3}+\frac{\alpha \gamma t_1 ^{\beta +4}}{2(\beta +4)}\right. \\&\left. +\,\frac{\alpha \gamma t_1 ^{\beta +4}}{(\beta +1)(\beta +4)}\right] . \end{aligned}$$

• (iii) Backordered cost per cycle is;

  $$\begin{aligned} { BC}= & {} c_2{\mathop {\int }\limits _{t_1 }^T} {-Q_2 (t)dt}.\\= & {} \frac{c_2 (a-p)}{\eta ^{2}}\left[ {\eta (T- t_1 )-\ln (1+\eta (T- t_1 )} \right] . \end{aligned}$$

• (iv) Cost due to lost sales per cycle;

  $$\begin{aligned} LS= & {} c_3 (a-p){\mathop {\int }\limits _{t_1 }^T} {\left( {1-\frac{1}{1+\eta (T-t)} } \right) dt} \\= & {} \frac{c_3 (a-p)}{\eta }\left[ {\eta (T- t_1 )-\ln (1+\eta (T- t_1 )} \right] . \end{aligned}$$

• (v) Purchase cost per cycle is

  $$\begin{aligned} { PC}= & {} c_1 \times Q\\\Rightarrow & {} { PC}=c_1 (a-p)\left[ t_1 +\frac{\alpha t_1 ^{\beta +1}}{\beta +1}+\frac{\gamma t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +2}+\frac{1}{\eta }\ln (1+\eta (T-t_1))\right] . \end{aligned}$$

• (vi) Sales revenue is given by;

  $$\begin{aligned} { SR}= & {} p{\mathop {\int }\limits _0^{t_1 }} {(a-p+\gamma Q_1 (t)} )dt+p{\mathop {\int }\limits _{t_1 }^T} {(a-p)dt}\\= & {} p(a-p)T+p\gamma (a-p)\left[ \frac{t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +3}-\frac{\alpha \gamma t_1 ^{\beta +3}}{\beta +1}-\frac{\alpha t_1 ^{\beta +2}}{(\beta +1)(\beta +2)}\right. \\&\left. +\,\frac{\gamma t_1 ^{3}}{6}+\frac{\alpha t_1 ^{\beta +2}}{\beta +2} +\frac{\alpha \gamma t_1 ^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma t_1 ^{\beta +3}}{(\beta +1)(\beta +3)}\right] . \end{aligned}$$

  Therefore, total profit per unit time is given by;

  $$\begin{aligned} P(T,t_1,p)= & {} \frac{1}{T}\left[ {{ SR}-{ OC}-{ IHC}-{ BC}-LS-{ PC}} \right] .\nonumber \\= & {} \frac{1}{T}\left[ p(a-p)T+p\gamma (a-p)\left[ \frac{t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +3}-\frac{\alpha \gamma t_1 ^{\beta +3}}{\beta +1}-\frac{\alpha t_1 ^{\beta +2}}{(\beta +1)(\beta +2)}\right. \right. \nonumber \\&\left. +\,\frac{\gamma t_1 ^{3}}{6}+\frac{\alpha t_1 ^{\beta +2}}{\beta +2} +\frac{\alpha \gamma t_1 ^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma t_1 ^{\beta +3}}{(\beta +1)(\beta +3)}\right] -A-h(a-p)\left[ \frac{t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +3}\right. \nonumber \\&\left. -\,\frac{\alpha \gamma t_1 ^{\beta +3}}{\beta +1}-\frac{\alpha t_1 ^{\beta +2}}{(\beta +1)(\beta +2)} \quad +\frac{\gamma t_1 ^{3}}{6}+\frac{\alpha t_1 ^{\beta +2}}{\beta +2}+\frac{\alpha \gamma t_1 ^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma t_1 ^{\beta +3}}{(\beta +1)(\beta +3)}\right] \nonumber \\&\left. -\,\delta (a-p)\left[ \frac{t_1 ^{3}}{6}+\frac{\alpha t_1 ^{\beta +3}}{2(\beta +1)}+\frac{\gamma t_1 ^{4}}{24}-\alpha \gamma t_1 ^{\beta +4} -\alpha t_1 ^{\beta +3}-\frac{\alpha \gamma t_1 ^{\beta +4}}{2(\beta +2)}-\frac{\alpha \gamma t_1 ^{\beta +4}}{3(\beta +1)}\right. \right. \nonumber \\&\left. -\,\frac{\alpha t_1 ^{\beta +3}}{(\beta +3)(\beta +1)}+\frac{\alpha t_1 ^{\beta +3}}{\beta +3}+\frac{\alpha \gamma t_1 ^{\beta +4}}{2(\beta +4)}+\frac{\alpha \gamma t_1 ^{\beta +4}}{(\beta +1)(\beta +4)}\right] \nonumber \\&-\,\frac{c_2 (a-p)}{\eta ^{2}}\left[ {\eta (T- t_1 )-\ln (1+\eta (T- t_1 )} \right] -\frac{c_3 (a-p)}{\eta }\left[ \eta (T- t_1 )\right. \nonumber \\&\left. -\,\ln (1+\eta (T- t_1 ) \right] -c_1 (a-p)\left[ t_1 +\frac{\alpha t_1 ^{\beta +1}}{\beta +1}+\frac{\gamma t_1 ^{2}}{2}-2\alpha \gamma t_1 ^{\beta +2}\right. \nonumber \\&\left. \left. +\,\frac{1}{\eta }\ln (1+\eta (T-t_1))\right] \right] . \end{aligned}$$

  (8)

Solution Procedure

Let $t_1 =\lambda T, 0<\lambda <1$ and putting $t_1$ values in Eq. (8) we have;

$$\begin{aligned} P(T,p)= & {} \frac{1}{T}\left[ {{ SR}-{ OC}-{ IHC}-{ BC}-{ LS}-{ PC}} \right] .\nonumber \\= & {} \frac{1}{T}\left[ p(a-p)T+p\gamma (a-p)\left[ \frac{\lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{\beta +1}\right. \right. \nonumber \\&\left. -\,\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{(\beta +1)(\beta +2)}+\frac{\gamma \lambda ^{3}T^{3}}{6} +\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{\beta +2}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{(\beta +1)(\beta +3)}\right] \nonumber \\&-\,A-h(a-p)\left[ \frac{\lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{ \beta +3}T^{\beta +3}}{\beta +1} -\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{(\beta +1)(\beta +2)}\right. \nonumber \\&\left. +\,\frac{\gamma \lambda ^{3}T^{3}}{6}+\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{\beta +2}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{(\beta +1)(\beta +3)}\right] -\delta (a-p)\left[ \frac{\lambda ^{3}T^{3}}{6}\right. \nonumber \\&+\,\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +1)}+\frac{\gamma \lambda ^{4}T^{4}}{24}-\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}-\alpha \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{2(\beta +2)}\nonumber \\&-\,\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{3(\beta +1)}-\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{(\beta +3)(\beta +1)} +\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{\beta +3}+\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{2(\beta +4)}\nonumber \\&\left. +\,\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{(\beta +1)(\beta +4)}\right] -\frac{c_2 (a-p)}{\eta ^{2}}\left[ {\eta (T-\lambda T)-\ln (1+\eta (T- \lambda T))} \right] \nonumber \\&-\,\frac{c_3 (a-p)}{\eta }\left[ {\eta (T- \lambda T)-\ln (1+\eta (T- \lambda T))} \right] -c_1 (a-p)\left[ \lambda T+\frac{\alpha \lambda ^{\beta +3}T^{\beta +1}}{\beta +1}\right. \nonumber \\&\left. \left. +\,\frac{\gamma \lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +2}T^{\beta +2} +\frac{1}{\eta }\ln (1+\eta (T-\lambda T))\right] \right] \end{aligned}$$

(9)

Proposition 1

When selling price p is fixed, the profit function P(T, p) is concave with respect to T.

Proof

The first and second partial derivatives of the profit function P(T, p) with respect to T are given below:

$$\begin{aligned} \frac{\partial P(T,p)}{\partial T}= & {} p\gamma (a-p)\left[ \frac{\lambda ^{2}}{2}-2\alpha (\beta +2)\gamma \lambda ^{\beta +3}T^{\beta +1}-\frac{\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{\beta +1}\right. \nonumber \\&-\,\frac{\alpha \lambda ^{\beta +2}T^{\beta }}{(\beta +2)} +\frac{\gamma \lambda ^{3}T}{3} +\frac{\alpha (\beta +1)\lambda ^{\beta +2}T^{\beta }}{\beta +2}+\frac{\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{2(\beta +3)}\nonumber \\&\left. +\,\frac{\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{(\beta +1)(\beta +3)}\right] +\frac{A}{T^{2}}-h(a-p)\left[ \frac{\lambda ^{2}}{2} -2\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}\right. \nonumber \\&-\,\frac{\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{\beta +1}-\frac{\alpha \lambda ^{\beta +2}T^{\beta }}{(\beta +2)}+\frac{\gamma \lambda ^{3}T}{3}+\frac{\alpha (\beta +1)\lambda ^{\beta +2}T^{\beta }}{\beta +2}\nonumber \\&\left. +\,\frac{\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{2(\beta +3)} +\frac{\alpha \gamma (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{(\beta +1)(\beta +3)}\right] -\delta (a-p)\left[ \frac{\lambda ^{3}T}{3}\right. \nonumber \\&+\,\frac{\alpha (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{2(\beta +1)}+\frac{\gamma \lambda ^{4}T^{2}}{8} -\alpha \gamma (\beta +3)\lambda ^{\beta +4}T^{\beta +2}-\alpha (\beta +2)\lambda ^{\beta +3}T^{\beta +1}\nonumber \\&-\,\frac{\alpha \gamma (\beta +3)\lambda ^{\beta +4}T^{\beta +2}}{2(\beta +2)}-\frac{\alpha \gamma (\beta +3)\lambda ^{\beta +4}T^{\beta +1}}{3(\beta +1)} -\frac{\alpha (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{(\beta +3)(\beta +1)}\nonumber \\&\left. +\,\frac{\alpha (\beta +2)\lambda ^{\beta +3}T^{\beta +1}}{\beta +3}+\frac{\alpha \gamma (\beta +3)\lambda ^{\beta +4}T^{\beta +2}}{2(\beta +4)}+\frac{\alpha \gamma (\beta +3)\lambda ^{\beta +4}T^{\beta +2}}{(\beta +1)(\beta +4)}\right] \nonumber \\&+\,\frac{c_2 (a-p)}{\eta ^{2}}\left[ {\frac{\eta (1-\lambda )}{T(1+\eta (T-\lambda T))}-\frac{\ln (1+\eta (T- \lambda T))}{T^{2}}} \right] \nonumber \\&+\,\frac{c_3 (a-p)}{\eta }\left[ {\frac{\eta (1-\lambda )}{T(1+\eta (T-\lambda T))}-\frac{\ln (1+\eta (T- \lambda T))}{T^{2}}} \right] -c_1 (a-p)\left[ \frac{\alpha \beta \lambda ^{\beta +3}T^{\beta -1}}{\beta +1}\right. \nonumber \\&\left. \left. +\,\frac{\gamma \lambda ^{2}}{2}-2\alpha \gamma (\beta +1)\lambda ^{\beta +2}T^{\beta }+\frac{1-\lambda }{T(1+\eta (T-\lambda T))}-\frac{\ln (1+\eta (T- \lambda T))}{\eta T^{2}}\right] \right] =0.\nonumber \\ \end{aligned}$$

(10)

and

$$\begin{aligned}&\frac{\partial ^{2}P(T,p)}{\partial T^{2}}=\frac{2A}{T^{3}}\nonumber \\&\quad +\,\frac{h(a-p)\lambda ^{2}(-2T(2+\beta )\gamma \lambda -6T^{\beta }\alpha \beta ^{2}\lambda ^{\beta }+3T^{1+\beta }\alpha (2+\beta )^{2}(5+4\beta )\gamma \lambda ^{1+\beta })}{6T(2+\beta )}\nonumber \\&\quad -\,\frac{(a-p)p\gamma \lambda ^{2}(-2T(2+\beta )\gamma \lambda -6T^{\beta }\alpha \beta ^{2}\lambda ^{\beta }+3T^{1+\beta }\alpha (2+\beta )^{2}(5+4\beta )\gamma \lambda ^{1+\beta })}{6T(2+\beta )}\nonumber \\&\quad -\,\frac{1}{12}(a-p)\delta \lambda ^{3}\left[ 4+3T\gamma \lambda -\frac{6T^{\beta }\alpha (6+13\beta +9\beta ^{2}+2\beta ^{3})\lambda ^{\beta }}{3+\beta }\right. \nonumber \\&\quad \left. -\,\frac{4T^{1+\beta }\alpha (3+\beta )(-6+35\gamma +22\beta ^{2}\gamma +3\beta ^{3}\gamma +\beta (-3+51\gamma ))\lambda ^{1+\beta }}{(1+\beta )(4+\beta )}\right] \nonumber \\&\quad -\,\frac{1}{T^{3}}(a-p)\left[ T\left[ \frac{2-2\lambda }{-1+T\eta (-1+\lambda )}-\frac{T\eta (-1+\lambda )^{2}}{(-1+T\eta (-1+\lambda ))^{2}}\right. \right. \nonumber \\&\quad \left. \left. -\,2T^{1+\beta }\alpha \beta (1+\beta )\gamma \lambda ^{2+\beta }+ \frac{T^{\beta }\alpha (-1+\beta )\beta \lambda ^{3+\beta }}{1+\beta }\right] +\frac{2Log[1+T\eta -T\eta \lambda ]}{\eta }\right] c_1\nonumber \\&\quad +\,\frac{(a-p)(-\frac{T\eta (-2+3T\eta (-1+\lambda ))(-1+\lambda )}{(-1+T\eta (-1+\lambda ))^{2}}+2Log[1+T\eta -T\eta \lambda ])c_2 }{T^{3}\eta ^{2}}\nonumber \\&\quad +\,\frac{(a-p)\left[ -\frac{T\eta (-2+3T\eta (-1+\lambda ))(-1+\lambda )}{(-1+T\eta (-1+\lambda ))^{2}}+2Log[1+T\eta -T\eta \lambda ]\right] c_3 }{T^{3}\eta }<0. \end{aligned}$$

(11)

Clearly, from (11), the profit function is concave in. Therefore; the search for the optimal ordering frequency is reduced to obtain a local optimum.

Proposition 2

There exists an unique $p^*$ that maximizes profit function P(T, p).

Proof

The first and second partial derivatives of the profit function P(T, p) with respect to p are presented below:

$$\begin{aligned}&\frac{\partial P(T,p)}{\partial p}=\frac{1}{T}\left[ (a-2p)T+\gamma (a-2p)\left[ \frac{\lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{\beta +1}\right. \right. \nonumber \\&\quad \left. -\,\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{(\beta +1)(\beta +2)} +\frac{\gamma \lambda ^{3}T^{3}}{6}+\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{\beta +2}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{(\beta +1)(\beta +3)}\right] \nonumber \\&\quad +\,h\left[ \frac{\lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{\beta +1} -\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{(\beta +1)(\beta +2)}+\frac{\gamma \lambda ^{3}T^{3}}{6}\right. \nonumber \\&\quad \left. +\,\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{\beta +2}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{(\beta +1)(\beta +3)}\right] +\delta \left[ \frac{\lambda ^{3}T^{3}}{6} +\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +1)}\right. \nonumber \\&\quad +\,\frac{\gamma \lambda ^{4}T^{4}}{24}-\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}-\alpha \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{2(\beta +2)}-\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{3(\beta +1)}\nonumber \\&\quad \left. -\,\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{(\beta +3)(\beta +1)} +\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{\beta +3}+\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{2(\beta +4)}+\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{(\beta +1)(\beta +4)}\right] \nonumber \\&\quad +\,\frac{c_2 }{\eta ^{2}}\left[ {\eta (T-\lambda T)-\ln (1+\eta (T- \lambda T))}\right] +\frac{c_3 }{\eta }\left[ {\eta (T- \lambda T)-\ln (1+\eta (T- \lambda T))} \right] \nonumber \\&\quad \left. +\,c_1 \left[ \lambda T+\frac{\alpha \lambda ^{\beta +3}T^{\beta +1}}{\beta +1}+\frac{\gamma \lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +2}T^{\beta +2} +\frac{1}{\eta }\ln (1+\eta (T-\lambda T))\right] \right] =0.\nonumber \\ \end{aligned}$$

(12)

By assuming that $\delta>0,\eta >0, 0<\lambda <1$ and $p<a<2p$ it is clear from (12) that $\frac{\partial P(T^*,p)}{\partial T}=0$ has a solution if $[(a-2p)+\gamma (a-2p)]<0.$

Further, the second-order derivations of $\frac{\partial P(T^*,p)}{\partial T}=0$ with respect to p, is

$$\begin{aligned}&\frac{\partial P^{2}(T,p)}{\partial p^{2}}=\frac{-2}{T}\left[ T+\gamma \left[ \frac{\lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{\beta +1}\right. \right. \nonumber \\&\quad \left. -\,\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{(\beta +1)(\beta +2)} +\frac{\gamma \lambda ^{3}T^{3}}{6}+\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{\beta +2}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{(\beta +1)(\beta +3)}\right] \nonumber \\&\quad +\,h\left[ \frac{\lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{\beta +1} -\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{(\beta +1)(\beta +2)}+\frac{\gamma \lambda ^{3}T^{3}}{6}\right. \nonumber \\&\quad \left. +\,\frac{\alpha \lambda ^{\beta +2}T^{\beta +2}}{\beta +2}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +3)}+\frac{\alpha \gamma \lambda ^{\beta +3}T^{\beta +3}}{(\beta +1)(\beta +3)}\right] +\delta \left[ \frac{\lambda ^{3}T^{3}}{6} +\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{2(\beta +1)}\right. \nonumber \\&\quad +\,\frac{\gamma \lambda ^{4}T^{4}}{24}-\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}-\alpha \lambda ^{\beta +3}T^{\beta +3}-\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{2(\beta +2)}-\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{3(\beta +1)}\nonumber \\&\quad \left. -\,\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{(\beta +3)(\beta +1)} +\frac{\alpha \lambda ^{\beta +3}T^{\beta +3}}{\beta +3}+\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{2(\beta +4)}+\frac{\alpha \gamma \lambda ^{\beta +4}T^{\beta +4}}{(\beta +1)(\beta +4)}\right] \nonumber \\&\quad +\,\frac{c_2 }{\eta ^{2}}\left[ {\eta (T-\lambda T)-\ln (1+\eta (T- \lambda T))} \right] +\frac{c_3 }{\eta }\left[ {\eta (T- \lambda T)-\ln (1+\eta (T- \lambda T))} \right] \nonumber \\&\quad \left. +\,c_1 \left[ \lambda T+\frac{\alpha \lambda ^{\beta +3}T^{\beta +1}}{\beta +1}+\frac{\gamma \lambda ^{2}T^{2}}{2}-2\alpha \gamma \lambda ^{\beta +2}T^{\beta +2} +\frac{1}{\eta }\ln (1+\eta (T-\lambda T))\right] \right] <0. \end{aligned}$$

Consequently, $P(T^*,p)$ is a concave function of p for a given $T^*$ hence a value of p that obtain from (12) is unique. As a result, we prove that exist a unique value of $p(p^*)$ which maximizes $P(T^*,p)p^*$ can be obtained by solving (12). The solution of $[(a-2p)+\gamma (a-2p)]=0$ is the lower bound for the optimal selling price $p^*$ such that $\frac{\partial P(T^*,p)}{\partial T}=0.$ Combining the above finding and theorem, we propose the following algorithm for solving the problem.

Proposition 3 is the grouping of Propositions 1 and 2.

Proposition 3

For optimal values of $p^*$, the optimal solution $(T^*,p^*)$ which maximizes the profit function $P(T^*,p)$ exists and is unique. The optimal solution is easily obtained the iterative algorithm.

Using the mathematical results obtained previously the following iterative algorithm is developed.

Algorithm

We can propose a simple algorithm to obtain the optimal solution $(p^*,T^*)$ of the problem.

Step 1::

Start with $j=0$ and the initial trial value of $p_j =p_1$. Which is a solution to $[(a-2p)+\gamma (a-2p)]=0$.

Step 2::

By using (10), find the optimum of $T^*$, for a given price $p_j$.

Step 3::

Use the result in step 2, and then determine the optimal $p_{j+1}$ by (12).

Step 4::

If the difference between $p_j$, $p_{j+1}$ is sufficiently small (i.e. $\left| {p_j -p_{j+1} } \right| \le 0.0001)$, set $p^*=p_{j+1}$, then $(p^*,T^*)$ is the optimal solution and stop. Otherwise, set $j=j+1$ and go back to step 2.

By using above algorithm, we obtain the optimal solution $(p^*,T^*)$ then; we can obtain $Q^*$ by using (7) and P(T, p) by using (9).

Numerical Example

To illustrate the solution procedure and the results, let us apply the proposed algorithm to solve the following numerical examples. The results can be found by applying the Mathematica 9.0.

Consider $A=\$ 260, a=120, c_1 =\$ 20, c_2 =\$ 30, c_3 =\$ 40, \alpha =0.02 \,\mathrm{unit}, \beta =4 \,\mathrm{unit}, \gamma =0.02 \,\mathrm{unit} \delta =4 \,\mathrm{units}, h=\$ 0.4, \eta =0.6 \,\mathrm{unit}$ and $\lambda =0.4 \,\mathrm{unit}$. Using propositions and algorithm, the optimum solution $T^*=1.02612\,\mathrm{year}, p^*=\$ 70.4367$. For these values of T and p, the second order derivative found to be $\frac{\partial ^{2}P(T^*,p^*)}{\partial T^{2}}=-2.00329<0$ and $\frac{\partial ^{2}P(T^*,p^*)}{\partial p^{2}}=-375082<0$. So the values of $T^*$ and $p^*$ are maximize the total average profit cost. Based on these input data, the computed outputs are $t_1 ^*=0.410448 \hbox {year }\, Q^*=46.3976 \,\mathrm{units}$ and $P(T^*,p^*)=\$ 2207.19.$

Graphical Proof for the Concavity of the Total Profit Function

If we plot the total cost function (9) with some values of p and T such that p is 40–100 and T is 1.01–1.03 then we get strictly concave graph of total cost function P(T, p) given by the Fig. 2. From Fig. 2, we observe that the optimal price and replenishment schedule uniquely exists and the total profit cost to the inventory system is a concave function. From Fig. 2, observed that the total cost function is a strictly concave function. Thus, the optimum values of T and p can be obtained with the help of the average net profit function of the model provided that the total profit per unit time of the inventory system is maximum.

Fig. 2

P(T, p) versus T and p

Sensitivity Analysis

In this section, the effects of studying the changes in the optimal value of total profit, cost per unit time and the optimal value of order quantity per cycle with respect to changes in parameters are discussed. Based on the example, the sensitivity analysis is performed by changing the value of each of the parameters by ${\pm } 25$ and ${\pm }\,50\,\%$, taking one parameter at a time and keeping the remaining parameters unchanged.

Table 2 Sensitivity analysis based on changes of parameters

Based on the results of Table 2, the following observations can be made (Figs. 3, 4).

• 1. $P(T^*,p^*)$ increases with increase in the values of model parameters $A, a, \alpha , \gamma , h$ and $\lambda$ while $P(T^*,p^*)$ decreases with increase in the value of $c_1 , c_2, c_3, \beta , \delta$ and $\eta$. $P(T^*,p^*)$is highly sensitive to changes in $A, a, c_2, c_3$ and $\lambda$. It is less sensitive to changes in $c_1, \eta$ and $\gamma$; and very less sensitive to change in $\alpha , \beta$ and $\delta$.

• 2. $P(T^*,p^*)$ decrease with decrease in the values of model parameters $A, a, \alpha , \gamma , h$ and $\lambda$ while $P(T^*,p^*)$ increase with decreases in the value of $c_1 , c_2, c_3, \beta , \delta$ and $\eta$. $P(T^*,p^*)$is highly sensitive to changes in $A, a, c_2, c_3$ and $\lambda$. It is less sensitive to changes in $c_1, \eta$ and $\gamma$; and very less sensitive to change in $\alpha , \beta$ and $\delta$.

Fig. 3

Behavior of optimal total profit cost

Fig. 4

Behavior of optimal ordering quantity

• 3. $Q^{^*}$ increases with increase in the values of model parameters $A, a, c_1, \alpha , \gamma$and $\lambda$ while $Q^{^*}$decreases with increase in the value of $c_2, c_3, \beta , \delta ,_{ }h$ and $\eta$. $Q^{^*}$ is highly sensitive to changes in $A, a, c_1, c_2, c_3, \eta$ and $\lambda$. It is less sensitive to changes in $h, \delta$ and $\gamma$; and very less sensitive to change in $\alpha$, and $\beta$.

• 4. $Q^{^*}$ decrease with decrease in the values of model parameters $A, a, c_1, \alpha , \gamma$ and $\lambda$ while $Q^{^*}$ increase with decreases in the value of $c_2, c_3, \beta , \delta$ ,$_{ }h$ and $\eta$.$Q^{^*}$ is highly sensitive to changes in $A, a, c_1, c_2, c_3, \eta$ and $\lambda$. It is less sensitive to changes in $h, \delta$ and $\gamma$; and very less sensitive to change in $\alpha$ and $\beta$.

Based on Sensitivity Analysis Results, We Can Obtain the Following Managerial Phenomena

• (a) When the value of parameters $A, c_2$ and $c_3$ increase; the optimal length of time in which there is no inventory shortage will increase while it decreases as the values of parameters h increase. From an economic viewpoint, this means that the retailer will avoid shortages when the order cost, shortage cost, and cost of lost sales are high.

• (b) When the values of parameters A and $\lambda$ increases; the optimal total profit per unit time $P(T^*,p^*)$ will increases. This implies that decreases p and the deterioration rate have a negative effect on the total profit per unit time.

Conclusion

In the above study an inventory model has been proposed in which demand rate as a function of stock level and selling price where the deterioration rate has been considered to follows two parameter Weibull deterioration. The model has been applied to optimize the total profit for the business enterprises where demand is stock and price dependent and shortages are partially backlogged. The model is solved by both mathematically and graphically by maximizes the profit. The outcome shows that a higher value of the deterioration rate causes the lower value of order quantity and lower value of inventory cost. The model can be applied to optimize the total inventory cost for the business enterprises, chemical industries where demand is stock and time dependent and shortages are partially backlogged as the proposed deterministic inventory model has been developed for perishable items with stock and time dependent demand where shortages are partially backlogged. Finally, the proposed model has been verified by the numerical and graphical analysis. This model can further be extended by taking more realistic assumptions, such as probabilistic demand rate, other functions of holding costs, non-zero lead time, etc. Also we may consider the permissible delay in payment or promotions in the model. Finally, we could extend the deterministic demand function to stochastic demand function.