An Improved FMEA Method Based on ANP with Probabilistic Linguistic Term Sets

Abstract

Failure modes and effects analysis (FMEA), as a practical and easy-to-use reliability assessment tool, has been widely applied across various fields of researches. At the same time, it also receives criticisms for its limited selection of risk factors as well as its discrete numerical ordinal scales. In an attempt to fill in this gap, this paper proposes an improved FMEA method based on analytic network process (ANP) with probabilistic linguistic term sets (PLTSs). Firstly, the three risk factors of FMEA, namely occurrence, severity and detection, are broken down to more elaborate and specific sub-factors, and a network representing the influential relationship between these sub-factors is constructed. ANP is then utilized to derive the relative weights of factors, sub-factors and failure modes by making pairwise comparisons with the help of PLTS. To verify the rationality and applicability of our proposed method, a case study of hospital information system reliability assessment is carried out. Comparative analyses with other existing FMEA methods are also undertaken to highlight the differences and advantages of our proposed method.

1 Introduction

Failure modes and effects analysis, FMEA [1,2,3] is the process of systematically identifying and reviewing all potential failure modes in a given system and their resultant effects on system operations. It is first introduced by the US military to serve as a reliability assessment tool to determine the effect of equipment failures in 1949 [4]. Then in the 1960s, the United States National Aeronautics and Space Administration (NASA) adopts the FMEA method in a series of programs including Apollo, Voyager, Galileo and etc. to ensure the desired reliability of space systems [5]. Due to its effectiveness and easy implementation, FMEA has been widely utilized in many different industries, such as aerospace [6, 7], nuclear power [8,9,10], automotive [11,12,13], medical [14,15,16,17], wind turbines [18], information security [2, 19, 20], etc.

The aim of FMEA is to guarantee that the potential failure modes that may threat the system’s normal functioning are well-addressed. To analyze the risk associated with such failure modes, the risk prioritization number (RPN) methodology is adopted in FMEA. Each failure mode is evaluated with respect to its “probability of occurrence ($O$)”, “severity ($S$)” and “likelihood of detection ($D$)”, each assessed with a discrete numerical scale of 1 to 10. The ratings of these three risk factors are multiplicated to obtain the RPN, i.e., ${\text{RPN}} = O \times S \times D$. The failure modes with higher RPNs are regarded to be more urgent and thus needing more immediate remedial action.

Despite its wide application, there still exists some criticisms of the classical FMEA method [4]. One of the shortcomings of FMEA is that it only considers three risk factors ($O$, $S$ and $D$). However, the concepts of these three factors are broad and vague, often varying considerably according to the context and application. For instance, one failure mode of the transportation system may lead to the delay of cargo’s delivery, while another failure mode of the same transportation system may result in personnel injuries. It is very hard, if not entirely impossible, to rate the time losses and human casualties uniformly under the risk factor severity.

Another disadvantage of classical FMEA method is that the risk factors’ relative weights are neglected. In other words, the equal importance of three risk factors translates to equal weight in the determination of RPN. Consequently, the same RPN may correspond to different combination of ratings on $O$, $S$, and $D$. This may cause the problem of indistinguishability that the failure mode with higher occurrence probability and lower severity is assigned the same RPN with the failure mode with lower probability of occurrence and higher severity.

Last but not least, the classical FMEA method is also criticized for its rating scale. Generally speaking, the ratings of risk factors are conducted with a discrete numerical scale of 1 to 10. For starter, this numerical scale of 1 to 10 is, in its essence, ordinal. Which is to say, the physical meanings of intervals between different consecutive ratings are not uniform. Besides, a change in the ratings of risk factors can cause significant change in the overall RPN, seeing that the multiplication operation is very sensitive to variation. What’s more, in practice, the rating of risk factors is inherently a human cognitive process, because it is conducted by experts and/or stakeholders whose opinion expression is bound to contain information uncertainty. It is very difficult to directly give an exact numerical evaluation on intangible factors such as $O$, $S$, and $D$, especially so under the circumstance that the definition and implication of these factors are vague and unclear.

Based on the above considerations, this paper proposes an improved FMEA method based on analytic network process, ANP [21,22,23,24] with probabilistic linguistic term sets, PLTSs [25] information. The three risk factors $O$, $S$, and $D$ are all broken down to more specific and precise sub-factors, and a network structure is constructed to represent the influential relationship between these sub-factors. Then ANP is taken advantage of to derive the relative weights of three main factors and failure modes by making pairwise comparisons. PLTS is made use of to facilitate the comparison process, where the expert can appoint a probability distribution over all possible comparison outcomes that he/she feels appropriate. A super-matrix is constructed and raised to very large powers to acquire the stable long-term weighting vector of sub-factors. Finally, RPN is calculated based on the relative weights obtained before, and failure modes can be prioritized accordingly.

The main contribution of our proposed method is three-fold:

• (1) The risk factors Occurrence, Severity and Detection are broken down to sub-factors, to accommodate the needs of practical applications, the relative weights of which are derived via ANP with full consideration of their influential relationships.

• (2) The PLTS is integrated into our proposed model to facilitate the pairwise comparisons between risk factors, sub-factors and failure modes, providing the necessary tools for the experts to express their uncertainty.

• (3) A case study of risk assessment for hospital information systems (HISs) is undertaken to verify the applicability. Comparative analysis with existing approaches also demonstrates the robustness of our proposed method.

The rest of this paper is organized as follows: Sect. 2 reviews some related works and latest developments of FMEA methods; in Sect. 3, some preliminaries of PLTS and the detailed calculation process of the proposed ANP-FMEA method is described; a case study of HIS reliability assessment is conducted in Sect. 4 to demonstrate the applicability of our proposed method; comparative analyses and experiments with other existing FMEA methods are carried out in Sect. 5; and finally, Sect. 6 marks the end of this paper with some concluding remarks.

2 Related Works

The traditional FMEA procedure can roughly be categorized into five steps [26]: (1) failure modes identification; (2) rating of risk factors; (3) total RPN calculation; (4) critical failure mode identification; and (5) corrective or prevention action. As mentioned before, the criticisms of classical FMEA methods are mainly directed to the second and third steps, where only three risk factors are being considered, the rating is performed with a numerical scale of 1 to 10, and equal weights are assigned to all the risk factors. Therefore, in this section, the related works of FMEA methods are briefly reviewed in three aspects: risk factor selection, weight determination, and information uncertainty.

To be more comprehensive, many researchers have proposed to take other risk factors into consideration as an improvement on classical FMEA method. Lo and Liou [27] integrated the expected cost of prevention actions as another risk factor to be evaluated in the FMEA procedure, and the weights of these risk factors are calculated via best–worst method (BWM) and RPN is obtained through Grey relation analysis (GRA). Similarly, in [28], Huai-Wei Lo et al. proposed to consider both the expected cost and the environmental awareness as risk factors. In the evaluation of agricultural risk management, Zandi et al. [29] broke down the risk factor severity to sub-factors, namely cost severity, time severity and quality of the project severity. Then the authors adopted fuzzy technique for order preference by similarity to an ideal solution (TOPSIS) and fuzzy analytic hierarchy process (AHP) to derive the weights associated with these risk factors. For oil and gas projects, in addition to three main risk factors $O$, $S$, and $D$, Khalilzadeh et al. [30] identified response time, cost and quality of remedy action to failures as risk factors. In [31], Kumar Dadsena et al. proposed to include the reduction of risk by implementing mitigation strategy as another risk factor.

Seeing that there are multiple factors that can impact the ranking of failure modes, and that treating all the risk factors with equal importance is unrealistic, a great deal of researches have undertaken the multi-criteria decision-making (MCDM) approaches to the weight determination problem in FMEA procedure. In [32], Kiani Aslani Reza et al. developed a mathematical model to determine the optimal weights of the three main risk factors based on AHP technique, and applied it to a real-world case study of alternator failure causes. Li et al. [33] integrated the fuzzy Petri nets with PLTS for the prioritization of failure modes in a marine-ship system. Kutlu and Ekmekçioğlu [34] combined the fuzzy TOPSIS and fuzzy AHP to assign weights to the risk factors based on expert judgements. For ship navigation safety, Başhan et al. [35] proposed a FMEA-based TOPSIS method under single-valued neutrosophic sets. Mete [36] incorporated the AHP–MOORA method under Pythagorean fuzzy environment into FMEA, and evaluated the occupational risks in a natural gas pipeline construction project. Huang et al. [37] devised a new FMEA model where TOPSIS was utilized to determine the relative weights of risk factors, and TODIM (an acronym in Portuguese for interactive MCDM) was used to obtain the priority ranking of failure modes. In [38], Yazdi M. utilized both the fuzzy AHP and entropy technique to derive the subjective and objective weights of the risk factors, and applied this method to the risk assessment of a gas refinery. To reflect the conditionality between failure modes, Yucesan et al. [39] proposed to derive the probability of failure occurrence with fuzzy Bayesian network, and BWM is used to weight the risk factors. Fattahi and Khalilzadeh [40] extended the fuzzy multiple multi-objective optimization by ratio analysis (MULTIMOORA) to compute the weights of failure modes, along with the weights of risk factors acquired through fuzzy AHP, a fuzzy weighted RPN is proposed.

To handle the uncertainty of experts’ evaluations, various types of fuzzy sets are taken advantage of. Liu et al. [41] proposed to use intuitionistic fuzzy hybrid Euclidean distance operator for the failure modes’ prioritization. Bhattacharjee et al. [42] transformed the FMEA process into a logistic regression model, where the risk factors are evaluated with interval numbers. In [43], Abdelgawad M. and A. R. Fayek utilized linguistic fuzzy sets with corresponding triangular fuzzy numbers (TFN) to overcome the limitation of classical FMEA method. Sayyadi Tooranloo and Saghafi [44] extended the FMEA method to the interval-valued intuitionistic fuzzy environment, and evaluated the failure causes of health information system implementation. In [45], Qin J. et al. combined the interval type-2 fuzzy sets with evidential reasoning to provide a more precise assessment of risk factors, and to gain their relative weights. Li et al. [46] presented an advanced FMEA method based on interval 2-tuple linguistic variables and TOPSIS method. Ko [47] exploited the 2-tuple linguistic representational model for the house of quality-based FMEA method. Chang et al. [48] integrates the ordered weighted geometric operator with hesitant fuzzy linguistic term sets (LTSs) to increase the effectiveness of soft FMEA.

The recent developments of FMEA methods mentioned above and their differences are summarized in Table 1. It is worthwhile to point out there are still some limitations to these existing approaches.

Table 1 Recent developments of FMEA methods compared to our proposed method

For one thing, in most literature, only the risk factor severity is broken down to more elaborate and specific sub-factors, while the factors occurrence and detection remain the same as in the classical FMEA. This hardly fits the demands of practical applications. For example, in the hospital service evaluation in [49], Huang Jia broke down the risk factor of occurrence into two sub-factors, frequency and repeatability. As for the risk factor of detection, it was also broken down to two sub-factors, chance of non-detection and difficulty of proactive inspection. It is reasonable to believe that FMEA woulds benefit a lot more if all three of the risk factors can be broken down and evaluated at a finer granularity.

For another, in the existing approaches, the influential relationship between sub-factors is also overlooked. Here we would like to argue that there are two types of dependence in the sub-factors of FMEA. One is the intra-dependence between the sub-factors within the same category. For instance, in the category of severity, environmental damage may lead to reputation damage, information loss may lead to financial loss; while in the category of detection, there is a trade-off relationship between false alarm and miss rate, the improvement of one index will inevitably lead to the deterioration of the other. The other is the outer-dependence between the sub-factors in different categories. For example, for failure modes causing information or time losses, a certain degree of miss rate or delay of detection is somewhat acceptable; but for failure mode that may lead to personnel casualties, the timeliness of detection is critical and a high degree of false alarm may be desired because otherwise the unfortunate outcome is unbearable. Failing to take these dependence relationships into consideration may result in unsatisfactory weight assignment to sub-factors, which is essential to the determination of the final RPNs.

Moreover, to help experts to express their evaluation results, the existing approaches mostly utilizes different types of fuzzy number, including the TFN, trapezoidal fuzzy number, intuitionistic fuzzy number and so on. But seeing that the experts’ evaluation is inherently a process of human thinking, it is more natural to use linguistic terms rather than numerical values like the one adopted in [46,47,48]. On top of that, in practical applications the experts’ opinion expression may come with a certain degree of hesitancy, thus it is preferable that the experts express their assessment results with a probability degree rather than settling on one certain value.

In an attempt to fill in this gap, this paper proposes an improved FMEA method based on ANP with PLTS, the details of which are described in the next section.

3 ANP-FMEA Method with PLTS

3.1 Preliminaries of PLTS

First, some preliminary concepts, notations and operators of PLTS are introduced. The concept of linguistic variable is first introduced by Zadeh [50] in 1975 to model the linguistic expressions verbalized by decision makers. Up till now, it has been developed and adopted by many researchers in various fields. Among them, the most widely used is the additive LTS [51], the formal definition of which is as follows:

$$T = \{ t_{\alpha } |\alpha = 0,\;1, \ldots ,\tau \} ,$$

(1)

where $t_{\alpha }$ denotes a possible value for linguistic variable, and $\tau$ is a positive integer. The LTS has the following property and operators:

• (1) The set is order: $t_{\alpha } > t_{\beta }$, if $\alpha < \beta$;

• (2) The negation operator is defined: ${\text{neg}}(t_{\alpha } ) = t_{\beta }$ s.t. $\alpha + \beta = \tau$;

• (3) The maximum operator is defined: $\max (t_{\alpha } ,\;t_{\beta } ) = t_{\alpha }$, if $t_{\alpha } > t_{\beta }$;

• (4) The minimum operator is defined: $\min (t_{\alpha } ,\;t_{\beta } ) = t_{\alpha }$, if $t_{\alpha } < t_{\beta }$.

Furthermore, for the convenience of calculation, in [52] Xu extended the discrete LTS to a continuous variation $\overline{T} = \{ t_{\alpha } |\alpha \in [0,\;\tau ]\}$.

Similar to hesitant fuzzy set, which is a generalization on classical fuzzy set, in [53] Rdoriguez et al. proposed to generalize LTS to hesitant LTS (HLTS), to accommodate the situation where decision makers may hesitate between several possible values for linguistic variable.

Definition 1

[53] Let $T = \{ t_{\alpha } |\alpha = 0,\;1, \ldots ,\tau \}$ be a LTS, then a HLTS $b_{T}$ is an ordered finite subset of consecutive linguistic terms of $T.$

However, there are several underlying assumptions in HLTS that hampers its potential application. For one thing, by definition, the linguistic terms in HLTS must be consecutive in order, which may limit the free expression of decision makers. For another thing, in HLTS all possible values provided by decision makers are assumed to have equal importance or weight, which is not in accordance to real-life scenarios. In light of this, to better model the uncertainty in linguistic decision-making problems, in [25] Pang et al. further extended HLTS and proposed the concept of PLTS, which is defined as follows.

Definition 2

[25] Let $T = \{ t_{\alpha } |\alpha = 0,\;1, \ldots ,\tau \}$ be a LTS, a PLTS $L(p)$ is defined as:

$$L(p) = \left\{ {L^{(k)} (p^{(k)} )|L^{(k)} \in T,\;p^{(k)} \ge 0,\;k = 1,\;2, \ldots ,\# L(p),\;\sum\limits_{k = 1}^{\# L(p)} {p^{(k)} \le 1} } \right\},$$

(2)

where $L^{(k)} (p^{(k)} )$ is the linguistic term $L^{(k)}$ associated with probability $p^{(k)}$, and $\# L(p)$ is the number of all different linguistic terms in $L(p)$.

From the definition, it is easy to see that HLTS can be regarded as a special type of PLTS consecutive linguistic terms and equal probabilities divided among them. Also note that the definition of PLTS only requires the sum of probabilities associated with linguistic terms is not greater than 1, i.e., $\sum\nolimits_{k = 1}^{\# L(p)} {p^{(k)} } \le 1$. When $\sum\nolimits_{k = 1}^{\# L(p)} {p^{(k)} } = 1$, it means that we have complete information regarding the probabilistic distribution of all probable linguistic terms; and when $\sum\nolimits_{k = 1}^{\# L(p)} {p^{(k)} } < 1$, it represents the partial ignorance situation where the information currently available for the decision maker is not sufficient for him/her to provide a complete evaluation result, which is not rare in decision-making problems.

Finally, to facilitate the calculation of principal eigenvectors in ANP, here we introduce the defuzzification function that can transform the PLTS to numerical scales.

Definition 3

[54] Let $L(p) = \{ L^{(k)} (p^{(k)} )|k = 1,\;2, \ldots ,\# L(p)\}$ be a PLTS, suppose $v^{(k)}$ is the subscript of linguistic term $L^{(k)}$, then the numerical score of $L(p)$ is defined as:

$$g\left( {L(p)} \right) = {{\sum\limits_{k = 1}^{\# L(p)} {v^{(k)} p^{(k)} } } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{\# L(p)} {v^{(k)} p^{(k)} } } {\sum\limits_{k = 1}^{\# L(p)} {p^{(k)} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{k = 1}^{\# L(p)} {p^{(k)} } }}.$$

(3)

Admittedly, there are a number of fuzzy sets in various forms. In this paper, PLTS is chosen mainly for the following reasons. On one hand, in FMEA procedure, the rating of risk factors is usually conducted by a group of stakeholders and/or experts in relative fields, based on their professional opinions. In this process, LTSs can better facilitate the expression of their judgements. Because for other type of fuzzy sets such as TFN, trapezoidal fuzzy number or intuitionistic fuzzy number, the experts usually need to convert their practical assessments to various types of fuzzy numbers based on a set of pre-determined rules. For experts who are not previously familiar with the fuzzy set theory, this conversion may be troublesome. On the other hand, compare to the HLTS, the unnecessary assumptions of consecutive linguistic terms and equal weights divided among them are lifted. This way, PLTS can provide the experts with more room to express their assessments, by associating the LTS with a probability distribution. Next, an illustrative example is given to demonstrate the calculation of PLTS’s numerical score.

Example 1

Let $T$ be a LTS with following linguistic terms:

$$T = \left\{ \begin{gathered} t_{0} = {\text{extremely}}\;{\kern 1pt} {\text{low}},\;t_{1} = {\text{low}},\;t_{2} = {\text{slightly}}\;{\text{low}},\;t_{3} = {\text{fair}}, \hfill \\ t_{4} = {\text{slightly}}\;{\kern 1pt} {\text{high}},\;t_{5} = {\text{high}},\;t_{6} = {\text{extremely}}\;{\text{high}} \hfill \\ \end{gathered} \right\}.$$

Suppose a client is invited to review the hospitality of the reception, then a PLTS $L(p) = \{ t_{4} (0.3),\;t_{5} (0.5)\}$ means that this client is 30% sure that the receptionist’s hospitality is “slightly high”, and 50% sure that the receptionist’s hospitality is “high”. Then via Eq. (3), the PLTS can be transformed into a numerical scale: $g(L(p)) = (5 \times 0.3 + 6 \times 0.5)/(0.3 + 0.5) = 5.625$.

3.2 Proposed Method

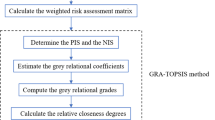
In this subsection, the ANP-FMEA method with PLTS information is proposed. Suppose $Z$ experts denoted as $e_{z} (z = 1:Z)$ are gathered together to prioritize several potential failure modes of a certain system. After careful consideration and evaluation, the experts are able to identify $M$ failure modes ${\text{FM}}_{m} \;(m = 1:M)$ that may have serious impact on system performance. Under the guidance of FMEA, the experts are supposed to evaluate each and every failure mode according to three main risk factors, namely “Occurrence ($O$)”, “Severity ($S$)”, and “Detection ($D$)”. As depicted in Fig. 1, the calculating process of ANP-FMEA is summarized below.

Fig. 1

The computation process of ANP-FMEA method with PLTS

Step 1::

Sub-factors selection and network construction. Experts collectively select appropriate sub-factors under the category of Occurrence, Severity, and Detection, and construct the network structure of sub-factors.

Step 2::

Individual evaluation.

Step 2.1::

Experts make pairwise comparisons of risk factors Occurrence, Severity, and Detection, and obtain the corresponding weighting vector;

Step 2.2::

Experts make pairwise comparisons of the importance of the same category’s sub-factors, and obtain the corresponding normalized principal eigenvector;

Step 2.3::

Experts construct the super-matrix by making pairwise comparisons of the influences of sub-factors on each other, and calculating the normalized principal eigenvector. Then the stable long-term weighting vector is obtained by raising the super-matrix to large powers;

Step 2.4::

Experts make pairwise comparisons of different failure modes under each sub-factor, and obtain the individual weighting vector of failure modes;

Step 2.5::

Experts obtain the RPN of different failure modes;

Step 3::

Group aggregation. The group opinion is derived via the weighted average operator on the basis of the individual evaluation results, and the failure modes are prioritized accordingly.

The computation procedures are detailed as follows.

Step 1: Sub-factors selection and network construction.

To better reflect the failure modes’ adverse effects on system performance, several sub-factors under the category Occurrence $O$, Severity $S$, and Detection $D$ are selected appropriately according to the specific application scenario, which can be denoted as $O_{i} \;(i = 1:h_{O} )$, $S_{i} \;(i = 1:h_{S} )$, and $D_{i} \;(i = 1:h_{D} )$ respectively. Then experts need to construct the network structure that can properly reflect the dependence between the sub-factors like depicted in Fig. 2.

Fig. 2

The network structure of ANP-FMEA

Step 2: Individual evaluation.

In step 2, each expert evaluates the effects of potential failure modes individually, the results of which are later aggregated into a collective group assessment result in Step 3. For brevity, in Step 2 the subscript $z$ of $e_{z} \;(z = 1:Z)$ is left out. It is assumed that all the calculation processes are carried out for each expert $e_{z} \;(z = 1:Z)$.

Step 2.1: Comparison of the importance of three main risk factors. Each expert makes pairwise comparisons regarding the importance of risk factors Occurrence $O$, Severity $S$ and Detection $D$, and verbalize his/her comparison results $A$ with the help of PLTS:

(4)

where $L_{ij} (p) = \{ L_{ij}^{(k)} (p_{ij}^{(k)} )|L_{ij}^{(k)} \in T,\;p_{ij}^{(k)} \ge 0,\;k = 1,\;2, \ldots ,\# L_{ij} (p),\;\sum\nolimits_{k = 1}^{{\# L_{ij} (p)}} {p_{ij}^{(k)} \le 1} \}$. Note that entry $L_{ij} (p)$ represents the result of comparing the $i$th risk factor to the $j$th risk factor, whereas the entry $L_{ji} (p)$ stands for the result of comparing the $j$th risk factor to the $i$th risk factor. By definition, between these two entries that are symmetric with respect to the diagonal of the comparison matrix, there should exist a reciprocal relationship:

$$L_{ji} (p) = \overline{{L_{ij} (p)}} = \left\{ {\overline{{L_{ij}^{(k)} }} (p_{ij}^{(k)} )|\overline{{L_{ij}^{(k)} }} = {\text{neg}}(L_{ij}^{(k)} )} \right\}.$$

(5)

Also note that the entries on the diagonal of the comparison matrix, $L_{ii} (p)$, represents the pairwise comparison result of one factor to itself. Therefore, we always have $L_{ii} (p) = \{ t_{\# L(P)/2} (1)\}$, which stands for absolute equality.

Besides the above two properties, consistency is another desirable characteristic of the comparison matrix. It is stemmed from the idea that if the $i$th risk factor is preferred over the $r$th risk factor, and $r$th risk factor outweighs the $j$th risk factor during their pairwise comparison, then it is only natural the expert would favor the $i$th risk factor over the $j$th risk factor. Following this intuition, next we give the formal definition of consistency level for PLTS comparison matrix.

Definition 4

[54] Assume that $A = [L_{ij} (p)]_{n \times n}$ and $G(A) = \left[ {g(L_{ij} (p))} \right]_{n \times n}$ are a comparison matrix with PLTS entries and its defuzzied form via Eq. (3). The consistent preference of the $i$th element over the $j$th element through the $r$th element is defined as:

$${\text{CL}}_{ij}^{r} = g(L_{ir} (p)) + g(L_{rj} (p)) - \# L(P)/2,\quad \forall i,\,j,\;r = 1:n.$$

(6)

Then the consistency level of $A$ is defined as:

$${\text{Consistency}}\;(G(A)) = \frac{{\Sigma_{i \ne j} {\text{DL}}_{ij} }}{{n^{2} - n}},$$

(7)

where

$${\text{DL}}_{ij} = \frac{{\Sigma_{r \ne i,j} |G(L_{ij} ) - {\text{CL}}_{ij}^{r} |}}{n - 2}\quad (\forall i,\;j = 1:n).$$

(8)

From the definition, it can be seen that the more consistent the comparison matrix, the smaller the consistency level. $A$ is said to be completely consistent if ${\text{Consistency}}\;(G(A)) = 0$.

Like depicted in Fig. 1, after experts provide the pairwise comparison matrix, a consistency check must be performed where the experts are advised to revise their evaluation results if the consistency level exceeds a certain threshold $\gamma$. This consistency check procedure is carried out for every comparison matrix provided by the experts. In the subsequent processes, the consistency checks are left out for brevity, and all comparison matrices are assumed to have passed the consistency test.

Then the comparison matrix $A$ is defuzzied via Eq. (3), and the normalized principal eigenvector of $G(A)$ is taken as the weighting vector of three main risk factors $w = (w^{O} ,\;w^{S} ,\;w^{D} )^{{\text{T}}}$.

Step 2.2: Comparison of the importance of sub-factors. Under each risk factor, $O$, $S$ or $D$, pairwise comparisons of sub-factors are performed by each expert to determine their importance in their respective categories. For instance, in the category of main risk factor Severity $S$, each expert provides the comparison results of sub-factors $S_{i} \;(i = 1:h_{S} )$ in the form of PLTS, and the consequent comparison matrix takes the form:

(9)

Similarly, $A^{S}$ is also defuzzied via function $G$ in Eq. (3), then the normalized principal eigenvector of $G(A^{S} )$ is calculated and denoted as $\omega^{S} = (\omega_{1}^{S} ,\;\omega_{2}^{S} , \ldots ,\omega_{{h_{S} }}^{S} )^{{\text{T}}}$. Identical calculations are also carried out for main risk factors $O$ and $D$, $\omega^{O}$ and $\omega^{D}$ are obtained accordingly.

Step 2.3: Comparison of the influence of sub-factors. Next the experts evaluate the influences of elements in the network on other elements by means of pairwise comparison, the result of which can be expressed as a super-matrix:

$$Q = \left[ {\begin{array}{*{20}c} {Q_{O}^{O} } & {Q_{O}^{S} } & {Q_{O}^{D} } \\ {Q_{S}^{O} } & {Q_{S}^{S} } & {Q_{S}^{D} } \\ {Q_{D}^{O} } & {Q_{D}^{S} } & {Q_{D}^{D} } \\ \end{array} } \right],$$

(10)

where a typical entry of the super-matrix, called a block of super-matrix, is also a matrix of the form:

$$Q_{O}^{O} = \left[ {\begin{array}{*{20}c} {\dot{\omega }_{O1}^{O1} } & {\dot{\omega }_{O1}^{O2} } & \cdots & {\dot{\omega }_{O1}^{{Oh_{O} }} } \\ {\dot{\omega }_{O2}^{O1} } & {\dot{\omega }_{O2}^{O2} } & \cdots & {\dot{\omega }_{O2}^{{Oh_{O} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {\dot{\omega }_{{Oh_{O} }}^{O1} } & {\dot{\omega }_{{Oh_{O} }}^{O2} } & \cdots & {\dot{\omega }_{{Oh_{O} }}^{{Oh_{O} }} } \\ \end{array} } \right].$$

(11)

Here each column of $Q_{O}^{O}$ is a normalized principal eigenvector representing the relative influences of the sub-factors in the category of Occurrence on one certain sub-factor in the same category. Which is to say, $\forall i = 1:h_{O}$, the expert makes pairwise comparisons of sub-factors $O_{j} \;(j = 1:h_{O} )$ regarding their influences on sub-factors $O_{i}$, the resulting comparison matrix is:

(12)

Then via the calculation of the normalized principal eigenvector of $G(A^{{O_{i} }} )$, the $i$th column in the block $(\dot{\omega }_{O1}^{Oi} ,\dot{\omega }_{O2}^{Oi} ,...,\dot{\omega }_{{Oh_{O} }}^{Oi} )^{T}$ is obtained. Similar computation procedures are also carried out to obtain the other blocks in the super-matrix. The final super-matrix should take the form of:

(13)

It is worthy to point out that since the primary purpose of the super-matrix is to describe the influence relationship between the elements in the network, if some sub-factor is determined to have zero influence on some other sub-factor, i.e., there is no link between these sub-factors in the network structure constructed in Step 1, then the pairwise comparison can be omitted for these sub-factors to simplify the computation process. In other words, the experts only need to perform comparison on sub-factors that have been previously identified as having potential non-zero influences on some other sub-factors.

Then the super-matrix $Q$ is raised to very large powers to obtain a long-term stable set of weights. Which is to say, a positive integer $c$ is found so that $||Q^{c} - Q^{c - 1} ||_{2} \le \varepsilon$, then the column vector of $Q^{c}$ is taken as the long-term stable weight vector of sub-factors, denoted as $\ddot{\omega } = (\ddot{\omega }_{1}^{O} , \ldots ,\ddot{\omega }_{{h_{O} }}^{O} ,\;\ddot{\omega }_{1}^{S} , \ldots ,\ddot{\omega }_{{h_{S} }}^{S} ,\;\ddot{\omega }_{1}^{D} , \ldots ,\ddot{\omega }_{{h_{D} }}^{D} )^{{\text{T}}}$.

Step 2.4: Comparison of failure modes. In this step, the failure modes ${\text{FM}}_{m} \;(m = 1:M)$ are evaluated under each sub-factor. For instance, under sub-factors $O_{i} \;(i = 1:h_{O} )$, the experts express their assessment results with PLTS in the comparison matrix:

(14)

Then via defuzzification and normalized principal eigenvector calculation, the weight of failure modes ${\text{FM}}_{m} \;(m = 1:M)$ with respect to sub-factors $O_{i} \;(i = 1:h_{O} )$ is obtained as $\varpi^{{O_{i} }} = (\varpi_{1}^{{O_{i} }} ,\;\varpi_{2}^{{O_{i} }} , \ldots ,\varpi_{M}^{{O_{i} }} )^{{\text{T}}}$. Similar results are also derived for other sub-factors $S_{i} \;(i = 1:h_{S} )$ and $D_{i} \;(i = 1:h_{D} )$.

Step 2.5: Calculation of RPN. Now with the weighting vectors obtained in the previous steps, the RPN of each failure mode ${\text{FM}}_{m} \;(m = 1:M)$ can be defined as:

$${\text{RPN}}_{m} = w^{O} \sum\limits_{i = 1}^{{h_{O} }} {\omega_{i}^{O} \ddot{\omega }_{i}^{O} \varpi_{m}^{{O_{i} }} } + w^{S} \sum\limits_{i = 1}^{{h_{S} }} {\omega_{i}^{S} \ddot{\omega }_{i}^{S} \varpi_{m}^{{S_{i} }} } + w^{D} \sum\limits_{i = 1}^{{h_{D} }} {\omega_{i}^{D} \ddot{\omega }_{i}^{D} \varpi_{m}^{{D_{i} }} } ,$$

(15)

where $w^{O}$, $w^{S}$, and $w^{D}$ are the importance weights of the three main risk factors; $\omega_{i}^{O}$, $\omega_{i}^{S}$, and $\omega_{i}^{D}$ are the respective importance weights of the sub-factors under the category Occurrence, Severity, and Detection; $\ddot{\omega }_{i}^{O}$, $\ddot{\omega }_{i}^{S}$, and $\ddot{\omega }_{i}^{D}$ are the sub-factors’ weights of influence on other sub-factors in the network; $\varpi_{m}^{{O_{i} }}$, $\varpi_{m}^{{S_{i} }}$, and $\varpi_{m}^{{D_{i} }}$ are the failure mode ${\text{FM}}_{m}$’s relative weights with respect to sub-factors $O_{i}$, $S_{i}$, and $D_{i}$.

Step 3: Group aggregation.

As indicated before, identical computation procedures in Step 2 are carried out for all experts involved in the risk prioritization task. Suppose under the evaluation of expert $e_{z} \;(z = 1:Z)$ the RPN of each failure mode ${\text{FM}}_{m} \;(m = 1:M)$ is denoted as ${\text{RPN}}_{m}^{z}$, and the weighting vector that reflects the experts’ credibility and trustworthiness is $\eta = (\eta_{1} ,\;\eta_{2} , \ldots ,\eta_{Z} )^{{\text{T}}}$. Then the individual evaluation results of each expert $e_{z} \;(z = 1:Z)$ are aggregated into a group collective assessment via the weighted average operator:

$${\text{RPN}}_{m}^{C} = {\text{WA}}(\eta_{1} ,\;{\text{RPN}}_{m}^{1} , \ldots ,\eta_{Z} ,\;{\text{RPN}}_{m}^{Z} ) = \sum\limits_{z = 1}^{Z} {\eta_{z} {\text{RPN}}_{m}^{z} } .$$

(16)

Then the failure modes can be ranked accordingly.

4 Case Study: Hospital Information System Reliability Analysis

4.1 Empirical Experiment

This study case is adapted from [49] and [55]. HIS [56,57,58,59] is a customized information system specifically designed to satisfy the needs of patients, physicians, nurses and other parties in a hospital, by collecting, recording, storing, managing and transmitting information about medical history of individual patients and treatment activities of medical staffs [44]. HIS can help to reduce medical errors, boost treatment efficiency, support timely decisions, and improve the overall health service qualities. In a word, the reliability of HIS is crucial to normal functioning of hospital and the well-beings of its patients. And in this section, our proposed method is applied to evaluate the reliability of one HIS.

Five experts, denoted as $e_{z} \;(z = 1:5)$, are consulted to evaluate the reliability of HIS according to their expertise. This expert committee includes two experts in safety engineering who has been working as risk auditors of information systems for more than 5 years, one practicing physician with more than 10 years of experiences, one senior management representative of the hospital, and one consultant as well as trainer for HIS. After conducting several interviews and a series of questionnaires in the preliminary assessment, as enlisted in Table 2, 14 potential failure modes are identified from 4 dimensions: database, network, software and hardware. Next the experts are guided to evaluate the reliability of the HIS via the ANP-FMEA method proposed in this paper, the specific steps are detailed as follows.

Table 2 Potential failure modes in the HIS

Step 1: Sub-factors selection and network construction. Under the category of Occurrence, Severity and Detection, a total of 11 relevant sub-factors are identified as listed in Table 3. These sub-factors are selected through reviewing existing literature on HIS risk assessment and brainstorming by said five experts. In [55], the authors identified seven factors that may influence the HIS’s failure modes’ impacts, including growth rate, non-detectability degree, human casualties/losses, financial losses, time losses, reputation losses and environmental degradation, which corresponds to the sub-factors $O_{3}$, $S_{1}$ to $S_{5}$ and $D_{1}$ in Table 3. Then in [49], the author broke down the risk factor Occurrence to sub-factors frequency and repeatability, which are included in Table 3 as $O_{1}$ and $O_{2}$. On this basis, the expert team have added sub-factors “false alarm” and “timeliness” as $D_{2}$ and $D_{3}$ under the category of risk factor Detection in Table 3. Here, the sub-factor “false alarm” is selected because if only the non-detectability degree is considered, then in the extreme case, a HIS that automatically reports all events as failures would be considered “best” in the aspect of detection. However, a high degree of false alarm rate may cause work overload for the emergence response team, or divert valuable resources away from legitimate emergencies. As for the “timeliness” of detection, here we would like to argue that for safety–critical systems like HIS, the time between the occurrence and detection of its failure modes is crucial, because the sooner the failures are detected, the sooner can mitigation or remedy actions can be taken, and the less damage can be done. Therefore, this paper takes the non-detection degree, false alarm and timeliness all into consideration, offering a more comprehensive view on HIS risk assessment in the aspect of Detection. The network structure representing the dependence relations between these sub-factors is depicted in Fig. 3.

Table 3 Sub-factors in the HIS reliability assessment and the corresponding descriptions

Fig. 3

The network structure of sub-factors for HIS reliability assessment

It can be seen from Fig. 3, the sub-factors of category Occurrence, Severity and Detection are interdependent on other sub-factors in the same category. For example, in the category of Detection, there is a trade-off relationship between the sub-factors miss rate and the sub-factors false alarm; also, to achieve lower miss rate may require more sophisticated and comprehensive inspection, which would inevitably prolong the time needed for detection. It can also be seen from Fig. 3 that there exists a bi-directional influential relationship between the sub-factors of the category Severity and Detection. Naturally, on one hand, a timelier detection of failure modes may prevent the situation from escalating and mitigate the subsequent damages; on the other hand, the greater the damages, or the broader the affected range, the more easily can a failure mode be detected since it may disrupt the normal functioning of the hospital.

Step 2: Individual evaluations. Here we make an illustrative example of expert $e_{1}$, similar computations are also carried out for other experts $e_{z} \;(z = 2:5)$, but left out here for brevity.

Step 2.1: With the linguistic terms defined in Table 4, expert $e_{1}$ makes pairwise comparisons of risk factors Occurrence, Severity and Detection. Here the pairwise comparison aims to answer the question: “In the determination of failure modes’ risk priority number, which one of the pair is more important, and to what extent?”

Table 4 Linguistic terms for pairwise comparisons

The evaluation result of expert $e_{1}$ is listed in Table 5. The entry on the first row and second column $\{ t_{4} (0.3),\;t_{5} (0.6)\}$ represents that expert $e_{1}$ is 30% confident that risk factor Occurrence is “slightly less important” than risk factor Severity, and 60% sure that risk factor Occurrence is “equally important” than risk factor Severity. Note that every entry on the diagonal of the comparison matrix is $\{ t_{4} (1)\}$, which is the linguistic term for “equally important”, because naturally the comparison of one risk factor to itself should yield equal result.

Table 5 Expert $e_{1}$’s pairwise comparison result of the three main risk factors

Let $\gamma = 0.1$, via Eqs. (6), (7) and (8), the consistency level of this comparison matrix is calculated as $0.075 < 0.1$, passing the consistency test. Thus, the calculation process carries on. The last row in Table 5 represents the normalized principal eigenvector of the defuzzied comparison matrix, which also serves as the weighting vector of risk factors Occurrence, Severity, and Detection.

Step 2.2: Next expert $e_{1}$ makes pairwise comparisons regarding the importance of the sub-factors in the same category. Take category Occurrence for instance, given any two sub-factors under the category of Occurrence, expert $e_{1}$ needs to answer the question: “In the determination of the failure modes’ occurrence, which one of the pair is more important, and to what extent?”.

The comparison matrix and the corresponding weighting vector are listed in Tables 6, 7, and 8 for Occurrence, Severity, and Detection respectively, with consistency level of $0.0499$, $0.0754$, and $0.0833$, all passing the consistency test.

Table 6 Expert $e_{1}$’s pairwise comparison result of sub-factors in the category of Occurrence

Table 7 Expert $e_{1}$’s pairwise comparison result of sub-factors in the category of Severity

Table 8 Expert $e_{1}$’s pairwise comparison result of sub-factors in the category of Detection

Step 2.3: According to the network structure constructed in Step 1, there exist interdependence relationships among the sub-factors in the same category, as well as bi-directional influential relationships between the sub-factors $S_{i} \;(i = 1:5)$ and $D_{i} \;(i = 1:3)$. Therefore, expert $e_{1}$ are instructed to make pairwise comparisons of the relative influences of these sub-factors.

Take the sub-factors of the category Occurrence as an example. Given a sub-factor $O_{i} \;(i = 1:3)$, expert $e_{1}$ needs to make pairwise comparisons between any two other sub-factors $O_{r}$ and $O_{j}$. The question that expert $e_{1}$ is supposed to answer is: “With respect to sub-factor $O_{i}$, which one of the pair $(O_{r} ,\;O_{j} )$ is more influential, and to what extent?” The resulting comparison results are listed in Tables 9, 10 and 11. Since the comparison matrices only have two elements, by definition the consistency level is 1.

Table 9 Expert $e_{1}$’s pairwise comparison result of sub-factors with respect to sub-factor $O_{1}$

Table 10 Expert $e_{1}$’s pairwise comparison result of sub-factors with respect to sub-factor $O_{2}$

Table 11 Expert $e_{1}$’s pairwise comparison result of sub-factors with respect to sub-factor $O_{3}$

Similar comparisons are also carried out for the other influential relationships in the network depicted in Fig. 3, but for the compactness of presentation, the results are left out for the time being.

On the basis of the computation results obtained, a super-matrix representing the influential relationships between all sub-factors can be constructed for expert $e_{1}$, as listed in Table 12. Setting $\varepsilon = 10e - 8$, we have $||Q^{43} - Q^{42} || < \varepsilon$. In other words, approximately, the super-matrix reaches convergence after raising it to the power $43$. The super-matrix after convergence is listed in Table 13, where each column can be viewed as the stable long-term weighting vector reflecting sub-factors’ influences in the network.

Table 12 The weighted original super-matrix before convergence

Table 13 The limit matrix after convergence

Step 2.4: Next expert $e_{1}$ makes pairwise comparisons of different failure modes with respect to each sub-factor. Take the sub-factor $O_{1}$ as an example, the question that expert $e_{1}$ is asked is: “Which one of the failure modes’ occurrences is more frequent?” For brevity, in Table 14 we only list the normalized principal eigenvector, and left out the comparison matrices.

Table 14 Expert $e_{1}$’s pairwise comparison result of failure modes with respect to different sub-factor

Step 2.5: With the weighting vector obtained in Steps 2.1–2.4, now the RPN of each failure mode can be calculated via Eq. (15). The normalized results are as shown in the first row of Table 15.

Table 15 The RPN of different failure modes under different experts’ evaluation and the final group assessment result

Step 3: Group aggregation. Up till now, the calculation process from Steps 2.1 to 2.5 are under the evaluations of expert $e_{1}$. The other 4 experts also undergo similar computation procedures, but the details are omitted, only the final RPN of different failure modes are listed in the second to fifth rows in Table 15.

Then, with the expert weights setting to be equal, i.e., $\eta = (1/5,\;1/5,\;1/5,\;1/5,\;1/5)^{{\text{T}}}$, the individual evaluations of these 5 experts are aggregated via the weighted average operator in Eq. (16), the result of which is shown in the second last row of Table 15. Now with the group collective ${\text{RPN}}_{m}^{C} \;(m = 1:14)$, the failure modes can be prioritized accordingly:

$\begin{gathered} {\text{FM}}_{14} \succ {\text{FM}}_{13} \succ {\text{FM}}_{1} \succ {\text{FM}}_{7} \succ {\text{FM}}_{4} \succ {\text{FM}}_{10} \succ {\text{FM}}_{6} \hfill \\ \succ {\text{FM}}_{11} \succ {\text{FM}}_{5} \succ {\text{FM}}_{12} \succ {\text{FM}}_{3} \succ {\text{FM}}_{8} \succ {\text{FM}}_{9} \succ {\text{FM}}_{2} . \hfill \\ \end{gathered}$.

4.2 Managerial Insights and Practical Implications

In this section, the risk assessment of HIS is investigated, with special attention paid to various types of risk sub-factors and their influential relationships. For hospital staff, the results in the above subsection offer some insights regarding HIS’s operation management. For one thing, when comparing the importance of sub-factors under the category of $O$, the expert committee deemed “Repeatability” as the most significant. Failure modes that happen repeatedly often lacks sufficient prevention strategy, therefore, corresponding mitigation actions are advised to be put in place. For another thing, in this paper “False alarm” and “Timeliness” are included as sub-factors in the category of $D$. The former is recommended because a high degree of false alarm will bring unnecessary workload to the medical staff, and the resulting fatigue may lead to the increase of misconducts. The latter is suggested because in the particular environment of hospital, any delay in the treatment of patients may incur devastating events. What’s more, according to the RPNs derived via our proposed method, the top three ranking failure modes are “Natural disasters”, “Hardware maintenance error and equipment failure” and “Server down”. This result suggests that important data should have back-ups in clouds, in case of hardware and equipment failures. Besides, in the unfortunate circumstance that HIS server is unavailable because of power outage or natural disasters, some paper records would also be very helpful.

5 Comparative Analyses

In this section, to highlight the differences and advantages of our proposed method, some comparative analyses with existing FMEA methods are performed. Without loss of generality, we only compare the evaluation result of expert $e_{1}$. What’s more, for the compactness of presentation, here only the computation results are provided, the detailed computation process can be found in “Appendix 2”.

5.1 Comparison with Classical FMEA

In the classical FMEA method, the expert is instructed to evaluate the failure modes’ criticality in three aspects: occurrence, severity and detection, with a discrete numerical scale of 1–10. To make fair comparison between the classical FMEA and our proposed method, firstly, expert $e_{1}$’s comparison matrices of failure modes under different sub-factors need to be converted to the numerical scale of 1–10. For instance, for the comparison matrix in Eq. (14), the first row can be seen as the criticality of failure mode ${\text{FM}}_{1}$ compared to all other failure modes with respect to sub-factor $O_{i} \;(i = 1:3)$. Thus, through defuzzification, the arithmetic mean of the entries in the first row of $G(A_{{{\text{FM}}}}^{{O_{i} }} )$ can be seen as the criticality of failure mode ${\text{FM}}_{1}$ with respect to sub-factor $O_{i}$. Then the failure mode ${\text{FM}}_{1}$’s criticality degrees under different $O_{i} \;(i = 1:3)$ is aggregated via the average operator to obtain the overall criticality degree in the aspect of occurrence.

Similar conversion procedures are also carried out for other failure modes and sub-factors, and the final RPN of classical FMEA method is listed in the second row of Table 16, along with the corresponding prioritization rank. From Fig. 4, it can be seen that the prioritization result obtained through our proposed method is in near accord with the one obtained via classical FMEA, with failure modes ${\text{FM}}_{14}$, ${\text{FM}}_{13}$ and ${\text{FM}}_{10}$ ranking as the failure modes with the highest criticality, and failure modes ${\text{FM}}_{2}$ and ${\text{FM}}_{9}$ ranking as the lowest ones, verifying the rationality of our proposed model. Compared with the classical FMEA, our proposed method has the following advantages:

• (1) The classical FMEA method only considers failure modes’ criticality in three main aspects, namely occurrence, severity, and detection. This type of over-generalization can result in troubling difficulties in the practical applications. For one thing, the concepts of these three main risk factors are too broad for experts to provide meaningful evaluation results, certain additional specifications are often needed in practical applications. For another thing, different failure modes may lead to different type of consequences with various categorizations of magnitudes, making it very hard to evaluate their criticality with a uniform numerical scale. Thus, it is safe to say that compared to the classical FMEA, our proposed method can provide a more through and comprehensive evaluation result, seeing that different sub-factors can be identified and selected based on the specific demands of application scenario.

• (2) In the classical FMEA method, the RPN of failure mode is defined as the product of criticality degrees of occurrence, severity, and detection. In other words, it is assumed that these three risk factors are equally important in the determination of failure modes’ RPN, thus sharing the same weight, which is rarely the case in practical applications. Besides, the equal weight also means that different combinations of occurrence, severity and detection may correspond to the same RPN, making it very difficult to distinguish between these particular failure modes. While in our proposed method, different weights are assigned to different risk factors based on the pairwise comparison matrix, reflecting their relative importance in the determination of overall RPN.

• (3) In the classical FMEA the experts’ evaluations results are represented with a numerical scale of 1–10, while in our proposed method the experts are instructed to express their assessment in the form of PLTS. On one hand, the linguistic terms are easier to utilize and fits more closely to the human way of thinking. On the other hand, the probability distribution in the PLTS allows more room for experts to express their hesitancy, providing more information to be processed.

Table 16 The failure modes’ RPNs and ranks of different methods

Fig. 4

Different methods’ normalized RPNs of failure modes

5.2 Comparison with AHP-FMEA

(1) Comparative analysis with Kiani Aslani et al.’s method [32]: In [32] Kiani Aslani R. et al. proposed to apply the fuzzy AHP to determine the relative weights of risk factors occurrence, severity and detection, and defined the RPN as the weighted sum of these three factors. To ensure the fairness of comparison, the PLTS entries in the comparison matrix in Table 5 is converted to the form of TFNs, by setting the lower and higher bounds of TFN as $\min \{ k|L^{(k)} (p^{(k)} ) \in L(p)\}$ and $\max \{ k|L^{(k)} (p^{(k)} ) \in L(p)\}$ respectively, and the center of TFN as $g(L(p))$. The entries in the comparison matrices of failure modes are also converted to the form of TFN, then aggregated in the similar procedure as described in Sect. 5.1. The final defuzzied RPN and the corresponding prioritization ranks of failure modes are shown in Table 16, as well as Fig. 4. It is easy to see that evaluation results obtained via Kiani Aslani R. et al.’s method and our proposed method is mostly consistent with each other. The primary differences between our proposed method and Kiani Aslani R. et al.’s are reflected in the following aspects:

• (1) Same as the classical FMEA, Kiani Aslani R. et al.’s method only takes into account the three broad risk factors, occurrence, severity and detection, without dividing them into more specific and comprehensive sub-factors.

• (2) The criticality degree of Kiani Aslani R. et al.’s method is directly given by the experts, whereas in our proposed method the weights of failure modes are derived from the pairwise comparison matrices. It has been a common understanding that as opposed to directly assigning a proper weight to each element, the pairwise comparisons are easier to conduct because the human mind is not very adequate at processing a lot of information at the same time [60, 61].

(2) Comparative analysis with Abdelgawad and Fayek’s method [43]: In [43], Abdelgawad M. and Fayek A. R. explored the concept of fuzzy expert system to map the relationship between risk factors occurrence, severity, detection and the overall RPN. Among these, the severity is further divided to sub-factors cost impact, time impact and scope/quality impact, the weights of which are determined by AHP. Similar to the conversion utilized in comparative analysis with Kiani Aslani R. et al.’s method, the comparison matrix with PLTS in Table 7 is defuzzied to form the comparison matrix for Abdelgawad M. and Fayek A. R.’s method. The resulting RPN and ranking of different failure modes are listed in sixth and seventh columns of Table 16, which are mostly in line with the results obtained via our proposed methods. That being said, our proposed method still shows some merits:

• (1) Abdelgawad M. and Fayek A. R.’s method only considers sub-factors under the category of severity, at the same time maintaining the broad concept of occurrence and detection as before. Whereas our proposed method divides all three main risk factors into more elaborate and specific sub-factors, making the evaluation results more comprehensive.

• (2) Abdelgawad M. and Fayek A. R.’s method only assigns different weight to the sub-factors, and assumes equal importance to the three main risk factors, same as the classical FMEA method. Just like discussed before, this over-simplification may lead to practical problems since expert’s emphasis on risk factors varies according to the application scenarios.

• (3) In Abdelgawad M. and Fayek A. R.’s method, the evaluation result of failure modes is expressed with crisp-valued real numbers. While in our proposed method PLTS is utilized, which not only better facilitates the experts’ opinion expression, but also allows the situation of hesitancy and incomplete information.

(3) Comparative analysis with Zandi et al.’s method [29]: In [29] Zandi P. et al. proposed to break down the risk factor severity to three sub-factors including severity on cost, severity on time, and severity on quality. Then Zandi P. et al. utilize AHP to derive the weights of both the main risk factors and the sub-factors. To make a fair comparison, the matrices in Tables 5 and 7 are converted as follows: for a PTLS $L(p)$, it is first defuzzied via Eq. (3), then $g(L(p))$ is rounded to an integer $\left\lfloor {g(L(p))} \right\rfloor$. The TFN corresponding to the linguistic term $t_{{\left\lfloor {g(L(p))} \right\rfloor }}$ as described in [29] is then taken as the conversion result. In Table 16, the eighth and ninth column represents the calculation results for Zandi P. et al.’s method. It can be seen from Fig. 4 that the results are basically consistent with the ones obtained via our proposed method. Apart from that, our proposed method also possesses the following desirable properties:

• (a) Like in [43], Zandi P. et al.’s method only considers the specification of risk factor severity, while our proposed method further breaks down the risk factors occurrence and detection as well.

• (b) Zandi P. et al.’s method adopts AHP for the weight assignment of risk factors and sub-factors, while our proposed method takes advantage of ANP for the same task. Seeing that AHP can only model the hierarchical architecture where the elements in the same level are independent from each other, ANP is a generalization developed on the basis on AHP, which can also model the dependence relationship between the elements in the same level. In the particular scenario of FMEA, this means that ANP can model and reflect the influential relationship between the sub-factors. For instance, a timelier detection may lead to lower financial losses, or a human casualty may cause serious damages to the organization’s reputation. The existence of these influential relationship makes ANP more suitable for the task of weight determination in FMEA, thus it is safe to say that the assessment result obtained through our proposed method is more reasonable and comprehensive.

5.3 Comparison with Crisp-Valued ANP-FMEA

In [62, 63], the authors also proposed to make use of ANP to improve the performance of FMEA. However, our proposed method inherently differs from the one put forward in [62, 63] in the following aspects. For starter, the methods in [62, 63] only considers the three main risk factors, same as the classical FMEA. Besides, in [62, 63] the authors utilizes crisp-valued real number as the opinion expression tool, while our proposed method makes use of PLTS. What’s more, the method in [62, 63] utilizes ANP to derive the relative weights of different failure modes with respect to the goal of failure mode prioritization. The network structures in [62, 63] represents the dependence relationship between the failure modes, i.e., the probability that one failure mode may lead to another. While in our proposed method, the network structure is constructed for the sub-factors, where a link exists if there is an influential relationship between said sub-factors. In other words, the methods in [62, 63] focuses on the common-cause phenomenon in FMEA, while our proposed method emphasis on the appropriate weight assignment to sub-factors in FMEA. Because of the different application field and the lack of necessary data, our proposed method cannot be applied to the case study in [62, 63], and vice versa.

6 Concluding Remarks

Classical FMEA method only considers three broad risk factors (occurrence, severity, and detection), and uses a discrete numerical scale of 1–10, which greatly limits its applicability and rationality. In light of this, this paper proposes an improved FMEA method based on ANP and PLTS. The three main risk factors are broken down to more elaborate and specific-to-application sub-factors, and a network is constructed to reflect the influential relationship between these sub-factors. ANP is taken advantage of to derive the relative weights of the main risk factors, sub-factors and failure modes with respect to the goal of failure mode prioritization. PLTS is utilized to facilitate the experts’ opinion expression, which allows for hesitancy and incomplete information. A case study on the reliability assessment of HIS, as well as comparative analysis with other existing FMEA methods, are carried out to demonstrate the applicability and rationality of our proposed method. The main findings of this paper are three-fold:

• (1) The specification of sub-factors and the consideration of their influential relationship help the experts tailor the evaluation process to better fit the application scenario, at the same time also improves the comprehensiveness of evaluation results.

• (2) The use of PLTS can better capture the subjectivity and ambiguity of the experts, maintaining more information during the evaluation process.

• (3) The case study of HIS risk assessment proves the applicability of our proposed method, further, comparative analyses with existing approaches validates its robustness.

However, there are also some limitations to our proposed method. In this paper, the calculation of RPNs follows the definition in classical FMEA method, with weights reflecting the relative importance of the risk factors. However, as discussed in Sect. 2, there are currently a number of researches that focus on integrating MCDM methods with FMEA process. The utilization of ANP in combination with other MCDM methods such as TOPSIS or VIKOR could be the future direction of our work. What’s more, the method proposed in this paper does not consider the common-cause failure effect often seen in application scenarios, which will be the future direction of our work. Last but not least, the risk assessment result provided in Sect. 4 are derived from the professional opinions of a committee consisting of five experts. Admittedly, the experiment results may differ if some other experts are consulted on this issue. Although this does not bring into question the rationality of our proposed method, in our future work a greater number of experts can be consulted with some techniques from social network group decision-making.

Appendices

Appendix 1: Abbreviation and Notation List

Abbreviation list

AHP	Analytic hierarchy process
ANP	Analytic network process
BWM	Best–worst method
COPRAS	COmplex PRoportional ASsessment of alternatives
FMEA	Failure modes and effects analysis
GRA	Grey relation analysis
HLTS	Hesitant linguistic term set
HIS	Hospital information system
LTS	Linguistic term set
MCDM	Multi-criteria decision making
MOORA	Multi-objective optimization by ratio analysis
MULTIMOORA	Multiple multi-objective optimization by ratio analysis
NASA	National Aeronautics and Space Administration
PLTS	Probabilistic linguistic term set
RPN	Risk prioritization number
SAW	Simple additive weighting
TFN	Triangular fuzzy numbers
TODIM	An acronym in Portuguese for interactive multi-criteria decision making
TOPSIS	Technique for order preference by similarity to an ideal solution
VIKOR	Vlse kriterijumska optimizacija kompromisno resenje

Notation list

$O$	Probability of occurrence
$S$	Severity
$D$	Likelihood of detection
${\text{RPN}}$	Risk prioritization number
$t_{\alpha }$	Linguistic terms
$T$	Additive linguistic term set
$\overline{T}$	Continuous linguistic term set
${\text{neg}}(t_{\alpha } )$	Negation operator of linguistic term set
$\max (t_{\alpha } ,\;t_{\beta } )$	Maximum operator of linguistic term set
$\min (t_{\alpha } ,\;t_{\beta } )$	Minimum operator of linguistic term set
$b_{T}$	Hesitant linguistic term set
$L(p)$	Probabilistic linguistic term set
$L^{(k)} (p^{(k)} )$	Linguistic term $L^{(k)}$ associated with probability $p^{(k)}$
$\# L(p)$	Number of all different linguistic terms in $L(p)$
$g\left( {L(p)} \right)$	Numerical score of $L(p)$
$e_{z} \;(z = 1:Z)$	The $z$th expert
${\text{FM}}_{m} \;(m = 1:M)$	The $m$th failure mode
$O_{i} \;(i = 1:h_{O} )$	The $i$th sub-factors under the category Occurrence $O$
$S_{i} \;(i = 1:h_{S} )$	The $i$th sub-factors under the category Severity $S$
$D_{i} \;(i = 1:h_{D} )$	The $i$th sub-factors under the category Detection $D$
$A$	Comparison matrix of risk factors $O$, $S$ and $D$
$L_{ij} (p)$	Comparing result of the $i$th risk factor to the $j$th risk factor
$\overline{{L_{ij} (p)}}$	Negation of $L_{ij} (p)$
$G(A)$	Crisp-valued matrix obtained by calculating the numerical score
${\text{CL}}_{ij}^{r}$	Consistent preference of the $i$th element over the $j$th element through the $r$th element
${\text{Consistency}}\;(G(A))$	Consistency level of $A$
$\gamma$	Required consistency level threshold
$w$	Weighting vector of three main risk factors
$A^{O} ,\;A^{S} ,\;A^{D}$	Comparison matrix of sub-factors
$\omega^{O} ,\;\omega^{S} ,\;\omega^{D}$	Weighting vector of sub-factors
$Q$	Super-matrix representing the influence of sub-factors
$A^{{O_{i} }}$	Comparison matrix of sub-factors regarding their influences on $O_{i}$
$(\dot{\omega }_{O1}^{Oi} ,\;\dot{\omega }_{O2}^{Oi} , \ldots ,\dot{\omega }_{{Oh_{O} }}^{Oi} )^{{\text{T}}}$	Normalized principal eigenvector of $G(A^{{O_{i} }} )$
$||Q^{c} - Q^{c - 1} ||_{2}$	Euclidean norm of the deviation between $Q^{c}$ and $Q^{c - 1}$
$\ddot{\omega }$	Long-term stable weight vector of sub-factors
$A_{FM}^{{O_{i} }}$	Comparison matrix of failure modes regarding the $i$th sub-factor $O_{i}$
$\varpi^{{O_{i} }}$	Weight of failure modes with respect to the $i$th sub-factor $O_{i}$
$RPN_{m}$	RPN of the $m$th failure mode
${\text{RPN}}_{m}^{C}$	group assessment of the RPN of the $m$th failure mode
$\varphi (L^{(k)} )$	Transformation function from linguistic terms to AHP scale
$\hat{\varphi }(\rho )$	Transformation function from PLTS numerical score to TFN scale

Appendix 2: Computation Process of Comparative Methods

1.1 Classical FMEA Method

As explained before, in classical FMEA method, the expert is instructed to rate the failure modes with a discrete numerical scale of 1–10. To ensure the fairness of comparison, the first step is to convert the entries in failure modes’ comparison matrix from PLTS to the numerical scale.

For example, the comparison of failure mode ${\text{FM}}_{1}$ to failure model ${\text{FM}}_{2}$ under sub-factor $O_{1}$ is $\{ t_{5} (0.8),\;t_{6} (0.2)\}$, then via Eq. (3) this entry is defuzzied to $5 \times 0.8 + 6 \times 0.2 = 5.2$, then rounded to $5$ because the ratings in classical FMEA is required to be integers. With similar calculations, expert $e_{1}$’s comparison matrices of failure modes with respect to sub-factor $O_{1}$ is obtained, as shown in Table 17.

Table 17 Comparison matrix of failure modes w.r.t. $O_{1}$ for classical FMEA method

In Table 17, the entries in the first row represents the criticality of failure mode ${\text{FM}}_{1}$ compared to all other failure modes with respect to sub-factor $O_{1}$. Thus, the arithmetic mean of the entries in the first row of Table 17 can be seen as the criticality rating of failure mode ${\text{FM}}_{1}$ with respect to sub-factor $O_{1}$. The same argument goes for other failure modes, and their criticality ratings are list in the first row of Table 18. Corresponding calculation results for sub-factor $O_{2}$ and $O_{3}$ are also listed in the second and third row of Table 18, with their calculation process omitted for compactness.

Table 18 Criticality rating of failure modes w.r.t. $O_{i} \;(i = 1:3)$ for classical FMEA method

Seeing that in classical FMEA method, only three main risk factors are considered, the criticality ratings of failure modes under sub-factors $O_{i} \;(i = 1:3)$ need to be further aggregated via the average operator, to derive the ratings under the main risk factor $O$, the result of which is listed in the first row of Table 19. Similar computations are also carried out for main risk factors $S$ and $D$, as shown in the second and third rows of Table 19. Finally, the ${\text{RPN}}$ can be calculated, and the ranking of failure modes via classical FMEA method can be obtained:

$$\begin{gathered} {\text{FM}}_{14} \succ {\text{FM}}_{13} \succ {\text{FM}}_{10} \succ {\text{FM}}_{11} \succ {\text{FM}}_{12} \succ {\text{FM}}_{1} \succ {\text{FM}}_{7} \hfill \\ \succ {\text{FM}}_{3} \succ {\text{FM}}_{8} \succ {\text{FM}}_{4} \succ {\text{FM}}_{5} \succ {\text{FM}}_{9} \succ {\text{FM}}_{6} \succ {\text{FM}}_{2} . \hfill \\ \end{gathered}$$

Table 19 Criticality ratings and RPNs of failure modes

1.2 Kiani Aslani et al.’s Method [32]

To counter the problem of equal weight assumption, Kiani Aslani R. et al. took the advantage of AHP to derive the relative weights of main risk factors, and defined the RPN as the weighted sum of these three factors. In [32], TFN is utilized to accommodate the uncertainty of expert judgements. Therefore, the comparison matrix in Table 5 needs to be converted into TFN to ensure the fairness of comparison. This conversion process is carried out in two steps. Firstly, the PLTS is converted into triangular forms by setting the lower and higher bounds as $L^{{(\min \{ k|L^{(k)} (p^{(k)} ) \in L(p)\} )}}$ and $L^{{(\max \{ k|L^{(k)} (p^{(k)} ) \in L(p)\} )}}$ respectively, and the center as $L^{(g(L(p)))}$. For instance, in Table 5, the comparison result of risk factor $O$ to risk factor $S$ is $\{ t_{3} (0.3),\;t_{4} (0.6)\}$. It is easy to see that $\min \{ 3,\;4\} = 3$, $\max \{ 3,\;4\} = 4$ and $g(L(p)) = 3 \times 0.3$$+ 4 \times 0.6 = 3.3$. Hence, the triangular form of $\{ t_{3} (0.3),\;t_{4} (0.6)\}$ is $(t_{3} ,\;t_{3.3} ,\;t_{4} )$.

Secondly, the triangular form of PLTS is transformed to TFN according to their practical meanings. In AHP method [64], the pairwise comparison of two elements are conducted with instructions in Table 20.

Table 20 Practical meanings of pairwise comparison result for AHP

Thus, according to the practical meanings in Table 4, the linguistic terms can be translated to the scale of AHP with the following equation:

$$\varphi (L^{(k)} ) = \left\{ {\begin{array}{*{20}c} {2(k - 4) + 1,} & {k \ge 4,} \\ {\frac{1}{2(4 - k) + 1},} & {{\text{otherwise}}.} \\ \end{array} } \right.$$

(17)

And the TFN obtained after conversion is:

$$\left( {\varphi (\min \{ k|L^{(k)} (p^{(k)} ) \in L(p)\} ),\;\varphi (g(L(p))),\;\varphi (\max \{ k|L^{(k)} (p^{(k)} ) \in L(p)\} )} \right).$$

(18)

Continuing with the above instance, via Eq. (17) the linguistic terms $t_{3}$, $t_{3.3}$ and $t_{4}$ are translated to:

$$\varphi (t_{3} ) = 1/(2 \times (4 - 3) + 1) = 1/3 \approx 0.33,$$

$$\varphi (t_{3.3} ) = 1/(2 \times (4 - 3.3) + 1) = 1/2.4 \approx 0.42,$$

$$\varphi (t_{4} ) = 1/(2 \times (4 - 4) + 1) = 1/1 = 1.$$

Therefore, the PLTS $\{ t_{3} (0.3),\;t_{4} (0.6)\}$ can be converted to a TFN $(0.33,\;0.42,\;1)$. Identical conversions are also carried out for other entries in Table 5, the results are presented in Table 21.

Table 21 Pairwise comparison matrix of the three main risk factors for method in [32]

For two TFNs $\lambda_{1} = (a_{1} ,\;b_{1} ,\;c_{1} )$ and $\lambda_{2} = (a_{2} ,\;b_{2} ,\;c_{2} )$, their operation laws [65] are defined as:

• (1) $(a_{1} ,\;b_{1} ,\;c_{1} ) \oplus (a_{2} ,\;b_{2} ,\;c_{2} ) = (a_{1} + a_{2} ,\;b_{1} + b_{2} ,\;c_{1} + c_{2} )$;

• (2) $(a_{1} ,\;b_{1} ,\;c_{1} ) \otimes (a_{2} ,\,b_{2} ,\;c_{2} ) = (a_{1} a_{2} ,\;b_{1} b_{2} ,\;c_{1} c_{2} )$;

• (3) $\mu \otimes (a_{1} ,\;b_{1} ,\;c_{1} ) = (\mu a_{1} ,\;\mu b_{1} ,\;\mu c_{1} )$;

• (4) $(a_{1} ,\;b_{1} ,\;c_{1} )^{ - 1} = (1/c_{1} ,\;1/b_{1} ,\;1/a_{1} )$;

• (5) $\tilde{g}(\lambda_{1} ) = (a_{1} + 4b_{1} + c_{1} )/6$.

Suppose the pairwise comparison matrix is $\tilde{A} = \left[ {\lambda_{i}^{j} } \right]_{n \times n}$, then the TFN weight of each element is calculated with the following formula [65]:

$$\tilde{w}_{i} = \sum\limits_{j = 1}^{n} {\lambda_{i}^{j} \otimes \left[ {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\lambda_{i}^{j} } } } \right]}^{ - 1} .$$

(19)

Thus, according to the comparison matrix in Table 21, the TFN weights of the three risk factors can be calculated via Eq. (19):

$$\tilde{w}_{O} = \left( {4.33,\;5.02,\;9} \right) \otimes \left( {\frac{1}{19.66},\;\frac{1}{12.1},\;\frac{1}{10.49}} \right) = \left( {0.22,\;0.41,\;0.86} \right),$$

$$\tilde{w}_{S} = \left( {4.83,\;5.60,\;9} \right) \otimes \left( {\frac{1}{19.66},\;\frac{1}{12.1},\;\frac{1}{10.49}} \right) = \left( {0.25,\;0.46,\;0.86} \right),$$

$$\tilde{w}_{D} = \left( {1.33,\;1.48,\;1.66} \right) \otimes \left( {\frac{1}{19.66},\;\frac{1}{12.1},\;\frac{1}{10.49}} \right) = \left( {0.07,\;0.12,\;0.16} \right).$$

Similar aggregation process as described in “Appendix 2.1” is also undertaken to derive the ratings of failure modes with respect to three main risk factors. The only difference is that in “Appendix 2.1” the ratings are given in integers, while here the ratings are transformed to TFNs, as shown in the second to fourth columns of Table 22.

Table 22 Ratings and RPNs of failure modes for Kiani Aslani et al.’s method [32]

Suppose the ratings of failure modes under risk factors $O$, $S$ and $D$ are $\lambda^{O}$, $\lambda^{S}$ and $\lambda^{D}$, respectively, then the RPN of failure modes are defined as:

$${\text{RPN}}_{i} = \tilde{g}\left( {(\tilde{w}_{O} \otimes \lambda^{O} ) \oplus (\tilde{w}_{S} \otimes \lambda^{S} ) \oplus (\tilde{w}_{D} \otimes \lambda^{D} )} \right).$$

The calculation results are shown in the last two columns of Table 22, and finally the ranking of failure modes can be obtained for Kiani Aslani R. et al.’s method [32]:

$\begin{gathered} {\text{FM}}_{14} \succ {\text{FM}}_{13} \succ {\text{FM}}_{10} \succ {\text{FM}}_{11} \succ {\text{FM}}_{12} \succ {\text{FM}}_{9} \succ {\text{FM}}_{7} \hfill \\ \succ {\text{FM}}_{1} \succ {\text{FM}}_{5} \succ {\text{FM}}_{4} \succ {\text{FM}}_{3} \succ {\text{FM}}_{6} \succ {\text{FM}}_{8} \succ {\text{FM}}_{2} . \hfill \\ \end{gathered}$.

1.3 Abdelgawad and Fayek’s Method [43]

In [43], the authors broke down risk factor $S$ to sub-factors and utilized classical AHP to derive their relative weights. Similar to the conversion process in “Appendix 2.2”, the entries of comparison matrix in Table 7 are first defuzzied via Eq. (3), then translated to the scale of AHP method via Eq. (17). Take the comparison result of sub-factor $S_{1}$ to sub-factor $S_{2}$ as an example, $\{ t_{5} (0.5),\;t_{6} (0.2)\}$ is first converted to $5 \times 0.5 + 6 \times 0.2 = 3.7$. Then according to the practical meanings listed in Table 20, linguistic term $t_{3.7}$ corresponds to $1/(2 \times (4 - 3.7) + 1) = 1/1.6 = 0.625$ in classical AHP method. The converted comparison matrix is as shown in Table 23. Moreover, the entries of the same column in Table 23 are normalized, then entries of the same row are summed together, which are then normalized to obtain the weights of corresponding sub-factors, as listed in the last column in Table 23.

Table 23 Comparison matrix and the corresponding weights of sub-factors for AHP method

Similar as in “Appendix 2.1”, the ratings of failure modes under different sub-factors are derived by calculating the arithmetic mean of the entries in the same row of the pairwise comparison matrices like Table 17. Because in [43] only the risk factor $S$ is broken down to sub-factors while $O$ and $D$ remains the same as in classical FMEA method, here the ratings of failure modes under risk factor $S$ is calculated as the weighted sum of ratings under $S_{i} \;(i = 1:5)$ with the weighting vector from Table 23. The ratings under risk factors $O$ and $D$ are the same as in “Appendix 2.1”, where sub-factors $O_{i} \;(i = 3)$ and $D_{i} \;(i = 1:3)$ are assigned equal importance. The calculation results are as listed in Table 24.

Table 24 Ratings and RPNs of failure modes for method in [43]

With the ratings under $O$, $S$ and $D$ obtained, the RPNs of failure modes can be calculated, as shown in the last column of Table 24. Thus, the ranking of failure modes via Abdelgawad and Fayek’s method [43] is:

$$\begin{gathered} {\text{FM}}_{14} \succ {\text{FM}}_{13} \succ {\text{FM}}_{10} \succ {\text{FM}}_{11} \succ {\text{FM}}_{12} \succ {\text{FM}}_{8} \succ {\text{FM}}_{1} \hfill \\ \succ {\text{FM}}_{4} \succ {\text{FM}}_{7} \succ {\text{FM}}_{6} \succ {\text{FM}}_{3} \succ {\text{FM}}_{5} \succ {\text{FM}}_{2} \succ {\text{FM}}_{9} . \hfill \\ \end{gathered}$$

1.4 Zandi et al.’s Method [29]

In [29], Zandi P. et al. broke down the risk factor $S$ to sub-factors and utilized AHP to derive both the weights of three main risk factors and the weights of sub-factors under the category of $S$. Seeing that in [29] the experts express their assessments in the form of TFNs, to ensure the fairness of comparison, first the comparison matrices in Tables 5 and 7 need to be converted to relevant forms.

As described in Table 25, a special kind of TFN scale is used in [29] where the deviation between lower bound and center of the TFN, as well as the deviation between the center and higher bound of the TFN is 2. In order to conform to this norm, first the PLTS entries in Tables 5 and 7 is defuzzied via the numerical score function in Eq. (3), then rounded to a positive integer. Suppose $\rho = \left\lfloor {g(L(p))} \right\rfloor$, then the conversion is completed by the following function:

$$\hat{\varphi }\left( \rho \right) = \left( {\begin{array}{*{20}c} {\left( {2(\rho - 4) - 1,\;2(\rho - 4) + 1,\;\min \left( {2(\rho - 4) + 3,\;9} \right)} \right),} & {\rho > 4,} \\ {\left( {1,\;1,\;1} \right),} & {\rho = 4,} \\ {(1/\min \left( {2(4 - \rho ) + 3,\;9} \right),\;1/(2(4 - \rho ) + 1),\;1/(2(4 - \rho ) - 1)),} & {{\text{otherwise}}{.}} \\ \end{array} } \right.$$

(20)

Table 25 Practical meaning of TFN scales used in [29]

The comparison result of risk factor $O$ to risk factor $S$ in Table 5, $\{ t_{3} (0.3),\;t_{4} (0.6)\}$, is taken once again as an example. It is easy to see that $g\left( {L(p)} \right) = 3 \times 0.3 + 4 \times 0.6 = 3.3$, then $\rho = \left\lfloor {g(L(p))} \right\rfloor$$= 3$. Via Eq. (20), the TFN scale after conversion is:

$$\hat{\varphi }\left( \rho \right) = (1/\min \left( {2(4 - 3) + 3,\;9} \right),\;1/(2(4 - 3) + 1),\;1/(2(4 - 3) - 1)) = (1/5,\;1/3,\;1).$$

Likewise, other entries in Tables 5 and 7 are converted following the above procedures, the results are presented in Tables 26 and 27.

Table 26 Pairwise comparison matrix of the three main risk factors for method in [29]

Table 27 Pairwise comparison matrix of sub-factors for method in [29]

Here, we introduce the principle of comparing TFNs. For any two TFNs $\lambda_{1} = (a_{1} ,\;b_{1} ,\;c_{1} )$ and $\lambda_{2} = (a_{2} ,\;b_{2} ,\;c_{2} )$, the possibility degree of $\lambda_{1} \ge \lambda_{2}$ is defined as:

$$\sigma \left( {\lambda_{1} \ge \lambda_{2} } \right) = \left\{ {\begin{array}{*{20}c} {1,} & {b_{1} \ge b_{2} ,} \\ {\frac{{a_{2} - c_{1} }}{{(b_{1} - c_{1} ) - (b_{2} - a_{2} )}},} & {{\text{otherwise}}.} \\ \end{array} } \right.$$

(21)

Moreover, the possibility degree that one TFN $\lambda = (a,\;b,\;c)$ is greater than $k$ other TFNs $\lambda_{i} \;(i = 1:k)$ is defined as:

$$\sigma \left( {\lambda \ge \lambda_{1} , \ldots ,\lambda_{k} } \right) = \min \left( {\sigma (\lambda \ge \lambda_{1} ), \ldots ,\sigma (\lambda \ge \lambda_{k} )} \right).$$

(22)

Next, let us suppose the pairwise comparison matrix is $\hat{A} = \left[ {\hat{\lambda }_{i}^{j} } \right]_{n \times n}$, then the synthetic extent with respect to the $i$th element is defined as:

$$V_{i} = \sum\limits_{j = 1}^{n} {\hat{\lambda }_{i}^{j} \otimes \left[ {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\hat{\lambda }_{i}^{j} } } } \right]}^{ - 1} .$$

(23)

Then, the normalized possibility degree of $V_{i} \ge V_{j} \;(j \ne i)$ is regarded as the weight of the $i$th element derived from comparison matrix.

For instance, according to the comparison matrix in Table 26, via Eq. (23) we have:

$$V_{1} = \left( {2.2,\;4.33,\;7} \right) \otimes \left( {\frac{1}{6.54},\;\frac{1}{10.86},\;\frac{1}{16.33}} \right) = \left( {0.13,\;0.40,\;1.07} \right),$$

$$V_{2} = \left( {3,\;5,\;7} \right) \otimes \left( {\frac{1}{6.54},\;\frac{1}{10.86},\;\frac{1}{16.33}} \right) = \left( {0.18,\;0.46,\;1.07} \right),$$

$$V_{3} = \left( {1.34,\;1.53,\;2.33} \right) \otimes \left( {\frac{1}{6.54},\;\frac{1}{10.86},\;\frac{1}{16.33}} \right) = \left( {0.08,\;0.14,\;0.36} \right).$$

Using Eqs. (21) and (22),

$$\sigma (V_{1} \ge V_{2} ) = \frac{0.18 - 1.07}{{(0.40 - 1.07) - (0.46 - 0.18)}} \approx 0.94,$$

$$\sigma (V_{1} \ge V_{3} ) = 1,\quad \sigma (V_{2} \ge V_{1} ) = 1,\quad \sigma (V_{2} \ge V_{3} ) = 1,$$

$$\sigma (V_{3} \ge V_{1} ) = \frac{0.13 - 0.36}{{(0.14 - 0.36) - (0.40 - 0.13)}} \approx 0.46,$$

$$\sigma (V_{3} \ge V_{2} ) = \frac{0.18 - 0.36}{{(0.14 - 0.36) - (0.46 - 0.18)}} \approx 0.35,$$

$$\sigma (V_{1} \ge V_{2} ,\;V_{3} ) = \min (0.94,\;1) = 0.94,$$

$$\sigma (V_{2} \ge V_{1} ,\;V_{3} ) = \min (1,\;1) = 1,$$

$$\sigma (V_{3} \ge V_{1} ,\;V_{2} ) = \min (0.46,\;0.35) = 0.35.$$

Furthermore, the vector $(0.94,\;1,\;0.35)^{{\text{T}}}$ is normalized to $(0.41,\;0.44,\;0.15)^{{\text{T}}}$, which serves as the weighting vector of the three main risk factors. The same computing process is also performed for the comparison matrix in Table 27, the result of which is shown in the first row of Table 28. Same as in “Appendix 2.3”, the ratings of failure modes are transformed to TFN then defuzzied, as shown in Table 28. Then, the RPN of failure modes can be defined as their weighted sum, as presented in the last column of Table 28. Finally, the ranking of failure modes via Zandi et al.’s method [29] is obtained:

Table 28 Ratings and RPNs of failure modes for method in [29]

$\begin{gathered} {\text{FM}}_{13} \succ {\text{FM}}_{14} \succ {\text{FM}}_{10} \succ {\text{FM}}_{11} \succ {\text{FM}}_{12} \succ {\text{FM}}_{1} \succ {\text{FM}}_{9} \hfill \\ \succ {\text{FM}}_{7} \succ {\text{FM}}_{4} \succ {\text{FM}}_{5} \succ {\text{FM}}_{6} \succ {\text{FM}}_{3} \succ {\text{FM}}_{8} \succ {\text{FM}}_{2} . \hfill \\ \end{gathered}$.