1 Introduction

In group decision-making (GDM) problems, the preferences among different experts are often inconsistent. Therefore, how to support experts to reach consensus on the final decision outcome has become a hot topic. Consensus model is an effective way which can be classified into two categories: (1) identification rules and direction rules [1,2,3]; (2) minimum adjustments or cost rules [4, 5]. In addition, Pérez et al. [6] believed that experts usually interact with each other. Therefore, the construction of consensus model in social networks has attracted the attention of many scholars [7,8,9].

Although all of the abovementioned methods have effectively improved the consensus degrees of experts, the improvement of collective intelligence (CI) level was rarely considered. Decomposing CI etymologically, the term “collective” describes a group of individuals who do not need to have the same attitude or viewpoint, and thus leading to better solutions to a given problem. “Intelligence” refers to the ability to learn, understand, and adapt to a changing and difficult environment by using own knowledge. The MIT Center for Collective Intelligence combined both terms to broadly describe groups of individuals doing things collectively that seem intelligent [10]. In addition, Woolley et al. [11] proposed that CI is a powerful concept to explain why some groups perform better than others on various tasks. Massari et al. [12] argued that when the consensus degree is too high, the CI level may diminish. The group is able to reach a higher CI level by exploiting the power of trust/distrust relationships, and distrust relationships make the group better explore the decision space without converging too soon on an agreed suboptimal solution. Inspired by this idea, a consensus model is constructed in this paper for the purpose of reaching a relatively high CI level.

As aforementioned, the trust/distrust relationships are important factors influencing the consensus model. It can be seen in Refs. [7, 8] that trust/distrust relationships among experts are usually given previously. Therefore, how to build trust/distrust relationships based on limited information is an important issue. The calculations of trust relationship are usually divided into two categories: (1) the similarity between experts in one or some aspects [13] and (2) some historical information of experts [14]. However, not all experts have direct contact with each other in a real social network, and they cannot obtain the information of other experts with whom they have indirect relationship. As a result, it is obviously unreasonable to use these methods to build a trust relationship between each pair of experts with indirect contact. To solve this problem, various propagation operators have been proposed to propagate trust/distrust relationships to connect experts [15, 16]. Nevertheless, the weakness of these operators is that both trust and distrust may decrease at the same time. It is inconsistent with human intuition because the propagation process using trusted third partners may generate information attenuation, which may result in the decrease of trust and increase of distrust [7]. In order to describe the information attenuation, we construct a propagation operator.

The main contributions of this paper are summarized as follows:

  1. (1)

    For two experts with a direct relationship, the trust/distrust relationships between them are constructed by fusing their knowledge levels and representativeness levels. And a trust function expressed by an intuitionistic fuzzy number is used to quantify the trust/distrust relationships between them.

  2. (2)

    For two experts with an indirect relationship, a new propagation operator is investigated to construct the trust/distrust relationships between them, which can interpret the phenomenon of information attenuation that the trust and distrust decreases and increases, respectively.

  3. (3)

    A consensus model based on the social network relationships density and the trust/distrust relationships is established, which not only improves the consensus degrees of experts but also improves the CI level.

The rest of this paper is organized as follows: Sect. 2 introduces some basic concepts which will be used to solve intuitionistic fuzzy GDM problems. In Sect. 3, the trust/distrust relationships are constructed or propagated for experts with direct or indirect relationships. In Sect. 4, a consensus model is established and the validity of the model is proved theoretically. In Sect. 5, a general alternatives selection process based on the trust/distrust relationships is presented, and Sect. 6 gives an example of GDM problem to demonstrate the effectiveness of the proposed method. This paper is concluded in Sect. 7.

2 Preliminaries

In this section, the necessary preliminaries which will be used in Sects. 3 and 4 are introduced. Specifically, the theory of social networks is briefly reviewed. In addition, the definitions of consistency and consensus degree are also presented.

2.1 Social Networks

The social network is a relatively stable system of social relations formed by the interactions among social individuals. A social network can be abstracted as a social structure composed of nodes and lines, where nodes represent individuals or organizations, and lines represent the connections of individuals or organizations. In social network analysis, this social structure is usually represented in three ways: graph theoretic, algebraic, and sociometric [17].

By far, the primary notational scheme is sociometric, because it is easy to be calculated. For instance, let \(E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}\) be the set of nodes and \(f:E \times E \to \left\{ {0,1} \right\}\) be the relationship between nodes. Then the social relationship from \(e_{i}\) to \(e_{j}\) is as follows:

$$f\left( {e_{i} ,e_{j} } \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if }}e_{i} {\text{is related to }}e_{j} ,} \hfill \\ {0,} \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right.$$
(1)

Let \(a_{ij} = f\left( {e_{i} ,e_{j} } \right)\); then a sociomatrix constructed among the nodes in \(E\) is denoted by \(A = \left( {a_{ij} } \right)_{m \times m}\), and it is asymmetric such that \(a_{ij} \ne a_{ji}\).

2.2 Intuitionistic Fuzzy Consistent Reciprocal Relation

In the process of solving GDM problems, a group of experts should firstly evaluate alternatives and express their opinions. When the GDM problem is complicated, it is not easy for experts to directly give the priority orders or utility values of alternatives, so the comparison between two alternatives is a feasible way for experts to apply. However, if experts are not very familiar with the problem, or the information about alternatives is incomplete, it will be difficult for expert to provide crisp preference values [18]. For example, in a social life cycle assessment (SLCA) problem, some uncertain quantitative and qualitative attributes derived from different dimensions are involved, such as added value from economic dimension and work satisfaction from social dimension. In such case, intuitionistic fuzzy number (IFN) is a suitable representation for the comparison of alternatives because experts could express their imprecise cognitions from positive, negative, and hesitative perspectives [19].

Definition 1

[20] Let a crisp set \(X\) be fixed and \(A \subset X\) be a fixed set. An intuitionistic fuzzy set (IFS) \(A\) in \(X\) is an object with the following form:

$$A = \left\{ {x,\mu_{A} \left( x \right),\gamma_{A} \left( x \right) |x \in X} \right\}.$$
(2)

Equation (2) is characterized by a membership function \(\mu_{A} \left( x \right):A \to \left[ {0,1} \right]\) and a non-membership function \(\gamma_{A} \left( x \right):A \to \left[ {0,1} \right]\) with the condition that \(0 \le \mu_{A} \left( x \right) + \gamma_{A} \left( x \right) \le 1\), \(\forall x \in X\).

Let \(\pi_{A} \left( x \right)\) be the hesitation degree of element \(x \in X\) to \(A\) such that \(\pi_{A} \left( x \right) = 1 - \mu_{A} \left( x \right) - \gamma_{A} \left( x \right)\) and \(0 \le \pi_{A} \left( x \right) \le 1\). Particularly, if \(\pi_{A} \left( x \right) = 0\), then IFS \(A\) is degenerated to a fuzzy set.

For convenience, \(a = \left( {\mu_{a} ,\gamma_{a} } \right)\) is called an IFN. An IFN representing the preference value is called intuitionistic fuzzy reciprocal relation (IFRR), and multiple IFRRs can form a judgment matrix which is called intuitionistic fuzzy reciprocal relation matrix (IFRRM).

Definition 2

[21] An IFRRM on a finite set of alternatives \(X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\) is denoted by \(R = \left( {r_{ij} } \right)_{n \times n}\), where \(r_{ij} =\langle \mu_{R} \left( {x_{i} ,x_{j} } \right),\gamma_{R} \left( {x_{i} ,x_{j} } \right)\rangle\). For convenience, let \(r_{ij} = \left( {\mu_{ij} ,\gamma_{ij} } \right)\), where \(\mu_{ij}\) denotes the degree to which \(x_{i}\) is preferred to \(x_{j}\), \(\gamma_{ij}\) indicates the degree to which \(x_{i}\) is non-preferred to \(x_{j}\), and \(\pi_{ij} = 1 - \mu_{ij} - \gamma_{ij}\) is interpreted as the hesitation degree to which \(x_{i}\) is preferred or non-preferred to \(x_{j}\). Furthermore, \(\mu_{ij}\) and \(\gamma_{ij}\) satisfy the following characteristics:

$$0 \le \mu_{ij} + \gamma_{ij} \le 1,\,\mu_{ij} = \gamma_{ji} ,\,\mu_{ii} = \gamma_{ii} = 0.5,\quad \forall i,j = 1,2, \ldots ,n .$$
(3)

In essence, an IFRRM is an extension of the fuzzy reciprocal relation matrix (FRRM). Therefore, an IFRRM can be transformed into the FRRM based on the closeness degree.

Definition 3

[22] Given an IFRRM \(R = \left( {r_{ij} } \right)_{n \times n}\) with \(r_{ij} = \left( {\mu_{ij} ,\gamma_{ij} } \right)\); then the FRRM based on the closeness degree of \(R\) is denoted by \(C = \left( {c_{ij} } \right)_{n \times n}\), where \(c_{ij} = \frac{{1 - \gamma_{ij} }}{{2 - \mu_{ij} - \gamma_{ij} }}\).

According to the definition of fuzzy consistent reciprocal relation (FCRR), the intuitionistic fuzzy consistent reciprocal relation (IFCRR) can be obtained.

Definition 4

[22] Given an IFRRM \(R = \left( {r_{ij} } \right)_{n \times n}\) with \(r_{ij} = \left( {\mu_{ij} ,\gamma_{ij} } \right)\), and the corresponding FRRM \(C = \left( {c_{ij} } \right)_{n \times n}\). If

$$c_{ij} = c_{ik} + c_{jk} - 0.5 ,\forall i,j,k = 1,2, \ldots ,n ,$$
(4)

i.e., \(\frac{{1 - \gamma_{ij} }}{{2 - \mu_{ij} - \gamma_{ij} }} = \frac{{1 - \gamma_{ik} }}{{2 - \mu_{ik} - \gamma_{ik} }} + \frac{{1 - \gamma_{jk} }}{{2 - \mu_{jk} - \gamma_{jk} }} - 0.5 ,\forall i,j,k = 1,2, \ldots ,n\), then \(R\) and \(C\) are an intuitionistic fuzzy consistent reciprocal relation matrix (IFCRRM) and a fuzzy consistent reciprocal relation matrix (FCRRM), respectively.

However, in real GDM problems, due to the complexity of the decision-making environment and experts’ understandings of things are bound to be subjective, one-sided, and ambiguous, it is difficult to ensure that the experts’ preference values satisfy the property of consistency. And then we can make \(\widehat{C} = \left( {\widehat{c}_{ij} } \right)_{n \times n}\) with \(\widehat{c}_{ij} = \frac{1}{n}\mathop \sum \limits_{k = 1}^{n} \left( {c_{ik} + c_{jk} } \right) - 0.5\), to construct a FCRRM. If \(R\) is an IFCRRM, then \(\widehat{C} = C\). In addition, a method has been proposed to measure the consistency degrees of experts.

Definition 5

[23] Suppose \(R = \left( {r_{ij} } \right)_{n \times n}\) is an IFRRM, \(C = \left( {c_{ij} } \right)_{n \times n}\) is the corresponding FRRM, and \(\widehat{C}\) = \(\left( {\widehat{c}_{ij} } \right)_{n \times n}\) is the corresponding FCRRM. Then the deviation between \(C\) and \(\widehat{C}\) represents the consistency degree of an expert, which can be defined as follows:

$${\text{CD}} = 1 - d\left( {C,\widehat{C}} \right) = 1 - \frac{2}{{n\left( {n - 1} \right)}}\mathop \sum \limits_{i = 1}^{n - 1} \mathop \sum \limits_{j = i + 1}^{n} \left| {c_{ij} - \widehat{c}_{ij} } \right| .$$
(5)

Obviously, \({\text{CD}} = 1\) means that \(C\) is completely consistent, i.e., \(R\) is completely consistent. If the value of \({\text{CD}}\) is smaller, the consistency of \(R\) is lower.

2.3 Consensus Measure

In order to obtain the consensus degree of an expert, consensus measures can be calculated for each expert at three different levels: (1) the element level; (2) the alternative level; and (3) the judgment matrix level [24].

  • Level 1. Consensus degree at the element level. The consensus degree between experts \(e_{h}\) and \(e_{k}\) on alternatives \(x_{i}\) against \(x_{j}\) is defined as follows:

    $${\text{CE}}_{ij} \left( {R^{h} ,R^{k} } \right) = 1 - \frac{{\left| {\mu_{ij}^{h} - \mu_{ij}^{k} } \right| + \left| {\gamma_{ij}^{h} - \gamma_{ij}^{k} } \right|}}{2} .$$
    (6)

  • Level 2. Consensus degree at the alternative level. The consensus degree of \(e_{h}\) with respect to the group on \(x_{i}\) against \(x_{j}\) is defined as follows:

    $${\text{ACE}}_{ij}^{h} = \frac{1}{m - 1}\mathop \sum \limits_{k \ne h,k = 1}^{m} {\text{CE}}_{ij} \left( {R^{h} ,R^{k} } \right).$$
    (7)

  • Level 3. Consensus degree at the judgment matrix level. Suppose the set composed of \(q\) elements with the lowest consensus degree of \(e_{h}\) is \({\text{APS}}^{h} = \left\{ {\left( {i,j} \right)} \right\}\), where \(\left( {i,j} \right)\) are the coordinates corresponding to the \(q\) elements and \(1 \le q \le n^{2}\). Then the consensus degree of \(e_{h}\) is defined as follows:

    $${\text{ACD}}^{h} = \frac{1}{q}\mathop \sum \limits_{{\left( {i,j} \right) \in {\text{APS}}^{h} }} {\text{ACE}}_{ij}^{h} .$$
    (8)

The higher the value of \({\text{ACD}}^{h}\) (\(0 \le {\text{ACD}}^{h} \le 1\)), the higher the consensus degree of \(e_{h}\).

3 The Construction and Propagation of Trust/Distrust Relationships

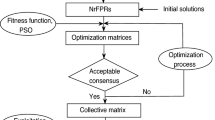
In recent years, the trust/distrust relationships among experts have increasingly played a key role in different phases of GDM problems, such as consensus model [9], aggregation [8], and incomplete preference values estimation [25]. In this paper, the sources of the trust/distrust relationships and their role in GDM process are depicted in Fig. 1.

Fig. 1
figure 1

The sources of the trust/distrust relationships and their role in GDM process

Full size image

3.1 The Construction of Trust/Distrust Relationships Among Experts with Direct Relationships

Trust is a relationship between a set of trusters and a set of trustees in a specified context. It can be conceptualized as follows: the truster is willing to depend upon the trustee and expects the trustee will do something that are important or valuable to the truster [26]. In GDM process, a more representative and knowledgeable expert is often more influential and easier to gain the trust of others.

The consistency degree is the similarity between the judgment matrix given by the expert and the completely consistent judgment matrix. The completely consistent judgment matrix is the optimal matrix, and the expert who gives this matrix has the highest knowledge level. The higher the consistency degree, the higher the knowledge level of the expert, and the easier it is for him/her to gain the trust of others. The consensus degree is defined by measuring the similarity between the expert’s judgment matrix and that of other experts. The expert with a high consensus degree can represent the opinions of the majority of experts, and he/she is more likely to win the trust of others.

Therefore, we use the expert’s consistency degree and consensus degree to represent his/her knowledge level and representative level, respectively. Here, we can give a definition of the trust/distrust relationships between two experts with a direct relationship.

Definition 6

Let \({\text{CD}}^{k}\) and \({\text{ACD}}^{k}\) be the consistency degree and the consensus degree of expert \(e_{k} ,\) respectively. If expert \(e_{h}\) is directly related to \(e_{k}\), then the trust degree of \(e_{h}\) to \(e_{k}\) is defined as follows:

$$T_{hk} = \omega_{1}^{h} {\text{CD}}^{k} + \omega_{2}^{h} {\text{ACD}}^{k} ,$$
(9)

where \(\omega_{1}^{h}\) and \(\omega_{2}^{h}\) are the weights of two factors given by \(e_{h}\), and they follow the conditions that \(0 \le \omega_{1}^{h} + \omega_{2}^{h} \le 1\) and \(0 \le \omega_{1}^{h} , \omega_{2}^{h} \le 1\).

Correspondingly, the distrust degree of \(e_{h}\) to \(e_{k}\) is defined as follows:

$$D_{hk} = \omega_{1}^{h} \left( {1 - {\text{CD}}^{k} } \right) + \omega_{2}^{h} \left( {1 - {\text{ACD}}^{k} } \right) .$$
(10)

Let \({{\lambda }}_{hk} = \left( {T_{hk} ,D_{hk} } \right)\) be a set of trust/distrust values expressed by IFN, called the trust function (TF), which can quantify the trust/distrust relationships from \(e_{h}\) to \(e_{k}\). The membership and non-membership degrees in IFN are replaced with \(T_{hk}\) and \(D_{hk} ,\) respectively. And the hesitation degree is \(1 - T_{hk} - D_{hk}\), which means the trust/distrust degrees from \(e_{h}\) to \(e_{k}\) cannot be exactly determined. In particular, when \(T_{hk} + D_{hk} = 1\), it means that \(e_{k}\) has complete trust/distrust state; otherwise, there exists trust/distrust knowledge with incompleteness.

3.2 The Propagation of Trust/Distrust Relationships for Experts with Indirect Relationships

Besides the direct relationships, there are indirect relationships between some experts, so they cannot acquire others’ information about knowledge and representativeness levels. A chain via trusted third partners (TTPs) can be built to propagate the trust/distrust relationships. During the propagation process, trust is decreasing, while distrust is increasing [7]. In order to describe this phenomenon, a new propagation operator \(P\) is proposed.

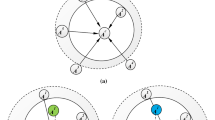
As shown in Fig. 2, there are three pairs of direct relationships, such as \(e_{1}\) to \(e_{2}\), \(e_{2}\) to \(e_{3}\), and \(e_{3}\) to \(e_{4}\). These direct relationships are represented by solid arrow lines. Obviously, \(e_{1}\) is not directly related to \(e_{3}\) and \(e_{4}\).

Fig. 2
figure 2

The propagation of trust/distrust relationships

Full size image

The trust/distrust relationships propagate from \(e_{1}\) to \(e_{3}\) via \(e_{2}\), which is defined as follows:

$$\left( {T_{13} ,D_{13} } \right) = P\left( {\left( {T_{12} ,D_{12} } \right),\left( {T_{23} ,D_{23} } \right)} \right) = \left( {T_{12} T_{23} ,D_{12} + T_{12} D_{23} } \right) .$$
(11)

Via \(e_{2}\), the trust degree of \(e_{1}\) to \(e_{3}\) is \(T_{13} = T_{12} T_{23}\). Because \(0 \le T_{12} , T_{23} \le 1\), there is \(T_{13} \le T_{12}\). The distrust degree of \(e_{1}\) to \(e_{3}\) is \(D_{13} = D_{12} + T_{12} D_{23}\), which indicates that the distrust of \(e_{1}\) to \(e_{3}\) inherits the distrust of \(e_{1}\) to \(e_{2}\). Because \(0 \le T_{12} , D_{23} \le 1\), there is \(D_{13} \ge D_{12}\). The propagation of trust/distrust relationships from \(e_{1}\) to \(e_{3}\) via \(e_{2}\) describes the reality that the trust decreases, while the distrust increases.

\(\left( {T_{12} ,D_{12} } \right)\) and \(\left( {T_{23} ,D_{23} } \right)\) are two TFs expressed by IFNs, so they meet the conditions of IFN, i.e., \(0 \le T_{12} + D_{12} \le 1\) and \(0 \le T_{23} + D_{23} \le 1\). It can be proved that the TF obtained by propagating the trust/distrust relationship from \(e_{1}\) to \(e_{3}\) via \(e_{2}\) also satisfies the condition of IFN, i.e., \(0 \le T_{13} + D_{13} \le 1\).

The trust/distrust relationships propagate from \(e_{1}\) to \(e_{4}\) via \(e_{3}\) is defined as follows:

$$\left( {T_{14} ,D_{14} } \right) = P\left( {\left( {T_{13} ,D_{13} } \right),\left( {T_{34} ,D_{34} } \right)} \right) = \left( {T_{13} T_{34} ,D_{13} + T_{13} D_{34} } \right),$$
(12)

where \(\left( {T_{13} ,D_{13} } \right)\) is calculated by Eq. (11).

Generally, the iterative formula of the trust/distrust relationships propagate from \(e_{1}\) to \(e_{j}\) is defined as follows:

$$\left( {T_{1j} ,D_{1j} } \right) = P\left( {\left( {T_{1,j - 1} ,D_{1,j - 1} } \right),\left( {T_{j - 1,j} ,D_{j - 1,j} } \right)} \right) = \left( {T_{1,j - 1} T_{j - 1,j} ,D_{1,j - 1} + T_{1,j - 1} D_{j - 1,j} } \right) .$$
(13)

If there is more than one trust/distrust relationships propagation path from \(e_{h}\) to \(e_{k}\), the shortest path should be selected to reduce information loss. If there are n shortest paths, the average value of the TF generated by each path is as follows:

$$\left( {T_{hk} ,D_{hk} } \right) = \frac{{\left( {T_{hk} ,D_{hk} } \right)^{{L_{1} }} + \left( {T_{hk} ,D_{hk} } \right)^{{L_{2} }} + \ldots + \left( {T_{hk} ,D_{hk} } \right)^{{L_{n} }} }}{n} ,$$
(14)

where \(\left( {T_{hk} ,D_{hk} } \right)^{{L_{\text{s}} }} \left( {s = 1,2, \ldots ,n} \right)\) represents the TF of \(e_{h}\) to \(e_{k}\) through the s-th shortest path.

The sociomatrix \(A = \left( {a_{ij} } \right)_{m \times m}\) is introduced in Sect. 2.1. When \(a_{hk} = 1\), it indicates that \(e_{h}\) is directly related to \(e_{k}\), and the knowledge level and representativeness level of \(e_{k}\) can be combined to build the trust/distrust relationships from \(e_{h}\) to \(e_{k}\). When \(a_{hk} = 0\), it means that there is indirect relationship from \(e_{h}\) to \(e_{k}\). Therefore, we need to propagate the trust/distrust relationships from \(e_{h}\) to \(e_{k}\) by using the propagation operator \(P\). Finally, we can constitute a complete trust/distrust relationships matrix \({\text{TM}} = \left( {{{\lambda }}_{hk} } \right)_{m \times m}\) according to direct and indirect relationships.

3.3 Comparisons with Existing Propagation Operators

Some existing propagation operators are shown in Table 1. Victor et al. [15] argued that trust is often a gradual phenomenon, and proposed t-norm to propagate trust and t-conorm to propagate distrust. Victor et al. [16] investigated three kinds of propagation operator, each with its own distinct behavior. Wang et al. [27] built a uninorm propagation operator that can propagate both trust and distrust simultaneously. Wu et al. [7] investigated a novel dual propagation operator based on the t-norm Einstein product and the t-conorm Einstein sum.

Table 1 Some existing propagation operators
Full size table

Some examples are given to compare the differences between these propagation operators and the propagation operator proposed in this paper. For convenience, the above propagation operators are abbreviated as \(P_{V1}\), \(P_{V2}\), \(P_{V3}\),\(P_{\text{TMAX}}\), \(P_{\text{DMAX}}\), \(P_{\text{KMAX}}\), \(P_{W} ,\) and \(P_{WU}\), and the propagation operator in this paper is abbreviated as \(P\).

There are three experts \(\left\{ {e_{1} ,e_{2} ,e_{3} } \right\}\) and two pairs of direct relationship, such as \(e_{1}\) to \(e_{2}\) and \(e_{2}\) to \(e_{3}\). But \(e_{1}\) is not directly related to \(e_{3}\).

Example 1

The TF of \(e_{1}\) to \(e_{2}\) is \(\left( {1,0} \right)\), and the TF of \(e_{2}\) to \(e_{3}\) is \(\left( {t,d} \right)\). The TFs of \(e_{1}\) to \(e_{3}\) calculated using the above propagation operators are shown in Table 2.

Table 2 The TFs of \(e_{1}\) to \(e_{3}\) in example 1
Full size table

In this example, \(e_{1}\) completely trusts \(e_{2}\), so the attitude of \(e_{1}\) to \(e_{3}\) should be the same as that of \(e_{2}\) to \(e_{3}\), i.e., \(\left( {T_{13} ,D_{13} } \right) = \left( {t,d} \right)\). \(P_{V1}\), \(P_{V2}\), \(P_{V3}\), \(P_{\text{WU}} ,\) and \(P\) can propagate the trust/distrust relationships from \(e_{1}\) to \(e_{3}\) well in this situation. \(P_{\text{TMAX}}\) selects the maximum trust degree in the propagation process, which is a most optimistic choice. \(P_{\text{DMAX}}\) selects the maximum distrust degree, which is a most pessimistic choice. \(P_{\text{KMAX}}\) selects the maximum trust degree and distrust degree simultaneously, which is a bold aggregation option. \(P_{\text{TMAX}}\), \(P_{\text{DMAX}}\), and \(P_{\text{KMAX}}\) do not embody the idea of propagation, so these three operators cannot well propagate the trust/distrust relationships from \(e_{1}\) to \(e_{3}\). Although \(P_{W}\) embodies the idea of propagation, it shares the limitation of decreasing trust and distrust simultaneously, which conflicts with human intuition because the propagating process via TTPs may produce information attenuation that makes trust degrees to decrease but distrust degrees to increase.

Example 2

The TF of \(e_{1}\) to \(e_{2}\) is \(\left( {0,1} \right)\), and the TF of \(e_{2}\) to \(e_{3}\) is \(\left( {t,d} \right)\). The TFs of \(e_{1}\) to \(e_{3}\) calculated using the above propagation operators are shown in Table 3.

Table 3 The TFs of \(e_{1}\) to \(e_{3}\) in Example 2
Full size table

In this example, \(e_{1}\) completely distrusts \(e_{2}\), so \(e_{1}\) should not trust \(e_{3}\) at all, i.e., \(\left( {T_{13} ,D_{13} } \right) = \left( {0,1} \right)\). Both \(P_{\text{WU}}\) and \(P\) can propagate the trust/distrust relationships from \(e_{1}\) to \(e_{3}\) well in this situation. \(P_{V1}\) uses t-norm to propagate trust and t-conorm to propagate distrust, which could not propagate both trust and distrust at the same time. When \(T_{12} + D_{12} = 1\), \(P_{V2}\) degrades to \(P_{V1}\), so they have the same disadvantage. Although \(P_{V3}\) can determine that the friend’s friend is a friend in Example 1, it cannot determine the information of enemy’s friend.

Example 3

The TF of \(e_{1}\) to \(e_{2}\) is \(\left( {0.5,0.5} \right)\), and the TF of \(e_{2}\) to \(e_{3}\) is \(\left( {0.5,0.5} \right)\). The TFs of \(e_{1}\) to \(e_{3}\) calculated using the above propagation operators are shown in Table 4.

Table 4 The TFs of \(e_{1}\) to \(e_{3}\) in Example 3
Full size table

In practice, propagating trust/distrust relationships via TTPs should result in trust degrees to decrease, while distrust degrees to increase. Therefore, \(D_{13}\) should be greater than \(T_{13}\) in this example. \(P_{V3}\), \(P_{\text{WU}} ,\) and \(P\) can all propagate the trust/distrust relationships from \(e_{1}\) to \(e_{3}\) well in this situation.

In conclusion, \(P\) has good properties like \(P_{\text{WU}}\), which not only calculates the TF in the hesitant fuzzy cases but also describes the fact that the trust decreases, while the distrust increases during the propagation process.

4 Consensus Model Based on the Social Network Relationships Density and the Trust/Distrust Relationships Matrix

It is necessary to reach consensus for experts in the process of solving GDM problems although the difference of experts’ preference values may be large. Set the threshold \(\delta\) such that \(\delta \in \left[ {0.5,1} \right]\). When the consensus degrees of all experts are not smaller than \(\delta\), the group reaches consensus; otherwise, consensus model will be used to modify the preference values of experts whose consensus degrees are less than \(\delta\).

The relationship between CI and consensus degree is not always monotonically increasing, i.e., the group with the highest consensus degree may not have the highest level of CI. When the consensus degree is too high, the distrust relationship is beneficial to the improvement of CI, because it allows the group to better explore the decision space rather than prematurely converging on an agreed suboptimal solution [12]. Therefore, in the consensus model constructed in this paper, both the preference values of trusted experts and distrusted experts should be considered for the purpose to improve the consensus degree and CI level simultaneously.

The findings in Ref. [12] showed that the social network relationships density affects the relationship between scopes of distrust and CI level. For low density (\(0 \le \rho \le 0.3\)), CI level diminishes as the scope of distrust rises. For medium or high density (\(\rho > 0.3\)), an inverted-U trend is achieved. Inspired by this idea, when establishing the consensus model, for low density, the expert’s preference values will be modified according to the preference values of trusted experts; for medium or high density, the expert’s preference values will be modified according to the preference values of both trusted and distrusted experts.

In this paper, we introduce the concept of the social network relationships density based on the sociomatrix and give the following definition according to the ideas of Geffroy et al. [28].

Definition 7

The social network relationships density \(\rho\) is defined as follows:

$$\rho = \frac{{\mathop \sum \nolimits_{i = 1}^{m} \mathop \sum \nolimits_{j = 1}^{m} a_{ij} }}{{m\left( {m - 1} \right)}} ,$$
(15)

where \(a_{ij}\) is the element in the sociomatrix \(\left( {a_{ij} } \right)_{m \times m}\), and \(m\left( {m - 1} \right)\) indicates the total number of possible social network relationships.

Let \(\alpha\) be the threshold. If \(\rho < \alpha\), then social network relationships density is low; otherwise, it is medium or high. According to the result in Ref. [12], let \(\alpha = 0.3\).

Suppose \(m\) experts form a group of experts \(\left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}\). Given the threshold \(\beta\), when \(T_{hk} \ge \beta\), there is a trust relationship between \(e_{h}\) and \(e_{k}\); otherwise, there is a distrust relationship. By this rule, let \({\text{TS}}^{h} = \left\{ {e_{\left( 1 \right)}^{h} ,e_{\left( 2 \right)}^{h} , \ldots ,e_{\left( t \right)}^{h} } \right\} \subseteq \left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}\) be the set of experts trusted by \(e_{h}\), where \(t\) is the number of trusted experts. Meanwhile, \({\text{DS}}^{h} = \left\{ {e_{\left[ 1 \right]}^{h} ,e_{\left[ 2 \right]}^{h} , \ldots ,e_{\left[ d \right]}^{h} } \right\} \subseteq \left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}\) is the set of experts distrusted by \(e_{h}\), where \(d\) is the number of distrusted experts.

Assume \(e_{x}\) is the expert with the lowest consensus degree, \({\text{APS}}^{x}\) is the set of \(q\) elements with the lowest consensus degree of \(e_{x}\). Then the elements in \({\text{APS}}^{x}\) are modified as follows:

$$\overline{r}_{ij}^{x} = \left\{ {\begin{array}{*{20}l} {\left( {1 - \theta_{1} } \right)r_{ij}^{x} + \theta_{1} r_{ijT}^{x} , \quad \quad \rho \le 0.3} \hfill \\ {\left( {1 - \theta_{2} - \theta_{3} } \right)r_{ij}^{x} + \theta_{2} r_{ijT}^{x} + \theta_{3} r_{ijD}^{x} , \quad \rho > 0.3} \hfill \\ \end{array} } \right.,$$
(16)

where \(r_{ijT}^{x} = \frac{{r_{ij\left( 1 \right)}^{x} + r_{ij\left( 2 \right)}^{x} + \ldots + r_{ij\left( t \right)}^{x} }}{t}\) and \(r_{ijD}^{x} = \frac{{r_{ij\left[ 1 \right]}^{x} + r_{ij\left[ 2 \right]}^{x} + \ldots + r_{ij\left[ d \right]}^{x} }}{d}\). \(\left\{ {r_{ij\left( 1 \right)}^{x} ,r_{ij\left( 2 \right)}^{x} , \ldots ,r_{ij\left( t \right)}^{x} } \right\}\) and \(\left\{ {r_{ij\left[ 1 \right]}^{x} ,r_{ij\left[ 2 \right]}^{x} , \ldots ,r_{ij\left[ d \right]}^{x} } \right\}\) are the preference values of trusted and distrusted experts, respectively. \(\theta_{1}\), \(\theta_{2} ,\) and \(\theta_{3}\) are modified parameters that satisfy the conditions of \(\theta_{1} ,\theta_{2} ,\theta_{3} \in \left[ {0,1} \right]\) and \(\theta_{2} + \theta_{3} \in \left[ {0,1} \right]\). However, excessive adoption of the preference values of distrusted experts is detrimental to the improvement of CI level, so there is \(\theta_{2} > \theta_{3}\).

According to the above analysis, the consensus model proposed in this paper can be summarized as follows:

Input: A problem with \(n\) alternatives. A group of experts \(\left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}\), whose sociomatrix and trust/distrust relationships are represented by \(A = \left( {a_{hk} } \right)_{m \times m}\) and \(TM = \left( {{{\lambda }}_{hk} } \right)_{m \times m} ,\) respectively. The judgment matrix given by each expert is \(R^{h} = \left( {r_{ij}^{h} } \right)_{n \times n}\) \(\left( {h = 1,2, \ldots ,m} \right)\). The threshold value of consensus degree is \(\delta\), the parameter in the consensus measurement is \(q\), the modified parameters are \(\theta_{1}\), \(\theta_{2} ,\) and \(\theta_{3}\), and the maximum number of consensus modification is limited to \(l_{\hbox{max} }\).

Output: \(R^{h} = R_{l}^{h}\).

  • Step 1. Set \(l = 0\), and \(R_{0}^{h} = \left( {r_{ij,0}^{h} } \right)_{n \times n}\).

  • Step 2. Use Eq. (15) to obtain \(\rho\).

  • Step 3. Compute \({\text{CE}}_{ijl} \left( {R^{h} ,R^{k} } \right)\) and \({\text{ACE}}_{ijl}^{h}\) by Eqs. (6) and (7), respectively.

  • Step 4. Identify the \(q\) elements and form \({\text{APS}}^{h}\).

  • Step 5. Calculate \({\text{ACD}}_{l}^{h}\) by Eq. (8).

  • Step 6. If \({\text{ACD}}_{l}^{h} \ge \delta\) or \(l \ge l_{\hbox{max} }\), output \(R^{h} = R_{l}^{h}\). Otherwise, identify the expert \(e^{x}\) \(\left( {e^{x} \in \left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}} \right)\) with the lowest consensus degree. Then ask \(e^{x}\) whether he/she agrees to change his/her preference values. If not, exclude \(e^{x}\) from the group and turn to Step 3. Otherwise, continue with the next step.

  • Step 7. Derive \({\text{TS}}^{x}\) and \({\text{DS}}^{x}\), and calculate \(r_{ijT}^{x}\) and \(r_{ijD}^{x}\). Set \(l = l + 1\). If \(\rho \le 0.3\), modify the preference values of \(e^{x}\) to \(r_{ij,l}^{x} = \left\{ {\begin{array}{*{20}l} {r_{ij,l - 1}^{x} ,} \hfill & {\left( {i,j} \right) \notin {\text{APS}}^{x} } \hfill \\ {\left( {1 - \theta_{1} } \right)r_{ij,l - 1}^{x} + \theta_{1} r_{ijT}^{x} ,} \hfill & {\left( {i,j} \right) \in {\text{APS}}^{x} } \hfill \\ \end{array} } \right..\) Otherwise, modify them to \(r_{ij,l}^{x} = \left\{ {\begin{array}{*{20}l} {r_{ij,l - 1}^{x} ,} \hfill & {\left( {i,j} \right) \notin {\text{APS}}^{x} } \hfill \\ {\left( {1 - \theta_{2} - \theta_{3} } \right)r_{ij,l - 1}^{x} + \theta_{2} r_{ijT}^{x} + \theta_{3} r_{ijD}^{x} , } \hfill & {\left( {i,j} \right) \in {\text{APS}}^{x} } \hfill \\ \end{array} } \right.\). The modified judgment matrix is denoted as \(R_{l}^{x} = \left( {r_{ij,l}^{x} } \right)_{n \times n}\). Then turn to Step 3.

Theorem 1

Suppose there are m experts \(e_{1} ,e_{2} , \ldots ,e_{m}\), and their judgment matrices are \(R^{1} ,R^{2} , \ldots ,R^{m}\). It can be assumed that the consensus degree of \(e_{m}\) is lower than the threshold value, and \(e_{m}\) is the expert with the lowest consensus degree. After modifying the preference values of \(e_{m}\) according to the consensus model, the new judgment matrix of \(e_{m}\) is \(\overline{R}^{m}\), and the consensus degree of \(e_{m}\) is improved, i.e., \(\overline{\text{ACD}}^{m} > {\text{ACD}}^{m}\).

The proof of Theorem 1 is shown in "Appendix A". Theorem 1 gives us a further insight into the consensus model. When we modify the preference values of experts whose consensus degree is lower than the predefined threshold value, we first modify the preference values of expert \(e_{m}\) with the lowest consensus degree. If the consensus degree of \(e_{m}\) does improve, then the consensus model is valid.

5 Alternatives Selection Process Based on the Trust/Distrust Relationships

When the consensus degrees of the experts are greater than the predefined threshold value, the group has reached consensus, and then we can select the optimal alternative. The process of alternatives selection can be divided into two stages: the aggregation of experts’ judgment matrices and the ranking of alternatives.

Generally, the more the trusted by other experts, the more influential power the expert has. Thus, he/she can be given a higher weight, so his/her preference values ought to be considered more in the process of aggregating the experts’ judgment matrices. Liang et al. [29] determined the importance score of the expert \(e^{h}\) by using the trust/distrust relationships matrix.

$${\text{IS}}_{h} = \frac{1}{{2\left( {m - 1} \right)}}\mathop \sum \limits_{k = 1,k \ne h}^{m} \left( {T_{kh} - D_{kh} + 1} \right) .$$
(17)

Thus, the importance vector of experts can be represented by \({\text{IS}} = \left( {{\text{IS}}_{1} ,{\text{IS}}_{2} , \ldots ,{\text{IS}}_{m} } \right)^{\text{T}}\), which is normalized as follows:

$$\overline{\text{IS}}_{h} = \frac{{{\text{IS}}_{h} }}{{{\text{IS}}_{1} + {\text{IS}}_{2} + \ldots + {\text{IS}}_{m} }} .$$
(18)

Then the weight of \(e^{h}\) is \(\omega_{h} = \overline{\text{IS}}_{h}\), and the weight vector of experts is denoted by \(\omega = \left( {\omega_{1} , \omega_{2} , \ldots ,\omega_{m} } \right)^{\text{T}}\).

In this paper, the judgment matrices of experts are aggregated by the intuitionistic fuzzy weighted average (IFWA) operator, and then the group judgment matrix \(S = \left( {s_{ij} } \right)_{n \times n}\) is generated as follows:

$$s_{ij} = {\text{IFWA}}_{\omega } \left( {r_{ij}^{1} ,r_{ij}^{2} , \ldots ,r_{ij}^{m} } \right) = \left( {1 - \mathop \prod \limits_{k = 1}^{m} \left( {1 - \mu_{ij}^{k} } \right)^{{\omega_{k} }} ,\mathop \prod \limits_{k = 1}^{m} \left( {\gamma_{ij}^{k} } \right)^{{\omega_{k} }} } \right).$$
(19)

Wang and Li [30] proposed Eq. (20) to obtain the score function of the i-th alternative. Then, the alternatives can be ranked in descending order of score.

$$f_{i} = \mathop \sum \limits_{j = 1}^{n} \left( {\mu_{ij} - \mu_{ji} } \right).$$
(20)

The larger the value of \(f_{i}\), the better the alternative \(x_{i}\). If two or more alternatives have the same score function value, then the exact function \(h_{i}\) [31] of these alternatives can be constructed as follows:

$$h_{i} = \mathop \sum \limits_{j = 1}^{n} \left( {\mu_{ij} + \gamma_{ij} } \right).$$
(21)

The alternative with the larger value of \(h_{i}\) is better provided that the value of score function is equal. In conclusion, we have the following properties:

  1. (1)

    If \(f_{1} > f_{2}\), then \(x_{1} \succ x_{2}\).

  2. (2)

    If \(f_{1} = f_{2}\), then

    1. (i)

      if \(h_{1} = h_{2}\), then \(x_{1} \sim x_{2}\);

    2. (ii)

      if \(h_{1} > h_{2}\), then \(x_{1} \succ x_{2}\);

    3. (iii)

      if \({\text{h}}_{1} < {\text{h}}_{2}\), then \({\text{x}}_{1} \prec {\text{x}}_{2}\).

Figure 3 shows the process of solving the intuitionistic fuzzy GDM problem discussed in this paper. Specifically, it consists of the following seven steps: (1) Convene a group of experts and obtain the sociomatrix; (2) Obtain the IFRRM of each expert; (3) Calculate the consensus degree and consistency degree of each expert; (4) Model the trust/distrust relationships among experts; (5) Modify the preference values of experts whose consensus degrees are lower than the predefined threshold value; (6) Aggregate the preference value of each expert; and (7) Derive the ranking order of alternatives.

Fig. 3
figure 3

The process of solving the intuitionistic fuzzy GDM problem

Full size image

The fourth and fifth steps are the main advantages of the methods proposed in this paper, which have been introduced in Sects. 3 and 4, respectively.

6 Illustrative Example and Comparative Analysis

In this section, we will illustrate an example and conduct comparative analysis to demonstrate the effectiveness and applicability of the proposed method.

6.1 Illustrative Example

The example of solving an intuitionistic fuzzy GDM problem in Ref. [32] is selected here. In the example, the selection of outstanding Ph.D. students for China scholarship council which has very practical significance is studied. To simplify the presentation, four candidate Ph.D. students represented by \(\left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right\}\) are evaluated by five experts represented by \(\left\{ {e_{1} ,e_{2} ,e_{3} ,e_{4} ,e_{5} } \right\}\). The social network relationships among the five experts is shown in Fig. 4.

Fig. 4
figure 4

The social network relationships of the five experts

Full size image

The corresponding sociomatrix of Fig. 4 is generated as follows:

$$A = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 1 \\ 1 & 0 \\ 1 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \\ \end{array} } \right).$$

The IFRRMs given by the five experts are shown as follows:

$$R^{1} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.5,0.2} \right)} \\ {\left( {0.2,0.5} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.7,0.1} \right)} & {\left( {0.5,0.3} \right)} \\ {\left( {0.6,0.2} \right)} & {\left( {0.3,0.6} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.1,0.7} \right)} & {\left( {0.2,0.6} \right)} \\ {\left( {0.3,0.5} \right)} & {\left( {0.6,0.3} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.3,0.6} \right)} \\ {\left( {0.6,0.3} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } \\ \end{array} } \right),$$
$$R^{2} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.6,0.2} \right)} \\ {\left( {0.2,0.6} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.8,0.2} \right)} & {\left( {0.6,0.3} \right)} \\ {\left( {0.5,0.3} \right)} & {\left( {0.3,0.5} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.2,0.8} \right)} & {\left( {0.3,0.5} \right)} \\ {\left( {0.3,0.6} \right)} & {\left( {0.5,0.3} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.3,0.6} \right)} \\ {\left( {0.6,0.4} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } \\ \end{array} } \right),$$
$$R^{3} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.6,0.2} \right)} \\ {\left( {0.2,0.6} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.8,0.1} \right)} & {\left( {0.6,0.2} \right)} \\ {\left( {0.6,0.3} \right)} & {\left( {0.3,0.4} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.1,0.8} \right)} & {\left( {0.3,0.6} \right)} \\ {\left( {0.2,0.6} \right)} & {\left( {0.4,0.3} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.2,0.5} \right)} \\ {\left( {0.5,0.2} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } \\ \end{array} } \right),$$
$$R^{4} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.6,0.2} \right)} \\ {\left( {0.2,0.6} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.7,0.2} \right)} & {\left( {0.6,0.3} \right)} \\ {\left( {0.5,0.3} \right)} & {\left( {0.3,0.4} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.2,0.7} \right)} & {\left( {0.3.0.5} \right)} \\ {\left( {0.3,0.6} \right)} & {\left( {0.4,0.3} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.3,0.6} \right)} \\ {\left( {0.6,0.3} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } \\ \end{array} } \right),$$
$$R^{5} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.7,0.1} \right)} \\ {\left( {0.1,0.7} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.6,0.2} \right)} & {\left( {0.4,0.3} \right)} \\ {\left( {0.6,0.1} \right)} & {\left( {0.3,0.6} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.2,0.6} \right)} & {\left( {0.1,0.6} \right)} \\ {\left( {0.3,0.4} \right)} & {\left( {0.6,0.3} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.5,0.5} \right)} & {\left( {0.3,0.5} \right)} \\ {\left( {0.5,0.3} \right)} & {\left( {0.5,0.5} \right)} \\ \end{array} } \\ \end{array} } \right).$$

  • Step 1. Calculate the consistency degree and consensus degree of each expert.

    From Eq. (5), we can obtain the consistency degrees of the five experts such that \({\text{CD}}^{1} = 0.9661\), \({\text{CD}}^{2} = 0.9833\), \({\text{CD}}^{3} = 0.9856\), \({\text{CD}}^{4} = 0.9912\), and \({\text{CD}}^{5} = 0.9298\).

    In this example, we select the parameter \(q = 5\). According to Eqs. (7) and (8), the consensus degrees of the five experts are generated such that \({\text{ACD}}^{1} = 0.9080\), \({\text{ACD}}^{2} = 0.9240\), \({\text{ACD}}^{3} = 0.9000\), \({\text{ACD}}^{4} = 0.9200\), and \({\text{ACD}}^{5} = 0.8680\).

  • Step 2. Construct the trust/distrust relationships.

    Assuming that the weight matrix of each expert in constructing the trust/distrust relationships based on the knowledge level and representativeness level is \(\begin{array}{*{20}c} { {\text{CD}} {\text{ACD}} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ {e_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {e_{4} } \\ {e_{5} } \\ \end{array} } \\ \end{array} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0.35} & {0.55} \\ {0.25} & {0.65} \\ {0.30} & {0.60} \\ \end{array} } \\ {\begin{array}{*{20}c} {0.35} & {0.55} \\ {0.25} & {0.65} \\ \end{array} } \\ \end{array} } \right)} \\ \end{array}\).

    The complete trust/distrust relationships matrix is generated by Eqs. (9)–(14) as follows:

    $${\text{TM}} = \left( {\begin{array}{*{20}l} {\left( { - , - } \right)} \hfill & {\left( {0.70,0.12} \right)} \hfill & {\left( {0.84,0.06} \right)} \hfill & {\left( {0.71,0.10} \right)} \hfill & {\left( {0.80,0.10} \right)} \hfill \\ {\left( {0.83,0.07} \right)} \hfill & {\left( { - , - } \right)} \hfill & {\left( {0.70,0.12} \right)} \hfill & {\left( {0.85,0.05} \right)} \hfill & {\left( {0.67,0.15} \right)} \hfill \\ {\left( {0.71,0.11} \right)} \hfill & {\left( {0.85,0.05} \right)} \hfill & {\left( { - , - } \right)} \hfill & {\left( {0.85,0.05} \right)} \hfill & {\left( {0.68,0.14} \right)} \hfill \\ {\left( {0.84,0.06} \right)} \hfill & {\left( {0.68,0.14} \right)} \hfill & {\left( {0.69,0.13} \right)} \hfill & {\left( { - , - } \right)} \hfill & {\left( {0.80,0.10} \right)} \hfill \\ {\left( {0.70,0.11} \right)} \hfill & {\left( {0.85,0.05} \right)} \hfill & {\left( {0.83,0.07} \right)} \hfill & {\left( {0.71,0.11} \right)} \hfill & {\left( { - , - } \right)} \hfill \\ \end{array} } \right).$$

  • Step 3. Modify the preference values of the expert with lowest consensus degree.

    First, the social network relationships density of the group is calculated by Eq. (15) as \(\rho = 0.5\), which means that the group belongs to the group with medium density. Therefore, the expert’s preference values will be modified according to the preference values of the trusted and distrusted experts.

    Then, we set the threshold values of consensus degree and trust as \(\delta = 0.9\) and \(\beta = 0.8\), respectively. Since \({\text{ACD}}^{5} = 0.8680\), which is smaller than the predefined threshold value, it is necessary to modify the preference values of \(e_{5}\). Suppose that \(e_{5}\) accepts the preference values modifications. Therefore, we obtain \({\text{TS}}^{5} = \left\{ {e_{2} ,e_{3} } \right\}\) and \({\text{DS}}^{5} = \left\{ {e_{1} ,e_{4} } \right\}\). We assume that the modified parameters \(\theta_{2} = 0.2\) and \(\theta_{3} = 0.1\); then the modified IFRRM of \(e_{5}\) is generated as follows:

    $$\overline{R}^{5} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.50,0.50} \right)} & {\left( {0.67,0.13} \right)} \\ {\left( {0.13,0.67} \right)} & {\left( {0.50,0.50} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.65,0.19} \right)} & {\left( {0.46,0.29} \right)} \\ {\left( {0.60,0.10} \right)} & {\left( {0.30,0.60} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.20,0.60} \right)} & {\left( {0.16,0.59} \right)} \\ {\left( {0.30,0.40} \right)} & {\left( {0.60,0.30} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.50,0.50} \right)} & { \left( {0.30,0.50} \right)} \\ {\left( {0.50,0.30} \right)} & {\left( {0.50,0.50} \right)} \\ \end{array} } \\ \end{array} } \right).$$

    After modifying the preference values of \(e_{5}\), we recalculate the consensus degrees of the five experts such that \(\overline{\text{ACD}}^{1} = 0.9172\), \(\overline{\text{ACD}}^{2} = 0.9300\), \(\overline{\text{ACD}}^{3} = 9052\), \(\overline{\text{ACD}}^{4} = 0.9284,\) and \(\overline{\text{ACD}}^{5} = 0.9016\). The group reaches the preset consensus degree threshold value, and the group judgment matrix can be calculated in Step 4.

  • Step 4. Generate the group judgment matrix.

    According to Eqs. (17) and (18), the weight vector of the five experts is generated as \(\omega = \left( {0.2005,0.20162,0.1997,0.2032,0.1951} \right)^{\text{T}}\). Thus, the group judgment matrix obtained by fusing each expert’s IFRRM through Eq. (19) is shown as follows:

    $$S = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {0.50,0.50} \right)} & {\left( {0.60,0.18} \right)} \\ {\left( {0.19,0.59} \right)} & {\left( {0.50,0.50} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.74,0.15} \right)} & {\left( {0.56,0.27} \right)} \\ {\left( {0.56,0.22} \right)} & {\left( {0.30,0.49} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {0.16,0.72} \right)} & {\left( {0.25,0.56} \right)} \\ {\left( {0.28,0.53} \right)} & {\left( {0.51,0.30} \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\left( {0.50,0.50} \right)} & { \left( {0.28,0.56} \right)} \\ {\left( {0.56,0.29} \right)} & {\left( {0.50,0.50} \right)} \\ \end{array} } \\ \end{array} } \right).$$

  • Step 5. Rank order of alternatives.

    According to Eq. (20), the score function values of alternatives are \(f_{1} = 1.76\), \(f_{2} = - 0.31\), \(f_{3} = - 1.17\) and \(f_{4} = 0.21\). So the ranking of these four alternatives is \(x_{1} \succ x_{4} \succ x_{2} \succ x_{3}\), which is the same as the results obtained by Liao et al. [32], indicating that the method proposed in this paper can effectively solve the GDM problem.

6.2 Comparative Analysis

Several representative and similar methods are selected here for the purpose to conduct comparative analysis against the method proposed in this paper. The differences among them are shown in Table 5.

Table 5 Comparisons of the proposed method against several typical methods
Full size table
  1. (1)

    In terms of the trust/distrust relationships construction.

    Although Capuano et al. [33], Liang et al. [29], and Kamis et al. [34] discussed the interactions among experts and studied the strength of the relationship among experts, the trust/distrust relationships among experts were not considered.

    Wu et al. [7] assumed that incomplete trust/distrust relationships were given previously, and used a propagation operator to construct the complete trust/distrust relationship. If there are multiple propagation paths between the two experts, Wu et al. [7] selected the shortest propagation path to reduce information loss. Dong et al. [35] reviewed some existing propagation operators and summarized two types of propagation operators based on one propagation path and multiple propagation paths.

    Li et al. [36] built a trust relationship between two experts by fusing information from three aspects: the social relations among experts, experts’ social statuses, and their knowledge abilities. For experts who are directly related to each other, this method can be used to build a trust relationship between them, but for experts who are not directly related to each other, they cannot possess the information about each other’s social status and knowledge ability. In order to solve these problems, we proposed to construct and propagate the trust/distrust relationships for experts with direct and indirect relationships, respectively.

  2. (2)

    In terms of the consensus model.

    Capuano et al. [33] proposed that each expert will take into account the preference values of other experts in the GDM process, which is called opinion evolution. After several rounds of opinion evolution, the experts’ preference values will be stable. Usually, experts cannot reach consensus on the preference values at this time, so an opinion management strategy is needed to help them reach consensus. The following approaches of managing opinions have been developed: changing the network structure and adjusting opinions.

    In the consensus model, it is assumed that \(e_{h}\) is an expert whose consensus degree is lower than the predefined threshold value. Liang et al. [29] suggested that \(e_{h}\) should modify his/her preference values closer to the preference values of \(e_{k}\) with the minimum preference similarity to \(e_{h}\). Kamis et al. [34] used the centrality concept as a way of determining the most important person in a network, and suggested that \(e_{h}\) should modify his/her preference values closer to the preference values of \(e_{k}\) with the highest centrality index. However, the same problem in Liang and Kamis’s methods is that \(e_{k}\) may not be the one \(e_{h}\) trusts, while \(e_{h}\) may not willing to be closer to \(e_{k}\).

Both Wu et al. [7] and Li et al. [36] proposed a consensus model to modify the preference values of \(e_{h}\) closer to the preference values of \(e_{k}\) trusted by him/her. Dong et al. [35] advised \(e_{h}\) to modify his/her preference values closer to the collective preference values, which can quickly improve the consensus of \(e_{h}\). However, the preference values of \(e_{k}\) and collective one may not be the optimal result, which may make the preference values of \(e_{h}\) quickly converge in an agreed suboptimal solution. Therefore, these three consensus models are not conducive to the improvement of CI level.

The above methods did not fully consider whether \(e_{h}\) is willing to modify his/her preference values. Liao et al. [32] proposed a consensus model that when \(e_{h}\) does not agree to modify his/her preference values, \(e_{h}\) will be excluded from the group because his/her preference values are quite different from the group; otherwise, \(e_{h}\) will modify his/her preference values. Comparing with other consensus models, the iterative consensus reaching process in Ref. [32] is more appropriate to some extent.

The consensus model given in this paper also considered whether experts are willing to modify their own preference values, and gave modification opinions for them. For the group with low density, only the preference values of trusted experts are considered when the preference values of \(e_{h}\) is modified. The reason lies in that the preference values of distrusted experts are not conducive to the improvement of CI level. For the group with medium or high density, the preference values of trusted and distrusted experts are considered when the preference values of \(e_{h}\) is modified, because preference values of distrusted experts make the group better explore the decision space.

7 Conclusion

In this paper, we proposed a method to solve the intuitionistic fuzzy GDM problem with low consensus degree considering social network. Its main advantages are as follows: (1) The trust/distrust relationships between two experts with direct relationships are established based on knowledge levels and representativeness levels, and the trust/distrust relationships between two experts with indirect relationships are built by using a new propagation operator. (2) A consensus model is proposed for the purpose of improving the consensus degree and CI level.

Although the consensus model proposed in this paper allows experts to reach consensus, it is not able to determine the exact values of the modified parameters to provide the optimal balance between group consensus and individual independence, i.e., the minimum change of the original preference values required to reach the consensus threshold. This aspect is worthy of further work, and thus, we will study the optimal choices of the modified parameters \(\theta_{1}\), \(\theta_{2} ,\) and \(\varepsilon_{2}\).