An Alternative Consensus Model of Additive Preference Relations for Group Decision Making Based on the Ordinal Consistency

Abstract

Pairwise comparison is a useful tool to express decision makers’ (DMs’) preferences in the group decision-making (GDM) problems. However, the preferences provided by pairwise comparisons could be self-contradictory, i.e., ordinal inconsistencies exist. Therefore, before reaching consensus, the first thing is to assure the DM’s judgments that are not contradictory. As the purpose of the GDM is to choose most preferred alternative, the consensus degree for each alternative of all the DMs should be measured. In the present paper, an alternative consensus model for additive preference relations (APRs) based on ordinal consistency (OC) is developed. An algorithm is applied to detect and adjust the ordinally inconsistent elements for APRs. Then the alternative rankings for each ordinally consistent APR and the aggregated APR is obtained, respectively. A model is designed to change the DMs’ importance, which increases the alternative consensus degree. The proposed model does not change the DMs’ preferences, aiming to make full use of the DMs’ judgements. Finally, an illustrative example and comparisons with the current approaches are furnished to demonstrate the effectiveness of the developed method.

1 Introduction

Group decision making (GDM) involves a set of decision makers (DMs) to take part in a decision-making process. Nowadays, numerous studies have been proposed to deal with GDM problems [1,2,3,4,5,6]. Generally, the consensus reaching process (CRP) and the selection process are performed to receive the final ranking of the alternatives [7, 8]: the consensus process and the selection process. Various consensus methods have been developed to manage diverse preference relations (PRs), such as additive preference relations (APRs) [9,10,11,12,13], multiplicative preference relations (MPRs) [14,15,16], linguistic preference relations (LPRs) [17,18,19,20], intuitionistic fuzzy preference relations (IFPRs) [21], hesitant fuzzy preference relations (HFPRs) [22,23,24,25,26,27], and heterogeneous preferences in GDM [28, 29]. In this paper, we applied a consistency process before the selection process and the consensus process, and the consensus model is based on the ordinal consistency (OC) of APRs.

Classically, it is rare to obtain the unanimous and complete agreement on a specific problem for all the DMs. Thus, a “soft” consensus [29,30,31] is adopted in real applications. At present, the majority of the research studies pay attention to making the individual DMs closer to the group, which generally includes the individual consistency process (ICP) and CRP [32]. The ICP is usually applied to transform an inconsistent preference relation into one with acceptable consistency. It is generally measured by a consistency index (CI) [10, 14, 15, 19]. The CRP is a negotiation process which involves some consensus rounds, in which the DMs revise their judgements according to the recommendations offered by a moderator. It is measured by a group consensus index (GCI) [10, 11, 24, 33,34,35,36]. Whether the CI and GCI are predefined in advance, and there is no rule to determine their threshold, then it is too arbitrary.

The OC means a logical person will not express contradictory judgments [37, 38]. Thus, it is the basic requirement that should be satisfied firstly. The CI is generally used to measure the cardinal consistency of a PR. However, if a PR is of cardinal consistency, it cannot assure the OC, and it may still contain contradictory information. Thus, the OC should be considered firstly. In the CRP, if the DMs change their preferences to narrow their judgments to the group judgements, it will distort the DMs’ original information. Thus, to develop a consensus model that does not change DMs’ judgements is a more rational way to deal with the consensus problem, which motivates us to change the weights of the DMs. Additionally, as the objective of the GDM problem is to choose the most preferred alternative(s), it is naturally that the best alternative should have the highest agreement level among all the DMs. Thus, the alternative consensus level should be measured. Recently, related lines of research have been hotly studied [4, 39].

Lots of the present consensus models have the drawbacks as below: (1) Some of them do not include the ICP [9, 11], or most of the ICPs are measured by the CI [10, 14], which is based on the cardinality consistency index. However, CI cannot assure whether the information provided by DM is self-contradictory. (2) Most of the consensus degrees are measured by the GCI [10, 11, 16], which measures the differences of preferences between a single DM and the group. However, in order to select the most preferred alternative, we should pay attention to the DMs’ consensus degree on the alternatives. (3) To sufficiently use the DMs’ judgments, it is mostly desired that the DMs’ original information unchanged.

In order to overcome the shortcomings of the present methods, this paper proposes a new consensus model for APRs, which contains the following three folds: (1) The OC of an APR is used in the ICP; (2) the alternative consensus level is proposed to measure the consensus degree; (3) a weight updating model is proposed to reaching consensus, while keeping the DMs’ preference information unchanged.

The main advantages of the proposed methods are:

• 1. As we use the OC to measure the consistency degrees of APRs, it does not need to give the CI in advance, and the OC can assure the basic reasonableness of the DMs’ judgements.

• 2. In the CRP, we measure the alternative consensus levels among all the DMs, which is different to the consensus of individual DM to the group one. It depends on how many alternatives the DMs want to select.

• 3. In the CRP, a weight-changing model is used to revise the DMs’ importance, which does not change the DMs’ judgements of ordinally consistent APRs. This will not distort the DMs’ original judgments.

The remainder of the paper is structured below. Section 2 gives the preliminaries of the paper, including the definition of APR, the weighted arithmetic averaging (WAA) operator, and the OC of an APR. Section 3 proposes an alternative consensus model of APRs based on OC. Section 4 provides an example, and a comparative analysis is also performed. The conclusions are given in Sect. 5.

2 Preliminaries

In the following, the definitions of the APR, the WAA operator, and the OC of APRs are reviewed. In addition, an algorithm to examine and improve the OC of an APR is also offered.

2.1 The APR

For the sake of simplicity, $N = \{ 1,2, \ldots ,n\}$, $M = \{ 1,2, \ldots ,m\}$. $X = \{ x_{1} ,x_{2} , \ldots ,x_{n} \}$$(n \ge 2)$ denotes a set of alternatives; $D = \{ d_{1} ,d_{2} , \ldots ,d_{m} \}$$\left( {m \ge 2} \right)$ denotes a set of DMs. Each DM $d_{k}$, $k \in M$, provides his/her comparisons on alternatives using a 0–1 scale, and all the preference values consist of an APR [40,41,42,43,44]. We use $P = (p_{ij} )_{n \times n}$ to represent the APR. $p_{ij}$ indicates the preference degree of the alternative $x_{i}$ over $x_{j}$:

• (1) $p_{ij} = 0.5$ indicates that $x_{i}$ and $x_{j}$ are equally important ($x_{i} \sim x_{j}$);

• (2) $0 \le p_{ij} < 0.5$ implies $x_{j}$ is better than $x_{i}$ ($x_{j} \succ x_{i}$). Particularly, $p_{ij} = 0$ denotes that $x_{j}$ is definitely better than $x_{i}$. While $0.5 < p_{ij} \le 1$ reverses.

Definition 1 ([ 40 ]).

Let $P = (p_{ij} )_{n \times n}$ be a PR, if $p_{ij} \in [0,1]$, $p_{ij} + p_{ji} = 1$ and $p_{ii} = 0.5$ for all $i,j \in N$, then $P$ is called an ARP.

2.2 The WAA Operator

In the GDM, APRs provided by different DMs generally have different levels of importance. Assume $w_{k}$ ($k \in M$) be the weight of a DM, where

$$ \sum\limits_{k = 1}^{m} {w_{k} } = 1,w_{k} \ge 0,\quad k \in M. $$

(1)

Then, the group APR $P = (p_{ij} )_{n \times n}$ obtained by the WAA operator [9] is:

$$ p_{ij} = \sum\limits_{k = 1}^{m} {w_{k} } p_{ij,k} ,\quad i,j \in N. $$

(2)

Notice that $P$ is also an APR.

There are so many methods to obtain the priority vector from an APR. One of the most used methods is the normalizing rank aggregation method [45]. Assume $v = (v_{1} ,v_{2} , \ldots ,v_{n} )^{T}$ be the priority vector of an APR $P = (p_{ij} )_{n \times n}$, then

$$ v_{i} = \frac{2}{{n^{2} }}\sum\limits_{j = 1}^{n} {p_{ij} } ,\quad i \in N. $$

(3)

Remark 1

Based on Eqs. (1) and (2), we can know that $P$ is also a APR. Here, we use WAA operator to aggregate the individual APRs to a group APR. However, other operators such as OWA operator also can be used to aggregate. If an OWA is used, in order to keep the reciprocity of group APR, the weights should be carefully chosen. Further, in this paper, we assume that initial weight vector is $w = (1/m,1/m, \ldots ,1/m)^{T}$, and this means all the DMs’ APRs play an equal role in the initial stage.

2.3 The OC of an APR

Consistency is very important for the GDM. If the DM’s judgments are ordinally inconsistent, it will result in wrong decisions. The OC is the basic requirement to avoid contradictory judgments. The OC is referred as weak transitivity [46, 47]. The concept of OC of APR was first proposed by Xu et al. [37], and a procedure to find and amend the inconsistency entries was also offered in Xu et al. [37].

Definition 2

An APR $P = (p_{ij} )_{n \times n}$ is OC when for all $i,j,k \in N$, $i \ne j \ne k$, the following properties are verified:

• 1. If $\left[ {p_{ik} > 0.5,p_{kj} \ge 0.5} \right]$ or $\left[ {p_{ik} \ge 0.5,p_{kj} > 0.5} \right]$, then $p_{ij} > 0.5$;

• 2. If $\left[ {p_{ik} = 0.5,p_{kj} = 0.5} \right]$, then $p_{ij} = 0.5$.

Remark 2

If the APR is ordinally inconsistent if it has contradictory elements $r_{ij} ,r_{ik} ,r_{kj}$ for $i,j,k \in N,i \ne j \ne k$ satisfying

$$ \left[ {p_{ik} > 0.5,p_{kj} \ge 0.5,p_{ij} < 0.5} \right] $$

or

$$ \left[ {p_{ik} \ge 0.5,p_{kj} > 0.5,p_{ij} < 0.5} \right] $$

or

$$ \left[ {p_{ik} = 0.5,p_{kj} = 0.5,p_{ij} \ne 0.5} \right]. $$

Xu et al. [37] investigated the OC of APRs by the graph theory. In each situation of Remark 1, a 3-cycle ($v_{i} \to v_{k} \to v_{j} \to v_{i}$) appears in the digraph. They also gave the below results:

Theorem 1 [37].

Let $P = (p_{ij} )_{n \times n}$ be an APR, if entries $p_{ik} ,p_{kj} ,p_{ij} ,\left( {i \ne j \ne k} \right)$ , satisfy:

• (a) $p_{ik} > 0.5,p_{kj} \ge 0.5$, or$p_{ik} \ge 0.5,p_{kj} > 0.5$, but$p_{ij} \le 0.5$.

• (b) $p_{ik} = 0.5,p_{kj} = 0.5$ , but $p_{ij} \ne 0.5.$

• (c) $p_{ik} = 0.5,p_{kj} = 0.5,p_{ij} = 0.5.$

Then, there exist 3-cycles in the digraph $G$ of $P$, and vice versa.

It should be noted that case (c) in Theorem 1 does not lead to ordinal inconsistency. When applying Xu et al. [37]’s method to identify the ordinal inconsistency elements, more attention should be paid to the case (c) in Theorem 1. In order to avoid this inconvenience, Xu et al. [48] devised an improved method, which designed a modified adjacency matrix as follows.

Definition 3 ([ 48 ]).

Let $P = (p_{ij} )_{n \times n}$ be an APR, the adjacency matrix $B = (b_{ij} )_{n \times n}$ of $P$ is

$$ b_{{ij}} = \left\{ {\begin{array}{*{20}l} {1,} & {p_{{ij}} > 0.5} \\ {f,} & {p_{{ij}} = 0.5,\quad i \ne j} \\ {0,} & {{\text{otherwise}}} \\ \end{array} } \right. $$

(4)

The “f” is a symbol that represents the indifference between $x_{i}$ and $x_{j}$. More detailed explanation can be found in Xu et al. [48].

Definition 4 ([ 48 ]).

Let $P = (p_{ij} )_{n \times n}$, $B = (b_{ij} )_{n \times n}$ be as before, and $E = (e_{ij} )_{n \times n} = B^{2} \circ B^{T}$, then the OC index (${\text{OCI}}$) of P is

$$ {\text{OCI}}(P) = \frac{1}{3}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {e_{ij} } }, $$

(5)

where $\circ$ denotes the Hadamard product operation, $f = 1$, $f^{2} = 1$, $f^{3} = 0$.

Based on the aforesaid concepts and results, Xu et al. [48] proposed an algorithm to detect and adjust the ordinally inconsistent entries for APRs.

Algorithm 1 ([ 48 ])

• Input: the APR $P = (p_{ij} )_{n \times n}$.

• Output: Output $t$, $E^{(t)}$, $B^{(t)}$, ${\text{OCI}}(P^{(t)} ),$ and $P^{(t)}$.

• Step 1. Let $P^{(t)} = (p_{ij}^{(t)} )_{n \times n} = (p_{ij} )_{n \times n}$, and $t = 0$.

• Step 2. Establish $E^{(t)} = (e_{ij}^{(t)} )_{n \times n}$, where

  $$ b_{ij}^{(t)} = \left\{ {\begin{array}{*{20}l} {1,} & {p_{ij}^{(t)} > 0.5} \\ {f,} & {p_{ij}^{(t)} = 0.5\text{, }i \ne j} \\ {0,} & {\text{otherwise}} \\ \end{array} } \right. $$

  (6)

• Step 3. Derive $E^{(t)}$, i.e.,

  $$ E^{(t)} = (e_{ij}^{(t)} )_{n \times n} = (B^{(t)} )^{2} \circ (B^{(t)} )^{T}. $$

  (7)

  That is,

  $$ e_{ij}^{(t)} = \sum\limits_{k = 1}^{n} {b_{ik}^{(t)} } b_{kj}^{(t)} b_{ji}^{(t)} ,\quad \forall i,j,k \in N $$

  (8)

• Step 4. Using Eq. (9) to obtain the ${\text{OCI}}(P^{(t)} )$:

  $$ {\text{OCI}}(P^{(t)} ) = \frac{1}{3}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {e_{ij}^{(t)} } } $$

  (9)

  If the value of ${\text{OCI}}(P^{(t)} )$ is 0, then go to Step 7. Otherwise, go to Step 5.

• Step 5. Find the maximum entry $e_{{i_{\sigma } j_{\sigma } }}^{(t)}$ in $E^{(t)}$(i.e., $e_{{i_{\sigma } j_{\sigma } }}^{(t)} = \max_{ij} \{ e_{ij}^{(t)} \}$). Then $p_{{j_{\sigma } i_{\sigma } }}^{(t)}$ is treated as the mostly ordinally inconsistent entry in $P^{(t)}$. If there are two or more mostly ordinally inconsistent entries, any inconsistent entry can be selected for repairing. Let $P^{(t + 1)} = (p_{ij}^{(t + 1)} )_{n \times n}$, where

  $$ \left( {p_{ij}^{(t + 1)} ,p_{ji}^{(t + 1)} } \right) = \left\{ {\begin{array}{*{20}l} {\left( {1 - p_{{i_{\sigma } j_{\sigma } }}^{(t)} ,p_{{i_{\sigma } j_{\sigma } }}^{(t)} } \right),} & {p_{{i_{\sigma } j_{\sigma } }}^{(t)} {\text{ is inconsistent entry and }}p_{{i_{\sigma } j_{\sigma } }}^{(t)} \ne 0.5} \\ {(0.4,0.6),} & { \, p_{{i_{\sigma } j_{\sigma } }}^{(t)} {\text{ is inconsistent entry and }}p_{{i_{\sigma } j_{\sigma } }}^{(t)} = 0.5} \\ {\left( {p_{ij}^{(t)} ,p_{ji}^{(t)} } \right),} & {\text{otherwise}} \\ \end{array} } \right. $$

  (10)

  So we can get a new modified APR $P^{(t + 1)}$.

• Step 6. Let $t = t + 1$, then go to Step 2.

• Step 7. Output $t$, $E^{(t)}$, $B^{(t)}$, ${\text{OCI}}(P^{(t)} ),$ and $P^{(t)}$. $P^{(t)}$ is now the modified APR.

• Step 8. End.

Please refer to [37, 48] for all the related information.

Remark 3

In Step 5, generally, there are two or more mostly ordinally inconsistent entries, we select the entry which is closest to 0.5 to be revised prior. The entry $p_{ij}$ is closer to 0.5, indicating that the DM does not have distinct preference between the alternative $x_{i}$ and $x_{j}$. At present, there are so many methods to measure the distances between two elements. For simplicity, the Hamming distance is used to measure the distance between the entry and 0.5, i.e., $d(p_{ij} ,0.5) = |p_{ij} - 0.5|.$

Remark 4

If an APR is of OC, the rankings can be derived immediately.

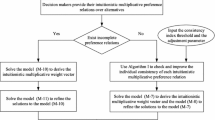
3 An Alternative Consensus Model of APRs Based on OC

In the GDM problems, when the APR $P_{k} = (p_{ij,k} )_{n \times n}$ of each DM is ordinally consistent, the order $O_{{x_{i} }}^{{d_{k} }}$ ($O_{{x_{i} }}^{{d_{k} }}$ is a permutation of 1, 2, …, n) of $x_{i}$ for APR $P_{k}$ can be obtained directly, and the order $O_{{x_{i} }}^{G}$ ($O_{{x_{i} }}^{G}$ is a permutation of 1, 2, …, n) of $x_{i}$ for the group APR P can be obtained by Eq. (3).

Definition 5

Let $w_{k}$ be the weight of the $k{\text{th}}$ DM, $O_{{x_{i} }}^{{d_{k} }}$ and $O_{{x_{i} }}^{G}$ be the order of the alternative $x_{i}$ from the DMs $d_{k}$’s APR $P_{k}$ and group APR P. Then the consensus degree (${\text{CD}}$) of the alternative $x_{i}$ is defined by

$$ {\text{CD}}_{i} = \sum\limits_{k = 1}^{m} {\left[ {\left( {1 - \frac{{\left| {O_{{x_{i} }}^{G} - O_{{x_{i} }}^{{d_{k} }} } \right|}}{n - 1}} \right) \times w_{k} } \right]} ,\quad i \in N. $$

(11)

Definition 6

Let $[i]$ be the alternative ranking in the $i{\text{th}}$ position. Then the group consensus degree (GCD) is defined by

$$ {\text{GCD}} = \hbox{min} \left\{ {{\text{CD}}_{[1]} , \ldots ,{\text{CD}}_{[i]} , \ldots ,{\text{CD}}_{[q]} } \right\}. $$

(12)

Remark 5

$q$ is the number of alternatives that the DM wants to choose in the group. If only one best alternative is needed to be selected, it needs the alternative that is ranked in the first position to achieve the desired consensus level. Similarly, if we want to choose q alternatives, we should ensure the minimum consensus level of the top q alternatives’ consensus levels over a certain level.

The aim of the GDM is to rank the alternatives and then select the best one, and the rankings can be obtained easily if an APR is ordinally consistent. Thus, OC of APRs is more suitable to rank the alternatives. In the following, a consensus model which will only update the DMs’ weights but do not modify the DMs’ ordinally consistent judgements will be developed. The main procedure of the consensus measure includes three steps:

• 1. The OC process. By Algorithm 1, we can obtain the ordinally consistent APRs.

• 2. The ranking process. The APRs are ordinally consistent, it is easy to rank the alternatives from the APRs, and the group ranking of alternatives can be obtained using Eqs. (2) and (3).

• 3. The CRP. If the alternative consensus level is lower than the predefined value, an algorithm is designed to adjust the weight of each DM based on his/her contribution to the group.

Algorithm 2

• Input: the ordinally consistent individual APRs $P_{k}^{(t)} = (p_{ij,k}^{(t)} )_{n \times n}$ ($k \in M$) using Algorithm 1, the group APR $P_{r} = (p_{ij,r} )_{n \times n}$, the weight vector $w^{(r)} = (w_{1}^{(r)} ,w_{2}^{(r)} , \ldots ,w_{m}^{(r)} )^{T}$ of the DMs in the $r{\text{th}}$ iteration, and we assume the weight vector in the initial iteration $w^{(0)} = (w_{1}^{(0)} ,w_{2}^{(0)} , \ldots ,w_{m}^{(0)} )^{T} = (1/m,1/m, \ldots ,1/m)$, parameter $\delta$, and $\delta \in [0,1]$.

• Output: the weight vector $w^{(r + 1)} = (w_{1}^{(r + 1)} ,w_{2}^{(r + 1)} , \ldots ,w_{m}^{(r + 1)} )^{T}$ of DMs after $(r + 1 ) {\text{th}}$ iteration, and the ${\text{GCD}}$ of each iteration.

• Step 1. Using Algorithm 1 to judge and rectify all the APRs $P_{k}^{(t)} = (p_{ij,k}^{(t)} )_{n \times n}$ to be ordinally consistent.

• Step 2. Obtain the orders $O_{{x_{i} ,r}}^{{d_{k} }}$ of all the alternatives $x_{i}$ for DM $d_{k}$ in the rth iteration.

• Step 3. Aggregate all the individual APRs into a collective APR $P^{(r)} = (p_{ij}^{(r)} )_{n \times n}$ using the WAA operator, and then by Eq. (3), we can get the orders $O_{{x_{i} ,r}}^{G}$ of the alternative $x_{i}$ from the group APR $P^{(r)}$.

• Step 4. Using Eqs. (11) and (12), the consensus degree ${\text{CD}}_{i,r}$ of $x_{i}$, and the group consensus degree ${\text{GCD}}_{r}$ can be obtained, respectively.

• Step 5. The consensus degree ${\text{CD}}_{i,r}^{{\bar{s}}}$ of $x_{i}$ without the DM $d_{s}$ can be obtained by Eq. (13):

  $$ {\text{CD}}_{i,r}^{{\bar{s}}} = \sum\limits_{{k \in M\backslash \{ s\} }} {\left[ {\left( {1 - \frac{{|O_{{x_{i} ,r}}^{{G\backslash \{ d_{s} \} }} - O_{{x_{i} ,r}}^{{d_{k} }} |}}{n - 1}} \right) \times u_{k,r} } \right]} ,{\text{where}}\quad u_{k,r} = \frac{{w_{k,r} }}{{\sum\limits_{{i \in M\backslash \{ s\} }} {w_{i,r} } }}, $$

  (13)

  where $k \in M\backslash \{ s\}$ denotes $k \in M$ and $k \ne s$. $O_{{x_{i} ,r}}^{{G\backslash \{ d_{s} \} }}$ denotes the ranking orders of the alternative $x_{i}$ from the group without DM $d_{s}$ in the rth round.

• Step 6. Calculate the individual contribution ${\text{IC}}_{i,r}^{s}$, which represents the contribution of DM $d_{s}$ on the alternative $x_{i}$ in the rth round, where

  $$ {\text{IC}}_{i,r}^{s} = {\text{CD}}_{r} - {\text{CD}}_{i,r}^{{\bar{s}}} ,\quad i \in N. $$

  (14)

• Step 7. Calculate the contribution ${\text{GC}}_{r}^{s}$, which represents the contribution of the DM $d_{s}$ on all alternatives, where

  $$ {\text{GC}}_{r}^{s} = \sum\limits_{i = 1}^{n} {{\text{IC}}_{i,r}^{s} } $$

  (15)

  As it can be seen from Eq. (15), the larger the value of ${\text{GC}}$ is, the more contribution the DM $d_{s}$ to the group decision, and the DM $d_{s}$ should be assigned a higher weight.

• Step 8. If ${\text{GCD}}_{r} \ge \delta$, then output $w^{(r + 1)} = \left( {w_{1}^{(r + 1)} ,w_{2}^{(r + 1)} , \ldots ,w_{m}^{(r + 1)} } \right)^{T}$. Otherwise, continue with the next step.

• Step 9. The DM $d_{k}$’s weight $w_{k}^{(r + 1)}$ is revised according to Eqs. (16) and (17):

  $$ \upsilon_{k}^{(r + 1)} = w_{k}^{(r)} .\left( {1 + {\rm GC}_{r}^{k} } \right)^{\beta }, $$

  (16)
  $$ w_{k}^{(r + 1)} = \frac{{\upsilon_{k}^{(r + 1)} }}{{\sum\nolimits_{k = 1}^{m} {\upsilon_{k}^{(r + 1)} } }}, $$

  (17)

  where $w_{k}^{(r)}$ represent the weight of the DM $d_{k}$ in the $r{\text{th}}$ iteration. $\beta$ is a parameter, denoting the influence of DM’s weight on its contribution, and the larger $\beta$ is, the faster it reaches the agreed level of consensus. Go to Step 3.

The above Algorithm 2 can be depicted in Fig. 1.

Fig. 1

Flowchart of the process of consensus model

4 Illustrative Example and Comparisons

We illustrate the following example and offer comparisons to demonstrate the effectiveness of the method.

4.1 Illustrative Example

Consider the example shown in [10, 49]. Let us suppose a group of four DMs $d_{k}$, ($k = 1,2, \ldots ,4$) and a set of four alternatives $x_{i}$ ($i = 1,2, \ldots ,4$). The DMs construct the following four APRs $P_{k} = (p_{ij,k} )_{4 \times 4}$$(k = 1,2, \ldots ,4)$.

$$ P_{1} = \left[ {\begin{array}{*{20}c} {0.5} & {0.2} & {0.6} & {0.4} \\ {0.8} & {0.5} & {0.9} & {0.7} \\ {0.4} & {0.1} & {0.5} & {0.3} \\ {0.6} & {0.3} & {0.7} & {0.5} \\ \end{array} } \right], \quad P_{2} = \left[ {\begin{array}{*{20}c} {0.5} & {0.7} & {0.9} & {0.5} \\ {0.3} & {0.5} & {0.6} & {0.7} \\ {0.1} & {0.4} & {0.5} & {0.8} \\ {0.5} & {0.3} & {0.2} & {0.5} \\ \end{array} } \right], $$

$$ P_{3} = \left[ {\begin{array}{*{20}c} {0.5} & {0.3} & {0.5} & {0.7} \\ {0.7} & {0.5} & {0.1} & {0.3} \\ {0.5} & {0.9} & {0.5} & {0.25} \\ {0.3} & {0.7} & {0.75} & {0.5} \\ \end{array} } \right],\quad P_{4} = \left[ {\begin{array}{*{20}c} {0.5} & {0.25} & {0.15} & {0.65} \\ {0.75} & {0.5} & {0.6} & {0.8} \\ {0.85} & {0.4} & {0.5} & {0.5} \\ {0.35} & {0.2} & {0.5} & {0.5} \\ \end{array} } \right]. $$

4.1.1 Stage 1. OC Process

Using Algorithm 1 to judge and improve the OC for all the APRs, let $P_{k}^{(0)} = P_{k} = (p_{ij,k} )_{4 \times 4} \quad (k = 1,2, \ldots ,4)$.

By Eq. (6), the adjacency matrices $B_{k}^{(0)} = (b_{ij,k}^{(0)} )_{4 \times 4} \quad (k = 1,2, \ldots ,4)$ of the APRs $P_{k}^{(0)} = (p_{ij,k}^{(0)} )_{4 \times 4} \quad (k = 1,2, \ldots ,4)$ are:

$$ B_{1}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ \end{array} } \right], \quad B_{2}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 1 & 1 & f \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ f & 0 & 0 & 0 \\ \end{array} } \right], $$

$$ B_{3}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 0 & f & 1 \\ 1 & 0 & 0 & 0 \\ f & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ \end{array} } \right], \quad B_{4}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & f \\ 0 & 0 & f & 0 \\ \end{array} } \right]. $$

By Eq. (7), we have

$$ E_{1}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right], \quad E_{2}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 2 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ \end{array} } \right], $$

$$ E_{3}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 2 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 2 & 0 & 0 & 0 \\ \end{array} } \right], \quad E_{4}^{(0)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right]. $$

By Eq. (9), we have

$$ {\text{OCI}}(P_{1}^{(0)} ) = 0,{\text{OCI}}(P_{2}^{(0)} ) = 2,{\text{OCI}}(P_{3}^{(0)} ) = 3,{\text{OCI}}(P_{4}^{(0)} ) = 1. $$

Thus, $P_{1}^{(0)}$ is ordinally consistent. There are two 3-cycles, three 3-cycles, one 3-cycle in $P_{2}^{(0)}$, $P_{3}^{(0)}$, $P_{4}^{(0)}$, respectively.

$P_{2}$ should be improved to be ordinally consistent, $e_{14,2}^{(0)} = \max_{ij} \left\{ {e_{ij,2}^{\left( 0 \right)} } \right\}{ = 2}$, $p_{41,2}^{(0)}$ is the mostly ordinally inconsistent element. By Eq. (10), $p_{41,2}^{(1)} = 0.4$, $p_{14,2}^{(1)} = 0.6$.

$$ P_{2}^{(1)} = \left[ {\begin{array}{*{20}c} {0.5} & {0.7} & {0.9} & {0.6} \\ {0.3} & {0.5} & {0.6} & {0.7} \\ {0.1} & {0.4} & {0.5} & {0.8} \\ {0.4} & {0.3} & {0.2} & {0.5} \\ \end{array} } \right] $$

and

$$ B_{2}^{(1)} = \left[ {\begin{array}{*{20}c} 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right], \quad E_{2}^{(1)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]. $$

By Eq. (9), ${\text{OCI}}(P_{2}^{(1)} ) = 0$. Therefore, $P_{2}^{(1)}$ is of OC.

For $P_{3}^{(0)}$, as $e_{12,3}^{(0)} = e_{41,3}^{(0)} { = 2}$, and $d(p_{21,3}^{(0)} ,0.5) = |0.7 - 0.5| = 0.2$, $d(p_{14,3}^{(0)} ,0.5) = |0.7 - 0.5 | = 0.2 ,$ thus, we choose $p_{21,3}^{(0)}$ to be repaired randomly. We set $p_{21,3}^{(1)} = 0.3$, $p_{12,3}^{(1)} = 0.7$. That is

$$ P_{3}^{(1)} = \left[ {\begin{array}{*{20}c} {0.5} & {0.7} & {0.5} & {0.7} \\ {0.3} & {0.5} & {0.1} & {0.3} \\ {0.5} & {0.9} & {0.5} & {0.25} \\ {0.3} & {0.7} & {0.75} & {0.5} \\ \end{array} } \right] .$$

By Eq. (9), ${\text{OCI}}(P_{3}^{(1)} ) = 1$, we set $p_{13,3}^{(2)} = 0.6$, $p_{31,3}^{(2)} = 0.4$. Then, we have

$$ P_{3}^{(2)} = \left[ {\begin{array}{*{20}c} {0.5} & {0.7} & {0.6} & {0.7} \\ {0.3} & {0.5} & {0.1} & {0.3} \\ {0.4} & {0.9} & {0.5} & {0.25} \\ {0.3} & {0.7} & {0.75} & {0.5} \\ \end{array} } \right], $$

and ${\text{OCI}}(P_{3}^{(2)} ) = 0$

Similarly, we set $p_{43,4}^{(1)} = 0.4$, $p_{34,4}^{(1)} = 0.6$. That is:

$$ P_{4}^{(1)} = \left[ {\begin{array}{*{20}c} {0.5} & {0.25} & {0.15} & {0.65} \\ {0.75} & {0.5} & {0.6} & {0.8} \\ {0.85} & {0.4} & {0.5} & {0.6} \\ {0.35} & {0.2} & {0.4} & {0.5} \\ \end{array} } \right], $$

and ${\text{OCI}}(P_{4}^{(1)} ) = 0$.

Then, the consensus process is activated.

4.1.2 Stage 2. Consensus Stage

• Step 1. According to the ordinally consistent APRs $P_{1}^{(0)}$, $P_{2}^{(1)}$, $P_{3}^{(2)}$, and $P_{4}^{(1)}$, the alternative rankings are detailed in Table 1.

  Table 1 Alternative orders from individual experts

• Step 2. When $r = 0$, $w^{(0)} = (w_{1} ,w_{2} ,w_{3} ,w_{4} )^{T} = (0.25,0.25,0.25,0.25)^{T}$. Then we can get the aggregated APR.

  $$ P^{(0)} = \left[ {\begin{array}{*{20}c} {0.5} & { 0. 4 6 2 5} & { 0. 5 6 2 5} & { 0. 5 8 7 5} \\ { 0. 5 3 7 5} & { 0. 5} & { 0. 5 5 0 0} & { 0. 6 2 5 0} \\ { 0. 4 3 7 5} & { 0. 4 5 0 0} & { 0. 5} & { 0. 4 8 7 5} \\ { 0. 4 1 2 5} & { 0. 3 7 5 0} & { 0. 5 1 2 5} & { 0. 5} \\ \end{array} } \right] $$

  Using Eq. (3), we obtain

  $$ v_{1} = (0.5+0.4625+0.5625+0.5875)/8 = 0.2641 ,$$

  and

  $$ v_{2} = 0.2766, v_{3} = 0.2344, v_{4} = 0.225.$$

  Thus, the ranking of the collective APR $P^{(0)}$ is $x_{2} \succ x_{1} \succ x_{3} \succ x_{4}$.

• Step 3. Based on the alternative rankings in Table 1 and the ranking of the group, using Eqs. (11) and (12), we can obtain the ${\text{CD}}_{i}$ ($i = 1,2,3,4$) for each alternative $x_{i}$ ($i = 1,2,3,4$). When the DM wants to select only one best alternative (i.e., $q = 1$), then ${\text{GCD}} = {\text{CD}}_{2} = 0.6667$ as alternative $x_{2}$ ranks first in the collective APR. Similarly, when the DM wants to select two alternatives (i.e., $q = 2$), then ${\text{GCD}} = {\text{min}}\{ {\text{CD}}_{2} ,{\text{CD}}_{1} \} = 0.6667$ as alternatives $x_{2}$ and $x_{1}$ are ranked in the first and second position. Table 2 lists the values of ${\text{CD}}_{i}$ ($i = 1,2,3,4$), and the group consensus level when $q = 1$ and $q = 2$ in the initial round $r = 0$, respectively.

  Table 2 The values of CD_i and GCD (r = 0)

• Step 4. Assume the threshold value $\delta = 0.99$ and the parameter $\beta = 1$. To measure the contribution of each DM, we obtain the aggregated values without one particular DM. The weight vector is $w^{(0)} = (1/3,1/3,1/3)^{T}$. Table 3 shows the new orders without one particular DM, and Table 4 lists the consensus degree by Eq. (13) without one particular DM.

  Table 3 New group orders without one particular DM (r = 0)

  Table 4 New alternative consensus level without one particular DM (r = 0)

• Step 5. Calculate ${\text{IC}}_{i,0}^{s}$ and ${\text{GC}}_{0}^{s}$ ($s = 1,2,3,4$) by Eqs. (14) and (15), which are displayed in Table 5.

  Table 5 Contribution of the experts (r = 0)

• Step 6. Using Eq. (16) and Eq. (17), we revise the weights of DMs based on their contributions to the group consensus, $w^{(1)} = ( 0. 2 6 5 6, 0. 2 6 5 6, 0. 2 0 3 1, 0. 2 6 5 6)^{T}$. By Eq. (2), we obtain the new APR:

  $$ P^{(1)} = \left[ {\begin{array}{*{20}c} {0.5} & { 0. 4 4 7 6} & { 0. 5 6 0 1} & { 0. 5 8 0 4} \\ { 0. 5 5 2 3} & {0.5} & { 0. 5 7 8 1} & { 0. 6 4 5 2} \\ { 0. 4 3 9 8} & { 0. 4 2 1 8} & {0.5} & { 0. 5 0 2 3} \\ { 0. 4 1 9 5} & { 0. 3 5 4 6} & { 0. 4 9 7 6} & {0.5} \\ \end{array} } \right] $$

  Therefore, the ranking of the collective APR $P^{(1)}$ is $x_{2} \succ x_{1} \succ x_{3} \succ x_{4}$. Tables 6, 7, 8, and 9 list the ${\text{CD}}_{i}$ ($i = 1,2,3,4$), and the GCD of alternatives, new group orders without one particular DM, the new alternative consensus level without one particular DM, the contributions of DMs for $r = 1$, respectively.

  Table 6 Consensus level to alternatives (r = 1)

  Table 7 New group orders without a particular DM (r = 1)

  Table 8 New alternative consensus level without one particular DM (r = 1)

  Table 9 Contribution of the DMs (r = 1)

  The algorithm stops after 10 iterations. The detailed weights of DMs, individual consensus degrees, and the GCD for each iteration are listed in Tables 10, 11, and 12, respectively.

  Table 10 Weights of experts for each iteration

  Table 11 Consensus degrees for each iteration

  Table 12 Group consensus for each iteration

  While the DM’s weights change, the group CRP achieved a predefined threshold gradually. Figure 2 shows the detailed process for $q = 1$ and $q = 2$.

  Fig. 2

  

  Group consensus process with the change of DM weights

From Fig. 2, we can obtain the characteristics of the developed method:

• 1. The GCD increases gradually while the weights of the DMs are changed. Specifically, the weight of DM $d_{2}$ increases, the weights of other three DMs decrease, and finally, the weight of DM $d_{2}$ almost equals to 1, which shows the DM $d_{2}$ is the most important in the group, and can be looked as an autocratic leader.

• 2. In the CRP, the group rankings for alternatives may be changed. In the 4th iteration ($r = 4$), the alternative ranking is $x_{2} \succ x_{1} \succ x_{3} \succ x_{4}$, and it is $x_{2} \succ x_{1} \succ x_{3} \succ x_{4}$ in the 5th iteration ($r = 5$), which is same as the DM $d_{2}$’s ranking. This is why the weight of DM $d_{2}$ increases, and the other three weights decrease while the consensus degree approaches the predefined threshold.

4.2 Comparisons with the Existing Methods

4.2.1 Comparison With Wu and Xu [10]’s Method

Wu and Xu [10] investigated the consensus problem for the illustrative example. Their method included two processes: individual consistency control process and the CRP. In the consistency control process, they used the additive consistency property of APRs to measure whether an APR is consistent and established an algorithm to make an inconsistent APR to turn into one with acceptable consistency. In the illustrative example, they set the consistency threshold $\overline{\text{CI}} = 0.1$, and obtained the ${\text{CI}}(P_{1} ) = 0$, ${\text{CI}}(P_{2} ) = 0.1417$, ${\text{CI}}(P_{3} ) = 0.1875$, ${\text{CI}}(P_{4} ) = 0.0917.$ As the consistency degrees of DMs $d_{2}$ and $d_{3}$ are higher than the threshold, they used their proposed algorithm to modify $P_{2}$ and $P_{3}$ to be additively consistent. The modified $P_{2}$ and $P_{3}$ are (here, they set $\beta = 0.9$):

$$ P_{2} = \left[ {\begin{array}{*{20}c} {0.5} & {0.67} & {0.83} & {0.59} \\ {0.33} & {0.5} & {0.59} & {0.68} \\ {0.17} & {0.41} & {0.5} & {0.72} \\ {0.41} & {0.32} & {0.28} & {0.5} \\ \end{array} } \right], \quad P_{3} = \left[ {\begin{array}{*{20}c} {0.5} & {0.44} & {0.48} & {0.58} \\ {0.56} & {0.5} & {0.22} & {0.32} \\ {0.52} & {0.78} & {0.5} & {0.36} \\ {0.42} & {0.68} & {0.64} & {0.5} \\ \end{array} } \right]. $$

It is obvious that the revised $P_{2}$ and $P_{3}$ are greatly different from the original ones. When setting different $\beta$s, it will get different results and the iterations are also different. Furthermore, if we use Algorithm 1 to verify the revised $P_{3}$, it still contains two 3-cycles. One of the cycles is $x_{1} \succ x_{4} \succ x_{2} \succ x_{1}$. Furthermore, Wu and Xu [10] thought $P_{4}$ is additively consistent. As we have verified, it contains one 3-cycle. Therefore, Wu and Xu [10]’s additive consistency cannot assure the DMs’ preferences without contradiction, which makes their results unreliable.

4.2.2 Comparison with Other Similar Methods

Chiclana et al. [49] first investigated the consensus problem for Example 1. The consensus model they presented for APRs dealt with consistency and consensus. In the consistency process, Chiclana et al. [49] regarded $P_{2}$ and $P_{3}$ are not of (additive) consistency (AC), but $P_{4}$ is of AC. Then, based on the AC consistency property, they developed a consistency model which generates the recommendations which help the DMs to modify their preferences to increase the consistency. The consensus model then is sought after. It also generates the advices to change the DMs’ preferences. In our OC process, it is verified that $P_{4}$ is not ordinally consistent, which means that there are contradictory judgements in $P_{4}$. Therefore, AC cannot assure whether there exist contradictory judgements for an APR. Furthermore, in the consistency and consensus processes, Chiclana et al. [49] changed so many pairwise comparisons, distorting the DMs’ initial judgements greatly. However, the proposed method in this paper can keep most of the DMs’ original judgements unchanged, which will make the final decision more reliable.

Based on the maximizing group consensus for APRs, Xu and Cai [9] established several goal programming models and quadratic programming models. There are two main drawbacks of Xu and Cai [9]’s method. First, they did not consider the individual consistency of APRs, which cannot assure whether the DMs’ information is reasonable. Actually, most of the APRs are not of OC, which makes the final decision unreliable. Second, in the CRP, Xu and Cai [9]’s method not only changes the DMs’ weights, but also modifies the DMs’ judgments, which will distort the DMs’ original information. There are also similar problem for Xu et al. [11]’s method.

5 Conclusion

In the above, we have proposed an alternative consensus model for APRs in the GDM problem. Its main characteristics are:

• 1. It has two courses: ICP and CRP. The OC of APRs is used in the ICP, while the cardinal consistency is generally used in the existing literature. As we know, cardinal consistency within a certain predefined level cannot assure that there are no contradictory judgments in the APRs. Thus, it is more reasonable to use the OC.

• 2. In the CRP, an alternative consensus level is defined to measure the group consensus level. As the aim of the group is to decide the best alternative, alternative consensus of all the DMs is more rationale to select the alternatives.

• 3. The weight updating does not modify the DMs’ ordinally consistent APRs, which intends to keep the DMs’ initial information to the greatest extent.

Nowadays, a GDM process generally involves a large scale of DMs. Therefore, it is unrealistic to modify most of the DMs’ judgements in the CRP. Thus, the proposed method has the potential to be extended to deal with large-scale GDM problems [36, 50,51,52], which will be left for our future research.