1 Introduction

It is no doubt that time-delay system has received considerable attention, and its research has been one of the active subjects in the field of nonlinear control because it widely exists and is inevitable in most real-world systems; see [1,2,3,4,5] and the references therein. Specifically, owing to the lack of unified method applicable to nonlinear control design, there are still many important and interesting control problems for time-delay nonlinear systems remaining unsolved. Fortunately, ever since the introduction of backstepping method into adaptive fuzzy control and Lyapunov–Krasovskii functionals, numerous interesting results on nonlinear time-delay systems have been achieved. For instance, an approximation-based adaptive fuzzy control method with only one adaptive parameter was presented in [6] for a class of strict-feedback nonlinear systems with unmodeled dynamics, dynamic disturbances, and unknown time delays. As for a class of stochastic nonlinear time-delay systems with a nonstrict-feedback structure, the problem of approximation-based adaptive fuzzy tracking control was studied in [7]. What is more, [8] studied the problem of adaptive output tracking control for a class of nonlinear systems subject to unknown time-delay and input saturation. If there are MIMO strict-feedback nonlinear systems with unknown time-varying delays, unmeasured states and input saturation, a hybrid fuzzy adaptive output feedback control approach was proposed in [9]. In a different direction, an adaptive indirect fuzzy sliding mode controller was designed in [10] for networked control systems subject to time-varying network-induced time delay. Yi et al. [11] investigated the adaptive fuzzy output feedback control problem for a class of nonstrict-feedback time-delay systems subject to full-state constraints. The studies [12,13,14,15,16] and the references therein also made significant contributions to the research of time-delay system.

On the other hand, constraints are everywhere for physical systems in the face of limitation of mathematical tools and methods. To guarantee the stability of various kinds of systems with the state or output constraints, numerous results have been proposed. For example, [17] and [18] investigated the adaptive neural tracking control problem for a class of DC motor systems with the full-state constraints and an uncertain n-link robot with full-state constraints, respectively. An adaptive neural network control method was investigated in [19] for a class of uncertain nonlinear strict-feedback systems with full-state constraints. Based on BLF-based backstepping, the control design for strict-feedback systems with constraints on the states was addressed in [20]. An finite-time adaptive control approach was designed in [21] for stochastic nonlinear systems with full-state constraints and parametric uncertainties. In a different direction, [22] studied the problem of output feedback control for a class of nonlinear systems with the full-state constraints. A composite adaptive fuzzy output feedback control approach was proposed in [23] for a class of strict-feedback nonlinear systems with unmeasured states and input saturation. Besides, [24,25,26,27] and the references therein reported several control strategies for nonlinear systems with the state or input constraints. However, to the best of our knowledge, there exist a few results of adaptive fuzzy control for nonlinear systems simultaneously subject to the full-state constraints and time delays, which motivates this paper.

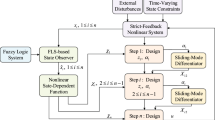
In this paper, the problem of adaptive fuzzy tracking control for a class of strict-feedback nonlinear time-delay systems with full-state constraints is studied. Compared with existing results on adaptive fuzzy control for nonlinear systems, the novelties and main contributions of this work are highlighted from three aspects: The simultaneous existence of the full-state constraints and time delays makes the design of controller very difficult. Correspondingly, the tan-type barrier Lyapunov functions and Lyapunov–Krasovskii functionals are introduced to deal with state constraints and time-delay terms, respectively. Fuzzy systems are adopted to identify the completely unknown package nonlinear functions and avoid the heavy computations at the same time. Therefore, the virtual and real control signals of the proposed scheme can be achieved simpler and easier. Only one parameter estimation is considered for the adaptive controller used; therefore, the dynamic order of the designed controller is minimum, which avoids the over-parametrization estimate phenomenon. In addition, the proposed control scheme can also work for systems when there is no state constraint, because the tan-type BLF can reduce to standard quadratic ones in this case.

This paper is organized as follows. After the introduction section, the problem statement and some preliminary results are introduced in Sect. 2. The control design schemes are given in Sect. 3. To verify the effectiveness of the proposed methodology, a numerical example is presented in Sect. 4. Finally, Sect. 5 concludes the paper.

2 Problem Statement and Preliminary Results

Consider the following strict-feedback nonlinear systems with full-state constraints

$$\left\{ \begin{array}{l} \dot{x}_i(t)=g_i({\bar{x}}_i(t))x_{i+1}(t)+f_i(\bar{x}_i(t))+h_i(\bar{x}_i(t-\tau _i)) +d_i(t,x),\\ \quad i=1, \ldots , n-1,\\ \dot{x}_n(t)=g_n(x(t))u+f_n(x(t))+h_n(\bar{x}(t-\tau _n)) +d_n(t,x),\\\quad y=x_1, \end{array} \right.$$
(1)

where \({{\bar{x}}}_i=[x_1, \ldots , x_i]^T\in R^i\), \(i=1,\ldots , n\), \(x=[x_1, x_2, \ldots , x_n]^{T}\in R^n\) and \(y\in R\) are system state vector and output, respectively, \(g_i({\bar{x}}_i)\ne 0\) is a known smooth nonlinear function, \(f_i(\bar{x}_i)\) and \(h_i(\bar{x}_i(t-\tau _i))\) are unknown continuous functions, \(d_i(t,x)\) is a bounded time-varying disturbance and u is the control signal to be designed. All the states are constrained in the compact set as

$$\begin{aligned} \Omega _{x}:=\{x_i\in R, |x_i(t)| \le k_{c_i}, i=1, \ldots , n\}, \end{aligned}$$
(2)

where \(k_{c_{i}}\) are known positive constants. Given a reference trajectory \(y_r\), the control objective is to design a fuzzy controller in the form as follows:

$$\left\{ \begin{array}{l} u(t)\,=u(x(t),\,{\hat{\Theta }}(t),\,y_r),\\ \dot{{\hat{\Theta }}}(t)=\Lambda (x(t),\,{\hat{\Theta }}(t),\,y_r),\quad {{\hat{\Theta }}}(0)={\hat{\Theta }}_0, \end{array} \right.$$

such that the system output y tracks the desired trajectory \(y_r\); all the signals in the closed-loop system are bounded, and the state constraint requirements are not violated, where \({\hat{\Theta }}(t)\) represents the estimate of an unknown positive constant \(\Theta\) which will be specified later. Sometimes, the arguments of the functions will be omitted or simplified, whenever no confusion can arise from the context. For instance, we sometimes denote a function f(t) by simply f.

First, the following fuzzy systems are employed to approximate the unknown functions.

IF-THEN rules: \(R_{i}\): If \(x_{1}\) is \(F^{i}_{1}\) and \(\cdots\) and \(x_{n}\) is \(F^{i}_{n}\), THEN y is \(B^{i},i=1,\ldots ,n\).

The fuzzy systems can be formulated as:

$$\begin{aligned} y(x)=\frac{\sum ^{N}_{i=1}\Phi _{i}\prod ^{n}_{j=1}\mu _{F^{i}_{j}}(x_{j})}{\sum ^{N}_{i=1}[\prod ^{n}_{j=1}\mu _{F^{i}_{j}} (x_{j})]}. \end{aligned}$$

where \(\mu _{F^{i}_{j}}\) is fuzzy membership function. Let

$$\begin{aligned} p_{i}(x)=\frac{\prod ^{n}_{j=1}\mu _{F^{i}_{j}}(x_{j})}{\sum ^{N}_{i=1}[\prod ^{n}_{j=1}\mu _{F^{i}_{j}}(x_{j})]}, \end{aligned}$$

where \(P(x)=[p_{1}(x),p_{2}(x),\ldots ,p_{N}(x)]^{T}\) and \(\Phi =[\Phi _{1},\ldots ,\Phi _{N}]^{T}\). Then, the fuzzy systems can be rewritten as follows:

$$\begin{aligned} y(x)=\Phi ^{T}P(x). \end{aligned}$$

Lemma 1

[28] f(x) is a continuous function defined on a compact set \(\Omega\), for any given constant \(\varepsilon >0\); there exists a fuzzy system \(\Phi ^{T}P(x)\) such that

$$\begin{aligned} sup_{x\in \Omega }\mid f(x)-\Phi ^{T}P(x)\mid \le \varepsilon . \end{aligned}$$

To reduce the number of adaptive laws, define \(\Theta\) as:

$$\begin{aligned} \Theta =\max \Big \{\parallel \Phi _i\parallel ^{2}\Big \}, i=1,\ldots , n, \end{aligned}$$

where \(\Phi _i\) is the unknown parameter vector in the fuzzy system. Next, the following transformations are introduced:

$$\left\{ \begin{array}{l} z_1=x_1-y_r, \\ z_i=x_i-x^*_{i-1},\quad i=2, \ldots , n, \end{array} \right.$$
(3)

where \(z_{i}\in R\) is the virtual state tracking error, \(x^*_{i}\in R\) is the virtual controller satisfying \(|x^*_{i}|<{x}_{i0}^*\), and \({x}_{i0}^*\) is a positive constant which will be specified later. To achieve the desired control objective, we make the following assumptions:

Assumption 1

For \(1\le i\le n\), there exists an unknown positive function \(\mu _i({\bar{x}}_i(t))\) such that \(|d_i(t,x)|\le \mu _i({\bar{x}}_i(t))\).

Assumption 2

For the unknown nonlinear smooth functions \(h_i({\bar{x}}_i(t))\), there exist unknown positive functions \(q_{ij}({\bar{x}}_i(t))\), such that

$$\begin{aligned} h_i({\bar{z}}_i(t)+ {{\bar{x}}}^*_{i-1}(t))\le \sum _{j=1}^i|z_j(t)|q_{ij}({\bar{z}}_i(t)), \end{aligned}$$

where \({\bar{z}}_i=[z_1,\ldots , z_i]^T\), \({{\bar{x}}}^*_{i-1}=[x^*_0,\ldots , x^*_{i-1}]^T\), \(x^*_0=y_r\).

Assumption 3

The desired signal \(y_r\) is bounded, i.e., \(|y_r|\le y_0\), and its time derivatives up to the n-th order are continuous and bounded; meanwhile \(y_0 <k_{c_i}\).

Remark 1

The above assumptions are all reasonable. Assumption 1 is common in conventional results. For the Assumption 2, the similar ones can be seen in [29, 30]. In particular, the \(q_{ij}\) is need to be known in [30]. The requirement on signal of Assumption 3 relies widely on backstepping control [31, 32]. To design the desired controller, the standard backstepping technique requires that the reference signal has to be continuous and derivable. \(y_0 <k_{c_i}\) in Assumption 3 is always true in practice for the requirement of output tracking control. A similar assumption is presented in the literatures [33].

Next, the following tan-type BLFs are introduced

$$\begin{aligned} V^{*}_i=\frac{k^{2}_{b_{i}}}{\pi }\tan \left( \frac{\pi z^2_{i}}{2k^{2}_{b_{i}}}\right) , \quad |z_{i}(0)|<k_{b_{i}},\quad i=1, \ldots , n, \end{aligned}$$

where \(z_i\in \Omega _{z}:=\{z_i\in R, |z_i|<k_{b_i}\}\) with \(k_{b_1}=k_{c_1}-y_0>0\) and \(k_{b_i}=k_{c_i}-{x}_{i-10}^*>0\), \(i=2,\ldots ,n\). Define \(v_{z_i}=\frac{z_i}{\cos ^{2}(\frac{\pi z^2_i}{2k^2_{b_i}})}\). In fact, \(k_{c_{i}}\rightarrow \infty\) implies \(k_{b_{i}}\rightarrow \infty\), and \(\tan \Big (\frac{\pi z^2_i}{2k^{2}_{b_{i}}}\Big ) \sim \frac{\pi z^2_i}{2k^{2}_{b_{i}}}\) can be obtained. With this in mind, the following equation can be further obtained

$$\begin{aligned} \lim _{k_{b_{i}}\rightarrow \infty } \frac{k^{2}_{b_{i}}}{\pi }\tan \left( \frac{\pi z^2_i}{2k^{2}_{b_{i}}}\right) = \frac{1}{2}z^2_i, \end{aligned}$$

this implies that the tan-type BLF reduces to standard quadratic ones when there is no constraint. Compared with the log-type BLF employed in [30, 34], using the tan-type BLF to deal with state constraints is a general approach that can also work for systems without state constraints.

3 Adaptive Fuzzy Control

3.1 Control Design

Step 1: Define a candidate BLF as

$$\begin{aligned} V_{1}=V^{*}_{1}+\sum _{i=1}^n\int _{t-\tau _i}^tW_{i1}(z_1(s))\hbox {d}s +\frac{1}{2}{\tilde{\Theta }}^2, \end{aligned}$$

where \({{\tilde{\Theta }}}=\Theta -{{\hat{\Theta }}}\) and the positive function \(W_{i1}(z_1(t))\) are specified later. Taking the derivative of \(V_{1}\) with respect to time, one has

$$\begin{aligned} {\dot{V}}_{1}= & {} v_{z_{1}}\left( g_1x_2 +f_1(x_1)+h_1(x_1(t-\tau _1))+ d_1-\dot{y_{r}}\right) \nonumber \\&\quad +\sum _{i=1}^nW_{i1}(z_1(t))-\sum _{i=1}^nW_{i1}(z_1(t-\tau _i)) -{\tilde{\Theta }}\dot{{{\hat{\Theta }}}}. \end{aligned}$$
(4)

In view of Assumptions 1 and  2, the following inequalities hold

$$\begin{aligned} v_{z_{1}}d_1\le & {} \frac{v_{z_{1}}^2\mu ^2_1( x_1)}{2a_{11}^2}+\frac{a_{11}^2}{2}, \end{aligned}$$
(5)
$$\begin{aligned} v_{z_{1}}h_1(x_1(t-\tau _1))\le & {} v_{z_{1}}^2+\frac{1}{2}z_1^2(t-\tau _1)q_{11}^2(z_1(t-\tau _1)). \end{aligned}$$
(6)

To cancel the unknown time-delay term \(h_1(x_1(t-\tau _1))\) in (4), \(W_{i1}(z_1(t))\) is chosen as:

$$\begin{aligned} W_{i1}(z_1(t))=\frac{1}{2}(n-i+1){z_1^2(t)}q^2_{i1}(z_1(t)). \end{aligned}$$
(7)

Substituting (5)–(7) into (4) results in

$$\begin{aligned}&{\dot{V}}_{1}\le v_{z_{1}}\left( g_1(x_1)x^*_1 +f_1(x_1)+\frac{v_{z_{1}}}{2}+ \frac{v_{z_{1}}\mu ^2_1( x_1)}{2a_{11}^2}-\dot{y_{r}} +\,\frac{1}{2}\sum _{i=1}^n(n-i+1){\cos ^{2}\left( \frac{\pi z^2_1}{2k^2_{b_1}}\right) z_1(t)}q^2_{i1}(z_1(t))\right) \nonumber \\ &\quad -\,\frac{1}{2}\sum _{i=1}^n(n-i+1){z_1^2(t-\tau _1)}q^2_{i1}(z_1(t-\tau _1))+\,\frac{1}{2}{z_1^2(t-\tau _1)q_{11}^2(z_1(t-\tau _1))} +\frac{a_{11}^2}{2}+g_1v_{z_1}z_2-{\tilde{\Theta }}\dot{{{\hat{\Theta }}}}. \end{aligned}$$
(8)

Let \({\bar{f}}_1=f_1(x_1)+ \frac{v_{z_{1}}\mu ^2_1( x_1)}{2a_{11}^2}-\dot{y_{r}} +\frac{1}{2}\sum _{i=1}^n(n-i+1){\cos ^{2}(\frac{\pi z^2_1}{2k^2_{b_1}})z_1(t)}q^2_{i1}(z_1(t))\). In view of Lemma 1, a fuzzy system \(\Phi _1P_1(X_1)\) can be used to approximate the unknown function \({{\bar{f}}}_1\). For any given \(\varepsilon _1>0\),

$$\begin{aligned} {\bar{f}}_1=\Phi _1^TP_1(X_1)+\delta _1(X_1), \end{aligned}$$

where \(\delta _{1}(X_1)\le \varepsilon _1\) is the approximation error. Based on Young’s inequality, one can obtain

$$\begin{aligned} v_{z_{1}}{\bar{f}}_1=v_{z_{1}}\Phi _1^TP_1(X_1)+v_{z_{1}}\delta _1(X_1) \le \frac{\Theta v^2_{z_1} P^{T}_1P_1}{2a^2_{1}}+\frac{a^2_{1}}{2}+ \frac{v^2_{z_1}}{2}+\frac{\varepsilon ^2_1}{2}, \end{aligned}$$
(9)

where \(a_1\) is a positive constant. A virtual controller \(x^*_1\) and the first tuning function \(\rho _1\) are designed as:

$$\begin{aligned} \left\{ \begin{array}{l} x^*_1= -\frac{1}{g_1}\left( \frac{k_{1}\sin \Big (\frac{\pi z^2_1}{2k^{2}_{b_{1}}}\Big )\cos \Big (\frac{\pi z^2_1}{2k^{2}_{b_{1}}}\Big )}{z_1} +\frac{{{\hat{\Theta }}} P^{T}_1P_1}{2a^2_{1}}v_{z_1}+\frac{2v_{z_1}}{2}\right) ,\\ \rho _1=\frac{ P^{T}_1P_1}{2a^2_{1}}v^2_{z_1}, \end{array} \right. \end{aligned}$$
(10)

where \(k_{1}\) is a positive gain constant. Then, the inequality (8) can be finally represented as:

$$\begin{aligned} \dot{V}_1\le & {} - k_1\tan \left( \frac{\pi z^2_1}{2k^2_{b_1}}\right) \nonumber \\&\quad +g_1v_{z_1}z_2-\sum _{i=1}^n(n-i+1)\frac{z_1^2(t-\tau _i)}{2}q^2_{i1}(z_1(t-\tau _i))+\frac{z_1^2(t-\tau _1)q_{11}^2(z_1(t-\tau _1))}{2}\nonumber \\&\quad +{{\tilde{\Theta }}}(\rho _1-\dot{{{\hat{\Theta }}}})+c_1, \end{aligned}$$
(11)

where \(c_1=\frac{a_{11}^2}{2}+\frac{a_{1}^2}{2}+\frac{\varepsilon ^2_1}{2}\).

Step 2: It follows from (1) and (3) that

$$\begin{aligned} \dot{z}_2&= g_2({\bar{x}}_2(t))x_3(t)+f_2(\bar{x}_2(t))+h_2(\bar{x}_2(t-\tau _2)) +d_2(t,x)\nonumber \\ &\quad -\left( \frac{\partial x^*_1}{\partial x_1}\dot{x}_1 +\frac{\partial x^*_1}{\partial {{\hat{\Theta }}}}\rho _1 +\sum ^{1}_{i=0}\frac{\partial x^*_1}{\partial y^{(i)}_r}y^{(i+1)}_r\right) \nonumber \\ &= g_2({\bar{x}}_2(t))x_3(t)+f_2(\bar{x}_2(t))+h_2(\bar{x}_2(t-\tau _2)) +d_2(t,x)\nonumber \\&\quad -\frac{\partial x^*_1}{\partial x_1}(h_1(x_1(t-\tau _1))+d_1)-\lambda _1, \end{aligned}$$
(12)

where \(\lambda _1=\frac{\partial x^*_1}{\partial x_1}(f_1+g_1x_2)+\frac{\partial x^*_1}{\partial {{\hat{\Theta }}}}\rho _1 +\sum ^{1}_{i=0}\frac{\partial x^*_1}{\partial y^{(i)}_r}y^{(i+1)}_r\). Consider the candidate BLF as

$$\begin{aligned} V_{2}=V_{1}+V^{*}_{2}+\sum _{i=2}^n\int _{t-\tau _i}^tW_{i2}({\bar{z}}_2(s))\hbox {d}s. \end{aligned}$$

The time derivative of \(V_{2}\) is

$$\begin{aligned} \dot{V}_2\le & {} \dot{V}_1 +v_{z_2}\Big (g_2({\bar{x}}_2(t))x_3(t)+f_2(\bar{x}_2(t))+h_2(\bar{x}_2(t-\tau _2)) +d_2(t,x)\nonumber \\&\quad -\frac{\partial x^*_1}{\partial x_1}(h_1(x_1(t-\tau _1))+d_1)-\lambda _1\Big )\nonumber \\&\quad +\sum _{i=2}^nW_{i2}(z_2)-\sum _{i=2}^nW_{i2}({\bar{z}}_2(t-\tau _i))\nonumber \\\le & {} - k_1\tan \Big (\frac{\pi z^2_1}{2k^2_{b_1}}\Big ) + g_1v_{z_1}z_2\nonumber \\&\quad -\sum _{i=1}^n(n-i+1)\frac{z_1^2(t-\tau _i)}{2}q^2_{i1}(z_1(t-\tau _i)) + \frac{z_1^2(t-\tau _1)q_{11}^2(z_1(t-\tau _1))}{2}\nonumber \\&\quad +c_1+v_{z_2}\Big (g_2({\bar{x}}_2(t))x_3(t)+f_2(\bar{x}_2(t))+h_2(\bar{x}_2(t-\tau _2)) +d_2(t,x)-\frac{\partial x^*_1}{\partial x_1}h_1(x_1(t-\tau _1))\nonumber \\&\quad -\frac{\partial x^*_1}{\partial x_1}d_1-\lambda _1\Big ) +\sum _{i=2}^nW_{i2}(z_2)-\sum _{i=2}^nW_{i2}({\bar{z}}_2(t-\tau _i))+{{\tilde{\Theta }}}(\rho _1-\dot{{{\hat{\Theta }}}}). \end{aligned}$$
(13)

In accordance with Assumptions 1 and  2, the following inequalities can be obtained:

$$\begin{aligned} v_{z_2}d_2\le & {} \frac{v_{z_2}^2\mu ^2_2( {\bar{x}}_2)}{2a_{21}^2}+\frac{a_{21}^2}{2}, \end{aligned}$$
(14)
$$\begin{aligned} v_{z_2}h_2({\bar{x}}_2(t-\tau _2))\le & {} v_{z_2}^2+\frac{1}{2}\sum _{j=1}^2 z_j^2(t-\tau _2)q_{2j}^2({\bar{z}}_j(t-\tau _2)), \end{aligned}$$
(15)
$$\begin{aligned} -v_{z_2}\frac{\partial x^*_1}{\partial x_1}h_1(x_1(t-\tau _1))\le & {} \frac{v_{z_{2}}^2}{2}\Big (\frac{\partial x^*_1}{\partial x_1}\Big )^2+\frac{1}{2}z_1^2(t-\tau _1)q_{11}^2(z_1(t-\tau _1)), \end{aligned}$$
(16)
$$\begin{aligned} -v_{z_2}\frac{\partial x^*_1}{\partial x_1}d_1\le & {} \frac{v_{z_2}^2\mu ^2_1( x_1)}{2a_{22}^2}\Big (\frac{\partial x^*_1}{\partial x_1}\Big )^2+\frac{a_{22}^2}{2}. \end{aligned}$$
(17)

Choosing \(W_{i2}({\bar{z}}_2(t))=\frac{1}{2}(n-i+1){z_2^2(t)}q^2_{i2}({\bar{z}}_2(t))\) and substituting (14)–(17) into (13) lead to the following inequality:

$$\begin{aligned} \dot{V}_2\le & {} v_{z_2}\left( g_2({\bar{x}}_2(t))x^*_2+f_2(\bar{x}_2(t))+\Upsilon _2+ v_{z_2} +\frac{v_{z_2}\mu ^2_2( {\bar{x}}_2)}{2a_{21}^2}+\frac{v_{z_{2}}}{2}\Big (\frac{\partial x^*_1}{\partial x_1}\Big )^2+\frac{v_{z_2}\mu ^2_1( x_1)}{2a_{22}^2}\Big (\frac{\partial x^*_1}{\partial x_1}\Big )^2-\lambda _1\right) \nonumber \\&+\sum _{j=2}^2\left( \sum _{l=j}^2(2-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l)) -\sum _{l=j}^n(n-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l))\right) \nonumber \\&+g_2({\bar{x}}_2(t))z_3 v_{z_2}- k_1\tan \Big (\frac{\pi z^2_1}{2k^2_{b_1}}\Big ) +{{\tilde{\Theta }}}(\rho _1-\dot{{{\hat{\Theta }}}})+c_1, \end{aligned}$$
(18)

where \(\Upsilon _2= g_1{\cos ^2\Big (\frac{\pi z^2_2}{2k^2_{b_2}}\Big )}/{\cos ^2\Big (\frac{\pi z^2_{1}}{2k^2_{b_1}}\Big )}z_1 +\frac{1}{2}\sum _{i=2}^n(n-i+1)q_{i2}^2({\bar{z}}_2){\cos ^2\Big (\frac{\pi z^2_2}{2k^2_{b_2}}\Big )}z_2\). Let \({\bar{f}}_2=f_2(\bar{x}_2(t))+\Upsilon _2 +\frac{v_{z_2}\mu ^2_2( {\bar{x}}_2)}{2a_{21}^2}+\frac{v_{z_{2}}}{2}\Big (\frac{\partial x^*_1}{\partial x_1}\Big )^2+\frac{v_{z_2}\mu ^2_1( x_1)}{2a_{22}^2}\Big (\frac{\partial x^*_1}{\partial x_1}\Big )^2-\lambda _1\). By using of Lemma1 again, the unknown function \({\bar{f}}_2\) can be modeled by the given fuzzy system \(\Phi _2P_2(X_2)\)

$$\begin{aligned} {\bar{f}}_2=\Phi _2^TP_2(X_2)+\delta _2(X_2), \end{aligned}$$

where \(\delta _2(X_2)\le \varepsilon _2\) is the approximation error. Notice that

$$\begin{aligned} v_{z_2}{\bar{f}}_2=v_{z_2}\Phi _2^TP_2 +v_{z_2}\delta _{2} \le \frac{\Theta v_{z_2}^2 P^{T}_2P_2}{2a^2_{2}}+\frac{a^2_{2}}{2}+ \frac{v^2_{z_2}}{2}+\frac{\varepsilon ^2_2}{2}, \end{aligned}$$
(19)

where \(a_2\) is a design parameter. The virtual controller \(x^*_2\) and tuning function \(\rho _2\) are constructed as:

$$\begin{aligned} \left\{ \begin{array}{l} x^*_2= -\frac{1}{g_2}\left( \frac{k_2\sin \Big (\frac{\pi z^2_2}{2k^2_{b_2}}\Big )\cos \Big (\frac{\pi z^2_2}{2k^2_{b_2}}\Big )}{z_2}+\frac{v_{z_2}{{\hat{\Theta }}} P^{T}_2P_2}{2a^2_2}+\frac{3v_{z_2}}{2}\right) ,\\ \rho _2=\rho _1+\frac{ P^{T}_2P_2}{2a^2_{2}}v^2_{z_2}, \end{array} \right. \end{aligned}$$
(20)

where \(k_{2}>0\) is a design parameter. By using of the virtual controller \(x^*_2\), we get

$$\begin{aligned} {\dot{V}}_{2}\le & {} \sum _{j=2}^2\left( \sum _{l=j}^2(2-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l)) -\sum _{l=j}^n(n-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l))\right) \nonumber \\&-\sum ^{2}_{i=1} k_{i}\tan \Big (\frac{\pi z^2_i}{2k^{2}_{b_{i}}}\Big ) + {\tilde{\Theta }}\Big (\rho _2-\dot{{\hat{\Theta }}}\Big )+g_2({\bar{x}}_2(t))z_3 v_{z_2}+\sum ^{2}_{i=1}c_i, \end{aligned}$$
(21)

where \(c_2=\frac{a^2_{21}}{2}+\frac{a^2_{22}}{2}+\frac{a^2_{2}}{2}+\frac{\varepsilon ^2_2}{2}\).

Step k\((3 \le k \le n-1)\): Similar to step 2, if we consider the candidate BLF as

$$\begin{aligned} V_k=V_{k-1}+V^{*}_k+\sum _{i=k}^n\int _{t-\tau _i}^tW_{ik}({\bar{z}}_k(s))\hbox {d}s, \end{aligned}$$

where \(W_{ik}({\bar{z}}_k(t))=\frac{1}{2}(n-i+1){z_k^2(t)}q^2_{ik}({\bar{z}}_k(t))\), the virtual controller \(x^*_k\) and the tuning function \(\rho _k\) are chosen as:

$$\begin{aligned} \left\{ \begin{array}{l} x^*_k= -\frac{1}{g_k}\left( \frac{k_k\sin \Big (\frac{\pi z^2_k}{2k^2_{b_k}}\Big )\cos \Big (\frac{\pi z^2_k}{2k^2_{b_k}}\Big )}{z_k}+\frac{v_{\eta _k}{{\hat{\Theta }}} P^{T}_kP_k}{2a^2_k}+\frac{3v_{z_k}}{2}\right) ,\\ \rho _k=\rho _{k-1}+\frac{ P^{T}_kP_k}{2a^2_k}v^2_{z_2}. \end{array} \right. \end{aligned}$$
(22)

Then, the derivative of \(V_k\) leads to the following:

$$\begin{aligned} {\dot{V}}_{k}\le & {} \sum _{j=1}^k\left( \sum _{l=j}^k(k-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l)) -\sum _{l=j}^n(n-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l))\right) \nonumber \\&-\sum ^k_{i=1} k_{i}\tan \Big (\frac{\pi z^2_i}{2k^{2}_{b_{i}}}\Big ) + {\tilde{\Theta }}\Big (\rho _k-\dot{{\hat{\Theta }}}\Big )+g_k({\bar{x}}_k(t))z_{k+1} v_{z_k}+\sum ^k_{i=1}c_i. \end{aligned}$$
(23)

Step n: From (1) and (3), the time derivative of \(z_n\) is

$$\begin{aligned}&\dot{z}_n = g_nu+f_n+h_2(x_n(t-\tau _n)) +d_n-\left( \sum ^{n-1}_{i=1}\frac{\partial x^*_{n-1}}{\partial x_i}\dot{x}_i +\frac{\partial x^*_{n-1}}{\partial {{\hat{\Theta }}}}\rho _{n-1} +\sum ^{n-1}_{i=0}\frac{\partial x^*_{n-1}}{\partial y^{(i)}_r}y^{(i+1)}_r\right) \nonumber \\&\quad = g_nu+f_n+h_2(x_n(t-\tau _n)) +d_n-\sum ^{n-1}_{i=1}\frac{\partial x^*_{n-1}}{\partial x_i}(h_i({\bar{x}}_i(t-\tau _i))+d_i) -\lambda _{n-1} \end{aligned}$$
(24)

where \(\lambda _{n-1} =\sum ^{n-1}_{i=1}\frac{\partial x^*_{n-1}}{\partial x_i}(f_i+g_ix_{i+1}) +\frac{\partial x^*_{n-1}}{\partial {{\hat{\Theta }}}}\rho _{n-1} +\sum ^{n-1}_{i=0}\frac{\partial x^*_{n-1}}{\partial y^{(i)}_r}y^{(i+1)}_r\). Choose the BLF as:

$$\begin{aligned} V_n=V_{n-1}+V^{*}_n+\int _{t-\tau _n}^tW_{nn}({\bar{z}}_n(s))\hbox {d}s. \end{aligned}$$

Then, the derivative of \(V_n\) is

$$\begin{aligned} \dot{V}_n\le & {} v_{z_n}\left( g_n({\bar{x}}_n(t))u+f_n(x_n(t))+h_n(x_n(t-\tau _n)) +d_n -\sum ^{n-1}_{i=1}\frac{\partial x^*_{n-1}}{\partial x_i}(h_i({\bar{x}}_i(t-\tau _i))+d_i) -\lambda _{n-1}\right) \nonumber \\&+\dot{V}_{n-1}+W_{nn}({\bar{z}}_n)-W_{nn}({\bar{z}}_n(t-\tau _n))\nonumber \\\le & {} \sum _{j=1}^{n-1}\left( \sum _{l=j}^{n-1}(n-l)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l)) -\sum _{l=j}^{n-1}(n-l+1)\frac{1}{2}z_j^2(t-\tau _l)q_{lj}^2({\bar{z}}_j(t-\tau _l))\right) \nonumber \\&-\sum ^{n-1}_{i=1} k_{i}\tan \Big (\frac{\pi z^2_i}{2k^{2}_{b_{i}}}\Big ) + g_{n-1}v_{z_{n-1}}z_n+c_{n-1}+W_{nn}({\bar{z}}_n(t))-W_{nn}({\bar{z}}_n(t-\tau _n))+{{\tilde{\Theta }}}(\rho _{n-1}-\dot{{{\hat{\Theta }}}})\nonumber \\&+v_{z_n}\Big (g_nu+f_n+h_2(x_n(t-\tau _n)) +d_n-\sum ^{n-1}_{i=1}\frac{\partial x^*_{n-1}}{\partial x_i}(h_i({\bar{x}}_i(t-\tau _i))+d_i) -\lambda _{n-1}\Big ). \end{aligned}$$
(25)

With Assumptions 1 and  2 in mind, one can immediately arrives at

$$\begin{aligned} v_{z_n}d_n\le & {} \frac{v_{z_n}^2\mu ^2_n( x_n)}{2a_{n1}^2}+\frac{a_{n1}^2}{2}, \end{aligned}$$
(26)
$$\begin{aligned} v_{z_n}h_n( x_n(t-\tau _n))\le & {} v_{z_n}^2+\frac{1}{2}\sum _{j=1}^n z_j^2(t-\tau _n)q_{nj}^2({\bar{z}}_j(t-\tau _n)),\end{aligned}$$
(27)
$$\begin{aligned} -v_{z_n}\frac{\partial x^*_{n-1}}{\partial x_i}h_i(x_i(t-\tau _i))\le & {} \frac{v_{z_n}^2}{2}\Big (\frac{\partial x^*_{n-1}}{\partial x_i}\Big )^2 +\frac{1}{2}\sum _{j=1}^iz_j^2(t-\tau _i)q_{ij}^2(z_i(t-\tau _i)),\end{aligned}$$
(28)
$$\begin{aligned} -v_{z_n}\frac{\partial x^*_{n-1}}{\partial x_i}d_i\le & {} \frac{v_{z_n}^2\mu ^2_n( x_n)}{2a_{n2}^2}\left( \frac{\partial x^*_{n-1}}{\partial x_i}\right) ^2+\frac{a_{n2}^2}{2}. \end{aligned}$$
(29)

Choosing \(W_{nn}( z_n(t))=\frac{1}{2}{z_n^2(t)}q^2_{nn}({\bar{z}}_n(t))\) and substituting (26)–(29) into (25) render

$$\begin{aligned} \dot{V}_n\le & {} v_{z_n}\left( g_n( x_n(t))u+f_n(x_n(t))+\Upsilon _n+ v_{z_n} +\frac{v_{z_n}\mu ^2_n( x_n)}{2a_{n1}^2}+\frac{v_{z_n}}{2}\Big (\frac{\partial x^*_{n-1}}{\partial x_i}\Big )^2+\frac{v_{z_n}\mu ^2_n( x_n)}{2a_{n2}^2}\Big (\frac{\partial x^*_{n-1}}{\partial x_i}\Big )^2 -\lambda _{n-1}\right)nonumber \\ - \sum ^{n-1}_{i=1} k_{i}\tan \Big (\frac{\pi z^2_i}{2k^{2}_{b_{i}}}\Big ) +{{\tilde{\Theta }}}(\rho _{n-1}-\dot{{{\hat{\Theta }}}})+c_1, \end{aligned}$$
(30)

where \(\Upsilon _n= g_{n-1}{\cos ^2\Big (\frac{\pi z^2_n}{2k^2_{b_n}}\Big )}/{\cos ^2\Big (\frac{\pi z^2_{n-1}}{2k^2_{b_{n-1}}}\Big )}z_{n-1} +\frac{1}{2}(n-i+1)q_{in}^2({\bar{z}}_n){\cos ^2\Big (\frac{\pi z^2_n}{2k^2_{b_n}}\Big )}z_n\). Let \({\bar{f}}_n=f_n({x}_n(t))+\Upsilon _n +\frac{v_{z_n}\mu ^2_n( x_n)}{2a_{n1}^2}+\frac{v_{z_n}}{2}\Big (\frac{\partial x^*_{n-1}}{\partial x_i}\Big )^2+\frac{v_{z_n}\mu ^2_n( x_n)}{2a_{n2}^2}\Big (\frac{\partial x^*_{n-1}}{\partial x_i}\Big )^2-\lambda _{n-1}\). According to Lemma 1, for any given \(\varepsilon _2>0\), there is a fuzzy system \(\Phi _2P_2(X_2)\) such that

$$\begin{aligned} {\bar{f}}_n=\Phi _n^TP_n(X_n)+\delta _n(X_n), \end{aligned}$$

where \(\delta _n(X_n)\le \varepsilon _n\) is the approximation error. Notice

$$\begin{aligned} v_{z_n}{\bar{f}}_n=v_{z_n}\Phi _n^TP_n +v_{z_n}\delta _{n} \le \frac{\Theta v_{z_n}^2 P^{T}_nP_n}{2a^2_n}+\frac{a^2_n}{2}+ \frac{v^2_{z_n}}{2}+\frac{\varepsilon ^2_n}{2}, \end{aligned}$$
(31)

where \(a_n>0\) is a design parameter, the controller u and adaptive law \(\dot{{{\hat{\Theta }}}}\) are constructed as:

$$\begin{aligned} \left\{ \begin{array}{l} u= -\frac{1}{g_n}\left( \frac{k_n\sin \Big (\frac{\pi z^2_n}{2k^2_{b_n}}\Big )\cos \Big (\frac{\pi z^2_n}{2k^2_{b_n}}\Big )}{z_n}+\frac{v_{z_n}{{\hat{\Theta }}} P^{T}_nP_n}{2a^2_n}+\frac{3v_{z_n}}{2}\right) ,\\ \dot{{{\hat{\Theta }}}}=\rho _{n-1}+\frac{ P^{T}_nP_n}{2a^2_n}v^2_{z_n}-\gamma {{\hat{\Theta }}}=\sum _{i=1}^n\frac{ P^{T}_iP_i}{2a^2_i}v^2_{z_i}-\gamma {{\hat{\Theta }}}, \end{array} \right. \end{aligned}$$
(32)

where \(k_n>0\) is a design parameter. By substituting (31)–(32) into (30) and using \(\gamma {{\tilde{\Theta }}}{\hat{\Theta \le }}-\frac{\gamma }{2}{\tilde{\Theta }}^2+\frac{\gamma }{2}\Theta ^2\), there holds

$$\begin{aligned} {\dot{V}}_n \le -b\left( \sum ^{n}_{i=1} \tan \left( \frac{\pi z^2_i}{2k^{2}_{b_{i}}}\right) +{{\tilde{\Theta }}}^2\right) +c\le {V}_n+c, \end{aligned}$$
(33)

where \(b=\min \{\frac{k_i\pi }{k^{2}_{b_{i}}},\frac{\gamma }{2}\}\), \(i=1,\ldots , n\) and \(c=\sum ^{n}_{i=1}c_i+\frac{\gamma }{2}\Theta ^2\).

3.2 Main Results

Theorem 1

Consider uncertain nonlinear time-delay systems (1) with the full-state constraints (2), a combined control law proposed in (32), the following properties are guaranteed:

  1. (1)

    All the signals in the closed-loop system are bounded.

  2. (2)

    The full-state constraints are not violated.

  3. (3)

    The tracking error \(z_1\) converges to a sufficiently small neighborhood of the origin.

Proof

In light of (33), one deduces that \(V_n\le (V_n(0)-\frac{c}{b})e^{-bt}+\frac{c}{b}\). Therefore, \(V_n\) is bounded; from the definition of \(V_n\), it concludes that both \(\frac{k^2_{b_i}}{\pi }\tan \Big (\frac{\pi z^2_i}{2k^2_{b_i}}\Big )\) and \({\tilde{\Theta }}\) are bounded, and then, it can also be obtained that \(|z_{i}|<k_{b_{i}}\) and \({\hat{\Theta }}(t)\) are bounded. Assumption 2 shows \(| x_{1}|\le |z_{1}|+| y_r|<k_{b_1}+y_0=k_{c_1}\). \(x^*_1\) is a continuous function, and all variables in \(x^*_1\) are bounded. Hence, \(x^*_1\) is bounded; that is, \(|x^*_1|\le x^*_{10}\). By the transformations (3) and boundedness of \(z_{2}\) and \(x^*_1\), it can be obtained that \(| x_{2}|\le | z_{2}|+| x^*_1|<k_{b_2}+x^*_{10}=k_{c_2}\). Taking the same manipulations, it can be proved that \(| x_i|\le k_{c_i}\). As a result, all the signals in the closed-loop system are bounded and the full-state constraints are not violated. In addition, \(\frac{1}{2}z_1^2\le \frac{k^{2}_{b_1}}{\pi }\tan \Big (\frac{\pi z^2}{2k^{2}_{b_1}}\Big ) \le (V_n(0)-\frac{c}{b})e^{-bt}+\frac{c}{b}\). Therefore, \(z_1\) will be exponentially convergent to the set \(|z_1|\le \sqrt{\frac{2c}{b}}\). Consequently, the appropriate parameters such as \(c_i\) and \(\varepsilon _i\) can be selected to make sure that c is small enough and b is large enough; it guarantees that the tracking error \(z_1\) can converge to a small neighborhood of origin. \(\square\)

Remark 2

This paper addresses the issue of adaptive fuzzy tracking control in the case of strict-feedback nonlinear time-delay systems with full-state constraints. Compared with [19,20,21,22], the simultaneous existence of the full-state constraints and time delays in the system makes the design of controller very difficult. Since the tan-type BLF also works when there is no state constraint, compared with the log-type BLF employed in [30, 34], using the tan-type BLF to deal with state constraints is a general approach.

4 Simulation Example

To demonstrate the effectiveness of the proposed control scheme, the following example is considered:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=x_2 +\theta _1x_1^2+\sin (x_1(t-\tau _1))+d_1(t),\\ \dot{x}_2=u +\theta _2x_1x_2-0.2x_1+x_2(t-\tau _2)\cos (x_2(t-\tau _2))+d_2(t),\\ \,\quad y=x_1. \end{array} \right. \end{aligned}$$
(34)

In the simulation, \(\tau _1=1\) and \(\tau _2=2\), the bounded time-varying disturbances are \(d_1(t)=d_2(t)=0.2\cos t\), a reference signal is given as \(y_r=0.5\cos 2t\). Suppose that all the states are strictly constrained in the following compact set:

$$\begin{aligned} \Omega _{x}:=\Big \{x_i(t)\in R, | x_i(t)| \le 1.5\Big \},\,i=1,2. \end{aligned}$$

Based on the design procedure in Sect. 2, the virtual and actual controllers are designed as:

$$\begin{aligned} \left\{ \begin{array}{l} \alpha _1=-\left( \frac{k_{1}\sin \Big (\frac{\pi z^2_1}{2k^{2}_{b_{1}}}\Big )\cos \Big (\frac{\pi z^2_1}{2k^{2}_{b_{1}}}\Big )}{z_1} +\frac{{{\hat{\Theta }}} P^{T}_1P_1}{2a^2_{1}}v_{z_1}+\frac{3v_{z_1}}{2}\right) , \\ \quad \,u=-\left( \frac{k_2\sin \Big (\frac{\pi z^2_2}{2k^2_{b_2}}\Big )\cos \Big (\frac{\pi z^2_2}{2k^2_{b_2}}\Big )}{z_2}+\frac{{{\hat{\Theta }}} P^{T}_2P_2}{2a^2_2}v_{z_2}+\frac{3v_{z_2}}{2}\right) , \end{array} \right. \end{aligned}$$

and adaptive law is chosen as

$$\begin{aligned} \dot{{{\hat{\Theta }}}}=\sum _{i=1}^2\frac{ P^{T}_iP_i}{2a^2_i}v^2_{z_i}-\gamma {{\hat{\Theta }}}, \end{aligned}$$

where \(P_i(x)=[p_{i1}(x),p_{i2}(x),\ldots ,p_{iN}(x)]^{T}\) with \(p_{ji}(x)=\frac{\prod ^{n}_{j=1}\mu _{F^{i}_{j}}(x_{j})}{\sum ^{N}_{i=1}[\prod ^{n}_{j=1}\mu _{F^{i}_{j}}(x_{j})]}\), \(v_{z_i}=\frac{z_i}{\cos ^2\Big (\frac{\pi z^2_i}{2k^2_{b_i}}\Big )}\), \(j=1,2\), \(i=1,\,2\), \(z_1=x_1-y_r\), \(z_2=x_2-\alpha _1\).

Fig. 1
figure 1

The trajectories of y and \(y_r\)

Full size image
Fig. 2
figure 2

The trajectories of \(x_1\) and \(x_2\)

Full size image
Fig. 3
figure 3

The trajectory of control input u

Full size image
Fig. 4
figure 4

The trajectory of parameter estimation \({{\hat{\Theta }}}\)

Full size image

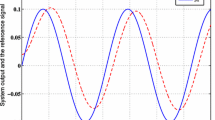
In the simulation, let \(\theta _1=0.1\) and \(\theta _2=0.2\), the initial values are chosen as \(x_1(0)=0.6\), \(x_2(0)=-0.2\) and \({{\hat{\Theta }}}(0)=0.1\). The parameters are designed as \(\gamma =1\), \(k_3=k_2=2\), \(a_1=a_2=1\) and \(k_{b_1}=k_{b_2}=1\). The results of the simulation are shown in Figs. 1, 2, 3 and 4. The system output y and reference trajectory \(y_r\) are illustrated in Fig. 1. It can be seen that the output y can primely track the desired trajectory \(y_r\). It is shown in Fig. 2 that all the states are strictly constrained in \(\{x_i| -1.5 \le x_i(t)\le 1.5 \},\,i=1, 2\). The input u and parameter updating law \({{\hat{\Theta }}}\) are all bounded as shown in Figs. 3 and 4, respectively. Therefore, it can be concluded that the proposed control scheme can deal with uncertain nonlinear time-delay systems with state constraints effectively.

5 Conclusions

This study carries out the adaptive fuzzy tracking control for a class of strict-feedback nonlinear time-delay systems with full-state constraints. Based on barrier Lyapunov functions, the backstepping design method and adaptive fuzzy control approach, an adaptive tracking controller is proposed to guarantee that the system tracking errors converge to a sufficiently small neighborhood of the origin, while the constraints on the states of system will not be violated during operation. Stability analysis of the proposed closed-loop control system is supported by the Lyapunov stability theory. In this direction, there are still remaining several problems to be investigated. For example, an interesting research problem is how to design an finite-time adaptive controller for strict-feedback nonlinear time-delay systems with full-state constraints.