Abstract
Individual consistency and group consensus are important topics in group decision-making process with preference relations. This study introduces a programming model to meet the individual consistency level and group consensus threshold value simultaneously. First, the distance measure between two probabilistic hesitant fuzzy preferences (PHFPRs) is proposed, and a consistency index for PHFPR is defined based on the proposed distance measure. Then, a mathematical programming model is constructed to improve its consistency when the PHFPR does not meet the consistency level. Second, considering that some values in PHFPRs provided by the decision makers may be missing in the decision-making process, a mathematical programming model is constructed to derive the missing values. Third, the proximity degree between any two decision makers is proposed, and a consensus index among the decision makers is defined based on the proposed proximity degree. Then, a mathematical programming model is constructed to obtain the expected consistency level and consensus threshold value simultaneously. Finally, an example is provided to illustrate the effectiveness of the proposed method. Comparative studies with several existing methods are also provided.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Group decision making is a type of decision problem where multiple decision makers analyze problems, evaluate alternatives, and select the best solution from a collection of alternatives [1,2,3]. Each decision maker expresses his/her own knowledge, motivations, and ideas over each alternative [4]. Many multi-attribute group decision-making (MAGDM) methods have been presented over the last decades [5,6,7]. Preference relation is one of the most useful tools to describe the preference of the decision maker. Consistency of preference relation plays a vital role because it is related to rationality, and inconsistency in the decision-making process often leads to misleading solutions. However, obtaining complete consistent preference relation in decision-making process is difficult. In such case, decision makers strive for an acceptable consistent preference relation. In addition, consensus is a fundamental issue widely employed in group decision making. Decision makers with different perceptions, motivations, and attitudes reach a collective decision in which the individual preference comparability is as high as possible. Thus, consistency and consensus are important topics in group decision-making process that have been studied within various fuzzy environments, such as, intuitionistic fuzzy environments [8], hesitant fuzzy linguistic environments [9], and incomplete linguistic environments [10].
Three processes must be performed to solve MAGDM problems based on consistency and consensus [11,12,13]. (1) Individual consistency checking and improving process aims to guarantee the rationality of evaluation values of decision makers to avoid misleading priority weights of alternatives [12]. When a desired consistency level is not yet achieved, developing some methods to improve individual consistency is necessary to obtain acceptable consistency. (2) Group consensus checking and improving process is a preferable process to find out the non-consensus decision makers, and then solve potential problems in group decision-making process [14]. A set of experts must reach a high degree of consensus among their opinions for large-scale group decision-making. (3) The best alternative selection process, which aims to select the best alternative from a set of alternatives, such alternatives are pairwise compared and represented with preference relations provided by decision makers. The first and second processes are the most important because the process of checking and improving individual consistency and group consensus met most challenges for many scholars.
Torra [15] first introduced the concept of hesitant fuzzy set (HFS), as a significant extension of fuzzy set, the primary advantage of it is the ability to specify membership within a set by assigning several values to each candidate membership [16]. Afterward, to incorporate distribution information in HFS, the probabilistic hesitant fuzzy set (PHFS) was proposed by Zhu [17] in 2014. It plays an important role in group decision-making process as a significant extension of HFS. PHFS describes not only the hesitancy of decision makers when making decisions, but also the hesitancy distribution information. Following Zhu [17], PHFS receives increasing attention [18,19,20,21,22,23]. For example, in Zhang et al. [20], an improved PHFS is proposed to incorporate incomplete evaluation information. Hao et al. [24] extended PHFS to probabilistic dual hesitant fuzzy set, whereas Zhai et al. [25] introduced the probabilistic interval intuitionistic hesitant fuzzy set. In addition, some group decision-making methods within probabilistic hesitant fuzzy environments are developed in [26,27,28,29,30].
The PHFS concept is proposed, and following studies on fuzzy preference relations [31], intuitionistic fuzzy preference relations [32], and hesitant fuzzy preference relations [33], some scholars focus on developing MAGDM methods based on probabilistic hesitant fuzzy preference relations (PHFPRs), and group consensus within the context of probabilistic hesitant fuzzy environments [16, 17, 34,35,36,37]. For example, Zhou and Xu [34] developed an iterative algorithm to improve group consistency with uncertain PHFPRs based on additive consistency. Wu et al. [35] introduced two local feedback strategies to improve individual consistency and group consensus. Later, a consensus model was constructed for a large-scale group decision making with probabilistic hesitant fuzzy information by Wu and Xu [36]. Moreover, Zhou and Xu [16] discussed the probability calculation for PHFPRs and developed an iterative optimization algorithm to improve individual consistency. Zhu [17] introduced two iterative algorithms to improve individual consistency and group consensus based on multiplicative consistency. Zhu et al. [37] developed the probabilistic hesitant multiplicative preference relations, which used 1/9–9 scale instead of 0.1–0.9 scale to represent membership degrees.
Although the PHFPR concept is introduced, and some decision-making methods based on PHFPR are studied, some critical issues require resolution. (1) The individual consistency and group consensus are important topics in a group decision-making process with preference relations. Thus, making decisions becomes comprehensive. Nevertheless, some group decision-making processes only consider the individual consistency checking and improving, paying less attention to group consensus [16, 34]. On the other hand, some group decision-making processes only consider group consensus checking and improving, paying less attention to individual consistency [36]. (2) When individual PHFPR does not meet the consistency level or group does not reach consensus threshold value, several algorithms have been developed to improve individual consistency level and group consensus, such as automatic iterative algorithms [17, 38], local feedback strategies [35, 36], and optimization iterative algorithms [16, 34]. Nevertheless, repeating these algorithms several times may be necessary to repair unacceptable consistent PHFPRs until they reach acceptable consistency or group consensus, which is time-consuming. (3) Some values in PHFPRs may be missing in the decision-making process. Unfortunately, only a few studies focus on deriving missing values in decision-making process within probabilistic hesitant fuzzy environments.
Therefore, the current study focuses on individual consistency, as well as group consensus checking and improving with PHFPRs. Moreover, a model is developed to derive missing information in PHFPRs, and a MAGDM method is proposed to meet the individual consistency level and group consensus threshold value simultaneously. The main motivations and contributions of this study are summarized as follows:
-
1.
To obtain comprehensive and reasonable decision information in the decision-making process. In this study, the proposed MAGDM method not only considers the individual consistency, but also the group consensus. Moreover, individual consistency level and group consensus threshold value can be obtained simultaneously.
-
2.
Several models are constructed to reduce the number of iterations in improving individual consistency and group consensus. In addition, the proposed models have a unified mathematical structure. Thus, the amount of computation can be reduced sharply with the assistance of programming software.
-
3.
Some values in PHFPRs may be missing in the decision-making process. In this study, a programming model is constructed to obtain the missing information.
The remainder of the paper is organized as follows. Section 2 reviews some basic concepts related to PHFS, PHFPR, and expected preference relation. In addition, a new distance measure between two PHFPRs is introduced. In Sect. 3, consistency index for PHFPR is introduced and a mathematical programming model is constructed to improve consistency level when individual PHFPR is unacceptable. In Sect. 4, the concept of incomplete PHFPR is defined, and a mathematical programming model is constructed to obtain missing values. In Sect. 5, the group consensus index among decision makers is defined, and a programming model is provided to obtain the expected consistency level and consensus threshold value simultaneously. The proposed algorithm is applied in selecting best green energy engineering problems, and a comparative study and discussion are demonstrated in Sect. 6. Finally, conclusions are presented in Sect. 7.
2 Preliminaries
In this section, we briefly review the definitions of PHFS and PHFPR. Furthermore, a new distance measure between two PHFPRs is proposed.
2.1 Probabilistic Hesitant Fuzzy Set
Zhu [17] first introduced the PHFS concept as an extension of HFS, which membership degrees are endowed with corresponding probabilities.
Definition 1
[17] Let \(X\) be a reference set, then a PHFS \(P\) on \(X\) can be defined as:
where the function \(h_{x}\) is a set of different values in [0, 1], which is described by the probability distribution \(p_{x}\); where \(h_{x}\) denotes the possible membership degree of element \(x\) in \(X\) to \(P\). For convenience, \(h_{x} \left( {p_{x} } \right)\) is named probabilistic hesitant fuzzy element (PHFE) and denoted as \(h\left( p \right)\). It is indicated by:
where \(p_{i}\) satisfying \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } = 1\), is the probability of the possible value \(\gamma_{i}\), and \(\# h\) is the number of all \(\gamma_{i} \left( {p_{i} } \right)\) in \(h\left( p \right)\).
Remark 1
Zhu [17] first introduced the PHFS concept with complete evaluation information. Later, an improved PHFS is proposed by Zhang et al. [20] to incorporate incomplete evaluation information. The difference of the definitions related to PHFS between Zhu [17] and Zhang et al. [20] is that the probability condition in PHFS satisfying \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } = 1\) in Zhu [17], whereas such condition satisfying \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } \le 1\) in Zhang et al. [20].
Xu and Zhou [39] proposed the score function and deviation function for PHFE with complete information to rank PHFEs, and these are as follows.
Definition 2
[39] Let \(h\left( p \right) = \left\{ {\left. {\gamma_{i} \left( {p_{i} } \right)} \right|i = 1,2, \ldots ,\# h} \right\}\) be a PHFE. Its score function is defined as follows:
Definition 3
[39] Let \(h\left( p \right) = \left\{ {\left. {\gamma_{i} \left( {p_{i} } \right)} \right|i = 1,2, \ldots ,\# h} \right\}\) be a PHFE. Its deviation function is defined as follows:
Based on score function and deviation function, the ranking law for two PHFEs is introduced as follows.
Definition 4
[39]. Let \(h_{1} \left( {p_{1} } \right) = \left\{ {\left. {\gamma_{1,i} \left( {p_{1,i} } \right)} \right|i = 1,2, \ldots ,\# h_{1} } \right\}\) and \(h_{2} \left( {p_{2} } \right) = \left\{ {\left. {\gamma_{2,j} \left( {p_{2,j} } \right)} \right|j = 1,2, \ldots ,\# h_{2} } \right\}\) be two PHFEs. Their ranking law is defined as follows:
-
(1)
If \(E\left( {h_{1} \left( {p_{1} } \right)} \right) < E\left( {h_{2} \left( {p_{2} } \right)} \right)\), then \(h_{1} \left( {p_{1} } \right) < h_{2} \left( {p_{2} } \right)\);
-
(2)
If \(E\left( {h_{1} \left( {p_{1} } \right)} \right) = E\left( {h_{2} \left( {p_{2} } \right)} \right)\), then
-
(a)
If \(V\left( {h_{1} \left( {p_{1} } \right)} \right) < V\left( {h_{2} \left( {p_{2} } \right)} \right)\), then \(h_{1} \left( {p_{1} } \right) > h_{2} \left( {p_{2} } \right)\);
-
(b)
If \(V\left( {h_{1} \left( {p_{1} } \right)} \right) = V\left( {h_{2} \left( {p_{2} } \right)} \right)\), then \(h_{1} \left( {p_{1} } \right) = h_{2} \left( {p_{2} } \right)\).
-
(a)
The expected valued and variance of PHFE proposed by Wu et al. [35] are similar to the score function and deviation function of PHFE proposed by Xu and Zhou [39]. Moreover, the comparison law for two PHFEs introduced in [35] is exactly the same as Definition 4.
2.2 Probabilistic Hesitant Fuzzy Preference Relations
Zhu [17] first developed PHFPRs, which were improved by Wu et al. [35], as follows.
Definition 5
[35] Let \(X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\) be a finite set of alternatives. A PHFPR \(H\) on \(X\) is represented by a matrix \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\), where \(h_{ij} \left( {p_{ij} } \right) = \left\{ {\left. {\gamma_{ij,l} \left( {p_{ij,l} } \right)} \right|l = 1,2, \ldots ,\# h_{ij} } \right\}\) is a PHFE, indicating all possible degrees of \(x_{i}\) preferred to \(x_{j}\). Moreover, \(h_{ij} \left( {p_{ij} } \right)\) should satisfy the following conditions:
where \(\gamma_{ij,l}\) is the \(l\)th possible value in \(h_{ij}\), and \(p_{ij,l}\) is the corresponding probability of \(\gamma_{ij,l}\). If the corresponding probability of the possible value \(\gamma_{ij,l}\) is 1, that is to say, only one element in PHFE exists. Thus, the probability of the possible value can be omitted, and the element can be denoted as \(h_{ij} \left( {p_{ij} } \right) = \left\{ {\gamma_{ij,l} } \right\}\).
Example 1
Suppose a decision maker provides a fuzzy preference relation for four alternatives \(\left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right\}\) as follows:
According to Definition 5, \(H\) is a PHFPR.
Zhu [17] proposed expected preference relations to understand the meaning of each element in a PHFPR as a determined value, and these are as follows.
Definition 6
[17] Let \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\) be a PHFPR, where \(h_{ij} \left( {p_{ij} } \right) = \left\{ {\left. {\gamma_{ij,l} \left( {p_{ij,l} } \right)} \right|l = 1,2, \ldots ,\# h_{ij} } \right\}\). Expected preference relations corresponding to \(H\) is denoted as \(E_{H} = \left( {eh_{ij} } \right)_{n \times n}\), where \(eh_{ij} = \sum\nolimits_{l = 1}^{{\# h_{ij} }} {\gamma_{ij,l} p_{ij,l} }\).
Expected preference relations \(E_{H} = \left( {eh_{ij} } \right)_{n \times n}\) are fuzzy preference relations, which are proven by Wu et al. [35].
In order to develop the fuzzy preference relations with multiplicative transitivity, the values with logarithms can be used to measure the distance of fuzzy preference relations. Motivated by Crawford and Williams [40], and Xia and Chen [41], the distance between two PHFPRs can be defined as follows.
Definition 7
Let \(H_{1} = \left( {h_{ij}^{1} \left( {p_{ij}^{1} } \right)} \right)_{n \times n}\) and \(H_{2} = \left( {h_{ij}^{2} \left( {p_{ij}^{2} } \right)} \right)_{n \times n}\) be two PHFPRs, where \(E_{{H_{1} }} = \left( {eh_{ij}^{1} } \right)_{n \times n}\) and \(E_{{H_{2} }} = \left( {eh_{ij}^{2} } \right)_{n \times n}\) be their corresponding expected preference relations. The distance between two PHFPRs is defined as follows:
Utilizing the above distance formula, the consistency index of PHFPRs can be obtained, which is discussed in the following section.
3 Consistency for Probabilistic Hesitant Fuzzy Preference Relations
In this section, the concept of multiplicative consistent expected preference relations of PHFPR is defined. Subsequently, PHFPR consistency index is introduced to check the PHFPR consistency level. Finally, a mathematical programming model is constructed to improve the consistency level when PHFPRs are unacceptably consistent.
3.1 Consistency Index of PHFPRs
Based on expected preference relations and multiplicative transitivity, the concept of multiplicative consistent expected preference relations of PHFPRs can be defined as follows.
Definition 8
Let \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\) be a PHFPR, and its expected preference relations are \(E_{H} = \left( {eh_{ij} } \right)_{n \times n}\). If the following multiplicative transitivity is satisfied:
then \(E_{H}\) is the multiplicative consistent expected preference relation of PHFPRs.
Given that the expected preference relations are fuzzy preference relations, we have \(eh_{ij} = 1 - eh_{ji} ,\) that is to say, components of the lower triangle of \(H\) can be determined according to the components of the upper triangle of \(H\). Then, Eq. (6) is equivalent to:
By taking logarithms on both sides of Eq. (7), an equivalent expression of Definition 8 can be obtained as follows.
Definition 9
Let \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\) be a PHFPR, and its expected preference relations be \(E_{H} = \left( {eh_{ij} } \right)_{n \times n}\). Then, \(E_{H}\) is multiplicative consistent if and only if:
Based on Definition 9, the consistency index of PHFPRs is defined as follows.
Definition 10
For a PHFPR \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\), and its expected preference relations be \(E_{H} = \left( {eh_{ij} } \right)_{n \times n} ,\) the consistency index of \(H\) is defined as:
If a PHFPR is multiplicative consistent, its consistency index \({\text{CI}}\left( H \right) = 1\). Conversely, if consistency index \({\text{CI}}\left( H \right) = 1\), the PHFPR is multiplicative consistent. Moreover, the larger the value \({\text{CI}}\left( H \right)\), the higher the multiplicative consistency level of PHFPR.
Remark 2
Let \({\text{CI}}_{0}\) be a predefined threshold value, it can be determined with respect to practical situation and decision makers’ preference, which is an issue to be further studied. And related work has been investigated intensively by Saaty [42], and Cutello and Montero [43].
3.2 A Method to Improve the Consistency Level of PHFPRs
Consistency of preference relation is related to rationality, and inconsistent decision making often leads to misleading solutions. Therefore, developing some methods to improve the consistency is necessary when a desired consistency level is not yet achieved. However, only few scholars focus on iterative-based method to improve the consistency of PHFPRs at present. In addition, studies using the optimization-based method are limited. Therefore, in this subsection, a mathematical programming model is proposed to obtain an acceptable consistent PHFPR when a desired consistency level is not yet achieved.
Given PHFPR \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\), where \(h_{ij} \left( {p_{ij} } \right) = \left\{ {\left. {\gamma_{ij,l} \left( {p_{ij,l} } \right)} \right|l = 1,2, \ldots ,\# h_{ij} } \right\}\). Utilizing Eq. (2), its expected preference relation \(E_{H} = \left( {eh_{ij} } \right)_{n \times n}\) can be obtained. Then, the consistency of \(H\) can be obtained by using Eq. (9). If a desired consistency level is not yet achieved, the consistency level of \(H\) can be improved by constructing new expected preference relations. To obtain new expected preference relations \(C_{H} = \left( {ch_{ij} } \right)_{n \times n}\), which are not only acceptably consistent, but also preserve the preference information implied in the given PHFPR \(H\), an optimal model can be constructed by minimizing the distance between \(E_{H}\) and \(C_{H}\) under the acceptable consistency constraint. The optimization model can be constructed in the following, and denoted as Model 1.
In Model 1, the first constraint is the consistency index which is proposed in Eq. (9); it ensures that \(C_{H}\) satisfies the acceptable consistency condition, and the rest of the constraints guarantee that \(C_{H}\) is an expected preference relation. By using Model 1, an acceptable consistent expected preference relation \(C_{H}\) can be obtained, which is applied to improve the consistency level of given individual PHFPRs.
The absolute in the object function is removed to simplify the presentation of Model 1. Some marks are adopted in the following. Denoted as \(s_{ij} = - \ln eh_{ij}\) and \(t_{ij} = - \ln ch_{ij}\). Given that \(0 < eh_{ij} ,\;ch_{ij} < 1\), we obtain \(s_{ij} ,\;t_{ij} > 0\). Let \(\xi_{ij} = s_{ij} - t_{ij}\), \(\xi_{ij}^{ + } = \left( {\left| {\xi_{ij} } \right| + \xi_{ij} } \right) /2\) and \(\xi_{ij}^{ - } = \left( {\left| {\xi_{ij} } \right| - \xi_{ij} } \right) /2\), then \(\left| {\xi_{ij} } \right| = \xi_{ij}^{ + } + \xi_{ij}^{ - }\). In this way, Model 1 can be transformed to Model 2:
Similarly, we denote \(\delta_{ijk} = t_{ij} + t_{jk} + t_{ki} - \left( {t_{ji} + t_{kj} + t_{ik} } \right)\), \(\delta_{ijk}^{ + } = \left( {\left| {\delta_{ijk} } \right| + \delta_{ijk} } \right) /2\), and \(\delta_{ijk}^{ - } = \left( {\left| {\delta_{ijk} } \right| - \delta_{ijk} } \right) /2\) to remove the absolute in the first constraint. Then, \(\left| {\delta_{ijk} } \right| = \delta_{ijk}^{ + } + \delta_{ijk}^{ - }\). In this way, Model 2 can be transformed to Model 3:
Suppose that the optimal solution of Model 3 is \(t_{ij}^{ * }\), \(\left( {i < j} \right)\). From \(t_{ij}^{ * } = - \ln ch_{ij}\), we obtain the upper triangular components of matrix \(C_{H}\) as \(ch_{ij} = e^{{ - t_{ij}^{ * } }}\), \(\left( {i < j} \right)\). According to the complementary, lower triangular components of matrix \(C_{H}\) can be obtained. Thus, an acceptable consistent expected preference relation \(C_{H} = \left( {ch_{ij} } \right)_{n \times n}\) is generated as,
Therefore, we obtain the acceptable consistent PHFPR \(H^{c}\) by adjusting expected values of PHFE in PHFPR H.
4 A Method to Determine Missing Information in Incomplete PHFPRs
Decision makers may have a difficult for providing complete preference relations over alternatives in the MAGDM process because of their lack of knowledge and the limited expertise. Therefore, developing some methods to manage incomplete information for PHFPRs is necessary. In this section, we first discuss the missing information for PHFPRs, and then the concept of incomplete PHFPRs is defined. Finally, a mathematical programming model is proposed to obtain the missing values by using complete expected preference relations.
Zhang et al. [20] proposed an improved PHFS indicated that a situation where not all decision makers provide complete evaluation information can possibly occur. That is to say, some information in the decision-making process is missing. In this case, the condition changes to \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } \le 1\). If \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } = 0\), information is complete missing. To estimate the missing probability \(1 - \sum\nolimits_{i = 1}^{\# h} {p_{i} }\) in a PHFE, Zhang et al. [20] asserted that the probability can be proportionally allocated to every membership degree, that is, the probability \(\frac{{p_{i} }}{{\sum\nolimits_{i = 1}^{\# h} {p_{i} } }} - p_{i}\) is allocated to the membership degree \(\gamma_{i}\), \(\left( {i = 1,2, \ldots ,\# h} \right)\), and then the condition \(\sum\nolimits_{i = 1}^{\# h} {\frac{{p_{i} }}{{\sum\nolimits_{i = 1}^{\# h} {p_{i} } }}} = 1\) can be obtained. The method presented in [20] is elaborated in the following example to understand this condition.
Example 2
Suppose a PHFPR \(H\) is given as follows:
For PHFE \(\left\{ {0.3\left( {0.2} \right),0.4\left( {0.3} \right)} \right\}\) in \(H\), the sum of all probabilities is not equal to 1, which means that some information provided by decision makers are missing, and the missing probability is 0.5. In the method proposed by Zhang et al. [20], the probability 0.2 is allocated to membership degree 0.3, whereas 0.3 is allocated to 0.4. In this case, the probability of the membership degree 0.3 becomes 0.4, whereas 0.4 becomes 0.6. Then, the complete PHFPR \(H^{c}\) is obtained as follows:
Evidently, the method presented in [20] is straightforward, and is an effective way to obtain the missing evaluation information. However, this method may result in loss of a certain amount of information. In the given example, decision makers may provide other membership degrees to PHFE \(\left\{ {0.3\left( {0.2} \right),0.4\left( {0.3} \right)} \right\}\). Therefore, they cannot provide complete information because they do not have enough capacity or other reasons. For example, some decision makers may provide PHFE \(\left\{ {0.3\left( {0.2} \right),0.4\left( {0.3} \right),0.5\left( {0.5} \right)} \right\}\) to represent their evaluation. Evidently, the above evaluation values are different from the method proposed by Zhang et al. [20], and it seems reasonable for decision makers to express their preferences. Therefore, further research must be conducted to obtain the missing evaluation information.
Based on the above analysis, incomplete PHFPRs can be defined as follows.
Definition 11
Let \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\), where \(h_{ij} \left( {p_{ij} } \right) = \left\{ {\left. {\gamma_{ij,l} \left( {p_{ij,l} } \right)} \right|l = 1,2, \ldots ,\# h_{ij} } \right\}\) be a PHFPR, then \(H\) is called an incomplete PHFPR when the condition \(\sum\nolimits_{l = 1}^{{\# h_{ij} }} {p_{ij,l} } < 1\) exists.
Remark 3
In an incomplete PHFPR, the number of incomplete membership degrees may be more than one in a PHFE, and complicated ways to solve this problem exist. In this study, we only discuss the case where only one incomplete membership degree in a PHFE exists. In this case, the probability of the missing membership degree is \(1 - \sum\nolimits_{l = 1}^{{\# h_{ij} }} {p_{ij,l} }\). If \(\sum\nolimits_{l = 1}^{{\# h_{ij} }} {p_{ij,l} } = 0\), only one element in a PHFE exists, and its probability is 1.
When some elements in \(H = \left( {h_{ij} \left( {p_{ij} } \right)} \right)_{n \times n}\) cannot be completely given by decision makers, corresponding expected preference relation \(E_{H} = \left( {eh_{ij} } \right)_{n \times n}\) is obtained, which is an incomplete preference relation. Let \(H\) be as before, \(U = \left\{ {{\text{There}}\;{\text{is}}\;{\text{an}}\;{\text{unknown}}\;{\text{value}}\;{\text{in}}\;h_{ij} \left( {p_{ij} } \right),\;{\text{where}}\;i,j = 1,2, \ldots ,n\;{\text{with}}\;i < j} \right\}\). The key task of calculating the missing values of \(E_{H}\) is to find a complete expected preference relation \(C_{H} = \left( {ch_{ij} } \right)_{n \times n}\) with \(eh_{ij} = ch_{ij}\) for \(eh_{ij} \notin U\). When elements for all unknown elements in \(E_{H}\) exist, the incomplete expected preference relation \(E_{H}\) becomes multiplicatively consistent. By maximizing the consistent level of \(C_{H}\), an optimization model to calculate missing values of incomplete expected preference relations is present in Model 4.
In Model 4, the first constraint ensures that \(C_{H}\) satisfies the acceptable consistency condition, the second to forth constraints guarantee that \(C_{H}\) is an expected preference relation, and the last constraint ensures that \(ch_{ij}\) is a constant when there is not unknown value in \(h_{ij} \left( {p_{ij} } \right)\). The following marks are adopted to remove logarithms in the object function: \(s_{ij} = - \ln eh_{ij}\), \(t_{ij} = - \ln ch_{ij}\). Given that \(0 < eh_{ij} ,\;ch_{ij} < 1\), we obtain \(s_{ij} ,\;t_{ij} > 0\). In this way, Model 4 can be transformed to Model 5.
We denote \(\delta_{ijk} = t_{ij} + t_{jk} + t_{ki} - \left( {t_{ji} + t_{kj} + t_{ik} } \right)\), \(\delta_{ijk}^{ + } = \left( {\left| {\delta_{ijk} } \right| + \delta_{ijk} } \right) /2\), and \(\delta_{ijk}^{ - } = \left( {\left| {\delta_{ijk} } \right| - \delta_{ijk} } \right) /2\) to remove the absolute in the object function. Then, \(\left| {\delta_{ijk} } \right| = \delta_{ijk}^{ + } + \delta_{ijk}^{ - }\). In addition, the maximum of the object function is equivalent to its contrary minimum. Then, Model 5 can be transformed to Model 6,
Missing values in \(E_{H}\) can be derived by solving Model 6 for each known element \(eh_{ij}\), \(\left( {i = 1,2, \ldots ,n - 1;\;i < j} \right)\).
Remark 4
The difference between the method proposed by Zhang et al. [20] and the proposed method is that the missing probability is allocated to an unknown evaluation value in the proposed method, which can be obtained by solving Model 6. By contrast, the missing probability in the method by Zhang et al. [20] is proportionally allocated to original evaluation values, without considering the consistency of PHFPRs. Therefore, the proposed method seems more reasonable and objective than that of Zhang et al. [20].
Example 3
Let \(H\) be as given in Example 2:
For the element \(t_{12} = \left\{ {0.3\left( {0.2} \right),0.4\left( {0.3} \right)} \right\}\), the condition is \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } = 0.2 + 0.3 = 0.5 < 1\), which suggests an incomplete PHFPR, and the missing probability value is \(1 - \sum\nolimits_{i = 1}^{\# h} {p_{i} } = 1 - 0.5 = 0.5\). Let \(x\) represent the missing evaluation value, then \(t_{12}\) can be represented as follows: \(t_{12} = \left\{ {0.3\left( {0.2} \right),0.4\left( {0.3} \right),x\left( {0.5} \right)} \right\}\). In Model 6, we obtain \(t_{12} = 1.14295\), that is, \(- \,\ln \left( {0.18 + 0.5x} \right) = 1.14295\). Then, \(x = 0. 2 7 7 8\approx 0.3\). The complete PHFPR of \(H\) can be obtained as follows:
5 A Method for MAGDM with PHFPRs
In this section, the consensus measure index among decision makers is introduced. Then, a programming model is constructed to improve the individual consistency and group consensus when the PHFPR is unacceptably consistent or the group consensus does not reach the threshold value.
Let \(A = \left\{ {A_{1} ,A_{2} , \ldots ,A_{n} } \right\}\) be a set of alternatives, \(E = \left\{ {D^{1} ,D^{2} , \ldots ,D^{m} } \right\}\) be a set of decision makers. Suppose \(\omega = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{m} } \right)\) is the weight vector of decision makers, such that \(0 \le \omega_{p} \le 1\), \(\sum\nolimits_{p = 1}^{m} {\omega_{p} } = 1\), and the weights of the decision makers are completely known. Each decision maker \(D^{p}\) provides his/her individual PHFPR on a basis of several chosen attributes, denotes \(D^{p} = \left( {h_{ij} \left( {p_{ij} } \right)^{p} } \right)_{n \times n}\), where \(h_{ij} \left( {p_{ij} } \right)^{p} = \left\{ {\left. {\gamma_{ij,l}^{p} \left( {p_{ij,l}^{p} } \right)} \right|l = 1,2, \ldots ,\# h_{ij} } \right\}\), \(\left( {p = 1,2, \ldots ,m;\;i,j = 1,2, \ldots ,n} \right)\). According to Eq. (2), the corresponding expected preference relations \(E^{p} = \left( {eh_{ij}^{p} } \right)_{n \times n}\) can be obtained. If some information in the PHFPR is missing, utilizing Model 6 can determine such information.
5.1 Consensus Measure Index with PHFPRs
In this subsection, a consensus measure index among decision makers is introduced. First, the similarity degree \({\text{SD}}\left( {E^{p} ,E^{q} } \right)\) between any two decision makers \(E^{p}\) and \(E^{q}\) is obtained based on the distance presented in Eq. (5). Then, based on \({\text{SD}}\left( {E^{p} ,E^{q} } \right)\), we can obtain the proximity degree \({\text{PD}}\left( {E^{p} } \right)\) related to \(E^{p}\) and other decision makers. Finally, the consensus measure index \({\text{Con}}\left( E \right)\) among decision makers \(E^{1} ,E^{2} , \ldots ,E^{m}\) can be obtained based on proximity degree \({\text{PD}}\left( {E^{p} } \right)\).
The smaller the distance between \(E^{p}\) and \(E^{q}\), the higher their similarity degree. Based on this consideration, we can use \(1 - d\left( {E^{p} ,E^{q} } \right)\) to calculate the similarity degree of \(E^{p}\) and \(E^{q}\). By substituting Eq. (5) in the above formula, the similarity degree \({\text{SD}}\left( {E^{p} ,E^{q} } \right)\) can be obtained as follows:
Similarly, the similarity degree between \(E^{p}\) and other decision makers \(E^{1} , \ldots ,E^{p - 1} ,E^{p + 1} , \ldots ,E^{m}\) can be obtained. Let \(\sum\nolimits_{q = 1,q \ne p}^{m} {{\text{SD}}\left( {E^{p} ,E^{q} } \right)}\) denote the sum of the similarity degree related to \(E^{p}\) and other decision makers, the proximity degree \({\text{PD}}\left( {E^{p} } \right)\) between \(E^{p}\) and other decision makers can be calculated as follows: \({\text{PD}}\left( {E^{p} } \right) = \frac{1}{m - 1}\sum\nolimits_{q = 1,q \ne p}^{m} {{\text{SD}}\left( {E^{p} ,E^{q} } \right)}\). Substituting Eq. (11) in the above formula, the proximity degree related to \(E^{p}\) and other decision makers can be obtained as follows:
Let \(\sum\nolimits_{p = 1}^{m} {{\text{PD}}\left( {E^{p} } \right)}\) denote the sum of all decision makers to the proximity degree of other decision makers. The consensus \({\text{Con}}\left( E \right)\) among all decision makers \(E^{1} ,E^{2} , \ldots ,E^{m}\) can be obtained as follows: \({\text{Con}}\left( E \right) = \frac{1}{m}\sum\nolimits_{p = 1}^{m} {{\text{PD}}\left( {E^{p} } \right)}\). Substituting Eq. (12) in the above formula, consensus index among decision makers can be obtained as follows:
Given that \({\text{SD}}\left( {E^{p} ,E^{q} } \right) = {\text{SD}}\left( {E^{q} ,E^{p} } \right)\), Eq. (13) is simplified as:
Let \({\text{GCI}}_{0}\) be a predefined consensus threshold value, if \({\text{Con}}\left( E \right) \ge {\text{GCI}}_{0}\), the group is an acceptable consensus. Otherwise, the group is an unacceptable consensus. In the following section, a programming model is constructed to improve the consensus when the group is an unacceptable consensus.
5.2 Improving the Individual Consistency and Group Consensus
Evaluation values provided based on the preferences of decision makers may vary because of their different experiences and knowledge background. Therefore, obtaining decision results, which can be accepted by most decision makers, is another principal issue in MAGDM problems. Therefore, the consensus reaching models are designed. Considering consistency and consensus as important topics in group decision-making process, in this subsection, we develop a mathematical programming model to improve the individual consistency and group consensus simultaneously.
Let \(E^{p} = \left( {eh_{ij}^{p} } \right)_{n \times n}\), where \(eh_{ij}^{p} = \sum\nolimits_{l = 1}^{{\# h_{ij} }} {\gamma_{ij,l}^{p} p_{ij,l}^{p} } ,\,\left( {p = 1,2, \ldots ,m} \right)\) denoted as expected preference relations obtained from \(m\) decision makers. If at least one of the individual PHFPR is unacceptably consistent or the group is an unacceptable consensus, then a mathematical programming model is constructed to derive a family of expected preference relations \(C^{p} = \left( {ch_{ij}^{p} } \right)_{n \times n}\), which meet the consistency level and reach the consensus threshold value simultaneously, the model is denoted as Model 7.
In Model 7, the first constraint ensures the obtained expected preference relation is an acceptable PHFPR, the second constraint ensures that the obtained expected preference relation is the group acceptable consensus, and the rest of the constraints guarantee that \(C^{p}\) are expected preference relations. Let \(s_{ij}^{p} = - \ln eh_{ij}^{p} ,\,t_{ij}^{p} = - \ln ch_{ij}^{p}\), \(\xi_{ij}^{p} = s_{ij}^{p} - t_{ij}^{p}\), \(\xi_{ij}^{p + } = \left( {\left| {\xi_{ij}^{p} } \right| + \xi_{ij}^{p} } \right) /2\) and \(\xi_{ij}^{p - } = \left( {\left| {\xi_{ij}^{p} } \right| - \xi_{ij}^{p} } \right) /2\), then \(\left| {\xi_{ij}^{p} } \right| = \xi_{ij}^{p + } + \xi_{ij}^{p - }\). In this way, Model 7 is equivalent to Model 8.
Furthermore, let \(\delta_{ijk}^{p} = t_{ij}^{p} + t_{jk}^{p} + t_{ki}^{p} - \left( {t_{ji}^{p} + t_{kj}^{p} + t_{ik}^{p} } \right)\), \(\delta_{ijk}^{p + } = \left( {\left| {\delta_{ijk}^{p} } \right| + \delta_{ijk}^{p} } \right) /2\) and \(\delta_{ijk}^{p - } = \left( {\left| {\delta_{ijk}^{p} } \right| - \delta_{ijk}^{p} } \right) /2\). Then, \(\left| {\delta_{ijk}^{p} } \right| = \delta_{ijk}^{p + } + \delta_{ijk}^{p - }\), and let \(\sigma_{ij}^{pq} = t_{ij}^{p} - t_{ij}^{q}\). \(\sigma_{ij}^{pq + } = \left( {\left| {\sigma_{ij}^{pq} } \right| + \sigma_{ij}^{pq} } \right) /2\) and \(\sigma_{ij}^{pq - } = \left( {\left| {\sigma_{ij}^{pq} } \right| - \sigma_{ij}^{pq} } \right) /2\), then \(\left| {\sigma_{ij}^{pq} } \right| = \sigma_{ij}^{pq + } + \sigma_{ij}^{pq - }\). Then, Model 8 can be transformed to Model 9.
Suppose that the optimal solution of Model 9 is \(t_{ij}^{p * }\), \(\left( {p = 1,2, \ldots ,m} \right)\), replace \(t_{ij}^{ * }\) with \(t_{ij}^{p * }\) in Eq. (10). Then, a family of consistency expected preference relations are derived. Model 9 not only obtains the acceptable consistent PHFPRs, but also meets the group consensus level.
5.3 Algorithm for Group Decision Making with PHFPRs
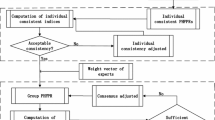
In this section, an algorithm is designed to solve MAGDM with PHFPRs. The main procedures are described as follows:
- Step 1 :
-
Determine individual PHFPR.
Each decision maker \(D^{p}\) provides his/her individual PHFPR on a basis of several chosen attributes, denotes \(D^{p} = \left( {h_{ij} \left( {p_{ij} } \right)^{p} } \right)_{n \times n} ,\) where \(h_{ij} \left( {p_{ij} } \right)^{p} = \left\{ {\left. {\gamma_{ij,l}^{p} \left( {p_{ij,l}^{p} } \right)} \right|l = 1,2, \ldots ,\# h_{ij} } \right\},\,\left( {p = 1,2, \ldots ,m;\;i,j = 1,2, \ldots ,n} \right)\).
- Step 2 :
-
Determine missing information.
If some information in PHFPRs is missing, then such values can be determined by solving Model 6. Otherwise, proceed to the next step.
- Step 3 :
-
Calculate expected preference relations.
Expected preference relations can be obtained according to Eq. (2).
- Step 4 :
-
Check individual consistency and group consensus.
The individual consistency can be checked by Eq. (9), and group consensus among decision makers can be checked by Eq. (14). If all individual PHFPRs meet the consistency level, and the group consensus reaches the threshold value, then proceed to Step 6. Otherwise, proceed to the next step.
- Step 5 :
-
Derive a group of expected preference relations.
If at least one of the individual PHFPRs does not meet the consistency level or the group consensus does not reach threshold value, then the individual consistency and group consensus can be improved by solving Model 9. Combined with Eq. (10), a group of expected preference relations can be derived which not only meets the consistency level, but also reaches the group consensus threshold value.
- Step 6 :
-
Calculate individual priority weights of alternatives.
The individual priority weights of alternatives can be calculated according to the following formula [44]:
- Step 7 :
-
Calculate overall priority weights of alternatives.
The overall priority weights of alternatives can be calculated according to the following formula:
where \(w = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{m} } \right)\) is the weight vector of decision makers.
- Step 8 :
-
Rank alternatives.
The ranking of alternatives can be obtained with respect to the values obtained from Eq. (16), and the largest value is the best alternative.
The above group decision-making process with PHFPRs is depicted in Fig. 1.
6 A Case Study
In this section, the best green energy engineering selection problem is provided to present the application of the proposed method.
6.1 Description of the Illustrate Problem
With the development of human society, the demand for energy is growing, but the traditional non-renewable energy is reducing. According to the storage report of the twenty-first century petrochemical energy, the world energy has entered a statement of crisis [45]. The development and utilization of new green energy becomes an important task all over the world. New green energy also becomes an important part in the structure of energy. In addition, advantages for underdeveloped countries or less developed areas to occupy the international market become a competition. Although new environmentally friendly energy cannot replace traditional energy, the supply of energy in the world and the change of climate provide a broad space for new green energy development. In other words, new green energy makes a great contribution to the world environment and economy.
With the rapidly growing energy consumption, a new energy development company experienced a growth in the demand of its products. Moreover, the company is dissatisfied with the size of its existing projects. Choosing a new energy engineering project to expand production and to solve the current difficulties in the company is the best way. The company decision to develop a new green energy engineering project is made after the discussion among the board of directors. After 3 months of market research in the demand of customers, three engineering are determined for the company to select, that is, (1) electrical engineering \(\left( {A_{1} } \right)\), (2) computer engineering \(\left( {A_{2} } \right)\), (3) and electronics engineering \(\left( {A_{3} } \right)\). The company focuses on the attributes of engineering including technological foundation \(\left( {c_{1} } \right)\), economic interest \(\left( {c_{2} } \right)\), market capacity \(\left( {c_{3} } \right)\), and future development \(\left( {c_{4} } \right)\).
The company invites four experts to participate in the decision-making process to select the best engineering project among three alternatives. Suppose the invited experts are familiar with engineering, and the weights of experts are completely known, \(\omega = \left( {0.2,0.3,0.3,0.2} \right)\). After adequately considering such attributes, four experts, respectively, provide pairwise comparison to alternatives with PHFPRs, which are shown in Tables 1, 2, 3, and 4.
The process of obtaining the best engineering is described in the following steps:
- Step 1 :
-
Determine individual PHFPR.
The individual PHFPR is provided by four experts. See Tables 1, 2, 3 and 4.
- Step 2 :
-
Determine missing information.
The complete information is shown in Tables 1, 2, 3 and 4, and no missing information must be determined. Thus, proceed to the next step.
- Step 3 :
-
Calculate expected preference relations.
Expected preference relations can be obtained according to Eq. (2) and are shown in Table 5.
- Step 4 :
-
Check individual consistency and group consensus.
According to Eq. (9), individual consistency index can be obtained as follows: \({\text{CI}}\left( {E^{1} } \right) = 0.9642\), \({\text{CI}}\left( {E^{2} } \right) = 0. 8 3 2 9\), \({\text{CI}}\left( {E^{3} } \right) = 0. 7 9 9 3\), and \({\text{CI}}\left( {E^{4} } \right) = 0. 7 4 2 2\). Utilizing Eq. (14), the consensus index among decision makers can be obtained as follows: \({\text{GCI}}\left( E \right) = 0. 9 8 4 4\). Suppose \({\text{CI}}_{0} = 0.9\) and \({\text{GCI}}_{0} = 0.8\), then \(E^{2}\), \(E^{2}\), and \(E^{3}\) are unacceptably consistent, \(E^{1}\) is acceptably consistent, and \(E = \left\{ {E^{1} ,E^{2} ,E^{3} ,E^{4} } \right\}\) is an acceptable group consensus.
- Step 5 :
-
Derive a group of expected preference relations.
A group of expected preference relations is derived via Model 9 and Eq. (10) and is shown in Table 6.
The individual consistency index derived from Eq. (9) can be obtained as follows: \({\text{CI}}\left( {E^{1 * } } \right) = 0.9642\), \({\text{CI}}\left( {E^{2 * } } \right) = 0. 9 7 4 5\), \({\text{CI}}\left( {E^{3 * } } \right) = 0. 9 2\), and \({\text{CI}}\left( {E^{4 * } } \right) = 0. 9 1 5 9\). The consensus index among three experts is: \({\text{GCI}}\left( {E^{ * } } \right) = 0. 9 8 6 2\). Given that \({\text{CI}}_{0} = 0.9\) and \({\text{GCI}}_{0} = 0.8\) derived expected preference relations \(E^{1 * }\), \(E^{2 * }\), \(E^{3 * }\), and \(E^{4 * }\) are acceptably consistent, and \(E^{ * } = \left\{ {E^{1 * } ,E^{2 * } ,E^{3 * } ,E^{4 * } } \right\}\) is an acceptable group consensus.
- Step 6 :
-
Calculate individual priority weights of alternatives.
According to Eq. (15), individual priority weights of alternatives can be obtained as follows:
- Step 7 :
-
Calculate the overall priority weights of alternatives.
According to Eq. (16), the overall priority weights of alternatives can be obtained as follows:
- Step 8 :
-
Rank alternatives.
Given that \(w_{1} > w_{3} > w_{2}\), the best alternative is electrical engineering project.
6.2 Comparative Studies and Discussions
To validate the feasibility of the proposed method, in this subsection, we conducted a comparative study with other methods based on the same illustrative example.
- Case 1 :
-
Compared with the method presented in Zhou and Xu [16].
In the following, the method was introduced in Zhou and Xu [16] is applied to the illustrative example. The process is described in the following steps:
- Step 1 :
-
Derive individual priority weight vector.
For \(D^{1}\), the programming model can be constructed according to Eq. (11) in Zhou and Xu [16] as follows:
By solving above programming model, we have
Similarly, for \(D^{2}\), we have
For \(D^{3}\), we have
For \(D^{4}\), we have
- Step 2 :
-
Consistency checking.
According to Eq. (13) in Zhou and Xu [16], consistency indexes for \(D^{1}\), \(D^{2}\), \(D^{3}\) and \(D^{4}\) can be obtained as follows: \({\text{ECI}}_{1} = 0. 0 0 1 7\), \({\text{ECI}}_{2} = 0. 0 0 6 9\), \({\text{ECI}}_{3} = 0. 0 0 5 6\) and \({\text{ECI}}_{4} = 0. 0 1 1 6\). Since all the consistency indexes less than \(0.02\), and thus, the consistencies of \(D^{1}\), \(D^{2}\), \(D^{3}\) and \(D^{4}\) are acceptable.
- Step 3 :
-
Derive the collective priority weight.
According to Eq. (17) in Zhou and Xu [16], the collective priority weight is obtained as follows: \(w_{1} = 0. 4 6 8 3\), \(w_{2} = 0. 2 2 4 6\) and \(w_{3} = 0. 3 0 7 0\).
- Step 4 :
-
Rank all the alternatives.
Since \(w_{1} > w_{3} > w_{2}\), we have, \(A_{1} \succ A_{3} \succ A_{2}\), which implies that electrical engineering project is the best alternative.
For a better comparison, the calculation results of the method Zhou and Xu [16], and the proposed method are listed in Table 7.
As shown in Table 7, the ranking result and the best alternative obtained by the proposed method is the same as that of the method of Zhou and Xu [16], indicating the validity of the proposed method. Moreover, the possible reason why the best alternative is the same between these two methods, i.e., these methods are both based on consistency checking and improvement. However, in the processes of these two methods we find that: the proposed method requires higher consistency than the method of Zhou and Xu [16]. In the illustrative example, only \(D^{1}\) is acceptable in the proposed method, whereas in the method of Zhou and Xu [16], the consistencies of \(D^{1}\), \(D^{2}\), \(D^{3}\) and \(D^{4}\) are acceptable. Furthermore, the method proposed by Zhou and Xu [16] pays less attention to the group consensus checking and improving in the group decision-making process, whereas the proposed method can overcome this shortcoming. Therefore, the group decision-making process presented in the proposed method is more reasonable.
- Case 2 :
-
Compared with the method presented in Zhou and Xu [34].
In the following, the method was introduced in Zhou and Xu [34] is applied to the illustrative example. The process is described in the following steps:
- Step 1 :
-
Derive individual priority weight vector.
For \(D^{1}\), the programming model can be constructed according to Eq. (13) in Zhou and Xu [34] as follows:
By solving above programming model, we have
Similarly, for \(D^{2}\), we have
For \(D^{3}\), we have
For \(D^{4}\), we have
- Step 2 :
-
Consistency checking.
According to the consistency index formula \({\text{CI}} = \frac{2}{{n\left( {n - 1} \right)}}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = 2,j > i}^{n} {\left| {\mathop {e_{ij} }\limits^{ - } - \left( {w_{i} - w_{j} } \right) - 0.5} \right|} }\) presented in Zhou and Xu [34], we have: \({\text{CI}}_{1} = 0. 0 0 3 3\), \({\text{CI}}_{2} = 0. 0 1\), \({\text{CI}}_{3} = 0. 0 1 6 7\) and \({\text{CI}}_{4} = 0. 0 2\). Since all the consistency indexes less than or equal to \(0.02\), and thus, the consistencies of \(D^{1} ,\,D^{2} ,\,D^{3}\) and \(D^{4}\) are acceptable.
- Step 3 :
-
Integrate the overall evaluation information.
With respective to Eq. (17) in Zhou and Xu [34], the evaluation information is integrated into one, and the results are listed as follows:
- Step 4 :
-
Derive the collective priority weight.
According to Eq. (13) in Zhou and Xu [34], we have: \(w_{1} = \, 0.412\), \(w_{2} = 0. 2 7 8\) and \(w_{3} = 0. 3 1\); \(d_{12}^{ + } = 0.02\), \(d_{12}^{ - } = 0\), \(d_{13}^{ + } = 0\), \(d_{13}^{ - } = 0\), \(d_{23}^{ + } = 0\), \(d_{23}^{ - } = 0\).
- Step 5 :
-
Collective consistency checking.
According to the consistency index formula presented in Step 2, we have:\({\text{CI}} = 0. 0 0 6 7< 0. 0 2\), then, the consistency of overall evaluation information are acceptable.
- Step 6 :
-
Rank all the alternatives.
Since \(w_{1} > w_{3} > w_{2}\), we have, \(A_{1} \succ A_{3} \succ A_{2}\), which implies that electrical engineering project is the best alternative.
For a better comparison, the calculation results of the method Zhou and Xu [34], and the proposed method are listed in Table 8.
As shown in Table 8, the ranking result and the best alternative obtained by the proposed method is the same as that of the method of Zhou and Xu [34], indicating the validity of the proposed method. The differences from different methods are explained similar to that for Case 1 and is thus omitted here. Moreover, we find that the integration results obtained using Zhou and Xu’s method [34] are complex and tedious. Take \(h_{23} \left( {p_{23} } \right)\) in Step 3 for example, we find that the integration results obtained using Zhou and Xu’s method [34] have 14 results, whereas the proposed method only has one result. Obviously, the burden of computation can be significantly decreased when using proposed method to integrate the evaluation values.
Consistency and consensus are important topics in the group decision-making process. Some scholars studied about these topics within probabilistic hesitant fuzzy environments. In the following section, the proposed method is compared with some existing consistency and consensus-based methods.
-
1.
In the method proposed by Zhu and Xu [38], the checking of individual consistency is based on the distance between individual PHFPR and a complete consistent PHFPR, whereas the checking of consensus is based on the distance between individual PHFPR and the collected PHFPR. When a desired consistency or consensus threshold value is not yet achieved, two automatic iterative algorithms are constructed to improve the individual consistency and the group consensus. In algorithms, several iterations must occur to achieve the consistency level or the consensus threshold value. However, the individual consistency and group consensus can be improved simultaneously by solving Model 9 in the proposed method. Combined with Eq. (10), a group of expected preference relations can be derived, which not only meets the consistency level, but also reaches the consensus threshold value.
-
2.
In the method proposed by Wu et al. [35], the checking of individual consistency is done by constructing a linear programming model, whereas the checking of group consensus is based on the sum of all distances between any two decision makers. When a desired consistency or consensus threshold value is not yet achieved, two local feedback strategies are provided to improve individual consistency and the group consensus. Unfortunately, the convergent is not presented in algorithm 1 of the proposed feedback mechanism [35]. If the algorithm is not convergent, time may be wasted, and acceptable individual PHFPRs cannot be obtained.
-
3.
In the method by Wu and Xu [36], the group consensus checking is based on the sum of all distances between any two decision makers, and local feedback strategies are provided to improve the group consensus. As the optimization iterative algorithms by Zhou and Xu [16, 34], several consensus rounds are necessary to reach the consensus level. In addition, the method by Wu and Xu [36] pays less attention to the individual consistency checking and improving in the group decision-making process.
Compared with these methods, the proposed method in this study has the following attractive features.
-
1.
Consistency and consensus are important topics in group decision-making process. In this study, the proposed MAGDM method not only considers the individual consistency checking and improving, but also the group consensus. Moreover, the proposed model can simultaneously meet the individual consistency level and group consensus threshold value.
-
2.
Proposed models have unified mathematical structure. Therefore, the amount of computation can be reduced sharply with the assistance of programming software.
-
3.
Some values in PHFPRs provided by decision makers may be missing in the decision-making process. In this study, a model is introduced to obtain such values. Therefore, the proposed MAGDM method has a wide application field.
7 Conclusion
The individual consistency and group consensus are important topics in a group decision-making process with preference relations. This study aims to develop the MAGDM method for checking and improving the individual consistency and group consensus with PHFPRs. First, the consistency index for PHFPRs is defined, and then a programming model is constructed to improve its consistency when a PHFPR does not meet the consistency level. Second, a programming model is constructed to obtain missing values. Third, a consensus index among the decision makers is defined, and then a programming model is constructed to obtain the expected consistency level and consensus threshold value simultaneously. Finally, an example is provided to illustrate the effectiveness of the proposed method.
This study makes several significant contributions to MAGDM problems, which are summarized as follows: (1) In this study, the proposed group decision-making method not only considers the individual consistency checking and improving, but also the group consensus. Thus, more comprehensive and reasonable decision information is obtained in the decision-making process than those only consider individual consistency or group consensus. (2) Several models are proposed to solve some MAGDM problems with PHFPRs, that is, consistency checking, determining missing values, and improving individual consistency and group consensus. (3) When the decision makers provide incomplete PHFPRs in MAGDM process, a programming model is constructed to obtain such missing values in PHFPRs. Therefore, the proposed MAGDM method has a wide application field than those with only complete PHFPRs. The MAGDM process with complete PHFPRs and incomplete PHFPRs are addressed. In future studies, we focus on expanding proposed models under probabilistic linguistic environments to solve other practical MAGDM problems.
References
Zhang, X.Y., Wang, J.Q., Hu, J.H.: On novel operational laws and aggregation operators of picture 2-tuple linguistic information for MCDM problems. Int. J. Fuzzy Syst. 20, 958–969 (2018)
Liang, R.X., Wang, J.Q., Zhang, H.Y.: Projection-based PROMETHEE methods based on hesitant fuzzy linguistic term sets. Int. J. Fuzzy Syst. (2017). https://doi.org/10.1007/s40815-40017-40418-40817
Liao, H.C., Mi, X.M., Xu, Z.S., Xu, J.P., Herrera, F.: Intuitionistic fuzzy analytic network process. IEEE Trans. Fuzzy Syst. (2018). https://doi.org/10.1109/TFUZZ.2017.2788881
Sun, R.X., Hu, J.H., Zhou, J.D., Chen, X.H.: A hesitant fuzzy linguistic projection-based MABAC method for Patients’ prioritization. Int. J. Fuzzy Syst. (2017). https://doi.org/10.1007/s40815-40017-40345-40817
Chen, S.Q., Wang, Y.M., Shi, H., Zhang, M.J., Lin, Y.: Alliance-based evidential reasoning approach with unknown evidence weights. Expert Syst. Appl. 78, 193–207 (2017)
Rezaei, J., Wang, J., Tavasszy, L.: Linking supplier development to supplier segmentation using Best Worst Method. Expert Syst. Appl. 42, 9152–9164 (2015)
Liao, H.C., Jiang, L.S., Xu, Z.S., Xu, J.P., Herrera, F.: A linear programming method for multiple criteria decision making with probabilistic linguistic information. Inf. Sci. 415, 341–355 (2017)
Chu, J.F., Liu, X.W., Wang, Y.M., Chin, K.S.: A group decision making model considering both the additive consistency and group consensus of intuitionistic fuzzy preference relations. Comput. Ind. Eng. 101, 227–242 (2016)
Wu, Z.B., Xu, J.P.: Managing consistency and consensus in group decision making with hesitant fuzzy linguistic preference relations. Omega 65, 28–40 (2016)
Zhao, M., Ma, X.Y., Wei, D.W.: A method considering and adjusting individual consistency and group consensus for group decision making with incomplete linguistic preference relations. Appl. Soft Comput. 54, 322–346 (2017)
Xu, G.L., Wan, S.P., Wang, F., Dong, J.Y., Zeng, Y.F.: Mathematical programming methods for consistency and consensus in group decision making with intuitionistic fuzzy preference relations. Knowl.-Based Syst. 98, 30–43 (2016)
Liao, H.C., Xu, Z.S., Zeng, X.J., Merigo, J.M.: Framework of group decision making with intuitionistic fuzzy preference information. IEEE Trans. Fuzzy Syst. 23, 1211–1227 (2015)
Zhang, X.Y., Wang, J.Q.: Discussing incomplete 2-tuple fuzzy linguistic preference relations inmulti-granular linguistic MCGDM with unknown weight information. Soft. Comput. (2017). https://doi.org/10.1007/s00500-00017-02915-x
Zhang, L.Y., Li, T., Xu, X.H.: Consensus model for multiple criteria group decision making under intuitionistic fuzzy environment. Knowl.-Based Syst. 57, 127–135 (2014)
Torra, V.: Hesitant fuzzy sets. Int. J. Intell. Syst. 25, 529–539 (2010)
Zhou, W., Xu, Z.S.: Probability calculation and element optimization of probabilistic hesitant fuzzy preference relations based on expected consistency. IEEE Trans. Fuzzy Syst. (2017). https://doi.org/10.1109/TFUZZ.2017.2723349
Zhu, B.: Decision Method for Research and Application Based on Preference Relation. Southeast University, Nanjing (2014)
Li, J., Wang, J.Q.: An extended QUALIFLEX method under probability hesitant fuzzy environment for selecting green suppliers. Int. J. Fuzzy Syst 19, 1866–1879 (2017)
Li, J., Wang, J.Q.: Multi-criteria outranking methods with hesitant probabilistic fuzzy sets. Cogn. Comput. 9, 611–625 (2017)
Zhang, S., Xu, Z.S., He, Y.: Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inf. Fusion 38, 1–11 (2017)
Peng, H.G., Zhang, H.Y., Wang, J.Q.: Cloud decision support model for selecting hotels on TripAdvisor.com with probabilistic linguistic information. Int. J. Hosp. Manag. 68, 124–138 (2018)
Yu, S.M., Wang, J., Wang, J.Q., Li, L.: A multi-criteria decision-making model for hotel selection with linguistic distribution assessments. Appl. Soft Comput. 67, 741–755 (2018)
Li, J., Wang, Z.X.: Multi-attribute decision-making based on prioritized operators under probabilistic hesitant fuzzy environments. Soft Comput. (2018). https://doi.org/10.1007/s00500-00018-03047-00507
Hao, Z.N., Xu, Z.S., Zhao, H., Su, Z.: Probabilistic dual hesitant fuzzy set and its application in risk evaluation. Knowl.-Based Syst. 127, 16–28 (2017)
Zhai, Y.L., Xu, Z.S., Liao, H.C.: Measures of probabilistic interval-valued intuitionistic hesitant fuzzy sets and the application in reducing excessive medical examinations. IEEE Trans. Fuzzy Syst. (2017). https://doi.org/10.1109/TFUZZ.2017.2740201
Wang, Z.X., Li, J.: Correlation coefficients of probabilistic hesitant fuzzy elements and their applications to evaluation of the alternatives. Symmetry 9, 259–377 (2017)
Zhou, W., Xu, Z.S.: Expected hesitant VaR for tail decision making under probabilistic hesitant fuzzy environment. Appl. Soft Comput. 60, 297–311 (2017)
Gao, J., Xu, Z.S., Liao, H.C.: A dynamic reference point method for emergency response under hesitant probabilistic fuzzy environment. Int. J. Fuzzy Syst. 19, 1261–1278 (2017)
Ding, J., Xu, Z.S., Zhao, N.: An interactive approach to probabilistic hesitant fuzzy multi-attribute group decision making with incomplete weight information. J. Intell. Fuzzy Syst. 32, 2523–2536 (2017)
Li, J., Wang, Z.X.: Consensus building for probabilistic hesitant fuzzy preference relations with expected additive consistency. Int. J. Fuzzy Syst. (2018). https://doi.org/10.1007/s40815-40018-40451-40811
Orlovsky, S.A.: Decision-making with a fuzzy preference relation. Fuzzy Sets Syst. 1, 155–167 (1978)
Liao, H.C., Xu, Z.S.: Consistency of the fused intuitionistic fuzzy preference relation in group intuitionistic fuzzy analytic hierarchy process. Appl. Soft Comput. 35, 812–826 (2015)
Xia, M.M., Xu, Z.S.: Managing hesitant information in GDM problems under fuzzy and multiplicative preference relations. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 21, 865–897 (2013)
Zhou, W., Xu, Z.S.: Group consistency and group decision making under uncertain probabilistic hesitant fuzzy preference environment. Inf. Sci. 414, 276–288 (2017)
Wu, Z.B., Jin, B.M., Xu, J.P.: Local feedback strategy for consensus building with probability-hesitant fuzzy preference relations. Appl. Soft Comput. 67, 691–705 (2018)
Wu, Z.B., Xu, J.P.: A consensus model for large-scale group decision making with hesitant fuzzy information and changeable clusters. Inf. Fusion 41, 217–231 (2018)
Zhu, B., Xu, Z.S., Zhang, R., Hong, M.: Hesitant analytic hierarchy process. Eur. J. Oper. Res. 250, 602–614 (2016)
Zhu, B., Xu, Z.S.: Probability-hesitant fuzzy sets and the representation of preference relations. Technol. Econ. Dev. Econ. (2017). https://doi.org/10.3846/20294913.2016.1266529
Xu, Z.S., Zhou, W.: Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optim. Decis. Making 16, 481–503 (2017)
Crawford, G., Williams, C.: A note on the analysis of subjective judgment matrices. J. Math. Psychol. 29, 387–405 (1985)
Xia, M.M., Chen, J.: Consistency and consensus improving methods for pairwise comparison matrices based on Abelian linearly ordered group. Fuzzy Sets Syst. 266, 1–32 (2015)
Saaty, T.L.: Multicriteria Decision Making: The Analytic Hierarchy Process. McGraw-Hill, NewYork (1980)
Cutello, V., Montero, J.: Fuzzy rationality measures. Fuzzy Sets Syst. 62, 39–54 (1994)
Xu, Z.S.: Algorithm for priority of fuzzy complementary judgement matrix. J. Syst. Eng. 16, 311–314 (2001)
Oncel, S.S.: Green energy engineering: opening a green way for the future. J. Clean. Prod. 142, 3095–3100 (2017)
Acknowledgements
The authors thank the editors and anonymous reviewers for providing thoughtful comments for the improvement of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, J., Wang, Zx. A Programming Model for Consistency and Consensus in Group Decision Making with Probabilistic Hesitant Fuzzy Preference Relations. Int. J. Fuzzy Syst. 20, 2399–2414 (2018). https://doi.org/10.1007/s40815-018-0501-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-018-0501-8