1 Introduction

Recurrent fuzzy systems have been designed and aimed for the processing of nonlinear dynamic systems. Contrasted with feed-forward fuzzy systems, recurrent fuzzy systems are characterized by having feedback loops in their structure. In processing the dynamic systems whose current outputs depend explicitly on the delayed past outputs, delayed past inputs or both, recurrent fuzzy systems have been demonstrated to be particularly useful due to its feedback structure [1,2,3,4,5,6,7,8,9,10]. If a feed-forward fuzzy system is employed to deal with such temporal characteristic problems, the number of lagged inputs and outputs of the dynamic model should be acquired in advance. Unfortunately, however, the exact order of the real-life dynamic systems to be processed usually is unknown. Moreover, these time-delayed input/output values provide the necessary information and thus have to be fed as the inputs to the feed-forward fuzzy system. This will increase the input dimension yielding less compact fuzzy system models and perhaps making the design more difficult. On the contrary, the recurrent fuzzy systems are able to store information from the past experiences due to the internal memory inherited in recurrent models and thus do not require necessarily such information from the external inputs. Therefore, the recurrent fuzzy systems are probably more suitable than the feed-forward fuzzy systems on processing dynamic systems with temporal characteristics.

The proposed recurrent fuzzy systems in the studies [1,2,3,4,5,6,7,8,9,10] differ mainly on the feedback structure. The examples of recurrent fuzzy systems in [1,2,3,4] feed the outputs of the fuzzy system back to its inputs. The recurrent fuzzy systems proposed in [5,6,7,8,9,10] use feedback loops from the internal state variables instead of the fuzzy outputs, which are further differentiated according to the recurrence property: local and global feedbacks. The recurrent systems in the studies [5, 6] feed the output of each membership function locally back to itself, so each membership value is only affected locally by its past values. In [7], a recurrent self-evolving fuzzy neural network with local feedback (RSEFNN-LF) feeds the output of temporal firing strength locally back to itself, so the temporal firing strength is affected locally by the current and past states. The examples of recurrent fuzzy systems with the global recurrence property are recurrent self-organizing neural fuzzy inference networks (RSONFIN) [8], Takagi–Sugeno–Kang (TSK)-type recurrent fuzzy networks (TRFN) [9], and interactively recurrent self-evolving fuzzy neural network (IRSFNN) [10]. In the TRFN, all rule firing strengths are linearly summed according to their weights and then fed back as internal network input variables. As a result, the firing strength of each rule depends not only on its own previous value but also on all other rules, making the global recurrence across all rules. Due to such global recurrence, the performance superiority of TRFN to recurrent fuzzy neural networks (RFNN) [5] was shown in [9]. However, given the fuzzy rules, the accurate design of fuzzy system, equivalent to the identification of the parameters in fuzzy systems, is always a time-consuming task. This is particularly difficult for recurrent fuzzy systems. Therefore, this study will aim on improving the accuracy of TRFN designs.

In the past decades, the designs of fuzzy systems have adopted the parameter learning methods used for the learning of artificial neural network to reduce the difficulty. This was accomplished by transforming such design task into solving an optimization problem of the parameters. One major approach for solving the optimization problems is the gradient-based learning algorithm in which the search direction is derived from the gradient of the objective function with respect to the parameters [1,2,3, 5,6,7,8,9,10]. The gradient-based learning requires the training input–output data pairs of the fuzzy system for calculating the gradient. However, this usually does not fit for control problems because the desired control outputs corresponding to the inputs are usually not directly available in advance. Moreover, the derivation of the gradient computation is usually complicated and is especially more complex for recurrent fuzzy systems. Another problem for the gradient-based method is that it is easily trapped in local minima/maxima, which is always an issue for the optimization problems where there are multiple minima/maxima in the search space.

To avoid issues above in gradient-based learning methods, derivative-free population-based evolutionary algorithms via computation techniques, such as genetic algorithms (GAs) [9, 11,12,13,14,15], particle swarm optimization (PSO) [16,17,18,19,20], and ant colony optimization (ACO) [21,22,23,24,25,26,27,28,29,30,31,32,33], have been proposed and investigated extensively for optimizing the parameters of fuzzy systems in the past. These evolutionary algorithms apply stochastic procedures on generating new solutions and evaluate many candidate solutions simultaneously, so they are more likely in probability to find the relatively better solution.

Genetic algorithm [11] was developed based on the principle of survival of fittest. The GA uses the crossover operation for exchanging the information between two randomly selected parent solutions, and the mutation technique for exploiting the solutions further to generate the offspring with optimistically better performance. In [13], the GA was employed to design fuzzy controller for the mobile robots. The design of neural fuzzy system optimized by the GA for temperature control was demonstrated in [14]. In [9], an elite genetic algorithm was employed to identify optimally the parameters of a TRFN for control problems. Particle swarm optimization (PSO) was invented based on the understanding of the social behavior of animals such as bird flocking, fish schooling [16]. For each particle in the PSO, its locally own and globally neighboring experiences stochastically determine its velocity for movement. The swarm of particles moves in the search space to find better solutions. In [17], the PSO was used for the automatic construction of fuzzy systems. The hybrid of GA and PSO (HGAPSO) was proposed to achieve better accuracy of the TFRN designs [19]. The study in [20] proposed to use interval type-2 fuzzy logic system for dynamic parameter adaption in PSO to improve the convergence and diversity of the swarm.

Inspired by the observations on real ant colony, the ACO technique was proposed and originally used for solving discrete combinational optimization problems (COP) [21,22,23,24]. The original ACO and its variants have been successfully applied to optimization problems and have good performances [25,26,27,28]. A rank-based ACO with the algorithm parameters being dynamically adjusted by type-1 fuzzy logic [25] or interval type-2 fuzzy logic [26] was proposed to optimize the membership functions of trajectory fuzzy controller for mobile robot. The design of a fuzzy controller for the ball and beam system using a modified ACO with ant set partition strategy was proposed in [27]. The proposed approach in [27] optimized in a systematic and hierarchical way the type of membership functions, the parameters of the membership function, and the fuzzy rules of a fuzzy controller. In the studies [25,26,27], the parameters of the membership functions of the fuzzy controller were discretized such that the discrete ACO variants can be applied to identify them optimally.

By extending the discrete ACO to continuous domains, a continuous ACO algorithm for solving continuous optimization problems with real-value parameters to be determined was proposed and named as ACOR [29]. The ACOR demonstrated good performances for continuous optimization in [29], and later became useful for the high-precision demanded problems such as the design of fuzzy controllers for dynamic systems. Motivated by the ACOR, several ACOR variants have been proposed to design fuzzy systems for accuracy-oriented problems [30,31,32,33]. A cooperative continuous ACO (CCACO) [30] and an assimilation–accommodation mixed continuous ant colony optimization (ACACO) [31] inspired by the cognitive psychology concepts were proposed for the designs of feed-forward fuzzy systems. The elite-guided continuous ACO (ECACO) as claimed to be the first application of continuous ACO to recurrent fuzzy system design was proposed in [32]. These ACOR variants achieved good performances on the designs of fuzzy systems. However, as far as accuracy of the fuzzy system design is concerned, there is still room for further improvement over the existing ACOR approaches in terms of convergence and accuracy of the optimization algorithms. Based on the ACOR framework, this paper proposes a new learning algorithm for TRFN design to improve further the accuracy.

The main contributions of this paper are twofold. First, a new continuous ACO, elite-mixed continuous ACO with central initialization (EMCACO-C) is proposed for TRFN designs. The EMCACO-C is developed based on the framework of the ACOR and can be regarded as a new population-based evolutionary optimization algorithm. The EMCACO-C proposes a centrally distributed initialization of the ant solutions for fuzzy system designs followed by a new approach for new solution generation at each iteration. The performance superiority of the EMCACO-C to the ACOR, PSO, and ACACO algorithms is demonstrated in five simulation examples of TRFN designs. Second, the advantage on the accuracy improvement for the TRFN designs gained by applying the central initialization to population-based algorithms is also demonstrated in this study. To the best of our knowledge, this is the first time to be studied.

This paper is organized as follows. The next section reviews the structure and the detailed operation of the TRFN. Section 3 proposes the EMCACO-C for TRFN design and provides the comparison of the algorithm with GA. The simulation results of the TRFNs designed by the EMCACO-C and other algorithms for several application problems are presented and discussed in Sect. 4. The application problems simulated in this paper include dynamic system control, chaotic series prediction, and dynamic system identification. Ultimately, Sect. 5 concludes this paper.

2 TSK-Type Recurrent Fuzzy Network

The TSK-type recurrent fuzzy network (TRFN) was proposed in [9], and its structure is shown in Fig. 1. Referring to [9], the detailed operation is reviewed as follows. Nodes in layer 1 are input nodes. The sole function of the input nodes is to transmit the input variables to layer 2. The nodes in layer 2 are input term nodes and they act as membership functions to express the input fuzzy linguistic variables. Two types of membership functions are employed in this layer. The first one is the Gaussian membership function, which is used for the external network input variable x and affects the fuzzy output based on the local rules. The second one is a global membership function, the sigmoid function, which is used for the internal network input variable h. Each node in layer 3 is a rule node and is to calculate the firing strength of a rule. The nodes in layer 4 are consequent nodes. Each consequent node corresponding to each rule node performs a TSK-type consequence which is the linearly weighted combination of the input variables x and h plus a constant. Context nodes in layer 5 operate as the defuzzifier for the inference output h. The link weights for inference output in the consequent part of the rules are represented with singleton values. The number of the internal variables h in this layer is the same as the ones of the rules nodes and the consequent nodes. The node in layer 6 is a defuzzification node and computes the output of the TRFN.

Fig. 1
figure 1

Structure of the TSK-type recurrent fuzzy network [9]

Full size image

The memory mechanism behaviour in the TRFN is explained as follows. In Fig. 1, the value of the internal variable \(h_{i}\) is derived from the firing strengths of all fuzzy rules and then its delayed version is fed back to layer 1 as the input for the corresponding rule. The sigmoid membership of each internal variable \(h_{i}\) corresponding to each rule can be regarded as the influence degree of the temporal history to the current rule. Thus, these internal network variables can memorize the temporal characteristics of the TRFN.

To be specific, a TRFN is represented by a set of the recurrent if–then fuzzy rules, which is described as follows:

$$\begin{aligned} {\text{Rule}}\,i :\, & {\text{If}}\,x_{1} (t)\,{\text{is}}\,A_{i1} , \ldots ,{\text{ and}}\;x_{n} (t)\,{\text{is}}\,A_{in} ,\;{\text{and}}\,h_{i} (t)\,{\text{is}}\,G, \\ & {\text{Then}}\,y(t + 1)\,{\text{is}}\;a_{i0} + a_{i1} x_{1} (t) + \cdots + a_{in} x_{n} (t) + a_{i(n + 1 )} h_{i} (t), \\ & \quad {\text{and}}\,h_{1} (t + 1)\,{\text{is}}\;v_{i1} ,\, \ldots ,\, {\text{and}}\,h_{r} (t + 1)\,{\text{is}}\,v_{ir} , \\ \end{aligned}$$
(1)

where \(A_{ij}\) and G are the fuzzy sets, and the variables \(x_{i}\) and \(h_{i}\) are the external network inputs and internal network inputs to the TRFN, respectively. The values of \(a_{ij}\) and \(v_{ij}\) are the consequent parameters for the external output y and internal inference outputs h, respectively. The external output y inferred from the TRFN with r fuzzy rules is calculated by

$$y(t + 1) = \frac{{\sum\nolimits_{i = 1}^{r} {\phi_{i} \left( {\vec{x}(t),h_{i} (t)} \right) \cdot f_{i} (t)} }}{{\sum\nolimits_{i = 1}^{r} {\phi_{i} \left( {\vec{x}(t),h_{i} (t)} \right)} }} , { }$$
(2)

and the internal inference output \(h_{i}\) is computed by

$$h_{i} (t + 1) = \sum\limits_{j = 1}^{r} {\phi_{j} \left( {\vec{x}(t),h_{j} (t)} \right) \cdot v_{ji} } ,\quad i = 1,2, \ldots ,r,$$
(3)

where

$$f_{i} (t) = a_{i0} + \sum\limits_{j = 1}^{n} {a_{ij} x_{j} (t) + a_{i(n + 1)} h_{i} } ,$$
(4)
$$\phi_{i} \left( {\vec{x}(t),h_{i} (t)} \right) = \frac{1}{{1 + \exp ( - h_{i} (t))}} \cdot \exp \left\{ { - \sum\limits_{j = 1}^{n} {\left( {\frac{{x_{j} (t) - m_{ij} }}{{b_{ij} }}} \right)}^{2} } \right\}.$$
(5)

where the values of antecedent parameters \(m_{ij}\) and \(b_{ij}\) are the centers and the widths of the Gaussian membership functions for the external input \(x_{i}\), respectively.

Therefore, given the fuzzy rules, the design of TRFN actually is to determine the parameters \(m_{ij} ,\,b_{ij} ,\,a_{ij} ,\) and \(v_{ij}\) as used in (3), (4) and (5). For a TRFN in (1) with n external input variables, r fuzzy rules, and a single output, all of the free parameters (decision variables) of the total number \(D = r \cdot (r + 3n + 2)\) can be represented as follows:

$$\begin{aligned} \vec{s} & = [m_{11} ,b_{11} , \ldots ,m_{1n} ,b_{1n} ,a_{10} ,a_{11} , \ldots ,a_{1(n + 1)} , \ldots ,m_{r1,} b_{r1} , \ldots , \\ & \quad m_{rn} ,b_{rn} ,a_{r0} ,a_{r1} , \ldots ,a_{r(n + 1)} ,v_{11} ,v_{12} , \ldots ,v_{1r} , \ldots ,v_{r1} , \ldots ,v_{rr} ] \\ & \equiv s\left[ {^{1} ,s^{2} , \ldots ,s^{D} } \right]. \\ \end{aligned}$$
(6)

The design of a TRFN can be accomplished by applying the optimization algorithm to determine the decision variables in (6) by minimizing or maximizing the value of the task-dependent objective function when the TRFN is employed for achieving such task.

3 Elite-Mixed Continuous ACO with Central Initialization (EMCACO-C) for TRFN Design

This section presents the proposed elite-mixed continuous ACO with central initialization (EMCACO-C) which will be used for TRFN designs. Since the proposed EMCACO-C is inspired by the ACOR, which is actually extended from the discrete ACO framework, we firstly review the operation of the original ACO and the ACOR in detail for easier explanation of the EMCACO-C later. The ACOR will also be used as the benchmark for comparison.

3.1 Discrete ACO Framework

The discrete ACO framework outlines a class of swarm-based evolutionary algorithms, which were inspired by the behavior of real ant colonies and now are largely applied to solve discrete combinational optimization problems. Ants deposited the pheromone trail when they foraged for food. Since the pheromone evaporates with the time, the path with a higher pheromone level guiding other ants is usually a shorter one to the food source. The first and best-known discrete ACO, named as ant system (AS) [21], was proposed and applied to solve the classical traveling salesman problem (TSP). In ant system for the TSP problem, each ant chooses probabilistically the next city to visit when it moves. At the time t, the transition probability with which ant k in city i chooses to move to city j is defined as

$$P_{ij}^{k} (t) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {\tau_{ij} (t)} \right)^{a} \left( {\eta_{ij} } \right)^{b} }}{{\sum\nolimits_{{l \in \mathop U\nolimits_{i}^{k} }} {\left( {\tau_{il} (t)} \right)^{a} \left( {\eta_{il} } \right)^{b} } }}} \hfill & {{\text{if }}\,j \in \mathop U\nolimits_{i}^{k} ,} \hfill \\ 0 \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right.$$
(7)

The parameters in (7) are described as follows. \(\tau_{ij} (t)\) is the pheromone trail on the edge (i, j) at the time t. \(\eta_{ij}\) is a prior heuristic information for moving from city i to city j. \(\mathop U\nolimits_{i}^{k}\) is the set of allowed neighborhood cities of city i for the ant k. The values of a and b determine the relative importance of pheromone trail at time t and heuristic information. Each ant constructs a feasible solution after it visited all cities only once. All feasible solutions the ant colony built by completing their visits are collected for the discrete ACO algorithm to update the pheromone information for the next ant cycle. Many variants of discrete ACO algorithms, such as ant colony system (ACS) [22] and max–min ant system (MMAS) [23] differing on the update rules for pheromone values, were proposed.

3.2 ACO for Continuous Domains (ACOR)

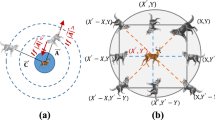
Many continuous ACO algorithms for continuous optimization problems were proposed and studied after the proposal of the discrete ACO. In particular, ACO for continuous domain (denoted as ACOR) proposed in [29] directly extended the discrete probability distributions (7) used in the discrete ACO to the continuous probability density functions (PDFs). In the ACOR, these PDFs are the Gaussian functions and can be derived from a maintained solution archive sketched in Fig. 2 for sampling values to generate new candidate solutions.

Fig. 2
figure 2

Solutions archive in the ACOR, where the weights \(w_{1} \ge w_{2} \ge \cdots \ge w_{N}\) and the objective values \(E\left( {\vec{s}_{1} } \right) \le E\left( {\vec{s}_{2} } \right) \le \cdots \le E\left( {\vec{s}_{N} } \right)\) [29]

Full size image

In the ACOR, each row vector in the solution archive represents a feasible solution to the optimization problem to be solved. The quality of each feasible solution \(\vec{s}_{l}\) is determined by the value of the objective function \(E\left( {\vec{s}_{l} } \right)\). All the feasible solutions in the archive are sorted and ranked from the best quality to the worst one in the table so that the solution \(\vec{s}_{l}\) has rank l. These ranks are used to determine the probabilities of each ant solution being selected in the next ant cycle to generate the new solutions. The procedure of the ACOR is detailed as follows.

Initially, in the archive of N solutions, each D-dimensional row vector \(\vec{s} = [s^{1} ,s^{2} , \ldots ,s^{D} ]\) with the continuous-valued components as in (6) is randomly generated within the specified search space. All solutions then are evaluated, sorted, and kept in the solution archive. Each solution \(\vec{s}_{l}\) (with rank l) in the sorted archive has associated with a weight \(w_{l}\):

$$w_{l} = \frac{1}{{qN\sqrt {2\pi } }}\exp \left\{ { - \frac{{\left( {l - 1} \right)^{2} }}{{2q^{2} N^{2} }}} \right\},$$
(8)

where q is a parameter of the ACOR.

The ACOR generates a new candidate solution in two phases. In the phase one, the ACOR chooses probabilistically one leading solution \(\vec{s}_{l}\) from the archive according to the following probability distribution:

$$p_{l} = \frac{{w_{l} }}{{\sum\nolimits_{m = 1}^{N} {w_{m} } }},\quad m = 1,2, \ldots ,N.$$
(9)

It is inferred from (8) and (9) that the solution with the better quality has the higher chances being chosen. Once a leading solution is chosen, a new candidate solution is constructed by completing the second phase. In the phase two, the new value for each variable \(s^{j}\) of a new candidate solution is sampled around the jth component value of the leading solution based on the Gaussian PDF \(g_{l}^{j} (s^{j} ;\mu_{l}^{j} ,\sigma_{l}^{j} )\) with the mean \(\mu_{l}^{j} = s_{l}^{j}\) and the standard deviation \(\sigma_{l}^{j}\)

$$g_{l}^{j} (s^{j} ;\mu_{l}^{j} ,\sigma_{l}^{j} ) = \frac{1}{{\sigma_{l}^{j} \sqrt {2\pi } }}\exp \left\{ { - \frac{{\left( {s^{j} - \mu_{l}^{j} } \right)^{2} }}{{2\left( {\sigma_{l}^{j} } \right)^{2} }}} \right\},$$
(10)
$$\sigma_{l}^{j} = \varepsilon \sum\limits_{m = 1}^{N} {\frac{{\left| {s_{m}^{j} - s_{l}^{j} } \right|}}{N - 1},}$$
(11)

where the pheromone evaporation rate \(\varepsilon > 0\) is a parameter of the ACOR. For constructing a new candidate solution, a leading solution \(\vec{s}_{l}\) from all archive solutions is chosen only once and the Gaussian PDFs \(g_{l}^{j} (s^{j} ;\mu_{l}^{j} ,\sigma_{l}^{j} )\) are sampled in sequence for \(\, j = 1,2, \ldots ,D\). Therefore, L new candidate solutions can be generated for consideration by repeating this two-phase process L times. These L new candidate solutions, together with the original N solutions in the previous ant cycle, are sorted again according to their values of objective function \(E\left( \cdot \right)\). At the end of each ant cycle, only the N top-best-performance solutions over the total (N + L) solutions are reserved and stored in the archive for next cycle.

3.3 EMCACO-C

The proposed algorithm, elite-mixed continuous ACO with central initialization (EMCACO-C), for improving the accuracy of TRFN designs differs from the ACOR on the initialization of ant solutions and the method of generating new candidate solution. The superiority of the proposed EMCACO-C for TRFN designs will be demonstrated in Sect. 4. The operation of the EMCACO-C is detailed as follows.

3.3.1 Central Initialization

The initial guesses of ant solutions in the EMCACO-C for TRFN design are not the same as most popular swarm-based algorithms, such as GA, PSO, and ACOR. Those well-known popular algorithms usually generate the initial population of solutions randomly and uniformly over the entire search space because of no a prior information in the beginning. In the EMCACO-C for TRFN designs, however, all the initial solutions are guessed uniformly within the certain width around the center point of the search space. Our idea for this is simply based on the case observations of some manually designed fuzzy systems. In some observed fuzzy systems, especially accuracy-oriented systems, one of the locations of the membership functions for each input in its antecedent part is usually designed around the input value which arises more frequently or is most concerned. The other membership functions for each input could be located in the positions symmetrically extending from that point. Therefore, we consider the central initialization for the archive solutions in the proposed EMCACO-C for fuzzy system designs. The centrally distributed initial ant solutions will be further optimized by the proposed algorithm.

The specific procedure for the initial guess of solutions in the EMCACO-C is as follows. In the first step, the entire search range for each decision variable to be optimized is normalized to the fixed range [0, 1], respectively. In fact, such normalization procedure for the decision variables to be learned is very common in the field of computational intelligence because it makes the learning rates for all the decision variables uniform. Then an initial ant solution in the archive is formed by generating random numbers uniformly over the range [0.5 − α/2, 0.5 + α/2] and scaling back to the original search range for each decision variable. The parameter α is defined as the guess width for initializing population solutions, and its value is a parameter of the EMCACO-C. The effects of the guess width α for initializing solutions on the performance of TRFN designs will be discussed through simulation results.

3.3.2 Elite-Mixed ACOR

In the ACOR, all N solutions in the archive are the candidates for being chosen as the leading solution. Around the leading solution, a series of D (the number of decision variables) corresponding Gaussian samplings are followed to generate a new solution. The probability of a solution to be chosen in (8) and (9) is inversely in exponential way proportional to its corresponding rank and depends on the value of the parameter q in (8). When q is small, the best-ranked solutions are intensely favored and thus the algorithm is easier to be stuck in one of the local optima while it converges faster. On the contrary, when q is too large, the probabilities for all archive solutions being selected become more uniform, and the algorithm has better chance to find the global optima while it converges more slowly.

The EMCACO-C mixes in scanning manner starting from the first solution component, the fixed number of the few best elites uniformly in probability to form a directional solution. The Gaussian random sampling procedure for exploiting further the directional solution then is employed to generate a new candidate solution. The entire process of the mixing operation followed by the Gaussian sampling is denoted as the elite-mixed ACOR to differentiate from the original ACOR. For example, we consider the EMCACO-C in which the Q best-ranked elites are involved for mixing. The EMCACO-C firstly constructs the directional solution, whose jth component \(s_{d(j)}^{j}\) is chosen identically and independently from the component set \(\left\{ {s_{1}^{j} ,s_{2}^{j} , \ldots ,s_{Q}^{j} } \right\}\). Around the constructed directional solution, a new candidate solution is generated by sampling the Gaussian PDF \(g_{d(j)}^{j} (s^{j} ;\mu_{d}^{j} ,\sigma_{d}^{j} )\) with \(\mu_{d}^{j} = s_{d(j)}^{j}\) and \(\sigma_{d(j)}^{j}\) as defined in (11) for \(j = 1,2, \ldots ,D.\) Therefore, the L new candidate solutions are generated for consideration by L repetitions of the elite-mixed ACOR. The value of Q is a parameter of the algorithm and its effect on the performance is discussed in Sect. 4.

3.3.3 Population Update

The L new candidate solutions above are evaluated by the values of the objective function \(E\left( \cdot \right)\). These L new candidate solutions, together with the original N solutions in the previous cycle, are sorted again according to their values of objective function. Similarly, at the end of each cycle, only the N top-best-performance solutions over the total (N + L) solutions are reserved and stored in the archive for next cycle, and the rest of them are discarded.

The EMCACO-C repeats generating the L new candidate solutions followed by the population update until the termination condition for the algorithm is satisfied. The pseudo code of the EMCACO-C algorithm is shown in Fig. 3.

Fig. 3
figure 3

EMCACO-C algorithm

Full size image

3.3.4 Qualitative Comparison of the EMCACO-C with GA

Though the EMCACO-C is inspired from the ACOR, its operation is more like the Genetic algorithms (GA). Referring to [32], the methodology similarities and differences between the EMCACO-C and GA are compared. In the EMCACO-C, the mixing operation of the elite-mixed ACOR can be regarded as the multi-parent scanning crossover in the GAs [34]. In general, the GA usually selects and recombines two parents to generate new solutions. The basic principle for selecting parents is that the better-quality parents are possibly selected with higher probability. The techniques of the tournament and the roulette wheel are two of the examples. The general recombination techniques include one-point, two-point, or arithmetic crossover operations. However, the mixing operation of the elite-mixed ACOR in the EMCACO-C selects multiple parents. These parents are the top-performed Q elites in the archive. Each of these Q elites is selected uniformly in probability. The scanning crossover used in the mixing operation of the elite-mixed ACOR essentially is (D − 1)-point crossover. Intuitively, the multi-parent scanning crossover probably could provide more diverse candidate solutions than the two-point crossover by two parents. However, the mixing operation of the elite-mixed ACOR does not handle the correlation information between each optimized variable in the TRFN [29], and thus, a larger value of Q may slow down the convergence speed.

In the elite-mixed ACOR, the Gaussian sampling around the directional solution plays the similar role as the mutation operation in the GA. In general GA mutation operation, the mutation probability is usually constant and small, and thus, at each iteration some offspring solutions might not be mutated. The deviation range in the GA mutation for each offspring solution component usually is set to be fixed and identical. Furthermore, the mutation in GA usually is implemented by sampling the uniform density function. On the contrary, the sampling in the EMCACO-C is based on Gaussian density function and is always realized for generating new candidate solution. Moreover, since the deviation range for the sampling in the EMCACO-C depends on the separate convergence status of each solution component in the archive, it is not fixed.

4 Simulation Results and Discussions

4.1 The Values of \(\varvec{\alpha}\) and Q

To determine suitable values of \(\alpha\) and Q in the EMCACO-C for TRFN designs, a validation procedure by employing various combinations of \(\alpha\) and Q has been conducted to optimize a TRFN. The TRFN for validation is used to produce the control input for controlling the nonlinear dynamic plant output to track the reference trajectory as detailed in Example 1 below. The computation environment is a personal computer with Intel CoreTM i5-4570 CPU@3.2 GHz and memory capacity of 4 GB running the program compiled by dev-C++ on Windows 7. In the EMCACO-C, the population size N is set to 20, the number of new solution candidates L is set to 20, and the parameter \(\varepsilon\) is set to 0.85 as that used in [29].

Example 1

(MISO dynamic plant control) As the same as that used in [9, 19, 32], the nonlinear dynamic plant to be controlled is given by

$$y(k + 1) = \frac{y(k)y(k - 1)(y(k) + 2.5)}{{1 + y^{2} (k) + y^{2} (k - 1)}} + \lambda (k),$$
(12)

where \(\lambda (k)\) is the control input to the plant and is limited within the range [− 4, 4] in this study. The system output in (12) depends on two previous outputs and is controlled by a control input. The objective is to design a TRFN for controlling the system output, initialized at \(y(0) = y(1) = 0.0,\) to track the reference trajectory \(y_{d} (k),\) which is guided by the reference input \(r(k)\) and is described as follows:

$$\begin{aligned} & y_{d} (k + 1) = 0.6y_{d} (k) + 0.2y_{d} (k - 1) + r(k), \\ & r(k) = 0.5 \cdot \sin \left( {\frac{2\pi k}{45}} \right) + 0.2 \cdot \sin \left( {\frac{2\pi k}{15}} \right) + 0.2 \cdot \sin \left( {\frac{2\pi k}{90}} \right), \\ \end{aligned}$$
(13)

where the initial reference states \(y_{d} (0)\) and \(y_{d} (1)\) are assumed to be 2.4 and 1.9, respectively.

The control configuration of the TRFN controller and the nonlinear plant is presented in Fig. 4 where the input–output variables of the TRFN are also illustrated. The only input variables to the TRFN are the desired plant output \(y_{d} (k + 1)\) and the current plant state \(y(k).\) Excited by these two external inputs as well as the internal states within the TRFN, the TRFN produces the output \(\lambda (k)\) to control the nonlinear dynamic plant governed by (12). The performance of the designed TRFN controller is evaluated by the root-mean-square error (RMSE) between the plant output \(y(k)\) and the reference trajectory \(y_{d} (k)\) over the 250 time steps and is calculated by

$${\text{RMSE}} = \left( {\sum\limits_{k = 1}^{250} {\frac{{(y_{d} (k + 1) - y(k + 1))^{2} }}{250}} } \right)^{{\frac{1}{2}}} .$$
(14)

This RMSE error is defined as the value of the objective function \(E( \cdot )\) for use in the EMCACO-C and other compared evolutionary algorithms. We firstly designed a TRFN with four fuzzy rules. The free parameters \(m_{ij} \in \left[ { - 3,3} \right],b_{ij} \in [0,3],a_{ij} \in [ - 4,4],v_{ij} \in [ - 4,4]\) as described in (6) are searched for finding a better controller so as to determine the suitable values of \(\alpha\) and Q. The 30,000 evaluations were performed in a single run of the optimization process to build a TRFN controller. With 100 independent runs, the validation results of the average, the standard deviation (SD), the best (minimum), and the worst (maximum) of RMSE errors are shown in Table 1. The results clearly indicate that the values of \(\alpha\) and Q should be selected as 0.2 and 2, respectively, for the EMCACO-C. These two values will be also adopted by the EMCACO-C to conduct other simulations later.

Fig. 4
figure 4

Configuration of evolutionary learning of TRFN for the control of nonlinear plant in Example 1

Full size image
Table 1 Cross-validation results for different values of \(\alpha\) and Q in the EMCACO-C for the four-rule TRFN in Example 1
Full size table

To validate the performance superiority of the proposed EMCACO-C using the determined values of \(\alpha\) and Q, some population-based optimization algorithms including the ACOR associated with several different q values, PSO, and assimilation–accommodation mixed continuous ant colony optimization (ACACO) [31] were also applied to the same TRFN design problem for comparison. The settings of parameters used in these algorithms are described as follows. In the ACOR, the population size of N = 50, the number of new candidate solutions L = 20 at each ant cycle, and the parameter of \(\varepsilon = 0.85\) are set. In the PSO, the number of particles, the inertia coefficient for previous velocity, the acceleration coefficient toward the globally best-known solution, and the acceleration coefficient toward the locally own best solution are set to 50, 0.5, 2.0, and 1.0, respectively. In the ACACO, the population size of N = 50 and the number of new candidate solutions L = 20 at each ant cycle are set. The ACACO set group size N1 = 2, N2 = 8, and N3 = 40 for group 1, group 2, and group 3, respectively, as those used in [31].

In addition to the TRFNs with four rules, we also compared the TRFNs composed of eight fuzzy rules. Figure 5 and Table 2 show the learned results of the TRFN systems optimized by the EMCACO-C, ACOR, PSO, and ACACO. The simulation results performed by the ACOR, PSO, and ACACO were obtained when the decision variables were initialized uniformly over the entire search space as usual, that is \(\alpha = 1.0\). Figure 5 shows the average best-so-far RMSE at each performance evaluation of each algorithm for the TRFN with eight rules. The numerical results in Table 2 demonstrate that the average error of the EMCACO-C is smaller than the ones of the ACOR, PSO, and ACACO for TRFNs with the same rule number. To verify the statistically significant difference between the EMCACO-C and the algorithms used for comparison, the nonparametric Wilcoxon signed-rank tests [35] for two related samples of RMSE errors were performed. For each algorithm, the null hypothesis claims that its average error is less than or equal to that of the EMCACO-C. The performance of the EMCACO-C is compared against each of the algorithms, and the resulting p value is presented. The p values in Table 2 indicate that the null hypothesis is rejected at the significant level of 5% for each comparison.

Fig. 5
figure 5

Average best-so-far RMSEs at each performance evaluation for the evolutionary TRFN controllers optimized by the EMCACO-C and different population-based optimization algorithms in Example 1 (eight rules)

Full size image
Table 2 Performances of the TRFN controllers designed by various population-based optimization algorithms for the MISO plant control problem in Example 1
Full size table

Moreover, we also observed that the performance of the TRFN with eight rules outperforms that with four rules when they were optimized by the EMCACO-C. However, this observation does not hold for the ACOR with larger q values. The possible reason for this is that the ACOR converges slower if the q value is larger. The best four-rule TRFN controller designed by the EMCACO-C is shown in Table 3, and the resulting control results are shown in Fig. 6. The results show that the controlled plant output is very close to the reference output except at the first few time steps because the initial conditions of the controlled plant are different from the reference.

Table 3 Obtained TRFN controller composed of four rules optimized by the EMCACO-C. The values are truncated to two fractional digits
Full size table
Fig. 6
figure 6

Control results of the TRFN controller optimized by the EMCACO-C in Example 1 (four rules)

Full size image

4.2 Application Examples

Example 2

(MIMO dynamic plant control) The nonlinear multiple-input multiple-output (MIMO) plant to be controlled by the TRFN is the same as that used in [19, 32] and is given by

$$y_{1} (k + 1) = 0.5 \cdot \left[ {\frac{{y_{1} (k)}}{{1 + y_{2}^{2} (k)}} + \lambda_{1} (k - 1)} \right]$$
(15)
$$y_{2} (k + 1) = 0.5 \cdot \left[ {\frac{{y_{1} (k)y_{2} (k)}}{{1 + y_{2}^{2} (k)}} + \lambda_{2} (k - 1)} \right].$$
(16)

The objective is to generate two sequences of control inputs \(\lambda_{1} (k)\) and \(\lambda_{2} (k)\) such that the controlled plant outputs \(y_{1} (k),y_{2} (k),\) initialized at \(y_{1} (0) = 0.2\) and \(y_{2} (0) = 0.0,\) follow the two desired sinusoidal reference outputs \(y_{d1} (k)\) and \(y_{d2} (k),\), respectively, as follows:

$$y_{d1} (k) = \sin \left( {\frac{k\pi }{45}} \right)$$
(17)
$$y_{d2} (k) = \cos \left( {\frac{k\pi }{45}} \right).$$
(18)

Similarly, the only input variables to the TRFN are the current plant states \(y_{1} (k),\,y_{2} (k)\) and the desired outputs \(y_{d1} (k + 1),\,y_{d2} (k + 1).\) Excited by these inputs, the TRFN produces two control inputs \(\lambda_{1} (k)\) and \(\lambda_{2} (k)\). The two delayed TRFN outputs \(\lambda_{1} (k - 1)\) and \(\lambda_{2} (k - 1)\) are used to control the plant governed by (15) and (16). The RMSE of the two tracking data over the 250 time steps is defined by

$${\text{RMSE}} = \left( {\sum\limits_{k = 1}^{250} {\frac{{\left( {y_{d1} (k + 1) - y_{1} (k + 1)} \right)^{2} + \left( {y_{d2} (k + 1) - y_{2} (k + 1)} \right)^{2} }}{250}} } \right)^{{\frac{1}{2}}} .$$
(19)

In this example, we designed the TRFN systems with two different numbers of rules as studied in [32]: six rules and eight rules. The free parameters \(m_{ij} \in \left[ { - \,1,\,1} \right],\,b_{ij} \in [0,\,1],\,a_{ij} \in [ - 2,2],\,v_{ij} \in [ - 2,2]\) are searched for finding a better-performed TRFN controller. The 15,000 evaluations were performed in a single run of the optimization process. With 100 independent runs of simulations, the average best-so-far RMSE at each performance evaluation of each algorithm for the eight-rule TRFN is shown in Fig. 7.

Fig. 7
figure 7

Average best-so-far RMSEs at each performance evaluation for the evolutionary TRFN controllers optimized by the EMCACO-C and different population-based optimization algorithms in Example 2 (eight rules)

Full size image

The learned results of the TRFNs with six and eight rules are shown in Table 4. The results show that the average error of the EMCACO-C is smaller than the ones of the ACOR, PSO, and ACACO for TRFNs with the same rule number. The p values in Table 4 indicate that the null hypothesis is rejected at the significance level of 5% for each comparison using the Wilcoxon test. Similarly, the performance of the TRFN with eight rules outperforms that with six rules when they were designed by the EMCACO-C. The control results of the TRFN controller optimized by the EMCACO-C are shown in Fig. 8. The results demonstrate that two controlled plant outputs are very close to the desired ones except at the first few time steps.

Table 4 Performances of the TRFN controllers designed by various population-based optimization algorithms for the MIMO plant control problem in Example 2
Full size table
Fig. 8
figure 8

Control results of the TRFN controller optimized by the EMCACO-C in Example 2 (six rules)

Full size image

Example 3

(Continuously stirred tank reactor control) In this example, we use a TRFN system to control a continuously stirred tank reactor (CSTR) in which the first-order, irreversible, exothermic reaction \(A\, \mapsto \,B\) is carried out. At the input, the fresh feed of chemical A is mixed with the recycle stream of unreacted material A with a recycle rate. Let t be the moment of time the output exits the CSTR. According to [36], the CSTR material and energy balance equations in dimensionless variables are

$$\begin{aligned} \dot{x}_{1} (t) & = f_{1} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} (t)) + \left( {\frac{1}{\lambda } - 1} \right)x_{1} (t - \tau ) \\ \dot{x}_{2} (t) & = f_{2} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} (t)) + \left( {\frac{1}{\lambda } - 1} \right)x_{2} (t - \tau ) + \beta u, \\ \end{aligned}$$
(20)

where

$$\begin{aligned} f_{1} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} (t)) & = \frac{ - 1}{\lambda }x_{1} (t) + D_{a} (1 - x_{1} (t))\exp \left( {\frac{{x_{2} (t)}}{{1 + x_{2} (t)/\gamma_{0} }}} \right) \\ f_{2} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} (t)) & = - \left( {\frac{1}{\lambda } + \beta } \right)x_{2} (t) + HD_{a} (1 - x_{1} (t))\exp \left( {\frac{{x_{2} (t)}}{{1 + x_{2} (t) /\gamma_{0} }}} \right), \\ \end{aligned}$$
(21)

where \(x_{i} (t) = \theta_{i}\) for \(t \in \left[ { - \tau ,0} \right], \, i = 1,2,\) and \(- 1 \le u(t) \le 1\) is the control input. The state \(x_{1} (t)\) represents the conversion rate of the reaction, \(0 \le x_{1} (t) \le 1,\) and \(x_{2} (t)\) is the dimensionless temperature. As the same as that used in the previous study [32], the constant parameters are given as \(\gamma_{0} = 20,H = 8,\beta = 0.3,D_{a} = 0.0072,\lambda = 0.8, \, \tau = 2,\) and the initial values of \(x_{i} (t)\) are \(\theta_{1} = 0.144\) and \(\theta_{2} = 0.8862\). The objective is to control the conversion rate \(x_{1} (t)\) to follow the pre-defined set points \(x_{d} (t)\) as given by

$$x_{d} (t) = \left\{ {\begin{array}{*{20}l} {0.4,} \hfill & {t \le 35,} \hfill \\ {0.6,} \hfill & {35 < t \le 70,} \hfill \\ {0.8,} \hfill & {70 < t \le 105,} \hfill \\ {0.6,} \hfill & {105 < t \le 150.} \hfill \\ \end{array} } \right.$$
(22)

The TRFN controller to be optimized is composed of six fuzzy rules and its inputs are the current states \(x_{1} (t),x_{2} (t),\) and the set point \(x_{d} (t)\). The free parameters \(m_{ij} \in \left[ {0,1} \right],\,b_{ij} \in [0,0.5],\,a_{ij} \in [ - \,1,1],\,v_{ij} \in [ - \,1,1]\) are searched for finding a better-performed TRFN controller. In the simulation, the controller commands a new control input u every 0.5 time interval. The simultaneous differential equations in (20) are solved by Euler method for simulations. The RMSE error for training is defined by

$${\text{RMSE}}_{\text{train}} = \left( {\sum\limits_{k = 1}^{300} {\frac{{W(k)\mathop {\left( {x_{1} (k) - x_{d} (k)} \right)}\nolimits^{2} }}{300}} } \right)^{{\frac{1}{2}}} ,$$
(23)

where the time step \(k\) is set to 2t and W(k) is defined by

$$W(k) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {70 \, n + 1 \le k \le 70 \, n + 5,\quad n = 0,1,2,3,} \hfill \\ {5,} \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right.$$
(24)

In the RMSEtrain, when the desired conversion rate changes from one set point to another, the regulation errors in the initial five steps of the transition state are weighted with \(W = 1,\) and the following errors in the steady state are weighted with \(W = 5.\) The 25,000 evaluations were performed in a single run of the training process. As considered in [32], by neglecting the initial transition errors, the evaluation RMSE for the obtained controller is defined by

$${\text{RMSE}}_{\text{eva}} = \left( {\sum\limits_{k = 21}^{300} {\frac{{W(k)\mathop {\left( {x_{1} (k) - x_{d} (k)} \right)}\nolimits^{2} }}{280}} } \right)^{{\frac{1}{2}}} .$$
(25)

where

$$W(k) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & { 70 \, n + 1 \le k \le 70 \, n + 5,\quad n = 1,2,3,} \hfill \\ {1,} \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right.$$
(26)

With 100 independent runs of simulations, the average best-so-far training RMSE at each performance evaluation of each algorithm for the TRFN is shown in Fig. 9. Table 5 shows the learned statistical results of training and evaluation RMSEs. The results show the average training error RMSEtrain of the EMCACO-C is smaller than the ones of the ACOR, PSO, and ACACO. Moreover, the average evaluation error RMSEeva of the EMCACO-C is also smaller than the ones of the population-based algorithms in comparison. The p values in Table 5 indicate that the null hypothesis is rejected at the significance level of 5% for each comparison using the Wilcoxon test for the samples of evaluation errors RMSEeva. The control results of the TRFN optimized by the EMCACO-C are shown in Fig. 10. The results demonstrate that the controlled plant output is very close to the desired set points except at the initial transition time steps.

Fig. 9
figure 9

Average best-so-far training RMSEs at each performance evaluation for the evolutionary TRFN CSTR controllers optimized by the EMCACO-C and different population-based optimization algorithms in Example 3

Full size image
Table 5 Performances of the TRFN controllers designed by various population-based optimization algorithms for the CSTR control problem in Example 3
Full size table
Fig. 10
figure 10

CSTR control result of the TRFN controller optimized by the EMCACO-C in Example 3

Full size image

Example 4

(Mackey–Glass Chaotic Series Prediction) This example considers the prediction of chaotic time series using a TRFN as studied in [7]. The time series to be predicted is generated by the well-known Mackey–Glass chaotic system, which is described by the delay differential equation:

$$\frac{{{\text{d}}x(t)}}{{{\text{d}}t}} = \frac{0.2x(t - \tau )}{{1 + x^{10} (t - \tau )}} - 0.1x(t),$$
(27)

where \(\tau\) is set to 17, and the initial value x(0) is 1.2 with x(t) = 0 for t < 0. The objective is to design a TRFN using the four past values of x(t − 24), x(t − 18), x(t − 12) and x(t − 6) as the external inputs for predicting x(t). The objective function is defined as the RMSE error between the sampled output of the system governed by (27) and the TRFN output.

In this example, the TRFN predictor to be optimized is composed of five fuzzy rules. The free parameters \(m_{ij} \in \left[ {0.4,1.4} \right],\,b_{ij} \in [0,0.5],\,a_{ij} \in [ - \,1.4,1.4],\,v_{ij} \in [ - \,1.4,1.4]\) are searched for finding a better-performed TRFN predictor. To evaluate the performances, the following experiment was conducted: First, the time series data governed by (27) were generated using Runge–Kutta numerical method. As discussed in [7], 500 data patterns from t = 124 to 623 extracted from the time series are used for training the TRFN and the other 500 data patterns from t = 624 to 1123 are for testing. The 100,000 evaluations were performed in a single run of the training process.

With 50 independent runs of simulations, the average best-so-far training RMSE at each performance evaluation of each algorithm for the TRFN is shown in Fig. 11. Table 6 presents the learned results of training errors RMSEtrain (the first 500 data) and testing errors RMSEtest (the second 500 data). The results show that the training error RMSEtrain and testing error RMSEtest of the EMCACO-C are smaller than the ones of the ACOR, PSO, and ACACO. The p values in Table 6 indicate that the null hypothesis is rejected at the significance level of 5% for each comparison using the Wilcoxon test for the samples of testing errors RMSEtest. In [7], the TRFN was trained by the gradient-based supervised learning (TRFN-S) for predicting the same chaotic time series. The testing RMSEtest using the TRFN-S is 0.012, which is larger than that by the EMCACO-C. The prediction outputs from t = 624 to 1123 of the optimized TRFN by the EMCACO-C are demonstrated in Fig. 12. The results show nearly undistinguishable difference between the actual chaotic series and the predicted series.

Fig. 11
figure 11

Average best-so-far training RMSEs at each performance evaluation for the evolutionary TRFN predictors optimized by the EMCACO-C and different population-based optimization algorithms in Example 4

Full size image
Table 6 Performances of the TRFN designed by various population-based optimization algorithms for the prediction of nonlinear chaotic time series in Example 4
Full size table
Fig. 12
figure 12

Test results of the TRFN predictor optimized by the EMCACO-C in Example 4

Full size image

Example 5

(Dynamic system identification) This example as taken from [9] uses a TRFN to identify a nonlinear dynamic system with multiple time delays. The nonlinear plant is described as follows:

$$y_{p} (k + 1) = f(y_{p} (k),y_{p} (k - 1),y_{p} (k - 2),\lambda (k),\lambda (k - 1))$$
(28)

where

$$f(x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ) = \frac{{x_{1} x_{2} x_{3} x_{5} (x_{3} - 1) + x_{4} }}{{1 + x_{3}^{2} + x_{2}^{2} }}.$$
(29)

The current output \(y_{p} (k)\) and the control input \(\lambda (k)\) are the inputs of the TRFN model, and the value of \(y_{p} (k + 1)\) is the target output for the TRFN. The objective function is defined as the RMSE between the plant output in (28) and the TRFN output.

The TRFN identification model to be optimized is composed of three fuzzy rules. The free parameters \(m_{ij} \in \left[ { - \,1.5,1.5} \right],\,b_{ij} \in [0,1.5],\,a_{ij} \in [ - \,1.5,1.5],v_{ij} \in [ - \,1.5,1.5]\) are searched for finding a better-performed TRFN model. The training data for the TRFN are the control inputs of 900 time steps and the corresponding outputs produced by the plant. The first 450 control inputs are independently and identically distributed uniform random sequences over [− 1, 1]. The remaining half control inputs are generated by a sinusoid 1.05sin(πk/45). The 100,000 evaluations were performed in a single run of the optimization process. To see the identification performance, the following guiding input signal is used for test:

$$\lambda (k) = \left\{ {\begin{array}{*{20}l} {\sin (\pi k /25),} \hfill & {k < 2 5 0} \hfill \\ {1.0,} \hfill & { 2 5 0\le k < 5 0 0} \hfill \\ { - 1.0,} \hfill & { 5 0 0\le k < 7 5 0} \hfill \\ {0.3\sin (\pi k /25) + 0.1\sin (\pi k /32) + 0.6\sin (\pi k /10),} \hfill & { 7 5 0\le k < 1 0 0 0.} \hfill \\ \end{array} } \right.$$
(30)

With 50 independent runs of simulations, the average best-so-far training RMSE at each performance evaluation of each algorithm for the TRFN is shown in Fig. 13. Table 7 shows the learned numerical results of statistical training and testing RMSEs. The results show that the training error RMSEtrain and testing error RMSEtest of the EMCACO-C are smaller than the ones of the ACOR, PSO, and ACACO. The p values in Table 7 indicate that the null hypothesis is rejected at the significance level of 5% for each comparison using the Wilcoxon test for the samples of testing errors RMSEtest. The same problem was also studied using TRFN-S [9]. The TRFN-S reached the testing error RMSEtest of 0.0346, which is larger than that by the EMCACO-C. The outputs of the optimized TRFN by the EMCACO-C for the test input in (30) are demonstrated in Fig. 14. The results show TRFN output is very close to the output of dynamic plant.

Fig. 13
figure 13

Average best-so-far training RMSEs at each performance evaluation for the evolutionary TRFN models optimized by the EMCACO-C and different population-based optimization algorithms in Example 5

Full size image
Table 7 Performances of the TRFN designed by various population-based optimization algorithms for the system identification problem in Example 5
Full size table
Fig. 14
figure 14

Test results of the TRFN model optimized by the EMCACO-C in Example 5

Full size image

4.3 Analysis of the EMCACO-C

4.3.1 Analysis of Computational Complexity

The time complexity of the EMCACO-C as applied to TRFN design is proportional to the number Ncycles of ant cycles (iterations), the number L of new candidate solutions, the runtime Tgen for generating a new ant, and the evaluation time Teva for a new solution, and can be computed as follows:

$$N_{\text{cycles}} \times \left( {L \times \left( {T_{\text{gen}} + T_{\text{eva}} } \right)} \right).$$
(31)

In the simulation results of Example 1 as an example, the computational time of each evolutionary learning for TRFN design for tracking control was also reported in Table 2. The results indicate the time the EMCACO-C consumed is comparable to that of the ACOR, which implies that in this example the runtime Tgen in the EMCACO-C is not much different from that in the ACOR or both of them are negligible compared to the evaluation time Teva for a new solution.

4.3.2 Performance Analysis of the Central Initialization on TRFN Designs

In addition to the results in Table 1, a cross-validation on three of the simulated examples has been conducted for discussing the advantages of the central initialization on the experimented TRFN designs. The validation results for the EMCACO-C, PSO, and ACOR are presented in Table 8. The results show that for each algorithm itself, the central initialization helps achieve the smaller error than the blind uniform initialization. This demonstrates that the proposed central initialization can help the investigated swarm-based algorithms including the EMCACO-C achieve the better performance on the TRFN designs for application examples.

Table 8 Performance comparisons of the EMCACO, ACOR, and PSO as applied to the TRFN designs by using the different guess widths for initialization
Full size table

Furthermore, to learn whether the proposed central initialization (\(\alpha = 0.2\)) confines the EMCACO-C convergence to the initial local guesses around or not, we need to examine the parameters of the designed TRFN. The parameters of the best designed TRFN controller optimized by the EMCACO-C in Example 1 are shown in Table 3. We found that 25% (12/48) of the parameters fall in the initially guessed region, which is slightly more than the case (20%) of the blind uniform guess. We also observed that some of the parameter values in the designed TRFN are equal or very close to the specified limit for search, which has demonstrated that if the proper guess width is used, the central initialization does not necessarily confine the search only toward the initial local guess.

4.3.3 Analysis of the Number of Elites and the Evaporation Rate

The value of 2 for Q currently used in the EMCACO-C for applications simulations was determined simply based on the cross-validation results for the four-rule TRFN in Example 1 when the evaporation rate \(\varepsilon\) is 0.85 as that used in [29]. To learn more about the influences of Q value on the performances of the EMCACO-C for TRFN designs, more experiments on Examples 1, 2, and 5 using the values of Q ranging from 1 to 10 were simulated. The results in Fig. 15 show that the best performances are achieved when two elites are used for mixing operation. It is also observed that the error decreased significantly when the value of Q was changed from one to two. When the value of Q is one, the EMCACO-C actually did not mix elites, and thus, the Gaussian sampling was the only operation in the algorithm, which is the possible reason for being inferior. Furthermore, the average error increases roughly with the value of Q starting from 2. One of the possible reasons is that a higher value of Q provides more exploration in search thus lower convergence speed and the worse performance.

Fig. 15
figure 15

Comparison about the performance achieved by the EMCACO-C with respect to different values of Q

Full size image

To verify the above reason, the normalized diversity of all ant solutions is defined to indicate the convergence of learning and is computed as follows:

$${\text{Diversity}}\,(t) = \frac{1}{N - 1}\sum\limits_{m = 1}^{N} {\frac{1}{D}\sum\limits_{j = 1}^{D} {\frac{{\left| {s_{m}^{j} (t) - s_{1}^{j} (t)} \right|}}{{L^{j} }}} } ,$$
(32)

where t is the iteration index and \(L^{j}\) is the search length for the parameter in the jth dimension. With 100 independent runs, the average normalized diversity of the EMCACO-C with each different Q value in Example 1 as an example is shown in Fig. 16. The results show that when \(\varepsilon\) is fixed to 0.85, the EMCACO-C with a higher value of Q converges slower than that with a lower value of Q. However, because a higher value of \(\varepsilon\) can provide more exploration in search and a lower value of \(\varepsilon\) can provide more exploitation in search, different values of \(\varepsilon\) can be used to respond to the selected Q value for balancing the exploration and exploitation based on the following guideline: the higher the value of Q is selected, the lower the value of \(\varepsilon\) is used. The diversity results using the different values of \(\varepsilon\) to respond to the selected Q value are also shown in Fig. 16 for comparison. The corresponding learning curves of performance evaluations are shown in Fig. 17, indicating that the resulting performances using the adjusted value of \(\varepsilon\) are much improved and some of them are even better than the case of \(Q = 2\) and \(\varepsilon = 0.85\).

Fig. 16
figure 16

Average normalized diversity of the TRFN parameters optimized by the EMCACO-C with different values of Q and \(\varepsilon\) in Example 1 (Dash lines are the cases of \(\varepsilon = 0.85\); solid lines are the cases for different values of \(\varepsilon\))

Full size image
Fig. 17
figure 17

Average best-so-far training RMSEs optimized by the EMCACO-C with different values of Q and \(\varepsilon\) in Example 1 (Dash lines are the cases of \(\varepsilon = 0.85\); solid lines are the cases for different values of \(\varepsilon\))

Full size image

5 Conclusions

This paper proposes an efficient continuous ACO, elite-mixed continuous ACO with central initialization (EMCACO-C), for improving the accuracy of TRFN designs. The EMCACO-C is developed based on the framework of the ACOR and can be regarded as a new population-based evolutionary optimization algorithm. Unlike most popular population-based algorithms, the EMCACO-C initializes the ant solutions on concentrative region around the center of the search range. The EMCACO-C mixes in scanning manner the fixed number of the few best elites uniformly in probability to form a directional solution. A new candidate solution is generated by sampling Gaussian density function around the constructed directional solution. The methodology similarities and differences between the EMCACO-C and GAs are also compared in this study.

In the TRFN designs for the problems of dynamic systems control, dynamic system identification, and chaotic series prediction, the simulation results demonstrated that the EMCACO-C achieved smaller errors than those by the algorithms of ACOR, PSO, and ACACO. The Wilcoxon signed-rank tests were conducted to verify the significant differences in comparisons.

In addition, the advantages on the accuracy improvement for TRFN designs gained by applying the central initialization to the ACOR and PSO were also demonstrated in this study. The selection guidelines for the number of elites for mixing operation and the value of the evaporation rate in the EMCACO-C for TRFN design were discussed and demonstrated by the simulation results of the application example.

In the future, the performances of the EMCACO-C for the designs of various types of recurrent and feed-forward fuzzy systems will be studied. The study of different skewed initializations and elites selection techniques for finding the performance improvement will also be considered. In addition, hybridization of other evolutionary optimization algorithms with the EMCACO-C may further improve optimization performance and thus will also be studied in the future.