A Framework of Group Decision Making with Hesitant Fuzzy Preference Relations Based on Multiplicative Consistency

Abstract

The purpose of this paper is to develop a general framework of group decision making with hesitant fuzzy preference relations based on the multiplicative consistency. First, we define a consistency index to measure whether or not a hesitant fuzzy preference relation is of acceptably multiplicative consistency. A consistency improving process is developed to improve the consistency level of a hesitant fuzzy preference relation with unacceptably multiplicative consistency until it is acceptably multiplicative. Then, we present a group consensus index to measure the deviation measure between the individual hesitant fuzzy preference relations and their collective hesitant fuzzy preference relation. A consensus reaching process is developed to help the decision makers improve the consensus level among hesitant fuzzy preference relations until they meet a predefined consensus level. Subsequently, we establish a complete framework of group decision making with hesitant fuzzy preference relations. In this framework, individual multiplicative consistency and group consensus are simultaneously highlighted and the acceptably multiplicative consistency of each hesitant fuzzy preference relation is still maintained in the achievement of the predefined consensus level. Finally, an illustrative numerical example is given to verify the effectiveness and practicality of the developed method.

1 Introduction

Owing to the fact that when defining the membership degree of an element to a set in some fuzzy decision settings, the difficulty of establishing the membership degree is not because we have a margin of error (as in intuitionistic fuzzy sets [4] and interval-valued fuzzy sets [38]) or some possibility distribution (as in type-2 fuzzy sets [10]) on the possible values, but because we have a set of possible values [20], Torra [20] developed the concept of hesitant fuzzy sets (HFSs) which permit the membership degree of an element to a set to be presented as several possible values between 0 and 1. For example, assume a group of DMs are required to assess the membership of x to the set A and they are hesitant about three possible values as 0.6, 0.7 and 0.8. This case differs from the situations of using Zadeh’s fuzzy sets [37], interval-valued fuzzy sets [38], intuitionistic fuzzy sets [4], type-2 fuzzy sets [10], or fuzzy multisets [16]. In such cases, the membership of x to A can be modeled by a HFS h = {0.6, 0.7, 0.8} rather than a single exact value, an interval number, or an intuitionistic fuzzy number. In a short period of time since its first appearance, HFSs have attracted more and more attention in different areas, mainly in decision making [8, 18, 31, 35, 39], because of its suitability to deal with hesitant situations that are quite usual in real-world decision-making problems.

As one of the most common activities in the real-world, group decision making (GDM) consists in finding the best alternative(s) from a set of feasible ones according to the preference information provided by a group of experts. In the practical process of GDM, sometimes, because of the time pressure and lack of knowledge or data, or because the decision makers (DMs) have limited attention and information processing capacities, the DMs cannot provide their preference with single exact value, a margin of error or some possibility distribution on the possible values, but several possible values, which is a common situation in our daily life. To circumvent this issue and motivated by HFSs, Zhu and Xu [42] introduced hesitant fuzzy preference relations (HFPRs) to deal with a hesitant situation that the decision group is hesitant about some possible values for the preference degrees over paired comparisons of alternatives. Then, they [42] proposed a regression method to transform HFPRs into fuzzy preference relations (FPRs) [17]. Xia and Xu [32] used the known hesitant fuzzy aggregation operators to develop an approach to GDM with HFPRs. Zhu [41] studied the additive consistency measure of HFPRs and proposed a regression method to transform the HFPR into a FPR, called a reduced HFPR, with the highest consistency level. Owing to the importance of consistency and consensus in GDM with preference relations, Zhu et al. [43] developed the consistency measures of HFPRs, established the consistency thresholds to measure whether or not an HFPR is of acceptable consistency, and built an optimization model to improve the consistency of inconsistent HFPRs until they are acceptable. Liao et al. [13] introduced the concepts of multiplicative consistency, perfect multiplicative consistency and acceptable multiplicative consistency for a HFPR, based on which two algorithms were given to improve the inconsistency level of a HFPR. Furthermore, the consensus of group decision making was studied based on the HFPRs. Zhang et al. [40] developed a consistency- and consensus-based decision support model for GDM with HFPRs.

Generally, GDM with hesitant fuzzy preference information is faced with three processes [14]:

• 1. The consistency checking and improving process of each HFPR. This process guarantees that the experts’ preferences yield no contradiction;

• 2. The consensus checking and reaching process of the group. Consensus makes it possible for a group to reach a final decision that all group members can support despite their differing opinions;

• 3. The selection process. The selection process is to find the final result that is accepted by most individuals.

It is noticed that the aforementioned work [13, 32, 40–43] about HFPRs has some limitations, which are shown as follows:

• 1. The additive consistency proposed by Zhu [41] and Zhu and Xu [42] is sometimes in conflict with the [0,1] scale used for providing the preference values, whereas the multiplicative consistency does not have this limitation [9, 36]. Additionally, Zhu [41] and Zhu and Xu [42] did not consider the consistency checking and improving process, the consensus checking and reaching process and the selection process.

• 2. The drawback of Xia and Xu [32]’s approach was that they did not consider the consistency and consensus checking processes; that is, they only considered the third step but ignore Step 1 and Step 2 in GDM with HFPRs.

• 3. Zhu et al. [43] proposed an optimization model for improving the multiplicative consistency of HFPRs in a group, but they did not pay much attention to the consensus process, which means that they did not consider Step 2 and consequently made the final result might not be supported by all the members in the group. In addition, the optimization model developed by Zhu et al. [43] is time-consuming, inconvenient, and complex to resolve (See a further analysis in Subsection 6.2.1).

• 4. The multiplicative consistency definition proposed by Liao et al. [13] holds only for the upper (or lower) triangular of the preference relation and does not hold in general cases (See a further analysis in Subsection 6.2.2). In addition, the multiplicative consistency of the collective HFPR did not been taken into account. Moreover, Liao et al. [13] did not organically combine the consistency with the consensus. That is to say, they did not discuss how to manage individual consistency in a consensus reaching process for GDM with HFPRs.

• 5. Although the decision support model developed by Zhang et al. [40] simultaneously considered Step 1, Step 2 and Step 3, this model was constructed based on the additive consistency. The drawback of the additive consistency has been pointed out in the above discussions.

It is noted that there exists lots of literature on multiplicative consistency property for additive reciprocal preference relations, interval-valued preference relations, intuitionistic preference relations and triangular fuzzy membership preference value relations. For example, Chiclana et al. [9] developed a characterization transitivity of multiplicative of reciprocal preference relation. Alonso et al. [3] presented a web consensus support system to deal with group decision-making problems with different kinds of incomplete preference relations (fuzzy, linguistic and multigranular linguistic preference relations) in which the consistency is modeled via the multiplicative consistency property used to estimate the unknown values of incomplete preference relations as well as to compute the needed consistency measures. Alonso et al. [2] proposed a consistency-based procedure to estimate missing pairwise preference values when dealing with pairwise comparison and heterogeneous information. Alonso et al. [1] developed an interactive decision support system based on consistency criteria. Xia et al. [33] investigated the consistency and consensus of fuzzy preference relations based on the multiplicative consistency property. Wu and Chiclana [25] investigated the multiplicative consistency property of interval-valued fuzzy reciprocal preference relations (IFRPRs) and defined the consistency indexes for the three different levels of an IFRPR. Xu and Chen [34] employed the feasible-region-based multiplicative transitivity condition to present the multiplicative consistency definition for interval fuzzy preference relations. Wang and Li [23] used the interval-arithmetic-based multiplicative transitivity condition to propose the multiplicative consistency definition for interval fuzzy preference relations. Wu and Chiclana [26] defined the multiplicative consistency property of intuitionistic reciprocal preference relations and applied it to missing values estimation and consensus building for intuitionistic reciprocal preference relations. Liao and Xu [12] gave a general definition of multiplicative consistent intuitionistic fuzzy preference relation (IFPR) and built some fractional programming models to generate the intuitionistic fuzzy priority weighting vector of the IFPR. Wu and Chiclana [27] presented a visual information feedback mechanism for GDM problems with triangular fuzzy complementary preference relations (TFCPRs). Xia and Xu [30] proposed a new method to construct the complete fuzzy complementary preference relation from n−1 preference values base on multiplicative consistency. Wang and Tong [24] introduced a cross-ratio-expressed triangular fuzzy multiplication-based transitivity equation to define multiplicatively consistent triangular fuzzy additive reciprocal preference relations (TFARPRs). Wu et al. [29] proposed uninorm trust propagation and aggregation methods for group decision making in social network with four tuple information: trust, distrust, hesitancy and inconsistency. Ureña et al. [21] used the multiplicative consistency property to drive decision-making approach with confidence and consistency properties and incomplete reciprocal intuitionistic preference relations. Wu and Chiclana [28] developed a risk attitudinal ranking method for interval-valued intuitionistic fuzzy numbers based on novel score and accuracy expected functions. In addition, there are a lot of references about consensus. For example, Mata et al. [15] proposed a new approach of a consensus reaching process based on the T1OWA operator to deal with GDM problems in multigranular linguistic contexts. Cabrerizo et al. [7] developed a method based on an allocation of information granularity as an important asset to increase the consensus achieved within the group of decision makers in GDM situations. Cabrerizo et al. [6] analyzed the different consensus approaches to compute soft consensus measures in fuzzy group decision-making problems and discussed their advantages and drawbacks. Cabrerizo et al. [5] presented some challenges and open questions about the software tools developed to carry out the consensus in a fuzzy group decision-making problem. Herrera-Viedma et al. [11] presented an overview of consensus models based on soft consensus measures, showing the pioneering and prominent papers, the main existing approaches and the new trends and challenges. However, the multiplicative consistency and consensus in the above studies [1–3, 5–7, 9, 11, 12, 15, 23–30, 33, 34] do not contain hesitant fuzzy information and thus fail to deal with hesitant fuzzy preference relations.

To circumvent all the above drawbacks, this paper presents a multiplicative consistency- and consensus-based framework for GDM with hesitant fuzzy preference information. All the three steps, i.e., the consistency checking and improving process, the consensus checking and reaching process and the selection process, are systematically discussed in this framework. The contributions of this paper are highlighted as follows.

• 1. We define a multiplicative consistency index to measure the multiplicative consistency degree of a HFPR, based on which we apply a new consistency checking method to check the multiplicative consistency of HFPRs. As to those HFPRs which are not of acceptably multiplicative consistency, we develop a consistency improving method to help the experts to repair them until the consistency is reached or accepted.

• 2. We introduce a group consensus index to measure the consensus of a group and propose a consensus reaching process to assist the group in achieving a predefined consensus level while keeping an acceptable multiplicative consistency for each HFPR.

• 3. After conducting the above two processes, a selection process is applied to achieve a higher level of multiplicative consistency and consensus solutions for a GDM with HFPRs.

• 4. We give a complete algorithm for GDM with HFPRs. Comparative analysis with the other methods in the existing literature shows that the developed algorithm is quite flexible, interactive and convenient and can match the practical GDM situation perfectly.

To do this, the paper is organized as follows. In Sect. 2, we briefly introduce the related work on HFSs and HFPRs. Section 3 defines a consistency index for HFPRs which can measure the consistency degree of a HFPR, based on which a convergent method is proposed to improve the consistency of a HFPR so as to ensure that the HFPR is of acceptably multiplicative consistency. Section 4 proposes a consensus index to measure the consensus level and develops a convergent iterative procedure to improve the consensus levels of the individual HFPRs so as to help experts achieve a predefined consensus level. Section 5 is devoted to presenting a complete framework which simultaneously addresses the individual consistency and group consensus for GDM with HFPRs. In Sect. 6, a numerical example is provided to demonstrate the application of the proposed method and to verify the theoretical results. Comparison analyses with some existing approaches in the literature are conducted to illustrate the advantages of the developed methods. Section 7 ends this paper with some concluding remarks.

2 Preliminaries

This section introduces the basic knowledge regarding hesitant fuzzy sets and hesitant fuzzy preference relations, which provide a basis for this study.

2.1 Hesitant Fuzzy Sets

Torra [20] originally proposed the concept of hesitant fuzzy sets to manage the situations in which several values are possible for the definition of the membership of an element.

Definition 2.1 [20]

Let X be a reference set, a hesitant fuzzy set (HFS) on X is in terms of a function that when applied to X returns a subset of [0,1], which can be represented as the following mathematical symbol [15]:

$$E = \left\{ {\left. {\left\langle {x,h_{\text{E}} \left( x \right)} \right\rangle } \right|x \in X} \right\}$$

(1)

where $h_{\text{E}} \left( x \right)$ is a set of some values in [0,1], denoting the possible membership degrees of the element $x \in X$ to the set E. For convenience, Xia and Xu [31] called $h = h_{\text{E}} \left( x \right)$ a hesitant fuzzy element (HFE). Let l _h denote the number of elements in the HFE h, and let Ω be the set of all hesitant fuzzy elements (HFEs).

To compare HFEs, Xia and Xu [31] defined the following comparison laws.

Definition 2.2 [31]

For a HFE h, $s\left( h \right) = \frac{{\sum\nolimits_{\gamma \in h} \gamma }}{{l_{\text{h}} }}$ is called the score function of h, where l _h is the number of elements in h. Assume two HFEs, h ₁ and h ₂, if $s\left( {h_{1} } \right) > s\left( {h_{2} } \right)$, then h ₁ > h ₂; if $s\left( {h_{1} } \right) = s\left( {h_{2} } \right)$, then h ₁ = h ₂.

In most situations, it is noted that the numbers of elements in two different HFEs h _i (i = 1,2) are different. In order to more accurately operation on h ₁ and h ₂, Zhu et al. [43] introduced a method to add some elements to HFEs.

Definition 2.3 [43]

Assume a HFE h, let h ⁺ and h ⁻ be the maximum and minimum elements in h, respectively, and $\varsigma$ ($0 \le \varsigma \le 1$) be an optimized parameter, which can be chosen by the decision makers according to their own risk preferences, then we call $\bar{h} = \varsigma h^{ + } + \left( {1 - \varsigma } \right)h^{ - }$ an added element.

Especially, $\bar{h} = h^{ + }$ and $\bar{h} = h^{ - }$ can be, respectively, derived from the conditions that $\varsigma = 1$ and $\varsigma = 0$, which correspond with the optimism and pessimism rules introduced by Xu and Xia [35], respectively.

2.2 Hesitant Fuzzy Preference Relations

Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a fixed set of alternatives. Assume that the DMs hesitate between some possible preferences to provide paired comparison judgments of alternatives, and these preferences are collected into HFEs. To address such situations, Zhu and Xu [42] developed a concept of hesitant fuzzy preference relations (HFPRs) as follows.

Definition 2.4 [42]

Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a fixed set. A hesitant fuzzy preference relation (HFPR) H on X is denoted by a matrix $H = \left( {h_{ij} } \right)_{n \times n} \subset X \times X$, where $h_{ij} = \left\{ {h_{ij}^{\rho \left( s \right)} \left| {s = 1,2, \ldots ,} \right.l_{{h_{ij} }} } \right\}$ is a HFE, indicating hesitant degrees to which x _i is preferred to x _j . For all $i,j = 1,2, \ldots ,n$, $h_{ij}$ should satisfy the following conditions:

$$h_{ij}^{\rho \left( s \right)} + h_{ji}^{{\rho \left( {l_{{h_{ij} }} - s + 1} \right)}} = 1,\;h_{ii} = \left\{ {0.5} \right\},\;l_{{h_{ij} }} = l_{{h_{ji} }}$$

(2)

where $h_{ij}^{\rho \left( s \right)}$ is the sth largest element in $h_{ij}$.

Based on Definition 2.3, Zhu et al. [43] used the optimized parameter $\varsigma$ to add some elements to a HFPR and obtained a normalized hesitant fuzzy preference relation (NHFPR) defined as follows.

Definition 2.5 [43]

Assume a HFPR, $H = \left( {h_{ij} } \right)_{n \times n}$, and an optimized parameter $\varsigma$ ($0 \le \varsigma \le 1$), where $\varsigma$ is used to add some elements to $h_{ij}$ ($i < j$), and $1 - \varsigma$ is used to add some elements to $h_{ji}$ ($i < j$) to obtain a HFPR $\overline{H} = \left( {\overline{h}_{ij} } \right)_{n \times n}$. And for all $i,j = 1,2, \ldots ,n$, this preference relation should satisfy the following conditions:

$$\left\{ \begin{aligned} & l_{{\bar{h}_{ij} }} = \hbox{max} \left\{ {\left. {l_{{h_{ij} }} } \right|i,j = 1,2, \ldots ,n,i \ne j} \right\} = l \\ & \bar{h}_{ij}^{\sigma \left( s \right)} + \bar{h}_{ji}^{\sigma \left( s \right)} = 1, \, \bar{h}_{ii} = \left\{ {0.5} \right\} \\ & \bar{h}_{ij}^{\sigma \left( s \right)} \le \bar{h}_{ij}^{{\sigma \left( {s + 1} \right)}} ,\bar{h}_{ji}^{{\sigma \left( {s + 1} \right)}} \le \bar{h}_{ji}^{\sigma \left( s \right)} , \, i < j \, \\ \end{aligned} \right.$$

(3)

where $\bar{h}_{ij}^{\sigma \left( s \right)}$ and $\bar{h}_{ji}^{\sigma \left( s \right)}$ are the sth elements in $\bar{h}_{ij}$ and $\bar{h}_{ji}$, respectively. Then, we call $\bar{H} = \left( {\bar{h}_{ij} } \right)_{n \times n}$ a NHFPR with the optimized parameter $\varsigma$, and $\bar{h}_{ij}$ is a normalized hesitant fuzzy element (NHFE).

We define the distance between two HFPRs as follows.

Definition 2.6

Assume two HFPRs $H_{1} = \left( {h_{ij,1} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{ij,1}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l_{{h_{ij,1} }} } \right\}} \right)_{n \times n}$ and $H_{2} = \left( {h_{ij,2} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{ij,2}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l_{{h_{ij,2} }} } \right\}} \right)_{n \times n}$, and $\varsigma$ ($0 \le \varsigma \le 1$), we get their normalized HFPRs as $\bar{H}_{1} = \left( {\bar{h}_{ij,1} } \right)_{n \times n} = \left( {\left\{ {\left. {\bar{h}_{ij,1}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ and $\bar{H}_{2} = \left( {\bar{h}_{ij,2} } \right)_{n \times n} = \left( {\left\{ {\left. {\bar{h}_{ij,2}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ satisfying $l = l_{{\bar{h}_{ij,1} }} = l_{{\bar{h}_{ij,2} }}$ ($i,j = 1,2, \ldots ,n$, $i \ne j$). Then

$$\begin{aligned} d\left( {H_{1} ,H_{2} } \right) & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\bar{h}_{ij,1}^{\sigma \left( s \right)} } \right) - \ln \left( {\bar{h}_{ji,1}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \ln \left( {\bar{h}_{ij,2}^{\sigma \left( s \right)} } \right) + \ln \left( {\bar{h}_{ji,2}^{\sigma \left( s \right)} } \right)} \right)^{2} \\ \end{aligned}$$

(4)

is called the distance between H ₁ and H ₂ with $\varsigma$.

Theorem 2.1

The distance $d\left( {H_{1} ,H_{2} } \right)$ between two HFPRs H ₁ and H ₂ satisfies the following properties:

• 1. $d\left( {H_{1} ,H_{2} } \right) \ge 0$;

• 2. $d\left( {H_{1} ,H_{2} } \right) = 0$ if and only if H ₁ = H ₂;

• 3. $d\left( {H_{1} ,H_{2} } \right) = d\left( {H_{2} ,H_{1} } \right)$.

3 Multiplicative Consistency Checking and Improving Process for a HFPR

Zhu et al. [43] defined the multiplicative consistent HFPR as follows.

Definition 3.1 [43]

Given a HFPR $H = \left( {h_{ij} } \right)_{n \times n}$ and its NHFPR $\bar{H} = \left( {\bar{h}_{ij} } \right)_{n \times n}$ with $\varsigma$, if for any $i,j,k = 1,2, \ldots ,n$, $i \ne j \ne k$,

$$\bar{h}_{ik}^{\sigma \left( s \right)} \bar{h}_{kj}^{\sigma \left( s \right)} \bar{h}_{ji}^{\sigma \left( s \right)} = \bar{h}_{ki}^{\sigma \left( s \right)} \bar{h}_{jk}^{\sigma \left( s \right)} \bar{h}_{ij}^{\sigma \left( s \right)}$$

(5)

where $\bar{h}_{ij}^{\sigma \left( s \right)}$ is the sth element in $\bar{h}_{ij}$, then H is called a multiplicative consistent HFPR with $\varsigma$.

The test of consistency measures is a critical step in decision making using preference relations. Consistent information which does not imply any kind of contradiction is more relevant or important than information containing some contradictions. When a HFPR fails to satisfy the consistency requirement, it is necessary to make revisions. In this section, we focus our discussion on the multiplicative consistency of HFPRs. We investigate the characterizations of multiplicative consistency property for HFPRs and propose some methods to measure and improve the multiplicative consistency level of a HFPR.

Based on a HFPR $H = \left( {h_{ij} } \right)_{n \times n}$ and its NHFPR $\bar{H} = \left( {\bar{h}_{ij} } \right)_{n \times n}$ with $\varsigma$, Zhu et al. [43] constructed a multiplicative consistent HFPR $\tilde{H} = \left( {\tilde{h}_{ij} } \right)_{n \times n}$ with $\varsigma$, where

$$\begin{aligned} \tilde{h}_{ij}^{\sigma \left( s \right)} & = \frac{{\sqrt[n]{{\prod\limits_{k = 1}^{n} {\bar{h}_{ik}^{\sigma \left( s \right)} \bar{h}_{kj}^{\sigma \left( s \right)} } }}}}{{\sqrt[n]{{\prod\limits_{k = 1}^{n} {\bar{h}_{ik}^{\sigma \left( s \right)} \bar{h}_{kj}^{\sigma \left( s \right)} } }} + \sqrt[n]{{\prod\limits_{k = 1}^{n} {\left( {1 - \bar{h}_{ik}^{\sigma \left( s \right)} } \right)\left( {1 - \bar{h}_{kj}^{\sigma \left( s \right)} } \right)} }}}}, \\ i,j & = 1,2, \ldots ,n,\;i \ne j \ne k,\;s = 1,2, \ldots ,l \\ \end{aligned}$$

(6)

Based on the distance measure of HFPRs proposed in Definition 2.6, we can define the multiplicative consistency index as follows.

Definition 3.2

Assume a HFPR $H = \left( {h_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l_{{h_{ij} }} } \right\}} \right)_{n \times n}$, an optimized parameter $\varsigma$ ($0 \le \varsigma \le 1$), its NHFPR $\bar{H} = \left( {\bar{h}_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {\bar{h}_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ with $\varsigma$, and its multiplicative consistent HFPR $\tilde{H} = \left( {\tilde{h}_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {\tilde{h}_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ with $\varsigma$, to make H approximate $\tilde{H}$ as much as possible, we define $d\left( {\bar{H},\tilde{H}} \right)$ as a consistency index (CI) with $\varsigma$ of the HFPR H as follows.

$$\begin{aligned} {\text{CI}}\left( H \right) = d\left( {\bar{H},\tilde{H}} \right) & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\bar{h}_{ij}^{\sigma \left( s \right)} } \right) - \ln \left( {\bar{h}_{ji}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \ln \left( {\tilde{h}_{ij}^{\sigma \left( s \right)} } \right) + \ln \left( {\tilde{h}_{ji}^{\sigma \left( s \right)} } \right)} \right)^{2} \\ \end{aligned}$$

(7)

According to Definition 3.2, the ${\text{CI}}\left( H \right)$ can be used to measure the distance between H and $\tilde{H}$. The smaller value the ${\text{CI}}\left( H \right)$, the more consistent the H. Especially, ${\text{CI}}\left( H \right) = 0$ if and only if H is a multiplicative consistent HFPR.

In most cases, it is unrealistic to expect a HFPR to be perfectly multiplicative consistent due to the reason that the DMs would be affected by many uncertainties. Consequently, a definition of acceptably multiplicative consistent HFPR will be further developed to allow a certain of level of acceptable deviation.

Definition 3.3

Let $H = \left( {h_{ij} } \right)_{n \times n}$ be a HFPR. Given a threshold value $\overline{\text{CI}}$, if the multiplicative consistency index satisfies the following,

$${\text{CI}}\left( H \right) \le \overline{\text{CI}}$$

(8)

then we call H a HFPR with acceptably multiplicative consistency.

The value of $\overline{\text{CI}}$ can be determined according to the decision makers’ preferences and the practical situations, which is an interesting topic and is worthy to be further studied in the future. Both Saaty [19] and Wang [22] suggested that the admissible bounds for checking the multiplicative consistency of H can be set at $\overline{\text{CI}} = 0.1$.

Owing to the lack of knowledge or the hardness of discriminating the degree to which some alternatives are better than the others, the HFPR H constructed by the decision maker is often always with unacceptably multiplicative consistency, i.e., ${\text{CI}}\left( H \right) > \overline{\text{CI}}$. To obtain a reasonable solution, H needs to be returned to the decision maker to reconstruct a new HFPR. To help the decision maker to obtain a multiplicative consistent HFPR, we provide the following formula to adjust or repair the inconsistent HFPR $H^{\left( t \right)} = \left( {h_{ij}^{\left( t \right)} } \right)_{n \times n} = \left( {\left\{ {\left. {\left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ until it has acceptably multiplicative consistency.

$$\left( {h_{ij}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} = \frac{{\left( {\left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{1 - \delta } \cdot \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{\delta } }}{{\left( {\left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{1 - \delta } \cdot \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{\delta } + \left( {1 - \left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{1 - \delta } \cdot \left( {1 - \left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{\delta } }}$$

(9)

Theorem 3.1

Let $H^{{\left( {t + 1} \right)}} = \left( {h_{ij}^{{\left( {t + 1} \right)}} } \right)_{n \times n} = \left( {\left\{ {\left. {\left( {h_{ij}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ be a HFPR defined by Eq. (9). Then, we have ${\text{CI}}\left( {H^{{\left( {t + 1} \right)}} } \right) < {\text{CI}}\left( {H^{\left( t \right)} } \right)$.

The proof of Theorem 3.1 is provided in the Appendix.

From Theorem 3.1, we can find that Eq. (9) can improve the multiplicative consistency level of a HFPR by producing a series of revised HFPRs with the monotonically decreasing multiplicative consistency levels.

Now let us consider a GDM problem with a finite set of alternatives $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$. Assume that $D = \left\{ {d_{1} ,d_{2} , \ldots ,d_{m} } \right\}$ are the group decision makers and the corresponding weight vector is $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)^{\text{T}}$ with $\sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1$, $\lambda_{k} \ge 0$. The kth DM compares each pair of the alternatives $x_{i}$ ($i = 1,2, \ldots ,n$) and gives his/her preference information as a HFPR $H_{k} = \left( {h_{ij,k} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{ij,k}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l_{{h_{ij,k} }} } \right\}} \right)_{n \times n}$, where $h_{ij,k}$ ($i,j = 1,2, \ldots ,n$, $i < j$) is a HFE, which indicates hesitant degrees to which x _i is preferred to x _j , and satisfies

$$\begin{aligned} h_{ij,k}^{\sigma \left( s \right)} + h_{ji,k}^{\sigma \left( s \right)} & = 1, \\ l_{{h_{ij,k} }} & = l_{{h_{ji,k} }} , \\ h_{ii,k} & = \left\{ {0.5} \right\},\;h_{ij,k}^{\sigma \left( s \right)} < h_{ij,k}^{{\sigma \left( {s + 1} \right)}} ,\;h_{ji,k}^{{\sigma \left( {s + 1} \right)}} < h_{ji,k}^{\sigma \left( s \right)} \\ \end{aligned}$$

(10)

where $h_{ij,k}^{\sigma \left( s \right)}$ and $h_{ji,k}^{\sigma \left( s \right)}$ are the sth elements in $h_{ij,k}$ and $h_{ji,k}$, respectively.

A collective matrix $H_{\text{c}} = \left( {h_{{ij,{\text{c}}}} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{{ij,{\text{c}}}}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ can be derived from all of the individual HFPRs $H_{k} = \left( {h_{ij,k} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{ij,k}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l_{{h_{ij,k} }} } \right\}} \right)_{n \times n}$ ($k = 1,2, \ldots ,m$) by the following fusion method:

$$\begin{aligned} h_{{ij,{\text{c}}}}^{\sigma \left( s \right)} & = \frac{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }}{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } + \prod\limits_{k = 1}^{m} {\left( {1 - \bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }}, \\ i,j & = 1,2, \ldots ,n,\;s = 1,2, \ldots ,l \\ \end{aligned}$$

(11)

where $\bar{H}_{k} = \left( {\bar{h}_{ij,k} } \right)_{n \times n} = \left( {\left\{ {\left. {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ are the corresponding normalized HFPRs of H _k ($k = 1,2, \ldots ,m$) with $\varsigma_{k}$ ($\varsigma_{k} \in \left[ {0,1} \right]$, $k = 1,2, \ldots ,m$).

Theorem 3.2

Let $H_{k} = \left( {h_{ij,k} } \right)_{n \times n}$ ($k = 1,2 \ldots ,m$) be a collection of m individual HFPRs associated with the weight vector $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)^{\text{T}}$, and let $H_{\text{c}} = \left( {h_{{ij,{\text{c}}}} } \right)_{n \times n}$ be a matrix defined by Eq. (11); then we have

• 1. H _c is a HFPR.

• 2. ${\text{CI}}\left( {H_{\text{c}} } \right) \le \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k} } \right)} \right\}$.

• 3. ${\text{CI}}\left( {H_{k} } \right) \le \alpha ,k = 1,2 \ldots ,m \Rightarrow {\text{CI}}\left( {H_{c} } \right) \le \alpha$.

The proof of Theorem 3.2 is provided in the Appendix.

Theorem 3.2 (2) shows that the consistency levels of the collective HFPR are better than any individual HFPRs. Theorem 3.2 (3) implies that if the multiplicative consistency indexes of individual HFPRs are smaller than a value, then the multiplicative consistency index of the collective HFPR is always smaller than this value. From Theorem 3.2, it can be easily observed that if H _k ($k = 1,2, \ldots ,m$) are of acceptably multiplicative consistency, then H _c is acceptably multiplicative consistent; if H _k ($k = 1,2, \ldots ,m$) are of multiplicative consistency, then H _c is multiplicative consistent.

4 Consensus Checking and Reaching Process for a Group of HFPRs

In the context of GDM, consensus decision making is often considered a desirable outcome. When consensus schemes are utilized, the DMs involved are supposed to participate in the discussions toward a consensus solution. In this section, we introduce a consensus index to measure the consensus level between the group members and develop a convergence method to help the decision makers reach a predefined consensus level.

Based on the distance measure of HFPRs, we next define a consensus index to measure the agreement between the individual HFPRs and the collective HFPR.

Definition 4.1

Assume m HFPRs $H_{k} = \left( {h_{ij,k} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$), an optimized parameter $\varsigma_{k}$ ($\varsigma_{k} \in \left[ {0,1} \right]$, $k = 1,2, \ldots ,m$), their NHFPRs $\bar{H}_{k} = \left( {\bar{h}_{ij,k} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$), and their collective HFPR $H_{\text{c}} = \left( {h_{{ij,{\text{c}}}} } \right)_{n \times n}$, a group consensus index of H _k can be defined to measure the distance between $\bar{H}_{k}$ and H _c, denoted as:

$$\begin{aligned} {\text{GCI}}\left( {H_{k} } \right) & = d\left( {\bar{H}_{k} ,H_{\text{c}} } \right) \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right) - \ln \left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \ln \left( {h_{{ij,{\text{c}}}}^{\sigma \left( s \right)} } \right) + \ln \left( {h_{{ji,{\text{c}}}}^{\sigma \left( s \right)} } \right)} \right)^{2} \\ \end{aligned}$$

(12)

From Definition 4.1, a group consensus index can be used to measure the closeness between the individual HFPRs and the collective HFPR. If ${\text{GCI}}\left( {H_{k} } \right) = 0$, then the kth decision maker has full consensus with the group preference. Otherwise, the smaller the value of ${\text{GCI}}\left( {H_{k} } \right)$, the closer that decision maker is to the group. In particular, if ${\text{GCI}}\left( {H_{k} } \right) = 0$, $k = 1,2, \ldots ,m$, then all the individual HFPRs H _k ($k = 1,2, \ldots ,m$) reach consensus, which seldom happens in the practical problems.

Definition 4.2

Assume m HFPRs $H_{k} = \left( {h_{ij,k} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$), an optimized parameter $\varsigma$ ($\varsigma_{k} \in \left[ {0,1} \right]$, $k = 1,2, \ldots ,m$), their NHFPRs $\bar{H}_{k} = \left( {\bar{h}_{ij,k} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$), their collective HFPR $H_{\text{c}} = \left( {h_{{ij,{\text{c}}}} } \right)_{n \times n}$, and a consensus index ${\text{GCI}}\left( {H_{k} } \right)$, then H _k and H _c are called to be of acceptable consensus, if

$${\text{GCI}}\left( {H_{k} } \right) \le \overline{\text{GCI}}$$

(13)

where $\overline{\text{GCI}}$ is the threshold of acceptable consensus, which can be determined by the DMs in advance in practical applications.

In a GDM problem, if ${\text{GCI}}\left( {H_{k} } \right) > \overline{\text{GCI}}$, then H _k and H _c are of unacceptable consensus. In this case, H _k needs to be returned to the decision maker d _k to reconstruct a new HFPR that is closer to the collective HFPR. This process will be repeated until the predefine consensus level is achieved, which we call the consensus reaching process. In the following, an automatic iterative equation is developed to improve the consensus levels of individual HFPRs.

$$\left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} = \frac{{\left( {\left( {h_{ij,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{1 - \eta } \cdot \left( {\left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{\eta } }}{{\left( {\left( {h_{ij,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{1 - \eta } \cdot \left( {\left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{\eta } + \left( {1 - \left( {h_{ij,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{1 - \eta } \cdot \left( {1 - \left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{\eta } }}$$

(14)

Theorem 4.1

Let $H_{k}^{\left( t \right)} = \left( {h_{ij,k}^{\left( t \right)} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$) be a collection of individual HFPRs associated with the weight vector $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)^{\text{T}}$, and let $H_{k}^{{\left( {t + 1} \right)}} = \left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$) be the adjusted HFPRs by Eq. (14), then we have

• 1. ${\text{GCI}}\left( {H_{k}^{{\left( {t + 1} \right)}} } \right) < {\text{GCI}}\left( {H_{k}^{\left( t \right)} } \right)$;

• 2. $\mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k}^{{\left( {t + 1} \right)}} } \right)} \right\} \le \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k}^{\left( t \right)} } \right)} \right\}$.

The proof of Theorem 4.1 is provided in the Appendix.

Theorem 4.1 (1) indicates that the consensus levels of the original HFPRs are improved by Eq. (14). Theorem 4.1 (2) tells us that the multiplicative consistency index of the original HFPR is bigger than that of the revised individual HFPR obtained by Eq. (14). Theorem 4.1 implies that Eq. (14) not only makes the revised HFPRs reach the predefined consensus level but also maintains the multiplicative consistency and the acceptably multiplicative consistency of the original HFPRs.

5 A Complete Framework for GDM with HFPRs

Through Sects. 3 and 4, in a rational GDM process, both consensus and consistency have be pursued and sought after. A solution with a high level of consensus is desirable, but additionally, a solution can be derived from information that is consistent enough. Once the consensus level among the DMs has been achieved, we can obtain a group decision matrix that represents the centralized opinions of the DMs. A selection process is applied to supply a selection set of alternatives. The selection process obtains the final solution according to the preferences that are given by the DMs; it involves two different steps: the aggregation of individual preferences and exploitation of the collective preference. We aggregate all of the preference information in the each row of the group HFPR and then obtain the overall preference degree of each alternative x _i ($i = 1,2, \ldots ,n$). We rank all of the alternatives x _i ($i = 1,2, \ldots ,n$) and then select the optimal one(s).

From the above analysis, we can design a complete framework of GDM with HFPRs. This framework accounts for the consistency and consensus simultaneously into account, and it is composed of the following steps:

5.1 Algorithm

Step 1 Input: m HFPRs $H_{k} = \left( {h_{ij,k} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$); the weight vector $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)^{\text{T}}$; the threshold of acceptably multiplicative consistency $\overline{\text{CI}}$; the threshold of acceptable consensus $\overline{\text{GCI}}$; the maximum number of iterative times $t_{\hbox{max} } \ge 1$; the controlling parameter $\delta_{k} ,\eta \in \left( {0,1} \right)$ ($k = 1,2, \ldots ,m$).

Step 2 Utilize the following equation

$$\left\{ \begin{aligned} & \hbox{min} {\kern 1pt} \;d\left( {\bar{H}_{k} ,\tilde{H}_{k} } \right) \\ & s.t.\;\;d\left( {\bar{H}_{k} ,\tilde{H}_{k} } \right) = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right) - \ln \left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \quad \quad \quad \quad \quad \quad \left. { - \;\ln \left( {\tilde{h}_{ij,k}^{\sigma \left( s \right)} } \right) + \ln \left( {\tilde{h}_{ji,k}^{\sigma \left( s \right)} } \right)} \right)^{2} \\ & 0 \le \varsigma_{k} \le 1 \\ \end{aligned} \right.$$

(15)

to obtain the value of $\varsigma_{k}$ ($k = 1,2, \ldots ,m$); then, determine $\bar{H}_{k} = \left( {\bar{h}_{ij,k} } \right)_{n \times n}$ and $\tilde{H}_{k} = \left( {\tilde{h}_{ij,k} } \right)_{n \times n}$ by Eqs. (3) and (6), respectively.

Let $H_{k}^{\left( 0 \right)} = \left( {h_{ij,k}^{\left( 0 \right)} } \right)_{n \times n} = \bar{H}_{k} = \left( {\bar{h}_{ij,k} } \right)_{n \times n}$, $\tilde{H}_{k}^{\left( 0 \right)} = \left( {\tilde{h}_{ij,k}^{\left( 0 \right)} } \right)_{n \times n} = \tilde{H}_{k} = \left( {\tilde{h}_{ij,k} } \right)_{n \times n}$, and $t = 0$.

Step 3 Compute the multiplicative consistent HFPRs $\tilde{H}_{k}^{\left( t \right)} = \left( {\tilde{h}_{ij,k}^{\left( t \right)} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$) by Eq. (6) and the multiplicative consistency index ${\text{CI}}\left( {H_{k}^{\left( t \right)} } \right)$ ($k = 1,2, \ldots ,m$) by Eq. (7).

Step 4 If ${\text{CI}}\left( {H_{k}^{\left( t \right)} } \right) \le \overline{\text{CI}}$ for all $k = 1,2, \ldots ,m$, then go to Step 6; otherwise, go to the next step.

Step 5 Let $K^{\left( t \right)} = \left\{ {k \in \left\{ {1,2, \ldots ,m} \right\}\left| {{\text{CI}}\left( {H_{k}^{\left( t \right)} } \right) > \overline{\text{CI}} } \right.} \right\}$. For $k \in K^{\left( t \right)}$, construct the modified HFPRs $H_{k}^{{\left( {t + 1} \right)}} = \left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)_{n \times n} = \left( {\left\{ {\left. {\left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ by Eq. (9). For $k \notin K^{\left( t \right)}$, let $H_{k}^{{\left( {t + 1} \right)}} = H_{k}^{\left( t \right)}$.

Let $t = t + 1$, and return to Step 3.

Step 6 Aggregate all of the individual HFPRs $H_{k}^{\left( t \right)} = \left( {h_{ij,k}^{\left( t \right)} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$) into the collective HFPR $H_{\text{c}}^{\left( t \right)} = \left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)_{n \times n}$ by Eq. (11).

Step 7 Calculate the group consensus index ${\text{GCI}}\left( {H_{k}^{\left( t \right)} } \right)$ ($k = 1,2, \ldots ,m$) by Eq. (12).

If ${\text{GCI}}\left( {H_{k}^{\left( t \right)} } \right) \le \overline{\text{GCI}}$ for all $k = 1,2, \ldots ,m$, or if $t \ge t_{\hbox{max} }$, then go to Step 9; otherwise, go to Step 8.

Step 8 Construct the modified HFPR $H_{k}^{{\left( {t + 1} \right)}} = \left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)_{n \times n}$ ($k = 1,2, \ldots ,m$) by Eq. (14).

Set $t = t + 1$ and go to Step 6.

Step 9 Utilize the following equation

$$\begin{aligned} \left( {h_{{i,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} & = \frac{{\prod\limits_{j = 1}^{n} {\left( {\left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{{\frac{1}{n}}} } }}{{\prod\limits_{j = 1}^{n} {\left( {\left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{{\frac{1}{n}}} } + \prod\limits_{j = 1}^{n} {\left( {1 - \left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)^{{\frac{1}{n}}} } }}, \\ i & = 1,2, \ldots ,n,\;s = 1,2, \ldots ,l \\ \end{aligned}$$

(16)

to aggregate the ith line of preferences $h_{{ij,{\text{c}}}}^{\left( t \right)}$ ($j = 1,2, \ldots ,n$) in $H_{\text{c}}^{\left( t \right)} = \left( {h_{{ij,{\text{c}}}}^{\left( t \right)} } \right)_{n \times n}$ and obtain the overall performance values $h_{{i,{\text{c}}}}^{\left( t \right)}$ ($i = 1,2, \ldots ,n$) corresponding to the alternatives x _i ($i = 1,2, \ldots ,n$).

Step 10 Rank all of the alternatives x _i ($i = 1,2, \ldots ,n$) by Definition 2.2.

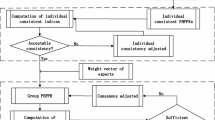
The proposed algorithm can also be described by using Fig. 1. To help the readers to understand our algorithm thoroughly, let us give more explanation step by step. In the above algorithm, the first step is to establish the input data of a GDM problem with HFPRs. Step 2 is the normalization and initialization process. Steps 3–5 make up of the consistency checking process and the consistency improving process. After Step 5, we would derive HFPRs which have the acceptably multiplicative consistency within the consistency threshold $\overline{\text{CI}}$. Steps 6–8 compose the consensus checking process and the consensus reaching process. After Step 8, all of the HFPRs are acceptably multiplicative consistent and the group consensus is also attained. The selection process consists of Steps 9 and 10. After Step 10, we can find out the final solution with sufficient consistency and consensus and then the algorithm ends.

Fig. 1

A complete framework of GDM with HFPRs

6 Illustrative Example and Comparative Analysis

In this section, we consider a practical example involving the investment selection problem to illustrate the implementation details of the proposed method. A comparative study is subsequently conducted to validate the results of the proposed method with the results from other approaches.

6.1 An illustrative Example

In this subsection, a practical example is provided to demonstrate how the proposed approach works in practice. An investment company wants to invest a sum of money in the best option. To reduce the risks involved in making decisions in this uncertain and highly competitive environment, the leader of the company invites a group of experts to participate in the decision and hopes to achieve a consensus solution. A panel with four alternatives is given as follows: x ₁ is a car industry, x ₂ is a food company, x ₃ is a computer company and x ₄ is an arms manufacturer. There are three experts, {d ₁, d ₂, d ₃} from three consultancy departments: the risk analysis department, the growth analysis department and the environmental impact analysis department. The weight vector of these three experts is $\lambda = \left( {0.2,0.5,0.3} \right)$. These experts provide their hesitant preferences over paired comparisons of these four decision alternatives and construct three HFPRs H _k ($k = 1,2,3$) as follows.

$$\begin{aligned} H_{1} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.3} \right\}} & {\left\{ {0.5,0.7} \right\}} & {\left\{ {0.4} \right\}} \\ {\left\{ {0.7} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7,0.9} \right\}} & {\left\{ {0.8} \right\}} \\ {\left\{ {0.5,0.3} \right\}} & {\left\{ {0.3,0.1} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.6,0.7} \right\}} \\ {\left\{ {0.6} \right\}} & {\left\{ {0.2} \right\}} & {\left\{ {0.4,0.3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ H_{2} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.3,0.5} \right\}} & {\left\{ {0.1,0.2} \right\}} & {\left\{ {0.6} \right\}} \\ {\left\{ {0.7,0.5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7,0.8} \right\}} & {\left\{ {0.1,0.3,0.5} \right\}} \\ {\left\{ {0.9,0.8} \right\}} & {\left\{ {0.3,0.2} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.4} \right\}} & {\left\{ {0.9,0.7,0.5} \right\}} & {\left\{ {0.5,0.4,0.3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ H_{3} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.3,0.5} \right\}} & {\left\{ {0.7} \right\}} & {\left\{ {0.7,0.8} \right\}} \\ {\left\{ {0.7,0.5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.2,0.3,0.4} \right\}} & {\left\{ {0.5,0.6} \right\}} \\ {\left\{ {0.3} \right\}} & {\left\{ {0.8,0.7,0.6} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7,0.8,0.9} \right\}} \\ {\left\{ {0.3,0.2} \right\}} & {\left\{ {0.5,0.4} \right\}} & {\left\{ {0.3,0.2,0.1} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ \end{aligned}$$

In the following, we use the proposed algorithm to derive a ranking among four alternatives, which includes the following steps:

Step 1 Utilize Eq. (15) to get the value of $\varsigma_{k}$ ($k = 1,2,3$): $\varsigma_{1} = 0$, $\varsigma_{2} = 0. 5 1 7 4$, $\varsigma_{3} = 1$. Then determine $H_{k}^{\left( 0 \right)}$ ($k = 1,2,3$) and $\tilde{H}_{k}^{\left( 0 \right)}$ ($k = 1,2,3$) as follows:

$$\begin{aligned} H_{1}^{\left( 0 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.3,0.3,0.3} \right\}} & {\left\{ {0.5,0.5,0.7} \right\}} & {\left\{ {0.4,0.4,0.4} \right\}} \\ {\left\{ {0.7,0.7,0.7} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7,0.7,0.9} \right\}} & {\left\{ {0.8,0.8,0.8} \right\}} \\ {\left\{ {0.5,0.5,0.3} \right\}} & {\left\{ {0.3,0.3,0.1} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.6,0.6,0.7} \right\}} \\ {\left\{ {0.6,0.6,0.6} \right\}} & {\left\{ {0.2,0.2,0.2} \right\}} & {\left\{ {0.4,0.4,0.3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ H_{2}^{\left( 0 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.3, 0. 4 0 3 5 ,0.5} \right\}} & {\left\{ {0.1, 0. 1 5 1 7 ,0.2} \right\}} & {\left\{ {0.6, 0. 6 , 0. 6} \right\}} \\ {\left\{ {0.7, 0. 5 9 6 5 ,0.5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7, 0. 7 5 1 7 ,0.8} \right\}} & {\left\{ {0.1,0.3,0.5} \right\}} \\ {\left\{ {0.9, 0. 8 4 8 3 ,0.8} \right\}} & {\left\{ {0.3, 0. 2 4 8 3 ,0.2} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.4, 0. 4 , 0. 4} \right\}} & {\left\{ {0.9,0.7,0.5} \right\}} & {\left\{ {0.5,0.4,0.3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ H_{3}^{\left( 0 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.3,0.5,0.5} \right\}} & {\left\{ {0.7,0.7,0.7} \right\}} & {\left\{ {0.7,0.8,0.8} \right\}} \\ {\left\{ {0.7,0.5,0.5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.2,0.3,0.4} \right\}} & {\left\{ {0.5,0.6,0.6} \right\}} \\ {\left\{ {0.3,0.3,0.3} \right\}} & {\left\{ {0.8,0.7,0.6} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7,0.8,0.9} \right\}} \\ {\left\{ {0.3,0.2,0.2} \right\}} & {\left\{ {0.5,0.4,0.4} \right\}} & {\left\{ {0.3,0.2,0.1} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ \end{aligned}$$

$$\begin{aligned} \tilde{H}_{1}^{\left( 0 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 2 5 2 9, 0. 2 5 2 9, 0. 2 2 9 9} \right\}} & {\left\{ { 0. 4 4 9 5, 0. 4 4 9 5, 0. 6 1 0 1} \right\}} & {\left\{ { 0. 5 0 8 3, 0. 5 0 8 3, 0. 5 8 8 0} \right\}} \\ {\left\{ { 0. 7 4 7 1, 0. 7 4 7 1, 0. 7 7 0 1} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 7 0 7 0, 0. 7 0 7 0, 0. 8 3 9 8} \right\}} & {\left\{ { 0. 7 5 3 4, 0. 7 5 3 4, 0. 8 2 7 0} \right\}} \\ {\left\{ { 0. 5 5 0 5, 0. 5 5 0 5, 0. 3 8 9 9} \right\}} & {\left\{ { 0. 2 9 3 0, 0. 2 9 3 0, 0. 1 6 0 2} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 5 8 8, 0. 5 5 8 8, 0. 4 7 6 9} \right\}} \\ {\left\{ { 0. 4 9 1 7, 0. 4 9 1 7, 0. 4 1 2 0} \right\}} & {\left\{ { 0. 2 4 6 6, 0. 2 4 6 6, 0. 1 7 3 0} \right\}} & {\left\{ { 0. 4 4 1 2, 0. 4 4 1 2, 0. 5 2 3 1} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ \tilde{H}_{2}^{\left( 0 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 6 9 6, 0. 3 5 6 7 , 0. 3 5 6 2} \right\}} & {\left\{ { 0. 2 6 9 5, 0. 3 3 6 0 , 0. 3 8 7 7} \right\}} & {\left\{ { 0. 2 4 8 3, 0. 3 9 2 8 , 0. 5 1 7 0} \right\}} \\ {\left\{ { 0. 6 3 0 4, 0. 6 4 3 3 , 0. 6 4 3 8} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 8 6 2, 0. 4 7 7 1 , 0. 5 3 3 6} \right\}} & {\left\{ { 0. 3 6 0 4, 0. 5 3 8 4, 0. 6 5 9 2} \right\}} \\ {\left\{ { 0. 7 3 0 5, 0. 6 6 4 0 , 0. 6 1 2 3} \right\}} & {\left\{ { 0. 6 1 3 8, 0. 5 2 2 9 , 0. 4 6 6 4} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 7 2 4, 0. 5 6 1 1, 0. 6 2 8 3} \right\}} \\ {\left\{ { 0. 7 5 1 7, 0. 6 0 7 2 , 0. 4 8 3 0} \right\}} & {\left\{ { 0. 6 3 9 6, 0. 4 6 1 6, 0. 3 4 0 8} \right\}} & {\left\{ { 0. 5 2 7 6, 0. 4 3 8 9, 0. 3 7 1 7} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ \tilde{H}_{3}^{\left( 0 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 8 5 8, 0. 6 6 1 2, 0. 6 3 6 1} \right\}} & {\left\{ { 0. 4 6 6 4, 0. 5 5 2 8, 0. 5 2 9 9} \right\}} & {\left\{ { 0. 6 5 3 7, 0. 7 9 4 6, 0. 8 2 5 7} \right\}} \\ {\left\{ { 0. 4 1 4 2, 0. 3 3 8 8, 0. 3 6 3 9} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 8 1 9, 0. 3 8 7 7, 0. 3 9 2 0} \right\}} & {\left\{ { 0. 5 7 1 7, 0. 6 6 4 6, 0. 7 3 0 5} \right\}} \\ {\left\{ { 0. 5 3 3 6, 0. 4 4 7 2, 0. 4 7 0 1} \right\}} & {\left\{ { 0. 6 1 8 1, 0. 6 1 2 3, 0. 6 0 8 0} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 6 8 3 6, 0. 7 5 7 9, 0. 8 0 7 8} \right\}} \\ {\left\{ { 0. 3 4 6 3, 0. 2 0 5 4, 0. 1 7 4 3} \right\}} & {\left\{ { 0. 4 2 8 3, 0. 3 3 5 4, 0. 2 6 9 5} \right\}} & {\left\{ { 0. 3 1 6 4, 0. 2 4 2 1, 0. 1 9 2 2} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ \end{aligned}$$

Step 2 Use Eq. (7) to compute the multiplicative consistency index ${\text{CI}}\left( {H_{k}^{\left( 0 \right)} } \right)$ ($k = 1,2,3$): ${\text{CI}}\left( {H_{1}^{\left( 0 \right)} } \right) = 0. 1 5 8 9 ,\;{\text{CI}}\left( {H_{2}^{\left( 0 \right)} } \right) = 0. 8 8 4 5 ,\;{\text{CI}}\left( {H_{3}^{\left( 0 \right)} } \right) = 0. 3 4 9 2$.

Step 3 Set $\overline{\text{CI}} = 0.1$. Consider ${\text{CI}}\left( {H_{k}^{\left( 0 \right)} } \right) > 0.1$ for all $k = 1,2,3$; therefore, we use Eq. (9) (suppose that $\delta_{1} = 0.1$, $\delta_{2} = 0.2$, and $\delta_{3} = 0.8$) to construct the acceptably multiplicative consistent HFPRs $H_{k}^{\left( 5 \right)}$ ($k = 1,2,3$) (after 5 iterations) follows:

$$\begin{aligned} H_{1}^{\left( 5 \right)} & = \left\{ {\begin{array}{*{20}c} { 0. 5} & {\left\{ { 0. 2 8 9 6, 0. 2 8 9 6, 0. 2 8 4 2} \right\}} & {\left\{ { 0. 4 8 9 0, 0. 4 8 9 0, 0. 6 8 1 9} \right\}} & {\left\{ { 0. 4 2 2 5, 0. 4 2 2 5, 0. 4 3 9 4} \right\}} \\ {\left\{ { 0. 7 1 3 8, 0. 7 1 3 8, 0. 7 2 1 0} \right\}} & { 0. 5} & {\left\{ { 0. 7 0 1 5, 0. 7 0 1 5, 0. 8 8 9 8} \right\}} & {\left\{ { 0. 7 9 1 2, 0. 7 9 1 2, 0. 8 0 6 1} \right\}} \\ {\left\{ { 0. 5 1 3 7, 0. 5 1 3 7, 0. 3 2 0 9} \right\}} & {\left\{ { 0. 2 9 8 3, 0. 2 9 8 3, 0. 1 1 0 8} \right\}} & { 0. 5} & {\left\{ { 0. 5 9 1 6, 0. 5 9 1 6, 0. 6 5 8 1} \right\}} \\ {\left\{ { 0. 5 7 1 1, 0. 5 7 1 1, 0. 5 4 9 7} \right\}} & {\left\{ { 0. 2 0 9 6, 0. 2 0 9 6, 0. 1 9 3 3} \right\}} & {\left\{ { 0. 4 1 0 0, 0. 4 1 0 0, 0. 3 4 8 6} \right\}} & { 0. 5} \\ \end{array} } \right\} \\ H_{2}^{\left( 5 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 5 5 8, 0. 3 6 6 6, 0. 3 8 5 6} \right\}} & {\left\{ { 0. 2 1 5 4, 0. 2 8 2 8, 0. 3 3 6 8} \right\}} & {\left\{ { 0. 3 2 6 8, 0. 4 4 4 7, 0. 5 3 8 6} \right\}} \\ {\left\{ { 0. 6 4 0 5, 0. 6 3 5 6, 0. 6 2 0 7} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 6 5 0, 0. 5 5 7 3, 0. 6 1 9 2} \right\}} & {\left\{ { 0. 2 6 3 9, 0. 4 7 9 4, 0. 6 2 6 2} \right\}} \\ {\left\{ { 0. 7 7 3 4, 0. 7 0 6 5, 0. 6 5 3 4} \right\}} & {\left\{ { 0. 5 4 7 3, 0. 4 5 1 5, 0. 3 8 8 2} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 8 0 5, 0. 5 7 1 8, 0. 6 4 8 1} \right\}} \\ {\left\{ { 0. 6 8 8 2, 0. 5 6 3 0, 0. 4 6 4 0} \right\}} & {\left\{ { 0. 7 2 0 2, 0. 5 1 1 2, 0. 3 6 9 6} \right\}} & {\left\{ { 0. 5 2 0 8, 0. 4 2 9 5, 0. 3 5 3 8} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ H_{3}^{\left( 5 \right)} & = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 2 6 9, 0. 3 6 6 6, 0. 6 0 9 9} \right\}} & {\left\{ { 0. 5 1 5 4, 0. 2 8 2 8, 0. 5 6 5 9} \right\}} & {\left\{ { 0. 6 6 3 3, 0. 4 4 4 7, 0. 8 2 0 8} \right\}} \\ {\left\{ { 0. 4 2 4 0, 0. 6 3 5 6, 0. 3 7 4 2} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 4 0 2, 0. 5 5 7 3, 0. 3 9 3 6} \right\}} & {\left\{ { 0. 5 5 7 5, 0. 4 7 9 4, 0. 7 0 6 6} \right\}} \\ {\left\{ { 0. 5 0 1 2, 0. 7 0 6 5, 0. 4 4 9 9} \right\}} & {\left\{ { 0. 6 4 4 4, 0. 4 5 1 5, 0. 6 2 9 0} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 6 8 6 9, 0. 5 7 1 8, 0. 8 3 0 4} \right\}} \\ {\left\{ { 0. 3 3 6 9, 0. 5 6 3 0, 0. 1 7 8 3} \right\}} & {\left\{ { 0. 4 4 5 1, 0. 5 1 1 2, 0. 2 8 8 4} \right\}} & {\left\{ { 0. 3 1 2 7, 0. 4 2 9 5, 0. 1 6 8 3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \\ \end{aligned}$$

Moreover, we use Eq. (7) to calculate the multiplicative consistency index ${\text{CI}}\left( {H_{k}^{\left( 5 \right)} } \right)$ ($k = 1,2,3$) as follows: ${\text{CI}}\left( {H_{1}^{\left( 5 \right)} } \right) = 0. 0 9 7 9 ,\;{\text{CI}}\left( {H_{2}^{\left( 5 \right)} } \right) = 0. 0 5 5 9 ,\;{\text{CI}}\left( {H_{3}^{\left( 5 \right)} } \right) = 0. 0 3 4 1$.

Because ${\text{CI}}\left( {H_{k}^{\left( 5 \right)} } \right) < 0.1$ for all $k = 1,2,3$, $H_{k}^{\left( 5 \right)}$ ($k = 1,2,3$) are of acceptably multiplicative consistency.

Step 4 Utilize Eq. (11) to aggregate all of the acceptably multiplicative consistent HFPRs $H_{k}^{\left( 5 \right)}$ ($k = 1,2,3$) into the collective HFPR $H_{\text{c}}^{\left( 5 \right)} = \left( {h_{{ij,{\text{c}}}}^{\left( 5 \right)} } \right)_{4 \times 4}$, which is shown as follows:

$$H_{\text{c}}^{\left( 5 \right)} = \left\{ {\begin{array}{*{20}c} {\left\{ { 0. 5} \right\}} & {\left\{ { 0. 3 9 9 1, 0. 4 3 0 4, 0. 4 3 1 0} \right\}} & {\left\{ { 0. 3 4 5 1, 0. 4 0 7 5, 0. 4 7 2 1} \right\}} & {\left\{ { 0. 4 4 2 9, 0. 5 5 7 2, 0. 6 1 9 6} \right\}} \\ {\left\{ { 0. 6 0 0 9, 0. 5 6 9 6, 0. 5 6 9 0} \right\}} & {\left\{ { 0. 5} \right\}} & {\left\{ { 0. 4 7 4 5, 0. 5 2 8 9, 0. 6 2 4 7} \right\}} & {\left\{ { 0. 4 5 7 9, 0. 6 0 4 1, 0. 6 9 3 8} \right\}} \\ {\left\{ { 0. 6 5 4 9, 0. 5 9 2 5, 0. 5 2 7 9} \right\}} & {\left\{ { 0. 5 2 5 5, 0. 4 7 1 1, 0. 3 7 5 3} \right\}} & {\left\{ { 0. 5} \right\}} & {\left\{ { 0. 5 6 6 9, 0. 6 3 9 7, 0. 7 1 2 7} \right\}} \\ {\left\{ { 0. 5 5 7 1, 0. 4 4 2 8, 0. 3 8 0 4} \right\}} & {\left\{ { 0. 5 4 2 1, 0. 3 9 5 9, 0. 3 0 6 2} \right\}} & {\left\{ { 0. 4 3 3 1, 0. 3 6 0 3, 0. 2 8 7 3} \right\}} & {\left\{ { 0. 5} \right\}} \\ \end{array} } \right\}$$

Step 5 Calculate the group consensus index ${\text{GCI}}\left( {H_{k}^{\left( 5 \right)} } \right)$ ($k = 1,2,3$) by Eq. (12): ${\text{GCI}}\left( {H_{1}^{\left( 5 \right)} } \right) = 0. 5 8 6 5 , {\text{ GCI}}\left( {H_{2}^{\left( 5 \right)} } \right) = 0. 1 7 0 8 , {\text{ GCI}}\left( {H_{3}^{\left( 5 \right)} } \right) = 0. 4 9 6 4$.

Step 6 Assume that $\overline{\text{GCI}} = 0.1$ and $\eta = 0.7$. Because ${\text{GCI}}\left( {H_{k}^{\left( 5 \right)} } \right) > 0.1$ for all $k = 1,2,3$, we utilize Eq. (14) to construct the modified HFPRs $H_{k}^{\left( 6 \right)}$ ($k = 1,2,3$) as below:

$$\begin{aligned} H_{1}^{\left( 6 \right)} = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 6 4 2, 0. 3 8 5 4, 0. 3 8 3 8} \right\}} & {\left\{ { 0. 3 8 6 2, 0. 4 3 1 2, 0. 5 3 6 9} \right\}} & {\left\{ { 0. 4 3 7 6, 0. 5 1 7 6, 0. 5 6 8 1} \right\}} \\ {\left\{ { 0. 6 1 6 1, 0. 5 9 0 2, 0. 5 9 1 7} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 4 6 1, 0. 5 8 3 6, 0. 7 2 7 5} \right\}} & {\left\{ { 0. 5 6 9 6, 0. 6 6 6 9, 0. 7 3 1 3} \right\}} \\ {\left\{ { 0. 6 2 6 0, 0. 5 7 4 5, 0. 4 7 7 6} \right\}} & {\left\{ { 0. 4 6 9 9, 0. 4 2 8 1, 0. 2 8 1 3} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 7 4 0, 0. 6 2 5 2, 0. 6 9 5 6} \right\}} \\ {\left\{ { 0. 5 5 6 4, 0. 4 6 3 0, 0. 4 0 9 9} \right\}} & {\left\{ { 0. 4 4 5 7, 0. 3 4 2 4, 0. 2 7 3 9} \right\}} & {\left\{ { 0. 4 2 7 1, 0. 3 7 0 0, 0. 3 0 0 2} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \hfill \\ H_{2}^{\left( 6 \right)} = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 3 8 6 3, 0. 4 1 0 6, 0. 4 1 6 5} \right\}} & {\left\{ { 0. 3 0 3 3, 0. 3 6 9 0, 0. 4 3 1 2} \right\}} & {\left\{ { 0. 4 0 5 2, 0. 5 2 2 5, 0. 5 9 5 4} \right\}} \\ {\left\{ { 0. 6 0 4 2, 0. 5 7 7 2, 0. 5 7 4 8} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 6 9 9, 0. 5 3 6 0, 0. 6 2 1 7} \right\}} & {\left\{ { 0. 3 9 6 7, 0. 5 6 8 7, 0. 6 7 5 0} \right\}} \\ {\left\{ { 0. 6 7 0 5, 0. 6 0 8 9, 0. 5 4 7 2} \right\}} & {\left\{ { 0. 5 2 6 7, 0. 4 6 5 1, 0. 3 7 4 1} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 4 1 0, 0. 6 1 9 5, 0. 6 9 3 7} \right\}} \\ {\left\{ { 0. 5 7 5 8, 0. 4 6 1 3, 0. 3 9 4 3} \right\}} & {\left\{ { 0. 5 6 4 8, 0. 4 1 6 5, 0. 3 1 9 4} \right\}} & {\left\{ { 0. 4 4 9 1, 0. 3 7 3 9, 0. 3 0 1 3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \hfill \\ H_{3}^{\left( 6 \right)} = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 4 4 9, 0. 4 9 4 7, 0. 4 8 8 1} \right\}} & {\left\{ { 0. 3 9 1 8, 0. 4 5 7 9, 0. 4 9 7 6} \right\}} & {\left\{ { 0. 5 1 0 7, 0. 6 3 8 5, 0. 6 8 9 9} \right\}} \\ {\left\{ { 0. 5 6 3 9, 0. 5 1 9 4, 0. 5 2 5 5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 3 4 6, 0. 4 8 0 1, 0. 5 5 3 8} \right\}} & {\left\{ { 0. 4 8 7 4, 0. 6 1 8 8, 0. 6 9 8 8} \right\}} \\ {\left\{ { 0. 6 2 3 3, 0. 5 5 6 6, 0. 5 0 8 6} \right\}} & {\left\{ { 0. 5 4 4 7, 0. 4 9 8 5, 0. 4 1 7 0} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 6 0 4 5, 0. 6 8 1 2, 0. 7 5 3 0} \right\}} \\ {\left\{ { 0. 5 0 5 5, 0. 3 7 2 9, 0. 3 1 8 6} \right\}} & {\left\{ { 0. 5 1 3 7, 0. 3 8 2 6, 0. 3 0 1 3} \right\}} & {\left\{ { 0. 4 0 3 6, 0. 3 2 5 7, 0. 2 5 1 9} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\} \hfill \\ \end{aligned}$$

Then, utilize Eq. (11) to aggregate all of the HFPRs $H_{k}^{\left( 6 \right)}$ ($k = 1,2,3$) into the collective HFPR $H_{\text{c}}^{\left( 6 \right)}$:

$$H_{\text{c}}^{\left( 6 \right)} = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 0 7 8, 0. 4 4 0 4, 0. 4 3 8 8} \right\}} & {\left\{ { 0. 3 5 4 6, 0. 4 1 6 0, 0. 4 8 1 3} \right\}} & {\left\{ { 0. 4 5 1 8, 0. 5 7 0 8, 0. 6 3 1 2} \right\}} \\ {\left\{ { 0. 5 9 8 7, 0. 5 6 7 1, 0. 5 6 7 0} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 4 8 1 7, 0. 5 3 4 4 , 0. 6 3 9 6} \right\}} & {\left\{ { 0. 4 8 2 3, 0. 6 1 2 5, 0. 6 9 6 9} \right\}} \\ {\left\{ { 0. 6 5 3 1, 0. 5 9 0 6, 0. 5 2 5 5} \right\}} & {\left\{ { 0. 5 2 3 6, 0. 4 6 9 6, 0. 3 7 0 7} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 5 7 0 5, 0. 6 4 3 3, 0. 7 1 5 9} \right\}} \\ {\left\{ { 0. 5 5 5 0, 0. 4 3 8 8, 0. 3 7 6 8} \right\}} & {\left\{ { 0. 5 3 5 8, 0. 3 9 3 3, 0. 3 0 5 1} \right\}} & {\left\{ { 0. 4 3 2 1, 0. 3 5 9 2, 0. 2 8 6 3} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\}$$

Calculate the group consensus index ${\text{GCI}}\left( {H_{k}^{\left( 6 \right)} } \right)$ ($k = 1,2,3$) by Eq. (12): ${\text{GCI}}\left( {H_{1}^{\left( 6 \right)} } \right) = 0. 0 3 6 8 , {\text{ GCI}}\left( {H_{2}^{\left( 6 \right)} } \right) = 0. 0 1 4 1 , {\text{ GCI}}\left( {H_{3}^{\left( 3 \right)} } \right) = 0. 0 2 9 3$.

Because ${\text{GCI}}\left( {H_{k}^{\left( 6 \right)} } \right) < 0.1$ for all $k = 1,2,3$, $H_{k}^{\left( 6 \right)}$ ($k = 1,2,3$) are of acceptable consensus.

Step 7 Use Eq. (16) to aggregate the ith line of preferences $h_{{ij,{\text{c}}}}^{\left( 6 \right)}$ ($j = 1,2,3,4$) in $H_{\text{c}}^{\left( 6 \right)}$ and derive the overall performance values $h_{{i,{\text{c}}}}^{\left( 6 \right)}$ ($i = 1,2,3,4$) corresponding to the alternatives x _i ($i = 1,2,3,4$), which are shown as follows:

$$\begin{aligned} h_{{1,{\text{c}}}}^{\left( 6 \right)} & = \left\{ { 0. 4 2 5 5 , 0. 4 7 8 7 , 0. 5 1 0 7} \right\}, \\ h_{{2,{\text{c}}}}^{\left( 6 \right)} & = \left\{ { 0. 5 1 2 2 , 0. 5 5 1 4 , 0. 6 0 0 3} \right\}, \\ h_{{3,{\text{c}}}}^{\left( 6 \right)} & = \left\{ { 0. 5 6 0 5 , 0. 5 5 0 1 , 0. 5 2 8 7} \right\}, \\ h_{{4,{\text{c}}}}^{\left( 6 \right)} & = \left\{ { 0. 5 0 2 1 , 0. 4 2 0 2 , 0. 3 6 2 5} \right\} \\ \end{aligned}$$

Step 8 Calculate the score functions $s\left( {h_{{i,{\text{c}}}}^{\left( 6 \right)} } \right)$ ($i = 1,2,3,4$) of the alternatives $x_{i}$ ($i = 1,2,3,4$) as follows: $s\left( {h_{{1,{\text{c}}}}^{\left( 6 \right)} } \right) = 0. 4 7 1 7 , { }s\left( {h_{{2,{\text{c}}}}^{\left( 6 \right)} } \right) = 0. 5 5 4 6 , { }s\left( {h_{{3,{\text{c}}}}^{\left( 6 \right)} } \right) = 0. 5 4 6 4 , { }s\left( {h_{{4,{\text{c}}}}^{\left( 6 \right)} } \right) = 0. 4 2 8 2$

According to Definition2.2, the ranking order of the four alternatives is determined as $x_{2} \succ x_{3} \succ x_{1} \succ x_{4}$. Therefore, the optimal alternative is x ₂.

6.2 Comparative Analysis and Discussions

In the following, we perform a comparison analysis between the developed algorithm and the previous methods in the existing literature and then highlight the main characteristics and advantages of the developed algorithm.

6.2.1 Comparison with Zhu et al. [43]’ Method

Zhu et al. [43] defined the multiplicative consistency of HFPRs and developed an optimization method to improve the consistency of inconsistent HFPRs until they are acceptably consistent. Zhu et al.’ method is briefly reviewed as follows: Assume an HFPR $H = \left( {h_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {h_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l_{{h_{ij} }} } \right\}} \right)_{n \times n}$ with the unacceptable consistency, according to Eq. (15), we can obtain its NHFPR $\bar{H} = \left( {\bar{h}_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {\bar{h}_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ ($l = \hbox{max} \left\{ {\left. {l_{{h_{ij} }} } \right|i,j = 1,2, \ldots ,n,i \ne j} \right\}$) and the optimal optimized parameter $\varsigma$. Let $\hat{H} = \left( {\hat{h}_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {\hat{h}_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ be the modified HFPR, where $\hat{h}_{ij}^{\sigma \left( s \right)} = \bar{h}_{ij}^{\sigma \left( s \right)} + x_{ij}^{\sigma \left( s \right)}$ ($i,j = 1,2, \ldots ,n$, $i < j$, $s = 1,2, \ldots ,l$), $x_{ij} = \left\{ {\left. {x_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}$ ($i,j = 1,2, \ldots ,n$, $i < j$) is the set of adjusted valuables represented by a HFE, then we build the model as follows:

$$\mathop {\hbox{min} }\limits_{x} \left( {\frac{2}{{n\left( {n - 1} \right)}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {x_{ij}^{\sigma \left( s \right)} } \right)^{2} } } } } \right)$$

(17)

with the conditions that

$$\left\{ \begin{aligned} & x_{ij}^{\sigma \left( s \right)} + x_{ji}^{\sigma \left( s \right)} = 0 \\ & {\text{CI}}\left( {\hat{H}} \right) \le \overline{\text{CI}} \\ \end{aligned} \right.$$

(18)

Therefore, Zhu et al. [43] built an optimization model as below:

$$\left\{ \begin{aligned} & \mathop {\hbox{min} }\limits_{x} \left( {\frac{2}{{n\left( {n - 1} \right)}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {x_{ij}^{\sigma \left( s \right)} } \right)^{2} } } } } \right) \\ & s.t.{\kern 1pt} \;\;\;x_{ij}^{\sigma \left( s \right)} + x_{ji}^{\sigma \left( s \right)} = 0 \\ & {\text{CI}}\left( {\hat{H}} \right) \le \overline{\text{CI}} \\ \end{aligned} \right.$$

(19)

By solving this optimization model, we can obtain the adjusted HFPR $\hat{H} = \left( {\hat{h}_{ij} } \right)_{n \times n} = \left( {\left\{ {\left. {\hat{h}_{ij}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$, where $\hat{h}_{ij}^{\sigma \left( s \right)} = \bar{h}_{ij}^{\sigma \left( s \right)} + x_{ij}^{\sigma \left( s \right)}$.

Compared to the developed algorithm in this paper, Zhu et al. [43]’ optimization model needs to calculate all the adjusted valuables. The number of all the adjusted valuables ($= \frac{{n\left( {n - 1} \right)l}}{2}$) is very large, especially when the number of alternatives (=n) and the number of elements in each HFE of a HFPR (=l) are very large. For example, suppose that the number of alternatives (n = 10) and the number of elements in each HFE of a HFPR (l = 5), then the number of all the adjusted valuables needed in Zhu et al.’ optimization model is 225. Thus, to input and output all these adjusted valuables is a very complex task in using the MATLAB optimization toolbox to resolve the model. In contrast, no the adjusted variables are needed in our developed algorithm. In addition, based on the adjusted valuables and the original NHFPR, the modified HFPR can be constructed. Because the values of the adjusted valuables are unconstrained, they can take the form of any real numbers. As a result, the number of the modified HFPRs $\hat{H}$ in Zhu et al.’ optimization model is very large. Zhu et al.’ optimization model needs to calculate the corresponding consistent HFPRs $\tilde{\hat{H}}$ of all of the modified HFPRs $\hat{H}$ and then calculate the consistency indexes ${\text{CI}}\left( {\hat{H}} \right)$ of all of the modified HFPRs $\hat{H}$, which is a considerably time-consuming and inconvenient process. However, our algorithm only needs to consider a modified HFPR in Eq. (9) and then calculates the consistent HFPR and the consistency index of this modified HFPR; thus, this process is time-saving and very convenient. The computational complexity of Zhu et al.’ optimization is much higher than that of our algorithm. A high computational complexity means a large amount of costs and time, which may not be preferred in the practical GDM process. Furthermore, Zhu et al.’ optimization model is a nonlinear programming model and it is not easy to be solved. On the contrary, our algorithm is not a nonlinear programming problem and we can directly obtain a HFPR with acceptably multiplicative consistency within several iterations by the developed algorithm without intermediate valuables and the construction process. Thus, our model is easier to solve than the Zhu et al.’ method. Finally, the number of iterations and the accuracy of modification can also be controlled by the adjusted parameter δ, where δ is determined by the decision makers in accordance with their knowledge and requirement over the specific decision-making problem. That is, our algorithm is interactive with the decision makers and thus is flexible and can match the practical group decision-making situation perfectly. In contrast, Zhu et al.’ optimization model has no any interactive action with the decision makers.

6.2.2 Comparison with Liao et al. [13]’ Method

Liao et al. [13] investigated the multiplicative consistency and consensus of hesitant fuzzy preference relations. First, Liao et al. defined the concept of multiplicative consistent HFPR as follows: Let $H = \left( {h_{ij} } \right)_{n \times n}$ be a HFPR, then $H = \left( {h_{ij} } \right)_{n \times n}$ is multiplicative consistent if

$$h_{ij}^{\rho \left( s \right)} = \left\{ \begin{aligned} & 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {h_{ik} ,h_{kj} } \right) \in \left\{ {\left( {\left\{ 0 \right\},\left\{ 1 \right\}} \right),\left( {\left\{ 1 \right\},\left\{ 0 \right\}} \right)} \right\},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ & \frac{{h_{ik}^{\rho \left( s \right)} h_{kj}^{\rho \left( s \right)} }}{{h_{ik}^{\rho \left( s \right)} h_{kj}^{\rho \left( s \right)} + \left( {1 - h_{ik}^{\rho \left( s \right)} } \right)\left( {1 - h_{kj}^{\rho \left( s \right)} } \right)}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{otherwise,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{all}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \le k \le j.{\kern 1pt} {\kern 1pt} \\ \end{aligned} \right.$$

(20)

where $h_{ik}^{\rho \left( s \right)}$ and $h_{kj}^{\rho \left( s \right)}$ are the sth smallest values in $h_{ik}$ and $h_{kj}$, respectively.

However, in Eq. (20), the transitivity of a HFPR is restricted by the condition: $i \le k \le j$; that is, Eq. (20) holds only for the upper triangular of the HFPR, while the transitivity of a HFPR in Definition 3.1 is unconstrained which satisfies for all $i,k,j = 1,2, \ldots ,n$ and is more general. If Eq. (20) is used to check the consistency of a HFPR for all $i,k,j = 1,2, \ldots ,n$, the transitivity and the consistency properties sometimes do not hold. This is because that when k comes from the row of lower triangular matrix, the equation does not hold. For example (see Example 2 in [13]):

$$H = \left\{ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ { 0. 1, 0.4} \right\}} & {\left\{ { 0. 0 4 6, 0.727} \right\}} & {\left\{ { 0.036, 0. 4 3 4} \right\}} \\ {\left\{ { 0. 6, 0. 9} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 3, 0. 8} \right\}} & {\left\{ { 0. 0 9 7, 0.903} \right\}} \\ {\left\{ { 0.273, 0. 9 5 4} \right\}} & {\left\{ { 0. 2, 0.7} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ { 0. 2, 0.7} \right\}} \\ {\left\{ { 0. 5 6 6, 0.964} \right\}} & {\left\{ { 0. 0 9 7, 0.903} \right\}} & {\left\{ { 0. 3, 0.8} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right\}$$

is a consistent HFPR in [13], and $h_{23} = \left\{ { 0. 3, 0. 8} \right\}$. If we relax the condition $i \le k \le j$, it follows that $h_{23} =\left\{ {\frac{{h_{21}^{\rho (1)} h_{13}^{\rho (1)} }}{{h_{21}^{\rho (1)} h_{13}^{\rho (1)} + \left( {1 - h_{21}^{\rho (1)} } \right)\left( {1 - h_{13}^{\rho (1)} } \right)}},\frac{{h_{21}^{\rho (2)} h_{13}^{\rho (2)} }}{{h_{21}^{\rho (2)} h_{13}^{\rho (2)} + \left( {1 - h_{21}^{\rho (2)} } \right)\left( {1 - h_{13}^{\rho (2)} } \right)}}} \right\} = \left\{ { 0. 0 6 7 4 , 0. 9 5 9 9} \right\}$. But $\left\{ { 0. 3, 0. 8} \right\} \ne \left\{ { 0. 0 6 7 4 , 0. 9 5 9 9} \right\}$, and then$h_{23} \ne \left\{ {\frac{{h_{21}^{\rho \left( 1 \right)} h_{13}^{\rho \left( 1 \right)} }}{{h_{21}^{\rho \left( 1 \right)} h_{13}^{\rho \left( 1 \right)} + \left( {1 - h_{21}^{\rho \left( 1 \right)} } \right)\left( {1 - h_{13}^{\rho \left( 1 \right)} } \right)}},\frac{{h_{21}^{\rho \left( 2 \right)} h_{13}^{\rho \left( 2 \right)} }}{{h_{21}^{\rho \left( 2 \right)} h_{13}^{\rho \left( 2 \right)} + \left( {1 - h_{21}^{\rho \left( 2 \right)} } \right)\left( {1 - h_{13}^{\rho \left( 2 \right)} } \right)}}} \right\}$.

From Eq. (20), we generally cannot derive the relationship $h_{ij}^{\rho \left( s \right)} = \frac{{h_{ik}^{\rho \left( s \right)} h_{kj}^{\rho \left( s \right)} }}{{h_{ik}^{\rho \left( s \right)} h_{kj}^{\rho \left( s \right)} + \left( {1 - h_{ik}^{\rho \left( s \right)} } \right)\left( {1 - h_{kj}^{\rho \left( s \right)} } \right)}}$ (for all $i,k,j = 1,2, \ldots ,n$) any more, and thus Eq. (20) loses the original foundation of multiplicative consistency. In other words, the multiplicative consistency conditions given in Eq. (20) may be too strict for a HFPR.

Second, in Liao et al.’s method, the adjusted hesitant fuzzy weighted averaging (AHFWA) operator or the adjusted hesitant fuzzy weighted geometric (AHFWG) operator is used to fuse all of the individual HFPRs into the collective HFPR. It is noticed that such collective HFPR derived by the AHFWA or AHFWG operator may not keep the consistency and the acceptable consistency. In contrast, our method uses Eq. (11) to fuse all of the individual HFPRs into the collective HFPR. Theorem 3.2 shows that such collective HFPR still keeps the consistency and the acceptable consistency.

Third, Liao et al. [13] developed some iterative algorithms to improve the consistency and consensus levels of individual HFPRs. However, the convergence of these algorithms is not been clearly stated and strictly proved. In contrast, the convergence of the proposed algorithm in this study is illustrated by several theorems. These results lay a solid theoretical foundation for the effectiveness and practicality of the developed method.

Finally, Liao et al. [13] only separately discussed the consistency and the consensus, and did not integrate them together. Liao et al. [13] did not argue that whether the consistency of the adjusted HFPRs is still been kept in a consensus reaching process. However, in this study, the consistency model and the consensus model are organically combined together. Theorem 4.1 ensures that each individual HFPR is of multiplicative consistency or acceptably multiplicative consistency when the predefined consensus level is achieved.

In conclusion, we develop a more flexible and reliable decision support model for solving GDM problems with HFPRs while accounting for the consistency and consensus. The numerical examples and comparison with other approaches in the literature illustrate the effectiveness, reasonableness and feasibility of the developed method.

7 Conclusions

In this paper, we have investigated the hesitant fuzzy group decision-making problem in which all the experts’ preference information is represented by HFPRs. First, an individual consistency index, which is based on the multiplicative consistency, has been developed to measure the consistency degree of each HFPR furnished by the group of experts. A consistency improving process has been designed to convert an unacceptably consistent HFPR to an acceptably consistent one. Then, we have defined a group consensus index to measure the consensus level among individual HFPRs. A consensus reaching process has been proposed to help the group reach a predefined consensus level. Furthermore, in order to make our approaches, more applicable, a complete framework, which simultaneously addresses the individual consistency and group consensus, has been presented to aid the whole GDM process based on HFPRs. Finally, we have given a numerical example to demonstrate the application of the proposed models and to verify the theoretical results. Additionally, a comparative analysis has been conducted to validate the solution results yielded by the proposed method with those by other methods.

Based on the comparative analysis between our approach and the existing hesitant fuzzy group decision-making methodologies in the literature, we can find that our method is the most comprehensive and convincing one among them as it takes the integral framework of hesitant fuzzy group decision making into account, including the consistency checking and improving process, the consensus checking and reaching process, and the selection process, while all the existing methods only focus on one or two process(es). Moreover, our approach is very flexible, convenient, and time-saving, and thus can fit well to the practical decision-making process.

Appendix

The proof of Theorem 3.1

$$\begin{aligned} {\kern 1pt} {\text{CI}}\left( {H^{{\left( {t + 1} \right)}} } \right) & = d\left( {H^{{\left( {t + 1} \right)}} ,\tilde{H}^{{\left( {t + 1} \right)}} } \right) \le d\left( {H^{{\left( {t + 1} \right)}} ,\tilde{H}^{\left( t \right)} } \right) \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left[ \begin{aligned} \ln \left( {\left( {h_{ij}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ - \ln \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) + \ln \left( {\left( {\tilde{h}_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ \end{aligned} \right]^{2} } } } \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left[ \begin{aligned} \left( {1 - \delta } \right)\ln \left( {\left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) + \delta \ln \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ - \left( {1 - \delta } \right)\ln \left( {\left( {h_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) - \delta \ln \left( {\left( {\tilde{h}_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ - \ln \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) + \ln \left( {\left( {\tilde{h}_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ \end{aligned} \right]}^{2} } } \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left[ \begin{aligned} \left( {1 - \delta } \right)\ln \left( {\left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) - \left( {1 - \delta } \right)\ln \left( {\left( {h_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ - \left( {1 - \delta } \right)\ln \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) + \left( {1 - \delta } \right)\ln \left( {\left( {\tilde{h}_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ \end{aligned} \right]}^{2} } } \\ & = \frac{{2\left( {1 - \delta } \right)^{2} }}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left[ \begin{aligned} \ln \left( {\left( {h_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ - \ln \left( {\left( {\tilde{h}_{ij}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) + \ln \left( {\left( {\tilde{h}_{ji}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) \hfill \\ \end{aligned} \right]}^{2} } } \\ & = \left( {1 - \delta } \right)^{2} d\left( {H^{\left( t \right)} ,\tilde{H}^{\left( t \right)} } \right) \le {\text{CI}}\left( {H^{\left( t \right)} } \right) \\ \end{aligned}$$

which completes the proof. Moreover, ${\text{CI}}\left( {H^{\left( t \right)} } \right) \ge 0$, for each t. Thus, the sequence $\left\{ {{\text{CI}}\left( {H^{\left( t \right)} } \right)} \right\}$ is monotonically decreasing and has lower bounds.

The proof of Theorem 3.2

(1) According to Eq. (11), for all $i,j = 1,2, \ldots ,n$, we have

$$\begin{aligned} h_{{ij,{\text{c}}}}^{\sigma \left( s \right)} + h_{{ji,{\text{c}}}}^{\sigma \left( s \right)} & = \frac{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }}{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } + \prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }} \\ & \quad + \;\frac{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }}{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } + \prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }} = 1 \\ \end{aligned}$$

$$\begin{aligned} h_{{ii,{\text{c}}}}^{\sigma \left( s \right)} & = \frac{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ii,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }}{{\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ii,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } + \prod\limits_{k = 1}^{m} {\left( {1 - \bar{h}_{ii,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } }} \\ & = 0.5 \\ \end{aligned}$$

According to Definition 2.4, H _c is a HFPR.

(2) Let $\tilde{H}_{\text{c}} = \left( {\tilde{h}_{{ij,{\text{c}}}} } \right)_{n \times n} = \left( {\left\{ {\left. {\tilde{h}_{{ij,{\text{c}}}}^{\sigma \left( s \right)} } \right|s = 1,2, \ldots ,l} \right\}} \right)_{n \times n}$ be the multiplicative consistent HFPR of $H_{\text{c}} = \left( {h_{{ij,{\text{c}}}} } \right)_{n \times n}$ obtained by Eq. (6), i.e., $\tilde{h}_{{ij,{\text{c}}}}^{\sigma \left( s \right)} = \frac{{\sqrt[n]{{\prod\limits_{k = 1}^{n} {h_{{ik,{\text{c}}}}^{\sigma \left( s \right)} \cdot h_{{kj,{\text{c}}}}^{\sigma \left( s \right)} } }}}}{{\sqrt[n]{{\prod\limits_{k = 1}^{n} {h_{{ik,{\text{c}}}}^{\sigma \left( s \right)} \cdot h_{{kj,{\text{c}}}}^{\sigma \left( s \right)} } }} + \sqrt[n]{{\prod\limits_{k = 1}^{n} {\left( {1 - h_{{ik,{\text{c}}}}^{\sigma \left( s \right)} } \right)\left( {1 - h_{{kj,{\text{c}}}}^{\sigma \left( s \right)} } \right)} }}}}$.

Let $\varepsilon_{ij,k}^{\sigma \left( s \right)} = \ln \left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right) - \ln \left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right) - \ln \left( {\tilde{h}_{ij,k}^{\sigma \left( s \right)} } \right) + \ln \left( {\tilde{h}_{ji,k}^{\sigma \left( s \right)} } \right)$, then we have

$$\begin{aligned} {\text{CI}}\left( {H_{\text{c}} } \right) = d\left( {H_{\text{c}} ,\tilde{H}_{\text{c}} } \right) & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {h_{{ij,{\text{c}}}}^{\sigma \left( s \right)} } \right) - \ln \left( {h_{{ji,{\text{c}}}}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \;\ln \left( {\tilde{h}_{{ij,{\text{c}}}}^{\sigma \left( s \right)} } \right) + \ln \left( {\tilde{h}_{{ji,{\text{c}}}}^{\sigma \left( s \right)} } \right)} \right)^{2} \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } } \right) - \ln \left( {\prod\limits_{k = 1}^{m} {\left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)^{{\lambda_{k} }} } } \right)} \right.} } } \\ & \quad \left. { - \;\ln \left( {\sqrt[n]{{\prod\limits_{t = 1}^{n} {h_{{it,{\text{c}}}}^{\sigma \left( s \right)} \cdot h_{{tj,{\text{c}}}}^{\sigma \left( s \right)} } }}} \right) + \ln \left( {\sqrt[n]{{\prod\limits_{t = 1}^{n} {h_{{jt,{\text{c}}}}^{\sigma \left( s \right)} \cdot h_{{ti,{\text{c}}}}^{\sigma \left( s \right)} } }}} \right)} \right)^{2} \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right) - \sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \;\sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\sqrt[n]{{\prod\limits_{t = 1}^{n} {\bar{h}_{it,k}^{\sigma \left( s \right)} \cdot \bar{h}_{tj,k}^{\sigma \left( s \right)} } }}} \right) + \sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\sqrt[n]{{\prod\limits_{t = 1}^{n} {\bar{h}_{jt,k}^{\sigma \left( s \right)} \cdot \bar{h}_{ti,k}^{\sigma \left( s \right)} } }}} \right)} \right)^{2} \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\bar{h}_{ij,k}^{\sigma \left( s \right)} } \right) - \sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\bar{h}_{ji,k}^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \;\sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\tilde{h}_{ij,k}^{\sigma \left( s \right)} } \right) + \sum\limits_{k = 1}^{m} {\lambda_{k} } \ln \left( {\tilde{h}_{ji,k}^{\sigma \left( s \right)} } \right)} \right)^{2} \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } \varepsilon_{ij,k}^{\sigma \left( s \right)} } \right)^{2} } } } \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\sum\limits_{k = 1}^{m} {\lambda_{k}^{2} } \left( {\varepsilon_{ij,k}^{\sigma \left( s \right)} } \right)^{2} + 2\sum\limits_{p = 1}^{m - 1} {\sum\limits_{q = p + 1}^{m} {\lambda_{p} \lambda_{q} \varepsilon_{ij,p}^{\sigma \left( s \right)} \varepsilon_{ij,q}^{\sigma \left( s \right)} } } } \right)} } } \\ & = \sum\limits_{k = 1}^{m} {\lambda_{k}^{2} } \left[ {\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\varepsilon_{ij,k}^{\sigma \left( s \right)} } \right)^{2} } } } } \right] \\ & \quad + \;2\sum\limits_{p = 1}^{m - 1} {\sum\limits_{q = p + 1}^{m} {\lambda_{p} \lambda_{q} \left[ {\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\varepsilon_{ij,p}^{\sigma \left( s \right)} \varepsilon_{ij,q}^{\sigma \left( s \right)} } } } } \right]} } \\ & \le \sum\limits_{k = 1}^{m} {\lambda_{k}^{2} } \left[ {\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\varepsilon_{ij,k}^{\sigma \left( s \right)} } \right)^{2} } } } } \right] \\ & \quad + \;2\sum\limits_{p = 1}^{m - 1} {\sum\limits_{q = p + 1}^{m} {\lambda_{p} \lambda_{q} \hbox{max} \left\{ {\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\varepsilon_{ij,p}^{\sigma \left( s \right)} } \right)^{2} } } } ,\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\varepsilon_{ij,q}^{\sigma \left( s \right)} } \right)^{2} } } } } \right\}} } \\ & \le \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } } \right)^{2} \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\varepsilon_{ij,k}^{\sigma \left( s \right)} } \right)^{2} } } } } \right\} \\ & = \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {\frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\varepsilon_{ij,k}^{\sigma \left( s \right)} } \right)^{2} } } } } \right\} = \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k} } \right)} \right\} \\ \end{aligned}$$

(3) can be directly derived from (2).

The proof of Theorem 4.1

(1) According to Eqs. (11), (12) and (14), for all $k = 1,2, \ldots ,m$, we have

$$\begin{aligned} {\text{GCI}}\left( {H_{k}^{{\left( {t + 1} \right)}} } \right) & = d\left( {H_{k}^{{\left( {t + 1} \right)}} ,H_{\text{c}}^{{\left( {t + 1} \right)}} } \right) \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \;\ln \left( {\left( {h_{{ij,{\text{c}}}}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) + \ln \left( {\left( {h_{{ji,{\text{c}}}}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right)} \right)^{2} \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \;\sum\limits_{p = 1}^{m} {\lambda_{p} } \ln \left( {\left( {h_{ij,p}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) + \sum\limits_{p = 1}^{m} {\lambda_{p} } \ln \left( {\left( {h_{ji,p}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right)} \right)^{2} \\ & = \frac{2}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\sum\limits_{p = 1}^{m} {\lambda_{p} \left( {\ln \left( {\left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji,k}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right)} \right.} } \right.} } } \\ & \quad \left. {\left. { - \ln \left( {\left( {h_{ij,p}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right) + \ln \left( {\left( {h_{ji,p}^{{\left( {t + 1} \right)}} } \right)^{\sigma \left( s \right)} } \right)} \right)} \right)^{2} \\ & = \frac{{2\left( {1 - \eta } \right)}}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\left( {h_{ij,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \sum\limits_{p = 1}^{m} {\lambda_{p} } \left( {\ln \left( {\left( {h_{ij,p}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)} \right) + \sum\limits_{p = 1}^{m} {\lambda_{p} } \left( {\ln \left( {\left( {h_{ji,p}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)} \right)} \right)^{2} \\ & = \frac{{2\left( {1 - \eta } \right)}}{{n\left( {n - 1} \right)l}}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{l} {\left( {\ln \left( {\left( {h_{ij,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) - \ln \left( {\left( {h_{ji,k}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right)} \right.} } } \\ & \quad \left. { - \ln \left( {\left( {h_{ij,c}^{\left( t \right)} } \right)^{\sigma \left( s \right)} } \right) + \ln \left( {\left( {h_{ji,c}^{\left( t \right)} } \right)} \right)} \right)^{2} \\ & = \left( {1 - \eta } \right){\text{GCI}}\left( {H_{k}^{\left( t \right)} } \right) < {\text{GCI}}\left( {H_{k}^{\left( t \right)} } \right) \\ \end{aligned}$$

(2) Let $\left\{ {H_{k}^{{\left( {t + 1} \right)}} = \left( {h_{ij,k}^{{\left( {t + 1} \right)}} } \right)_{n \times n} } \right\}$ ($k = 1,2, \ldots ,m$) be the HFPR sequence in the iteration t+1 derived by Eq. (14). From Eq. (14), we know that $H_{k}^{{\left( {t + 1} \right)}}$ is the combination of $H_{k}^{\left( t \right)}$ and $H_{\text{c}}^{\left( t \right)}$. According to Theorem 3.2, we have ${\text{CI}}\left( {H_{k}^{{\left( {t + 1} \right)}} } \right) \le \hbox{max} \left\{ {{\text{CI}}\left( {H_{k}^{\left( t \right)} } \right),{\text{CI}}\left( {H_{\text{c}}^{\left( t \right)} } \right)} \right\} \le \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k}^{\left( t \right)} } \right)} \right\}$. Consequently, $\mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k}^{{\left( {t + 1} \right)}} } \right)} \right\} \le \mathop {\hbox{max} }\limits_{1 \le k \le m} \left\{ {{\text{CI}}\left( {H_{k}^{\left( t \right)} } \right)} \right\}$.