Group Multi-criteria Decision Making Method with Triangular Type-2 Fuzzy Numbers

Abstract

Type-2 fuzzy sets/numbers (T2FSs/T2FNs) attract more and more attention in fuzzy decision field. The existing studies mostly focus on the general properties of T2FS, or interval type-2 fuzzy number whose membership degrees are denoted by intervals. A new form of T2FN named triangular type-2 fuzzy number is proposed, whose primary and secondary memberships both have the continuous triangular feature. For aggregating the triangular type-2 fuzzy information, two operators are also defined. Based on them, a method is developed to handle the duplex linguistic group multi-criteria decision making problems and rank the alternatives. Finally, an example is provided to show the feasibility of the method.

1 Introduction

In group multi-criteria decision making (GMCDM) problems, the decision information is usually fuzzy [1] so that explicit decision is difficult due to the limit of knowledge or lack of data. Therefore, handling the fuzziness is important. The fuzzy set theory was developed by Zadeh [2]. A bounded convex fuzzy set with continuous membership function is called a fuzzy number. The fuzzy models became a research focus in multi-criteria decision making (MCDM) [3–5], where the information is denoted by fuzzy numbers or fuzzy sets such as trapezoidal fuzzy numbers [6], intuitionistic fuzzy sets (IFS) [7–9], interval valued intuitionistic fuzzy sets (IVIFS) [10], trapezoidal or triangular intuitionistic fuzzy numbers [11].

Using fuzzy criteria values and weights is the common paradigm of these researches [12–16], where the membership degrees reflect the confidence of the decision maker (DM). But recently, researchers also found such degrees perhaps should also be represented by fuzzy sets, namely the information in MCDM has the type-2 fuzziness.

The so-called T2FS [17] is the fuzzy sets with fuzzy membership degrees. And T2FNs are the fuzzy numbers whose membership degrees denoted by fuzzy sets (or fuzzy numbers). Properties of general T2FS have been studied [18, 19]. Gera and Dombi [20] considered fuzzy truth values. Harding et al. [21]. addressed questions of the variety generated by the algebra of values of T2FS. Hwang et al. [22]. proposed the new similarity, inclusion and entropy measure formulas between T2FS based on the Sugeno integral. Zhai and Mendel [23] generalized five uncertainty measures of interval T2FS.

Many MCDM related type-2 fuzzy studies are found in the literature survey. For example, Hu et al. [24]. considered the MCDM based on the possibility degree of interval T2FN. Dereli et al. [25] reviewed the industrial applications of T2FS. Wu [26] proposed a ranking method and a similarity measure of T2FS for uncertainty linguistic decision problems. Wang [27, 28] used interval type-2 fuzzy number in handling MCDM problems. Akay [29] proposed a decision making method by using fuzzy information axiom and T2FS. Qin [30] introduced T2FS in a generalized DEA model. Ngan [31] studied type-2 linguistic set theory.

We notice that these studies usually use discrete numbers or intervals to denote the membership degrees of T2FS [32–35]. However, it perhaps cannot reflect the DMs’ confidence well. For example, DM believes his/her confidence level (membership degree) is “about 0.5, at least 0.4, and at most 0.6”. Using a discrete set {0.4, 0.5, 0.6} or an interval [0.4, 0.6] are both inadequate. In such case, using a group of triangular fuzzy numbers to denote these continuous fuzzy memberships is more appropriate. Thus, we put forward the notion of triangular type-2 fuzzy number (TT2FN) in this study.

In addition, triangular fuzzy numbers have shown the outstanding applicability, especially in expressing the semantics of linguistic fuzziness [36–38]. In real decision problems, the complex linguistic information like “I am very sure that it is good”, namely the duplex linguistic information [39], is common. It contains the evaluation itself (good), as well as the DM’s confidence degree about it (very sure). But the semantics of this type of linguistic variables is not expressed by fuzzy sets explicitly yet. In fact, the second linguistic variable, which expresses the confidence of DM, denotes the membership of the alternative to the evaluation (the first linguistic variable) from the view of fuzzy sets theory. Obviously, such linguistic membership must involve the fuzzy semantics like the linguistic evaluation itself as well. Naturally, such fuzziness could also be expressed by relative triangular fuzzy number.

Therefore, semantics of such important duplex linguistic variables can be represented by the proposed TT2FN actually. The linguistic evaluation is related to the primary triangular membership function, and the linguistic confidence is related to the secondary triangular membership function. In this way, we can compute and aggregate the duplex linguistic information using TT2FN.

The rest of the paper is organized as follows: in Sect. 2, the definitions related to TT2FN are introduced. In Sect. 3, some aggregation operators are proposed, and a GMCDM method based on the triangular type-2 fuzzy information is discussed. Section 4 is a numerical example. Section 5 is the discussion. Finally, the paper is concluded in Sect. 6.

2 Triangular Type-2 Fuzzy Numbers

2.1 Definition and Operation Rules

A T2FS in a universe set $X$ is an object $\tilde{a} = \left\{ {\left( {\left( {x,u} \right),\gamma_{{\tilde{u}_{x} }} \left( {x,u} \right)} \right)\left| {\forall x \in X,\forall u \in u_{x} \subseteq \left[ {0,1} \right]} \right.,0 \le \gamma_{{\tilde{u}_{x} }} \left( {x,u} \right) \le 1} \right\}$, where $u_{x}$ and $\gamma_{{\tilde{u}_{x} }} \left( {x,u} \right)$ are called the primary and secondary membership, respectively. This object can also be defined as $\tilde{a} = \smallint_{x \in X} \smallint_{{u \in u_{x} }} \gamma_{{\tilde{u}_{x} }} \left( {x,u} \right)/\left( {x,u} \right)$. Particularly, if $\gamma_{{\tilde{u}_{x} }} (x,u) = 1$, then $\tilde{a} = \smallint_{x \in X} \smallint_{{u \in u_{x} }} 1/\left( {x,u} \right)$ is called interval T2FS [40].

Definition 1

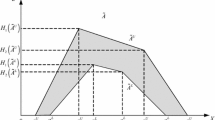
A triangular type-2 fuzzy number (TT2FN) $\tilde{a}$ can be defined as $\tilde{a} = \left\langle {\left[ {a,b,c} \right];\left[ {\mu^{L} ,\mu^{M} ,\mu^{R} } \right]} \right\rangle ,\left( {a \le b \le c,0 \le \mu^{L} \le \mu^{M} \le \mu^{R} \le 1} \right)$, which is illustrated in Fig. 1.

Fig. 1

Triangular type-2 fuzzy number $\tilde{a}$ in $x - \mu - \gamma$ space

Its primary membership function can be defined as

$$\begin{aligned} \mu _{{\tilde{a}}} \left( x \right) & = \left[ {\mu ^{L} \left( x \right),\mu ^{M} \left( x \right),\mu ^{R} \left( x \right)} \right] \\& = \left\{ \begin{array}{*{20}c} {\frac{{x - a}}{{b - a}}\left[ {\mu ^{L} ,\mu ^{M} ,\mu ^{R} } \right],} & {a \le x \le b} \\ {\frac{{c - x}}{{c - b}}\left[ {\mu ^{L} ,\mu ^{M} ,\mu ^{R} } \right],} & {b < x \le c} \\ {0,} & {{\text{others}}} \\ \end{array} \right. \\ \end{aligned}$$

And the secondary membership function can be defined as

$$\begin{aligned} \gamma_{{\tilde{\mu }\left( x \right)}} \left( \mu \right) = \left\{ \begin{array}{ll} \frac{{\mu - \mu^{L} \left( x \right)}}{{\mu^{M} \left( x \right) - \mu^{L} \left( x \right)}},&\quad \mu^{L} \left( x \right) \le \mu \le \mu^{M} \left( x \right) \hfill \\ \frac{{\mu^{R} \left( x \right) - \mu }}{{\mu^{R} \left( x \right) - \mu^{M} \left( x \right)}},&\quad \mu^{M} \left( x \right) < x \le \mu^{R} \left( x \right) \hfill \\ 0,&\quad{\text{others}} \hfill \\ \end{array} \right. \end{aligned}$$

Clearly, there is $0 \le \gamma_{{\tilde{\mu }\left( x \right)}} \le 1$.

Thus, the primary and secondary membership of the elements $x$ and $x^{\prime}$ are shown in Fig. 2.

Fig. 2

The primary and secondary membership of the elements $x$ and $x^{\prime}$

Definition 2

If $\tilde{a}\, = \,\left\langle {\left[ {a,b,c} \right];\left[ {\mu^{L} ,\mu^{M} ,\mu^{R} } \right]} \right\rangle$ is a TT2FN and $a \ge 0$, then $\tilde{a}$ is called a positive triangular type-2 fuzzy number (PTT2FN).

Be similar with [41], the following operation rules are proposed:

Definition 3

Let $\tilde{a}_{1} \, = \,\left\langle {\left[ {a_{1} ,b_{1} ,c_{1} } \right];\left[ {\mu_{1}^{L} ,\mu_{1}^{M} ,\mu_{1}^{R} } \right]} \right\rangle$ and $\tilde{a}_{2} \, = \,\left\langle {\left[ {a_{2} ,b_{2} ,c_{2} } \right];\left[ {\mu_{2}^{L} ,\mu_{2}^{M} ,\mu_{2}^{R} } \right]} \right\rangle$ be two PTT2FNs. The operations of them are:

• (1)
  $$\tilde{a}_{1} + \tilde{a}_{2} \, = \,\left\langle {\left[ {a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} } \right];\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}}} \right]} \right\rangle$$

  where $\left\| {\tilde{a}_{i} } \right\| = \frac{{a_{i} + 2b_{i} + c_{i} }}{4}.$

• (2)
  $$\tilde{a}_{1} - \tilde{a}_{2} \, = \,\left\langle {\left[ {a_{1} - c_{2} ,b_{1} - b_{2} ,c_{1} - a_{2} } \right];\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}}} \right]} \right\rangle$$
• (3)
  $$\lambda \tilde{a}_{1} \, = \,\left\langle {\left[ {\lambda a_{1} ,\lambda b_{1} ,\lambda c_{1} } \right];\left[ {\mu_{1}^{L} ,\mu_{1}^{M} ,\mu_{1}^{R} } \right]} \right\rangle \quad \left( {\lambda \ge 0} \right)$$

Particularly, if $\left\| {\tilde{a}_{1} } \right\| = \left\| {\tilde{a}_{2} } \right\| = 0$, then $\mu_{{\tilde{a}_{1} + \tilde{a}_{2} }} = \frac{{\mu_{{\tilde{a}_{1} }} + \mu_{{\tilde{a}_{2} }} }}{2}$, and $\gamma_{{\tilde{a}_{1} + \tilde{a}_{2} }} = \frac{{\gamma_{{\tilde{a}_{1} }} + \gamma_{{\tilde{a}_{2} }} }}{2}$.

Example 1

Given $\tilde{a}_{1} = \left\langle {\left[ { 7,{ 9},{ 1}0} \right];\left[ {0. 3,0. 5,0. 7} \right]} \right\rangle$, $\tilde{a}_{2} = \left\langle {\left[ { 5,{ 7},{ 9}} \right];\left[ {0. 7,0. 9, 1.0} \right]} \right\rangle$, and λ = 3, there is $\left\| {\tilde{a}_{1} } \right\| = 8. 7 5$ and $\left\| {\tilde{a}_{2} } \right\| = 7$. From Definition 3, there are

• (1)
  $$\tilde{a}_{1} + \tilde{a}_{2} = \left\langle {\left[ {12, \, 16, \, 19} \right];\left[ {0.48,0.68,0.83} \right]} \right\rangle$$
• (2)
  $$\tilde{a}_{1} - \tilde{a}_{2} = \left\langle {\left[ { - 2,2,5} \right];\left[ {0.48,0.68,0.83} \right]} \right\rangle$$
• (3)
  $$\lambda \tilde{a}_{1} = \left\langle {\left[ {21, \, 27, \, 30} \right];\left[ {0.3,0.5,0.7} \right]} \right\rangle$$

Property 1

Let $\tilde{a}_{i} \, = \,\left\langle {\left[ {a_{i} ,b_{i} ,c_{i} } \right];\left[ {\mu_{i}^{L} ,\mu_{i}^{M} ,\mu_{i}^{R} } \right]} \right\rangle$ $(i = 1,2,3)$ be three PTT2FNs, then the operations in Definition 3 have the following properties:

• (1)
  $$\tilde{a}_{1} + \tilde{a}_{2} = \tilde{a}_{2} + \tilde{a}_{1}$$
• (2)
  $$(\tilde{a}_{1} + \tilde{a}_{2} ) + \tilde{a}_{3} = \tilde{a}_{1} + (\tilde{a}_{2} + \tilde{a}_{3} )$$
• (3)
  $$\lambda_{1} \tilde{a}_{1} + \lambda_{2} \tilde{a}_{1} = (\lambda_{1} + \lambda_{2} )\tilde{a}_{1} ,\left( {\lambda_{1} ,\lambda_{2} \ge 0} \right)$$
• (4)
  $$\lambda \tilde{a}_{1} + \lambda \tilde{a}_{2} = \lambda (\tilde{a}_{1} + \tilde{a}_{2} ),\left( {\lambda \ge 0} \right)$$

The proof of property 1 is shown in Appendix.

Property 2

All the operations on PTT2FNs comprise the operations of positive triangular fuzzy numbers, i.e., a positive triangular fuzzy number can be looked as a special PTT2FN with $\mu^{L} = \mu^{M} = \mu^{R} = 1$ and then the operations of positive triangular fuzzy numbers comes:

• (1)
  $$\tilde{a}_{1} + \tilde{a}_{2} = \left[ {a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} } \right]$$
• (2)
  $$\tilde{a}_{1} - \tilde{a}_{2} = \left[ {a_{1} - c_{2} ,b_{1} - b_{2} ,c_{1} - a_{2} } \right]$$
• (3)
  $$\lambda \tilde{a}_{1} = [\lambda a_{1} ,\lambda b_{1} ,\lambda c_{1} ]\begin{array}{*{20}c} {} & {(\lambda \ge 0)} \\ \end{array}$$

2.2 Comparison Rules of TT2FNs

Definition 4

Let $\tilde{a}_{1} \, = \,\left\langle {\left[ {a_{1} ,b_{1} ,c_{1} } \right];\left[ {\mu_{1}^{L} ,\mu_{1}^{M} ,\mu_{1}^{R} } \right]} \right\rangle$ and $\tilde{a}_{2} \, = \,\left\langle {\left[ {a_{2} ,b_{2} ,c_{2} } \right];\left[ {\mu_{2}^{L} ,\mu_{2}^{M} ,\mu_{2}^{R} } \right]} \right\rangle$ be two PTT2FNs, $c_{i} \ge a_{i} \ge 0\,(i = 1,2)$, if $\tilde{a}_{1}$ and $\tilde{a}_{2}$ satisfy $0.5 \le P(\tilde{a}_{1} \ge \tilde{a}_{2} ) \le 1$, then $\tilde{a}_{1} \ge \tilde{a}_{2}$, otherwise $\tilde{a}_{1} < \tilde{a}_{2}$. Where

$$P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,\hbox{max} \left( {\left( {b_{1} + c_{1} } \right)\mu_{1} - \left( {a_{2} + b_{2} } \right)\mu_{2} ,0} \right)} \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }}$$

(1)

is called the probability degree of $\tilde{a}_{1} \ge \tilde{a}_{2}$. And $l_{i} = c_{i} - a_{i}$, $\mu_{i} = \frac{{\mu_{i}^{L} + 2\mu_{i}^{M} + \mu_{i}^{R} }}{4}\quad (i = 1,2)$.

Property 3

In probability degree, there is $0 \le P(\tilde{a}_{1} \ge \tilde{a}_{2} ) \le 1$ and $P(\tilde{a}_{1} \ge \tilde{a}_{1} ) = 0.5$.

Property 4

In probability degree, there is $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1$.

The proofs of Properties 3 and 4 are shown in Appendix.

Supposing that there are $g$ PTT2FNs $\tilde{a}_{i} \, = \,\left\langle {\left[ {a_{i} ,b_{i} ,c_{i} } \right];\left[ {\mu_{i}^{L} ,\mu_{i}^{M} ,\mu_{i}^{R} } \right]} \right\rangle \;(i = 1,2, \ldots ,g)$, then compare each PTT2FN $\tilde{a}_{i}$ with all PTT2FNs $\tilde{a}_{j} (j = 1,2, \ldots ,g)$ using Eq. (1), namely

$$p_{ij} = P\left( {\tilde{a}_{i} \ge \tilde{a}_{j} } \right) = \frac{{\hbox{min} \left\{ {l_{i} \mu_{i} + l_{j} \mu_{j} ,\hbox{max} \left( {\left( {b_{i} + c_{i} } \right)\mu_{i} - \left( {a_{j} + b_{j} } \right)\mu_{j} ,0} \right)} \right\}}}{{l_{i} \mu_{i} + l_{j} \mu_{j} }},$$

where $l_{i} = c_{i} - a_{i}$, $\mu_{i} = \frac{{\mu_{i}^{L} + 2\mu_{i}^{M} + \mu_{i}^{R} }}{4}$ $(i = 1,2, \ldots ,g)$

Then we can construct a complementary fuzzy matrix as follows:

$$P = \left[ {\begin{array}{*{20}l} {p_{11} } \hfill & {\quad p_{12} \, } \hfill & {\quad \cdots } \hfill & {\quad p_{1g} } \hfill \\ {p_{21} } \hfill & {\quad p_{22} \, } \hfill & {\quad \cdots } \hfill & {\quad p_{2g} } \hfill \\ \, \hfill & \, \hfill & {\quad \vdots \, } \hfill & \, \hfill \\ {p_{g1} } \hfill & {\quad p_{g2} \, } \hfill & {\quad \cdots } \hfill & {\quad p_{gg} } \hfill \\ \end{array} } \right],$$

where $p_{ij} \ge 0$, $p_{ij} + p_{ji} = 1$, and $p_{ii} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}$

Theorem 1

According to [19], let $P = (p_{ij} )_{g \times g}$ be a fuzzy complementary matrix, its priority index vector $v$ can be expressed as follows:

$$v = (v_{1} ,v_{2} , \ldots ,v_{n} ),{\text{where }}v_{i} = \frac{1}{g(g - 1)}\left( {\sum\limits_{j = 1}^{g} {p_{ij} + \frac{g}{2} - 1} } \right)$$

(2)

Definition 5

Let $\tilde{a}_{1} \, = \,\left\langle {\left[ {a_{1} ,b_{1} ,c_{1} } \right];\left[ {\mu_{1}^{L} ,\mu_{1}^{M} ,\mu_{1}^{R} } \right]} \right\rangle$ and $\tilde{a}_{2} = \left\langle {\left[ {a_{2} ,b_{2} ,c_{2} } \right];\left[ {\mu_{2}^{L} ,\mu_{2}^{M} ,\mu_{2}^{R} } \right]} \right\rangle$ be two PTT2FNs with the priority indexes $v_{1}$ and $v_{2}$, and then there are:

• (1) if $v_{1} > v_{2}, \quad {\text{then}}\quad \tilde{a}_{1} > \tilde{a}_{2};$

• (2) if $v_{1} = v_{2}, \quad {\text{then}}\quad \tilde{a}_{1} = \tilde{a}_{2};$

• (3) if $v_{1} < v_{2}, \quad {\text{then}}\quad \tilde{a}_{1} < \tilde{a}_{2}.$

Definition 6

Let PTT2FNs $(\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{g} )$ with priority index vector $(v_{1} ,v_{2} , \ldots ,v_{g} )$, then the larger the element of priority index vector is, the larger the PTT2FN is.

Example 2

Let $\tilde{a}_{1} = \left\langle {\left[ {6.4,8.0,9.5} \right];\left[ {0.62,0.8,0.94} \right]} \right\rangle$; $\tilde{a}_{2} \, = \,\left\langle {\left[ {8.7,9.9,10} \right];\left[ {0.6,0.7,0.88} \right]} \right\rangle$; $\tilde{a}_{3} \, = \,\left\langle {\left[ {7.1,8.9,9.9} \right];\left[ {0.6, \, 0.8,0.92} \right]} \right\rangle$ be three PTT2FNs, a fuzzy complementary matrix can be constructed:

$$\left( {\begin{array}{*{20}c} {0.500} & {\quad 0.077} & {\quad 0.254} \\ {0.923} & {\quad 0.500} & {\quad 0.592} \\ {0.746} & {\quad 0.408} & {\quad 0.500} \\ \end{array} } \right)$$

According to the Eq. (2), there are

$$\nu_{1} = \frac{1}{3 \times (3 - 1)}\left( {0.500 + 0.077 + 0.254 + \frac{3}{2} - 1} \right) = 0.223;\,\nu_{2} = 0.419;\nu_{3} = 0.359;\,\nu_{1} < \nu_{3} < \nu_{2}$$

So there is $\tilde{a}_{2} > \tilde{a}_{3} > \tilde{a}_{1}$, the $\tilde{a}_{2}$ is the best one(s).

2.3 Using TT2FNs Represent the Semantics of Duplex Linguistic Variables

Definition 7 [ 42 ]

Let X be a finite universal set. A duplex linguistic set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}$ is an object with the following form:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} = \left\{ {\left( {x, < s_{\theta (x)} ,h_{\sigma (x)} > } \right)|x \in X} \right\},$$

where

$$s_{\theta } :X \to S,\;\;x \mapsto s_{\theta (x)} \in S,h_{\sigma } :X \to H,\;\;x \mapsto h_{\sigma (x)} \in H.$$

S and H are two linguistic ordered scales, $h_{\sigma (x)}$ is the linguistic membership degree of the element $x \in X$ to the linguistic evaluation $s_{\theta (x)}$. The duplex linguistic set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}$ can also be denoted by

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} = \left\{ {\left\langle {s_{\theta (x)} ,h_{\sigma (x)} } \right\rangle |x \in X} \right\}$$

and by $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} \, = \,\left\langle {s_{\theta (x)} ,h_{\sigma (x)} } \right\rangle$ for short if there is only one element $x$.

The semantics of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} \, = \,\left\langle {s_{\theta (x)} ,h_{\sigma (x)} } \right\rangle$ can be represented by PTT2FNs if the linguistic values are translated into triangular fuzzy numbers. That is, if the semantics of $s_{\theta (x)}$ and $h_{\sigma (x)}$ is represented by triangular fuzzy numbers $[a,b,c]$ and $\left[ {\mu^{L} ,\mu^{M} ,\mu^{R} } \right]$ respectively, the semantics of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} \, = \,\left\langle {s_{\theta (x)} ,h_{\sigma (x)} } \right\rangle$ thus represented by the TT2FN $\left\langle {\left[ {a,b,c} \right];\left[ {\mu^{L} ,\mu^{M} ,\mu^{R} } \right]} \right\rangle$.

3 GMCDM Method Based on Triangular Type-2 Fuzzy Averaging Operators

3.1 Operators of Triangular Type-2 Fuzzy Numbers

For aggregating the decision information on different criteria or from different people, weighted arithmetic averaging (WAA) operator and ordered weighted averaging (OWA) operator [43–46] are the most common tools. Thus, triangular type-2 fuzzy WAA and OWA operators are proposed.

Definition 8

Let $\tilde{a}_{i} \, = \,\left\langle {\left[ {a_{i} ,b_{i} ,c_{i} } \right];\left[ {\mu_{i}^{L} ,\mu_{i}^{M} ,\mu_{i}^{R} } \right]} \right\rangle (i = 1,2, \ldots ,n)$ be a group of PTT2FNs, $a_{i}^{{}} \ge 0,\mu_{i}^{R} \le 1$. A mapping ${\text{TT2WAA}}:\varOmega^{n} \to \varOmega^{ + }$, where $\varOmega^{ + }$ is the set of PTT2FNs, such that ${\text{TT2WAA}}\left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right) = \sum\limits_{i = 1}^{n} {\omega_{i} \tilde{a}_{i} }$, where $\omega = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right)^{T}$ is a weight vector which is correlative with $\tilde{a}_{i} (i = 1,2, \ldots ,n)$, satisfying $\omega_{i} \in [0,1]$ $(i = 1, \ldots ,n)$ and $\sum\limits_{i = 1}^{n} {\omega_{i} = 1}$. Then the function ${\text{TT2WAA}}$ is called triangular type-2 fuzzy WAA operator.

Theorem 2

Let PTT2FNs $\tilde{a}_{i} = \left\langle {\left[ {a_{i} ,b_{i} ,c_{i} } \right];\left[ {\mu_{i}^{L} ,\mu_{i}^{M} ,\mu_{i}^{R} } \right]} \right\rangle (i = 1,2, \ldots ,n)$, where $a_{i}^{{}} \ge 0,\mu_{i}^{R} \le 1$. Then

$${\text{TT2WAA}}_{\omega } (\tilde{a}_{i} ) = \left\langle {\left[ {\sum\limits_{i = 1}^{n} {\omega_{i} a_{i}^{{}} } ,\sum\limits_{i = 1}^{n} {\omega_{i} b_{i}^{{}} } ,\sum\limits_{i = 1}^{n} {\omega_{i} c_{i}^{{}} } } \right];\left[ {\frac{{\sum\nolimits_{i = 1}^{n} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|\mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{n} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{n} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|\mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{n} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{n} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|\mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{n} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }}} \right]} \right\rangle$$

(3)

where $\left\| {\tilde{a}_{i} } \right\| = \frac{{a_{i} + 2b_{i} + c_{i} }}{4}$.

The proof is shown in Appendix.

Example 3

There are three PTT2FNs $\tilde{a}_{1} = \left\langle {\left[ {5, \, 7, \, 9} \right];\left[ {0.7,0.9,1.0} \right]} \right\rangle$, $\tilde{a}_{2} = \left\langle {\left[ {7, \, 9, \, 10} \right];\left[ {0.9,1.0,1.0} \right]} \right\rangle$ and $\tilde{a}_{3} = \left\langle {\left[ {5, \, 7, \, 9} \right];\left[ {0.5,0.7,0.9} \right]} \right\rangle$, and $\omega = \left( {0.33,0.34,0.33} \right)$ is the weight vector. Then the aggregation result ${\text{TT2WAA}}_{\omega } (\tilde{a}_{1} ,\tilde{a}_{2} ,\tilde{a}_{3} ) = \left\langle {\left[ {3.43,4.64,5.65} \right];\left[ {0.72,0.88,0.97} \right]} \right\rangle$.

Definition 9

Let $\tilde{a}_{i} = \left\langle {\left[ {a_{i} ,b_{i} ,c_{i} } \right];\left[ {\mu_{i}^{L} ,\mu_{i}^{M} ,\mu_{i}^{R} } \right]} \right\rangle$ be a group of PTT2FNs, $a_{i}^{{}} \ge 0,\mu_{i}^{R} \le 1$. A mapping ${\text{TT2OWA}}:\varOmega^{n} \to \varOmega^{ + }$, where $\varOmega^{ + }$ is the set of PTT2FNs, such that ${\text{TT2OWA}}\left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right) = \sum\limits_{i = 1}^{n} {\varphi_{i} \tilde{b}_{i} }$, where $\varphi = \left( {\varphi_{1} ,\varphi_{2} , \ldots ,\varphi_{n} } \right)^{T}$ is a weight vector which is correlative with ${\text{TT2OWA}}$, satisfying $\varphi_{i} \in [0,1](i = 1,2, \ldots ,n)$ and $\sum\limits_{i = 1}^{n} {\varphi_{i} = 1}$; $\tilde{b}_{i}$ is the $i$-th largest one of all numerical values $\tilde{a}_{s} (s = 1,2, \ldots ,n)$. Then the function ${\text{TT2OWA}}$ is called triangular type-2 fuzzy OWA operator.

Theorem 3

Assume a sequence of PTT2FNs $\tilde{a}_{i} = \left\langle {\left[ {a_{i} ,b_{i} ,c_{i} } \right];\left[ {\mu_{i}^{L} ,\mu_{i}^{M} ,\mu_{i}^{R} } \right]} \right\rangle$, where $a_{i}^{{}} \ge 0,\mu_{i}^{R} \le 1$. $\tilde{b}_{i} = \left\langle {\left[ {a_{\left( i \right)} ,b_{\left( i \right)} ,c_{\left( i \right)} } \right];\left[ {\mu_{{i\tilde{b}_{i} }}^{L} ,\mu_{{i\tilde{b}_{i} }}^{M} ,\mu_{{i\tilde{b}_{i} }}^{R} } \right]} \right\rangle$ is the $i$ th-largest element in $\left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right)$. Then

$${\text{TT2OWA}}_{\varphi } (\tilde{a}_{i} ) = \left\langle {\left[ {\sum\limits_{i = 1}^{n} {\varphi_{i} a_{\left( i \right)}^{{}} } ,\sum\limits_{i = 1}^{n} {\varphi_{i} b_{\left( i \right)}^{{}} } ,\sum\limits_{i = 1}^{n} {\varphi_{i} c_{\left( i \right)}^{{}} } } \right];\left[ {\frac{{\sum\nolimits_{i = 1}^{n} {\varphi_{i} \left\| {\tilde{b}_{i} } \right\|\mu_{{i\tilde{b}_{i} }}^{L} } }}{{\sum\nolimits_{i = 1}^{n} {\varphi_{i} \left\| {\tilde{b}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{n} {\varphi_{i} \left\| {\tilde{b}_{i} } \right\|\mu_{{i\tilde{b}_{i} }}^{M} } }}{{\sum\nolimits_{i = 1}^{n} {\varphi_{i} \left\| {\tilde{b}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{n} {\varphi_{i} \left\| {\tilde{b}_{i} } \right\|\mu_{{i\tilde{b}_{i} }}^{R} } }}{{\sum\nolimits_{i = 1}^{n} {\varphi_{i} \left\| {\tilde{b}_{i} } \right\|} }}} \right]} \right\rangle$$

(4)

where $\left\| {\tilde{a}_{i} } \right\| = \frac{{a_{i} + 2b_{i} + c_{i} }}{4}$.

The proof of Theorem 3 is just like the proof of the Theorem 2, so the detail of the proof is omitted.

Example 4

There are five PTT2FNs $a_{i} :\left\langle {\left[ {3.43,4.64,5.65} \right];\left[ {0.72,0.88,0.97} \right]} \right\rangle ,\left\langle {\left[ {3.36,4.71,5.83} \right];\left[ {0.9,1,1} \right]} \right\rangle ,\left\langle {\left[ {3.54,4.8,5.63} \right];\left[ {0.74,0.92,1} \right]} \right\rangle ,\left\langle {\left[ {5.61,6.5,6.73} \right];\left[ {0.9,1,1} \right]} \right\rangle ,\left\langle{\left[{1.27,2.12,2.97} \right];\left[ {0.43,0.63,0.83} \right]} \right\rangle$, $\omega = \left( {0.2,0.22,0.21,0.22,0.14} \right)$, $S(\tilde{a}_{1} ) = 63.1$; $S(\tilde{a}_{2} ) = 72.6$; $S(\tilde{a}_{3} ) = 67.4$; $S(\tilde{a}_{4} ) = 98.8$; $S(\tilde{a}_{5} ) = 21.5$, $S(\tilde{a}_{4} )\rangle S(\tilde{a}_{2} )\rangle S(\tilde{a}_{3} )\rangle S(\tilde{a}_{1} )\rangle S(\tilde{a}_{5} )$, so ${\text{TT2OWA}}(\tilde{a}_{i} ) = 0.2 \times a_{4} + 0.22 \times a_{2} + 0.21 \times a_{3} + 0.22 \times a_{1} + 0.14 \times a_{5} = \left\langle {\left[ {3.57,4.71,5.52} \right];\left[ {0.8,0.92,0.98}\right]}\right\rangle .$

3.2 GMCDM Method Based on TT2WAA and TT2OWA Operators

Suppose that there are $m$ alternatives $A_{i} (i = 1,2, \ldots ,m)$ and $n$ criteria $C_{j} (j = 1,2, \ldots ,n)$ with the criteria weight vector $\eta = \left( {\eta_{1} ,\eta_{2} , \ldots ,\eta_{n} } \right)^{T}$ where $\eta_{j} \in [0,1]$ and $\sum {\eta = 1}$. There are $g$ DMs in total, whose weight vector is $\beta = (\beta_{1} ,\beta_{2} , \ldots ,\beta_{g} )^{T}$, where $\beta_{l} \in [0,1]$ and $\sum {\beta = 1}$. The judgment information given by the $d$ th DM is $\tilde{X}_{d} = \left( {\tilde{x}_{ij}^{\left( d \right)} } \right)_{m \times n}$, whose elements $\tilde{x}_{ij}^{\left( d \right)} = \left\langle {\left[ {x_{ij}^{\left( d \right)1} ,x_{ij}^{\left( d \right)2} ,x_{ij}^{\left( d \right)3} } \right];\left[ {\mu_{rij}^{\left( d \right)L} ,\mu_{rij}^{\left( d \right)M} ,\mu_{rij}^{\left( d \right)R} } \right]} \right\rangle$ are PTT2FNs. The best alternative is needed to be selected. For solving this problem, the following decision making method is given:

Step 1 If the DM uses different scales to measure the alternatives’ performance on different criteria, we need to transfer these scales into a comparable one by normalizing them. Calculate the normalized decision matrix $\tilde{R}_{d}$ whose element $\tilde{r}_{ij}^{\left( d \right)} = \left\langle {\left[ {r_{ij}^{\left( d \right)1} ,r_{ij}^{\left( d \right)2} ,r_{ij}^{\left( d \right)3} } \right];\left[ {\mu_{rij}^{\left( d \right)L} ,\mu_{rij}^{\left( d \right)M} ,\mu_{rij}^{\left( d \right)R} } \right]} \right\rangle$. The following method is used to obtain these normalized values as $B$ or $C$.

$$\begin{aligned} \hfill \\ \left\{ \begin{aligned} &r_{ij}^{\left( d \right)k} = \frac{{x_{ij}^{\left( d \right)k} - \mathop {\hbox{min} }\limits_{i} x_{ij}^{\left( d \right)1} }}{{\mathop {\hbox{max} }\limits_{i} x_{ij}^{\left( d \right)3} - \mathop {\hbox{min} }\limits_{i} x_{ij}^{\left( d \right)1} }},\quad i = 1,2,\ldots,n,k = 1,2,3.\quad c_{j} \in B \hfill \\ &r_{ij}^{\left( d \right)k} = \frac{{\mathop {\hbox{min} }\limits_{i} x_{ij}^{\left( d \right)1} - x_{ij}^{\left( d \right)k} }}{{\mathop {\hbox{max} }\limits_{i} x_{ij}^{\left( d \right)3} - \mathop {\hbox{min} }\limits_{i} x_{ij}^{\left( d \right)1} }},\quad i = 1,2,\ldots,n,k = 1,2,3.\quad c_{j} \in C \hfill \\ &\mu_{rij}^{(d)s} = \mu_{ij}^{(d)s} ;\quad \quad \quad \quad \quad \quad \quad \;s = L,M,R. \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$

(5)

where $B$ and $C$ are the set of benefit criteria and cost criteria, respectively.

Otherwise, if all the criteria have the same performance scale, then we can simply let $\tilde{R}_{d} = \tilde{X}_{d}$

Step 2 Use ${\text{TT2WAA}}$ operator to aggregate the information from different DMs to get the comprehensive decision matrix $\tilde{R} = \left( {\tilde{r}_{ij} } \right)_{m \times n}$, where $\tilde{r}_{ij}^{{}} = {\text{TT2WAA}}_{\beta } \left( {\tilde{r}_{ij}^{\left( 1 \right)} , \ldots ,\tilde{r}_{ij}^{\left( g \right)} } \right) = \sum\limits_{d = 1}^{g} {\beta_{d} \tilde{r}_{ij}^{\left( d \right)} }$.

Step 3 Aggregate the $i$th row in the comprehensive decision matrix with ${\text{TT2OWA}}$ operator for getting the overall performance of alternative $A_{i}$. $\tilde{z}_{i} = {\text{TT2OWA}}_{\eta } (\tilde{r}_{i1} ,\tilde{r}_{i2} , \ldots ,\tilde{r}_{in} ) = \sum\limits_{j = 1}^{n} {\eta_{j} \tilde{b}_{ij} }$, where $\tilde{b}_{ij}$ is the $j$th largest one of all numerical values $\tilde{r}_{is}^{{}} (s = 1,2, \ldots ,n)$.

Step 4 Rank all the alternatives according to the possibility degree and priority vector of $\tilde{z}_{i}^{{}}$, and then select the best one. Based on the Definition 4, the possibility degree matrix $P = (p_{ij} )_{m \times m}$ is established and the ranking vector $\nu_{i} = (\nu_{1} ,\nu_{2} , \ldots ,\nu_{m} )$ is got according to the Theorem 1. Then the ranking order of all alternatives is in accordance with the decreasing order of $\nu_{i}$.

4 Numerical Example

In this section, an example modified from [47] is employed to illustrate the proposed method. In the example, a software company needs an engineer. There are three candidates $A_{1}$, $A_{2}$ and $A_{3}$. Three decision-makers $d_{1}$, $d_{2}$ and $d_{3}$ interview them. Five benefit criteria are considered:

• (1) emotional steadiness ($C_{1}$),

• (2) oral communication skill ($C_{2}$),

• (3) personality ($C_{3}$),

• (4) past experience ($C_{4}$),

• (5) self-confidence ($C_{5}$).

The weight vector of the criteria is $\eta = \left( {0.2,0.22,0.21,0.22,0.14} \right)$. And the weight vector of the DMs is $\beta = \left( {0.33,0.34,0.33} \right)$. The decision matrixes by three DMs under all criteria are shown in Tables 1, 2 and 3 (modified from [47]). The proposed method is currently applied to solve this problem. The computational procedures are summarized as follows:

Table 1 The fuzzy decision table of three alternatives by DM $d_{1}$

Table 2 The fuzzy decision table of three alternatives by DM $d_{ 2}$

Table 3 The fuzzy decision table of three alternatives by DM $d_{ 3}$

Step 1 Tables 4 and 5 shows the transformation from linguistic values to triangular fuzzy numbers in [47]. Base on it, a transformation from duplex linguistic numbers to PTT2FNs is designed. The decision matrixes with PTT2FNs are shown in Tables 6, 7 and 8.

Table 4 Linguistic variables for the ratings

Table 5 Linguistic variables for the confidence

Table 6 The transformed fuzzy decision table of three alternatives by DM $d_{1}$

Table 7 The transformed fuzzy decision table of three alternatives by DM $d_{ 2}$

Table 8 The transformed fuzzy decision table of three alternatives by DM $d_{ 3}$

Step 2 As there are only benefit criteria and the scale is the same, there is no need to normalize the decision matrixes. Calculate the decision matrixes given by DMs with ${\text{TT2WAA}}$ operator. Then the comprehensive decision matrix shown in Table 9 is got.

Table 9 Comprehensive decision table

Step 3 Calculate the probability degree of the criterion values. Then rank the criteria under every candidate. Aggregate the $i$ th row in the comprehensive decision matrix with ${\text{TT2OWA}}$ operator and then the comprehensive criterion values are got: $\tilde{z}_{1} = \left\langle {\left[ {3.57,4.71,5.52} \right];\left[ {0.8,0.92,0.98} \right]} \right\rangle$; $\tilde{z}_{2} = \left\langle { \left[ {4.94,5.78,6.06} \right];\left[ {0.79,0.92,0.98} \right]} \right\rangle$; $\tilde{z}_{3} = \left\langle { \left[ {4.16,5.2,5.83} \right];\left[ {0.79,0.93,0.98} \right]} \right\rangle$.

Step 4 Rank all the alternatives according to the possibility degree and priority vector, and then select the best one. The possibility degree matrix is established by the definition 4 and the ranking vector $\nu_{i} = (\nu_{1} ,\nu_{2} , \ldots ,\nu_{n} )$ is acquired based on Eq. (2).

$$\left( {\begin{array}{*{20}c} {0.500} & {\quad 0.054} & {\quad 0.233} \\ 1 & {\quad 0.500} & {\quad 0.636} \\ 1 & {\quad 0.283} & {\quad 0.500} \\ \end{array} } \right)$$

$\nu_{1} = 0.215;\nu_{2} = 0.439;\nu_{3} = 0.381.$ $\nu_{2} > \nu_{3} > \nu_{1}$, So there is $A_{2} \succ A_{3} \succ A_{1}$, the most desired one is $A_{2}$.

5 Discussion

From the theoretical point, we get a new form of T2FN, whose primary and secondary memberships both have the continuous triangular feature. Why do we need this somewhat complex fuzzy number? The initial motivation is to handle a common but new type of linguistic information in the fuzzy decision making namely the duplex linguistic information [39]. We represent its semantics by the proposed TT2FNs. The linguistic evaluation is related to the primary triangular membership function, and the linguistic confidence is related to the secondary triangular membership function.

We solve a group decision making problem with triangular type-2 fuzzy information. Since the existing methods cannot solve it, we just can compare the proposed method with other methods from the methodology rather than by computing-results.

The first obvious difference between our method and others of course is in whether the method can handle the triangular type-2 fuzzy information. But is it really important? Can we really encounter such type of information in real decisions? In fact, it is not fabulous. We can relate it with the semantics of duplex linguistic variables at least.

Then, this semantic representation is the second feature of the proposed method. Although duplex linguistic variables are very common and important in fuzzy decisions, their semantics have not been exactly represented by fuzzy sets or other arithmetic materials yet.

There is the study that using an outranking method to solve the duplex linguistic decision problem [39], but our method also has notable differences being compared to it. Firstly, the method in [39] can only handle the problems with single DM, but it cannot solve group decision making problems. Secondly, since it is an order-based method, it can only result in a particular order of alternatives. The proposed method can output a totally order. Thirdly, the proposed method is a parameter-independent method, which needs no additional parameters to get the final result. However, the method of [39] requires some additional parameters to help the DM confirming the outranking relations between alternatives and then ranking them.

6 Conclusion

In general, in real decision problems, information is usually imprecise and uncertainty. A new form of T2FN named triangular type-2 fuzzy number is proposed, whose primary and secondary memberships both have the continuous triangular feature. Its operation rules, aggregation operators and other properties are introduced. Based on TT2WAA and TT2OWA operators, a GMCDM method is proposed.

As a new type of fuzzy number, we believe that the application of TT2FN perhaps is not limited to above mentioned field only. We do not provide more examples to show the potential applications of TT2FN here. Nonetheless, we expect and believe this work can stimulate more interests of relational researchers.

Appendix

The Proof of Property 1

Since the properties (1), (3), (4) are easy to proof, here the property (2) is proofed. As $a_{i} \ge 0$ $\left( {i = 1,2,3} \right)$, from definition 3:

$$\tilde{a}_{1} + \tilde{a}_{2} = \left\langle {\left[ {a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} } \right];\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}}} \right]} \right\rangle$$

Thus,

$$(\tilde{a}_{1} + \tilde{a}_{2} ) + \tilde{a}_{3} = \left\langle {[a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} ];\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu _{2}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu _{2}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu _{2}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}}} \right]} \right\rangle + \left\langle {\left[ {a_{3} ,b_{3} ,c_{3} } \right];\left[ {\mu _{3}^{L} ,\mu _{3}^{M} ,\mu _{3}^{R} } \right]} \right\rangle = \left\langle [(a_{1} + a_{2} ) + a_{3} ,(b_{1} + b_{2} ) + b_{3} ,(c_{1} + c_{2} ) + c_{3} ];\left[\frac{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) \cdot \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{L} }}{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) + \frac{1}{4}(a_{3} + c_{3} + 2b_{3} )}}, \frac{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) \cdot \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{M} }}{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) + \frac{1}{4}(a_{3} + c_{3} + 2b_{3} )}},\frac{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) \cdot \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{R} }}{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) + \frac{1}{4}(a_{3} + c_{3} + 2b_{3} )}}\right] \right\rangle = \left\langle [a_{1} + a_{2} + a_{3} ,b_{1} + b_{2} + b_{3} ,c_{1} + c_{2} + c_{3} ];\left[\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{L} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{M} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}, \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{R} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}\right]\right\rangle$$

Similarly,

$$\begin{aligned} \tilde{a}_{1} + (\tilde{a}_{2} + \tilde{a}_{3} ) &= \left\langle {\left[ {a_{1} ,b_{1} ,c_{1} } \right];\left[ {\mu _{1}^{L} ,\mu _{1}^{M} ,\mu _{1}^{R} } \right]} \right\rangle\,+\,\left\langle {[a_{2} + a_{3} ,b_{2} + b_{3} ,c_{2} + c_{3} ]; \left[ {\frac{{\left\| {\tilde{a}_{2} } \right\|\mu _{2}^{L} + \left\| {\tilde{a}_{3} } \right\|\mu _{3}^{L} }}{{\left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{2} } \right\|\mu _{2}^{M} + \left\| {\tilde{a}_{3} } \right\|\mu _{3}^{M} }}{{\left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{2} } \right\|\mu _{2}^{R} + \left\| {\tilde{a}_{3} } \right\|\mu _{3}^{R} }}{{\left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}} \right]} \right\rangle \\ & = \left\langle {\left[ {a_{1} + a_{2} + a_{3} ,b_{1} + b_{2} + b_{3} ,c_{1} + c_{2} + c_{3} } \right];\left[ \begin{aligned} \frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{{\tilde{a}_{1} }}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu_{{\tilde{a}_{2} }}^{L} + \left\| {\tilde{a}_{3} } \right\|\mu_{{\tilde{a}_{3} }}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{{\tilde{a}_{1} }}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu_{{\tilde{a}_{2} }}^{M} + \left\| {\tilde{a}_{3} } \right\|\mu_{{\tilde{a}_{3} }}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}, \hfill \\ \quad \frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{{\tilde{a}_{1} }}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu_{{\tilde{a}_{2} }}^{R} + \left\| {\tilde{a}_{3} } \right\|\mu_{{\tilde{a}_{3} }}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}} \hfill \\ \end{aligned} \right]} \right\rangle \\ \end{aligned}$$

So $(\tilde{a}_{1} + \tilde{a}_{2} ) + \tilde{a}_{3} = \tilde{a}_{1} + (\tilde{a}_{2} + \tilde{a}_{3} )$.□

The Proof of Property 3

$0 \le P(\tilde{a}_{1} \ge \tilde{a}_{2} ) \le 1$ is easy to proof.

$$\begin{aligned} P(\tilde{a}_{1} \ge \tilde{a}_{1} ) & = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{1} \mu_{1} ,\hbox{max} ((b_{1} + c_{1} )\mu_{1} - (a_{1} + b_{1} )\mu_{1} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{1} \mu_{1} }} \\ & = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{1} \mu_{1} ,\hbox{max} (\mu_{1} l_{1} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{1} \mu_{1} }} = \frac{{l_{1} \mu_{1} }}{{l_{1} \mu_{1} + l_{1} \mu_{1} }} = 0.5. \\ \end{aligned}$$

□

The Proof of Property 4

$$P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,\hbox{max} ((b_{1} + c_{1} )\mu_{1} - (a_{2} + b_{2} )\mu_{2} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }}$$

$$P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,\hbox{max} ((b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }}$$

• (1) If $(b_{1} + c_{1} )\mu_{1} \le (a_{2} + b_{2} )\mu_{2}$, So, $(a_{1} + b_{1} )\mu_{1} \le (b_{1} + c_{1} )\mu_{1} \le (a_{2} + b_{2} )\mu_{2} \le (b_{2} + c_{2} )\mu_{2}$,

  $$P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = 0,$$
  $$\begin{aligned} P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} } \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }} \hfill \\ \quad \quad \quad \quad \,\, = \frac{{\hbox{min} \left\{ {(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} ,(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} } \right\}}}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}. \hfill \\ \end{aligned}$$

  Because $[(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} ] - [(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} ] = (\mu_{1} c_{1} - \mu_{2} a_{2} ) - (\mu_{2} b_{2} - \mu_{1} b_{1} )$, and $(\mu_{1} c_{1} - \mu_{2} a_{2} ) - (\mu_{2} b_{2} - \mu_{1} b_{1} ) = (b_{1} + c_{1} )\mu_{1} - (a_{2} + b_{2} )\mu_{2} \le 0$, so $\mu_{1} c_{1} - \mu_{2} a_{2} \le \mu_{2} b_{2} - \mu_{1} b_{1}$,$(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} \le (b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1}$. That is $P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1$. So $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1.$

• (2) If $(b_{1} + c_{1} )\mu_{1} > (a_{2} + b_{2} )\mu_{2}$, $(b_{2} + c_{2} )\mu_{2} \le (a_{1} + b_{1} )\mu_{1}$, it is the same as 1)

• (3) If $(b_{1} + c_{1} )\mu_{1} > (a_{2} + b_{2} )\mu_{2}$, $(b_{2} + c_{2} )\mu_{2} > (a_{1} + b_{1} )\mu_{1}$, then

  $$\begin{aligned} P(\tilde{a}_{1} \ge \tilde{a}_{2} ) & = \frac{{\hbox{min} \left\{ {(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} ,(b_{1} + c_{1} )\mu_{1} - (a_{2} + b_{2} )\mu_{2} } \right\}}}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }} \\ & = \frac{{\hbox{min} \left\{ {c_{1} \mu_{1} - a_{1} \mu_{1} + c_{2} \mu_{2} - a_{2} \mu_{2} ,b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} } \right\}}}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}. \\ \end{aligned}$$

  Because $(c_{1} \mu_{1} - a_{1} \mu_{1} + c_{2} \mu_{2} - a_{2} \mu_{2} ) - (b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} ) = c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} + b_{2} \mu_{2}$, and $c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} + b_{2} \mu_{2} = (b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} > 0$, so $c_{1} \mu_{1} - a_{1} \mu_{1} + c_{2} \mu_{2} - a_{2} \mu_{2} > b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2}$, that is $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = \frac{{b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}$. There also have $P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = \frac{{(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} }}{{l_{1} \mu_{1} + l_{2} \mu_{2} }} = \frac{{b_{2} \mu_{2} + c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}$, and $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} )$ $= \frac{{b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }} + \frac{{b_{2} \mu_{2} + c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }} = \frac{{c_{1} \mu_{1} - a_{2} \mu_{2} + c_{2} \mu_{2} - a_{1} \mu_{1} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}$ $= 1$. So $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1$. □

The Proof of Theorem 2

Obviously, from definition 3, the sum of PTT2FNs is also a PTT2FN. In the following, equation (2) is proved by using mathematical induction on $n$.

• (1) For $n = 2$, since

  $$\begin{aligned} &\sum\limits_{i = 1}^{2} {\omega_{i} \tilde{a}_{i} } = \langle \left[ {\omega_{1} a_{1} + \omega_{2} a_{2} ,\omega_{1} b_{1} + \omega_{2} b_{2} ,\omega_{1} c_{1} + \omega_{2} c_{2} } \right]; \\ &\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\omega_{1} \mu_{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\omega_{2} \mu_{2}^{L} }}{{\omega_{1} \left\| {\tilde{a}_{1} } \right\| + \omega_{2} \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\omega_{1} \mu_{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\omega_{2} \mu_{2}^{M} }}{{\omega_{1} \left\| {\tilde{a}_{1} } \right\| + \omega_{2} \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\omega_{1} \mu_{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\omega_{2} \mu_{2}^{R} }}{{\omega_{1} \left\| {\tilde{a}_{1} } \right\| + \omega_{2} \left\| {\tilde{a}_{2} } \right\|}}} \right]\rangle \\ \end{aligned}$$

  then the Eq. (2) is clearly true.

• (2) If Eq. (2) holds for $n = k$, that is

  $$\sum\limits_{i = 1}^{k} {\omega_{i} \tilde{a}_{i} = \left\langle {\left[ {\sum\limits_{i = 1}^{k} {\omega_{i} a_{i}^{{}} } ,\sum\limits_{i = 1}^{k} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k} {\omega_{i} c_{i} } } \right];\left[ {\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }}} \right]} \right\rangle }$$

Then, when $n = k + 1$, by the operational laws in Definition 3, there is:

$$\sum\limits_{i = 1}^{k + 1} {\omega_{i} \tilde{a}_{i} } = \sum\limits_{i = 1}^{k} {\omega_{i} \tilde{a}_{i} } + \omega_{k + 1} \tilde{a}_{k + 1} = \left\langle \left[ {\sum\limits_{i = 1}^{k} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k} {\omega_{i} c_{i} } } \right]; \left[ {\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }}} \right] \right\rangle + \left\langle {\left[ {\omega_{k + 1} a_{k + 1} ,\omega_{k + 1} b_{k + 1} ,\omega_{k + 1} c_{k + 1} } \right];\mu_{k + 1}^{L} ,\mu_{k + 1}^{M} ,\mu_{k + 1}^{R} } \right\rangle = \left\langle \left[ {\sum\limits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} ,\sum\limits_{i = 1}^{k} {\omega_{i} b_{i} } + \omega_{k + 1} b_{k + 1} ,\sum\limits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right]; \left[\frac{{\frac{{\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\mu_{i}^{L} } }}{{4\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|} }}\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{L} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} }}, \frac{{\frac{{\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\mu_{i}^{M} } }}{{4\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|} }}\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{M} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} }}, \frac{{\frac{{\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\mu_{i}^{R} } }}{{4\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|} }}\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{R} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} }}\right] \right\rangle = \left\langle \left[\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } \right];\left[\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{L} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} + 2\sum\nolimits_{i = 1}^{k} {\omega_{i} b_{i} } + 2\omega_{k + 1} b_{k + 1} + \sum\nolimits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right)}}, \frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{M} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} + 2\sum\nolimits_{i = 1}^{k} {\omega_{i} b_{i} } + 2\omega_{k + 1} b_{k + 1} + \sum\nolimits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right)}}, \frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{R} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} + 2\sum\nolimits_{i = 1}^{k} {\omega_{i} b_{i} } + 2\omega_{k + 1} b_{k + 1} + \sum\nolimits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right)}}\right] \right\rangle = \left\langle \left[\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } \right];\left[\frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{L} } + \frac{{a_{k + 1} + 2b_{k + 1} + c_{k + 1} }}{4}\omega_{k + 1} \mu_{k + 1}^{L} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} a_{i} } + 2\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} b_{i} } + \sum\nolimits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right)}}, \frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{M} } + \frac{{a_{k + 1} + 2b_{k + 1} + c_{k + 1} }}{4}\omega_{k + 1} \mu_{k + 1}^{M} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} a_{i} } + 2\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} b_{i} } + \sum\nolimits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right)}},\;\frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{R} } + \frac{{a_{k + 1} + 2b_{k + 1} + c_{k + 1} }}{4}\omega_{k + 1} \mu_{k + 1}^{R} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} a_{i} } + 2\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} b_{i} } + \sum\nolimits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right)}}\right] \right\rangle = \left\langle {\left[ {\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right];\frac{{\sum\nolimits_{i = 1}^{k + 1} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }}} \right\rangle = \left\langle {\left[ {\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right];\left[ {\frac{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }}} \right]} \right\rangle.$$

i.e. equation (2) holds for $n = k + 1$.

Therefore, based on (1) and (2), Eq. (2) holds for all $n \in N$, which completes the proof.□