1 Introduction

In various fields, production planning, financial and corporate planning, marketing and media selection, university planning and student admissions, health care and hospital planning, etc. often face problems to take decisions that optimize profit/cost, department/equity ratio, inventory/sales, actual cost/standard cost, output/employee, student/cost, nurse/patient ratio, etc. Such problems can be solved efficiently through linear fractional programming problems (LFPPs). The coefficients of LFPPs are assumed to be exactly known. However, in practice the coefficients (some or all) are not exact due to the errors of measurement or vary with market conditions or some uncontrollable problems (Climate, Traffic, Customers awareness, etc.). In this complex system, it is very common to hesitate the decision makers (DMs) in predicting their aspiration level of objective function as well as the parameters of the problem. In such cases, a DM has to suffer through uncertainty with hesitation. These situations can be modeled efficiently through intuitionistic fuzzy linear fractional programming problems (IFLFPPs).

Many researchers have investigated different kinds of fuzzy linear fractional programming problems (FLFPPs) so far. The FLFPP can be classified into two categories such as LFPP with fuzzy goals and LFPP with fuzzy coefficients. Most of the FLFPPs can be modeled and solved by fuzzy goal programming approach [1–8], but very few authors considered FLFPP where coefficients are fuzzy numbers. Mehra et al. [9] proposed a method to compute an \((\alpha ; \beta )\) acceptable optimal solution where \(\alpha , \beta \in [0, 1]\) are the grades of satisfaction associated with the fuzzy objective function and with the fuzzy constraints, respectively. Pop and Stancu-Minasian [10] analyzed a method to solve the fully fuzzified LFP problem, where all the variables and parameters are represented by triangular fuzzy numbers. Most of the work listed above deal with fuzziness either in the constraint inequalities and/or in the aspiration levels of the DMs. Veeramani and Sumathi [11] proposed a method for solving FLFPP where the cost of the objective function, the resources, and the technological coefficients are triangular fuzzy numbers. To the best of our knowledge, no work has been studied on intuitionistic fuzzy linear fractional programming with intuitionistic fuzzy coefficients. In this paper, we consider the IFLFPP with cost, technological coefficient, and resources are triangular intuitionistic fuzzy numbers. First, the given IFLFPP is transformed into a deterministic multi-objective LFPP (MOLFPP). By using fuzzy mathematical programming approach, the transformed MOLFPP is reduced to a single objective LPP.

The paper is organized as follows: Sect. 2 deals with some definitions from literature [12, 13]. In Sect. 3, we discussed about LFPP with Charnes and Cooper’s transformation and deals with fuzzy mathematical programming approach for solving MOLFPP. In Sect. 4, we have proposed IFLFPP with solution procedure. We have illustrated our methodology by suitable numerical example in Sect. 5 followed by conclusion in Sect. 6.

2 Some Definitions

Definition 1

Let X be a universe of discourse. Then an intuitionistic fuzzy set (IFS) \(\tilde{A}^{I}\) in X is defined by a set of ordered triples \(\tilde{A}^{I}=\{{<x,\mu _{\tilde{A}^{I}}(x),\nu _{\tilde{A}^{I}}(x)>: x\in X}\}\), where \(\mu _{\tilde{A}^{I}},\nu _{\tilde{A}^{I}}:X\rightarrow [0, 1]\) are functions such that \(0 \le \mu _{\tilde{A}^{I}}(x) + \nu _{\tilde{A}^{I}}(x) \le 1, \forall x\in X\). The value \(\mu _{\tilde{A}^{I}}(x)\) represents the degree of membership and \(\nu _{\tilde{A}^{I}}(x)\) represents the degree of non-membership of the element \(x\in X\) being in \(\tilde{A}^{I}\). \(h(x)=1-\mu _{\tilde{A}^{I}}(x) - \nu _{\tilde{A}^{I}}(x)\) is degree of hesitation of the element \(x\in X\) being in \(\tilde{A}^{I}\).

Definition 2

An IFS \(\tilde{A}^{I}=\{{<x,\mu _{\tilde{A}^{I}}(x),\nu _{\tilde{A}^{I}}(x)>: x\in X}\}\) is called an intuitionistic fuzzy number (IFN) if the following hold:

  • There exists \(\ m\in R \) such that \(\mu _{\tilde{A}^{I}}(m)=1\) and \(\nu _{\tilde{A}^{I}}(m)=0\) ( m is called the mean value of \(\tilde{A}^{I}\)),

  • \(\mu _{\tilde{A}^{I}}\) and \(\nu _{\tilde{A}^{I}}\) are piecewise continuous functions from R to the closed interval [0, 1] and \( 0 \le \mu _{\tilde{A}^{I}}(x) + \nu _{\tilde{A}^{I}}(x) \le 1, \forall x\in R\), where

    $$ \mu _{\tilde{A}^{I}}(x)=\left\{ \begin{array}{ll} g_{1}(x), & \quad { m-a\le x<m}\\ 1, & \quad {x=m}\\ h_{1}(x), &\quad {m<x\le m+b }\\ 0, &\quad {\text{otherwise}}, \end{array}\right. $$

    and

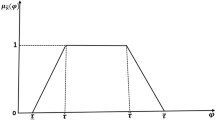
    $$\nu _{\tilde{A}^{I}}(x)=\left\{ \begin{array}{ll} g_{2}(x), & \quad { m-a^{\prime }\le x<m; 0\le g_{1}(x)+g_{2}(x)\le 1} \\ 0, &\quad {x=m}\\ h_{2}(x), & \quad {m<x\le m+b^{\prime }; 0\le h_{1}(x)+h_{2}(x)\le 1} \\ 1, & \quad {\text{otherwise}}. \end{array}\right. $$

    Here m is the mean value of \(\tilde{A}^{I}\); a and b are the left and right spreads of membership function \(\mu _{\tilde{A}^{I}}\), respectively; \(a^{\prime }\) and \(b^{\prime }\) are the left and right spreads of non-membership function \(\nu _{\tilde{A}^{I}}\), respectively; \(g_{1}\) and \(h_{1}\) are piecewise continuous, strictly increasing, and strictly decreasing functions in \([m-a, m)\) and \( (m, m+b]\), respectively; \(g_{2}\) and \(h_{2}\) are piecewise continuous, strictly decreasing, and strictly increasing functions in \([m-a^{\prime }, m]\) and \([m, m+b^{\prime }]\), respectively. The IFN \(\tilde{A}^{I}\) is represented by \(\tilde{A}^{I}=(m; a, b; a^{\prime }, b^{\prime })\).

Definition 3

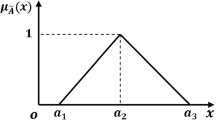
A triangular intuitionistic fuzzy number (TIFN) \(\tilde{A}^{I}\) is an IFN with the membership function \(\mu _{\tilde{A}^{I}}\) and non-membership function \(\nu _{\tilde{A}^{I}}\) given by

$$\mu _{\tilde{A}^{I}}(x)=\left\{ \begin{array}{ll} \dfrac{x-a}{b-a}, & \quad { a< x\le b}\\ 1, &\quad {x=b }\\ \dfrac{c-x}{c-b}, & \quad { b\le x< c}\\ 0, &\quad \text{otherwise}, \end{array}\right. $$

and

$$\nu _{\tilde{A}^{I}}(x)=\left\{ \begin{array}{ll} \dfrac{b-x}{b-a^{\prime }}, & \quad { a^{\prime }< x\le b}\\ 0, & \quad {x=b}\\ \dfrac{x-b}{c^{\prime }-b}, & \quad { b\le x< c^{\prime }}\\ 1, &\quad {\text{otherwise}}, \end{array}\right. $$

where \(a^{\prime }\le a\le b\le c\le c^{\prime }\). This TIFN is denoted by \(\tilde{A}^{I}=(a, b, c;a^{\prime }, b, c^{\prime })\).

Definition 4

Arithmetic operations on TIFNs:

Let \(\tilde{A}^{I}=(a_1, a_2, a_3; a_1^{\prime }, a_2, a_3^{\prime })\) and \(\tilde{B}^{I}=(b_1, b_2, b_3; b_1^{\prime }, b_2, b_3^{\prime }).\)

Addition \(\tilde{A}^{I}\oplus \tilde{B}^{I}=(a_1+b_1, a_2+b_2, a_3+b_3; a_1^{\prime }+b_1^{\prime }, a_2+b_2, a_3^{\prime }+b_3^{\prime }).\)

Subtraction \(\tilde{A}^{I}\ominus \tilde{B}^{I}=(a_1-b_3, a_2-b_2, a_3-b_1; a_1^{\prime }-b_3^{\prime }, a_2-b_2, a_3^{\prime }-b_1^{\prime }).\)

Multiplication \(\tilde{A}^{I}\otimes \tilde{B}^{I}=(l_1, l_2, l_3; l_1^{\prime }, l_2, l_3^{\prime }),\) where \(l_1= \min \{a_1b_1,a_1b_3, a_3b_1, a_3b_3\}, l_3= \max \{a_1b_1,a_1b_3, a_3b_1, a_3b_3\}\)

\(l_1^{\prime }= \min \{a_1^{\prime }b_1^{\prime },a_1^{\prime }b_3^{\prime }, a_3^{\prime }b_1^{\prime }, a_3^{\prime }b_3^{\prime }\}, l_3^{\prime }= \max \{a_1^{\prime }b_1^{\prime },a_1^{\prime }b_3^{\prime }, a_3^{\prime }b_1^{\prime }, a_3^{\prime }b_3^{\prime }\}\), \(l_2=a_2b_2\).

Division \(\tilde{A}^{I}\oslash \,\tilde{B}^{I}=(a_1/b_3, a_2/b_2, a_3/b_1; a_1^{\prime }/b_3^{\prime }, a_2/b_2, a_3^{\prime }/ b_1^{\prime }).\)

Scalar multiplication

  1. 1.

    \(k\tilde{A}^{I}=(ka_1, ka_2, ka_3; ka_1^{\prime }, ka_2, ka_3^{\prime }), k>0.\)

  2. 2.

    \(k\tilde{A}^{I}=(ka_3, ka_2, ka_1; ka_3^{\prime }, ka_2, ka_1^{\prime }), k<0.\)

Definition 5

Ordering of TIFNs: Let \(\tilde{A}^{I}=(a_1, a_2, a_3; a_1^{\prime }, a_2, a_3^{\prime })\) and \(\tilde{B}^{I}=(b_1, b_2, b_3; b_1^{\prime }, b_2, b_3^{\prime })\), and we define the ordering based on the components of TIFNs as follows:

  1. (i)

    \( \tilde{A}^{I}\ge \tilde{B}^{I}\Rightarrow (a_1 \ge b_1, a_2\ge b_2 , a_3\ge b_3; a_1^{\prime }\ge b_1^{\prime }, a_3^{\prime }\ge b_3^{\prime } )\)

  2. (ii)

    \(\tilde{A}^{I}\le \tilde{B}^{I}\Rightarrow (a_1 \le b_1, a_2\le b_2 , a_3\le b_3; a_1^{\prime }\le b_1^{\prime }, a_3^{\prime }\le b_3^{\prime } )\)

  3. (iii)

    \( \tilde{A}^{I}= \tilde{B}^{I}\Rightarrow (a_1 = b_1, a_2 = b_2 , a_3 = b_3; a_1^{\prime }= b_1^{\prime }, a_3^{\prime }= b_3^{\prime } )\)

  4. (iv)

    \(\min (\tilde{A}^{I}, \tilde{B}^{I})=\tilde{A}^{I}\), If \(\tilde{A}^{I}\le \tilde{B}^{I}\) or \(\tilde{B}^{I}\ge \tilde{A}^{I}\)

  5. (v)

    \(\max (\tilde{A}^{I}, \tilde{B}^{I})=\tilde{A}^{I}\), If \(\tilde{A}^{I}\ge \tilde{B}^{I}\) or \(\tilde{B}^{I}\le \tilde{A}^{I}\).

3 Linear Fractional Programming Problem (LFPP)

In this section, the general form of LFPP is discussed. Also, Charnes and Cooper’s [14] linear transformation is summarized. The general LFPP can be written as

$$\begin{aligned}&{\mathrm{Max}} \,Z(x)=\frac{\sum {c_j}x_j+p}{\sum {d_j}x_j+q}=\frac{c^Tx+p}{d^Tx+q}=\frac{N(x)}{D(x)}, \\&{\mathrm{s.t.}}\,x \in S=\{x \in R^n: Ax = b, x \ge 0\},z, \end{aligned}$$
(3.1)

where \(j=1,2,\ldots ,n, A \in R^{m\times n}, b \in R^m, c_j, d_j \in R^n\), and \(p, q \in R.\) For some values of x, D(x) may be zero. To avoid such cases, we require either \(\{AX = b, x \ge 0, D(x)>0\}\) or \(\{Ax = b, x \ge 0, D(x)<0\}.\) For convenience here, we consider the first case, i.e.,

$$ \{Ax = b, x \ge 0, D(x)>0\}. $$
(3.2)

Definition 6

([11]) The two mathematical programming \({\mathrm{(i)}}{\mathrm{Max}} \,F(x), {\mathrm{subject\,to}} \,x\in S \, {\mathrm{and (ii)}} {\mathrm{Max}} \,G(x), {\mathrm{subject\, to}} \,x\in U\) will be said to be equivalent iff there is a one to one map f of the feasible set of (i), onto the feasible set of (ii), such that \(F (x) =G(f (x))\) for all \(x \in S\).

Theorem 1

([14, 15]) Equivalence of LFP and LP. Assume that no point (y, 0) with \(y\ge 0\) is feasible for the following LPP:

$$\begin{aligned}&{\mathrm{Max}}\, c^Ty+pt,\\&{\mathrm{s.t.}}\, d^Ty+qt=1, \\&Ay-bt=0, \\&t \ge 0, y\ge 0, y\in R^n, t\in R. \end{aligned}$$
(3.3)

Now, assume the condition (3.2), i.e., \(\{Ax = b, x \ge 0, D(x)>0\}\) ; then the LFP (3.1) is equivalent to linear program (3.3).

3.1 Concave–Convex Problems

Consider the fractional programming

$$\begin{aligned}&{\mathrm{Max}}\,\frac{N(x)}{D(x)},\\&{\mathrm{s.t.}}\, Ax\le b, x\ge 0, \\&x\in \triangle =\{x: Ax\le b, x\ge 0, D(x)>0\}. \end{aligned}$$
(3.4)

Let us consider the following two related problems:

$$\begin{aligned}&{\mathrm{Max}}\, t N(y/t),\\&{\mathrm{s.t.}} \, A(y/t)- b\le 0, \\&t D(y/t)=1,\\&t>0,y\ge 0, \end{aligned}$$
(3.5)

and

$$\begin{aligned}&{\mathrm{Max}}\, t N(y/t),\\&{\mathrm{s.t.}}\, A(y/t)- b\le 0,\\&t D(y/t)\le 1,\\&t>0,y\ge 0, \end{aligned}$$
(3.6)

where (3.5) is obtained from (3.4) by the transformation \(t=1/D(x),y=tx \) and (3.6) differs from (3.5) by replacing the equality constraint \(tD(y/t)=1\) by an inequality constraint \(tD(y/t)\le 1\).

Definition 7

([15]). The program (3.4) will be said to be standard concave–convex fractional programming problem (SCCFP) if N(x) is concave on \(\triangle \) with \(N(\tau )\ge 0\) for some \(\tau \in \triangle \) and D(x) is convex and positive on \(\triangle \).

Theorem 2

([15]) Let for some \(\tau \in \triangle \), \(N(\tau )\ge 0\), and if (3.4) reaches a (global) maximum at \(x=x^*\) , then (3.6) reaches a (global) maximum at a point \((t, y)=(t^*,y*)\), where \(y^*/t^*=x^*\) and the objective functions at these points are equal.

Theorem 3

([15]) If (3.4) is a SCCFP which reaches a (global) maximum at a point \(x^*\), then the corresponding transformed problem (3.6) attains the same maximum value at a point \((t^*,y^*)\), where \(x^*=y^*/t^*\). Moreover (3.6) has a concave objective function and a convex feasible set.

Instead of this, if in (3.4), N(x) is concave, D(x) is concave and positive on \( \triangle \), and N(x) is negative for each \(x\in \triangle \), then \({\mathrm{Max}}_{x\in \triangle }\frac{N(x)}{D(x)}\Leftrightarrow {\mathrm{Min}}_{x\in \triangle }\frac{-N(x)}{D(x)}\Leftrightarrow {\mathrm{Max}}_{x\in \triangle }\frac{D(x)}{-N(x)}\), where \(-N(x)\) is convex and positive. Now, with the application of Theorem 1 and under the present hypotheses, the fractional program (3.4) transformed to the following LPP:

$$\begin{aligned}&{\mathrm{Max}}\, t D(y/t),\\&{\mathrm{s.t.}}\, A(y/t)- b\le 0,\\&-t N(y/t)\le 1,\\&t>0,y\ge 0. \end{aligned}$$
(3.7)

3.2 Multi-Objective Linear Fractional Programming Problem (MOLFPP)

The general MOLFPP may be written as

$$\begin{aligned}&{\mathrm{Max}} \,Z(x)=[Z_1(x),Z_2(x),\ldots ,Z_K(x)],\\&{\mathrm{s.t.}} \,x\in \triangle =\{x: Ax\le b, x\ge 0\}. \end{aligned}$$
(3.8)

with \(b \in R^m, A \in R^{m\times n}\), and \(Z_i(x)=\frac{c_i x+p_i}{d_i x+q_i}=\frac{N_i(x)}{D_i(x)}, c_i,d_i\in R^n\) and \(p_i,q_i\in R,i=1,2,\ldots , K.\)

Let I be the index set such that \(I=\{i: Ni(x)\ge 0 for \,x\in \triangle \}\) and \(I^c=\{i: Ni(x)<0 for \,x\in \triangle \}\), where \(I\cup I^c=\{1,2,\ldots ,K\}\). Let D(x) be positive on \(\triangle \) where \(\triangle \) is non-empty and bounded. For simplicity, let us take the least value of \(1/(d_i x+q_i)\) and \(1/[-(c_i x+ p_i)]\) is t for \(i\in I\) and \(i\in I^c\), respectively, i.e.,

$$\bigcap _{i\in I} \frac{1}{(d_i x+q_i)}=t \,{\mathrm{and}}\, \bigcap _{i\in I^c} \frac{-1}{(c_i x+ p_i)}=t,$$

which is equivalent to

$$\bigcap \frac{1}{(d_i x+q_i)}\ge t \quad{\mathrm{for}} \,i\in I \,{\mathrm{and}}\, \bigcap \frac{-1}{(c_i x+ p_i)}\ge t \quad{\mathrm{for}} \,i\in I^c.$$
(3.9)

By using the transformation \(y = tx(t > 0)\), Theorems 2 and 3, and using (3.9), MOLFPP (3.8) may be written as follows:

$$\begin{aligned}&{\mathrm{Max}} \,f_i(y,t)=\{t N_i(y/t) \quad {\mathrm{for}}\, i\in I; \\&t D_i(y/t) \quad {\mathrm{for}}\, i\in I^c\}\\&{\mathrm{s.t.}}\, t D_i(y/t)\le 1, \quad {\mathrm{for}} \, i\in \, I,\\&-t N_i(y/t)\le 1, \quad {\mathrm{for} }\, i\in I^c,\\&A(y/t)-b\le 0,\\&t, y\ge 0. \end{aligned}$$
(3.10)

3.2.1 Fuzzy Mathematical Programming Approach for Solving MOLFPP

In an extension of classical linear programming with objective functions represented by fuzzy numbers, the complete solution set (y, t) from well-defined membership function \(\mu _D(y,t) =\bigcap _{i=1}^K\mu _i(y, t)\), Zimmermann [16] proved that if \(\mu _D(y,t)\) has a unique maximum value \(\mu _D(y^*,t^*)={\mathrm{Max}} \mu _D(y,t)\), then \((y^*,t^*)\) which is an element of complete solution set (y, t) can be derived by solving a classical linear programming with one variable \(\lambda \). The complete solution set is composed of all those solution vectors which result \(\mu _D(y,t) > 0\). If no solution vector (y, t) can result \(\mu _D(y,t) > 0\), we say that the complete solution set does not exist [15]. If a complete solution set contains all solutions vectors with \(\mu _D(y,t) > 0\) and if an \((y^*,t^*)\) with the unique \(\mu _D(y^*,t^*)={\mathrm{Max}} \mu _D(y,t)\) exists, it must be included in the complete solution set. If \(i\in I\), then membership function of each objective function can be written as

$$ \mu _i(t N_i(y/t))=\left\{ \begin{array}{lll} 0, & \quad {\mathrm{if}}\;{ t N_i(y/t)\le 0},\\ \frac{t N_i(y/t)}{Z_i}, & \quad {\mathrm{if}}\;{0 \le t N_i(y/t) \le Z_i},\\ 1, & \quad {\mathrm{if}}\; {t N_i(y/t) \ge Z_i}. \end{array}\right. $$
(3.11)

If \(i\in I^c\), then membership function of each objective function can be written as

$$\mu _i(t D_i(y/t))=\left\{ \begin{array}{lll} 0, & \quad {\mathrm{if}}\; { t D_i(y/t)\le 0},\\ \frac{t D_i(y/t)}{Z_i}, & \quad {\mathrm{if}}\;{0 \le t D_i(y/t) \le Z_i},\\ 1, & \quad{ \mathrm{if}}\;{t D_i(y/t) \ge Z_i}. \end{array}\right.$$
(3.12)

Using Zimmermann’s min operator, the model (3.10) transformed to the crisp model as

$$\begin{aligned}&{\mathrm{Max}} \,\lambda ,\\&{\mathrm{s.t.}}\,\mu _i(t N_i(y/t))\ge \lambda \quad {\mathrm{for}}\, i\in I \\&\mu _i(t D_i(y/t))\ge \lambda \quad {\mathrm{for}}\, i\in I^c \\&t D_i(y/t)\le 1, \quad {\mathrm{for}} \, i\in \, I,\\&-t N_i(y/t)\le 1, \quad {\mathrm{for}}\,i\in I^c,\\&A(y/t)-b\le 0,\\&t, y\ge 0. \end{aligned}$$
(3.13)

4 Intuitionistic Fuzzy Linear Fractional Programming Problem (IFLFPP)

In a fractional programming problem, the parameters can be uncertain due to various uncontrollable factors. Also the DM may hesitate in predicting the values of the parameters. Thus, the modeling of the problem constitutes uncertainty with hesitation. Thus, intuitionistic fuzzy parameters are the best candidates to deal such situations. We use TIFNs as parameters in this section. This problem differs from the crisp problem by parametric values. In crisp or non-fuzzy models, the parameters are known exactly, whereas in this section, the parameters are uncertain quantities.

In this section, we develop a procedure for solving IFLFPP where the cost of the objective function, the resources, and the technological coefficients are TIFNs. Let us consider the IFLFPP:

$$\begin{aligned}&{\mathrm{Max}} \,\tilde{Z(x)}^I=\frac{\sum \tilde{c_j}^I x_j\oplus \tilde{p}^I}{\sum \tilde{d_j}^I x_j\oplus \tilde{q}^I}\\&{\mathrm{s.t.}}\, \sum \tilde{a_{ij}}^I x_j\le \tilde{b}_i^I, i=1,2,\ldots ,m,\\&x_j\ge 0, j=1,2,\ldots ,n. \end{aligned}$$
(4.1)

We assume that \(\tilde{c_j}^I, \tilde{p}^I, \tilde{d_j}^I , \tilde{q}^I, \tilde{a_{ij}}^I\) and \(\tilde{b}_i^I\) are TIFNs for each \(i = 1,2,\ldots ,m\) and \(j = 1,2,\ldots , n\). Therefore, the problem (4.1) can be written as

$$\begin{aligned}&{\mathrm{Max}} \,\tilde{Z(x)}^I=\frac{\sum (c_{j1}, c_{j2},c_{j3};c_{j1}^{\prime },c_{j2},c_{j3}^{\prime })x_j\oplus (p_1,p_2,p_3;p_1^{\prime },p_2,p_3^{\prime })}{\sum (d_{j1}, d_{j2},d_{j3};d_{j1}^{\prime },d_{j2},d_{j3}^{\prime }) x_j\oplus (q_1,q_2,q_3;q_1^{\prime },q_2,q_3^{\prime })}\\&{\mathrm{s.t.}} \sum (a_{ij1},a_{ij2},a_{ij3};a_{ij1}^{\prime },a_{ij2},a_{ij3}^{\prime }) x_j\le (b_{i1},b_{i2},b_{i3};b_{i1}^{\prime },b_{i2},b_{i3}^{\prime }), i=1,2,\ldots ,m,\\&x_j\ge 0, j=1,2,\ldots ,n. \end{aligned}$$
(4.2)

Using the concept of componentwise optimization, the problem (4.2) reduces to an equivalent MOLFPP as follows:

$$\begin{aligned}&{\mathrm{Max}} \,Z_1(x)=\frac{\sum c_{j1}x_j+p_1}{\sum d_{j3} x_j+q_3},\\&{\mathrm{Max}} \,Z_2(x)=\frac{\sum c_{j2}x_j+p_2}{\sum d_{j2} x_j+q_2},\\&{\mathrm{Max}} \,Z_3(x)=\frac{\sum c_{j3}x_j+p_3}{\sum d_{j1} x_j+q_1},\\&{\mathrm{Max}} \,Z_4(x)=\frac{\sum c_{j1}^{\prime }x_j+p_1^{\prime }}{\sum d_{j3}^{\prime } x_j+q_3^{\prime }},\\&{\mathrm{Max}} \,Z_5(x)=\frac{\sum c_{j3}^{\prime }x_j+p_3^{\prime }}{\sum d_{j1}^{\prime } x_j+q_1^{\prime }},\\&{\mathrm{s.t.}}\sum a_{ij1}x_j\le b_{i1},\\&\quad\,\sum a_{ij2}x_j\le b_{i2},\\&\quad\,\sum a_{ij3}x_j\le b_{i3},\\&\quad\,\sum a_{ij1}^{\prime }x_j\le b_{i1}^{\prime },\\&\quad\,\sum a_{ij3}^{\prime }x_j\le b_{i3}^{\prime },\\&\quad\,x_j\ge 0, i=1,2,\ldots ,m; j=1,2,\ldots ,n. \end{aligned}$$
(4.3)

Let us assume that \(Z_1, Z_2, Z_3, Z_4\) and  \(Z_5 \ge 0\) for the feasible region. Hence, by using the above procedure, the MOLFPP can be converted into the following MOLPP:

$$\begin{aligned}&{\mathrm{Max}} \,Z_1(y,t)=\sum c_{j1}y_j+p_1 t ,\\&{\mathrm{Max}} \,Z_2(y,t)=\sum c_{j2}y_j+p_2 t,\\&{\mathrm{Max}} \,Z_3(y,t)=\sum c_{j3}y_j+p_3 t ,\\&{\mathrm{Max}} \,Z_4(y,t)=\sum c_{j1}^{\prime }y_j+p_1^{\prime }t ,\\&{\mathrm{Max}} \,Z_5(y,t)=\sum c_{j3}^{\prime }y_j+p_3^{\prime }t,\\&{\mathrm{s.t.}}\sum d_{j3} y_j+q_3 t\le 1,\\&\quad\,\sum d_{j2} y_j+q_2 t\le 1,\\&\quad\,\sum d_{j1} y_j+q_1 t\le 1,\\&\quad\,\sum d_{j3}^{\prime } y_j+q_3^{\prime }t\le 1,\\&\quad\,\sum d_{j1}^{\prime } y_j+q_1^{\prime }t\le 1,\\&\quad\,\sum a_{ij1}y_j- b_{i1} t\le 0,\\&\quad\,\sum a_{ij2}y_j -b_{i2}t \le 0,\\&\quad\,\sum a_{ij3}y_j- b_{i3}t \le 0,\\&\quad\,\sum a_{ij1}^{\prime }y_j- b_{i1}^{\prime }t \le 0,\\&\quad\,\sum a_{ij3}^{\prime }y_j-b_{i3}^{\prime }t \le 0,\\&\quad\,t, y_j\ge 0, i=1,2,\ldots ,m; j=1,2,\ldots ,n. \end{aligned}$$
(4.4)

Solving the transformed MOLPP for each objective function, we obtain \(Z_1^*, Z_2^*, Z_3^*, Z_4^*\), and \(Z_5^*\). Using the membership function defined in (3.11) and (3.12), the above model reduces to

$$\begin{aligned}&{\mathrm{Max}}\, \lambda ,\\&{\mathrm{s.t.}}\sum c_{j1}y_j+p_1 t-Z_1^*\lambda \ge 0,\\&\quad\,\sum c_{j2}y_j+p_2 t-Z_2^*\lambda \ge 0,\\&\quad\,\sum c_{j3}y_j+p_3 t -Z_3^*\lambda \ge 0,\\&\quad\,\sum c_{j1}^{\prime }y_j+p_1^{\prime }t-Z_4^*\lambda \ge 0,\\&\quad\,\sum c_{j3}^{\prime }y_j+p_3^{\prime }t-Z_5^*\lambda \ge 0,\\&\quad\,{\text{and constraints of (4.4).}} \end{aligned}$$
(4.5)

4.1 Algorithm

The proposed approach for solving IFLFPP can be summarized as follows:

Step 1 The IFLFPP is converted into MOLFPP using componentwise optimization of intuitionistic fuzzy numbers.

Step 2 The MOLFPP is transformed into MOLPP using the method proposed by Charnes and Cooper.

Step 3 Maximize each objective function \(Z_i(i=1,2,3,4,5)\), subject to the given set of constraints. Let \(Z_i^*(i=1,2,\ldots ,5)\) be the maximum value of \(Z_i (i=1,2,3,4,5),\) respectively.

Step 4 Examine the nature of \(Z_i^* (i=1,2,3,4,5)\). If \(Z_i^*\ge 0\) (for some i), then \(i \in I\), and if \(Z_i^*< 0\)(for some i), then \(i\in I^c\).

Step 5 If \(i \in I\), then we may assume the maximum aspiration level is \(Z_i^*\) and if \(i \in I^c\), then we may assume the maximum aspiration level is \(-1/Z_i^*\).

Step 6 Using the membership function defined in (3.11) and (3.12), the MOLPP reduces to the crisp model which can be solved using suitable algorithm.

5 Numerical Example

A company manufactures 3 kinds of products \(P_1, P_2\), and \(P_3\) with profit around 8, 7, and 9 dollars per unit, respectively. However, the cost for each one unit of the products is around 8, 9, and 6 dollars, respectively. Also it is assumed that a fixed cost of around 1.5 dollars is added to the cost function due to expected duration through the process of production. Suppose the raw materials needed for manufacturing the products \(P_1, P_2\), and \(P_3\) are about 4, 3, and 5 units per pound, respectively. The supply for this raw material is restricted to about 28 pounds. Man-hours availability for product \(P_1\) is about 5 hours, for product \(P_2\) is about 3 hours, and that for \(P_3\) is about 3 hours in manufacturing per units. Total man-hours availability is around 20 hours daily. Determine how many products of \(P_1, P_2\), and \(P_3\) should be manufactured in order to maximize the total profit. Also during the whole process, the manager hesitates in prediction of parametric values due to some uncontrollable factors.

Let \(x_1, x_2\), and \(x_3\) units be the amount of products \(P_1, P_2\), and \(P_3,\) respectively to be produced. In the problem, all parameters are with fuzziness and hesitation. So, after prediction of estimated parameters, the above problem can be formulated as the following IFLFPP:

$$\begin{aligned}&{\mathrm{Max}}\, \tilde{Z(x)}^I=\frac{\tilde{8}^I x_1+\tilde{7}^I x_2+\tilde{9}^I x_3}{\tilde{8}^I x_1+\tilde{9}^I x_2+\tilde{6}^I x_3+\tilde{1.5}^I},\\&{\mathrm{s.t.}}\, \tilde{4}^I x_1+\tilde{3}^I x_2+\tilde{5}^I x_3\le \tilde{28}^I,\\&\tilde{5}^I x_1+\tilde{3}^I x_2+\tilde{3}^I x_3 \le \tilde{20}^I,\\&x_1, x_2, x_3\ge 0. \end{aligned}$$
(5.1)

with \(\tilde{8}^I=(7,8,9;6,8,10), \tilde{9}^I=(8,9,10;8,9,11), \tilde{7}^I=(6,7,8;5,7,10), \tilde{6}^I=(4,6,8;4,6,8), \tilde{1.5}^I=(1,1.5,2;1,1.5,2.5), \tilde{4}^I=(3,4,5;2,4,6), \tilde{3}^I=(2,3,4;1.5,3,4.5), \tilde{5}^I=(4,5,6;3,5,7), \tilde{28}^I=(25,28,30;24,28,32),\) and \(\tilde{20}^I=(18,20,22;16,20,24)\).

This problem is equivalent to the following MOLFPP:

$$\begin{aligned}&{\mathrm{Max}} \,Z_1(x)=\frac{7x_1+6x_2+8x_3}{9x_1+10x_2+8x_3+2},\\&{\mathrm{Max}} \,Z_2(x)=\frac{8x_1+7x_2+9x_3}{8x_1+9x_2+6x_3+1.5},\\&{\mathrm{Max}} \,Z_3(x)=\frac{9x_1+8x_2+10x_3}{7x_1+8x_2+4x_3+1},\\&{\mathrm{Max}} \,Z_4(x)=\frac{6x_1+5x_2+8x_3}{10x_1+11x_2+8x_3+2.5},\\&{\mathrm{Max}}\, Z_5(x)=\frac{10x_1+10x_2+11x_3}{6x_1+8x_2+4x_3+1},\\&{\mathrm{s.t.}}\, 3x_1+2x_2+4x_3\le 25,\\&\,\quad 4x_1+3x_2+5x_3\le 28,\\&\,\quad 5x_1+4x_2+6x_3\le 30,\\&\,\quad 2x_1+1.5x_2+3x_3\le 24,\\&\,\quad 6x_1+4.5x_2+7x_3\le 32,\\&\,\quad 4x_1+2x_2+2x_3\le 18,\\&\,\quad 5x_1+3x_2+3x_3\le 20,\\&\,\quad 6x_1+4x_2+4x_3\le 22,\\&\,\quad 3x_1+1.5x_2+1.5x_3\le 16,\\&\,\quad 7x_1+4.5x_2+4.5x_3\le 24,\\&\,\quad x_1,x_2,x_3\ge 0. \end{aligned}$$
(5.2)

Using the transformation, the problem (5.2) is equivalent to following MOLPP:

$$\begin{aligned}&{\mathrm{Max}} \,Z_1(y,t)=7y_1+6y_2+8y_3,\\&{\mathrm{Max}} \,Z_2(y,t)=8y_1+7y_2+9y_3,\\&{\mathrm{Max}} \,Z_3(y,t)=9y_1+8y_2+10y_3,\\&{\mathrm{Max}} \,Z_4(y,t)=6y_1+5y_2+8y_3,\\&{\mathrm{Max}} \,Z_5(y,t)=10y_1+10y_2+11y_3,\\&{\mathrm{s.t.}}\, 9y_1+10y_2+8y_3+2t\le 1,\\&\quad \,8y_1+9y_2+6y_3+1.5t\le 1,\\&\quad \,7y_1+8y_2+4y_3+t\le 1,\\&\quad \,10y_1+11y_2+8y_3+2.5t\le 1,\\&\quad \,6y_1+8y_2+4y_3+t\le 1,\\&\quad \,3y_1+2y_2+4y_3- 25t \le 0,\\&\quad \,4y_1+3y_2+5y_3- 28t \le 0,\\&\quad \,5y_1+4y_2+6y_3- 30t \le 0,\\&\quad \,2y_1+1.5y_2+3y_3- 24t \le 0,\\&\quad \,6y_1+4.5y_2+7y_3- 32t \le 0,\\&\quad \,4y_1+2y_2+2y_3- 18t \le 0,\\&\quad \,5y_1+3y_2+3y_3- 20t \le 0,\\&\quad \,6y_1+4y_2+4y_3- 22t \le 0,\\&\quad \,3y_1+1.5y_2+1.5y_3- 16t \le 0,\\&\quad \,7y_1+4.5y_2+4.5y_3- 24t \le 0,\\&\quad \,y_1,y_2,y_3\ge 0, t>0. \end{aligned}$$
(5.3)

Solving each objective at a time, we get \(Z_1=0.9360, Z_2=1.0530, Z_3=1.1700, Z_4=0.9360, Z_5=1.2870\). Now using fuzzy approach, the problem reduced to the following LPP:

$$\begin{aligned}&{\mathrm{Max}} \,\lambda \\&{\mathrm{s.t.}}\, 7y_1+6y_2+8y_3-0.9360\lambda \ge 0,\\&\,\quad 8y_1+7y_2+9y_3-1.0530\lambda \ge 0,\\&\,\quad 9y_1+8y_2+10y_3-1.1600\lambda \ge 0,\\&\,\quad 6y_1+5y_2+8y_3-0.9360\lambda \ge 0,\\&\,\quad 10y_1+10y_2+11y_3-1.2870\lambda \ge 0,\\&\,\quad {\text{and constraints of (5.3)}}. \end{aligned}$$
(5.4)

Solving by LINGO, we have \(y_1=0, y_2=0, y_3=0.1170, \lambda =1, t=0.2559E-01\). The solution of the original problem is obtained as \(x_1=0, x_2=0,x_3=4.57, \tilde{Z}^I=(0.9481, 1.422, 2.370; 0.935, 1.422, 2.607).\)

6 Conclusion

In this paper, a method for solving the IFLFPPs where the cost of the objective function, the resources, and the technological coefficients are TIFNs is proposed. In the proposed method, IFLFPP is transformed to a MOLFPP and the resultant problem is converted to a LP problem, using fuzzy mathematical programming method. In future, the proposed approach can be extended for solving LFPPs, where the cost of the objective function, the resources, and the technological coefficients are trapezoidal intuitionistic fuzzy numbers or non-linear membership functions, and for solving multi-objective IFLFPPs.