1 Introduction

Industrial processes are usually controlled by a conventional PID controller since it is easy to use. However, a PID controller cannot precisely control nonlinear systems. It is better to use modern control techniques for nonlinear systems, but these require a lot of computational time for a real-time system [1, 2]. This also increases the cost of manufacturing in an industrial process. Temperature control problems often involve a time delay and the control method must be easily implemented.

Previously, a robust self-tuning PD-type fuzzy controller (PDFC) has been presented, wherein the fuzzy logic control (FLC) is tuned on-line by modifying the output scaling factor of an existing FLC [3]. This scheme was used to control a wide range of different linear and nonlinear processes. The PD-type FLC is used for the purpose of comparison with the proposed method. For temperature control, Khalid and Omatu compared the performance of a multilayered neural network controller (NNC) to three other different kinds of controllers, in identical conditions [4]. In this control, the weights of the NNC are not kept constant, but are improved on-line by backpropagation of the traveling error. It was demonstrated that NNC can be used for real-time control. In [5], Li and Lee presented a combination of fuzzy logic and a neural network. They used the advantages of fuzzy data representation, fuzzy inference, parallel processing, and learning ability.

Recently, some optimization algorithms have been combined with an FLC to control the termperature of a water bath [6, 7]. A recurrent fuzzy controller (RFC) that uses direct inverse control was proposed in [6]. For the learning algorithm, a particle swarm optimization was used. Because of this effective learning algorithm, three rules are used for the RFC. An ant colony optimization has been proposed for an FLC [7]. Since it takes long time for the particle swarm and ant colony optimization search, this control method is not suitable for a real-time control system. In [8], a self-tuning fuzzy logic control was proposed to control the temperature of the water bath . The input and output scaling factors are tuned using a fuzzy gain scheduling algorithm. The gain-tuning fuzzy logic control (GTFC) partly eliminates the huge design steps required by a conventional FLC, such as manual tuning. Since the water bath temperature control system is a time-delay system, a more easily implemented and more effective control algorithm is worthy of development.

Design of a sliding-mode controller incorporating fuzzy control to achieve reduced chatter and robustness has been discussed for various applications such as a coupled tank system [9], an electroheat system [10], an ecological system [11], electro-hydraulic servo system [12], missile guidance [13], and nonlinear uncertain chaotic system [14]. However, in the fuzzy control system, IF–THEN rules are constructed, based on the qualitative aspects of human knowledge. Creating appropriate fuzzy rules requires time-consuming trial-and-error procedures. To handle this problem, Lian [15, 16] used an adaptive self-organizing fuzzy sliding-mode controller for active suspension and robotic systems where two parameters were considered as input variables of an FLC, instead of only using sliding surface. However, it increases the number of fuzzy rules that leads to computational complexity.

To avoid this problem and enhance the effectiveness, robustness, and simplicity, a self-learning fuzzy sliding-mode controller (SLFSMC) is proposed in this paper to control the temperature of the water bath.

The SLFSMC learns through a rule modifier in which a fuzzy learning algorithm is used to modify the control rules. The modification value of each rule is based on the fuzzy firing weight, so the fuzzy learning algorithm is reasonable and quick. A comparison between the PDFC [3], the GTFC [8] and the proposed SLFSMC for controlling the temperature of the water bath is presented. All of the control inputs and outputs of these three controllers have the same interval and an equal number of linguistic variables, for this comparison.

This paper is organized as follows. Section 2 describes the water bath temperature control system. Section 3 explains the formal structure of the controller design for PDFC, GTFC, and SLFSMC. Section 4 presents the simulation results and the comparison among different control methods. Finally, conclusions are drawn in Sect. 5.

2 Model of the Water Bath Temperature Control System

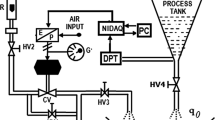
The schematic diagram of the water bath temperature control system is shown in Fig. 1. The water bath is heated by a heater, which is connected to a thyristor circuit. To ensure a uniform distribution of temperature, a stirrer is used. A sensor module is used to sense the temperature and provides a corresponding voltage to an A/D converter. A microprocessor reads the temperature and produces a control signal. The control signal is limited between 0 and 5 V and is used to control the thyristor circuit. The thyristor is then used to switch the heater on and off, depending on the control signal.

Fig. 1
figure 1

Water bath temperature control system

Full size image

The discrete-time water bath temperature control system is described by [5]

$$y\left( {k + 1} \right)\; = \;a\left( {T_{s} } \right)y\left( k \right)\; + \;\frac{{b\left( {T_{s} } \right)}}{{1 + {\text{e}}^{0.5y\left( k \right) - \gamma } }}u\left( k \right)\; + \left[ {1 - a\left( {T_{s} } \right)} \right]y_{0}$$
(1)
$$a\left( {T_{s} } \right) = {\text{e}}^{{ - \alpha \left( {T_{s} } \right)}}$$
(2)
$$b\left( {T_{s} } \right) = \left( {\frac{\beta }{\alpha }} \right)\left( {1 - {\text{e}}^{{ - \alpha \left( {T_{s} } \right)}} } \right),$$
(3)

where k is the discrete-time index, T s the sampling period, and y 0 is the initial temperature of water bath. The system input and output are represented by u(k) and y(k), respectively. The parameters for the plant are α = 1.00151e−4, β = 8.67973e−3, γ = 40 and y 0 = 25 °C [5, 7]. The sampling period is limited to T s  > 10 s. The system contains a saturating nonlinearity, such that the system exhibits a linear characteristic until about 70 °C and becomes nonlinear and then saturates at about 80 °C [8].

3 Design of the Temperature Control System

3.1 Self-learning Fuzzy Sliding-Mode Control System

The proposed SLFSMC consists of two sets of fuzzy inference logic: one for control and the other for rule modification. The temperature tracking error is defined as

$$e\left( k \right) = y_{r} \left( k \right) - y\left( k \right),$$
(4)

where y r (k) is the reference temperature and y(k) is the measured temperature. The change of error is defined as

$${{\Delta }}e\left( k \right) = e\left( k \right) - e\left( {k - 1} \right).$$
(5)

The sliding surface is chosen as the input variable for the fuzzy inference rules, so that the number of the fuzzy control rules can be reduced. The sliding surface is defined by the following scale function:

$$s\left( k \right) = {{\Delta }}e\left( k \right) + \lambda e\left( k \right),$$
(6)

where λ > 0 is a given positive constant value. The SLFSMC water bath temperature control system is shown in Fig. 2a. The fuzzy control rules are as follows:

$$\begin{gathered} {\text{Rule}}\;i:{\text{ IF }}s{\text{ is}}\;F_{s}^{i} \hfill \\ \qquad \qquad \quad {\text{THEN }}u_{{sl\,f\,smc}} \,is\,r_{i} ,\,i = 1,2, \ldots ,n \hfill \\ \end{gathered}$$
(7)
Fig. 2
figure 2

The structure of the three control schemes developed for the water bath temperature control system: a SLFSMC, b PDFC, and c GTFC

Full size image

where \(F_{s}^{i}\) represents the fuzzy set of s and r i is the singleton control action. The defuzzification of the controller output is accomplished using the center-of-gravity method.

$$u_{\text{slfsmc}} \left( {s,r_{i} } \right)\; = \;\frac{{\sum\limits_{i = 1}^{n} {w_{i} \; \times \;r_{i} } }}{{\sum\limits_{i = 1}^{n} {w_{i} } }},$$
(8)

where w i is the firing weight of the ith rule. The defuzzified value u slfsmc, in (8) represents the control effort.

3.1.1 Fuzzy Learning Algorithm

The central part of the iterative learning algorithm for the SLFSMC system changes the control effort in the direction of the negative gradient of a performance index, I, which is defined as a function of e and \({{\Delta }}e\) as [17]

$$I = \mathop \sum \limits_{k = 1}^{m} \sqrt {e^{2} \left( k \right) + \rho \left[ {{{\Delta }}e\left( k \right)} \right]^{2} },$$
(9)

where m is the total number of time intervals and \(\rho \; > \;0\) is the weight factor. The partial derivatives of I with respect to e and \({{\Delta }}e\) are obtained as follows:

$$\frac{\partial I}{\partial e\left( k \right)} = \frac{e\left( k \right)}{{\sqrt {e^{2} \left( k \right) + \rho \left[ {{{\Delta }}e\left( k \right)} \right]^{2} } }}$$
(10)
$$\frac{\partial I}{{\partial {{\Delta }}e\left( k \right)}} = \frac{{\rho {{\Delta }}e\left( k \right)}}{{\sqrt {e^{2} \left( k \right) + \rho \left[ {{{\Delta }}e\left( k \right)} \right]^{2} } }}.$$
(11)

The negative gradient for the optimal performance is expressed as

$$\left. { - \left| {\nabla I} \right| = - \left\{ {\left| {\frac{e\left( k \right)}{{\sqrt {e^{2} \left( k \right)\; + \;\rho \left[ {\Delta e\left( k \right)} \right]^{2} } }}} \right|} \right.\; + \;\rho \left| {\frac{\Delta e\left( k \right)}{{\sqrt {e^{2} \left( k \right) + \rho \left[ {\Delta e\left( k \right)} \right]^{2} } }}} \right|} \right\}.$$
(12)

Depending on the optimal control, the adjust control signal, u slfsmc, is chosen as

$$\delta u_{\text{slfsmc}} \left( k \right) = \eta \left( { - \left| {\nabla I} \right|} \right)\left[ {s\left( k \right)} \right],$$
(13)

where η is a positive learning rate. The fuzzy rules modification algorithm is

$$\Delta r_{i} = \delta u_{\text{slfsmc}} \frac{{w_{i} }}{{\sum \limits_{i = 1}^{n} {w_{i} } }}$$
(14)
$$r_{i} = r_{i} + \Delta r_{i},$$
(15)

where \(\Delta r_{i}\) is the modified value that is added to the ith control rule in (7). Equation (14) shows that the modified value of each control rule is proportional to its firing weight of fuzzy inference.

For comparison, a proportional derivative-type fuzzy logic control (PDFC) system [3] and a GTFC system [8] are also used for the water bath temperature control. These are described in the following.

3.2 Proportional Derivative-Type Fuzzy Logic Control System

The PDFC water bath temperature control system is shown in Fig. 2b. The gains of the inputs and the output are adjusted manually. Because the characteristic of the PDFC depends on G e , G ce, and G u gains, the inputs for this controller are the error (e) and the change of error (\(\Delta e\)). All of the membership functions (MF) in the controller are a Gaussion MF, which is defined over a common interval [−1, 1], and the linguistic variables are quantized into seven fuzzy subsets, from negative big (NB) to positive big (PB), as shown in Fig. 3.

Fig. 3
figure 3

The Gaussian membership function for the fuzzy controller

Full size image

The parameters of the Gaussian membership functions are used with the mean value \(\mu = \left[ { - 1 \; - 0.666 \; - 0.3334 \; 0 \;0.3334\; 0.6666 \;1} \right]\) and the variance value σ = 0.1416.

The fuzzy rules for the PDFC are defined as

$$\begin{aligned} {\text{Rule}}\;i:{\text{ IF}}\;e\;{\text{is}}\;A_{i} \;{\text{and}}\;\Delta e\;{\text{is}}\;B_{i} \hfill \\ {\text{ THEN}}\;u_{\text{PDFC}} \;{\text{is}}\;C_{i} \hfill \\ \end{aligned},$$
(16)

where A i , B i , and C i , i = 1, 2, …, n are the linguistic values of the linguistic variables.

The fuzzy rules are shown in Table 1. Instead of 49 rules, only 25 rules are picked up and formulated [4]. The centroid defuzzification method is used, which allows a lower mean square error.

Table 1 The inference rules for the PDFC
Full size table

3.3 Gain-Tuning Fuzzy Control System

The GTFC water bath temperature control system is shown in Fig. 2c. The GTFC is tuned by a gain scheduling, which uses fuzzy rule bases to produce tuning parameters.

The inputs and output gains of the controller are regulated and modified on-line. The modified value depends on the trend in the controlled process output. In this design, four sets of fuzzy rule bases are constructed. One is for fuzzy control, similar to the PDFC system, but different membership functions and rules are used for the other three. Triangular membership functions are used to tune the inputs and output gains, as shown in Figs. 4a, b, respectively [4]. In both cases, all of the triangular membership functions have the same width and isosceles, with 50 % overlapped, except for the two extreme ends. The extreme ends are rectangular trapezoids.

Fig. 4
figure 4

The triangular membership function for tuning. a input gain and b output gain

Full size image

The fuzzy rules for the gain scheduling are defined as

$$\begin{aligned} {\text{Rule}}\;i:{\text{ IF}}\;e\;{\text{is}}\;A_{i} \;{\text{and}}\;\Delta e\, {\text{is}}\;B_{i} \; {\text{THEN}}\;\hfill \hfill \\ \, G_{e} \;{\text{is}}\;C_{i} {\text{ and}}\,G_{\text{ce}} \,{\text{is}}\;D_{i} \;{\text{and}}\;G_{u} \;{\text{is}}\;E_{i} \end{aligned},$$
(17)

where A i , B i , C i , D i and E i , i = 1, 2, …, n are the linguistic values of the linguistic variables. The centroid defuzzification method is used for the gain scheduling.

The inference rules used to tune the input gains, G e and G ce, are given in Tables 2 and 3, respectively. The inference rules for the input gains, G e and G ce, are opposing, so if PB is replaced by NB, then PS is replaced by NS and so on. The MFs for the output gain, G u , are shown in Table 4. By trial-and-error method, a total of 100 rules are constructed and used for the GTFC, instead of the 196 rules in Tables 1, 2, 3, and 4.

Table 2 The inference rules used to tune the input gain, G e
Full size table
Table 3 The inference rules used to tune the input gain, G ce
Full size table
Table 4 The inference rules used to tune output gain, G u
Full size table

4 Simulation Results

All three algorithms were simulated using the same conditions for the water bath temperature control system. Each simulation was 180 min in duration. The sampling period T s was 25 s. The reference signal was as seen in Table 5. For each control system, the output variable, u(k), is a voltage between 0 and 5 V, which is quantized into six fuzzy singletons: 0.0, 1.0, 2.0, 3.0, 4.0, and 5.0 V [6].

Table 5 The reference signal for the water bath control system
Full size table

A summation of the absolute error (SAE) was calculated and tabulated. The SAE is defined as follows:

$${\text{SAE}} = \mathop \sum \limits_{k = 1}^{180} \left| {y_{r} \left( k \right) - y\left( k \right)} \right|.$$
(18)

In the first set of simulations, the tracking performance of the three control systems was compared. A satisfactory performance for the PDFC was obtained when the input and output gains were G e  = 0.1, G ce = 0.01, and G u  = 450. These three gains were determined by experience and after much trial and error. It was time consuming to tune these parameters manually.

For the GTFC, all of the parameters and design procedures were the same as those in [8]. The initial values of G e and G ce were randomized and G u was set as 450. After tuning, it was observed that G e  = 0.0419, G ce = −0.0419, and G u  = 1.0454.

For the third method, which is the proposed SLFSMC system, the parameters were ρ = 15, λ = 4, and η = 0.01. The initial values of the rules were set to zero, and the rules obtained after training are as shown in Table 6.

Table 6 The trained rules for the SLFSMC system for the water bath plant
Full size table

The simulation results for these three control systems are shown in Fig. 5a–c. It is seen that the SLFSMC system performs better than the other two algorithms. The SLFSMC system also has a considerably lower SAE than the other two methods, with fewer fuzzy rules. A comparison of the SAE values is shown in Table 7.

Fig. 5
figure 5

The performance of the simulated systems (\(T_{s} = 25 \; {\text{s}}\)): a PDFC, b GTFC, and c SLFSMC

Full size image
Table 7 A comparison of the SAE values for the simulated control systems
Full size table

The robustness of SLFSMC was also analyzed by applying disturbances of −5 and +10 °C at 45 and 80 min, respectively.

The proposed SLFSMC quickly counters any disturbance during the process, as shown in Fig. 6. This result also confirms the robustness of the proposed SLFSMC method.

Fig. 6
figure 6

The performance of the proposed SLFSMC system with disturbance

Full size image

The proper sampling time was also verified by setting T s  = 15, 25, and 35 s, as shown in Fig. 7. The best results are for a sampling time of T s  = 25 s. When the sampling time is decreased to 15 s, the system response is slower and when the sampling time is increased to 35 s, the response is faster. However, there is an overshoot, so a sampling time T s  = 25 s is preferable.

Fig. 7
figure 7

Sampling time analysis for the proposed SLFSMC

Full size image

Compared to the other methods shown in [8], the proposed SLFSMC also has the smallest SAE, as shown in Table 8.

Table 8 A comparison of the SAE values for the existing techniques and the proposed approach
Full size table

A simulation to determine the tracking performance of the SLFSMC used the following reference profile:

$$\left\{ \begin{aligned} {\text{Initial condition: }}Y_{0} & = \;25\;^{ \circ } {\text{C}} \\ {\text{Reference}}\;{\text{curve:}} \\ {\text{Temperature}} & = \;\left\{ \begin{array} {ll} 40\;^{\circ } {\text{C,}} & 0\; \le \;\;t\;\; \le { 30}\;{ \text{min} } \\ 30 + {t/3}, & 30 < \;t \;\le \;90\;{\text{min}} \hfill \\ 45 + {t/6}, & 90 < \;t\; \le \;150\;{\text{min}} \\ 70^{\; \circ } {\text{C,}} & 150 < \;t\; \le \;180\;{\text{min}} \\ \end{array} \right. \hfill \\ \end{aligned} \right.$$

The result is shown in Fig. 8. It is seen that the proposed SLFSMC system can also track different trajectories.

Fig. 8
figure 8

The tracking performance for the proposed SLFSMC

Full size image

Initially, the water bath temperature has a large negative error, compared to its reference value, but within 15 s it recovers the trajectory without overshoot. After that, the controller is forced toward the constant reference and then remains at that value. The slope of the reference signal is steep, and the control signal has frequent spikes between the 30th second and the 90th second. Compared with this period for the reference signal, the next period, between the 90th second and the 150th second has a more gradual slope. In this period, the control signal is smooth and has few spikes.

A comparison of computational complexity is given in Table 9. The computation time for the GTFC is longer than that for the other two methods, as it involves many calculations. The computation time for the proposed SLFSMC is very fast, as it involves comparatively fewer logic operations and calculations. This is a desirable characteristic for ease of implementation and cost-effectiveness.

Table 9 A comparison of the computational complexity
Full size table

5 Conclusions

This study proposes an SLFSMC system to control the temperature of a water bath, which is compared with two other control methods. All of these three control schemes use fuzzy logic control. With fuzzy logic control, it is possible to tune rules, membership functions, and gains.

The rules for the proposed method do not have permanent values, so the learning algorithm approaches the reference value more rapidly. The proposed method has a better response, in terms of fitness with the sum of the absolute error. The proposed rule tuning fuzzy control also uses sliding-mode control, which uses a sliding surface to reduce the number of fuzzy rules and reduce the computation loading. Therefore, the SLFSMC can be used for real-time control.