Bayesian Reliability Analysis of Marshall and Olkin Model

Abstract

In this paper, an endeavor has been made to fit three distributions Marshall–Olkin with exponential distributions, Marshall–Olkin with exponentiated exponential distributions and Marshall–Olkin with exponentiated extension distribution keeping in mind the end goal to actualize Bayesian techniques to examine visualization of prognosis of women with breast cancer and demonstrate through utilizing Stan. Stan is an abnormal model dialect for Bayesian displaying and deduction. This model applies to a genuine survival controlled information with the goal that every one of the ideas and calculations will be around similar information. Stan code has been created and enhanced to actualize a censored system all through utilizing Stan technique. Moreover, parallel simulation tools are also implemented and additionally actualized with a broad utilization of rstan.

1 Introduction

Survival analysis is the name for a collection of statistical techniques used to describe and quantify time to event data. In survival analysis we use the term failure to define the occurrence of the event of interest. The term ‘survival time species’ is the length of time taken for failure to occur. Types of studies with survival outcomes include clinical trials, time from birth until death. Survival analysis arises in many fields of study including medicine, biology, engineering, public health, epidemiology and economics. In this paper, an attempt has been made to outline how Bayesian approach proceeds to fit Marshall–Olkin exponential model, Marshall–Olkin exponentiated exponential and Marshall–Olkin exponential extension for lifetime data using Stan. The tools and techniques used in this paper are in Bayesian environment, which are implemented using rstan package [21]. Exponential, Weibull and Gamma are some of the important distributions widely used in reliability theory and survival analysis [19]. But these distributions have a limited range of behavior and cannot represent all situations found in applications. For example; although the exponential distribution is often described as flexible, of the major disadvantages of the exponential distribution is that it has a constant hazard function. The limitations of standard distributions often arouse the interest of researchers in finding new distributions by extending existing ones. The procedure of expanding a family of distributions for added flexibility or constructing covariate models is a well known technique in the literature. For instance the family of Weibull distributions contains exponential distribution and is constructed by taking powers of exponentially distributed random variables. Marshall and Olkin [15] introduced a new method of adding a parameter into a family of distributions. Stan is a probabilistic programming language for specifying statistical models. Bayesian inference is based on the Bayes rule which provides a rational method for updating our beliefs in the light of new information. The Bayes rule states that posterior distribution is the combination of prior and data information. It does not tell us what our beliefs should be, it tells us how they should change after seeing new information. The prior distribution is important in Bayesian inference since it influences the posterior. When no information is available, we need to specify a prior which will not influence the posterior distribution. Such priors are called weakly-informative or non-informative, such as, Normal, Gamma and half-Cauchy prior, this type of priors will be used throughout the paper. The posterior distribution contains all the information needed for Bayesian inference and the objective is to calculate the numeric summaries of it via integration. In cases, where the conjugate family is considered, posterior distribution is available in a closed form and so the required integrals are straightforward to evaluate. However, the posterior is usually of non-standard form, and evaluation of integrals is difficult. For evaluating such integrals, various methods are available such as Laplace’s method (see, for example, [5, 18, 22]) and numerical integration methods of [8]. Simulation can also be used as an alternative technique. Simulation based on Markov chain Monte Carlo (MCMC) is used when it is not possible to sample $\theta$ directly from posterior $p(\theta |y)$ . For a wide class of problems, this is the easiest method to get reliable results [11]. Gibbs sampling, Hamiltonian Monte Carlo and Metropolis–Hastings algorithm are the MCMC techniques which render difficult computational tasks quite feasible. A variant of MCMC techniques are performed such as independence Metropolis, and Metropolis within Gibbs sampling. To make computation easier, software such as R, Stan [full Bayesian inference using the No-U-Turn sampler (NUTS), a variant of Hamiltonian Monte Carlo (HMC)] are used. Bayesian analysis of proposal appropriation has been made with the following objectives:

• To define a Bayesian model, that is, specification of likelihood and prior distribution.

• To write down the R code for approximating posterior densities with Stan.

• To illustrate numeric as well as graphic summaries of the posterior densities.

2 Analysis of Marshall–Olkin Distribution

Marshall and Olkin [15] introduced a new way of incorporating a parameter to expand a family of distributions. Marshall–Olkin distribution as mentioned by Marshall and Olkin [15]

The probability density function (pdf) and cumulative distribution function (cdf) of Marshall–Olkin distribution which are given by (2.1) and (2.2), respectively,

$$\begin{aligned} f(t)&=\frac{bg(t)}{[b+(1-b)G(t)]^2} \end{aligned}$$

(2.1)

$$\begin{aligned} F(t)&=\frac{G(t)}{[b+(1-b)G(t)]} \end{aligned}$$

(2.2)

where g(t) and G(t) are corresponding pdf and cdf of t, respectively.

2.1 The Marshall–Olkin Exponential Distribution

In this section, we introduce a Marshall–Olkin exponential distribution. The pdf, cdf, survival function and hazard function of exponential distribution when $g(t)\sim exp(\theta )$ are given by (2.3), (2.4), (2.5) and (2.6), respectively, as in Fig. 1.

$$\begin{aligned} f(t)&=\frac{b/\theta exp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))]^2} \end{aligned}$$

(2.3)

$$\begin{aligned} F(t)&=\frac{1-exp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))]} \end{aligned}$$

(2.4)

$$\begin{aligned} S(t)&=1-F(t) =\frac{bexp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))]} \end{aligned}$$

(2.5)

$$\begin{aligned} h(t)&=\frac{f(t)}{S(t)} \end{aligned}$$

(2.6)

If $b= 1$, then we obtain exponential distribution with parameter $\theta > 0$.

Fig. 1

Probability density plots, cdf, survival and hazard curves of Marshall–Olkin Exponential Distribution for different values of $\theta$

2.2 The Marshall–Olkin Exponentiated Exponential Distribution

Marshall–Olkin extra shapes parameter to the two-parameter exponentiated exponential distribution. It is observed that the new three-parameter distribution is very flexible. When the pdf, cdf, survival function and hazard function of exponentiated exponential distribution is $g(t)\sim expexp(\theta ,\alpha )$, the results are (2.7), (2.8), (2.9) and (2.10), respectively, as in Fig. 2.

$$\begin{aligned} f(t)&=\frac{b\alpha /\theta (1-exp(-t/\theta ))^{\alpha -1} exp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))^\alpha ]^2} \end{aligned}$$

(2.7)

$$\begin{aligned} F(t)&=\frac{(1-exp(-t/\theta ))^\alpha }{[b+(1-b) (1-exp(-t/\theta ))^\alpha ]}\end{aligned}$$

(2.8)

$$\begin{aligned} S(t)&=\frac{1-(1-exp(-t/\theta )^\alpha }{[1+(1/b-1) (1-exp(-t/\theta ))^\alpha ]}\end{aligned}$$

(2.9)

$$\begin{aligned} h(t)&=\frac{f(t)}{S(t)} \end{aligned}$$

(2.10)

It may be observed that several special cases can be obtained from (2.8). For example, if we set $b = 1$ in (2.8), then we obtain the exponentiated exponential distribution as introduced by Gupta and Kundu [12]. If $\alpha = 1$, we obtain the Marshall–Olkin exponential distribution introduced by Marshall and Olkin [15]. If $\alpha = 1$ and $b = 1$, we obtain the exponential distribution with parameter $\theta$.

Fig. 2

Probability density plots, cdf, survival and hazard curves of Marshall–Olkin exponentiated exponential distribution for different values of b, $\alpha$ and at $\theta = 1$

2.3 The Marshall–Olkin Exponential Extension Distribution

When the pdf, cdf, survival function and hazard function of exponential extension distribution is $g(t)\sim expext(\theta ,\alpha )$, the results are (2.11), (2.12), (2.13) and (2.14), respectively, as in Fig. 3

$$\begin{aligned} f(t)&=\frac{b\alpha /\theta (1+t/\theta )^{\alpha -1} exp(1-(1+t/\theta )^\alpha }{[1-(1-b)exp(1-(1+t/\theta )^\alpha )]^2}\end{aligned}$$

(2.11)

$$\begin{aligned} F(t)&=\frac{1-exp(1-(1+t/\theta )^\alpha )}{1-(1-b) exp(1-(1+t/\theta )^\alpha )}\end{aligned}$$

(2.12)

$$\begin{aligned} S(t)&=1-F(t) =\frac{bexp(1-(1+t/\theta )^\alpha )}{1-(1-b)exp(1-(1+t/\theta )^\alpha )}\end{aligned}$$

(2.13)

$$\begin{aligned} h(t)&=\frac{f(t)}{S(t)} \end{aligned}$$

(2.14)

Fig. 3

Probability density plots, cdf, survival and hazard curves of Marshall–Olkin exponential extension distribution for different values of b, $\alpha$ and at $\theta = 1$

3 Bayesian Inference

Gelman [11] break applied Bayesian modeling into the following three steps:

• 1. Set up a full probability model for all observable and unobservable quantities. This model should be consistent with existing knowledge of the data being modeled and how it was collected.

• 2. Calculate the posterior probability of unknown quantities conditioned on observed quantities. The unknowns may include unobservable quantities such as parameters and potentially observable quantities such as predictions for future observations.

• 3. Evaluate the model fit to the data. This includes evaluating the implications of the posterior.

Typically, this cycle will be repeated until a sufficient fit is achieved in the third step. Stan automates the calculations involved in the second and third steps [6].

We have to specify here the most vital in Bayesian inference which are as per the following:

• prior distribution: $p(\theta )$: The parameter $\theta$ can set a prior distribution elements that using probability as a means of quantifying uncertainty about $\theta$ before taking the data into a count.

• Likelihood $p(y|\theta )$: likelihood function for variables are related in full probability model.

• Posterior distribution $p(\theta |y)$: is the joint posterior distribution that expresses uncertainty about parameter $\theta$ after considering about the prior and the data, as in equation.

  $$\begin{aligned} P(\theta |y)=p(y|\theta )\times p(\theta ) \end{aligned}$$

  (3.1)

4 The Prior Distributions

Section 3, the Bayesian inference has the prior distribution which represents the information about an uncertain parameter $\theta$ that is combined with the probability distribution of data to get the posterior distribution $p(\theta |y)$. For Bayesian paradigm, it is critical to indicate prior information with the value of the specified parameter or information which are obtained before analyzing the experimental data by using a probability distribution function which is called the prior probability distribution (or the prior). In this paper, we use three types of priors which are half-Cauchy prior, Gamma prior and Normal prior. The simplest of all priors is a conjugate prior which makes posterior calculations easy. Also, a conjugate prior distribution for an unknown parameter leads to a posterior distribution for which there is a simple formulae for posterior means and variances. Akhtar and Khan [4] use the half-Cauchy distribution with scale parameter $\alpha = 25$ as a prior distribution for scale parameter.

Hereinafter we will discuss the types of prior distribution:

• Half-Cauchy prior.

• Normal prior.

First, the probability density function of half-Cauchy distribution with scale parameter $\alpha$ is given by

$$\begin{aligned} f(x)=\dfrac{2\alpha }{\pi (x^2+\alpha ^2)} \quad x>0,\alpha >0. \end{aligned}$$

The mean and variance of the half-Cauchy distribution do not exist, but its mode is equal to 0. The half-Cauchy distribution with scale $\alpha =25$ is a recommended, default, weakly informative prior distribution for a scale parameter. At this scale $\alpha =25$, the density of half-Cauchy is nearly flat but not completely (see Fig. 4), prior distributions that are not completely flat provide enough information for the numerical approximation algorithm to continue to explore the target density; the posterior distribution. The inverse-gamma is often used as a non-informative prior distribution for scale parameter, however; this model creates a problem for scale parameters near zero; Gelman et al. [9] recommend that, the uniform, or if more information is necessary, the half-Cauchy is a better choice. Thus, in this paper, the half-Cauchy distribution with scale parameter $\alpha =25$ is used as a weakly informative prior distribution. Second, in the normal (or Gaussian), each parameters is assigned a weak information Gaussian prior probability distribution. In this paper, we use the parameters $\beta _i$ independently in the normal distribution with mean=0 and standard deviation=1000, that is, $\beta _j \sim N(0,1000)$, for this, we obtain a flat prior. From Fig. 4, we see that the large variance indicates a lot of uncertainty about each parameter and hence, a weak informative distribution.

Fig. 4

Half-Cauchy, Gamma and Normal priors

5 Stan Modeling

Stan is a high level language written in a C++ library for Bayesian modeling and [6] is a new Bayesian software program for inference that primarily uses the No-U-Turn sampler (NUTS) [13] to obtain posterior simulations given a user-specified model and data. Hamiltonian Monte Carlo (HMC) is one of the algorithms belonging to the general class of MCMC methods. In practice, HMC can be very complex, because in addition to the specific computation of possibly complex derivatives, it requires fine tuning of several parameters. Hamiltonian Monte Carlo takes a bit of effort to program and tune. In more complicated settings, though, HMC to be faster and more reliable than basic Markov chain simulation, Gibbs sampler and the Metropolis algorithm because they explores the posterior parameter space more efficiently. they do so by pairing each model parameter with a momentum variable, which determines HMC’s exploration behavior of the target distribution based on the posterior density of the current drawn parameter and hence enable HMC to “suppress the random walk behavior in the Metropolis algorithm” [11]. Consequently, Stan is considerably more efficient than the traditional Bayesian software programs. However, the main function in the rstan package is stan, which calls the Stan software program to estimate a specified statistical model, rstan provides a very clever system in which most of the adaptation is automatic. Statistical model through a conditional probability function $p(\theta |y,x)$ can be classified by Stan program, where $\theta$ is a sequence of modeled unknown values, y is a sequence of modeled known values, and x is a sequence of un-modeled predictors and constants (e.g., sizes, hyperparameters) [21]. A Stan program imperatively defines a log probability function over parameters conditioned on specified data and constants. Stan provides full Bayesian inference for continuous-variable models through Markov chain Monte Carlo methods [16], an adjusted form of Hamiltonian Monte Carlo sampling [17]. Stan can be called from R using the rstan package, and through Python using the pystan package. All interfaces support sampling and optimization-based inference with diagnostics and posterior analysis. rstan and pystan also provide access to log probabilities, parameter transforms, and specialized plotting. Stan programs consist of variable type declarations and statements. Variable types include constrained and unconstrained integer, scalar, vector, and matrix types. Variables are declared in blocks corresponding to the variable use: data, transformed data, parameter, transformed parameter, or generated quantities.

6 Bayesian Analysis of Model

Bayesian analysis is the method to obtain the marginal posterior distribution of the particular parameters of interest. In principle, the route to achieving this aim is clear; first, we require the joint posterior distribution of all unknown parameters, then, we integrate this distribution over the unknowns parameters that are not of immediate interest to obtain the desired marginal distribution. Or equivalently, using simulation, we draw samples from the joint posterior distribution, then, we look at the parameters of interest and ignore the values of the other unknown parameters.

6.1 Marshall–Olkin Exponential Model

Now, the probability density function (pdf) is given by

$$\begin{aligned} f(t,b,\theta )=\frac{b/\theta exp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))]^2}. \end{aligned}$$

Also, the survival function is given by

$$\begin{aligned} S(t,b,\theta )=1-F(y) = \frac{bexp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))]}. \end{aligned}$$

We can state the likelihood function for right censored (as is our case the data are right censored)as

$$\begin{aligned} L= & {} {\displaystyle \prod _{i=0}^{n}}Pr(t_i,\delta _i) \\= & {} {\displaystyle \prod _{i=0}^{n}}[f(t_i)]^{\delta _i}[S(t_i)]^{1-\delta _i} \end{aligned}$$

where $\delta _i$ is an indicator variable which takes value 0 if observation is censored and 1 if observation is uncensored. Thus, the likelihood function is given by AbuJarad and Khan [2]

$$\begin{aligned} L={\displaystyle \prod _{i=0}^{n}}\bigg [ \frac{b/\theta exp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))]^2}\bigg ]^{\delta _i} \bigg [\frac{bexp(-t/\theta )}{[b+(1-b)1-exp(-t/\theta )]} \bigg ]^{1-\delta _i}. \end{aligned}$$

(6.1)

Thus, the joint posterior density is given by

$$\begin{aligned}&p(b,\beta |t,X)\propto L(t|X,b,\beta )\times p(\beta )\times p(b) \nonumber \\&\quad \propto {\displaystyle \prod _{i=0}^{n}}\bigg [ \frac{b/e^{X\beta } exp(-t/e^{X\beta })}{[b+(1-b)(1-exp(-t/e^{X\beta }))]^2}\bigg ]^{\delta _i} \bigg [\frac{bexp(-t/e^{X\beta })}{[b+(1-b)1-exp(-t/e^{X\beta })]} \bigg ]^{1-\delta _i}\nonumber \\&\qquad \times {\displaystyle \prod _{i=0}^{J}}\frac{1}{\sqrt{2\pi \times 10^3 }}exp\bigg (-\frac{1}{2}\frac{\beta _{j}^{2}}{10^3}\bigg )\times \frac{2\times 25}{\pi (b^2+25^2)}. \end{aligned}$$

(6.2)

To carry out Bayesian inference in the Marshall–Olkin exponential model, we should determine an prior distribution for b and $\beta 's$. We discussed the issue associated with specifying prior distributions in Sect. 4, but for simplicity at this point, we assume that the prior distribution for b is half-Cauchy on the interval [0, 25] and for $\beta$ is Normal with [0, 1000]. Elementary application of Bayes rule as displayed in (3.1), applied to (6.1), then gives the posterior density for b and $\beta$ as Eq. (6.2). Result for this marginal posterior distribution get high-dimensional integral over all model parameters $\beta _j$ and b. To solve this integral, we employ the approximated using Markov Chain Monte Carlo methods. However, due to the availability of computer software package like rstan, this required model can easily be fitted in Bayesian paradigm using Stan as well as MCMC techniques.

6.2 Marshall–Olkin Exponentiated Exponential Model

Now, the probability density function (pdf) is given by

$$\begin{aligned} f(t,b,\alpha ,\theta )=\frac{b\alpha /\theta (1-exp(-t/\theta ))^{\alpha -1} exp(-t/\theta )}{[b+(1-b)(1-exp(-t/\theta ))^\alpha ]^2}. \end{aligned}$$

Also, the survival function is given by

$$\begin{aligned} S(t,b,\alpha ,\theta )=\frac{1-(1-exp(-t/\theta ))^\alpha }{[1+(1/b-1)(1-exp(-t/\theta ))^\alpha ]}. \end{aligned}$$

In the presence of censoring, the resulting log-likelihood function is modified to account for the possibility of partially observed data (in correspondence with censoring) We can write the likelihood function for right censored (as is our case the data are right censored) as [3]

$$\begin{aligned} L= & {} {\displaystyle \prod _{i=0}^{n}}Pr(t_i,\delta _i) \\= & {} {\displaystyle \prod _{i=0}^{n}}[f(t_i)]^{\delta _i}[S(t_i)]^{1-\delta _i}, \end{aligned}$$

where $\delta _i$ is an indicator variable which takes value 0 if observation is censored and 1 if observation is uncensored. Thus, the likelihood function is given by

$$\begin{aligned} L&={\displaystyle \prod _{i=0}^{n}}\bigg [ \frac{b\alpha /\theta (1-exp(-t/\theta ))^{\alpha -1}exp(-t/\theta )}{[b+(1-b) (1-exp(-t/\theta ))^\alpha ]^2}\bigg ]^{\delta _i} \bigg [\frac{1-(1-exp(-t/\theta ))^\alpha }{[1+(1/b-1) (1-exp(-t/\theta ))^\alpha ]}\bigg ]^{1-\delta _i} . \end{aligned}$$

(6.3)

Thus, the joint posterior density is given by

$$\begin{aligned}&p(\alpha ,\beta ,b|t,X)\propto L(t|X,\alpha ,\beta ,b)\times p(\beta )\times p(\alpha )\times p(b) \nonumber \\&\quad \propto {\displaystyle \prod _{i=0}^{n}}\bigg [ \frac{b\alpha /e^{X\beta } (1-exp(-t/e^{X\beta }))^{\alpha -1} exp(-t/e^{X\beta })}{[b+(1-b)(1-exp(-t/e^{X\beta }))^\alpha ]^2} \bigg ]^{\delta _i} \nonumber \\&\qquad \times \bigg [\frac{1-(1-exp(-t/e^{X\beta }))^\alpha }{[1+(1/b-1) (1-exp(-t/e^{X\beta }))^\alpha ]}\bigg ]^{1-\delta _i}\nonumber \\&\qquad \times {\displaystyle \prod _{i=0}^{J}}\frac{1}{\sqrt{2\pi \times 10^3 }}exp\bigg (-\frac{1}{2}\frac{\beta _{j}^{2}}{10^3}\bigg )\times \frac{2\times 25}{\pi (\alpha ^2+25^2)} \times \frac{2\times 25}{\pi (b^2+25^2)}. \end{aligned}$$

(6.4)

To carry out Bayesian inference in the Marshall–Olkin exponentiated exponential model, we must specify a prior distribution for $\alpha$, b and $\beta 's$. We discussed the issue associated with specifying prior distributions in Sect.  4, but for simplicity at this point, we assume that the prior distribution for $\alpha$ and b is half-Cauchy on the interval [0, 25] and for $\beta$ is Normal with [0, 1000]. Elementary application of Bayes rule as displayed in (3.1), applied to (6.3), then gives the posterior density for $\alpha$, b and $\beta$ as Eq. (6.4). The result for this marginal posterior distribution get high-dimensional integral over all model parameters $\beta _j$, b and $\alpha$. To resolve this integral we use the approximated using Markov chain Monte Carlo methods. However, due to the availability of computer software package like rstan, this required model can easily fit in Bayesian paradigm using Stan as well as MCMC techniques.

6.3 Marshall–Olkin Exponential Extension Model

The probability density function (pdf) given by

$$\begin{aligned} f(t,\alpha ,\theta ,b)=\frac{b\alpha /\theta (1+t/\theta )^{\alpha -1} exp(1-(1+t/\theta )^\alpha }{[1-(1-b)exp(1-(1+t/\theta )^\alpha )]^2}; \end{aligned}$$

The survival function is given by

$$\begin{aligned} S(t,\alpha ,\theta ,b)=\frac{bexp(1-(1+t/\theta )^\alpha )}{1-(1-b) exp(1-(1+t/\theta )^\alpha )}; \end{aligned}$$

We can state the likelihood function for right censored (as is our case the data are right censored) as

$$\begin{aligned} L= & {} {\displaystyle \prod _{i=0}^{n}}Pr(t_i,\delta _i) \\= & {} {\displaystyle \prod _{i=0}^{n}}[f(t_i)]^{\delta _i}[S(t_i)]^{1-\delta _i}, \end{aligned}$$

where $\delta _i$ is an indicator variable which takes value 0 if observation is censored and 1 if observation is uncensored. Thus, the likelihood function is given by

$$\begin{aligned} L&={\displaystyle \prod _{i=0}^{n}}\bigg [ \frac{b\alpha /\theta (1+t/\theta )^{\alpha -1} exp(1-(1+t/\theta )^\alpha }{[1-(1-b) exp(1-(1+t/\theta )^\alpha )]^2}\bigg ]^{\delta _i} \nonumber \\&\quad \bigg [\frac{bexp(1-(1+t/\theta )^\alpha )}{1-(1-b) exp(1-(1+t/\theta )^\alpha )}\bigg ]^{1-\delta _i} . \end{aligned}$$

(6.5)

Thus, the joint posterior density is given by [1]

$$\begin{aligned}&p(\alpha ,\beta ,b|t,X)\propto L(t|X,\alpha ,\beta ,b)\times p(\beta )\times p(\alpha )\times p(b) \nonumber \\&\quad \propto {\displaystyle \prod _{i=0}^{n}}\bigg [ \frac{b\alpha /e^{X\beta } (1+t/e^{X\beta })^{\alpha -1} exp(1-(1+t/e^{X\beta })^\alpha }{[1-(1-b) exp(1-(1+t/e^{X\beta })^\alpha )]^2}\bigg ]^{\delta _i} \nonumber \\&\qquad \times \bigg [\frac{bexp(1-(1+t/e^{X\beta })^\alpha )}{1-(1-b) exp(1-(1+t/e^{X\beta })^\alpha )}\bigg ]^{1-\delta _i}\nonumber \\&\qquad \times {\displaystyle \prod _{i=0}^{J}}\frac{1}{\sqrt{2\pi \times 10^3 }}exp\bigg (-\frac{1}{2}\frac{\beta _{j}^{2}}{10^3}\bigg )\times \frac{2\times 25}{\pi (\alpha ^2+25^2)} \times \frac{2\times 25}{\pi (b^2+25^2)}. \end{aligned}$$

(6.6)

To carry out Bayesian inference in the Marshall–Olkin exponential extension model, we must specify a prior distribution for $\alpha$, b and $\beta 's$. We discussed the issue associated with specifying prior distributions in Sect. 4, but for simplicity at this point, we assume that the prior distribution for $\alpha$ and b is half-Cauchy on the interval [0, 25] and for $\beta$ is Normal with [0, 1000]. Elementary application of Bayes rule as displayed in (3.1), applied to (6.5), then gives the posterior density for $\alpha$, b and $\beta$ as equation (6.6). The result for this marginal posterior distribution get high-dimensional integral over all model parameters $\beta _j$, b and $\alpha$. To resolve this integral we use the approximated using Markov chain Monte Carlo methods. However, due to the availability of computer software package like rstan, this required model can easily fit in Bayesian paradigm using Stan as well as MCMC techniques.

6.4 The Data: Prognosis of Women with Breast Cancer Survival Data

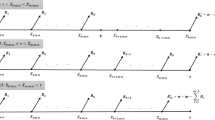
Breast cancer is one of the most common forms of cancer occurring in women living in the Western World. The data given in Table refers to the survival times (in months) of women who had received a simple or radical mastectomy to treat a tumour. The data is carried out at the Middlesex Hospital, and documented in [14] and is also discussed by Collet [7]. In the table, the survival times of each woman are classied according to whether their tumour was positively or negatively stained. Censored survival times are labeled with an asterisk:

Negatively stained: 23, 47, 69, 70*, 71*, 100*, 101*, 148, 181, 198*, 208*, 212*, 224*

Positively stained: 5, 8, 10, 13, 18, 24, 26, 26, 31, 35, 40, 41, 48, 50, 59, 61, 68, 71, 76*, 105*, 107*, 109*, 113, 116*, 118, 143*, 154*, 162*, 188*, 212*, 217*, 225*

7 Implementation Using Stan

Bayesian modeling of Marshall–Olkin models in rstan package includes the creation of blocks, data, transformed data, parameter, transformed parameter, or generated quantities. To use the method for Marshall–Olkin exponential model, Marshall–Olkin exponentiated exponential, and Marshall–Olkin exponential extension, we will follow the following steps; starting with build a function for the model containing the accompanying items:

• Define the log survival.

• Define the log hazard.

• Define the sampling distributions for right censored data.

At that point the distribution ought to be built on the function definition blocks. The function definition block contains user defined functions. The data block states the needed data for the model. The transformed data block permits the definition of constants and transforms of the data. The parameters block declares the model’s parameters. The transformed parameters block allows variables to be defined in terms of data and parameters that may be used later and will be saved. The model block is where the log probability function is defined.

file A stands for character string file name or a connection that R supports containing the text of a model specification in the Stan modeling language; a model may also be specified directly as a character string using parameter model_code, or through a previous fit using parameter fit. When fit is specified, the parameter file is ignored. model_name A is a character string naming the model; defaults to anon_model. However, the model name would be drawn from file or model_code (if model_code is the name of a character string object) if model_name is not specified. model_code A is a character string either containing the model definition or the name of a character string object in the workspace. This parameter is used only if parameter file is not specified. When fit is specified and the previously compiled model is used, we can ignor so specifying model_code. data A is a named list or environment providing the data for the model, or a character vector for all the names of objects used as data. pars A is a vector of character strings specifying parameters of interest. The default is NA indicating all parameters in the model. If include = TRUE, only samples for parameters named in pars are stored in the fitted results. Conversely, if include = FALSE, samples for all parameters except those named in pars are stored in the fitted results. chains A is a positive integer specifying the number of Markov chains. iter A is a positive integer specifying the number of iterations for each chain (including warmup). warmup A is a positive integer specifying the number of warmup (aka burnin) iterations per chain. As step-size adaptation is on (which it is by default), this controls the number of iterations for which adaptation is run (and hence these warmup samples should not be used for inference). The number of warmup iterations should not be larger than iter and the default is iter/2. thin A is a positive integer specifying the period for saving samples. The default is 1, which is usually the recommended value. init can be the digit 0, the strings 0 or random, a function that returns a named list, or a list of named lists [20].

7.1 Model Specification

Now we will examine the posterior estimates of the parameters when the Marshall–Olkin exponential, Marshall–Olkin exponentiated exponential and Marshall–Olkin exponential extension model’s are fitted to the above mentioned information (data). Thus the meaning of the probability (likelihood) becomes the topmost necessity for the Bayesian fitting. Here, we have likelihood as:

$$\begin{aligned} L(\theta |t)= & {} \prod \limits _{i=1}^{n}f(t_i)^{\delta _i}S(t_i)^{1-\delta _i} \\= & {} \prod \limits _{i=1}^{n}\bigg (\frac{f(t_i)}{S(t_i)}^{\delta _i}S(t_i)\bigg ) \\= & {} \prod \limits _{i=1}^{n}h(t_i)^{\delta _i}S(t_i), \end{aligned}$$

this way, our log-likelihood progresses toward becoming

$$\begin{aligned} log L= {\sum }_{i=i}^{n}\bigg (log\bigg [h(t_i)\bigg ]^{\delta _i}+log(S_t)\bigg ). \end{aligned}$$

7.1.1 Marshall–Olkin Exponential Model

The first model is Marshall–Olkin exponential :

$$\begin{aligned} y\sim MOexp(\theta ,b), \end{aligned}$$

where $\theta =exp(X\beta )$ is a linear combination of explanatory variables, log is the natural log for the time to failure event. The Bayesian system requires the determination and specification of prior distributions for the parameters. Here, we stick to subjectivity and thus introduce weakly informative priors for the parameters. Priors for the $\beta$ and $\alpha$ are taken to be normal and half-Cauchy as follows:

$$\begin{aligned} \beta _j&\sim N(0,1000);\quad j=1,2,3,\ldots J \\ b&\sim HC(0,25). \\ \end{aligned}$$

To fit this model in Stan, we first write the Stan model code and save it in a separated text-file with name “model_code1”.:

In this manner, we acquire the survival and hazard of the Marshall–Olkin exponential model.

7.1.2 Marshall–Olkin Exponentiated Exponential Model

The second model is Marshall–Olkin exponentiated exponential model:

$$\begin{aligned} y\sim MOexpexp(\alpha ,b,\theta ), \end{aligned}$$

where $\theta =exp(X\beta )$. The Bayesian framework requires the specification of prior distributions for the parameters. Here, we stick to subjectivity and thus introduce weakly informative priors for the parameters. Priors for the $\beta$, $\alpha$, and b are taken to be normal and half-Cauchy as follows:

$$\begin{aligned} \beta _j&\sim N(0,1000); \quad j=1,2,3,\ldots J \\ \alpha&\sim HC(0,25). \\ b&\sim HC(0,25). \end{aligned}$$

To fit this model in Stan, we first write the Stan model code and save it in a separated text-file with name “model_code2”.:

Therefore, we obtain the survival and hazard of the Marshall–Olkin exponentiated exponential model .

7.1.3 Marshall–Olkin Exponential Extension Model

The third model is Marshall–Olkin exponential extension model:

$$\begin{aligned} y\sim MOexpext(\alpha ,b,\theta ), \end{aligned}$$

where $\theta =exp(X\beta )$. The Bayesian framework requires the specification of prior distributions for the parameters. Here, we stick to subjectivity and thus introduce weakly informative priors for the parameters. Priors for the $\beta$, $\alpha$, and b are taken to be normal and half-Cauchy as follows:

$$\begin{aligned} \beta _j&\sim N(0,1000); {\quad } j=1,2,3,\ldots J \\ \alpha&\sim HC(0,25). \\ b&\sim HC(0,25). \end{aligned}$$

To fit this model in Stan, we first write the Stan model code and save it in a separated text-file with name “model_code3”.:

Therefore, we obtain the survival and hazard of the Marshall–Olkin exponential extension model .

7.2 Build the Stan

Stan contains an arrangement of blocks as stated previously; in the first block we will define the data block, in which we include the number of the observations, observed times, censoring indicator (1 $=$ observed, 0 $=$ censored), number of covariates, and build the matrix of covariates (with N rows and M columns). Then we create the parameter in block parameters, since we have more one parameter, we will do some changes for the parameters in side transformed parameters block. Finally, we arrange the model in blocks model. In these blocks, we put the prior for the parameters and the likelihood to get the posterior distribution for these model. We save this work in a file to use it in rstan package.

7.2.1 Marshall–Olkin Exponential Model

7.2.2 Marshall–Olkin Exponentiated Exponential Model

7.2.3 Marshall–Olkin Exponential Extension Model

7.3 Creation of Data for Stan

In this part, we are going to arrange the data that we need to employ for analysis, data arrangement requires model matrix X, number of predictors M, information regarding censoring and response variable. The number of observations is specified by N, that is, 45. Censoring is taken into account, where 0 stands for censored and 1 for uncensored values. Lastly, every one of these things are consolidated in a recorded list as dat.

7.4 Runing the Model Using Stan for Marshall–Olkin Exponential Model

Now we run Stan with 2 chains for 5000 iterations and display the results numerically and graphically:

7.4.1 Summarizing Output

A summary of the parameter distributions can be obtained by using print(S1), which provides posterior estimates for each of the parameters in the model. Before any inferences can be made, however, it is critically important to determine whether the sampling process has converged to the posterior distribution. Convergence can be diagnosed in several different ways. One way is to look at convergence statistics such as the potential scale reduction factor, Rhat [10], and the effective number of samples, n_eff [11], both of which are outputs in the summary statistics with print(S1). The function rstan approximates the posterior density of the fitted model and posterior summaries can be seen in the following tables. Table 1, which contain summaries for for all chains merged and individual chains, respectively. Included in the summaries are (quantiles),(means), standard deviations (sd), effective sample sizes (n_eff), and split (Rhats) (the potential scale reduction derived from all chains after splitting each chain in half and treating the halves as chains). For the summary of all chains merged, Monte Carlo standard errors (se_mean) are also reported.

Table 1 Summary of the simulated results using rstan function with mean stands for posterior mean, se_mean, sd for posterior standard deviation, LB, Median, UB are 2.5%, 50%, 97.5% quantiles, n_eff for number effective sample size, and Rhat, respectively

Fig. 5

Caterpillar plot for Marshall–Olkin exponential model

The inference of the posterior density after fitting the (Marshall–Olkin Exponential model) for prognosis of women with breast cancer data using stan are reposted in Table 1. The posterior estimate for $\beta _{0}$ is $6.79\pm 1.25$ and 95% credible interval is (4.99, 9.86), which is statistically significant. Rhat is close to 1.0, indication of good mixing of the three chains and thus approximate convergence. posterior estimate for $\beta _{1}$ is $-1.11\pm 0.59$ and 95% credible interval is ($-$ 2.39, $-$ 0.09), which is statistically significant. Rhat is close to 1.0, indication of good mixing of the three chains and thus approximate convergence. The table displays the output from Stan. Here, the coefficient beta[0] is the intercept, while the coefficient beta[1] is the effect of the only covariate included in the model. The effective sample size given an indication of the underlying autocorrelation in the MCMC samples values close to the total number of iterations. The selection of appropriate regressor variables can also be done by using a caterpillar plot. Caterpillar plots are popular plots in Bayesian inference for summarizing the quantiles of posterior samples. We can see in this Fig. 5, that the caterpillar plot is a horizontal plot of 3 quantiles of selected distribution. This may be used to produce a caterpillar plot of posterior samples. In MCMC estimation, it is important to thoroughly assess convergence as it in Fig. 6, the rstan contains specialized function to visualise the model output and assess convergence.

Fig. 6

Checking model convergence using rstan, through inspection of the traceplots or the autocorrelation plot

7.5 Runing the Model Using Stan for Marshall–Olkin Exponentiated Exponential Model

Now we run Stan with 2 chains for 5000 iterations and display the results numerically and graphically:

7.5.1 Summarizing Output

The function rstan approximates the posterior density of the fitted model and posterior summaries can be seen in the following tables. Table 2, contains summaries for for all chains merged and individual chains, respectively. Included in the summaries are (quantiles),(means), standard deviations (sd), effective sample sizes (n_eff), and split (Rhats) (the potential scale reduction is derived from all chains after splitting each chain in half and treating the halves as chains). For the summary of all chains merged, Monte Carlo standard errors (se_mean) are also reported. The inference of the posterior density after fitting the (Marshall–Olkin exponential exponential model) for prognosis of women with breast cancer data using stan are reposted in Table 2. The posterior estimate for $\beta _{0}$ is $6.74\pm 1.24$ and 95% credible interval is (5.04, 9.82), which is statistically significant. Rhat is close to 1.0, indication of good mixing of the three chains and thus approximate convergence. posterior estimate for $\beta _{1}$ is $-1.12\pm 0.55$ and 95% credible interval is ($-$ 2.32, $-$ 0.12), which is statistically significant. Rhat is close to 1.0, indication of good mixing of the three chains and thus approximate convergence. The selection of appropriate regressor variable can also be done by using a caterpillar plot. Caterpillar plots are popular plots in Bayesian inference for summarizing the quantiles of posterior samples. we can see in this Fig. 7, that the caterpillar plot is a horizontal plot of 3 quantiles of selected distribution. In MCMC estimation, it is important to thoroughly assess convergence as in Fig. 8, the rstan contains specialized function to visualise the model output and assess convergence.

Table 2 Summary of the simulated results using rstan function with mean stands for posterior mean, se_mean, sd for posterior standard deviation, LB, Median, UB are 2.5%, 50%, 97.5% quantiles, n_eff for number effective sample size, and Rhat, respectively

Fig. 7

Caterpillar plot for Marshall–Olkin exponentiated exponential model

Fig. 8

Checking model convergence using rstan, through inspection of the traceplots or the autocorrelation plot

7.6 Runing the Model Using Stan for Marshall–Olkin Exponential Extension Model

Now we run Stan with 2 chains for 5000 iterations and display the results numerically and graphically:

Table 3 Summary of the simulated results using rstan function with mean stands for posterior mean, se_mean, sd for posterior standard deviation, LB, Median, UB are 2.5%, 50%, 97.5% quantiles, n_eff for number effective sample size, and Rhat, respectively

7.6.1 Summarizing Output

The function rstan approximates the posterior density of the fitted model, and posterior summaries can be seen in the following tables. Table 3, contains summaries for for all chains merged and individual chains, respectively. Included in the summaries are (quantiles),(means), standard deviations (sd), effective sample sizes (n_eff), and split (Rhats) (the potential scale reduction derived from all chains after splitting each chain in half and treating the halves as chains). For the summary of all chains merged, Monte Carlo standard errors (se_mean) are also reported. The inference of the posterior density after fitting the (Marshall–Olkin exponential extension model) for prognosis of women with breast cancer data using stan are reposted in Table 3. The posterior estimate for $\beta _{0}$ is $7.53\pm 2.97$ and 95% credible interval is (1.92, 13.10), which is statistically significant. Rhat is close to 1.0, indication of good mixing of the three chains and thus approximate convergence. posterior estimate for $\beta _{1}$ is $-1.16\pm 0.60$ and 95% credible interval is ($-$ 2.41, $-$ 0.09), which is statistically significant. Rhat is close to 1.0, indication of good mixing of the three chains and thus approximate convergence. The selection of appropriate regressor variable can also be done by using a caterpillar plot. Caterpillar plots are popular plots in Bayesian inference for summarizing the quantiles of posterior samples. we can see in Fig. 9, that the caterpillar plot is a horizontal plot of 3 quantiles of selected distribution. In MCMC estimation, it is important to thoroughly assess convergence as it in Fig. 10, the rstan contains specialized function to visualise the model output and assess convergence.

Fig. 9

Caterpillar plot for Marshall–Olkin exponential extension model

Fig. 10

Checking model convergence using rstan, through inspection of the traceplots or the autocorrelation plot

Table 4 Model comparison of Marshall–Olkin exponential, Marshall–Olkin exponentiated exponential and Marshall–Olkin exponential extension models for the prognosis of women with breast cancer data

8 Conclusion

To display choice in this segment, we need to looking into the model which best suits the purpose. Here, therefore, Table 4 clearly demonstrates that Marshall–Olkin exponential extension is the most proper model for the Stan as it has least estimation of deviance when contrasted with Marshall–Olkin exponential and Marshall–Olkin exponentiated exponential. Finally, we can conclude that deviance is great criteria of model examination.