Exponentiated Generalized Power Series Family of Distributions

Abstract

In this paper, a new family of distributions called the exponentiated generalized power series family is proposed and studied. Statistical properties such as stochastic order, quantile function, entropy, mean residual life and order statistics were derived. Bivariate and multivariate extensions of the family was proposed. The method of maximum likelihood estimation was proposed for the estimation of the parameters. Some special distributions from the family were defined and their applications were demonstrated with real data sets.

1 Introduction

The development of generalized classes of distributions by researchers has become an interesting area of research in recent time. Several generalized classes of distributions have been proposed in statistical literature with the motivation of defining models with different types of failure rates, construct heavy-tailed distributions for modeling different kinds of data sets, generate distributions with left skewed, right skewed, symmetric, or reversed J shape and to consistently provide a reasonable parametric fits to data sets. This is necessary because the nature of data arising from different areas of study such as lifetime analysis, insurance, engineering, finance and biological science among others require extended forms of the existing statistical distributions before a better fit can be obtained.

Some of the generalized classes of distributions in literature includes: the transmuted geometric-G family [1]; Kumaraswamy transmuted-G family [2]; beta transmuted-H family [3]; generalized transmuted-G family [18]; transmuted exponentiated generalized-G family [22]; Kumaraswamy family [10]; Weibull-G family [9]; beta extended Weibull family [12]; exponentiated generalized class [11]; odd generalized exponential family [21]; transformed-transformer (T–X) method [4]; exponentiated generalized T–X method [16]; exponentiated T–X method [5] and exponentiated generalized exponential-X family [15].

This study proposes a new class of distributions called the exponentiated generalized power series (EGPS) family of distributions by compounding the exponentiated generalized (EG) class of distributions and the power series (PS) family of distributions. The rest of the paper is organized as follows: In Sect. 2, the cumulative distribution function (CDF), probability density function (PDF), survival function and hazard function of the EGPS family of distributions were defined. In Sect. 3, some sub-classes of the new family were discussed. In Sect. 4, statistical properties of the EGPS class were proposed using copula. In Sect. 7, special distributions from the EGPS family were discussed. In Sect. 8, simulations was performed to examine the finite sample properties of the estimators for the parameters of the special distributions. In Sect. 9, applications of the special distributions were demonstrated using real data sets. Finally, the concluding remarks of the study were given in Sect. 10.

2 Exponentiated Generalized Power Series Family

Let $N$ represent the number of independent subsystems of a system functioning at a given time. Suppose that $N$ has zero truncated PS distribution with probability mass function given by

$$ P(N = n) = \frac{{a_{n} \lambda^{n} }}{C(\lambda )},\quad n = 1,2, \ldots , $$

(1)

where $a_{n} > 0,C(\lambda ) = \sum_{i = 1}^{\infty } {a_{n} \lambda^{n} }$ and $\lambda \in (0,s)$($s$ can be $\infty$) is chosen such that $C(\lambda )$ is finite and its first, second and third derivatives are defined and shown by $C^{'} ( \cdot ),C^{''} ( \cdot )$ and $C^{'''} ( \cdot )$. The PS family includes; binomial, Poisson, geometric and logarithmic distributions. Detailed information of the PS family can be found in [17]. Suppose the failure time of each subsystem follows the EG class of distributions with CDF given by

$$ H_{c,d} (x) = \left( {1 - \left( {1 - G(x;\varvec{\psi})} \right)^{d} } \right)^{c} ,\quad x \in {\mathbb{R}}, $$

(2)

where $c,d > 0$ are extra shape parameters, $G(x;\varvec{\psi})$ is the baseline CDF depending on parameter $\varvec{\psi}$ and $g(x;\varvec{\psi})$ is its corresponding density function. For simplicity, $G(x;\varvec{\psi})$ is written as $G(x)$. If $T_{j}$ is the failure time of the jth subsystem and $X$ represents the time to failure of the first out of the $N$ operating subsystems such that $X = \hbox{min} (T_{1} ,T_{2} , \ldots ,T_{N} )$. Then the conditional CDF of $X$ given $N$ is

$$ \begin{aligned} F(x|N = n) & = 1 - P(X > x|N) \\ & = 1 - P(T_{1} > x,T_{2} > x, \ldots T_{N} > x) \\ & = 1 - \left( {1 - P(T_{1} \le x)} \right)^{n} \\ & = 1 - \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]^{n} . \\ \end{aligned} $$

(3)

Hence, the marginal CDF of $X$ is given by

$$ \begin{aligned} F(x) & = \sum_{i = 1}^{\infty } {\frac{{a_{n} \lambda^{n} }}{C(\lambda )}} \left\{ {1 - \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]^{n} } \right\} \\ & =1 - \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}. \\ \end{aligned} $$

(4)

The PDF is given by

$$ f(x) = \lambda cdg(x)(1 - G(x))^{d - 1} \left( {1 - (1 - G(x))^{d} } \right)^{c - 1} \frac{{C^{'} \left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}. $$

(5)

Table 1 summarizes some particular cases of zero truncated PS distributions.

Table 1 Useful quantities for some power series distributions

The survival function and the hazard rate function of the EGPS class of distributions are respectively given by

$$ S(x) = \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}, $$

(6)

and

$$ \tau (x) = \lambda cdg(x)(1 - G(x))^{d - 1} \left( {1 - (1 - G(x))^{d} } \right)^{c - 1} \frac{{C^{'} \left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}. $$

(7)

Remark 1

If $X = \hbox{max} (T_{1} ,T_{2} , \ldots ,T_{N} )$, then the CDF of the EGPS class is given by

$$ F(x) = \frac{{C\left( {\lambda \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right)}}{C(\lambda )}. \, $$

(8)

Remark 2

If $C(\lambda ) = \lambda$, then the EG class is a special case of the EGPS class.

Proposition 1

The EG class is a limiting case of the EGPS class when$\lambda \to 0^{ + }$.

Proof

$$ \begin{aligned} \mathop {\lim }\limits_{{\lambda \to 0^{ + } }} F(x) & = 1 - \mathop {\lim }\limits_{{\lambda \to 0^{ + } }} \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )} \\ & =1 - \mathop {\lim }\limits_{{\lambda \to 0^{ + } }} \frac{{\sum_{n = 1}^{\infty } {a_{n} \lambda^{n} \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]^{n} } }}{{\sum_{n = 1}^{\infty } {a_{n} \lambda^{n} } }}. \\ \end{aligned} $$

Applying L’Hôpital’s rule

$$ \begin{aligned} \mathop {\lim }\limits_{{\lambda \to 0^{ + } }} F(x) & = 1 - \mathop {\lim }\limits_{{\lambda \to 0^{ + } }} \frac{{\sum_{n = 1}^{\infty } {na_{n} \lambda^{n - 1} \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]^{n} } }}{{\sum_{n = 1}^{\infty } {na_{n} \lambda^{n - 1} } }} \\ & =1 - \mathop {\lim }\limits_{{\lambda \to 0^{ + } }} \frac{{a_{1} \left[ {\left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right] + \sum_{n = 2}^{\infty } {na_{n} \lambda^{n - 1} \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]^{n} } }}{{a_{1} + \sum_{n = 2}^{\infty } {na_{n} \lambda^{n - 1} } }} \\ & =\left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} . \\ \end{aligned} $$

Proposition 2

The exponentiated PS class is a limiting special case of the EGPS class when$d \to 1$.

Proof

$$ \begin{aligned} \mathop {\lim }\limits_{d \to 1} F(x) & = 1 - \mathop {\lim }\limits_{d \to 1} \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )} \\ & =1 - \frac{{C\left( {\lambda \left( {1 - G(x)^{c} } \right)} \right)}}{C(\lambda )}. \\ \end{aligned} $$

Lemma 1

The EGPS class density has a linear representation of the form

$$ f(x) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {g(x)G(x)^{k} } \right],} } $$

(9)

where $E_{N} ( \cdot )$ is the expectation with respect to the random variable $N$ and

$$ \omega_{ijk} = \frac{{( - 1)^{i + j + k} \varGamma (n + 1)\varGamma (c(i + 1))\varGamma (d(j + 1))}}{i!j!k!\varGamma (n - i)\varGamma (c(i + 1) - j)\varGamma (d(j + 1) - k)}. $$

Proof

The EGPS PDF can be written as

$$ f(x) = cd\sum_{n = 1}^{\infty } {P(N = n)ng(x)(1 - G(x))^{d - 1} \left( {1 - \left( {1 - G(x)} \right)^{d - 1} } \right)}^{c - 1} \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]^{n - 1} . $$

For a real non-integer $\eta > 0$, a series representation for $(1 - z)^{\eta - 1}$, for $\left| z \right| < 1$ is

$$ (1 - z)^{\eta - 1} = \sum_{i = 0}^{\infty } {\frac{{( - 1)^{i} \varGamma (\eta )}}{i!\varGamma (\eta - i)}} z^{i} . $$

(10)

Using the series expansion in Eq. (10) thrice and the fact that $0 \le 1 - G(x) \le 1$, yields

$$ f(x) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {g(x)G(x)^{k} } \right] .} } $$

The linear representation of the density function makes it easy to study the statistical properties of the EGPS class. Alternatively it can be written in terms of the exp-G function as

$$ f(x) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk}^{*} } E_{N} \left[ {\varphi_{k + 1} } \right]} , $$

(11)

where $\omega_{ijk}^{*} = \frac{{\omega_{ijk} }}{(k + 1)}$ and $\varphi_{k + 1} = (k + 1)g(x)G(x)^{k}$ is the exp-G density with power parameter $k + 1$.

3 Sub-Families

In this section, a number of sub-families of the EGPS family were discussed. These include: EG Poisson (EGP), EG binomial (EGB), EG geometric (EGG) and logarithmic (EGL) classes of distributions.

3.1 Exponentiated Generalized Poisson Class

The zero truncated Poisson distribution is a special case of PS distribution with $a_{n} = \frac{1}{n!}$ and $C(\lambda ) = e^{\lambda } - 1,(\lambda > 0)$. Using the CDF in Eq. (4), the CDF and PDF of the EGP class of distributions are respectively given by

$$ F(x) = \frac{{e^{\lambda } - e^{{\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]}} }}{{e^{\lambda } - 1}}, $$

(12)

and

$$ f(x) = \lambda cdg(x)(1 - G(x))^{d - 1} \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c - 1} \frac{{e^{{\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]}} }}{{e^{\lambda } - 1}}. $$

(13)

3.2 Exponentiated Generalized Binomial Class

The zero truncated binomial distribution is a special case of PS distribution $a_{n} = \left( \begin{aligned} m \hfill \\ n \hfill \\ \end{aligned} \right)$ and $C(\lambda ) = (1 + \lambda )^{m} - 1,(\lambda > 0)$, where $m(n \le m)$ is the number of replicas and is a positive integer. The CDF of the EGB class of distributions are respectively

$$ F(x) = 1 - \frac{{\left[ {1 + \lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right]^{m} - 1}}{{(1 + \lambda )^{m} - 1}}, $$

(14)

and

$$ f(x) = m\lambda cdg(x)(1 - G(x))^{d - 1} \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c - 1} \frac{{\left[ {1 + \lambda \left[ {1 - \left( {1 - \left( {1 - g(x)} \right)^{d} } \right)^{c} } \right]} \right]^{m - 1} }}{{\left( {\left( {1 + \lambda } \right)^{m} - 1} \right)}}. $$

(15)

The EGP class is a limiting case of the EGB class if $m\lambda \to \theta > 0$, when $m \to \infty$.

3.3 Exponentiated Generalized Geometric Class

The zero truncated geometric distribution is a special case of PS distributions with $a_{n} = 1$ and $C(\lambda ) = \frac{\lambda }{1 - \lambda },(0 < \lambda < 1)$. The CDF and PDF of the EGG class of distributions are respectively given by

$$ F(x) = 1 - \frac{{(1 - \lambda )\left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]}}{{1 - \lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]}}, $$

(16)

and

$$ f(x) = \frac{{(1 - \lambda )cdg(x)(1 - G(x))^{d - 1} \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c - 1} }}{{\left[ {1 - \lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right]^{2} }}. $$

(17)

3.4 Exponentiated Generalized Logarithmic Class

The zero truncated logarithmic distribution is another special case of the PS distribution with $a_{n} = \frac{1}{n}$ and $C(\lambda ) = - \log (1 - \lambda ),(0 < \lambda < 1)$. The CDF and PDF of the EGL class are respectively given by

$$ F(x) = 1 - \frac{{\log \left[ {1 - \lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right]}}{\log (1 - \lambda )}, $$

(18)

and

$$ f(x) = \frac{{\lambda cdg(x)(1 - G(x))^{d - 1} \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c - 1} }}{{\log (1 - \lambda )\left[ {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right] - 1} \right]}}. $$

(19)

4 Statistical Properties

In this section, the statistical properties of the EGPS class of distributions were discussed. These include: the quantile function, moment, moment generating function, incomplete moment, mean residual life, stochastic property, reliability, Shannon entropy and order statistics.

4.1 Quantile Function

The quantile function is another way of describing the distribution of a random variable. It plays a key role when simulating random numbers from a distribution and it provides an alternative means for describing the shapes of a distribution.

Proposition 3

The quantile function of the EGPS class is given by

$$ Q_{F} (u) = G^{ - 1} \left\{ {1 - \left[ {1 - \left( {1 - \frac{{C^{ - 1} \left( {(1 - u)C(\lambda )} \right)}}{\lambda }} \right)^{{\tfrac{1}{c}}} } \right]^{{\tfrac{1}{d}}} } \right\}, $$

(20)

where$u \in \left[ {0,1} \right]$and$C^{ - 1} ( \cdot )$is the inverse of$C( \cdot )$.

Proof

By definition, the quantile function is given by $F(x_{u} ) = P\left( {X \le x_{u} } \right) = u$. Thus, setting $Q_{F} (u) = x_{u}$ in Eq. (4) and solving for it yields the quantile function of the EGPS class.

The median of the EGPS class is obtained by substituting $u = 0.5$ into Eq. (20).

4.2 Moment, Generating Function and Incomplete Moment

In this subsection, the moment, moment generating function (MGF) and incomplete moment were presented.

Proposition 4

The rth non-central moment of the EGPS class is given by

$$ \mu_{r}^{'} = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{ - \infty }^{\infty } {x^{r} g(x)G(x)^{k} dx} } \right]} } ,\quad r = 1,2, \ldots . $$

(21)

Proof

By definition, the rth non-central moment is given by

$$ \mu_{r}^{'} = \int\limits_{ - \infty }^{\infty } {x^{r} f(x)dx.} $$

Substituting the linear representation of the density function into the definition and simplifying yields the non-central moment.

Alternatively, the moment can be expressed in terms of the quantile function of the baseline. Let $G(x) = u$, then

$$ \mu_{r}^{'} = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{0}^{1} {Q_{G} (u)^{r} u^{k} du} } \right]} } . $$

(22)

Proposition 5

The MGF of EGPS class of distributions is given by

$$ M_{X} (t) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{ - \infty }^{\infty } {e^{tx} g(x)G(x)^{k} dx} } \right]} } . $$

(23)

Proof

The proof of MGF directly follows from the definition $M_{X} (t) = \int\limits_{ - \infty }^{\infty } {e^{tx} f(x)dx}$.

In terms of the quantile function of the baseline, the MGF is given by

$$ M_{X} (t) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{0}^{1} {e^{{tQ_{G} (u)}} u^{k} du} } \right]} } . $$

(24)

Proposition 6

The rth incomplete moment of the EGPS class of distributions is given by

$$ M_{r} (t) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{ - \infty }^{t} {x^{r} g(x)G(x)^{k} dx} } \right]} } ,\quad r = 1,2 \ldots . $$

(25)

Proof

The proof can easily be obtained from the definition $M_{r} (t) = \int\nolimits_{ - \infty }^{t} {x^{r} f(x)dx}$. Letting $u = G(x)$, the incomplete moment can be expressed in terms of the baseline quantile function as

$$ M_{r} (t) = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{0}^{G(t)} {Q_{G} (u)^{r} u^{k} du} } \right].} } $$

(26)

Using the power series expansion of the quantile function of the baseline as $Q_{G} (u) = \sum_{h = 0}^{\infty } {e_{h} u^{h} }$, where $e_{h} (h = 0,1, \ldots )$ are suitably chosen real numbers that depend on the parameters of the $G(x)$ distribution.

$$ \left( {Q_{G} (u)} \right)^{r} = \left( {\sum_{h = 0}^{\infty } {e_{h} u^{h} } } \right)^{r} = \sum_{h = 0}^{\infty } {e_{r,h}^{'} u^{h} ,} $$

where $e_{r,h}^{'} = \left( {he_{0} } \right)^{ - 1} \sum_{z = 1}^{h} {\left[ {z(r + 1) - h} \right]e_{z} e_{r,h - z}^{'} } ,e_{r,0}^{'} = \left( {e_{0} } \right)^{h}$ and $r(r \ge 1)$ is a positive integer. For more details on quantile power series expansion see [13]. The incomplete moment can now be expressed as

$$ \begin{aligned} M_{r} (t) & = cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\sum_{h = 0}^{\infty } {e_{r,h}^{'} \int\limits_{0}^{G(t)} {u^{k + h} du} } } \right]} } \\ & =cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\sum_{h = 0}^{\infty } {\frac{{e_{r,h}^{'} G(t)^{k + h + 1} }}{k + h + 1}} } \right]} } . \\ \end{aligned} $$

4.3 Residual and Mean Residual Life

A system’s residual lifetime when it is still operating at time $t$, is $X_{t} = X - t|X > t$ which has the PDF

$$ \begin{aligned} f(x;t) & = \frac{f(x)}{1 - F(t)} \\ & =\lambda cdg(x)(1 - G(x))^{d - 1} \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c - 1} \frac{{C^{'} \left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}. \\ \end{aligned} $$

Proposition 7

The mean residual life of$X_{t}$is given by

$$ m(t) = \frac{1}{1 - F(t)}\left[ {\mu - cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\sum_{h = 0}^{\infty } {\frac{{e_{h} G(t)^{k + h + 1} }}{k + h + 1}} } \right]} } } \right] - t, $$

(27)

where$\mu = \mu_{1}^{'}$is the mean and$e_{h} (h = 0,1, \ldots )$are suitably chosen real numbers that depend on the parameters of the$G(x)$distribution.

Proof

The mean residual life is defined as

$$ m(t) = E\left[ {X - t|X > t} \right] = \frac{{\int\limits_{t}^{\infty } {(x - t)f(x)dx} }}{1 - F(t)} = \frac{{\mu_{1}^{'} - \int\limits_{ - \infty }^{t} {xf(x)dx} }}{1 - F(t)} - t. $$

(28)

The integral $\int\nolimits_{ - \infty }^{t} {xf(x)dx}$ is the first incomplete moment. Thus substituting the first incomplete moment into Eq. (28) yields the mean residual life.

4.4 Stochastic Ordering Property

Stochastic ordering is the common way of showing ordering mechanism in lifetime distribution. A random variable $X_{1}$ is said to be greater than a random variable $X_{2}$ in likelihood ratio order if $\frac{{f_{{X_{1} }} (x)}}{{f_{{X_{2} }} (x)}}$ is an increasing function of $x$.

Proposition 8

Let$X_{1} \sim EGPS(x;c,d,\lambda ,\varvec{\psi})$and$X_{2} \sim EG(x;c,d,\varvec{\psi})$, then$X_{2}$is greater than$X_{1}$in likelihood ratio order$(X_{1} \le_{lr} X_{2} )$provided$\lambda > 0$.

Proof

$$ \frac{{f_{{X_{1} }} (x)}}{{f_{{X_{2} }} (x)}} = \frac{{\lambda C^{'} \left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}, $$

which is decreasing in $x$ provided $\lambda > 0$.

From Proposition 8, it can be considered that the hazard rate order, the usual stochastic order and the mean residual life order between $X_{1}$ and $X_{2}$ hold.

4.5 Stress-Strength Reliability

Reliability plays a useful role in the analysis of stress-strength of models. If $X_{1}$ is the strength of a component and $X_{2}$ is the stress, then the component fails when $X_{1} \le X_{2}$. The estimate of the reliability of the component $R$ is $P(X_{2} < X_{1} )$.

Proposition 9

If$X_{1} \sim EGPS(x;c,d,\lambda ,\varvec{\psi})$and$X_{2} \sim EGPS(x;c,d,\lambda ,\varvec{\psi})$, then reliability is given by

$$ R = 1 - \sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{0}^{1} {u^{k} \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}} du} \right]} } . $$

(29)

Proof

The reliability is defined as

$$ \begin{aligned} R & = \int\limits_{ - \infty }^{\infty } {f(x)F(x)dx} \\ & { = 1 - }\int\limits_{ - \infty }^{\infty } {f(x)S(x)dx} \\ & { = 1 - }\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{ - \infty }^{\infty } {g(x)G(x)^{k} S(x)dx} } \right].} } \\ \end{aligned} $$

Letting $G(x) = u$ yields

$$ R = 1 - \sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\int\limits_{0}^{1} {u^{k} \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - u} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}} du} \right]} } . $$

4.6 Shannon Entropy

The entropy of a random variable is a measure of variation or uncertainty of the random variable. The Shannon entropy of a random variable $X$ with PDF $f(x)$ is given by $\eta_{X} = E\left\{ { - \log f(x)} \right\}$ [19].

Proposition 10

The Shannon entropy of the EGPS class random variable is given by

$$ \eta_{X} = - \log \left( {\frac{cd\lambda }{C(\lambda )}} \right) - E\left[ {\log g(X)} \right] + (1 - d)\delta_{1} + (1 - c)\delta_{2} - E\left[ {\log C^{'} \left( {\lambda \left[ {1 - H_{c,d} (X)} \right]} \right)} \right], $$

(30)

where$H_{c,d} (x)$is the CDF of the EG class,

$$ \delta_{1} = - cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\sum_{q = 1}^{\infty } {\frac{1}{q(k + q + 1)}} } \right]} } , $$

and

$$ \delta_{2} = - cd\sum_{j,k = 0}^{\infty } {\sum_{i = 0}^{n - 1} {\omega_{ijk} E_{N} \left[ {\sum_{s = 0}^{\infty } {\sum_{q = 1}^{\infty } {\frac{{( - 1)^{s} \left( \begin{aligned} dq \hfill \\ s \hfill \\ \end{aligned} \right)}}{q(k + q + 1)}} } } \right]} } . $$

Proof

By definition

$$ \begin{aligned} \eta_{X} & = - \log \left( {\frac{cd\lambda }{C(\lambda )}} \right) - E\left[ {\log g(X)} \right] + (1 - d)E\left[ {\log (1 - G(X))} \right] + (1 - c)E\left[ {\log (1 - (1 - G(x))^{d} )^{c} } \right] \\ & \quad - E\left[ {\log C^{'} \left( {\lambda \left[ {1 - H_{c,d} (X)} \right]} \right)} \right] .\\ \end{aligned} $$

(31)

Let $\delta_{1} = E\left[ {\log (1 - G(X))} \right]$ and $\delta_{2} = E\left[ {\log \left( {1 - \left( {1 - \left( {1 - G(X)} \right)^{d} } \right)^{c} } \right)} \right]$. Using the identity $\log (1 - z) = - \sum_{q = 1}^{\infty } {\frac{{z^{q} }}{q},\left| z \right| < 1}$, yields

$$ \begin{aligned} & \log (1 - G(x)) = - \sum_{q = 1}^{\infty } {\frac{{G(x)^{q} }}{q}} , \\ & \log \left( {1 - (1 - G(x))^{d} } \right) = - \sum_{s = 0}^{\infty } {\sum_{q = 1}^{\infty } {\frac{{( - 1)^{s} \left( \begin{aligned} dq \hfill \\ s \hfill \\ \end{aligned} \right)G(x)^{s} }}{q}} } . \\ \end{aligned} $$

Putting $G(x) = u$ and taking the expectation with respect to the random variable $X$, give the value of $\delta_{1}$ and $\delta_{2}$ after some algebraic manipulation.

4.7 Order Statistics

Let $X_{1} ,X_{2} , \ldots ,X_{n}$ be a random sample of size $n$ from EGPS, then the PDF of the pth order statistic, say $X_{p:n}$ is given by

$$ f_{p:n} (x) = \frac{1}{B(p,n - p + 1)}\left[ {F(x)} \right]^{p - 1} \left[ {1 - F(x)} \right]^{n - p} f(x), $$

where $F(x)$ and $f(x)$ are the CDF and PDF of the EGPS class of distributions respectively, and $B( \cdot , \cdot )$ is the beta function. Thus,

$$ \begin{aligned} f_{p:n} (x) & = \frac{n!f(x)}{(p - 1)!(n - p)!}\left[ {1 - \frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}} \right]^{p - 1} \\ & \quad \times \left[ {\frac{{C\left( {\lambda \left[ {1 - \left( {1 - \left( {1 - G(x)} \right)^{d} } \right)^{c} } \right]} \right)}}{C(\lambda )}} \right]^{n - p} . \\ \end{aligned} $$

(32)

5 Parameter Estimation

Different methods for parameter estimation exist in literature but the maximum likelihood approach is the most commonly used. The maximum likelihood estimators have several desirable properties and can be used for constructing confidence intervals and regions. Thus, in this study, the maximum likelihood method was employed for the estimation of the parameters of the EGPS distribution. Let $X_{1} ,X_{2} , \ldots ,X_{n}$ be a random sample of size $n$ from the EGPS distribution. Let $z_{i} = 1 - G(x_{i} ;\varvec{\psi})$, then the log-likelihood is given by

$$ \begin{aligned} \ell & = n\log (\lambda cd) + \sum_{i = 1}^{n} {\log g(x_{i} ;\varvec{\psi})} + (d - 1)\sum_{i = 1}^{n} {\log (z_{i} ) + (c - 1)\sum_{i = 1}^{n} {\log (1 - z_{i}^{d} ) - n\log C(\lambda )} } \\ & \quad + \sum_{i = 1}^{n} {\log C^{'} \left( {\lambda \left[ {1 - \left( {1 - z_{i}^{d} } \right)^{c} } \right]} \right)} .\\ \end{aligned} $$

(33)

Taking the partial derivatives of the log-likelihood function with respect to the parameters yields the following score functions:

$$ \frac{\partial \ell }{\partial \lambda } = \frac{n}{\lambda } - \frac{{nC^{'} (\lambda )}}{C(\lambda )} + \sum_{i = 1}^{n} {\frac{{[1 - (1 - z_{i}^{d} )^{c} ]C^{''} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}{{C^{'} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}} , $$

(34)

$$ \frac{\partial \ell }{\partial c} = \frac{n}{c} + \sum_{i = 1}^{n} {\log (1 - z_{i}^{d} ) - \sum_{i = 1}^{n} {\frac{{\lambda (1 - z_{i}^{d} )^{c} \log (1 - z_{i}^{d} )C^{''} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}{{C^{'} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}} } , $$

(35)

$$ \frac{\partial \ell }{\partial d} = \frac{n}{d} + \sum_{i = 1}^{n} {\log (z_{i} ) - (c - 1)\sum_{i = 1}^{n} {\frac{{z_{i}^{d} \log (z_{i} )}}{{1 - z_{i}^{d} }} + \sum_{i = 1}^{n} {\frac{{\lambda c(1 - z_{i}^{d} )^{c - 1} z_{i}^{d} \log (z_{i} )C^{''} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}{{C^{'} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}} } } , $$

(36)

$$ \begin{aligned} \frac{\partial \ell }{{\partial\varvec{\psi}}} & = \sum_{i = 1}^{n} {\frac{{g^{'} (x_{i} ;\varvec{\psi})}}{{g(x_{i} ;\varvec{\psi})}}} - (d - 1)\sum_{i = 1}^{n} {\frac{{G^{'} (x_{i} ;\varvec{\psi})}}{{z_{i} }} + (c - 1)\sum_{i = 1}^{n} {\frac{{dz_{i}^{d - 1} G^{'} (x_{i} ;\varvec{\psi})}}{{1 - z_{i}^{d} }}} } \\ & \quad - \sum_{i = 1}^{n} {\frac{{\lambda cdz_{i}^{d - 1} (1 - z_{i}^{d} )^{c - 1} G^{'} (x_{i} ;\varvec{\psi})C^{''} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}{{C^{'} (\lambda [1 - (1 - z_{i}^{d} )^{c} ])}}} , \\ \end{aligned} $$

(37)

where $g^{'} (x_{i} ;\varvec{\psi}) = \frac{{\partial g(x_{i} ;\varvec{\psi})}}{{\partial\varvec{\psi}}}$ and $G^{'} (x_{i} ;\varvec{\psi}) = \frac{{\partial G(x_{i} ;\varvec{\psi})}}{{\partial\varvec{\psi}}}$. The score functions do not have close form, thus it is more convenient to solve them using nonlinear optimization techniques such as the quasi-Newton algorithm. For the purpose of interval estimation of the parameters, a $p \times p$ observed information matrix can be obtained as $J(\varvec{\vartheta}) = \frac{{\partial^{2} \ell }}{\partial q\partial r}$ (for $q,r = \lambda ,c,d,\varvec{\psi}$), whose elements can be computed numerically. Under the usual regularity conditions as $n \to \infty$, the distribution of $\widehat{\varvec{\vartheta}} = (\widehat{\lambda },\widehat{c},\widehat{d},\widehat{{\varvec{\psi}^{T} }})^{T}$ approximately converges to a multivariate normal $N_{p} ({\mathbf{0}},J(\widehat{\varvec{\vartheta}})^{ - 1} )$ distribution. $J(\widehat{\varvec{\vartheta}})$ is the observed information matrix evaluated at $\widehat{\varvec{\vartheta}}$. The asymptotic normal distribution is useful for constructing approximate $100(1 - \alpha )\%$ confidence intervals, where $\alpha$ is the significance level.

6 Extension via Copula

In this section, bivariate and multivariate extensions of the EGPS class of distributions were proposed using Clayton copula. Consider a random pair $(X_{1} ,X_{2} )$, a copula $C^{*}$ associated with the pair is simply a joint distribution of the random vector $(F_{{X_{1} }} (x_{1} ),F_{{X_{2} }} (x_{2} ))$. Suppose that $F_{{X_{1} }} (x_{1} )$ and $F_{{X_{2} }} (x_{2} )$ are the marginal CDFs of the random variables $X_{1}$ and $X_{2}$ respectively and $C^{*}$ is the copula associated to $(X_{1} ,X_{2} )$. Sklar [20] established that the joint CDF $F_{{X_{1} X_{2} }} (x_{1} ,x_{2} )$ of the pair $(X_{1} ,X_{2} )$ is given by

$$ F_{{X_{1} X_{2} }} (x_{1} ,x_{2} ) = C^{*} (F_{{X_{1} }} (x_{1} ),F_{{X_{2} }} (x_{2} )). $$

Suppose $(X_{1} ,X_{2} )$ follows bivariate EGPS random variables with marginal distributions $F_{{X_{1} }} (x_{1} )$ and $F_{{X_{2} }} (x_{2} )$. Let the copula associated to $(X_{1} ,X_{2} )$ belong to Clayton copula family given by

$$ C^{*} (z_{1} ,z_{2} ) = [z_{1}^{ - \theta } + z_{2}^{ - \theta } - 1]^{{\tfrac{ - 1}{\theta }}} ,\theta \ge 0. $$

The joint CDF $F_{{X_{1} X_{2} }} (x_{1} ,x_{2} )$, of the bivariate EGPS class is given by

$$ \begin{aligned} & F_{{X_{1} X_{2} }} (x_{1} ,x_{2} ) \\ & \quad = \left\{ {\left[ {1 - \frac{{C(\lambda_{1} [1 - (1 - (1 - G(x_{1} ;\varvec{\psi}_{1} ))^{{d_{1} }} )^{{c_{1} }} ])}}{{C(\lambda_{1} )}}} \right]^{ - \theta } }\right.\\&\qquad\quad \left.{+ \left[ {1 - \frac{{C(\lambda_{2} [1 - (1 - (1 - G(x_{2} ;\varvec{\psi}_{2} ))^{{d_{2} }} )^{{c_{2} }} ])}}{{C(\lambda_{2} )}}} \right]^{ - \theta } - 1} \right\}^{{\tfrac{ - 1}{\theta }}} , \\ \end{aligned} $$

(38)

where $\lambda_{1} ,\lambda_{2} ,c_{1} ,c_{2} ,d_{1} ,d_{2} ,\varvec{\psi}_{1}$ and $\varvec{\psi}_{2}$ describe the marginal parameters while $\theta$ is the Clayton copula parameter. A p-dimensional multivariate extension from the above is given by

$$ F_{{X_{1} X_{2} \ldots X_{p} }} (x_{1} ,x_{2} , \ldots ,x_{p} ) = \left\{ {\sum_{i = 1}^{p} {\left[ {1 - \frac{{C(\lambda_{i} [1 - (1 - (1 - G(x_{i} ;\varvec{\psi}_{i} ))^{{d_{i} }} )^{{c_{i} }} ])}}{{C(\lambda_{i} )}}} \right]} - p + 1} \right\}^{{\tfrac{ - 1}{\theta }}} . $$

(39)

7 Special Distribution

In this section, four special distributions were presented. These include EGP inverse exponential (EGPIE) distribution, EGB inverse exponential (EGBIE) distribution, EGG inverse exponential (EGGIE) distribution and EGL inverse exponential (EGLIE) distribution. Suppose the baseline distribution follows an inverse exponential distribution with CDF $G(x) = e^{{ - \gamma x^{ - 1} }} ,\gamma > 0,x > 0$. The densities, hazard rate functions and quantiles of the EGPIE, EGBIE, EGGIE and EGLIE distributions are defined as follows:

7.1 EGPIE Distribution

The density function of the EGPIE distribution is obtained by substituting the baseline CDF and its corresponding PDF into Eq. (13). Thus, the PDF of EGPIE distribution is given by

$$ \begin{aligned} f(x) & = \lambda \gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d - 1} \left( {1 - \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d} } \right)^{c - 1} \frac{{e^{{\lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]}} }}{{e^{\lambda } - 1}}, \\ & \quad \quad \lambda ,\gamma ,c,d > 0,x > 0. \, \\ \end{aligned} $$

(40)

The corresponding hazard rate function is given by

$$ \begin{aligned} \tau (x) & = \lambda \gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d - 1} \left( {1 - \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d} } \right)^{c - 1} \frac{{e^{{\lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]}} }}{{e^{{\lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]}} - 1}}, \\ & \quad \quad \lambda ,\gamma ,c,d > 0,x > 0. \, \\ \end{aligned} $$

(41)

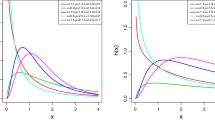
Figure 1 displays the plots of the density and hazard rate function of the EGPIE distribution. From the figure, the density exhibit right skewed shape with varied degrees of kurtosis and an approximately symmetric shape. The hazard rate function shows an upside down bathtub shapes.

Fig. 1

Plots of EGPIE a PDF and b hazard rate function

The quantile function of the EGPIE distribution is given by

$$ Q(u) = \left\{ {\frac{ - 1}{\gamma }\log \left[ {1 - \left[ {1 - \left( {1 - \frac{{\log (e^{\lambda } - u(e^{\lambda } - 1))}}{\lambda }} \right)^{{\tfrac{1}{c}}} } \right]^{{\tfrac{1}{d}}} } \right]} \right\}^{ - 1} . $$

(42)

7.2 EGBIE Distribution

Using Eq. (15), the PDF of EGBIE distribution is given by

$$ \begin{aligned} f(x) & = m\lambda \gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d - 1} \left( {1 - \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d} } \right)^{c - 1} \frac{{[1 + \lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]]^{m - 1} }}{{(1 + \lambda )^{m} - 1}}, \\ & \quad \quad \lambda ,\gamma ,c,d > 0,x > 0. \\ \end{aligned} $$

(43)

The corresponding hazard rate function is given by

$$ \begin{aligned} \tau (x) & = m\lambda \gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d - 1} \left( {1 - \left( {1 - e^{{ - \gamma x^{ - 1} }} } \right)^{d} } \right)^{c - 1} \frac{{[1 + \lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]]^{m - 1} }}{{[1 + \lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]]^{m} - 1}}, \\ & \quad \quad \lambda ,\gamma ,c,d > 0,x > 0. \\ \end{aligned} $$

(44)

The plots of the density and hazard rate functions of the EGNIE distribution for $m = 5$ are shown in Fig. 2. The density function exhibits right skewed and approximately symmetric shapes. The hazard rate function exhibits an upside down bathtub shapes and an upside down bathtub shape followed by a bathtub and then upside down bathtub shape.

Fig. 2

Plots of EGBIE a PDF and b hazard rate function

The quantile function of the EGBIE distribution is given by

$$ Q(u) = \left\{ {\frac{ - 1}{\gamma }\log \left[ {1 - \left[ {1 - \left( {1 - \frac{{(((1 + \lambda )^{m} - 1)(1 - u) + 1)^{{\tfrac{1}{m}}} - 1}}{\lambda }} \right)^{{\tfrac{1}{c}}} } \right]^{{\tfrac{1}{d}}} } \right]} \right\}^{ - 1} $$

(45)

7.3 EGGIE Distribution

From Eq. (17), the PDF of EGGIE distribution is given by

$$ f(x) = \frac{{(1 - \lambda )\gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} (1 - e^{{ - \gamma x^{ - 1} }} )^{d - 1} (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c - 1} }}{{[1 - \lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]]^{2} }},0 < \lambda < 1,\gamma ,c,d > 0,x > 0. $$

(46)

The associated hazard rate function is given by

$$ \begin{aligned} \tau (x) = \frac{{\gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} (1 - e^{{ - \gamma x^{ - 1} }} )^{d - 1} (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c - 1} }}{{[1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ][1 - \lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]]}},0 < \lambda < 1,\gamma ,c,d > 0,x > 0. \hfill \\ \hfill \\ \end{aligned} $$

(47)

The density and hazard rate function plots of the EGGIE distribution are displayed in Fig. 3. The density and hazard rate function exhibits similar shapes like that of the EGBIE distribution.

Fig. 3

Plots of EGGIE a PDF and b hazard rate function

The quantile function of the EGGIE distribution is given by

$$ Q(u) = \left\{ {\frac{ - 1}{\gamma }\log \left[ {1 - \left( {1 - \left( {\frac{u(1 - \lambda )}{1 - u\lambda }} \right)^{{\tfrac{1}{c}}} } \right)^{{\tfrac{1}{d}}} } \right]} \right\}^{ - 1} . $$

(48)

7.4 EGLIE Distribution

From Eq. (19), the PDF of EGLIE distribution is given by

$$ f(x) = \frac{{\lambda \gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} (1 - e^{{ - \gamma x^{ - 1} }} )^{d - 1} (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c - 1} }}{{\log [1 - \lambda ][\lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ] - 1]}},0 < \lambda < 1,\gamma ,c,d > 0,x > 0. \, $$

(49)

The corresponding hazard rate function is given by

$$ \begin{aligned} \tau (x) & = \frac{{\lambda \gamma cdx^{ - 2} e^{{ - \gamma x^{ - 1} }} (1 - e^{{ - \gamma x^{ - 1} }} )^{d - 1} (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c - 1} }}{{\log [1 - \lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ]][\lambda [1 - (1 - (1 - e^{{ - \gamma x^{ - 1} }} )^{d} )^{c} ] - 1]}}, \\ & \quad \quad 0 < \lambda < 1,\gamma ,c,d > 0,x > 0. \, \\ \end{aligned} $$

(50)

Figure 4 shows the density and hazard rate function of the EGLIE distribution. The density exhibits approximately symmetric shapes with different degrees of kurtosis. The hazard rate function shows upside down bathtub shapes.

Fig. 4

Plots of EGLIE a PDF and b hazard rate function

The quantile function of the EGLIE distribution is given by

$$ Q(u) = \left\{ {\frac{ - 1}{\gamma }\log \left[ {1 - \left( {1 - \left( {1 - \frac{{1 - (1 - \lambda )^{1 - u} }}{\lambda }} \right)^{{\tfrac{1}{c}}} } \right)^{{\tfrac{1}{d}}} } \right]} \right\}^{ - 1} . $$

(51)

8 Monte Carlo Simulation

In this section, Monte Carlo simulations were performed to examine the finite sample properties of the maximum likelihood estimators for the parameters of the EGPIE, EGBIE, EGGIE and EGLIE distributions. For the case of the EGBIE distribution, $m = 5$ was used during the simulation. The simulation steps are as follows

• 1. Specify the values of the parameters $\lambda ,c,d,\gamma$ and the sample size $n$.

• 2. Generate random samples of size $n = 25,50,75,100$ from EGPIE, EGBIE, EGGIE and EGLIE distributions using their respective quantiles.

• 3. Find the maximum likelihood estimates of the parameters.

• 4. Repeat steps 2–3 for $N = 1500$ times.

• 5. Calculate the average estimates (AE) and root mean square error (RMSE) for the estimators of the parameters of the distributions.

Table 2 shows the simulation results for the EGPIE and EGBIE distributions whereas Table 3 displays that of the EGGIE and EGLIE distributions. From both tables it can be seen that the AE of the parameters were quite close to the actual values of the parameters. The RMSEs of the parameters were smaller and decay towards zero as the sample size increases.

Table 2 Monte Carlo simulation results: AE and RMSE for EGPIE and EGBIE distributions

Table 3 Monte Carlo simulation results: AE and RMSE for EGGIE and EGLIE distributions

9 Applications

The applications of the EGPIE, EGBIE (with $m = 5$), EGGIE and EGLIE distributions were demonstrated in this section using real data sets. The performance of the distributions with regards to providing reasonable parametric fit to the data sets were compared using the Kolmogorov–Smirnov (K–S) statistic, Cramér-von (W*) misses distance values, Akaike information criterion (AIC), corrected Akaike information criterion (AIC_c), and Bayesian information criterion (BIC). The maximum likelihood estimates for the parameters of the models were estimated by maximizing the log-likelihood functions of the models via the subroutine mle2 using the bbmle package in R [8]. This was carried out using a wide range of initial values. The process often results into more than one maximum, hence in such situation, the maximum likelihood estimates corresponding to the largest maxima was chosen.

9.1 First Data Set

The data set comprises 101 observations corresponding to the failure time in hours of Kevlar 49/epoxy strands with pressure at 90%. The data set displayed in Table 4 can be found in [7, 6].

Table 4 Failure times of Kevlar 49/epoxy strands with pressure at 90%

Table 5 displays the maximum likelihood estimates of the parameters of the fitted distributions with their corresponding standard errors in brackets. The parameters of the EGPIE and EGGIE distributions were all significant at the 5% level with the exception of the parameter $\gamma$ for the two distributions. The parameters of the EGBIE distribution were all significant at the 5% level. The EGLIE distribution parameters were all significant at the 5% level with the exception of the parameter $\lambda$.

Table 5 Maximum likelihood estimates of parameters and standard errors

The EGPIE distribution provides a better fit to the data set compared to the other models. From Table 6, the EGPIE distribution has the highest log-likelihood and the smallest K–S, W*, AIC, AIC_c and BIC values compared to the other fitted models.

Table 6 Log-likelihood, goodness-of-fit statistics and information criteria

The plots of the empirical density, the fitted densities, the empirical CDF and the CDF of the fitted distributions are shown in Fig. 5. It is obvious the EGPIE distribution provides a better fit to the data compared to the other fitted models.

Fig. 5

Empirical and fitted density and CDF plots of Kevlar data

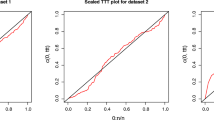
In addition, the P–P plots in Fig. 6 shows that the EGPIE and EGBIE distributions provide a more reasonable fit to the data compared to the EGGIE and EGLIE distributions.

Fig. 6

P–P plots of the fitted distributions

9.2 Second Data Set

The data set comprises monthly actual taxes revenue in Egypt from January 2006 to November 2010 in 1000 million Egyptian pounds. The data can be found in [14] and are given in Table 7.

Table 7 Egypt tax data in 1000 million Egyptian pounds

The maximum likelihood estimates with their corresponding standard errors in brackets for the fitted distributions are given in Table 8.

Table 8 Maximum likelihood estimates of parameters and standard errors

The EGLIE distribution provides a better fit to the tax data as compared to the other fitted distributions. With the exception of the K–S, all other model selection technique selected the EGLIE distribution as the best distribution for the tax data as shown in Table 9.

Table 9 Log-likelihood, goodness-of-fit statistics and information criteria

Figure 7 displays the plots of the empirical density, the fitted distributions, the empirical CDF and the CDF of the fitted distributions for the tax data.

Fig. 7

Empirical and fitted density and CDF plots of tax data

The P–P plots for the fitted distributions are given in Fig. 8. From Fig. 8, it can be seen that the EGLIE distribution provides a more reasonable parametric fit to the tax data.

Fig. 8

P–P plots of the fitted distributions for tax data

10 Conclusion

This study proposed and studied the properties of the EGPS family of distributions. Various statistical properties such as the quantile function, moment, moment generating function, incomplete moment, reliability, residual life, mean residual life, Shannon entropy and order statistics were derived. The method of maximum likelihood estimation was proposed for the estimation of the parameters of the family. Bivariate and multivariate extensions of the family was proposed using the Clayton copula. Some special distributions were defined and Monte Carlo simulations were performed to investigate the finite sample properties of the estimators for the parameters of the special distributions. The results of the simulation revealed the parameters of the distributions were stable with regards to the estimation techniques. Finally, applications of the special distributions were illustrated using real data sets.