The Exponentiated Generalized Marshall–Olkin Family of Distribution: Its Properties and Applications

Abstract

A new generator of continuous distributions called Exponentiated Generalized Marshall–Olkin-G family with three additional parameters is proposed. This family of distribution contains several known distributions as sub models. The probability density function and cumulative distribution function are expressed as infinite mixture of the Marshall–Olkin distribution. Important properties like quantile function, order statistics, moment generating function, probability weighted moments, entropy and shapes are investigated. The maximum likelihood method to estimate model parameters is presented. A simulation result to assess the performance of the maximum likelihood estimation is briefly discussed. A distribution from this family is compared with two sub models and some recently introduced lifetime models by considering three real life data fitting applications.

1 Introduction

In recent years, many different methods of generating new continuous distributions by adding one or more parameters to the classical ones were developed and some new families of distributions have been introduced in the statistical literature. The Marshall–Olkin generated family by Marshall and Olkin [16], exponentiated generalized class of distribution studied by Cordeiro et al. [4], exponentiated Marshall–Olkin-G family Dias et al. [7], exponentiated generalized Half-logistic distribution by Thiago et al. [22], Marshall–Olkin Kumaraswamy-G family by Handique et al. [12], Kumaraswamy Marshall–Olkin-G family Alizadeh et al. [2], Kumaraswamy generalized Marshall–Olkin-G family by Chakraborty and Handique [6], generalized Marshall–Olkin Kumaraswamy-G family by Chakraborty and Handique [5], beta Marshall–Olkin-G family by Alizadeh et al. [3], beta generalized Marshall–Olkin-G family by Handique and Chakraborty [9], beta generated Kumaraswamy-G family by Handique et al. [13], beta generated Kumaraswamy Marshall–Olkin-G by Handique and Chakraborty [10] and beta generalized Marshall–Olkin Kumaraswamy-G by Handique and Chakraborty [11] are some of the notable ones among others.

In this paper we introduce a new extension of Marshall–Olkin-G [${\text{MO-G}}(\alpha ,\varvec{\eta})$] family of distribution by considering it as the baseline distribution in the exponentiated generalized [${\text{E-G}}(a,b,\varvec{\eta})$] class of distribution studied by Cordeiro et al. [4]. We refer to this new family of distribution as the Exponentiated Generalized Marshall–Olkin [${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ for short] which encompasses many known families of distributions and study some of its general properties, parameter estimation and data modelling applications. The cumulative distribution function (cdf), probability density function (pdf), survival function (sf) and hazard rate function (hrf) of this proposed family of distribution are respectively given by

$$ F^{\text{EGMO-G}} (x;a,b,\alpha ,\varvec{\eta}) = [1 - [{{\alpha \bar{G}(x)}/ {\{ 1 - \bar{\alpha }\bar{G}(x)\} }}]^{a} ]^{b} , $$

(1)

$$ f^{\text{EGMO-G}} (x;a,b,\alpha ,\varvec{\eta}) = \frac{{ab\alpha^{a} g(x)\bar{G}(x)^{a - 1} [\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} ]^{b - 1} }}{{[1 - \bar{\alpha }\bar{G}(x)]^{ab + 1} }}, $$

(2)

$$ \bar{F}^{\text{EGMO-G}} (x;a,b,\alpha ,\varvec{\eta}) = 1 - [1 - [{{\alpha \bar{G}(x)} / {\{ 1 - \bar{\alpha }\bar{G}(x)\} }}]^{a} ]^{b} $$

(3)

$$ {\text{and}}\;{\text{hrf}}\;h^{\text{EGMO-G}} (x;a,b,\alpha ,\varvec{\eta}) = \frac{{ab\alpha^{a} g(x)\bar{G}(x)^{a - 1} [\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} ]^{b - 1} }}{{[1 - \bar{\alpha }\bar{G}(x)]\{ [1 - \bar{\alpha }\bar{G}(x)]^{ab} - [\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} ]^{b} \} }}. $$

(4)

where $\bar{G}(x)$ and $g(x)$ is the baseline sf and pdf respectively and $- \infty < x < \infty ,\alpha > 0,a > 0,b > 0$ and $\varvec{\eta}$ is the parameter vector of the baseline distribution.

For $\alpha = 1$, we get back ${\text{E-G}}(a,b,\varvec{\eta})$, which in turn reduces to ${\text{MO-G}}(\alpha ,\varvec{\eta})$ when $a,b = 1$.

1.1 Physical Basis of EGMO-G

For $a\;{\text{and}}\;b$ are positive integers consider a parallel system comprising of b independent components. Suppose that, each of this component again comprises of a serially connected subcomponents which are identically independently distributed with cdf $F^{\text{MOG}} (x; \alpha, {\varvec{\eta}})$. Let $X_{i1} ,X_{i2} , \ldots ,X_{ia}$ denote the lifetimes of the subcomponents within the jth component, $j = 1,2, \ldots ,b$ and $X_{j}$ denote the lifetime of the jth component. Then for the lifetime of the system $X$ we have

$$ \begin{aligned} P(X \le x) & = P(X_{1} \le x,X_{2} \le x, \ldots ,X_{b} \le x) = P(X_{1} \le x)^{b} = [1 - P(X_{1} > x)]^{b} \\ & = [1 - P(X_{11} > x,X_{12} > x, \ldots ,X_{1a} > x)]^{b} \\ & = [1 - P(X_{11} > x)^{a} ]^{b} \\ & = [1 - \{ 1 - P(X_{11} \le x)\}^{a} ]^{b} = [1 - \{ 1 - F^{{{\text{MOG}}}} (x; \alpha, \varvec{\eta})\}^{a} ]^{b} \\ & = [1 - [{{\alpha \bar{G}(x)} / {\{ 1 - \bar{\alpha }\bar{G}(x)\} }}]^{a} ]^{b} \\ \end{aligned} $$

This is the cdf of ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$.

The primary motivation of proposed family is to derived a new extension of the MO-G distribution by inducting three additional parameters with an aim of (1) bring in more flexibility with respect to skewness, kurtosis, tail weight and length, (2) Covering some important known distributions as particular and related cases and (3) Providing significant improvement in data modelling.

The rest of this article is organized in five more Sections. In Sect. 2 some important sub models are derived drop these words for the family. In the next section we discuss few important general results of the proposed family. In Sect. 4 different methods of estimation of parameters are presented. We present real life examples of comparative data fitting in Sect. 5. The paper ends with concluding remarks in the final Section.

2 Special Models and Shapes of the Density and Hazard Function

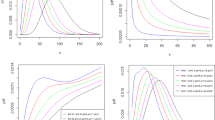
In this section we provide some special cases of the ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ family of distributions of namely (a) $\text{EGMO-E}(a,b,\alpha ,\lambda )$, (b) $\text{EGMO-W}(a,b,\alpha ,\beta ,\gamma )$ and (c) $\text{EGMO-L}(a,b,\alpha ,\beta ,\gamma )$ by taking Exponential $(\lambda )$, Weibull $(\beta ,\gamma )$ and Lomax $(\beta ,\gamma )$ as the base line G and plotted the pdf and hrf for some choices of the parameters to study the variety of shapes assumed by the family.

2.1 The EGMO-Exponential (EGMO-E) Distribution

Let the base line distribution be exponential with parameter $\lambda > 0,g(x) = \lambda e^{ - \lambda x}$ and $G(x) = 1 - e^{ - \lambda x} ,$$x > 0$, then for the $\text{EGMO-E}(a,b,\alpha ,\lambda )$ model we get the pdf, cdf and hrf respectively as

$$ \begin{aligned} f^{\text{EGMO-E}} (x;a,b,\alpha ,\lambda ) & = \frac{{ab\alpha^{a} \lambda (e^{ - \lambda x} )^{a} [\{ 1 - \bar{\alpha }e^{ - \lambda x} \}^{a} - \alpha^{a} (e^{ - \lambda x} )^{a} ]^{b - 1} }}{{[1 - \bar{\alpha }e^{ - \lambda x} ]^{ab + 1} }}, \\ F^{\text{EGMO-E}} (x;a,b,\alpha ,\lambda ) & = [1 - [{{\alpha e^{ - \lambda x} } / {\{ 1 - \bar{\alpha }e^{ - \lambda x} \} }}]^{a} ]^{b} \;{\text{and}} \\ h^{\text{EGMO-E}} (x;a,b,\alpha ,\lambda ) & = \frac{{ab\alpha^{a} \lambda (e^{ - \lambda x} )^{a} [\{ 1 - \bar{\alpha }e^{ - \lambda x} \}^{a} - \alpha^{a} (e^{ - \lambda x} )^{a} ]^{b - 1} }}{{[1 - \bar{\alpha }e^{ - \lambda x} ]\{ [1 - \bar{\alpha }e^{ - \lambda x} ]^{ab} - [\{ 1 - \bar{\alpha }e^{ - \lambda x} \}^{a} - \alpha^{a} (e^{ - \lambda x} )^{a} ]^{b} \} }}. \\ \end{aligned} $$

2.2 The EGMO-Weibull (EGMO-W) Distribution

Taking the Weibull distribution [23] with parameters $\beta > 0$ and $\gamma > 0$ having pdf and cdf $g(x) = \gamma \beta x^{\beta - 1} e^{{ - \gamma x^{\beta } }}$ and $G(x) = 1 - e^{{ - \gamma x^{\beta } }}$, $x > 0$ respectively we get the pdf, cdf and hrf of $\text{EGMO-W}(a,b,\alpha ,\beta ,\gamma )$ distribution respectively as

$$ \begin{aligned} f^{{{\text{EGMO-W}}}} (x;a,b,\alpha ,\beta ,\gamma ) & = \frac{{ab\alpha ^{a} \gamma \beta x^{{\beta-1}} (e^{{-\gamma x^{\beta } }} )^{a} [\{ 1-\bar{\alpha }e^{{-\gamma x^{\beta } }} \} ^{a}-\alpha ^{a} (e^{{-\gamma x^{\beta } }} )^{a} ]^{{b-1}} }}{{[1-\bar{\alpha }e^{{-\gamma x^{\beta } }} ]^{{ab + 1}} }}, \\ F^{{{\text{EGMO-W}}}} (x;a,b,\alpha ,\beta ,\gamma ) & = [1-[\alpha e^{{-\gamma x^{\beta } }} /\{ 1-\bar{\alpha }e^{{-\gamma x^{\beta } }} \} ]^{a} ]^{b} \;{\text{and}} \\ h^{{{\text{EGMO-W}}}} (x;a,b,\alpha ,\beta ,\gamma ) & = \frac{{ab\alpha ^{a} \gamma \beta x^{{\beta-1}} (e^{{-\gamma x^{\beta } }} )^{a} [\{ 1-\bar{\alpha }e^{{-\gamma x^{\beta } }} \} ^{a}-\alpha ^{a} (e^{{-\gamma x^{\beta } }} )^{a} ]^{{b-1}} }}{{[1-\bar{\alpha }e^{{-\gamma x^{\beta } }} ] [(1-\bar{\alpha }e^{{-\gamma x^{\beta } }} )^{{ab}}-\{( 1-\bar{\alpha }e^{{-\gamma x^{\beta } }} ) ^{a}-\alpha ^{a} (e^{{-\gamma x^{\beta } }} )^{a} \}^{b} ] }}. \\ \end{aligned} $$

2.3 The EGMO-Lomax (EGMO-L) Distribution

Considering the Lomax distribution [15] with pdf and cdf given by $g(x) = ({{\beta } / \gamma })[1 + ({x / \gamma })]^{ - (\beta + 1)}$ and $G(x) = 1 - [1 + ({x / \gamma })]^{ - \beta } ,$$x > 0,\beta > 0$ and $\gamma > 0$ the pdf, cdf and hrf of $\text{EGMO-L}(a,b,\alpha ,\beta ,\gamma )$ distribution are respectively given by

$$ \begin{aligned} f^{\text{EGMO-L}} (x;a,b,\alpha ,\beta ,\gamma ) & = \frac{{ab\alpha^{a} ({{\beta } / \gamma })[1 + ({x / \gamma })]^{ - (a\beta + 1)} }}{{[1 - \bar{\alpha }\{ [1 + ({x / \gamma })]^{ - \beta } \} ]^{ab + 1} }} \times [\{ 1 - \bar{\alpha }[1 + ({x / \gamma })]^{ - \beta } \}^{a} \\ & \quad - \alpha^{a} [1 + ({x / \gamma })]^{ - \beta a} ]^{b - 1} , \\ F^{\text{EGMO-L}} (x;a,b,\alpha ,\beta ,\gamma ) & = [1 - [{{\alpha [1 + ({x / \gamma })]^{ - \beta } } / {\{ 1 - \bar{\alpha }[1 + ({x / \gamma })]^{ - \beta } \} }}]^{a} ]^{b} \;{\text{and}} \\ h^{\text{EGMO-L}} (x;a,b,\alpha ,\beta ,\gamma ) & = \frac{{ab\alpha^{a} ({{\beta } / \gamma })[1 + ({x / \gamma })]^{ - (\beta + 1)} \{ [1 + ({x /\gamma })]^{ - \beta } \} ^{a - 1} }}{{[1 - \bar{\alpha }[1 + ({x / \gamma })]^{ - \beta } ]\left( {[1 - \bar{\alpha }[1 + ({x /\gamma })]^{ - \beta } ]^{ab} } \right.}} \\ & \quad \times \frac{{[\{ 1 - \bar{\alpha }\{ [1 + ({x /\gamma })]^{ - \beta } \} \}^{a} - \alpha^{a} [1 + ({x / \gamma })]^{ - \beta a} ]^{b - 1} }}{{\left. { - [\{ 1 - \bar{\alpha }[1 + ({x / \gamma })]^{ - \beta } \}^{a} - \alpha^{a} [1 + ({x /\gamma })]^{ - \beta a} ]^{b} \} } \right)}}. \\ \end{aligned} $$

From the plots in Figs. 1 and 2 it can be seen that the family is very flexible and can offer different types of shapes for density and hazard like increasing, decreasing, right skewed, including bathtub shape for hazard.

Fig. 1

Density plots of a EGMO-E, b EGMO-W and c EGMO-L

Fig. 2

Hazard plots of a EGMO-E, b EGMO-W and c EGMO-L

3 Mathematical and Statistical Properties

3.1 Linear Representation in Terms of Exponentiated-${\text{MO-G}}(\alpha ,\varvec{\eta})$

We consider the binomial expansion

$$ (1 - z)^{c} = \sum\limits_{k = 0}^{\infty } {( - 1)^{k} } \left( \begin{array}{c} c \\ k \end{array} \right)z^{k} , $$

(5)

which holds for any integer $c\;{\text{and}}\;\left| z \right| < 1$. Using expansion (5) in Eq. (1), for $\alpha \in (0,1)$, we can express the ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ cdf as

$$ \begin{aligned} F^{\text{EGMO-G}} (x;a,b,\alpha ,\varvec{\eta}) & = [1 - [{{\alpha \bar{G}(x)} / {\{ 1 - \bar{\alpha }\bar{G}(x)\} }}]^{a} ]^{b} \\ & = \sum\limits_{m = 0}^{\infty } {( - 1)^{m} \left( \begin{array}{c} b \\ m \end{array} \right)} \bar{F}^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{am} \\ & = \sum\limits_{m = 0}^{\infty } {( - 1)^{m} \left( \begin{array}{c} b \\ m \end{array} \right)\sum\limits_{j = 0}^{\infty } {( - 1)^{j} \left( \begin{array}{c} am \\ j \end{array} \right)} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j} \\ & = \sum\limits_{j = 0}^{\infty } {\omega_{j} ^{\prime}} F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j} \\ \end{aligned} $$

(6)

By differentiating (6), we obtain

$$ f^{\text{EGMO-G}} (x;a,b,\alpha ,\varvec{\eta}) = f^{\text{MO-G}} (x;\alpha )\sum\limits_{j = 0}^{\infty } {\omega_{j} } F^{\text{MO}} (x;\alpha ,\varvec{\eta})^{j-1} $$

(7)

$$ = \sum\limits_{j = 0}^{\infty } {\omega_{j}^{\prime} } \frac{d}{dx}F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j} $$

(8)

where $\omega_{j}^{\prime} = \sum\nolimits_{m = 0}^{\infty } {( - 1)^{j + m} \left( \begin{array}{c} b \\ m \end{array} \right)\left( \begin{array}{c} ma \\ j \end{array} \right)}$ and $\omega_{j} = j\omega_{j}^{\prime}$.

Equations (6) and (8) reveal that the cdf and pdf of ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ are linear combination of corresponding functions of exponentiated-${\text{MO-G}}(\alpha ,\varvec{\eta})$.

3.2 Quantile Function and Related Results

Inverting the cdf we get

$$ x = G^{ - 1} \left[ {1 - \frac{{\{ 1 - F^{\text{EGMO-G}} (x;a, b, \alpha, \varvec{\eta})^{1/b} \}^{1/a} }}{{\alpha + \bar{\alpha }\{ 1 - F^{\text{EGMO-G}} (x;a, b, \alpha, \varvec{\eta})^{1/b} \}^{1/a} }}} \right]. $$

Using this formula we can generate a random number x from ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ given a uniform random number u as

$$ x = G^{ - 1} [1 - \{ {{(1 - u^{1/b} )^{1/a} } / {(\alpha + \bar{\alpha }(1 - u^{1/b} )^{1/a} )\} }}]. $$

The pth quantile $x_{p}$ for ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ can be easily seen as

$$ x_{p} = G^{ - 1} [1 - \{ {{(1 - p^{1/b} )^{1/a} } / {(\alpha + \bar{\alpha }(1 - p^{1/b} )^{1/a} )\} }}], $$

hence the median is given by

$$ x_{0.5} = G^{ - 1} [1 - \{ {{(1 - 0.5^{1/b} )^{1/a} } / {(\alpha + \bar{\alpha }(1 - 0.5^{1/b} )^{1/a} )\} }}] $$

The Bowley skewness [14] measures and Moors kurtosis [17] measure are robust and less sensitive to outliers and exist even for distributions without moments. For ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ family these measures are given by

$$ B = \frac{{x_{(3/4)} + x_{(1/4)} - 2x_{(1/2)} }}{{x_{(3/4)} - x_{(1/4)} }}\quad {\text{and}}\quad M = \frac{{x_{(3/8)} - x_{(1/8)} + x_{(7/8)} - x_{(5/8)} }}{{x_{(6/8)} - x_{(2/8)} }} $$

For example, when G is taken as the exponential distribution with parameter $\lambda > 0$, the pth quantile is given by $- (1/\lambda )\log [1 - p]$. Therefore, the pth quantile $x_{p}$, of $\text{EGMO-E}(a,b,\alpha ,\lambda )$ is obtained as

$$ x_{p} = - \frac{1}{\lambda }\log [1 - [1 - \{ (1 - u^{1/b} )^{1/a} /(\alpha + \bar{\alpha }(1 - u^{1/b} )^{1/a} )\} ]] $$

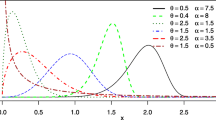
3.2.1 Plots of the Bowley Skewness and Moors Kurtosis

From the Figs. 3 and 4 it is easily seen that the flexibility of both the skewness and kurtosis are controlled by the additional parameters $a,b\;{\text{and}}\;\alpha$.

Fig. 3

Bowley skewness of EGMO-E distribution in (i) and (ii) as a function of $a$ when $\alpha = 1.5,\lambda = 1$ for some values $b > 1\;{\text{and}}\;b < 1$ respectively and in (iii) and (iv) as a function of $a$ when $b = 0.6,\lambda = 1$ for some values $\alpha > 1\;{\text{and}}\;\alpha < 1$ respectively

Fig. 4

Moors Kurtosis of EGMO-E distribution in (i) and (ii) as a function of $a$ when $\alpha = 1.5,\lambda = 5.5$ for some values $b > 1\;{\text{and}}\;b < 1$ respectively and in (iii) and (iv) as a function of $a$ when $b = 1.6,\lambda = 1$ for some values $\alpha > 1\;{\text{and}}\;\alpha < 1$ respectively

3.3 Distribution of Order Statistics

Suppose $X_{1} ,X_{2} , \ldots ,X_{n}$ is a random sample from any distribution belonging ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ family. Let $X_{r:n}$ denote the rth order statistics. The pdf of $X_{r:n}$ can be expressed as

$$ f_{r:n} (x) = \frac{n!}{(r - 1)!(n - r)!}\sum\limits_{j = 0}^{n - r} {( - 1)^{j} \left( \begin{array}{c} n - r \\ j \end{array} \right)} f^{{{\text{EGMO-G}}}} (x;a, b, \alpha, \varvec{\eta})F^{{{\text{EGMO-G}}}} (x;a, b, \alpha, \varvec{\eta})^{j + r - 1} $$

Now using the general expansions of the ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ pdf and cdf in Sect. 3.1 we get the pdf of the rth order statistics for of the ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ as

$$ \begin{aligned} f_{r:n} (x) & = \frac{n!}{(r - 1)!(n - r)!}\sum\limits_{j = 0}^{n - r} {( - 1)^{j} \left( {\begin{array}{*{20}c} {n - r} \\ j \\ \end{array} } \right)} f^{\text{MO-G}} (x;\alpha ,\varvec{\eta})\sum\limits_{k = 0}^{\infty } {\omega_{k} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{k - 1} \\ & \quad \times \left[ {\sum\limits_{l = 0}^{\infty } {\omega_{l}^{\prime } } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{l} } \right]^{j + r - 1} \\ \end{aligned} $$

where $\omega_{k}$ and $\omega_{l}^{\prime }$ are defined Sect. 3.1.

Now

$$ \left[ {\sum\limits_{l = 0}^{\infty } {\omega_{l}^{{\prime }} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{l} } \right]^{j + r - 1} = \sum\limits_{l = 0}^{\infty } {d_{j + r - 1,l} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{l} $$

where $d_{j + r - 1,l} = \frac{1}{{l\omega_{0}^{\prime } }}\sum\nolimits_{c = 1}^{l} {[c(j + r) - k]\omega_{l}^{\prime } d_{j + r - 1,l - c} }$ [19].

Therefore the pdf of the rth order statistic of ${\text{EGMO-G}}(a,b,\alpha ,\varvec{\eta})$ distribution can be expressed as

$$ \begin{aligned} f_{r:n} (x) & = \frac{n!}{(r - 1)!(n - r)!}\sum\limits_{j = 0}^{n - r} {( - 1)^{j} \left( \begin{array}{c} n - r \\ j \end{array} \right)} f^{\text{MO-G}} (x;\alpha ,\varvec{\eta})\sum\limits_{k = 0}^{\infty } {\omega_{k} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{k - 1} \\ & \quad \times \sum\limits_{l = 0}^{\infty } {d_{j + r - 1,l} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{l} \\ & = \frac{n!}{(r - 1)!(n - r)!}\sum\limits_{j = 0}^{n - r} {( - 1)^{j} \left( \begin{array}{c} n - r \\ j \end{array} \right)}\\ & \quad \times\,\left[ {f^{\text{MO-G}} (x;\alpha ,\varvec{\eta})} { \sum\limits_{k,l = 0}^{\infty } {\omega_{k} } d_{j + r - 1,l} F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{k + l - 1} } \right] \\ & = f^{\text{MO-G}} (x;\alpha ,\varvec{\eta})\sum\limits_{k,l = 0}^{\infty } {\lambda_{k,l} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{k + l - 1} \\ \end{aligned} $$

(9)

where $\lambda_{k,l} = \frac{n!}{(r - 1)!(n - r)!}\sum\nolimits_{j = 0}^{n - r} {{\mkern 1mu} ( - 1)^{{{\kern 1pt} j}} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {\begin{array}{*{20}c} {n - r} \\ j \\ \end{array} } \right)} \omega_{k} d_{j + r - 1,l}$, $d_{j + r - 1,l} = \frac{1}{{l\omega_{0}^{\prime } }}\sum\nolimits_{c = 1}^{l} {{\mkern 1mu} [c{\mkern 1mu} (j + r) - k]{\mkern 1mu} \omega_{{{\kern 1pt} l}}^{\prime } {\mkern 1mu} d_{{j + r - 1{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} l{\kern 1pt} - c}} }$, $\omega_{k}$ and $\omega_{l}^{\prime}$ defined in above.

3.4 Probability Weighted Moment

The probability weighted moments (PWMs), first proposed by Greenwood et al. [8], are expectations of certain functions of a random variable whose mean exists. The $(p,q,r){\text{th}}$ PWM of $X$ is having cdf $F(x)$ defined by

$$ \varGamma_{p,q,r} = \int\limits_{ - \infty }^{\infty } {x^{p} } [F(x)]^{q} [1 - F(x)]^{r} f(x)dx $$

From Eq. (7) the sth moment of $X$ can be expressed as

$$ \begin{aligned} E(X^{s} ) & = \int\limits_{ - \infty }^{ + \infty } {x^{s} f^{\text{MO-G}} (x;\alpha ,\varvec{\eta})\sum\limits_{j = 0}^{\infty } {\omega_{j} } F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j - 1} dx} \\ & = \sum\limits_{j = 0}^{\infty } {\omega_{j} } \int\limits_{ - \infty }^{ + \infty } {x^{s} F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j - 1} f^{\text{MO-G}} (x;\alpha ,\varvec{\eta})} dx \\ & = \sum\limits_{j = 0}^{\infty } {\omega_{j} \varGamma_{s,j - 1,0}^{\text{MO-G}} } \\ \end{aligned} $$

where $\Gamma _{p,q,r}^{\text{MO-G}} = \int\limits_{ - \infty }^{\infty } {x^{p} } \{ F^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})\}^{q} \{ \bar{F}^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})\}^{r} [f^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})]dx$ is the PWM of ${\text{MO-G}}(\alpha ,\varvec{\eta})$ distribution.

Proceeding as above we can derive sth moment of the rth order statistic $X_{r:n}$, on using Eq. (9) as $E(X_{r,n}^{s} ) = \sum\nolimits_{k,l = 0}^{\infty } {\lambda_{k,l} \varGamma_{sk + l - 1,0}^{\text{MO-G}} }$, where $\omega_{j}$ and $\lambda_{k,l}$ are defined in Sect. 3.1 and 3.2.

3.5 Moment Generating Function (mgf)

The mgf of $\text{EGMO-G}(a,b,\alpha ,\varvec{\eta})$ family can be easily expressed in terms of those of the exponentiated ${\text{MO-G}}(\alpha ,\varvec{\eta})$ distribution using the results of Sect. 3.1. For example, using Eq. (8), it can be seen that

$$ \begin{aligned} M_{X} (s) = E[e^{sx} ] & = \int\limits_{ - \infty }^{\infty } {e^{sx} } f^{{{\text{EGMO-G}}}} (x;a, b, \alpha, \varvec{\eta})dx \\ & = \int\limits_{ - \infty }^{\infty } {e^{st} } \sum\limits_{j = 0}^{\infty } {\omega_{j}^{\prime } } \frac{d}{dx}F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j} dx \\ & = \sum\limits_{j = 0}^{\infty } {\omega_{j}^{\prime} } \int\limits_{ - \infty }^{\infty } {e^{sx} } \frac{d}{dx}F^{\text{MO-G}} (x;\alpha ,\varvec{\eta})^{j} dx = \sum\limits_{j = 0}^{\infty } {\omega_{j} } M_{X} (s), \\ \end{aligned} $$

where $\omega_{j}$ is define in Sect. 3.1 and X has exponentiated ${\text{MO-G}}(\alpha ,\varvec{\eta})$ distribution.

3.6 Rényi Entropy

The entropy of a random variable is a measure of uncertainty. The Rényi entropy is defined as $I_{R} (\delta ) = (1 - \delta )^{ - 1} \log \left( {\int\nolimits_{ - \infty }^{\infty } {f(t)^{\delta } dt} } \right)$ (for details, see [21]), where $\delta > 0$ and $\delta \ne 1$. Using expansion given in Eq. (5) in Eq. (2) we can write for $\alpha \in (0,1)$

$$ \begin{aligned} f^{\text{EGMO-G}} (x)^{\delta } & = \{ ab[\bar{F}^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})]^{a - 1} [1 - \{ \bar{F}^{{{\text{MO}}}} (x;\alpha ,\varvec{\eta})\}^{a} ]^{b - 1} f^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})\}^{\delta } \\ & = (ab)^{\delta } f^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})^{\delta } \sum\limits_{j,k = 0}^{\infty } {( - 1)^{j + k} } \left( {\begin{array}{*{20}c} {\delta (b - 1)} \\ j \\ \end{array} } \right){\mkern 1mu} \left( {\begin{array}{*{20}c} {a{\mkern 1mu} (j + \delta ) - \delta } \\ k \\ \end{array} } \right)\{ F^{{{\text{MO-G}}}} (x;\alpha ,\varvec{\eta})\}^{k} \\ \end{aligned} $$

Thus for $\alpha \in (0,1)$, the Rényi entropy of $\text{EGMO-G}(a,b,\alpha ,\varvec{\eta})$ can be obtained as

$$ I_{R} (\delta ) = (1 - \delta )^{ - 1} \log \left( {\sum\limits_{j,k = 0}^{\infty } {\xi_{j,k} } \int\limits_{ - \infty }^{\infty } {\left[ {\frac{\alpha g(x)}{{[1 - \bar{\alpha }\bar{G}(x)]^{2} }}} \right]^{\delta } \left[ {\frac{G(x)}{{\{ 1 - \bar{\alpha }\bar{G}(x)\} }}} \right]^{k} dx} } \right), $$

where $\xi_{j,k} = (ab)^{\delta } ( - 1)^{j + k} \left( {\begin{array}{*{20}c} {\delta (b - 1)} \\ j \\ \end{array} } \right){\mkern 1mu} {\mkern 1mu} \left( {\begin{array}{*{20}c} {a{\mkern 1mu} (j + \delta ) - \delta } \\ k \\ \end{array} } \right)$.

3.7 Shapes

The shapes of the pdf and hrf can be described analytically. The critical points of the pdf of the EGMO-G family are the roots of the equation: $\frac{d}{dx}\log [f^{{{\text{EGMO-G}}}} (x;a, b, \alpha, \varvec{\eta})] = 0$

$$\begin{aligned} &\Rightarrow \frac{{g^{\prime}(x)}}{g(x)} + (1 - a)\frac{g(x)}{{\bar{G}(x)}} + (b - 1)\frac{{a(1 - \bar{\alpha }\bar{G}(x))^{a - 1} \bar{\alpha }g(x) + a\alpha^{a} \bar{G}(x)^{a - 1} g(x)}}{{\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} }}\\ &\quad - (ab + 1)\frac{{\bar{\alpha }g(x)}}{{1 - \bar{\alpha }\bar{G}(x)}} = 0 \end{aligned}$$

(10)

The critical point of the hrf of the EGMO-G family the roots of the equation: $\frac{d}{dx}\log [h^{\text{EGMO-G}} (x;a, b, \alpha, \varvec{\eta})] = 0$

$$ \begin{aligned} & \Rightarrow \frac{{g^{\prime}(x)}}{g(x)} + (1 - a)\frac{g(x)}{{\bar{G}(x)}} + (b - 1)\frac{{a(1 - \bar{\alpha }\bar{G}(x))^{a - 1} \bar{\alpha }g(x) + a\alpha^{a} \bar{G}(x)^{a - 1} g(x)}}{{\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} }} - \frac{{\bar{\alpha }g(x)}}{{1 - \bar{\alpha }\bar{G}(x)}} \\ & \quad - \frac{{ab[1 - \bar{\alpha }\bar{G}(x)]^{ab} - \{ [\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} ]^{b - 1} a(1 - \bar{\alpha }\bar{G}(x))^{a - 1} \bar{\alpha }g(x) + a\alpha^{a} \bar{G}(x)^{a - 1} g(x)\} }}{{[1 - \bar{\alpha }\bar{G}(x)]^{ab} - [\{ 1 - \bar{\alpha }\bar{G}(x)\}^{a} - \alpha^{a} \bar{G}(x)^{a} ]^{b} }} = 0 \\ \end{aligned} $$

(11)

There may be more than one root Eqs. (10) and (11). If $x = x_{0}$ is a root of the (10) then it corresponds to a local maximum, a local minimum or a point of inflexion depending on whether $\psi (x_{0} ) < 0,\psi (x_{0} ) < 0\,or\,\psi (x_{0} ) = 0$ and similarly for (11) $\omega (x_{0} ) < 0,\omega (x_{0} ) < 0\,or\,\omega (x_{0} ) = 0$ where $\psi (x) = {{(d^{2} } / {dx^{2} }})\log [f^{\text{EGMO-G}} (x;a, b, \alpha, {\varvec{\eta}})]$ and $\omega (x) = {{(d^{2} } / {dx^{2} }})\log [h^{\text{EGMO-G}} (x;a, b, \alpha, \varvec{\eta})]$.

We have illustrated the application of the above results graphically for EGMO-E by considering same set of values of the parameters for which we have plotted its pdfs in Fig. 1a. It can be seen that except for the yellow coloured all the other curves of ${{(d} / {dx)}}\log [f^{\text{EGMO-E}} (x)]$ cuts the horizontal axis (form Fig. 5a) and $\psi (x) = {{(d^{2} } / {dx^{2} }})\log [f^{\text{EGMO-E}} (x)] < 0$ (see Fig. 5b) i.e. the corresponding pdfs $f^{\text{EGMO-E}} (x)$ are log-concave and unimodal. The exception of yellow coloured curve is because the corresponding pdf $f^{\text{EGMO-E}} (x)$ is a decreasing function (see Fig. 1a) with maximum at zero. Similar conclusion can be drawn for the plots of ${{(d} / {dx)}}\log [h^{\text{EGMO-E}} (x)]$ and $\omega (x) = {{(d^{2} } / {dx^{2} }})\log [h^{\text{EGMO-E}} (x)] < 0$ (see Fig. 6a, b).

Fig. 5

1st and 2nd derivative of the log of density function of the EGMO-E

Fig. 6

1st and 2nd derivative of the log of hazard function of the EGMO-E

4 Estimation

In this section, parameters estimation of the $\text{EGMO-G}(a,b,\alpha ,\varvec{\eta})$ distribution is presented using the maximum likelihood method.

4.1 Maximum Likelihood Estimation

The model parameters of the $\text{EGMO-G}(a,b,\alpha ,\varvec{\eta})$ distribution can be estimated by maximum likelihood. Let ${\mathbf{X}} = (x_{1} ,x_{2} , \ldots ,x_{r} )^{\prime }$ be a random sample of size $r$ from $\text{EGMO-G}(a,b,\alpha ,\varvec{\eta})$ with parameter vector $\vartheta = (a,b,\alpha ,\varvec{\eta}^{T} )^{\prime}$, where $\varvec{\eta}= (\eta_{1} ,\eta_{2} , \ldots ,\eta_{q} )^{\prime}$ corresponds to the parameter(s) of the baseline distribution G. Then the log-likelihood function is given by

$$ \begin{aligned} \ell = \ell (\vartheta ) & = r\log (ab) + ra\log (\alpha ) + \sum\limits_{i = 1}^{r} {\log [g(x_{i} ,\varvec{\eta})]} + (a - 1)\sum\limits_{i = 1}^{r} {\log [\bar{G}(x_{i} ,\varvec{\eta})]} \\ & \quad + (b - 1)\sum\limits_{i = 1}^{r} {\log [\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a} ]} - \alpha^{a} \bar{G}(x_{i} ,\varvec{\eta})^{a} ] \\ \end{aligned} $$

This log-likelihood function can not be solved analytically because of its complex form but it can be maximized numerically by employing global optimization methods in R.

By taking the partial derivatives of the log-likelihood function with respect to $a,b,\alpha$ and $\varvec{\eta}$ components of the score vector $U_{\vartheta } = (U_{a} ,U_{b} ,U_{\alpha } ,U_{{\varvec{\eta}^{T} }} )^{T}$ can be obtained as follows:

$$ \begin{aligned} U_{a} & = \frac{\partial \ell }{\partial a} = \frac{r}{a} + r\log (\alpha ) + \sum\limits_{i = 1}^{r} {\log [\bar{G}(x_{i} ,\varvec{\eta})]} + (b - 1) \\ & \quad \times \sum\limits_{i = 1}^{r} {\frac{{\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a} \log [1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})] - [\alpha \bar{G}(x_{i} ,\varvec{\eta})]^{a} \log [\alpha \bar{G}(x_{i} ,\varvec{\eta})]}}{{\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a} - [\alpha \bar{G}(x_{i} ,\varvec{\eta})]^{a} }}} \\ & \quad - b\sum\limits_{i = 1}^{r} {\log [1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})} ] \\ U_{b} & = \frac{\partial \ell }{\partial b} = \frac{r}{b} + \sum\limits_{i = 1}^{r} {\log [\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a} ]} - \alpha^{a} \bar{G}(x_{i} ,\varvec{\eta})^{a} ] - a\sum\limits_{i = 1}^{r} {\log [1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})} ] \\ U_{\alpha } & = \frac{\partial \ell }{\partial \alpha } = \frac{r}{\alpha } + (b - 1)\sum\limits_{i = 1}^{r} {\frac{{a\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a - 1} \bar{G}(x_{i} ,\varvec{\eta}) - a\alpha^{a - 1} \bar{G}(x_{i} ,\varvec{\eta})^{a} }}{{\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a} - [\alpha \bar{G}(x_{i} ,\varvec{\eta})]^{a} }}} \\ & \quad - (ab + 1)\sum\limits_{i = 1}^{r} {\frac{{\bar{G}(x_{i} ,\varvec{\eta})}}{{1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})}}} \\ U_{{\varvec{\eta}}} & = \frac{\partial \ell }{{\partial \varvec{\eta}}} = \sum\limits_{i = 1}^{n} {\frac{{g^{{(\varvec{\eta})}} (x_{i} ,\varvec{\eta})}}{{g(x_{i} ,\varvec{\eta})}} + (a - 1)\sum\limits_{i = 1}^{n} {\frac{{G^{{(\varvec{\eta})}} (x_{i} ,\varvec{\eta})}}{{G(x_{i} ,\varvec{\eta})}}} } \\ & \quad + (b - 1)\sum\limits_{i = 1}^{r} {} \frac{{a\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a - 1} \bar{G}^{{(\varvec{\eta})}} (x_{i} ,\varvec{\eta}) - \alpha a\bar{G}(x_{i} ,\varvec{\eta})^{a - 1} \bar{G}^{{(\varvec{\eta})}} (x_{i} ,\varvec{\eta})}}{{\{ 1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})\}^{a} - [\alpha \bar{G}(x_{i} ,\varvec{\eta})]^{a} }} \\ & \quad - (ab + 1)\sum\limits_{i = 1}^{r} {\frac{{\bar{\alpha }\bar{G}^{{({\varvec{\upbeta}})}} (x_{i} ,\varvec{\eta})}}{{1 - \bar{\alpha }\bar{G}(x_{i} ,\varvec{\eta})}}} \\ \end{aligned} $$

4.1.1 Asymptotic Standard Error for the MLEs

For large sample the standard error for the MLE of jth parameter $\vartheta_{j}$ is approximated by $\sqrt {\hat{v}_{jj} }$, where $\hat{\nu }_{jj} = (\hat{V}_{n} ) = I_{n}^{ - 1} (\hat{\vartheta })$, where $\hat{I}_{n} (\hat{\vartheta }) = ({\hat{\text{I}}}_{ij} )$ is the observed Fisher’s information matrix defined as ${\hat{\text{I}}}_{ij} \approx ( - \partial^{2} \ell (\vartheta )/\partial \vartheta_{i} \partial \vartheta_{j} )_{{\vartheta = \hat{\vartheta }}} ,i,j = 1,2, \ldots ,3 + q$.

4.2 Simulation Study

Here, we examine the performance of the maximum likelihood method for estimating the EGMO-E parameters by using the Monte Carlo simulation study with 10,000 replications. We calculate the average of estimated parameters, bias and mean square errors (MSE).

• Data is generated using the inversion of cdf given in Sect. 3.2.

• (0.5, 1.5, 0.8 and 0.3) are taken as the true parameter values $a,b,\alpha \;{\text{and}}\;\lambda$. Simulation is conducted for the sample sizes $n = 100,200,300\;{\text{and}}\;500.$

The numerical results of the Monte Carlos simulation study are given in the Table 1. We evaluate the average of estimated parameters, bias, standard error and mean square errors (MSE). Based on these results we can conclude that, the biases and MSE decreases as the sample size increases.

Table 1 Means, standard error estimates, Biases and RMSEs of $\hat{a},\hat{b},\hat{\alpha }\;{\text{and}}\;\hat{\lambda }$ for the EGMO-Exponential model with true values $a = 0.5,b = 1.5,\alpha = 0.8\;{\text{and}}\;\lambda = 0.3$

5 Real Life Applications

Here we consider modelling of the three real life data sets, two positively skewed and other negatively skewed to illustrate the suitability of the $\text{EGMO-G}(a,b,\alpha ,\varvec{\eta})$ distribution in comparison to some existing distributions by estimating the parameters through numerical maximization of log-likelihood functions taking exponential distribution as the base line G.

We have compared the $\text{EGMO-E}(a,b,\alpha ,\lambda )$ distribution with some of its sub models namely the Marshall Olkin-exponential [$\text{MO-E}(\alpha \text{,}\lambda )$], Exponentiated generalized-exponential [$\text{EG-E}(a,b,\lambda )$] and exponential [${\text{E}}(\lambda )$] distributions, and also with useful lifetime model moment exponential [${\text{ME}}(\beta )$], exponentiated moment exponential [${\text{E-ME}}(\alpha ,\beta )$], exponentiated exponential [${\text{E-E}}(\beta ,\lambda )$], beta exponential [${\text{B-E}}(\alpha ,\beta ,\lambda )$] distributions for all three data sets.

The best model is chosen as the one having lowest AIC (Akaike Information Criterion), BIC (Bayesian Information Criterion), CAIC (Consistent Akaike Information Criterion) and HQIC (Hannan–Quinn Information Criterion). It may be noted that $AIC = 2k - 2l$; $BIC = k\log (n) - 2l$; $CAIC = AIC + (2k(k + 1))/(n - k - 1)$; and $HQIC = 2k\log [\log (n)] - 2l$, where $k$ is the number of parameters in the statistical model, $n$ the sample size and $l$ is the maximized value of the log-likelihood function under the considered model. Moreover the Anderson–Darling (A), Cramer–von Mises (W) and Kolmogorov–Smirnov (K–S) statistics are also used to compare the fitted models.

5.1 Likelihood Ratio Test for Nested Models

The $\text{EGMO-E}(a,b,\alpha ,\lambda )$ distribution reduces to ${\text{E}}(\lambda )$ when $a,b,\alpha = 1$ to $\text{MO-E}(\alpha \text{,}\lambda )$ when $a,b = 1$ and to $\text{EG-E}(a,b,\lambda )$ if $\alpha = 1$.

Here we have employed likelihood ratio criterion to test the following hypotheses:

• 1. $H_{0} {:}\;a,b,\alpha = 1$, that is the sample is from ${\text{E}}(\lambda )$

  $H_{1} {:}\;a \ne 1,b \ne 1,\alpha \ne 1$, that is the sample is $\text{EGMO-E}(a,b,\alpha ,\lambda )$

• 2. $H_{0} {:}\;a,b = 1$, that is the sample is from $\text{MO-E}(\alpha \text{,}\lambda )$

  $H_{1} {:}\;a \ne 1,b \ne 1$, that is the sample is $\text{EGMO-E}(a,b,\alpha ,\lambda )$.

• 3. $H_{0} {:}\;\alpha = 1$, that is the sample is from $\text{EG-E}(a,b,\lambda )$

  $H_{1} {:}\;\alpha \ne 1$, that is the sample is $\text{EGMO-E}(a,b,\alpha ,\lambda )$.

The likelihood ratio test statistic is given by LR = $- 2\ln (L(\hat{\vartheta }^{*} ;x)/L(\hat{\vartheta },x))$, where $\hat{\vartheta }^{*}$ is the restricted ML estimates under the null hypothesis $H_{0}$ and $\hat{\vartheta }$ is the unrestricted ML estimates under the alternative hypothesis $H_{1}$. Under the null hypothesis $H_{0}$ the LR criterion follows Chi square distribution with degrees of freedom (df) $(df_{alt} - df_{null} )$. The null hypothesis is rejected for p value less than 0.05.

First data set is about 346 nicotine measurements of cigarettes (http://www.ftc.gov/reports/tobacco or http://pw1.netcom.com/rdavis2/smoke.html). Second data set consists of 153 observations, of which 85 are classified as failed windshields, and the remaining 68 are service times of windshields that had not failed at the time of observation is taken from Murthy et al. [18]. Third data set consists of 63 observations about strengths of 1.5 cm glass fibres are taken from Smith and Naylor [20].

In data modelling applications, information about the shape of the hazard function can help us in deciding a particular model. To meet this objective, the concept of total time on test (TTT) plot was proposed by Aarset [1]. The TTT is drawn by plotting $T({i / n}) = {\left.{\left\{ {\left( {\sum\nolimits_{r = 1}^{i} {y_{(r)} } } \right) + (n - i)y_{(i)} } \right\}}\right / {\sum\nolimits_{r = 1}^{n} {y_{(r)} } }}$ where, $i = 1,2, \ldots ,n\;{\text{and}}\;y_{(r)} (r = 1,2, \ldots ,n)$ are the order statistics of the sample, against $i/n$. The hazard of the given data set is constant, decreasing and increasing depending on the shape of the TTT plot being a straight diagonal line, is of convex shape and concave shape respectively. The TTT plots for the data sets considered here are presented Fig. 7 indicate that the all the three data sets have increasing hazard rate. We have also presented the descriptive statistics of the data sets in Table 2 and findings of the data fitting for set-I, II and III Tables 3, 4, 5, 6, 7 and 8 respectively.

Fig. 7

TTT-plots for the a Data set I, b Data set II and c Data set III

Table 2 Descriptive Statistics for the data set I, II and III

Table 3 MLEs, standard error’s and confidence interval (in parentheses) values for the data set I

Table 4 AIC, BIC, CAIC, HQIC, A, W, KS (p value) and L-R (p value) values for the data set I

Table 5 MLEs, standard error’s and confidence interval (in parentheses) values for the data set II

Table 6 AIC, BIC, CAIC, HQIC, A, W, KS (p value) and L-R (p value) values for the data set II

Table 7 MLEs, standard error’s and confidence interval (in parentheses) values for the data set III

Table 8 AIC, BIC, CAIC, HQIC, A, W, KS (p value) and L-R (p value) values for the data set III

For the data sets I, II and III, the MLEs of the parameters with their standard errors for all the competing models are respectively presented in the Tables 3, 5, and 7 while corresponding AIC, BIC, CAIC, HQIC, A, W, KS and LR statistic with p value are shown in Tables 4, 6 and 8. For the all data sets, it is evident that the EGMO-E distribution is the best model with lowest AIC, BIC, CAIC, HQIC, A, W and highest p value of K–S statistic. Moreover the LR tests reject the two sub models in favour of the EGMO-E distribution. Therefore we may conclude that it is a better model than the sub models MO-E, EG-E, E and also useful lifetime models like moment exponential (ME), exponentiated moment exponential (E-ME), exponentiated exponential (E-E), beta exponential (B-E) distributions for all three data sets.

Also plots of fitted densities with histogram of the observed data in Figs. 8a, 9a, 10a and cdf of the best fitted distribution with ogive of observed data in Figs. 8b, 9b, 10b for the data sets I, II and III respectively show the adequacy of the proposed distributions for all the observed data sets.

Fig. 8

a Observed histogram and fitted densities of the EGMO-E distribution and other competitive models. b Estimated cdf of the EGMO-E model and the empirical cdf for the data set I

Fig. 9

a Observed histogram and fitted densities of the EGMO-E distribution and other competitive models. b Estimated cdf of the EGMO-E model and the empirical cdf for the data set II

Fig. 10

a Observed histogram and fitted densities of the EGMO-E distribution and other competitive models. b Estimated cdf of the EGMO-E model and the empirical cdf for the data set III

6 Conclusions

In this paper, a new G family extension of the Marshall–Olkin is proposed with more flexibility to analyze real life data. We study some of its statistical and mathematical properties including estimation of the model parameters by maximum likelihood method. New distribution applied to three real data sets provides better fit than its sub model and some other recently introduced distributions. It is therefore a useful new contribution to the pool of existing extensions of Marshall–Olkin models.