1 Introduction

Human immune deficiency virus (HIV) is a virus that causes acquired immuno deficiency syndrome (AIDS). The virus attacks the body’s immune system and destroys the CD4 cells that are crucial to the normal function of the immune system which defends the body against illness.

As HIV/AIDS is not a curable disease, patients are being treated by the combination of two or more classes of antiretroviral drugs, called highly active antiretroviral therapy (HAART), throughout their life time. The success of this lifelong HAART treatment in improving the health status of the patient depends on a number of factors. [5] indicated that CD4 count, viral load, total lymphocytes, body mass index and adherence to the treatment are significant predictors of mortality due to the disease. Of these and other factors, several cohort studies and clinical trials have shown that CD4 count is the strongest predictor of subsequent disease progression and survival [6, 13]. For example, CD4 counts below 200 cells per mm\(^3\) indicate occurrence of the greater risk of the disease, while the risk of progression increases substantially at CD4 counts \(<\)350 cells per mm\(^3\) and CD4 counts from 350 to 500 cells per mm\(^3\) are associated with risks of \(\le \)5 % across all ages [18]. Thus, lower CD4 counts are associated with greater risk of disease progression.

Many researchers have carried out studies on the change in CD4 cell counts of HIV patients. Several of these studies have look at change from the cross sectional point of view without considering the pattern of change over the period of study. For example, [11] used linear regression models to study some predictors of CD4 cell counts recovery in HIV-1 positive patients receiving Antiretroviral Therapy and showed that the change in CD4 cells is linear. [1] used a longitudinal approach and suggested that the pattern of growth in CD4 cell was not linear. In addition, [17] reveals that the mean square root CD4 cell counts of HIV/AIDS patients has a quadratic relationship with time. Therefore, several studies arrive at different relationship of the CD4 count over time.

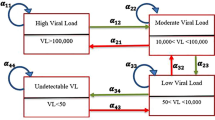
The basis of this paper is, therefore, modeling of the progression of HIV/AIDS disease using random intercepts and random coefficients ordinal response models. The progression of the disease represent the seriousness of HIV/AIDS sickness which is determined by splitting the immunological indicator namely the CD4 count into four stages as in [8]. These stages are CD4 count \(<200\) cells per mm\(^3\), \(200 \le \) CD4 count \(<\)350 cells per mm\(^3\), \(350\le \) CD4 \(< 500\) cells per mm\(^3\) and CD4 count \(\ge 500\) cells per mm\(^3\). Thus, by considering changes over time, the main focus is to compare two approaches of the generalized multilevel ordinal models; namely the proportional odds model and the non-proportional odds model. The random part of both models include random intercepts and random coefficients.

Following parts of the paper are organized as follows. Section 2 describes the materials and methods used in the study. Section 3 presents the results and discussion. Finally, conclusions are provided in Sect. 4.

2 Materials and Methods

2.1 Description of the HAART Data

The HAART data used for this study is the data used by [17] which was obtained from Jimma University Specialized Hospital HIV Outpatient Clinic, South West of Ethiopia. It consists of 1464 HIV/AIDS patients who were 18 years old or older, and started the HAART treatment any time in between 1st January 2007 to 31st December 2011.

The response variable is CD4 representing the progression of the disease as described previously. Thus, it has four values; 1 if the CD4 count \(<200\) cells per mm\(^3\), 2 if \(200 \le \) CD4 count \(< 350\) cells per mm\(^3\), 3 if \(350\le \) CD4 \(< 500\) cells per mm\(^3\) and 4 if the CD4 count \(\ge 500\) cells per mm\(^3\).

This study considers 5 explanatory variables. These are CD4 observation time in months (Time), baseline age of the patient in years (Age), gender (Female, Male), baseline clinical stage of the patient (Stage I, Stage II, Stage III, Stage IV) and baseline functional status of the patient (Working, Ambulatory, Bedridden).

2.2 Multilevel Ordinal Models

Multilevel data are a commonly encountered phenomenon especially in the fields of medical, biological and social sciences. Statistical modeling of multilevel data has been in discussion for many years and many developments have been made [2, 9, 10]. In such studies, the interest lies in drawing inference about the regression parameters of a marginal model for correlated responses while the association structure between the responses is of secondary importance [3]. As most of the early developments are concentrated in the area of continuous response variables, the field of multilevel modeling for discrete categorical responses is a relatively new approach [7, 16].

In this study, a two-level analysis is employed. Consider a response variable Y having k categories \((s=1,2,\ldots ,k)\). Suppose category k is chosen as a reference category. Let j represent the higher level (level-2) units and let i represent the lower level (level-1) units (nested observations). In this particular study, the level-2 units are patients (identified by card numbers) and the level-1 units are the CD4 observation times. Thus, each observed response is identified by the combination of card numbers and observation times.

Assume that there are \(j=1,2,\ldots ,N\) level-2 units and \(i=1,2,\ldots ,n_j\) level-1 units within each patient (level-2 unit). The total number of level-1 observations across level-2 units is given by \(\displaystyle n=\sum \nolimits _{j=1}^Nn_j\).

Let \(Y_{ij}\) be the value of the ordinal response associated with level-1 unit i nested within level-2 unit j. Thus, \(\pi _{ij}^{(s)}\) denotes the probability of patient j having a response variable value of s at the observation time i. The cumulative response probabilities are:

$$\begin{aligned} P(Y\le s)=\gamma _{ij}^{(s)}=\sum _{h=1}^s\pi _{ij}^{(h)}, \ \ \ s=1,2,\cdots ,k-1 \end{aligned}$$
(1)

where \(\gamma _{ij}^{(s)}\) represents the expected cumulative proportion (out of the total \(n_i\) observations) for the \(j^{th}\) patient at time i. Thus, expressing the category probabilities in terms of the cumulative probabilities:

$$\begin{aligned} \pi _{ij}^{(h)}=\gamma _{ij}^{(h)}-\gamma _{ij}^{(h-1)}; \ \ \ 1<h<k \end{aligned}$$
(2)

but \(\pi _{ij}^{(1)}=\gamma _{ij}^{(1)}\) and \(\gamma _{ij}^{(k)}=1\).

The choice of the marginal model depends on the nature of the response scale. The basic ordinal response model often utilize the cumulative comparisons of the ordinal outcome with the logit link function.

$$\begin{aligned} \text {logit } (\gamma _{ij}^{(s)})=\alpha ^{(s)}+\varvec{x}_{ij}\varvec{\beta }+\varvec{z}_{ij}\varvec{u}_j \end{aligned}$$
(3)

where

$$\begin{aligned} \gamma _{ij}^{(s)}= \frac{\exp (\alpha ^{(s)}+\varvec{x}_{ij}\varvec{\beta }+\varvec{z}_{ij}\varvec{u}_j)}{1+\exp (\alpha ^{(s)}+\varvec{x}_{ij}\varvec{\beta }+\varvec{z}_{ij}\varvec{u}_j)}. \end{aligned}$$

In this model, the term \(\varvec{u}_j\) are random effects specific to the second level. The \(\varvec{x}\) represents the fixed effect variables and the \(\varvec{z}\) (subset of the \(\varvec{x}\) variables) are the variables associated with the random effects. Here, it is assumed that \(\varvec{u}_j\sim N(\varvec{0},\varvec{\varPsi })\) where \(\varvec{\varPsi }\) is the variance covariance matrix of the random effects.

It is worth mentioning that the linear predictor differs in the marginal model (3) above. First, the category specific intercepts need to satisfy a monotonicity condition \(\alpha ^{(1)} \le \alpha ^{(2)} \le \cdots \le \alpha ^{(k-1)}\) only when the family of cumulative link models are employed. Second, the regression parameter coefficients \((\varvec{\beta })\) of the covariates are category specific (do not vary across categories). Thus, the relationship between the explanatory variables and the cumulative logits does not depend on s. [14] calls this assumption of identical odds ratios across the \(k-1\) cut-offs the proportional odds assumption. As written above, a positive coefficient for an explanatory variable indicates that as the values of the explanatory variable increase so do the odds that the response is greater than or equal to s.

Assuming an underlying multinomial distribution for the category probabilities, the covariance matrix of the the cumulative proportions is given by:

$$\begin{aligned} cov(y_{ij}^{(s)},y_{ij}^{(r)})=\frac{\gamma _{ij}^{(s)}(1-\gamma _{ij}^{(r)})}{n_i}; \ \ \ s\le r \end{aligned}$$
(4)

As noted by [15], violation of the proportional odds assumption is common. Thus, they described a (fixed-effects) partial proportional odds model in which the covariates are allowed to have differential effects on the \(t-1\) cumulative logits. Hence, this non-proportional odds model is widely used in situations where there is no evidence to suggest the effect of certain variables do not behave proportionality across response categories. In such case, the cumulative proportions is modeled as:

$$\begin{aligned} \text {logit } (\gamma _{ij}^{(s)})=\alpha ^{(s)}+\varvec{x}_{ij}\varvec{\beta }^{(s)}+\varvec{z}_{ij}\varvec{u}_j \end{aligned}$$
(5)

where the term \(\varvec{\beta }^{(s)}\) depict the estimated coefficients that vary across the logits.

2.3 Bayesian Estimation and the Likelihood Function

Estimation of both proportional and nonproportional odds models are estimated under a Bayesian framework through Markov chain Monte Carlo (MCMC) methods using the specialized software package for fitting multilevel models MLwiN [4]. For this study, I used the Stata command runmlwin to fit the models in MLwiN 2.32 seamlessly from within Stata. The command allows to fit models by both the IGLS and MCMC algorithms and provides full control over all aspects of model specification and estimation [12].

Bayesian inference is based on the posterior distribution given the observed data. For the ordinal models, the probability of a response in category s for a given level-2 unit j, conditional on the random effects \(\varvec{\theta }\) is equal to

$$\begin{aligned} \pi _{ij}^{(s)}=P(Y_{ij}=s|\varvec{\theta })=\gamma _{ij}^{(s)}-\gamma _{ij}^{(s-1)}. \end{aligned}$$

In what follows, the general model allowing for nonproportional odds is considered, since the more restrictive proportional odds model is just a special case.

Let \(\varvec{Y}_j\) denote the vector of ordinal responses from level-2 unit j (for the \(n_j\) level-1 units nested within). The probability of any pattern \(\varvec{Y}_j\) conditional on \(\varvec{\theta }\) is equal to the product of the probabilities of the level-1 responses,

$$\begin{aligned} \ell (\varvec{Y}_j|\varvec{\theta })= \prod _{i=1}^{n_j} \prod _{s=1}^k(\gamma _{ij}^{(s)}-\gamma _{ij}^{(s-1)})^{y_{ij}^{(s)}} \end{aligned}$$

where \(y_{ij}^{(s)}=1\) if \(Y_{ij}^{(s)}=s\) and 0 otherwise (i.e., for each ij-th observation \(y_{ij}^{(s)}=1\) for only one of the k categories).

Since Bayesian analysis combines the prior distribution of parameters with the likelihood function of the observed data, the marginal density of \(\varvec{Y}_j\) in the population is expressed as the integral of the likelihood \(\ell (\cdot )\) weighted by the prior density \(g(\cdot )\),

$$\begin{aligned} h(\varvec{Y}_j)=\int _{\varvec{\theta }}\ell (\varvec{Y}_j|\varvec{\theta })g(\varvec{\theta })d\varvec{\theta } \end{aligned}$$

where \(g(\varvec{\theta })\) is prior distribution of the parameters. For this study, multivariate normal and inverse gamma priors are used for the fixed effects parameter vector and the variance of the random effects, respectively. Hence, \(g(\varvec{\theta })\) represents the multivariate standard normal and inverse gamma densities.

The marginal loglikelihood from the N level-2 units is then given by,

$$\begin{aligned} \displaystyle \log L=\sum _{j=1}^N\log h(\varvec{Y}_j) =\sum _{j=1}^N\log \left( \int _{\varvec{\theta }}\ell (\varvec{Y}_j|\varvec{\theta })g(\varvec{\theta })d\varvec{\theta }\right) . \end{aligned}$$

which should be maximized to obtain the MCMC parameter estimates.

3 Results and Discussion

The HAART data used consists of \(N=1464\) patients (level-2 units). Also the indicator of the progression of the disease, the CD4 count, was measured approximately every six months for a maximum of successive five years. Thus, there are 1–10 (\(n_j=1,2,\ldots ,10; \ j=1,2,\ldots ,1464\)) level-1 units (recoded responses) for each patient. Therefore, there are about \(\displaystyle n=4655\) observations across all 1464 patients.

The four categories of the response variable (CD4) can be viewed as being increasingly good progression of the disease. The lowest value of the response variable (\(CD4_{ij}=1\)) represents the bad progression and the largest value (\(CD4_{ij}=4\)) represents good progression of the disease. The fourth category of the response (\(CD4_{ij}=4\) or CD4 \(>500\) cells per mm\(^3\)) is taken as the reference category. Thus, \(CD4_{ij}\sim \text {Multinomial } \left( \pi _{ij}^{(1)},\pi _{ij}^{(2)}, \pi _{ij}^{(3)}\right) \) where \(\pi _{ij}^{(1)}\), \(\pi _{ij}^{(2)}\) and \(\pi _{ij}^{(3)}\) denote the probabilities of having \(CD4<200\), \(200\le CD4<350\) and \(350\le CD4 <500\) for the jth patient at the ith observation time, respectively.

To assess the progression of the HIV/AIDS disease, two ordinal multilevel models are fitted to the HAART data, the first assuming a proportional odds model and the second relaxing this assumption. For both analyses, the repeated ordinal responses (progression stages) are modeled in terms of the time-varying observation time effect and the other baseline covariates. In terms of the multilevel part of the model, both a random intercept (patient) effect and random coefficient (random intercept for each patient and random slope for the observation time) are included in both analyses.

Each model is, first, fitted by iteratively generalized least squares (IGLS) to obtain starting values for the model parameters for the Markov Chain Monte Carlo (MCMC) estimation. In all of the models, the MCMC estimation is based on a sampling of 50,000 iterations following a 25,000 iteration “burn-in” period.

3.1 Random Intercepts Model

Random intercepts model (i.e., \(\varvec{z}_j =\varvec{1}_{n_j}\)) is used for both the proportional odds model and nonproportional odds model. The random intercepts proportional odds model is of the form:

$$\begin{aligned} \begin{aligned} \log \left( \pi _{ij}^{(1)}/\pi _{ij}^{(2,3,4)}\right) =\;&\alpha _0^{(1)}+\beta _1\text {Time}_{ij}+\beta _2\text {Age}_{j} +\beta _3\text {Gender}_{j} \\&+\beta _4\text {Stage II}_{j}+ \beta _5\text {Stage III}_{j} +\beta _6\text {Stage IV}_{j} \\&+\beta _7\text {Ambulatory}_{j}+\beta _8\text {Bedridden}_{j}+u_{0j} \\ \log \left( \pi _{ij}^{(1,2)}/\pi _{ij}^{(3,4)}\right) =\;&\alpha _0^{(2)}+\beta _1\text {Time}_{ij}+\beta _2\text {Age}_{j} +\beta _3\text {Gender}_{j} \\&+\beta _4\text {Stage II}_{j}+ \beta _5\text {Stage III}_{j} +\beta _6\text {Stage IV}_{j} \\&+\beta _7\text {Ambulatory}_{j}+\beta _8\text {Bedridden}_{j}+u_{0j} \\ \log \left( \pi _{ij}^{(1,2,3)}/\pi _{ij}^{(4)}\right) =\;&\alpha _0^{(3)}+\beta _1\text {Time}_{ij}+\beta _2\text {Age}_{j} +\beta _3\text {Gender}_{j} \\&+\beta _4\text {Stage II}_{j}+ \beta _5\text {Stage III}_{j} +\beta _6\text {Stage IV}_{j} \\&+\beta _7\text {Ambulatory}_{j}+\beta _8\text {Bedridden}_{j}+u_{0j} \\ \end{aligned} \end{aligned}$$
(6)

where \(u_{0j}\) is the random effect associated with each patient (card number). It is assumed that \(u_{0j}\sim N(0,\sigma _{u0}^2)\).

Since the response variable has four categories, the model is set up as three log-odds contrasts (logits). The first log odds contrast model is the log odds of \(CD4<200\) versus \(CD4\ge 200\) which can be interpreted as the logit of the expected probability that patient j has CD4 count less than 200 at time i, given the values of the explanatory variables. The second log odds contrast model, the log odds of \(CD4<350\) versus \(CD4\ge 350\) compares the log odds of that patient j has CD4 count less than 200 instead of having CD4 count 200 or more at time i, given the values of the explanatory variables. Similarly, the third log odds contrast model, the log odds of \(CD4<500\) versus \(CD4\ge 500\) shows, for given the values of the explanatory variables, the logit of the expected probability that patient j has CD4 count less than 500 at time i. Also, separate intercepts (threshold parameters) are estimated in each log-odds contrast. The effects of all predictor variables are assumed constant across the log-odds contrasts (proportional odds assumption).

Similarly the nonproportional random intercepts model is of the form:

$$\begin{aligned} \begin{aligned} \log \left( \pi _{ij}^{(1)}/\pi _{ij}^{(2,3,4)}\right) =\;&\alpha _0^{(1)}+\beta _1^{(1)}\text {Time}_{ij} +\beta _2^{(1)}\text {Age}_{j} +\beta _3^{(1)}\text {Gender}_{j} \\&+\beta _4^{(1)}\text {Stage II}_{j}+ \beta _5^{(1)}\text {Stage III}_{j} +\beta _6^{(1)}\text {Stage IV}_{j} \\&+\beta _7^{(1)}\text {Ambulatory}_{j}+\beta _8^{(1)}\text {Bedridden}_{j}+u_{0j} \\ \log \left( \pi _{ij}^{(1,2)}/\pi _{ij}^{(3,4)}\right) =\;&\alpha _0^{(2)}+\beta _1^{(2)}\text {Time}_{ij} +\beta _2^{(2)}\text {Age}_{j} +\beta _3^{(2)}\text {Gender}_{j} \\&+\beta _4^{(2)}\text {Stage II}_{j}+ \beta _5^{(2)}\text {Stage III}_{j} +\beta _6^{(2)}\text {Stage IV}_{j} \\&+\beta _7^{(2)}\text {Ambulatory}_{j}+\beta _8^{(2)}\text {Bedridden}_{j}+u_{0j} \\ \log \left( \pi _{ij}^{(1,2,3)}/\pi _{ij}^{(4)}\right) =\;&\alpha _0^{(3)}+\beta _1^{(3)}\text {Time}_{ij} +\beta _2^{(3)}\text {Age}_{j} +\beta _3^{(3)}\text {Gender}_{j} \\&+\beta _4^{(3)}\text {Stage II}_{j}+ \beta _5^{(3)}\text {Stage III}_{j} +\beta _6^{(3)}\text {Stage IV}_{j} \\&+\beta _7^{(3)}\text {Ambulatory}_{j}+\beta _8^{(3)}\text {Bedridden}_{j}+u_{0j} \\ \end{aligned} \end{aligned}$$
(7)

where \( u_{0j}\sim N(0,\sigma _{u_0}^2)\).

The parameter estimates of Model (6) and Model (7) together with their 95 % credible interval are presented in Table 1. In both models, the result show that all explanatory variables, except age, are significant at 5 % level of significance in the proportional odds model. But in the nonproportional odds models, at least one of the design variables of the corresponding categorical variable is significant. Even, age is significant in the third contrast of the nonproportional odds model. Thus, all variables are significantly associated with the progression of the disease in the proportional odds model.

In terms of the random patient effects, the estimated between-patient variance for the proportional odds model is 2.3416 with the 95 % credible interval (1.9809, 2.7434) and for the nonproportional odds model is 2.4712 with its corresponding 95 % credible interval (2.1018, 2.8891). It can be easily observed that the estimated between patient variance is smaller in the proportional odds model than that of the nonproportional odds model. And also the credible interval in the proportional odds model is wider than that of the nonproportional odds model. Therefore, the credible intervals for the between patient variance in both models clearly indicate that the between patient variance is significant or the data are correlated within patients.

Table 1 Bayesian estimates and the 95 % credible intervals for parameters of the random intercept models
Full size table

Generally, for a random intercepts model, it is often of interest to express the level-2 variance in terms of an intra-class correlation. For the ordinal multilevel model assuming normally distributed random effects, the estimated intra-class correlation is \(\hat{\sigma }_{u_0}^2/(\hat{\sigma }_{u_0}^2+\pi ^2/3)\) where the term in the denominator represents the variance of the underlying latent response tendency.

As said before, the significance of the random patient effects in Table 1 shows that the data are correlated within subjects. Expressing this as an intra-class correlation, the attributable variance at the patient level equals 0.4158 (41.58 %) and 0.4289 (42.89 %) for proportional odds and nonproportional odds models respectively. This means that about 41 % of the variation in the response (progression of the disease) is explained by the difference among patients.

Table 2 Bayesian estimates and the 95 % credible intervals for parameters of the random coefficient models
Full size table

3.2 Random Coefficients Model

Similar to the random intercepts model, both the proportional and nonproportional odds models are also fitted in a random coefficients form. The random coefficients model fitted, here, includes a random slope for each observation time in addition to a random intercept for each patient. The proportional odds model analysis assumes the effects of the explanatory variables are the same across the three cumulative logits of the model, whereas the nonproportional odds model analysis estimates effects for each explanatory variable on each of the three cumulative logits.

The random coefficients proportional odds model has the form:

$$\begin{aligned} \begin{aligned} \log \left( \pi _{ij}^{(1)}/\pi _{ij}^{(2,3,4)}\right) =\;&\alpha _0^{(1)}+\beta _1\text {Time}_{ij}+\beta _2\text {Age}_{j} +\beta _3\text {Gender}_{j} \\&+\beta _4\text {Stage II}_{j}+ \beta _5\text {Stage III}_{j} +\beta _6\text {Stage IV}_{j} \\&+\beta _7\text {Ambulatory}_{j}+\beta _8\text {Bedridden}_{j}+u_{0j}+u_{1j}\text {Time}_{ij} \\ \log \left( \pi _{ij}^{(1,2)}/\pi _{ij}^{(3,4)}\right) =\;&\alpha _0^{(2)}+\beta _1\text {Time}_{ij}+\beta _2\text {Age}_{j} +\beta _3\text {Gender}_{j} \\&+\beta _4\text {Stage II}_{j}+ \beta _5\text {Stage III}_{j} +\beta _6\text {Stage IV}_{j} \\&+\beta _7\text {Ambulatory}_{j}+\beta _8\text {Bedridden}_{j}+u_{0j}+u_{1j}\text {Time}_{ij} \\ \log \left( \pi _{ij}^{(1,2,3)}/\pi _{ij}^{(4)}\right) =\;&\alpha _0^{(3)}+\beta _1\text {Time}_{ij}+\beta _2\text {Age}_{j} +\beta _3\text {Gender}_{j} \\&+\beta _4\text {Stage II}_{j}+ \beta _5\text {Stage III}_{j} +\beta _6\text {Stage IV}_{j} \\&+\beta _7\text {Ambulatory}_{j}+\beta _8\text {Bedridden}_{j}+u_{0j}+u_{1j}\text {Time}_{ij} \\ \end{aligned} \end{aligned}$$
(8)

where \(u_{0j}\) and \(u_{1j}\) are the random intercept for each patient and random slope associated with the observation time. Here \(u_{0j}\sim N(0,\sigma _{u_0}^2)\), \(u_{1j}\sim N(0,\sigma _{u_1}^2)\) and \(\text {cov}(u_{0j},u_{1j})=\sigma _{01}\).

Similar to the random coefficients proportional odds models, the random coefficients nonproportional odds model is expressed as:

$$\begin{aligned} \begin{aligned} \log \left( \pi _{ij}^{(1)}/\pi _{ij}^{(2,3,4)}\right) =\;&\alpha _0^{(1)}+\beta _1^{(1)}\text {Time}_{ij} +\beta _2^{(1)}\text {Age}_{j} +\beta _3^{(1)}\text {Gender}_{j} \\&+\beta _4^{(1)}\text {Stage II}_{j}+ \beta _5^{(1)}\text {Stage III}_{j} +\beta _6^{(1)}\text {Stage IV}_{j} \\&+\beta _7^{(1)}\text {Ambulatory}_{j}+\beta _8^{(1)}\text {Bedridden}_{j} +u_{0j} +u_{1j}\text {Time}_{ij} \\ \log \left( \pi _{ij}^{(1,2)}/\pi _{ij}^{(3,4)}\right) =\;&\alpha _0^{(2)}+\beta _1^{(2)}\text {Time}_{ij} +\beta _2^{(2)}\text {Age}_{j} +\beta _3^{(2)}\text {Gender}_{j} \\&+\beta _4^{(2)}\text {Stage II}_{j}+ \beta _5^{(2)}\text {Stage III}_{j} +\beta _6^{(2)}\text {Stage IV}_{j} \\&+\beta _7^{(2)}\text {Ambulatory}_{j}+\beta _8^{(2)}\text {Bedridden}_{j} +u_{0j} +u_{1j}\text {Time}_{ij} \\ \log \left( \pi _{ij}^{(1,2,3)}/\pi _{ij}^{(4)}\right) =\;&\alpha _0^{(3)}+\beta _1^{(3)}\text {Time}_{ij} +\beta _2^{(3)}\text {Age}_{j} +\beta _3^{(3)}\text {Gender}_{j} \\&+\beta _4^{(3)}\text {Stage II}_{j}+ \beta _5^{(3)}\text {Stage III}_{j} +\beta _6^{(3)}\text {Stage IV}_{j} \\&+\beta _7^{(3)}\text {Ambulatory}_{j}+\beta _8^{(3)}\text {Bedridden}_{j} +u_{0j} +u_{1j}\text {Time}_{ij} \\ \end{aligned} \end{aligned}$$
(9)

where as usual \(u_{0j}\sim N(0,\sigma _{u_0}^2)\), \(u_{1j}\sim N(0,\sigma _{u_1}^2)\) and \(\text {cov}(u_{0j},u_{1j})=\sigma _{01}\).

The parameter estimates of both of the models in a random coefficient terms are summarized in Table 2. Again when the random coefficient models are considered, the random patient effect is significant in both models. Also, the random linear time effect is significant in both analysis. The estimated covariance between the subject and time effects is negative but it is not significantly different from zero.

3.3 Model Comparison

Having fitted models by MCMC, then comparison of the models is done via the hierarchical modeling generalization of the Akaike Information Criterion (AIC) called deviance information criterion (DIC) [19]. The DIC is the sum of the posterior expectation (mean) of the deviance function (\(\bar{D}\)) and the effective number of parameters (pD). The term \(\bar{D}\) measures the goodness-of-fit of the model and the term pD measures the model complexity. Since a smaller \(\bar{D}\) indicates a better fit and a smaller pD indicates a parsimonious model, small value of the sum (DIC) indicates preferred model.

Table 3 Comparison of the estimated models using DIC
Full size table

Table 3 presents \(\bar{D}\), \(p_D\) and DIC values for the four models fitted previously. When the posterior mean of the deviance function is examined, the value decreases from Model (6) to Model (9), it seems that the random coefficient nonproportional odds model fits the HAART data better. Turning to the effective number of parameters, the values increase from Model (6) to Model (9). But to select a model as best among other candidate models, both of the values should be small. Hence, when the sum of the two (DIC) is considered, the random coefficient nonproportional odds model has the smallest value. Therefore, among the four candidate models, the nonproportional odds model in a random coefficients basis fits better for the HAART data used.

4 Conclusions

In this study, a novel application of Bayesian multilevel modeling for an ordinal categorical response has been discussed. Proportional odds and nonproportional odds models are considered for the analysis of the HAART data. In terms of the multilevel part of the model, both random intercepts models and models incorporating random patient intercepts and linear trends are investigated.

Specifically, four different two-level ordinal models are explored. Then, the models are compared using the Deviance Information Criteria. Of the four models, the random coefficients nonproportional odds model is the best fit for the HAART data as it has the smallest DIC value.

All the variables included in the model, except age, are found to be significantly associated with the progression of the HIV/AIDS disease. In particular, the progression of the disease increases as the time under HAART increases, assuming all the other variables constant. Also, male patients are more likely to have better progression as compared to female patients if all the other explanatory variables are assumed to be fixed. Similarly the baseline clinical stage and functional status of the patients have differential effects on the progression of the disease.

In general, the modeling technique used in this study has not been widely used for modeling medical data with hierarchical structures. Hence the contribution of the paper would be invaluable for medical researchers and statisticians.