1 Introduction

In recent decades, due to the significant ability to generate electrical energy from wasted vibration to serve as power sources, energy harvesting (EH) techniques have been attracted. The power generated by vibration energy harvesting (V–EH) techniques can be applied for low power electronic devices, for instance, wireless sensor networks [1], self-powered sensors [2] and self-powered RFID tags [3], etc. For converting vibration into electricity, there are mainly five transduction mechanisms, which are, respectively, based on electrostatic [4], electromagnetic [5], piezoelectric [6], magnetostrictive [7] and triboelectric [8] effects. Due to the advantages of simple assembly and high performance of energy transduction, piezoelectric materials, serving as energy transducers, are usually applied intensively for transforming the mechanical strain into electrical charge [9,10,11,12,13,14,15]. Potential vibration sources providing kinetic energy captured by piezoelectric plate are classified as environmental, industrial, structural, vehicle and human motions according to the stiffness characteristics [16]. It is found that vibrations in many practical applications are with small-energy and ultralow frequencies, for instance, human motion, sea waves and dropping rain. The frequency band of human walking is reported in the range of 2–3 Hz [17] and dropping rain is with very small energy [18]. Thus, it needs to design and fabricate energy harvester triggered by small-energy or ultralow-frequency vibration resources. For external perturbation from human motion, the development on piezoelectric energy harvesting devices for low frequency (0–100 Hz) mechanical vibrations is reviewed and methods to improve the power outputs are proposed. In [19, 20], biomechanical EHs with little extra metabolic energy for generating electricity are carried out. In addition, various V-EHs for other vibration energy sources have also been exploited in many industrial areas including vehicle [21, 22], architectural structures [23,24,25,26,27,28] and even natural phenomena [29, 30].

Considering the energy sources we harvest are often from human motions, sea waves and some natural phenomena such as raindrop, the vibration sources are always with small energy and changeable frequencies at low or ultralow frequency band rather than a single frequency. The design of V-EH for small-amplitude or ultralow-frequency external excitations still remains a tough task. To harvest the energy from small-energy perturbation or ultralow-frequency vibrations, researchers have designed some novel structures with nonlinearity. For instance, Leadenham et al. [31] realized the cubic nonlinearity in a cantilever beam at reasonable excitation levels by using M-shaped bent beam. The vibrating frequency of the beams containing energy transducers is up-converted to a higher one which can be determined by the physical parameters of the beams. Liu et al. [32] and Chen et al. [33] utilized the concept of nonlinear structural design in V-EH, which reveals that adjustable stiffness property has advantages in the improvement of energy amplification by resonance. The energy harvesting devices are more applicable if the resonance frequency reduces and the resonance band extends. The so-called quasi-zero-stiffness system is utilized in EH, realized by pre-deformation elastic components [34] or magnetic interaction [35,36,37]. It finds that the single magnet can induce nonlinearity of stiffness, which can enhance EH effect for random vibrations. Recently, Nguyen [38] and Kim et al. [39] utilize bistable property to harvest the vibration energy realized by magnetic interaction because of the drop between two equilibriums.

In order to realize the requirements of effective energy harvesting for small perturbation and in ultralow-frequency excitation, this paper develops a novel V-EH with different numbers of equilibriums in potential energy by adjustable nonlinearity. The magnets are assembled similarly as the QZS system to result multiple equilibriums by adjustable nonlinearity property. Referring the interaction force of magnets with relative motion [40, 41], based on theoretical and experimental analysis, it shows that the mono-stable, tri-stable and multi-stable configurations can be obtained by matching the structural parameters of the piezoelectric beam and magnets. The V-EH proposed has multi-stable configurations, which not only keeps the stable zero equilibrium but also reserves potential energy for vibration. The experimental results show that the effect of V–EH is better for multi-stable configuration than the case for mono-stable or tri-stable configurations. The voltage obtained by the appropriate structural parameters is raised by 50% than other cases for potential energy. In addition, because of the adjustable nonlinearity, for time-lasting vibration excitation, the frequency bandwidth of effective energy harvesting can be further extended to ultralow-frequency band. Also, the proposed energy harvesting device can generate large output voltages which illustrates that it is a feasible design for collecting energy from ultralow frequency excitation.

According to the theoretical and experimental analysis in this manuscript, it concludes that the concept of the utilization of multi-stable equilibrium property by QZS assembled magnets to realize the energy harvesting is highly economical. Firstly, the energy resources considered are from natural phenomena such as dropping rain, human walking or falling ball; Secondly, the proposed V–EH can magnify the external energy or excitation by mechanical structure without any extra/assistant electric power; Thirdly, the present system has ultralow resonance frequency, which is suitable for energy harvesting for changing excitation. Therefore, this study not only proposes a novel V–EH with multi-stable equilibrium configuration for potential energy reservation, but also realizes adjustable nonlinearity property for ultralow-frequency vibration sources.

2 The Proposed Energy Harvesting Structure

2.1 Introduction of the Structure

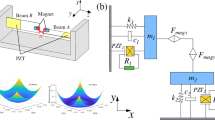
In the previous studies of novel energy harvesters [35,36,37,38,39], it discovers that introducing the adjustable nonlinearity into energy harvesting system by applying magnetic force exhibits significant improvement of performances. Figure 1 shows the proposed energy harvesting system consisted of a cantilever beam with symmetric piezoelectric layers and two pairs of magnets. Different from the assembly and configuration of magnets in normal nonlinear energy harvesting system, two pairs of magnets are assembled similarly to the so-called quasi-zero-stiffness (QZS) system. For the relative motion \(\hat{y}\), the magnets induce adjustable nonlinear interaction force as shown in Fig. 1. Then, Mono-stable, tri-stable and multi-stable configurations can be obtained by matching the structural parameters of the piezoelectric beam and magnets.

Fig. 1
figure 1

a Diagram of the proposed piezoelectric energy harvesting structure with designed magnetic field for small-amplitude and ultralow-frequency excitation; b force field applied on mass by magnetic interaction under vibration

Full size image

In this study, we prospect to design the structure and magnetic field to realize an energy harvesting system for small-amplitude or ultralow-frequency excitations such as dropping rain and falling ball. It has known that the impact of a raindrop can be described by using impact parameters [40]. Thus, the structure should be designed with stable static zero equilibrium but large potential energy drop for another equilibrium, which can be activated by a very small external impact.

2.2 The Interaction Energy of Magnets

From Fig. 1, the two magnets constructed as a pair to induce nonlinear interaction force parallel to the vibration motion. We analyse one pair of magnets to obtain the interaction energy for motion \(\hat{y}\). The configuration and motions of the right-side magnets are shown in Fig. 2.

Fig. 2
figure 2

The configuration, location and relative motion of the right-side pair magnets

Full size image

Referring the Refs. [40, 41], as shown in Fig. 2, for the motion \(\hat{y}\) at the free-end of the piezoelectric beam in y direction and the magnetizations J and J′ are considered rigid and uniform, the interaction energy V1 is expressed as

$$V_{1} = \int_{{ - \frac{a}{2}}}^{{\frac{a}{2}}} {dx} \int_{{ - \frac{b}{2}}}^{{\frac{b}{2}}} {dy} \int_{{ - \frac{A}{2}}}^{{\frac{A}{2}}} {dx^{\prime}} \int_{{ - \frac{B}{2}}}^{{\frac{B}{2}}} {dy^{\prime}} \frac{{JJ^{\prime}}}{{4\pi \mu_{0} r}},$$
(1)

where \(r = \sqrt {\left( {x^{\prime} - x} \right)^{2} + \left( {\hat{y} + y^{\prime} - y} \right)^{2} + d^{2} }\). After integration, the expression of V1 is written as:

$$V_{1} = \frac{{JJ^{\prime}}}{{4\pi \mu_{0} }}\sum\limits_{i = 0}^{1} {\sum\limits_{j = 0}^{1} {\sum\limits_{k = 0}^{1} {\sum\limits_{l = 0}^{1} {\sum\limits_{p = 0}^{1} {\sum\limits_{q = 0}^{1} {\left( { - 1} \right)^{i + j + k + k + p + q} \psi \left( {u_{ij} ,v_{kl} ,w_{pq} ,r} \right)} } } } } } ,$$
(2)

where \(\psi \left( {u,v,w,r} \right) = \frac{1}{2}u\left( {v^{2} - w^{2} } \right)\ln \left( {r - u} \right) + \frac{1}{2}v\left( {u^{2} - w^{2} } \right)\ln \left( {r - v} \right)\)\(+ \frac{r}{6}\left( {u^{2} + v^{2} - 2w^{2} } \right) + uvw\arctan \left( {\frac{uv}{rw}} \right)\), with

$$\begin{aligned} u_{ij} &= \left( { - 1} \right)^{j} \frac{A}{2} - \left( { - 1} \right)^{i} \frac{a}{2}, \\ v_{kl} &= \hat{y} + \left( { - 1} \right)^{l} \frac{B}{2} - \left( { - 1} \right)^{k} \frac{b}{2}, \\ w_{pq} &= d + \left( { - 1} \right)^{q} \frac{C}{2} - \left( { - 1} \right)^{b} \frac{c}{2}, \\ r &= \sqrt {u_{ij}^{2} + v_{kl}^{2} + w_{pq}^{2} }. \hfill \\ \end{aligned}$$
(3)

From Eqs. (1–3), the value of the interaction energy V1 can be easily calculated by substituting the locations and structural parameters. The variations of interaction energy V1 are demonstrated in Fig. 3 for different structural parameters of magnet.

Fig. 3
figure 3

The interaction energy for a and b different relative distances d between magnets; c and d different widths b of the magnet fixed on base

Full size image

From Fig. 3, it reveals the effects of structural parameters on the interaction energy of the magnets. First, the two structural parameters d and b of the magnets change the interaction energy and stability of equilibriums; second, the zero equilibrium is unstable for smaller d since reducing induces stronger repulsive magnetic force, while the zero equilibrium is an indifferent equilibrium and this region is wider for stronger magnetic field for larger b; Third, for stronger magnetic field with smaller d or larger b, there occur two stable equilibriums for large motion, which has obvious drop from the zero equilibrium.

2.3 Multiple Steady Points

In the expression of the interaction energy of one pair of magnets as Eq. (2), with the positive elastic potential energy of the piezoelectric beam, there can result multiple stabilities. The elastic potential energy of the piezoelectric beam is written as:

$$V = V_{1} + V_{2} = \frac{1}{2}K_{\text{eq}} \hat{y}^{2} + 2\frac{{JJ^{\prime}}}{{4\pi \mu_{0} }}\sum\limits_{i = 0}^{1} {\sum\limits_{j = 0}^{1} {\sum\limits_{k = 0}^{1} {\sum\limits_{l = 0}^{1} {\sum\limits_{p = 0}^{1} {\sum\limits_{q = 0}^{1} {\left( { - 1} \right)^{i + j + k + k + p + q} \psi \left( {u_{ij} ,v_{kl} ,w_{pq} ,r} \right)} } } } } } ,$$
(4)

where Keq is the equivalent stiffness coefficient for piezoelectric beam, defined as \(K_{\text{eq}} = EI\int_{0}^{L} {\phi_{j} \left( x \right)\frac{{\partial^{4} \phi_{i} \left( x \right)}}{{\partial x^{4} }}{\text{d}}x}\). The modal function is chosen as same as the cantilever beam due to the displacement boundary condition of the proposed structure. The Fixing Keq = 0.1, Fig. 4 shows the classification on the plane of the two adjustable structural parameters d and b for different number and stability of equilibrium.

Fig. 4
figure 4

a The classification of different numbers and stability of equilibrium on structural parametrical plane (d, b); b the potential energy of the system when fixing the parameters in different regions and the critical curves

Full size image

In Fig. 4, there are three regions I, II and III in the plane of adjustable structural parameters d and b, which reflect the three cases for mono-stable, tri-stable and multi-stable equilibriums, respectively; the three regions are divided by three critical curves C1, C2 and C3. The potential energy curves in the three regions and on the critical curves are shown in Fig. 4b. On the critical boundary curves C1 and C2, the system has zero-stiffness property at zero equilibrium, and on the curve C3, the zero-stiffness property occurs at the non-zero equilibrium, since the value of two derivatives of potential energy there equals to zero. In conclusion, in order to realize the requirements that a static stable zero equilibrium and very large vibration energy for a small external disturbance, the potential energy in region III in Fig. 4a can satisfy the proposed requirements.

2.4 Design Criterion

When the appropriate structural parameters d and b are chosen in Region III, the potential energy between the zero equilibrium and non-zero equilibriums has height difference, which can be utilized in vibration energy harvesting for a small perturbation. Figure 5 shows the variation of potential energy and the interval for zero-stiffness property under different structural parameters for b = 30 mm in Figs. 5a, b and d = 10 mm in Figs. 5c, d.

Fig. 5
figure 5

The potential energy of the system for a and b different relative distances d between magnets when fixing b = 30 mm; c and d different widths b of the magnet fixed on base when fixing d = 10 mm

Full size image

Figure 5 verifies the classification of potential energy by different number of equilibriums. As shown in Fig. 5, there are Mono-stable, tri-stable and multi-stable forms of the potential energy for different structural parameters d and b. As shown in Figs. 5a, b, when the values of d are fixed as d = 9.5 mm and d = 18 mm for b = 30 mm, the indifferent stable zero equilibrium is realized with a large range for zero-stiffness property; and as shown in Figs. 5c, d, for b = 33 mm and d = 10 mm, the zero-stiffness property can be realized.

In order to realize stable zero equilibrium but large vibration for an external perturbation with small energy, it needs a stable zero equilibrium with great height difference from another stable equilibrium. It has known that the appropriate potential energy curve is obtained by the structural parameters in Region III as d = 7 mm in Fig. 5b and b = 33 mm in Fig. 5d. The height of potential energy at zero equilibrium is defined as H1, the height at the unstable equilibrium is defined as H2 and the height at the stable non-zero equilibrium is H3. The design criterion is as small difference between H1 and H2 with as large falling from H2 to H3, which is proposed as:

$$I = \left\{ {\left. {\left( {d,b} \right)} \right|H_{2} - H_{1} \ge V_{e} \& \hbox{max} \left( {H_{2} - H_{3} } \right)} \right\}.$$
(5)

where Ve reflects the energy from external perturbation or excitation at the initial moment. Based on the design criterion as Eq. (5), high potential energy is reserved for the highest drop from H2 to H3 as the external perturbation beyond the difference from H1 to H2.

3 Equivalent Vibration System

3.1 Equivalent Restoring Force Under Appropriate Design

For the expression of the potential energy V as Eq. (4), the interaction force \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}\) is obtained by \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F} = - \nabla V = \left( {F_{x} ,F_{y} ,F_{z} } \right)\). Here, as shown in Fig. 1, only Fy participate in the restoring force for vibration since the vibration motion is in y-direction and the magnetic interaction forces in x-(z-) direction are in static equilibrium. The expression of the equivalent restoring force Fy is

$$\begin{aligned} &F_{y} = K_{eq} \hat{y} \\ &+ \frac{{JJ^{\prime}}}{{2\pi \mu_{0} }}\sum\limits_{i = 0}^{1} {\sum\limits_{j = 0}^{1} {\sum\limits_{k = 0}^{1} {\sum\limits_{l = 0}^{1} {\sum\limits_{p = 0}^{1} {\sum\limits_{q = 0}^{1} {\left( { - 1} \right)^{i + j + k + k + p + q} \psi_{y} \left( {u_{ij} ,v_{kl} ,w_{pq} ,r} \right)} } } ,} } } \hfill \\ \end{aligned}$$
(6)

where \(\psi_{y} \left( {u,v,w,r} \right) = \frac{1}{2}\left( {u^{2} - w^{2} } \right)\ln \left( {r - v} \right) + uv\ln \left( {r - u} \right)\)\(+ uw\arctan \left( {\frac{uv}{rw}} \right) + \frac{rv}{2}\), the symbols uij, vkl, wpq and r are same as Eq. (3). The variation of the restoring force is shown in Fig. 6 for different structural parameters.

Fig. 6
figure 6

The restoring force Fy for a and b different relative distances d between magnets when fixing b = 30 mm; c and d different widths b of the magnet fixed on base when fixing d = 10 mm

Full size image

From the restoring force Fy shown in Fig. 6, the results verify the conclusion in the analysis of potential energy. With stronger magnetic field by reducing d, the nonlinear effect is more obvious as Figs. 6a, b; while for stronger magnetic field by increasing the width of magnetic field b, the zero equilibrium changes from unstable to stable.

For appropriate structural parameters, for instant, the case for d = 7 mm and b = 30 mm in Fig. 6b or the case for d = 10 mm and b = 33 mm, the zero equilibrium is stable with positive restoring force and there are two non-zero equilibriums symmetrically with large drop from zero equilibrium. Since the restoring force is always positive for large motion, on one hand, when the small external perturbation excites the vibration at the non-zero equilibrium, the vibration is with large amplitude due to the energy drop around the non-zero equilibrium; on the other hand, for time-lasting external excitation with large energy, the vibration occurs in a large range. Also, the slope of restoring force over the non-zero equilibrium is much higher than the value around the zero equilibrium, so the quasi-zero-stiffness can be realized and it needs little energy to vibration at ultralow frequency. Thus, the continuous piezoelectric structure with appropriate designed structural parameters of magnetic field, the required nonlinear restoring force can be realized without mechanical contact.

3.2 Equivalent Mechanical Model

According to the restoring force as Eq. (6), the equivalent model is shown in Fig. 7, which can be simplified as a vibration system with designed nonlinearity and energy harvesting device. Since magnets induce uncontacted interaction effect, the damping is from the piezoelectric cantilever beam, which is considered as linear function of motion.

Fig. 7
figure 7

The equivalent model with nonlinearity and EH

Full size image

In Fig. 7, the function \(K\left( {\hat{y}} \right)\) is the equivalent stiffness of the system including the equivalent stiffness of the piezoelectric beam and interaction of magnets; c is the damping coefficient; the coefficient α is the electromechanical coupling coefficient, Cp is the equivalent capacitance and RL is the resistance load. The dynamical equation of the equivalent model can be written as:

$$\left\{ \begin{aligned} &M\ddot{\hat{y}} + K\left( {\hat{y}} \right)\hat{y} + c\dot{\hat{y}} + \alpha V_{0} \left( t \right) = M\ddot{z}\left( t \right) \\& \alpha \dot{\hat{y}}\left( t \right) = C_{p} \dot{V}\left( t \right) + {{V_{0} \left( t \right)} \mathord{\left/ {\vphantom {{V_{0} \left( t \right)} {R_{L} }}} \right. \kern-0pt} {R_{L} }}. \hfill \\ \end{aligned} \right.$$
(7)

In Eq. (7), M is the equivalent mass, considering the mass in the end of piezoelectric since its mass is much larger than the beam; z(t) is the external excitation from base. For M = 0.01 kg, the structural parameters are fixed in the three regions in Fig. 4a. The vibration responses with magnetic interaction for small perturbation, small-amplitude and large-amplitude excitations are shown in Figs. 8, 9.

Fig. 8
figure 8

The vibration responses for small perturbation with different potential energy curves under different structural parameters

Full size image
Fig. 9
figure 9

The vibration responses with different potential energy curves under different structural parameters for a small-amplitude excitation as z0 = 0.4 mm and b large-amplitude excitation as z0 = 2.3 mm

Full size image

From Figs. 8, 9, it shows that the V–EH system with different potential energy displays different responses. For small perturbation and time-lasting excitations, the vibration amplitude for the potential energy curve with multi-stable equilibriums is larger than the other two cases.

4 Experimental Results

4.1 Experimental Diagram

For small external perturbation, the proposed V–EH can obviously multiply the small external energy. The experimental diagram of structure is shown in Fig. 10. In Fig. 10a, the experimental structure is consisted of the piezoelectric cantilever beam and magnets. The width of magnets fixed on the base is as b = 40 mm and the distance in one pair of magnets d can be adjusted. The vibration response of the piezoelectric beam and the external excitation are measured by laser. The voltage induced by the PZT is measured by the oscilloscope. The experimental procedure is as follow (shown in Fig. 10b): first, the equivalent stiffness Keq and damping coefficient c of the piezoelectric are identified by the decay transients of response; second, the vibration responses for two values of d in the Region I and Region III are measured for comparison for the two kinds of potential energy curves for different external perturbations; third, the highest output voltages obtained the PZT for different values of d are measured and compared.

Fig. 10
figure 10

a The experimental diagram of the proposed structure; b experimental setups

Full size image

4.2 The Parameters of Piezoelectric Beam by Identification

The equivalent stiffness Keq and damping coefficient c are obtained by experiment and identification. Providing an external excitation, the piezoelectric vibrates with decay. The vibration response and the relation between vibration resonance frequency and amplitude are shown in Fig. 11.

Fig. 11
figure 11

a Vibration decay of the piezoelectric beam and the envelope; b the relation between resonance frequency and amplitude

Full size image

From Fig. 11a, the envelope curve describes the velocity of vibration decay, and from Fig. 11b, the backbone curve shows the value of resonance frequency. Thus, from the vibration decay signal as shown in Fig. 11, the equivalent stiffness Keq and coefficient damping c is obtained by:

$$\left\{ \begin{aligned} K_{\text{eq}} = \omega^{2} M \hfill \\ c = \frac{1}{2\pi \cdot 4}\ln \left( {\frac{{x_{0} }}{{x_{4} }}} \right)\sqrt {MK_{eq} } \hfill \\ \end{aligned} \right..$$
(8)

According to Fig. 11, it can be obtained that the resonance frequency ω = 26.6 rad/s, x0 = 4 mm and x4 = 1 mm. The equivalent stiffness and coefficient damping are Keq ≈ 7 N m−1 and c = 0.0146 N s m−1. Then, in the following experiments, the distances in one pair of magnets are set as d = 30 mm and d = 10 mm, corresponding to the potential energy curves for region I and III, respectively.

4.3 Responses and Voltages as d = 30 mm and d = 10 mm

4.3.1 For Small-energy Impact Perturbation

The distance in one pair of magnets are fixed as d = 30 mm and d = 10 mm. For a small external excitation, the responses of the piezoelectric beam and the output voltages for the two structural parameters are shown and compared in Fig. 12.

Fig. 12
figure 12

Vibration responses under a small external perturbation for ad = 30 mm and bd = 10 mm; the output voltage for cd = 30 mm and dd = 10 mm

Full size image

From Fig. 12, the piezoelectric beam vibrates for different magnetic field. For the two cases, the zero equilibrium is static stable and after applying a very small external perturbation, the system vibrates. For d = 10 mm, the vibration occurs around non-zero equilibrium with larger amplitude than the case for d = 30 mm since the system reserves the potential energy as d = 10 mm. Therefore, the amplitude of the voltage obtained for the case d = 10 mm is much larger than the case d = 30 mm, which is brought by the designed potential energy as the curve in Region III in Fig. 4a.

4.3.2 For Ultralow-frequency Periodic Excitation

From the experiment of response of the piezoelectric beam without the magnetic interaction as Fig. 10, the resonance frequency is about 26.6 rad/s (about 4.235 Hz). From the results in Fig. 11, for d = 30 mm, the resonance frequency is 23.248 rad/s (about 3.701 Hz); and for d = 10 mm, the resonance frequency is reduced to 15.96 rad/s (about 2.541 Hz). Then, we measure the vibration response of the piezoelectric beam and output voltage for the two cases for time-lasting external excitation with different frequencies, as shown in Fig. 13.

Fig. 13
figure 13

Vibration responses under time-lasting external excitation for ad = 30 mm; b the output voltage for excitation with 3.7 Hz frequency; vibration responses for cd = 10 mm and d the output voltage for 2.5 Hz excitation frequency

Full size image

From the Fig. 13, it can be seen that the proposed V–EH can harvest the ultralow-frequency external excitation. For reducing the structural parameter d from d = 30 mm to d = 10 mm, the resonance frequency is reduced from 3.7 Hz to 2.5 Hz, which approaches to the applications of the proposed device for EH from nature. Also, for d = 30 mm as shown in Fig. 13a, the input excitation is amplified from 3 Hz to 4.5 Hz and after 4.6 Hz, the excitation is restrained; while for d = 10 mm in Fig. 13b, from 2 to 4.8 Hz, the excitation is amplified several times. Therefore, in the vibration resonance band, the appropriate design of structure has wider frequency band for V–EH.

5 Conclusions

In this manuscript, we propose a novel V-EH with adjustable nonlinearity to realize multiple equilibriums for small-amplitude and ultralow-frequency external excitations. According to the theoretical and experimental studies, it discovers only two pairs of magnets can form a magnetic field for mono-stable, tri-stable and multi-stable configurations. The parallel assembly of two pairs of the magnets like so-called QZS system not only realizes multi-stable equilibrium potential energy, but also reserves the energy. From the theoretical analysis of potential energy of the system, for appropriate structural parameters of the magnetic field, the multi-stable configurations can reserve large potential energy due to the huge drop from zero equilibrium to non-zero equilibrium. In addition, since in one pair of magnets, there is more than one adjustable structural parameter, the nonlinearity could be optimized for highest energy storage to result largest output power by the PZT. Also, the experimental results verify the effects and advantages brought by adjustable nonlinearity.

Based on the theoretical analysis and structural design, the proposed V-EH has adjustable nonlinearity properties to realize the vibration energy harvesting for small-amplitude and ultralow-frequency external excitations, and thus it can be widely applied for the natural phenomena such as dropping rain, falling balls and wind power. On the other hand, the remarkable EH effects from external excitation is induced by passive design and nonlinearity, which can amplify the vibration excitation effectively without any extra energy sources including fossil fuels and electric power. In addition, for time-lasting ultralow-frequency excitation, since sustainable and steady output voltage can be guaranteed, the output power can be utilized directly in applications such as people walk through. Therefore, the proposed V–EH in this study helps the sustainable development in green architecture, public facilities by taking full advantage of nonlinearity by piezoelectric structure and magnetic field.