Gravity-induced bistable 2DOF piezoelectric vibration energy harvester for broadband low-frequency operation

Abstract

Bistability has been proven beneficial for vibration energy harvesting. However, previous bistable harvesters are usually cumbersome in structure and are not necessarily capable of low-frequency operation. To resolve this issue, this paper proposes a compact two-degree-of-freedom (2DOF) bistable piezoelectric energy harvester with simple structure by using an inverted piezoelectric cantilever beam elastically coupled with a swinging mass-bar. The swinging mass-bar possesses bistable property due to the combined effect of the gravity and the elastic joint. It is revealed that, under the inter-well periodic motion pattern which has large swinging amplitude, the swinging mass-bar can exert large force and moment on the piezoelectric cantilever beam, thereby generating large electrical output in this process. Moreover, the inter-well periodic swinging motion can occur in a very broad low-frequency region, enabling broadband low-frequency energy harvesting. An experimental prototype is tested under harmonic excitation and sine frequency sweeping excitation; high electrical output is gained in the frequency range of 2 Hz to 12.6 Hz with a peak power of 3.558mW and a normalized power density of 19.52mW/(g²·cm³), which validates the broadband low-frequency energy harvesting capability.

1 Introduction

Vibration is a ubiquitous phenomenon in the natural world and engineering systems [1], which manifests continuous mechanical energy flow [2], referred to as the vibration energy. In recent decades, it has become a hot research topic to harvest vibration energy and convert it into useful electrical energy. The vibration energy harvesting technologies can be applied to many low-power electronic devices such as wireless sensors, portable devices, and medical gadgets and implants [3], thereby achieving self-powered purpose [4], which provides a solution for mitigating the issues associated with chemical batteries such as limited lifespan, environmental pollution and high maintenance cost [5]. There are five main transduction mechanisms for converting vibration energy into electrical energy, namely piezoelectric [6], electromagnetic [7], electrostatic [8], magnetostrictive [9] and triboelectric [10] mechanisms, based on the underlying physical principles that have been developed by researchers. These transduction mechanisms can be exploited for developing vibration energy harvesters. However, many energy harvesters are linear designs and generate useful output power only near the resonant frequency [11], which results in narrow operation bandwidth [12]. Besides, the linear energy harvesters are difficult to efficiently generate electrical output at low frequencies, which hinders the application for low-frequency ambient vibration [13].

A lot of effort has been invested attempting to overcome the drawbacks of linear energy harvesters, and some methodologies have been put forward such as the multi-resonance method and the nonlinear method. The essence of the multi-resonance method is to construct a multi-degree-of-freedom (MDOF) vibrating structure which possesses multiple close resonant peaks and consequently the effective bandwidth of energy harvesting can be broadened [14]; a typical example is the multi-branch harvesters composed of a main cantilever beam on which the piezoelectric patch is bonded and multiple branches with tip masses at their free ends [15]. The nonlinear harvesters are essentially different from the linear ones in terms of dynamic response characteristics [16], because their frequency response curves usually bend to the right (for hardening stiffness) or left (for softening stiffness) [17], which therefore broadens the bandwidth of resonance region for effective energy harvesting. As a large category of generic methodology, the nonlinear energy harvesting technology involves many diverse implementations, such as the quasi-zero-stiffness (QZS) harvester [18], the nonlinear energy sink (NES)-based harvester [19], and the multi-stable harvester [20]. The multi-stable harvester possesses multiple potential wells, allowing the occurrence of large amplitude snap-through oscillation among these potential wells for high electrical output [21]. Usually, multi-stable harvester is composed of a piezoelectric cantilever beam with tip magnet and several fixed magnets that interact with the tip magnet [22]. Based on different numbers and layouts of the fixed magnets, various multi-stable harvesters can be built, including the bistable harvester [23], the tristable harvester [24], the quad-stable harvester [25] and the penta-stable harvester [26].

The bistable energy harvesters have a variety of construction ways in addition to the aforementioned piezomagnetoelastic cantilever configuration and therefore received the most attention in recent decade. Naseer et al. [27] employed the piezomagnetoelastic bistable energy harvester for harvesting energy from vortex-induced vibration. Li et al. [28] changed the fixed magnet to movable magnet, resulting in variable potential well. Xu et al. [29] studied a bistable harvester using the simply supported piezoelectric buckled beam and demonstrated that the output properties and bandwidth of this bistable harvester under harmonic excitation could be improved dramatically compared with traditional linear harvester. Pan et al. [30] built a bistable harvester using the hybrid composite laminate with well-designed stacking sequence, which had some unique features such as uniform strain of piezoelectric elements and symmetric stable configurations. Inspired by the flight mechanism of dipteran, Zhou et al. [31] proposed a novel bistable harvester using two flexible piezoelectric beams and two rigid rods for low-frequency energy harvesting, which generated 0.143mW power under 0.7 g excitation at 4 Hz. Wu et al. [32] integrated a U-shaped torsional structure into the middle of a pre-deformed piezoelectric beam with sinusoidal shape to facilitate the occurrence of snap-through and thus improve the energy harvesting efficiency, which generated a maximum average output power of 0.179mW. Hao et al. [33] proposed a nanomaterial-based broadband piezoelectric energy harvester with local bistability inspired by the structure of soybean pods. Qian et al. [34] proposed a broadband bistable harvester based on the bio-inspiration from the rapid shape transition of the Venus flytrap, in which two sub-beams with bending and twisting deformations were mutually constrained at their free ends to produce the snap-through ability. Tu et al. [35] proposed a bistable vibration energy harvester with spherical moving magnets, combining the restoring force of limit spring, attractive magnetic force and gravity to achieve bistability. Wang et al. [36] proposed a rolling magnet bistable electromagnetic harvester utilizing the rolling motion of a magnetically levitated magnet. Li et al. [37] proposed a novel bistable electromagnetic energy harvester coupled with appended nonlinear elastic boundary to enhance energy harvesting performance. Xing et al. [38] proposed a rotational hybrid energy harvester utilizing bistability for low-frequency applications. Hou et al. [39] proposed a novel bistable energy harvesting backpack to improve the biomechanical energy harvesting performance. Wu et al. [40] proposed a bistable piezoelectric energy harvester realizing by combining the elastic potential energy of a bridge-type compliant mechanism and the gravitational potential energy. Rezaei et al. [41] utilized a magnetic bistable PZT-based absorber for concurrent energy harvesting and vibration mitigation. Liu et al. [42] placed a spring below the bistable magnetostrictive energy harvester as displacement amplification mechanism to boost the electrical output. Tan et al. [43] proposed a sliding-impact bistable triboelectric nanogenerator to enhance the efficiency of harvesting energy from low-frequency intrawell oscillation. Bai et al. [44] proposed a snap-through triboelectric nanogenerator with magnetic coupling and buckled bistable mechanism to harvest rotational energy.

From the literature review, it can be seen that the structures of existing bistable energy harvesters are usually cumbersome for the purpose of realizing bistable property, and they are not necessarily capable of low-frequency energy harvesting in spite of broad operation bandwidth. In order to reduce the structural complexity and enable low-frequency operation, a compact bistable energy harvester with simple structure by using an inverted piezoelectric cantilever beam elastically coupled with a swinging mass-bar is proposed in this paper. The bistable property exists in the swinging mass-bar, which is produced by the combined effect of the gravity and the elastic joint. Due to the bistable property, the swinging mass-bar is expected to execute large amplitude inter-well swinging oscillation in a broadband frequency range, provided that the excitation is enough to break through the potential barrier. Then, the swinging mass-bar can exert large force and moment on the piezoelectric cantilever beam, thereby generating large output voltage. The biggest difference from the previous bistable harvesters is that the proposed bistable harvester is a two-degree-of-freedom (2DOF) system, whereas the previous bistable harvesters are single-degree-of-freedom (SDOF) systems. The composition of the proposed bistable harvester is very simple, which does not involve magnetic interaction or complex structure. Moreover, the elastic swinging mass-bar, similar to an inverted pendulum in a broad sense, has low characteristic frequency, which makes the large amplitude inter-well swinging oscillation easily activated at low frequencies. Therefore, the proposed bistable harvester possesses broadband low-frequency energy harvesting capability.

2 Structural configuration

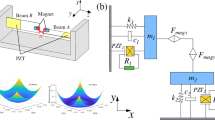
Figure 1(a) shows the schematic diagram of the proposed 2DOF bistable energy harvester, which is composed of an inverted cantilever beam, a piezoelectric patch, an elastic joint, a rigid bar and a tip body. The piezoelectric patch is bonded on the surface of the inverted cantilever beam near the clamped end. The electrical load is simply represented as a resistance [the load resistance and the electric wires are not displayed in Fig. 1(a)]. The cantilever beam and the rigid bar are connected via the elastic joint at the free end of the cantilever beam. The tip body is fixed at the upper end of the rigid bar and thus they can be considered as a whole, hereafter referred to as the mass-bar. The mass-bar can swing (upside down) about the elastic joint. The restoring moment of the swinging motion of the mass-bar is provided by its gravity and the elastic joint: The moment of gravity with respect to the rotation center (i.e. the elastic joint) produces negative restoring moment, while the elastic joint produces positive restoring moment. By selecting the rotational stiffness of the elastic joint properly, it is achievable to obtain the bistable property for the swinging mass-bar. The position in Fig. 1(a) is just an unstable equilibrium state, and the two stable equilibrium states are depicted schematically in Fig. 1(b) and (c). Due to the bistable property, the mass-bar can execute large amplitude inter-well swinging oscillation in broadband frequency range, which exerts large force on the cantilever beam. Moreover, the gravity of the tip body can produce an additional moment on the cantilever beam. As a result, the vibration intensity of the cantilever beam is significantly boosted, thereby generating higher output voltage. The swinging mass-bar also has another merit: Its characteristic frequency for the swinging motion is inherently low [45] and thus the large amplitude inter-well swinging oscillation can be easily activated at low frequencies. Therefore, the bistable property and the low characteristic frequency guarantee the capability of broadband low-frequency energy harvesting.

Fig. 1

a Schematic diagram of the proposed energy harvester; b first stable state; c second stable state

An experimental prototype is fabricated as shown in Fig. 2. The cantilever beam and the elastic joint are made of 65Mn spring steel; the rigid bar is made of polymethyl methacrylate (PMMA); the tip body is made of aluminum alloy; the piezoelectric patch is made of lead zirconate titanate piezoelectric ceramics (PZT-5H). The parameter values of the experimental prototype are listed in Table 1.

Fig. 2

Photograph of the experimental prototype

Table 1 Parameter values of the experimental prototype

3 Analysis and methodology

In this section, the bistable property of the elastic swinging mass-bar is analyzed; the electromechanical coupled equations are derived starting from the most elementary mechanical and electrical knowledge, which will be used for numerical simulations to obtain theoretical results; the experimental principle is given for frequency sweeping tests and harmonic excitation tests to obtain experimental results.

3.1 Bistable property of the elastic swinging mass-bar

The swinging mass-bar hinged at the elastic joint is examined to elucidate the bistable property. For simplicity, it is assumed that the mass of the swinging mass-bar is concentrated on the tip body. The swinging motion of the mass-bar is described by the swinging angle denoted as $\beta$ ($- {\pi / 2} < \beta < {\pi / 2}$). The potential energy of this system is

$$E_p = \frac{1}{2}k_0 \beta^2 - m_0 gL\left( {1 - \cos \beta } \right)$$

(1)

where $k_0$ is the rotational stiffness of the elastic joint, $m_0$ is the mass of the tip body, $g$ is the gravitational acceleration ($g = 9.8{{\text{m}} / {{\text{s}}^2 }}$), and $L$ is the length of the rigid bar. Figure 3 shows the potential energy plotted against the swinging angle, from which it can be seen that there are three situations for different values of the rotational stiffness: (1) When the rotational stiffness is relatively large, the potential energy has only one local minimum, which corresponds to the mono-stable case; (2) when the rotational stiffness is chosen in a certain range, the potential energy has two local minima and one local maximum, which corresponds to the bistable case; (3) when the rotational stiffness is relatively small, the potential energy has only one local maximum and no local minimum, which corresponds to the null-stable case. In fact, if the range of $\beta$ is extended beyond $\pm {\pi / 2}$, case 3 can also have two local minima; however, it makes sense only in purely mathematical aspect, but is totally meaningless in physical aspect.

Fig. 3

Potential energy versus swinging angle

The different stable state scenarios can also be observed from the unperturbed phase diagrams. As a conservative system, the Hamiltonian function of the elastic swinging mass-bar is

$$H\left( {\beta ,\dot{\beta }} \right) = \frac{1}{2}m_0 L^2 \dot{\beta }^2 + \frac{1}{2}k_0 \beta^2 - m_0 gL\left( {1 - \cos \beta } \right)$$

(2)

Based on the Hamiltonian function, the unperturbed phase diagrams are plotted in Fig. 4 for different values of the rotational stiffness. The mono-stable case is depicted in Fig. 4(a) which has one center (red point); the bistable case is depicted in Fig. 4(b) which has two centers and one saddle (green point); the null-stable case is depicted in Fig. 4(c) which has one saddle.

Fig. 4

Unperturbed phase diagrams of the elastic swinging mass-bar: a $k_0 = 0.023{\text{N}} \cdot {\text{m/rad}}$; b $k_0 = 0.02016{\text{N}} \cdot {\text{m/rad}}$; c $k_0 = 0.013{\text{N}} \cdot {\text{m/rad}}$

It is necessary to determine the range of the rotational stiffness that can lead to the bistable property for the elastic swinging mass-bar. To achieve this, the second derivative of the potential energy with respect to the swinging angle at $\beta = 0$ must be negative, and the first derivative at $\beta = {\pi / 2}$ must be positive, i.e.

$$\left\{ {\begin{array}{*{20}l} {\left. {\frac{{{\text{d}}^2 E_p }}{{{\text{d}}\beta^2 }}} \right|_{\beta = 0} < 0} \hfill \\ {\left. {\frac{{{\text{d}}E_p }}{{{\text{d}}\beta }}} \right|_{\beta = \frac{\pi }{2}} > 0} \hfill \\ \end{array} } \right.$$

(3)

which yields

$$\frac{2}{\pi }m_0 gL < k_0 < m_0 gL$$

(4)

Figure 5 gives the static bifurcation diagram of equilibrium positions with the variation of the rotational stiffness. It can be seen that, if $0 < k_0 < \left( {2 / \pi } \right)m_0 gL$, there is one unstable equilibrium position; if $\left( {2 / \pi } \right)m_0 gL < k_0 < m_0 gL$, there are two symmetrical stable equilibrium positions and one unstable equilibrium position; if $k_0 > m_0 gL$, there is one stable equilibrium position. Therefore, $k_0 = \left( {2 / \pi } \right)m_0 gL$ and $k_0 = m_0 gL$ are just two static bifurcation points of the rotational stiffness. In order to realize the bistable property, the rotational stiffness must be chosen between the two bifurcation points, i.e. $\left( {2 / \pi } \right)m_0 gL < k_0 < m_0 gL$.

Fig. 5

Static bifurcation diagram of equilibrium positions versus the rotational stiffness

3.2 Formulation of electromechanical coupled equations

In order to conduct numerical simulations for theoretical study, the electromechanical coupled equations of the proposed 2DOF bistable energy harvester must be derived. To proceed, some reasonable assumptions concerning the electromechanical coupled modeling are given here: (1) The beam is considered as an Euler–Bernoulli beam; (2) the longitudinal compression of the beam is ignored as it is very insignificant compared to the bending deformation; (3) the strain of the piezoelectric patch is considered uniform in the thickness direction (but non-uniform in the length direction) since it is very thin; (4) the electric field in the piezoelectric patch is also considered uniform in the thickness direction.

Strictly speaking, the cantilever beam is an elastic continuum with infinite vibration modes, and therefore, the whole harvester is an infinite-DOF system. However, the second-order and higher-order natural frequencies of the cantilever beam with tip mass are much larger than the first-order natural frequency, making it difficult to activate the second-order and higher-order vibration modes under normal external excitation especially the low-frequency excitation as discussed in this paper. Therefore, the cantilever beam vibrates in almost only the first-order mode and behaves as a SDOF vibrator, and then, the whole harvester becomes a 2DOF system accordingly. A direct way of establishing the SDOF model for a beam is to find a proper normalized shape function so as to describe the deformation of the beam by only one time-dependent variable. Previous studies have indicated that it is feasible to use the fundamental mode shape as the shape function to establish a SDOF beam model [46], which has satisfactory accuracy especially when the mass of the beam is much smaller than the attached mass [47]. Since the length of the bar is much smaller than the length of the beam, it is reasonable to assume that the fundamental mode shape of the cantilever beam with swinging tip mass is approximately the same as the cantilever beam with fixed tip mass, which is [48]

$$\Phi \left( s \right) = \left[ {\cos \left( {qs} \right) - \cosh \left( {qs} \right)} \right] - \frac{{\cos \left( {qL_b } \right) + \cosh \left( {qL_b } \right)}}{{\sin \left( {qL_b } \right) + \sinh \left( {qL_b } \right)}}\left[ {\sin \left( {qs} \right) - \sinh \left( {qs} \right)} \right]$$

(5)

where $s$ is the longitudinal coordinate along the cantilever beam, and $q$ is solved from the following characteristic equation:

$$\frac{m_0 }{{\rho_b b_b h_b L_b }}\left( {qL_b } \right)\left[ {\cos \left( {qL_b } \right)\sinh \left( {qL_b } \right) - \sin \left( {qL_b } \right)\cosh \left( {qL_b } \right)} \right] + \cos \left( {qL_b } \right)\cosh \left( {qL_b } \right) + 1 = 0$$

(6)

where $\rho_b$, $b_b$, $h_b$ and $L_b$ are the mass density, width, thickness and length of the cantilever beam, respectively. The normalized shape function is thus taken as $\phi \left( s \right) = {{\Phi \left( s \right)} / {\Phi \left( {L_b } \right)}}$ to give

$$\begin{gathered} \phi \left( s \right) = \hfill \\ \frac{{\left[ {\sin \left( {qL_b } \right) + \sinh \left( {qL_b } \right)} \right]\left[ {\cos \left( {qs} \right) - \cosh \left( {qs} \right)} \right] - \left[ {\cos \left( {qL_b } \right) + \cosh \left( {qL_b } \right)} \right]\left[ {\sin \left( {qs} \right) - \sinh \left( {qs} \right)} \right]}}{{2\left[ {\cos \left( {qL_b } \right)\sinh \left( {qL_b } \right) - \sin \left( {qL_b } \right)\cosh \left( {qL_b } \right)} \right]}} \hfill \\ \end{gathered}$$

(7)

By using the normalized shape function, the deformation of the beam can be described as

$$w\left( {s,t} \right) = \phi \left( s \right)x\left( t \right)$$

(8)

where $x\left( t \right)$ is the transverse displacement of the tip of the cantilever beam (hereafter called the beam tip for short) relative to the moving base. The strain of the beam is therefore

$$\varepsilon_b \left( {s,y,t} \right) = - y\frac{{\partial^2 w\left( {s,t} \right)}}{\partial s^2 } = - yx\phi^{\prime \prime}\left( s \right)$$

(9)

where $y$ is the transverse coordinate from the neutral surface. The stress of the beam is

$$\sigma_b \left( {s,y,t} \right) = Y_b \varepsilon_b \left( {s,y,t} \right) = - Y_b yx\phi^{\prime \prime}\left( s \right)$$

(10)

where $Y_b$ is the Young’s modulus of the beam. The strain of the piezoelectric patch is equal to the strain of the beam surface on which the piezoelectric patch is bonded, which is

$$\varepsilon_p \left( {s,t} \right) = \varepsilon_b \left( {s,\frac{h_b }{2},t} \right) = - \frac{1}{2}h_b x\phi^{\prime \prime}\left( s \right)$$

(11)

The piezoelectric patch works in 31-mode since the electric field direction is perpendicular to the stress direction. The reduced constitutive equations of the piezoelectric patch in 31-mode are [49]

$$\sigma_p \left( {s,t} \right) = Y_p \varepsilon_p - e_{31} E_3$$

(12)

$$D_3 \left( {s,t} \right) = e_{31} \varepsilon_p + \eta_{33} E_3$$

(13)

where $\sigma_p$ is the stress of the piezoelectric patch, $Y_p$ is the Young’s modulus of the piezoelectric patch, $e_{31}$ is the piezoelectric stress constant, $E_3$ is the electric field intensity, $D_3$ is the electric displacement (also known as the charge density in some articles [50]), and $\eta_{33}$ is the dielectric permittivity at constant strain. The relation between the electric field intensity $E_3$ and the output voltage $v$ is

$$E_3 = - \frac{v}{h_p }$$

(14)

where $h_p$ is the thickness of the piezoelectric patch. The relation between the electric displacement $D_3$ and the electric current $I$ is

$$\begin{gathered} I = \frac{{\text{d}}}{{{\text{d}}t}}\int_{A_p } {D_3 \left( {s,t} \right){\text{d}}A_p } = \frac{{\text{d}}}{{{\text{d}}t}}\int_{A_p } {\left( { - \frac{1}{2}e_{31} h_b x\phi^{\prime \prime}\left( s \right) - \frac{{\eta_{33} }}{h_p }v} \right){\text{d}}A_p } \\ = - \frac{1}{2}e_{31} b_p h_b \phi^{\prime}\left( {L_p } \right)\dot{x} - \frac{{\eta_{33} b_p L_p }}{h_p }\dot{v} \\ \end{gathered}$$

(15)

where $A_p$ stands for the surface of the piezoelectric patch, $b_p$ and $L_p$ are the width and length of the piezoelectric patch, and overdot denotes differentiation with respect to time $t$. Substituting Eq. into the expression of Ohm's law ($v = IR$), we have

$$\frac{v}{R} = - \frac{1}{2}e_{31} b_p h_b \phi^{\prime}\left( {L_p } \right)\dot{x} - \frac{{\eta_{33} b_p L_p }}{h_p }\dot{v}$$

(16)

where $R$ is the load resistance. This equation is just the coupled electrical equation (Fig. 6).

Fig. 6

a Force analysis diagram of the inverted cantilever beam; b force analysis diagram of the swinging mass-bar; c acceleration analysis diagram of the tip body

Next, we formulate the coupled mechanical equations. Here, we use the Principle of Virtual Work (which means that the virtual work done by the external forces/moments is equal to the virtual strain energy) to derive the coupled mechanical equation of the cantilever beam. With a transverse virtual displacement $\delta x$ (relative to the moving base) at the beam tip, the virtual strain energy of the piezoelectric cantilever beam is

$$E_{{\text{virtual}}} = \int_{V_b } {\sigma_b \cdot \delta \varepsilon_b } {\text{d}}V_b + \int_{V_p } {\sigma_p \cdot \delta \varepsilon_p } {\text{d}}V_p = \int_0^{L_b } {\int_{ - \frac{h_b }{2}}^{\frac{h_b }{2}} {b_b \sigma_b \cdot \delta \varepsilon_b } {\text{d}}y{\text{d}}s} + \int_0^{L_p } {b_p h_p \sigma_p \cdot \delta \varepsilon_p } {\text{d}}s$$

(17)

where $V_b$ and $V_p$ stand for the volumes of the beam and the piezoelectric patch, respectively. Substituting Eqs. ~ and into Eq. yields

$$E_{{\text{virtual}}} = \left\{ {\left[ {\frac{1}{12}Y_b b_b h_b^3 \int_0^{L_b } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} + \frac{1}{4}Y_p b_p h_p h_b^2 \int_0^{L_p } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} } \right]x - \frac{1}{2}e_{31} b_p h_b \phi^{\prime}\left( {L_p } \right)v} \right\} \cdot \delta x$$

(18)

To find the virtual work, we should first identify the external forces/moments for the cantilever beam. As depicted in Fig. 6(a), at the tip of the beam, there exist a horizontal force (denoted as $F_h$), a vertical force (denoted as $F_v$) and a moment (denoted as $M$). Since the deformation of the cantilever beam is much smaller than the swinging motion of the mass-bar, the nonlinearity mainly exists in the swinging mass-bar system, and the linear deformation assumption can be applied for the cantilever beam. Under this assumption, the vertical displacement of the beam tip is a higher-order infinitesimal quantity relative to the transverse displacement and the deflection angle at the beam tip, so the virtual work done by the vertical force is also a higher-order infinitesimal quantity and thus can be ignored when calculating the total virtual work. Based on the D’Alembert’s principle, the inertia forces of the beam and the piezoelectric patch are also treated as external forces when applying the Principle of Virtual Work, which are given by

$${\text{d}}F_{{\text{beam}}} = - \rho_b b_b h_b \left( {\ddot{z} + \ddot{w}} \right){\text{d}}s{\text{ d}}F_{{\text{piezo}}} = - \rho_p b_p h_p \left( {\ddot{z} + \ddot{w}} \right){\text{d}}s$$

(19)

where $\ddot{z}$ is the acceleration of the moving base and $\rho_p$ is the mass density of the piezoelectric patch. The total virtual work is calculated by

$$\begin{gathered} W_{{\text{virtual}}} = F_h \cdot \delta x + M \cdot \delta \left( {\left. {\frac{\partial w}{{\partial s}}} \right|_{s = L_b } } \right) + \int_0^{L_b } {\delta w \cdot {\text{d}}F_{{\text{beam}}} } + \int_0^{L_p } {\delta w \cdot {\text{d}}F_{{\text{piezo}}} } \\ = \left\{ {F_h + M\phi^{\prime}\left( {L_b } \right) - \left[ {\rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \right]\ddot{z}} \right. \\ \, \left. { - \left[ {\rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \right]\ddot{x}} \right\} \cdot \delta x \\ \end{gathered}$$

(20)

By letting $E_{{\text{virtual}}} = W_{{\text{virtual}}}$ and eliminating $\delta x$, we can obtain

$$\begin{gathered} \left[ {\rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \right]\ddot{x} + \left[ {\rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \right]\ddot{z} \hfill \\ + \left[ {\frac{1}{12}Y_b b_b h_b^3 \int_0^{L_b } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} + \frac{1}{4}Y_p b_p h_p h_b^2 \int_0^{L_p } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} } \right]x - \frac{1}{2}e_{31} b_p h_b \phi^{\prime}\left( {L_p } \right)v = F_h + M\phi^{\prime}\left( {L_b } \right) \hfill \\ \end{gathered}$$

(21)

The horizontal force $F_h$ and the moment $M$ at the beam tip are still unknown here. Therefore, we need to analyze the swinging mass-bar to associate $F_h$ and $M$ with the kinematic state of the swinging mass-bar. As depicted in Fig. 6(c), the tip body has a radial acceleration $\dot{\beta }^2 L$ and a tangential acceleration $\ddot{\beta }L$ relative to the rotation center (i.e. the elastic joint) which itself also has a horizontal acceleration $\ddot{x} + \ddot{z}$. Therefore, the horizontal (rightward) absolute acceleration of the tip body is

$$a_h = \dot{\beta }^2 L\sin \beta - \ddot{\beta }L\cos \beta - \ddot{x} - \ddot{z}$$

(22)

The vertical (downward) absolute acceleration of the tip body is

$$a_v = \dot{\beta }^2 L\cos \beta + \ddot{\beta }L\sin \beta$$

(23)

From the perspective of the D’Alembert’s principle, the existence of acceleration is equivalent to being subjected to the inertia force in the opposite direction. Based on the force analysis diagram of the swinging mass-bar [Fig. 6(b)], to achieve force balance in the vertical and horizontal directions, respectively, we have

$$F_h = m_0 a_h = m_0 \left( {\dot{\beta }^2 L\sin \beta - \ddot{\beta }L\cos \beta - \ddot{x} - \ddot{z}} \right)$$

(24)

$$F_v = m_0 g - m_0 a_v = m_0 \left( {g - \dot{\beta }^2 L\cos \beta - \ddot{\beta }L\sin \beta } \right)$$

(25)

The moment at the rotation center (i.e. the elastic joint) is

$$M = k_0 \beta$$

(26)

To achieve moment balance, we have

$$m_0 a_h L\cos \beta + \left( {m_0 g - m_0 a_v } \right)L\sin \beta = M$$

(27)

Substituting Eqs., and into Eq. yields

$$m_0 L\left[ { - \ddot{\beta }L - \left( {\ddot{x} + \ddot{z}} \right)\cos \beta + g\sin \beta } \right] = k_0 \beta$$

(28)

Substituting Eqs. and into Eq. yields

$$\begin{gathered} \left[ {m_0 + \rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \right]\ddot{x} + \left[ {m_0 + \rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \right]\ddot{z} \hfill \\ + \left[ {\frac{1}{12}Y_b b_b h_b^3 \int_0^{L_b } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} + \frac{1}{4}Y_p b_p h_p h_b^2 \int_0^{L_p } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} } \right]x - \frac{1}{2}e_{31} b_p h_b \phi^{\prime}\left( {L_p } \right)v \hfill \\ = m_0 \left( {\dot{\beta }^2 L\sin \beta - \ddot{\beta }L\cos \beta } \right) + k_0 \phi^{\prime}\left( {L_b } \right)\beta \hfill \\ \end{gathered}$$

(29)

Eqs., and are the electromechanical coupled equations of the whole energy harvester. Now we rearrange and rewrite them with extracting meaningful coefficients:

$$\left\{ {\begin{array}{*{20}l} {\left( {m_0 + m_{eq} } \right)\ddot{x} + k_{eq} x - m_0 \left( {L\dot{\beta }^2 \sin \beta - L\ddot{\beta }\cos \beta } \right) - k_0 \phi^{\prime}\left( {L_b } \right)\beta + \Theta v = - \left( {m_0 + m_{eq} } \right)\ddot{z}} \hfill \\ {m_0 L^2 \ddot{\beta } + m_0 L\ddot{x}\cos \beta - m_0 gL\sin \beta + k_0 \beta = - m_0 L\ddot{z}\cos \beta } \hfill \\ {\frac{v}{R} + C_p \dot{v} - \Theta \dot{x} = 0} \hfill \\ \end{array} } \right.$$

(30)

where

$$\left\{ {\begin{array}{*{20}c} {m_{eq} = \rho_b b_b h_b \int_0^{L_b } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} + \rho_p b_p h_p \int_0^{L_p } {\left( {\phi \left( s \right)} \right)^2 {\text{d}}s} } \\ {k_{eq} = \frac{1}{12}Y_b b_b h_b^3 \int_0^{L_b } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} + \frac{1}{4}Y_p b_p h_p h_b^2 \int_0^{L_p } {\left( {\phi^{\prime \prime}\left( s \right)} \right)^2 {\text{d}}s} } \\ {\Theta = - \frac{1}{2}e_{31} b_p h_b \phi^{\prime}\left( {L_p } \right)} \\ {C_p = \frac{{\eta_{33} b_p L_p }}{h_p }} \\ \end{array} } \right.$$

(31)

where $m_{eq}$ and $k_{eq}$ can be regarded as the equivalent mass and equivalent stiffness of the piezoelectric cantilever beam, and $\Theta$ and $C_p$ can be regarded as the electromechanical coupling coefficient and internal capacitance of the piezoelectric patch. The acceleration of the base excitation can be written in the form $\ddot{z}\left( t \right) = B\cos \left( {\omega t} \right)$ with $B$ being the excitation amplitude and $\omega$ being the excitation frequency. The above analysis procedure does not take energy dissipation into consideration. In order to consider energy dissipation in a simple manner, we can introduce linear viscous damping in the cantilever beam (with damping coefficient $c_1$) and the elastic joint (with damping coefficient $c_2$), and then, the damping force and damping moment terms can directly be added to the derived electromechanical coupled equations. In doing so, the electromechanical coupled equations are modified as

$$\left\{ {\begin{array}{*{20}l} {\left( {m_0 + m_{eq} } \right)\ddot{x} + c_1 \dot{x} + k_{eq} x - m_0 \left( {L\dot{\beta }^2 \sin \beta - L\ddot{\beta }\cos \beta } \right) - k_0 \phi^{\prime}\left( {L_b } \right)\beta + \Theta v = - \left( {m_0 + m_{eq} } \right)B\cos \left( {\omega t} \right)} \hfill \\ {m_0 L^2 \ddot{\beta } + m_0 L\ddot{x}\cos \beta + c_2 \dot{\beta } - m_0 gL\sin \beta + k_0 \beta = - m_0 LB\cos \beta \cos \left( {\omega t} \right)} \hfill \\ {\frac{v}{R} + C_p \dot{v} - \Theta \dot{x} = 0} \hfill \\ \end{array} } \right.$$

(32)

In order to facilitate numerical simulations, it is better to transform the electromechanical coupled equations Eq. into the state-space equation, which is

$$\left[ {\begin{array}{*{20}c} {\dot{u}_1 } \\ {\dot{u}_2 } \\ {\dot{u}_3 } \\ {\dot{u}_4 } \\ {\dot{u}_5 } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {u_2 } \hfill \\ {\frac{{\left( {Lu_4^2 - g\cos u_3 } \right)m_0 \sin u_3 + k_0 \phi^{\prime}\left( {L_b } \right)u_3 + \frac{c_2 u_4 + k_0 u_3 }{L}\cos u_3 - c_1 u_2 - k_{eq} u_1 - \Theta u_5 }}{{m_0 \sin^2 u_3 + m_{eq} }} - B\cos \left( {\omega t} \right)} \hfill \\ {u_4 } \hfill \\ {\frac{g}{L}\sin u_3 - \frac{{\left( {m_0 + m_{eq} } \right)\left( {c_2 u_4 + k_0 u_3 } \right)}}{{m_0 L^2 \left( {m_0 \sin^2 u_3 + m_{eq} } \right)}} - \frac{{\left( {Lu_4^2 - g\cos u_3 } \right)m_0 \sin u_3 + k_0 \phi^{\prime}\left( {L_b } \right)u_3 - c_1 u_2 - k_{eq} u_1 - \Theta u_5 }}{{\left( {m_0 \sin^2 u_3 + m_{eq} } \right){L / {\cos u_3 }}}}} \hfill \\ {\frac{\Theta }{C_p }u_2 - \frac{u_5 }{{RC_p }}} \hfill \\ \end{array} } \right]$$

(33)

where $\left[ {u_1 ,u_2 ,u_3 ,u_4 ,u_5 } \right]^{\text{T}}$ is defined as $\left[ {u_1 ,u_2 ,u_3 ,u_4 ,u_5 } \right]^{\text{T}} = \left[ {x,\dot{x},\beta ,\dot{\beta },v} \right]^{\text{T}}$.

3.3 Experimental setup

The experimental principle is shown in Fig. 7, which comprises a computer, a controller, a power amplifier, a shaker, the experimental prototype, a PCB accelerometer, a resistor and an oscilloscope. The shaker is turned to render its vibration direction horizontal. The base of the experimental prototype is fixed on the shaker table. The excitation signal is set on the computer and then transmitted to the controller to generate control signal; then, the control signal is amplified by the power amplifier to drive the shaker. The accelerometer is placed at the base of the experimental prototype to acquire the real-time acceleration of the base excitation (i.e. the acceleration of the shaker table), which is fed back to the controller for closed-loop negative feedback control to enhance the vibrating accuracy of the shaker table. The two electrodes of the piezoelectric patch are connected to the resistor whose resistance value can be adjusted. The oscilloscope is used to monitor and record the voltage across the resistor (i.e. the output voltage). Both the frequency sweeping tests and the harmonic excitation tests are conducted in this study.

Fig. 7

Experimental principle and apparatuses

4 Results and discussions

4.1 Numerical simulations

In the numerical simulations, the values of the four extracted lumped parameters are calculated according to Eq. to give $m_{eq} = 0.016{\text{kg}}$, $k_{eq} { = 547}{\text{.64N/m}}$, $\Theta =$$1.136 \times 10^{ - 3} {\text{N/V}}$ and $C_p = {2}{\text{.3901}} \times 10^{ - 7} {\text{F}}$; the damping coefficients are set as $c_1 =$${0}{\text{.0915N}} \cdot {\text{s/m}}$ and $c_2 = 3.43 \times 10^{ - 4} {\text{N}} \cdot {\text{m}} \cdot {\text{s/rad}}$; the excitation amplitude is set as $B = 0.5g = 4.9{\text{m/s}}^{2}$; the electrical load resistance is set as $R = 2 \times 10^5 \Omega$. By using the fourth-order Runge–Kutta algorithm, the theoretical dynamic response and output voltage of the proposed energy harvester can be obtained.

Figure 8 presents the forward frequency sweeping results from 0 to 14 Hz. It can be seen that the swinging motion of the mass-bar may be inter-well motion or intra-well motion in different frequency regions. In the frequency regions of 1.9 Hz ~ 2.1 Hz, 2.3 Hz ~ 2.7 Hz and 3 Hz ~ 12.2 Hz, the inter-well motion occurs. In the frequency regions of 0 Hz ~ 1.9 Hz, 2.1 Hz ~ 2.3 Hz, 2.7 Hz ~ 3 Hz and 12.2 Hz ~ 14 Hz, the intra-well motion occurs. For the intra-well motion pattern, although the offset of the oscillation center of the swinging mass-bar is very noticeable, the offset of displacement response and the offset of output voltage are not very obvious. The swinging amplitude of the inter-well motion is much larger than that of the intra-well motion (removing the offset). For this reason, the displacement response of the beam tip and the output voltage are also relatively large when the swinging mass-bar is in the inter-well motion pattern: The maximum output voltage is 28.9 V at 11 Hz at which the inter-well motion occurs, whereas the output voltage under the intra-well motion pattern is only about 0 ~ 3 V. An interesting phenomenon is that the displacement response and the output voltage suddenly drop down at 11.1 Hz. This is because, at this frequency, the motion pattern of the swinging mass-bar changes from the inter-well periodic motion to the inter-well chaotic motion. In general, the inter-well periodic motion can produce larger force/moment between the cantilever beam and the swinging mass-bar than the inter-well chaotic motion, and the inter-well chaotic motion can produce larger force/moment than the intra-well motion. According to the above results, the effective frequency band of energy harvesting includes two tiny regions (1.9 Hz ~ 2.1 Hz and 2.3 Hz ~ 2.7 Hz) and a large region (3 Hz ~ 11.1 Hz), which constitute a very broad low-frequency band. Figure 9 presents the backward frequency sweeping results from 14 to 0 Hz. The biggest difference from the forward frequency sweeping results is that the displacement response and the output voltage suddenly jump up at 9 Hz (instead of 11.1 Hz) when decreasing frequency, at which the motion pattern of the swinging mass-bar changes from the inter-well chaotic motion to the inter-well periodic motion. Besides, the effective frequency band of energy harvesting includes four tiny regions (1.5 Hz ~ 1.6 Hz, 1.8 Hz ~ 2 Hz, 2.2 Hz ~ 2.5 Hz and 2.9 Hz ~ 3.4 Hz) (instead of two tiny regions) and a large region (4 Hz ~ 9 Hz). Both the forward and backward frequency sweeping results reveal that the proposed harvester can generate considerable output voltage in broadband low-frequency range.

Fig. 8

Forward frequency sweeping results: a displacement response; b swinging angle; c output voltage

Fig. 9

Backward frequency sweeping results: a displacement response; b swinging angle; c output voltage

In order to expound the three kinds of dynamic response patterns, Figs. 10, 11, 12 present the numerical simulation results at 8 Hz, 11.3 Hz and 13 Hz, respectively, which correspond to the inter-well periodic motion pattern, the inter-well chaotic motion pattern and the intra-well motion pattern, respectively. Each figure displays the zoomed segment of the steady-state time history (including the displacement, the swinging angle and the output voltage), the phase trajectory with attractors, and the frequency spectrum of the output voltage. The frequency spectrum is obtained by discrete Fourier transform (DFT) of the steady-state time history of the output voltage. Among the three displayed cases, the voltage at 8 Hz (inter-well periodic motion) is the maximum (17.42 V), the voltage at 11.3 Hz (inter-well chaotic motion) is the second (9.3 V), and the voltage at 13 Hz (intra-well motion) is the minimum (3.64 V). From the number of attractors, it can be deduced that, under the inter-well periodic motion pattern and the intra-well motion pattern, the period of response is the same as the period of excitation, or in other words, the fundamental frequency of the response is the same as the excitation frequency. However, from the frequency spectra, it can be seen that the output voltage contains not only the fundamental frequency component but also some other frequency components. Under 8 Hz excitation, the frequency components of the output voltage include 8 Hz, 24 Hz and 40 Hz; under 13 Hz excitation, the frequency components of the output voltage include 13 Hz, 26 Hz and 39 Hz; for the inter-well chaotic motion, the frequency components of the output voltage constitute a continuous spectrum in which there is one distinct spectral line at the excitation frequency 11.3 Hz. The above results from frequency spectra indicate that there exist third-order and fifth-order superharmonic resonances for the inter-well periodic motion pattern, whereas there exist second-order and third-order superharmonic resonances for the intra-well motion pattern. Figure 13 shows the effect of rotational stiffness on the power–frequency curve. It can be seen that the rotational stiffness has only small influence on the peak power but significant influence on the frequency at which the power reaches the maximum, and the latter is increased with the increase in rotational stiffness.

Fig. 10

Numerical simulation results at 8 Hz (inter-well periodic response): a–c zoomed segment of the steady-state time history for displacement, swinging angle and output voltage, respectively; d–e phase trajectory and attractors; (f) frequency spectrum of the output voltage

Fig. 11

Numerical simulation results at 11.3 Hz (inter-well chaotic response): a–c zoomed segment of the steady-state time history for displacement, swinging angle and output voltage, respectively; d–e phase trajectory and attractors; f frequency spectrum of the output voltage

Fig. 12

Numerical simulation results at 13 Hz (intra-well response): a–c zoomed segment of the steady-state time history for displacement, swinging angle and output voltage, respectively; d–e phase trajectory and attractors; f frequency spectrum of the output voltage

Fig. 13

Effect of rotational stiffness on the power–frequency curve

4.2 Frequency sweeping tests

The frequency sweeping tests were carried out in the frequency range of 2 Hz ~ 14 Hz with the excitation amplitude of 0.5 g ($g = 9.8{\text{m/s}}^{2}$) and the load resistance of 200 ${\text{K}}\Omega$. Figures 14 and 15 show the forward and backward frequency sweeping test results, respectively. For the forward frequency sweeping test, the voltage is initially small and jumps up to 14.6 V at 2.37 Hz, but then it jumps down to a small value at 2.67 Hz; next, the voltage re-jumps up to 15.2 V at 2.98 Hz and high voltage is maintained until 10.61 Hz at which the voltage jumps down. Therefore, the effective energy harvesting frequency band in forward frequency sweeping test includes 2.37 Hz ~ 2.67 Hz and 2.98 Hz ~ 10.61 Hz. For the backward frequency sweeping test, the results are similar but slightly different in value: The effective energy harvesting frequency band includes 2.36 Hz ~ 2.63 Hz and 3.51 Hz ~ 9.9 Hz. It can be seen that, for both forward and backward frequency sweeping tests, the energy harvesting frequency band is broad and lies in low-frequency range, implying broadband low-frequency energy harvesting capability. Here, we make a comparison between the experimental results and the theoretical results. By comparing Fig. 14 with Fig. 8(c) and comparing Fig. 15 with Fig. 9(c), it is seen that their general characteristics are basically similar, although some quantitative details are somewhat different. We mainly focus on two important indices: One is the peak output voltage and the other is the maximum jump frequency (jump-down frequency for forward frequency sweeping; jump-up frequency for backward frequency sweeping). The maximum jump frequency reflects the upper bound of the energy harvesting frequency band. Table 2 shows the two indices obtained by theoretical numerical simulations and by experimental tests. The experimental peak voltage in forward frequency sweeping test, 25.32 V, is a little smaller than the theoretical one, 28.92 V, while the experimental peak voltage in backward frequency sweeping test, 22.43 V, is slightly larger than the theoretical one, 21.04 V. The experimental maximum jump-down frequency in forward frequency sweeping test, 10.61 Hz, is slightly smaller than the theoretical one, 11.1 Hz, while the experimental maximum jump-up frequency in backward frequency sweeping test, 9.9 Hz, is a little larger than the theoretical one, 9.03 Hz. Therefore, the theoretical electrical output indices are fairly close to the experimental ones, which validates the acceptable accuracy of the formulated theoretical model.

Fig. 14

Forward frequency sweeping test results

Fig. 15

Backward frequency sweeping test results

Table 2 Comparison between theoretical and experimental results regarding peak power and jump frequency

4.3 Harmonic excitation tests

The harmonic excitation test results at three different frequencies (6 Hz, 8 Hz and 10 Hz) are presented with the excitation amplitude of 0.5 g and the load resistance of 200 ${\text{K}}\Omega$, as shown in Fig. 16. According to the frequency sweeping results in Sect. 4.2, all the three examined frequencies lie in the energy harvesting frequency band. Note that the test under 10 Hz excitation needs a small initial disturbance. As expected, the output voltage signals are approximately periodic and symmetrical with respect to the 0 V line due to the inter-well periodic motion pattern, generating relatively large output voltage. The voltage amplitudes are, respectively, 15.62 V, 19.13 V and 24.51 V under 6 Hz, 8 Hz and 10 Hz excitations, which basically match well with the frequency sweeping test results. The waveforms of the output voltage signals are not harmonic; each one of them contains three main frequency components. The frequency spectrum of the output voltage under 6 Hz excitation has three main sharp peaks at 6 Hz, 18 Hz and 30 Hz; the frequency spectrum of the output voltage under 8 Hz excitation has three main sharp peaks at 8 Hz, 24 Hz and 40 Hz; the frequency spectrum of the output voltage under 10 Hz excitation has three main sharp peaks at 10 Hz, 30 Hz and 50 Hz (the amplitude of the 30 Hz component is even larger than that of the 10 Hz component). The frequency spectrum results indicate that there exist third-order and fifth-order superharmonic resonances for the excitation frequency lying in the energy harvesting frequency band, which also accords with the theoretical findings.

Fig. 16

Harmonic excitation test results: a, d, g time history of the output voltage under 6 Hz, 8 Hz and 10 Hz excitation, respectively; b, e, h zoomed segment of the time history under 6 Hz, 8 Hz and 10 Hz excitation, respectively; c, f, i frequency spectrum of the output voltage under 6 Hz, 8 Hz and 10 Hz excitation, respectively

4.4 Output power

The instantaneous output power varies with time, as the vibration energy harvesting, is a dynamic process and generates AC electrical output (time-varying voltage). Therefore, it is more reasonable to consider the average output power, which is defined as the time-domain average of the instantaneous power over a period of time. For the experimentally obtained output voltage under harmonic excitation at each individual frequency, the average output power is calculated by

$$P = \frac{1}{N}\sum_{i = 1}^N {\frac{v_i^2 }{R}}$$

(34)

where $v_i$ is the sample point of the output voltage signal, $N$ is the number of sample points, and $R$ is the load resistance. Hereafter, the output power refers to the average output power.

Figure 17(a) shows the output power versus frequency under different excitation amplitudes (0.4 g, 0.5 g, 0.6 g and 0.7 g). The excitation frequencies are from 2 to 14 Hz with an interval of 0.2 Hz. At each frequency, the harmonic excitation lasts for 5 s and then immediately switches to the next harmonic excitation with the frequency increased by 0.2 Hz, which is similar to “discrete frequency sweeping excitation” from a global perspective but is still harmonic excitation at each individual frequency. Based on the frequency response characteristics, the upper bound of the frequency band for effective energy harvesting can be regarded as the frequency at which the output power suddenly drops down (i.e. the jump-down frequency). Under 0.4 g excitation, the energy harvesting frequency band ranges from 4.8 Hz to 9.6 Hz with a peak power of 0.963mW, whereas little output power is generated at frequencies below 4.8 Hz due to the occurrence of intra-well motion. Under 0.5 g excitation, the energy harvesting frequency band includes 2.4 Hz ~ 2.6 Hz and 3 Hz ~ 10.6 Hz with a peak power of 1.616mW, and in the frequency region of 2 Hz ~ 2.4 Hz and 2.6 Hz ~ 3 Hz, the intra-well motion still occurs, which leads to little output power. Under 0.6 g and 0.7 g excitation, the energy harvesting frequency band ranges from 2 Hz to 11.8 Hz and from 2 Hz to 12.6 Hz, respectively, with a peak power of 2.505mW and 3.558mW, respectively, and the intra-well motion, which produces little output power, fully disappears in ultra-low frequency region. From these results, it is seen that the proposed energy harvester can indeed achieve broadband low-frequency energy harvesting with considerable output power. It can also be seen that larger excitation amplitude leads to higher output power and broader energy harvesting frequency band. In fact, it is easy to understand that the output power increases with the increase in excitation amplitude, since a larger excitation amplitude can input more energy into the harvester and thus generate higher output power. Therefore, it is meaningful to plot the normalized output power, which is defined as the power divided by the square of the excitation amplitude, as shown in Fig. 17(b). Under 0.4 g, 0.5 g, 0.6 g and 0.7 g excitation, the peak value of the normalized output power is 6.018mW/g², 6.462mW/g², 6.957mW/g² and 7.261mW/g², respectively, which means that the normalized peak power is still boosted with the increase in excitation amplitude.

Fig. 17

a Output power and b normalized output power versus frequency under different excitation amplitudes

In order to examine the output power under different load resistances, we vary the resistance value of the resistor and test the corresponding output voltage at 4 Hz, 6 Hz, 8 Hz and 10 Hz, respectively, to calculate the output power, as shown in Fig. 18. The excitation amplitude is fixed at 0.5 g. Under very small or very large load resistance, the output power is relatively small. For example, the output power under 10 ${\text{K}}\Omega$ resistance (a small resistance) is 0.159mW, 0.23mW, 0.388mW and 0.721mW, respectively, for 4 Hz, 6 Hz, 8 Hz and 10 Hz excitation, and the output power under 500 ${\text{K}}\Omega$ resistance (a large resistance) is 0.171mW, 0.282mW, 0.378mW and 0.595mW, respectively, for 4 Hz, 6 Hz, 8 Hz and 10 Hz excitation. As the load resistance varies from a small value to a large value, the variation of the output power is not monotonic. For 4 Hz, 6 Hz and 8 Hz excitation, the output power is increased and then decreased with the increase in load resistance. The maximum output power for 4 Hz excitation is 0.564mW, obtained at 90 ${\text{K}}\Omega$ resistance. The maximum output power for 6 Hz excitation is 0.796mW, obtained at 100 ${\text{K}}\Omega$ resistance. The maximum output power for 8 Hz excitation is 1.185mW, obtained at 110 ${\text{K}}\Omega$ resistance. For 10 Hz excitation, with the increase in load resistance, the output power experiences four variation processes: firstly rapid increase, secondly slight decrease, then slight increase, and finally gradual decrease; the maximum output power is 1.974mW, obtained at 50 ${\text{K}}\Omega$ and 110 ${\text{K}}\Omega$ resistance. In general, small resistance results in large electric current but small voltage, while large resistance results in large voltage but small electric current, which may qualitatively explain the influence of the load resistance on the output power.

Fig. 18

Output power with the variation of load resistance

A brief comparison with three previous bistable piezoelectric energy harvesters is conducted in terms of the peak power, the normalized peak power, the normalized power density (defined as the normalized power divided by the effective volume), and the effective energy harvesting frequency band, which are shown in Table 3. Note that some of the indices are not directly given in the references and therefore are calculated according to their presented results. It can be seen that the proposed 2DOF bistable piezoelectric energy harvester has larger normalized power density than the three previous bistable piezoelectric energy harvesters; most importantly, its effective energy harvesting frequency band extends to low-frequency range, and the bandwidth is much broader than that of the three previous counterparts. The comparison clearly validates the broadband low-frequency energy harvesting capability of the proposed harvester.

Table 3 Comparison with previous bistable piezoelectric energy harvesters

5 Conclusions

A compact 2DOF bistable piezoelectric energy harvester with simple structure is proposed and studied in this paper. The bistable property is realized by the combined effect of gravity and elastic joint. The electromechanical coupled equations are formulated for numerical simulations. An experimental prototype is fabricated for frequency sweeping tests and harmonic excitation tests. The simulation results indicate that there are three motion patterns for the swinging mass-bar, namely the inter-well periodic swinging motion, the inter-well chaotic swinging motion and the intra-well swinging motion. The inter-well periodic swinging motion has the largest oscillation amplitude and can thus exert large force and moment on the piezoelectric cantilever beam, thereby generating large electrical output. Besides, due to the structural merits, it is also indicated that the inter-well periodic swinging motion can occur in a very broad low-frequency range, thus enabling broadband low-frequency energy harvesting. The general electrical output characteristics in experimental results are basically consistent with those in simulation results. The peak output voltage is 25.32 V and 22.43 V, respectively, in the forward and backward frequency sweeping tests, which are close to the theoretical ones. In harmonic excitation tests, the third-order and fifth-order superharmonic components are observed, which also accords with the theoretical findings. The output power (time-domain average of the instantaneous power) is examined under different excitation amplitudes and load resistances. It is shown that larger excitation amplitude can produce higher peak power, higher normalized peak power and broader energy harvesting frequency band. Under 0.7 g excitation, the peak power and the normalized power density are, respectively, 3.558mW and 19.52mW/(g²·cm³), with the effective operation band from 2 Hz to 12.6 Hz, which manifests broadband low-frequency energy harvesting capability.