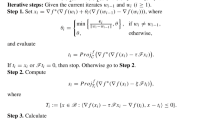Modified inertial subgradient extragradient method in reflexive Banach spaces

Abstract

In this paper, we study a modified inertial subgradient extragradient algorithm in reflexive Banach spaces and prove a strong convergence theorem for approximating common solutions of a fixed point equation of a demigeneralized mapping and a variational inequality problem of a monotone and Lipschitz mapping. Our result extends and improves important recent results announced by many authors.

1 Introduction

Variational inequality problems were formulated in 1967 by Lions and Stampaccia [23]. These problems have been studied extensively by several authors [2, 13, 15]. In many models for solving real-life problems arising in areas such as image processing, machine learning and signal processing, the constraints are expressed as variational inequality problems and as fixed point problems. Consequently, this problem has attracted the attention of many researchers working on nonlinear operator theory (see, for example, [2, 3, 26] and the references therein).

Throughout this paper, we shall assume E to be a real reflexive Banach space with dual $E^*$, C a nonempty, closed and convex subset of E and $f:{E \rightarrow (-\infty ,+\infty ]}$ to be a proper, lower semi-continuous and convex function. We denote by dom$f:=\{x \in E:f(x)<+\infty \}$, the domain of f. Let $x \in$ int(domf); the subdifferential of f at x is the convex set defined by

$$\begin{aligned} \partial f(x)=\{x^* \in E^*:f(x)+ \langle x^*,y-x \rangle \le f(y),\; \forall y \in E \}. \end{aligned}$$

Let $A:C\rightarrow E$ be a map. Then A is said to be

• 1. $k-$Lipschitz continuous if $\exists \;k\ge 0$, such that

  $$\begin{aligned} ||Ax-Ay||\le k||x-y||,\quad \forall x,y \in C \end{aligned}$$

• 2. Monotone, if the following inequality holds:

  $$\begin{aligned} \langle Ax-Ay,x-y \rangle \ge 0, \;\; \forall x, y \in C; \end{aligned}$$

• 3. $\alpha$-inverse strongly monotone if $\exists \;\alpha > 0$, such that

  $$\begin{aligned} \langle Ax-Ay,x-y \rangle \ge \alpha ||Ax-Ay||^2, \;\; \forall x, y \in C; \end{aligned}$$

• 4. Maximal monotone if the graph of A is not properly contained in the graph of any other monotone map.

The convex feasibility problem is to find a point $z \in C:=\cap _{i=1}^{k}C_i$, where $C_i$ is a convex set for each i.

The variational inequality problem is to find a point $z\in C$, such that

$$\begin{aligned} \langle v-z,Az \rangle \ge 0, \quad \forall v\in C. \end{aligned}$$

The solution set of the variational inequality problem is denoted by VI(C, A).

For any $x \in$ int(domf) and $y \in E$, the right-hand derivative of f at x in the direction of y is defined by

$$\begin{aligned} f^{\circ }(x,y):= \lim _{t \rightarrow 0^+} \frac{f(x+ty)-f(x)}{t}. \end{aligned}$$

The function f is said to be Gâteaux differentiable at x if $\lim _{{t \rightarrow {0}}} \frac{f(x+ty)-f(x)}{t}$ exists for any y. In this case, the gradient of f at x is the function ${\nabla }{f(x)}: E \rightarrow (-\infty , +\infty ]$ defined by $\langle \nabla f(x), y \rangle = f^{\circ }(x,y)$ for any $y \in E$. The function f is said to be Gâteaux differentiable if it is Gâteaux differentiable for any $x\,{\in }\,$ int(domf). The function f is said to be Fréchet differentiable at x if this limit is attained uniformly in y with $\Vert y\Vert =1$. Also f is said to be uniformly Fréchet differentiable on a subset C of E if the limit is attained uniformly for $x\,{\in }\,C$ and $\Vert y\Vert =1$. It is well known that if f is Gâteaux differentiable (resp. Fréchet differentiable) on int(domf), then f is continuous and its Gâteaux derivative ${\nabla }f$ is norm-to-weak$^*$ continuous (resp. norm-to-norm continuous) on int(dom(f)) (see [6, 9]).

A function f on E is coercive [18] if the sublevel sets are bounded; equivalently

$$\begin{aligned} \lim _{{\Vert x\Vert \rightarrow +\infty }}f(x)=+\infty . \end{aligned}$$

A function f on E is said to be strongly coercive [33] if

$$\begin{aligned} \lim _{{\Vert x\Vert \rightarrow +\infty }} \frac{f(x)}{\Vert x\Vert }=+\infty . \end{aligned}$$

Definition 1.1

[8] The function f is said to be:

• (1) Essentially smooth, if $\partial f$ is both locally bounded and single-valued on its domain;

• (ii) Essentially strictly convex, if ${(\partial f)}^{-1}$ is locally bounded on its domain and f is strictly convex on every subset of domf;

• (iii) Legendre, if it is both essentially smooth and essentially strictly convex.

The Fenchel conjugate of f is the function $f^*:{E^* \rightarrow (-\infty ,+\infty ]}$ defined by

$$\begin{aligned} f^*(x^*)= \sup \{ \langle x^*,x \rangle - f(x) :x \in E \}. \end{aligned}$$

Remark 1.2

If E is a reflexive Banach space, then we have the following results:

• (i) f is essentially smooth if and only if $f^*$ is essentially strictly convex (see [8], Theorem 5.4).

• (ii) ${(\partial f)}^{-1}= \partial f^*$ (see [9]).

• (iii) f is Legendre if and only if $f^*$ is Legendre (see [8], Corollary 5.5).

• (iv) If f is Legendre, then ${\nabla }f$ is a bijection satisfying ${\nabla }f =({\nabla }f^*)^{-1}$, ran${\nabla }f =$ dom${\nabla }(f^*)=$ int(dom$f^*$) and ran ${\nabla }f^*=$ dom$f=$ int(domf) (see [8], Theorem 5.10 ), where ran stands for the range.

Examples of Legendre function were given in [7, 8]. One important and interesting Legendre function is $\frac{1}{p} {\Vert \cdot \Vert }^p \;{ (1< p < \infty )}$ when E is a smooth and strictly convex Banach space; in particular Hilbert spaces.

In the rest of this paper, we always assume that ${f:E \rightarrow (-\infty ,+\infty ]}$ is Legendre.

Let ${f:E \rightarrow (-\infty ,+\infty ]}$ be a convex and Gâteaux differentiable function. The function

$D_f:$ dom$f \times$ int(dom$f)\rightarrow (-\infty ,+\infty ]$, defined as follows:

$$\begin{aligned} D_f(x,y):=f(x)-f(y)- \langle {\nabla }f(y),x-y \rangle , \end{aligned}$$

(1.1)

is called the Bregman distance with respect to f (see [14] ). It is obvious from the definition of $D_f$ that

$$\begin{aligned} D_f(z,x):=D_f(z,y)+D_f(y,x)+ \langle {\bigtriangledown } f(y)-{\bigtriangledown }f(x),z-y \rangle . \end{aligned}$$

(1.2)

Let $T:C \rightarrow E$ be a map and let $F(T)=\{x:Tx=x\}$ denote the set of fixed points of T.

A point $p \in C$ is said to be asymptotic fixed point of map T, if there exists a sequence $\{x_n\}$ in C which converges weakly to p such that $\lim _{n \rightarrow +\infty } \Vert x_n-Tx_n \Vert =0$. We denote by $\hat{F}(T)$ the set of asymptotic fixed points of T. A point $p \in C$ is said to be a strong asymptotic fixed point of map T, if there exists a sequence $\{x_n\}$ in C which converges strongly to p such that $\lim _{n \rightarrow +\infty } \Vert x_n-Tx_u \Vert =0$. We denote by $\tilde{F}(T)$ the set of strong asymptotic fixed points of T. T is said to be quasi-Bregman relatively nonexpansive if $F(T) \ne \emptyset$, $\hat{F}(T)= F(T)$ and $D_f(Tx,p)\le D_f(x,p)$ for all $x \in C$ and $p \in F(T)$.

If E is a smooth Banach space, the Lyapunov functional $\phi :E \times E \rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} \phi (x,y)= ||x||^2 - 2\langle x, Jy \rangle + ||y||^2, \quad \forall x,y \in E. \end{aligned}$$

where J denotes the normalized duality mapping.

Let $\eta$ and s be real numbers with $\eta \in (-\infty ,1)$ and $s \in [0, \infty )$, respectively. Then the map $T:C \rightarrow E$ with $F(T) \ne \emptyset$ is called $(\eta ,s)-$demigeneralized, if for any $x\in C$ and $q \in F(T)$,

$$\begin{aligned} \langle x-q,Jx-JTx \rangle \ge (1-\eta )\phi (x,Tx)+s\phi (Tx,x). \end{aligned}$$

(1.3)

In particular, if $s=0$ in (1.3), then

$$\begin{aligned} \langle x-q,Jx-JTx \rangle \ge (1-\eta )\phi (x,Tx), \end{aligned}$$

holds for any $x\in C$ and $q \in F(T)$, and in this case T is $(\eta ,0)-$demigeneralized map.

Remark 1.3

If E is smooth and strictly convex Banach space and $f(x)=||x||^2$ for all $x\in E$, then we have $\nabla f(x)=2Jx$, for all $x\in E$ and hence the function $D_f(x,y)$ reduces to $\phi (x,y).$

Definition 1.4

[5] Let E be a reflexive Banach space, C a nonempty closed and convex subset of E, and $\eta$ be a real number with $\eta \in (-\infty ,1)$. Then the map $T:C \rightarrow E$ with $F(T) \ne \emptyset$ is called $(\eta ,0)$-Bregman demigeneralized map, if for any $x\in C$ and $q \in F(T)$,

$$\begin{aligned} \langle x-q,\nabla f(x)-\nabla f(Tx)\rangle \ge (1-\eta )D_f(x,Tx). \end{aligned}$$

The following facts illustrate that the class of Bregman demigeneralized maps is very important.

• (i) [31] Let C be a nonempty, closed and convex subset of a reflexive Banach space E. Let k be real number in (0, 1), the map $T:C \rightarrow E$ is called quasi-Bregman strictly pseudocontractive map if $F(T)\ne \emptyset$, $x\in C$ and $\; p \in F(T),$ then we have

  $$\begin{aligned} D_f(p,Tx)\le D_f(p,x)+kD_f(x,Tx). \end{aligned}$$

  (1.4)

  From (1.4), we have

  $$\begin{aligned} D_f(p,Tx)\le D_f(p,x)+D_f(x,Tx)-D_f(x,Tx)+kD_f(x,Tx), \end{aligned}$$

  which by (1.2), implies

  $$\begin{aligned} (1-k)D_f(x,Tx)\le & D_f(p,x) + D_f(x,Tx)- D_f(p,Tx)\\=\,\, & \langle x-p,\nabla f(x)-\nabla f(Tx)\rangle . \end{aligned}$$

  This shows that T is (k, 0)-Bregman demigeneralized map.

• (ii) Let E be a reflexive Banach space, let $f:{E \rightarrow \mathbb {R}}$ be strongly coercive function and let A be a maximal monotone operator with $A^{-1}(0)\ne \emptyset$ . Let $Res^f_{\lambda A}$ be the resolvent of A, $\lambda >0$ for any $x\in E$ and $z\in A^{-1}(0),$ then we have

  $$\begin{aligned} \langle Res^f_{\lambda A}(x)-z, {\nabla } f(x)-{\nabla }f(Res^f_{\lambda A}(x))\rangle \ge 0, \end{aligned}$$

  which implies

  $$\begin{aligned} \langle Res^f_{\lambda A}(x)-x+x-z, {\nabla } f(x)-{\nabla }f(Res^f_{\lambda A}(x))\rangle \ge 0, \end{aligned}$$

  hence

  $$\begin{aligned} \langle x-z, {\nabla } f(x)-{\nabla }f(Res^f_{\lambda A}(x))\rangle\ge & \langle x-Res^f_{\lambda A}(x), {\nabla } f(x)-{\nabla }f(Res^f_{\lambda A}(x))\rangle \\=\,\, & D_f(x,Res^f_{\lambda A}(x))+ D_f(Res^f_{\lambda A}(x),x)\\\ge & D_f(x,Res^f_{\lambda A}(x)). \end{aligned}$$

  This shows that $Res^f_{\lambda A}$ is (0, 0)-Bregman demigeneralized mapping.

• (iii) Let E be a reflexive Banach space and C a nonempty, closed and convex subset of E and let $f:{E \rightarrow \mathbb {R}}$ be a Fréchet differentiable convex function. A map $T: C\rightarrow E$ is called quasi-Bregman nonexpansive map if $F(T)\ne \emptyset$ and for all $x\in C, \; p\in F(T),$

  $$\begin{aligned} D_f(p,Tx)\le & D_f(p,x), \end{aligned}$$

  which gives by (1.2)

  $$\begin{aligned} D_f(p,x)+D_f(x,Tx) + \langle p-x, \nabla f(x)-\nabla f(Tx) \rangle \le D_f(p,x) \end{aligned}$$

  and hence

  $$\begin{aligned} D_f(x,Tx)\le & \langle x-p, \nabla f(x)-\nabla f(Tx) \rangle . \end{aligned}$$

  This implies that T is (0, 0)-Bregman demigeneralized map.

Example 1.5

Let $E=\mathbb {R},\; C=[-1,0]$ and define $T,f:[-1,0]\rightarrow \mathbb {R}$ by $f(x)=x^3$ and $Tx=2x$, for all $x\in [-1,0]$. Then T is $(\eta ,0)$-Bregman demigeneralized map but not $(\eta ,0)$-demigeneralized map.

Bregman [10] introduced an effective technique through Bregman distance function $D_f$ for designing and analyzing feasibility and optimization algorithms. This opened a new area of research in which Bregman’s technique is applied in various ways to iterative algorithm for solving not only feasibility and optimization pro blems, but also algorithms for solving fixed point problems for nonlinear mappings (see, e.g., [11, 22, 31] and the references therein).

Many researchers have proposed and analyzed different iterative algorithms for solving variational inequality problems, approximating fixed points of nonexpansive mappings and their generalizations. Initially, in most of the algorithms for approximating solutions of variational inequality problems, the operator A was often assumed to be inverse strongly monotone (see, e.g, [4, 12, 15] and the references in them). In order to relax the inverse strong monotonicity of the operator A, Korpelevic [21] introduced the following extragradient method in the finite dimensional Euclidean space $\mathbb {R}^n$:

$$ {\left\{ \begin{array}{ll} x_0=x_1 \in C;\\ x_{n+1} = P_C(x_n-\lambda A[P_C(x_n-\lambda Ax_n)]), \quad \forall n \in \mathbb {N} \end{array}\right. }$$

(1.5)

where the operator A is monotone and Lipschitz and $P_C$ denotes the metric projection.

However, in the extragradient method, two projections onto a closed and convex subset C of H at each step of the iteration process need to be computed.

Censor et al. [16] observed that this may affect the efficiency of the method if the set C is not simple enough. They introduced and studied the following modified extragradient method by replacing the second projection onto a closed and convex subset C with a projection onto a specific constructable half-space $T_n$:

$${\left\{ \begin{array}{ll} x_0 = H; \\ y_n=P_C(x_n-\tau Ax_n);\\ T_n=\{w\in H:\langle x_n-\tau Ax_n-y_n,w-y_n \le 0 \}; \\ x_{n+1}=P_{T_n}(x_n-\tau Ay_n), \forall n \in \mathbb {N}. \end{array}\right. } $$

(1.6)

and they proved that the sequence generated by (1.6) converges weakly to the solution of a variational inequality problem in real Hilbert spaces under some mild assumptions. Since the set $T_n$ is a Half-space; therefore, algorithm (1.6) is simpler to implement than algorithm (1.5)

To get strong convergence, Kraikaew and Saejung [20] introduced the following hybridization of the subgradient extragradient method (1.6) as a Halpern method:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 = H; \\ y_n=P_C(x_n-\tau Ax_n);\\ T_n=\{w\in H:\langle x_n-\tau Ax_n-y_n,w-y_n \le 0 \}; \\ z_n= \alpha _nx_0 + (1-\alpha _n)P_{T_n}(x_n-\tau Ay_n);\\ x_{n+1}=\beta _n x_n + (1-\beta _n)Sz_n, \forall n \ge 0, \end{array}\right. } \end{aligned}$$

(1.7)

where $\beta _n \subset [a,b]\subset (0,1),$ for some $a,b \in (0,1)$ and $\{\alpha _n\}$ is a sequence in [0, 1] satisfying $\lim _{n\rightarrow \infty } \alpha _n=0$ and $\sum _{n=1}^{\infty } \alpha _n=\infty .$ They proved that the sequence generated by algorithm (1.7) converges strongly to a point $p\in VI(C,A)\cap F(S)$ in a real Hilbert space.

In 2018, Chidume et al. [13] introduced the following Krasnoselskii-type algorithm in a uniformly smooth and $2-$uniformly convex real Banach space for approximating common element of solutions of a variational inequality problem and common fixed point of a countable family of relatively nonexpansive maps, under some mild assumptions:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 = x \in E,\\ y_n = \Pi _CJ^{-1}(Jx_n-\lambda _n Ax_n);\\ T_n=\{z\in E: \langle z-y_n, Jx_n-\lambda Ax_n-Jy_n \rangle \le 0 \};\\ t_n= \Pi _{T_n}(Jx_n-\lambda _n Ax_n);\\ z_n= J^{-1}(\alpha _n Jx_0 + (1-\alpha _n)Jt_n);\\ x_{n+1}= J^{-1}(\lambda Jx_n + (1-\lambda )JS^n_iz_n), \quad n\ge 0. \end{array}\right. } \end{aligned}$$

(1.8)

Polyak [28] was first to propose an acceleration process called inertial-type algorithm for solving a smooth convex minimization problem. Incorporating an inertial term in an algorithm accelerates the rate of convergence of the sequence generated by the algorithm. Consequently, many researchers are applying inertial-type algorithms in their investigations (see [1, 17, 24] and references contained therein).

Khan et al. [19] introduced a modified inertial subgradient extragradient algorithm in a 2-uniformly convex and uniformly smooth real Banach space and proved a strong convergence theorem for approximating common solution of fixed point of a (k, 0)-demigeneralized mapping and solution of variational inequality problem, under some appropriate conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0, x_1 \in E,\\ w_n = J^{-1}(Jx_n+\delta _n(Jx_{n-1}-Jx_n))\\ y_n = \Pi _CJ^{-1}(Jw_n-\tau Aw_n);\\ T_n=\{z\in E: \langle z-y_n, Jw_n-\tau Aw_n-Jy_n \rangle \le 0 \};\\ z_n= \Pi _{T_n}(Jw_n-\tau Ay_n);\\ v_n= J^{-1}((1-\lambda _n) Jz_n + \lambda _nJTz_n);\\ x_{n+1}= J^{-1}(\alpha _nJx_n + \beta _nJv_n + \gamma _n Ju), \quad n\ge 1. \end{array}\right. } \end{aligned}$$

(1.9)

Motivated and inspired by the above-mentioned results, we proposed and studied a modified inertial subgradient extragradient algorithm in a reflexive Banach space and proved a strong convergence theorem for approximating common element of solutions of a variational inequality problem and a common fixed point of Bregman demigeneralized mappings. Our work extends and generalizes the result of Khan et al. [19] and many other related results announced recently.

2 Preliminaries

Recall that the Bregman projection [10] of $x \in$ int(domf) onto nonempty, closed and convex set $C \subset$ domf is the unique vector $P^f_C(x) \in C$ satisfying

$$\begin{aligned} D_f(P^f_C(x),x)= \inf \{ D_f(y,x): y \in C \}. \end{aligned}$$

The function f is called totally convex at x if $v_f(x,t)=\inf \{ D_f(y,x): y \in$ Dom$f, ||x-y||=t \}>0$ whenever $t>0$. The function f is called convex if it is totally convex at any point $x \in$ int(domf) and is said to be totally convex on bounded set if $v_f(B,t)>0$ for any nonempty bounded subset B of E and $t>0,$ where the modulus of total convexity of the function f on the set B is the function $v_f:$ int(dom$f) \times [0,+\infty ) \rightarrow [0,+\infty )$ defined by

$v_f(B,t):= \inf \{v_f(x,t):x \in B\, \cap \,$ dom$f \}.$

Concerning the Bregman projection, the following facts are well-known.

Lemma 2.1

[11] Let C be a nonempty, closed and convex subset of a reflexive Banach space E. Let ${f:E \rightarrow \mathbb {R}}$ be a Gâteaux differentiable and totally convex function. Then

(a):

$z=P^f_C(x)$ if and only if $\langle {\nabla } f(x)-{\nabla }f(z),y-z \rangle \le 0, \quad \forall x \in E$ and $y \in C;$

(b):

$D_f(y,P^f_C(x))+D_f(P_C(x),x) \le D_f(y,x), \quad \forall x \in E,\,y \in C.$

Lemma 2.2

[25] Let E be a Banach space and $f:E\rightarrow \mathbb {R}$ be a Gâteaux differentiable function which is uniformly convex on bounded subsets of E. Let $\{x_n\}_{n\in \mathbb {N}}$ and $\{y_n\}_{n\in \mathbb {N}}$ be bounded sequences in E. Then

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }D_{f}(x_{n},y_{n})=0\quad if\; and \; only \; if\quad \underset{n\rightarrow \infty }{\lim }||x_n-y_n||=0. \end{aligned}$$

Lemma 2.3

[29] Let ${f:E \rightarrow \mathbb {R}}$ be Gâteaux differentiable and totally convex function. If $x_{0} \in E$ and the sequence $\{D_f(x_n,x_{0})\}$ is bounded, then sequence $\{x_n\}$ is bounded too.

Recall that the function f is called sequentially consistent if for bounded sequences $\{u_n \}$ and $\{y_n \}$ in E

$$\begin{aligned} \lim _{n \rightarrow +\infty } D_f(y_n,u_n)=0 \qquad implies \qquad \lim _{n \rightarrow +\infty } \Vert y_n-u_n \Vert =0. \end{aligned}$$

The following two results are well-known; see ([33])

Theorem 2.4

Let E be a reflexive Banach space and let $f: E \rightarrow \mathbb {R}$ be a convex function which is bounded on bounded subsets of E. Then, the following assertions are equivalent:

(1):

f is strongly coercive and uniformly convex on bounded subsets of E;

(2):

$dom f^* = E^*$, $f^*$ is bounded on bounded subsets and uniformly smooth on bounded subsets of $E^*$;

(3):

$dom f^* = E^*, f^*$ is Fréchet differentiable and $\nabla f^*$ is norm-to-norm uniformly continuous on bounded subsets of $E^*$.

Theorem 2.5

Let E be a reflexive Banach space and let $f : E\rightarrow \mathbb {R}$ be a continuous convex function which is strongly coercive. Then the following assertions are equivalent:

(1) :

f is bounded on bounded subsets and uniformly smooth on bounded subsets of E ;

(2) :

$f^*$ is Fréchet differentiable and $f^*$ is uniformly norm-to-norm continuous on bounded subsets of $E^*$ ;

(3) :

$dom f^* = E^*, f^*$ is strongly coercive and uniformly convex on bounded subsets of $E^*$.

The following result was first proved in [11].

Lemma 2.6

Let E be a reflexive Banach space, $f : E\rightarrow \mathbb {R}$ be a strongly coercive Bregman function. V is the function defined by

$$\begin{aligned} V(x,x^*)=f(x)-\langle x,x^*\rangle +f^*(x^*),~~x\in E,~~x^*\in E^*. \end{aligned}$$

Then, the following assertions hold:

(1) :

$D_{f} (x,\nabla f(x^*)) = V(x, x^*)$ for all $x\in E$ and $x^*\in E^*$.

(2) :

$V(x, x^*) +\langle \nabla f^*(x^*)-x,y^*\rangle \le V(x, x^* + y^*)$ for all $x \in E$ and $x^*, y^*\in E^*$.

Lemma 2.7

[25] Let E be a Banach space and $f:E\rightarrow \mathbb {R}$ be a convex function which is uniformly convex on bounded subsets of E. Let $r>0$ be a constant and $\rho _{r}$ be the gauge of uniform convexity of f . Then

(i):

For any $x,y\in B_{r}=\{x\in :||x||\le 1 \}$ and $\alpha \in (0,1)$,

$$\begin{aligned} f(\alpha x+(1-\alpha )y)\le \alpha f(x)+(1-\alpha )f(y)-\alpha (1-\alpha )\rho _{r}(||x-y||). \end{aligned}$$

(ii):

For any $x,y\in B_{r}$,

$$\begin{aligned} \rho _{r}(||x-y||)\le D_{f}(x,y). \end{aligned}$$

(iii):

If, in addition, g is bounded on bounded subsets and uniformly convex on bounded subsets of E then, for any $x\in E, y^*,z^*\in B_{r}$ and $\alpha \in (0,1)$

$$\begin{aligned}&V_{f}(x,\alpha y^*+(1-\alpha )z^*)\le \alpha V_{f}(x,y^*)+(1-\alpha )V_{f}(x,z^*)\\&\quad -\alpha (1-\alpha )\rho ^*_{r}(||y^*-x^*||). \end{aligned}$$

Lemma 2.8

[30] Let C be a nonempty closed and convex subset of a reflexive Banach space E and $A:C \rightarrow E^*$ be a monotone and hemicontinuous map. Let $T:E \rightarrow 2^{E^*}$ be an operator defined by

$$\begin{aligned} Tu={\left\{ \begin{array}{ll} Au+N_C(u), \quad u\in C,\\ \emptyset ,\qquad \qquad \qquad u\notin C, \end{array}\right. } \end{aligned}$$

(2.1)

where $N_C(u)$ is defined as follows:

$N_C(u)=\{w^*\in E^*:\langle u-z,w^*\rangle \ge 0, \; \forall z \in C \}.$

Then, T is maximal monotone and $T^{-1}0=VI(C,A).$

Lemma 2.9

[32] Let $\{a_n\}$, $\{\gamma _n\}$, $\{\delta _n\}$ and $\{t_n\}$ be sequences of nonnegative real numbers satisfying the following relation:

$$\begin{aligned} a_{n+1}\le (1-t_n-\gamma _n)a_n+\gamma _nn a_{n-1}+t_ns_n + \delta _n, \; n\ge 0, \end{aligned}$$

where $\sum _{n=n_0}^{\infty }t_n= +\infty ;$ $\sum _{n=n_0}^{\infty } \delta _n < +\infty ;$ for each $n\ge n_0$ (where $n_0$ is a positive integer) and $\{\gamma _n\} \subset [0,\frac{1}{2}],$ $\limsup _{n \rightarrow \infty } s_n \le 0$. Then, the sequence $\{a_n\}$ converges to zero.

Lemma 2.10

[27] Let $\Gamma _n$ be a sequence of real numbers that does not decrease at infinity, in the sense that there exists a subsequence $\{\Gamma _{n_j}\}_{j\ge 0}$ of $\{\Gamma _n\}$ which satisfies $\Gamma _{n_j} \le \Gamma _{n_j+1}$ for all $j\ge 0$. Also consider a sequence of integers $\{ \tau (n)\}_{n\ge n_0}$ defined by

$$\begin{aligned} \tau (n)=\max \{k \le n \mid \Gamma _{n_k} \le \Gamma _{n_k+1}\}. \end{aligned}$$

Then $\{ \tau (n)\}_{n\ge n_0}$ is a nondecreasing sequence satisfying $\lim _{n \rightarrow \infty }\tau (n)=\infty$.

If it holds that $\Gamma _{\tau (n)}\le \Gamma _{\tau (n)+1}$ for all $n \ge n_0$ then we have

$$\begin{aligned} \Gamma _n \le \Gamma _{\tau (n)+1}. \end{aligned}$$

3 Main Results

Lemma 3.1

Let E be a reflexive Banach space and C a nonempty, closed and convex subset of E and let $f:{E \rightarrow \mathbb {R}}$ be a Fréchet differentiable convex function. Let $\eta$ be a real number with $\eta \in (-\infty ,0]$ and let $T:C \rightarrow E$ be $(\eta ,0)$-Bregman demigeneralized map with $F(T) \ne \emptyset$. Let $\alpha$ be a real number in [0, 1) and let $S= \nabla f^*((1-\alpha ) \nabla f + \alpha \nabla f(T))$. Then $S:C \rightarrow E$ is a quasi-Bregman nonexpansive map.

Proof

It is obvious that $F(T)=F(S)$. Since S is $(\eta ,0)$-Bregman demigeneralized map, for any $x \in C$, we obtain

$$\begin{aligned} D_f(x,Sx)=\,\, & D_f(x,\nabla f^*((1-\alpha ) \nabla f(x) + \alpha \nabla f(Tx)))\nonumber \\\le & (1-\alpha ) D_f(x,x) +\alpha D_f(x,Tx)\nonumber \\=\,\, & \alpha D_f(x,Tx), \end{aligned}$$

(3.1)

and letting $p \in F(S)$, we get

$$\begin{aligned} \langle x-p,\nabla f(x)-\nabla f(Sx)\rangle=\,\, & \langle x-p,\nabla f(x)- (1-\alpha ) \nabla f(x) - \alpha \nabla f(Tx)\rangle \nonumber \\=\,\, & \alpha \langle x-p,\nabla f(x) - \nabla f(Tx)\rangle \nonumber \\\ge & \alpha (1-\eta )D_f(x,Tx), \end{aligned}$$

(3.2)

from (3.1), (3.2) and the fact that $\eta \in (-\infty ,0]$,we have

$$\begin{aligned} \langle x-p,\nabla f(x)-\nabla f(Sx)\rangle \ge \alpha (1-\eta )D_f(x,Tx) \ge \alpha D_f(x,Tx) \end{aligned}$$

(3.3)

from (1.2) and (3.3), we have

$$\begin{aligned} D_f(p,x)-D_f(p,Sx)+D_f(x,Sx) \ge \alpha D_f(x,Tx); \end{aligned}$$

this and (3.1) imply

$$\begin{aligned} D_f(p,x)-D_f(p,Sx)\ge & \alpha D_f(x,Tx)-D_f(x,Sx)\\\ge & \alpha D_f(x,Tx) - \alpha D_f(x,Tx). \end{aligned}$$

Hence

$$\begin{aligned} D_f(p,Sx)\le D_f(p,x). \end{aligned}$$

$\square$

Lemma 3.2

Let C be a nonempty closed and convex subset of a reflexive Banach space E and $f:{E \rightarrow \mathbb {R}}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E. Let $A:C\rightarrow E$ be a monotone map and $L-$Lipschitz on E with $L>0$ and let $T:C \rightarrow E \quad$ be a $(k,0)-$Bregman demigeneralized mapping. Suppose that $\Omega = F(T)\cap V(C,A)\ne \emptyset$ . Define a sequence $\{x_n\}_{n=1}^{\infty }$ generated by arbitrarily chosen $x_0,x_1 \in E$ and any fixed $u \in E:$

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n = \nabla f^*(\nabla f(x_n)+\sigma _n(\nabla f(x_{n-1})-\nabla f(x_n))\\ y_n = P_C\nabla f^*(\nabla f(w_n)-\lambda Aw_n);\\ T_n=\{z\in E: \langle z-y_n, \nabla f(w_n)-\lambda Aw_n-\nabla f(y_n) \rangle \le 0 \};\\ z_n= P_{T_n}\nabla f^*(\nabla f(w_n)-\lambda Ay_n);\\ v_n= \nabla f^*((1-\alpha _n)\nabla f(z_n) + \alpha _n \nabla f(Tz_n));\\ x_{n+1}= \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n)+\gamma _n \nabla f(u)), \quad n\ge 0 \end{array}\right. } \end{aligned}$$

(3.4)

where $\lambda \in (0,\frac{\alpha }{L}),\; \{\sigma _n\} \subset [0,\frac{1}{2}],\; \{\alpha _n\}, \{\delta _n\}, \{\beta _n\}, \{\gamma _n\}$ are sequences in (0, 1) such that $\delta _n + \beta _n + \gamma _n = 1$ and the following conditions are satisfied:

(C1):

$0<a\le \sigma _n < \beta _n \le \frac{1}{2}, \; \forall n\ge 1$,

(C2):

$\lim _{n\rightarrow \infty }\gamma _n =0$ and $\sum _{n=1}^{\infty } \gamma _n =\infty$,

(C3):

$0< \liminf _{n\rightarrow \infty }\delta _n \le \delta _n \le \limsup _{n\rightarrow \infty } \delta _n< 1.$

Then, the sequence $\{x_n\}$ is bounded.

Proof

For this, we first show that

$$\begin{aligned} D_f(p,z_n)\le D_f(p,w_n)- \Big (1-\frac{L\lambda }{\alpha }\Big )\Big ( D_f(y_n,w_n)+ D_f(z_n,y_n)\Big ). \end{aligned}$$

Let $p \in \Omega .$ Then using Lemma 2.6, Lemma 2.1 (b) and (1.2), we have

$$\begin{aligned} D_f(p,z_n)\le & D_f(p,\nabla f^*(\nabla f(w_n)-\lambda Ay_n))-D_f(z_n,\nabla f^*(\nabla f(w_n)-\lambda Ay_n))\\=\,\, & V_f(p,\nabla f(w_n)-\lambda Ay_n)-V_f(t_n,\nabla f(w_n)-\lambda Ay_n)\\=\,\, & D_f(p,w_n)-D_f(z_n,x_n)+\lambda \langle p-z_n,Ay_n \rangle \\=\,\, & D_f(p,w_n)-D_f(z_n,x_n)+\lambda \langle p-y_n,Ay_n \rangle +\lambda \langle y_n-z_n,Ay_n \rangle \\=\,\, & D_f(p,w_n)-D_f(z_n,y_n)-D_f(y_n,w_n)-\langle \nabla f(y_n)-\nabla f(w_n),z_n-y_n\rangle \\&+\lambda \langle y_n-z_n,Ay_n \rangle \\=\,\, & D_f(p,w_n)-D_f(z_n,y_n)-D_f(y_n,w_n)\\&+\langle z_n-y_n, \nabla f(w_n)-\lambda Ay_n -\nabla f(y_n)\rangle . \end{aligned}$$

Using the fact that A is Lipschitz continuous, we estimate

$$\begin{aligned} \langle z_n-y_n, \nabla f(w_n)-\lambda Ay_n -\nabla f(y_n)\rangle=\,\, & \langle z_n-y_n, \nabla f(w_n)-\lambda Aw_n -\nabla f(y_n)\rangle \\&+ \lambda \langle z_n-y_n,Aw_n- Ay_n \rangle \\\le & \lambda \langle z_n-y_n,Aw_n- Ay_n \rangle \\\le & \lambda ||z_n-y_n||||Aw_n-Ay_n||\\\le & k\lambda ||z_n-y_n||||w_n-y_n||\\\le & \frac{ L\lambda }{2}\Big (||z_n-y_n||^2+||y_n-w_n||^2 \Big )\\\le & \frac{ L\lambda }{\alpha }\Big (D_f(z_n,y_n)+ D_f(y_n,w_n\Big ). \end{aligned}$$

It follows that

$$\begin{aligned} D_f(p,z_n)\le & D_f(p,w_n)-D_f(z_n,y_n)-D_f(y_n,w_n)\nonumber \\&+ \frac{ L\lambda }{\alpha }\Big (D_f(z_n,y_n)+ D_f(y_n,w_n\Big )\nonumber \\=\,\, & D_f(p,w_n)- \Big ( D_f(z_n,y_n)+D_f(y_n,w_n)\nonumber \\&- \frac{ L\lambda }{\alpha }\Big (D_f(z_n,y_n)+ D_f(y_n,w_n\Big )\Big )\nonumber \\=\,\, & D_f(p,w_n)-\Big (1-\frac{ L\lambda }{\alpha }\Big )\Big (D_f(z_n,y_n)+ D_f(y_n,w_n)\Big ) \end{aligned}$$

(3.5)

Also from (3.4), we have

$$\begin{aligned} D_f(p,w_n)=\,\, & D_f(p,\nabla f^*(\nabla f(x_n)+\sigma _n(\nabla f(x_{n-1})-\nabla f(x_n)))\nonumber \\\le & (1-\sigma _n)D_f(p,x_n)+\sigma _nD_f(p,x_{n-1}). \end{aligned}$$

(3.6)

Since T is $(k,0)-$Bregman demigeneralized mapping, $S_n= \nabla f^*((1-\alpha _n)\nabla f(I) + \alpha _n \nabla f(T))$ is relatively nonexpansive mapping and $F(S_n)=F(T)$. Hence, from (3.4), we have

$$\begin{aligned} D_f(p,v_n)=\,\, & D_f(p,\nabla f^*((1-\alpha _n)\nabla f(z_n) + \alpha _n \nabla f(Tz_n)))\nonumber \\=\,\, & D_f(p,S_nz_n)\nonumber \\\le & D_f(p,z_n). \end{aligned}$$

(3.7)

Let $\rho ^*_r :E \rightarrow \mathbb {R}$ be the gauge function of uniform convexity of the conjugate function $f^*$. By (3.4), (3.5),(3.6),(3.7) and Lemma 2.7, we obtain

$$\begin{aligned} D_f(p,x_{n+1})\le & D_f(p, \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u)))\nonumber \\=\,\, & V_f(p, \delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u))\nonumber \\=\,\, & f(p)- \langle p, \delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u) \rangle \nonumber \\&+ f^*( \delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u))\nonumber \\\le & \delta _n f(p)+ \beta _n f(p) +\gamma _n f(p) - \delta _n \langle p,\nabla f(x_n) \rangle - \beta _n \langle p,\nabla f(v_n) \rangle \nonumber \\&-\gamma _n \langle p,\nabla f(u) \rangle + \delta _n f^*(\nabla f(x_n)) + \beta _n f^*(\nabla f(v_n)) + \gamma _n f^*(\nabla f(u))\nonumber \\&- \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) - \delta _n \gamma _n \rho ^*_r(||\nabla f(x_n)- \nabla f(u)||)\nonumber \\&- \beta _n \gamma _n \rho ^*_r(||\nabla f(v_n)- \nabla f(u)||) \nonumber \\\le & \delta _n (f(p) - \langle p, \nabla f(x_n)\rangle + f^*(\nabla f(x_n))) + \beta _n (f(p) - \langle p, \nabla f(v_n)\rangle \nonumber \\&+ f^*(\nabla f(v_n))) + \gamma _n (f(p) - \langle p, \nabla f(u)\rangle + f^*(\nabla f(u)))\nonumber \\&- \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\=\,\, & \delta _n V_f(p,\nabla f(x_n)) + \beta _n V_f(p,\nabla f(v_n)) + \gamma _n V_f(p,\nabla f(u))\nonumber \\&- \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||)\nonumber \\=\,\, & \delta _n D_f(p,x_n) + \beta _n D_f(p,v_n) + \gamma _n D_f(p,u) \nonumber \\&- \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n D_f(p,z_n) + \gamma _n D_f(p,u) \nonumber \\&- \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n \Big [ D_f(p,w_n) \nonumber \\&-\Big (1-\frac{ L\lambda }{\alpha }\Big )\Big (D_f(z_n,y_n)+ D_f(y_n,w_n)\Big )\Big ]\nonumber \\&+ \gamma _n D_f(p,u) - \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n(1-\sigma _n)D_f(p,x_n)+\beta _n \sigma _nD_f(p,x_{n-1})\nonumber \\&-\beta _n\Big (1-\frac{ L\lambda }{\alpha }\Big )\Big (D_f(z_n,y_n)+ D_f(y_n,w_n)\Big )\nonumber \\&+ \gamma _n D_f(p,u) - \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n D_f(p,x_n) -\beta _n \sigma _nD_f(p,x_{n}) + \beta _n \sigma _nD_f(p,x_{n-1})\nonumber \\&-\beta _n \Big (1-\frac{ L\lambda }{\alpha }\Big )\Big (D_f(z_n,y_n)+ D_f(y_n,w_n)\Big )\nonumber \\&+ \gamma _n D_f(p,u) - \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\\le & (1-\gamma _n -\beta _n \sigma _n)D_f(p,x_n)+\beta _n \sigma _nD_f(p,x_{n-1})\nonumber \\&+ \gamma _n D_f(p,u) -\beta _n \Big (1-\frac{ L\lambda }{\alpha }\Big )\Big (D_f(z_n,y_n)+ D_f(y_n,w_n)\Big )\nonumber \\&- \delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) \nonumber \\\le & (1-\gamma _n -\beta _n \sigma _n)D_f(p,x_n)+\beta _n \sigma _nD_f(p,x_{n-1})+ \gamma _n D_f(p,u)\nonumber \\\le & \max \Big \{D_f(p,x_n), D_f(p,x_{n-1}), D_f(p,u)\Big \} \quad \forall n \ge 1. \end{aligned}$$

(3.8)

By induction, we get

$$\begin{aligned} D_f(p,x_{n})\le \max \Big \{D_f(p,x_1), D_f(p,x_{0}), D_f(p,u)\Big \}. \end{aligned}$$

Hence, $\{D_f(p,x_n)\}$ is bounded which by Lemma 2.3 implies that $\{x_n\}$ is bounded. Furthermore, $\{y_n\}$, $\{z_n\}$, $\{v_n\}$, $\{w_n\}$ and $\{Tz_n\}$ are bounded. $\square$

Now, we prove the following strong convergence theorem.

Theorem 3.3

Let C be a nonempty closed and convex subset of a reflexive Banach space E and $f:{E \rightarrow \mathbb {R}}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E. Let $A:C\rightarrow E$ be a monotone map and $L-$Lipschitz on E with $L>0$ and let $T:C \rightarrow E \quad$ be a $(k,0)-$Bregman demigeneralized mapping. Suppose that $\Omega = F(T)\cap V(C,A)\ne \emptyset$ . Let $\{x_n\}_{n=1}^{\infty }$ be the sequence generated by (3.4) where $\lambda \in (0,\frac{\alpha }{L}),\; \{\sigma _n\} \subset [0,\frac{1}{2}],\; \{\alpha _n\}, \{\delta _n\}, \{\beta _n\}, \{\gamma _n\}$ are sequences in (0, 1) such that $\delta _n + \beta _n + \gamma _n = 1$ and the following conditions are satisfied:

(C1):

$0<a\le \sigma _n < \beta _n \le \frac{1}{2}, \; \forall n\ge 1$,

(C2):

$\lim _{n\rightarrow \infty }\gamma _n =0$ and $\sum _{n=1}^{\infty } \gamma _n =\infty$,

(C3):

$0< \liminf _{n\rightarrow \infty }\delta _n \le \delta _n \le \limsup _{n\rightarrow \infty } \delta _n< 1.$

Then, the sequence $\{x_n\}$ generated by (3.4) converges strongly to the point $p=P^f_{\Omega }u.$

Proof

Let $p \in \Omega .$ From (3.8), we have

$$\begin{aligned}&\delta _n \beta _n \rho ^*_r(||\nabla f(x_n)- \nabla f(v_n)||) +\beta _n\big (1-\frac{ L\lambda }{\alpha }\big )\big (D_f(z_n,y_n)\nonumber \\&\quad + D_f(y_n,w_n)\big )\le (D_f(p,x_n) -D_f(p,x_{n+1}))\nonumber \\&\quad +\beta _n \sigma _nD_f((p,x_{n-1})- D_f(p,x_{n}))+ \gamma _n D_f(p,u). \end{aligned}$$

(3.9)

We consider two cases.

Case 1. Assume $D_f(p,x_{n+1})\le D_f(p,x_n)$, such that $D_f(p,x_n)\le M ,$ for all $n \ge 1$, where $M:=\max \{D_f(p,x_1),D_f(p,x_0),D_f(p,u)\}$. Then $\{D_f(p,x_n)\}_{n=1}^{\infty }$ is convergent. Therefore, $\lim _{n\rightarrow \infty }(D_f(p,x_n)-D_f(p,x_{n+1}))=\lim _{n\rightarrow \infty }(D_f(p,x_{n-1})- D_f(p,x_{n}))=0$.

Since $\beta _n \sigma _n > 0$ and $\big (1-\frac{ L\lambda }{\alpha }\big )>0$, therefore, by (3.9), we get

$$\begin{aligned} \lim _{n\rightarrow \infty } D_f(z_n,y_n)= \lim _{n\rightarrow \infty } D_f(y_n,w_n)= \lim _{n\rightarrow \infty }\rho ^*_r( ||\nabla f(x_n)- \nabla f(v_n)||)=0. \end{aligned}$$

Thus, it follows by Lemma 2.2 and the property of $\rho ^*_r$ that

$$\begin{aligned} \lim _{n\rightarrow \infty } ||z_n-y_n||= \lim _{n\rightarrow \infty } ||y_n-w_n||=0 \end{aligned}$$

(3.10)

and

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(x_n)- \nabla f(v_n)||=0. \end{aligned}$$

(3.11)

Since $\nabla f$ is norm to norm uniformly continuous on bounded subsets of $E^*$, (3.10) becomes

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(z_n)-\nabla f(y_n)||= \lim _{n\rightarrow \infty } ||\nabla f(y_n)-\nabla f(w_n)||=0. \end{aligned}$$

(3.12)

From (4.3), we have

$$\begin{aligned} ||\nabla f(x_{n+1})- \nabla f(x_n)||+\beta _n ||\nabla f(x_{n})- \nabla f(v_n)||+\gamma _n ||\nabla f(x_{n})- \nabla f(u)||=0. \end{aligned}$$

(3.13)

Using (C2) and (3.11) in (3.13), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(x_{n+1})- \nabla f(x_n)||=0. \end{aligned}$$

(3.14)

Since $\nabla f$ is norm to norm uniformly continuous on bounded subsets of $E^*$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||x_{n+1}- x_n||=0. \end{aligned}$$

(3.15)

Also from (3.4) we have

$$\begin{aligned} ||\nabla f(w_{n})- \nabla f(x_n)||=\sigma _n||\nabla f(x_{n-1})- \nabla f(x_n)||, \end{aligned}$$

which by (3.14) implies

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(w_{n})- \nabla f(x_n)||=0. \end{aligned}$$

(3.16)

From (3.12), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(z_{n})- \nabla f(w_n)||=0. \end{aligned}$$

(3.17)

In addition, from (3.11) and (3.16), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(w_{n})- \nabla f(v_n)||=0. \end{aligned}$$

(3.18)

Now, (3.17) and (3.19), give that

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(z_{n})- \nabla f(v_n)||=0. \end{aligned}$$

(3.19)

Again, from (3.11) and (3.19), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||\nabla f(x_{n})- \nabla f(z_n)||=0. \end{aligned}$$

(3.20)

Since $\nabla f$ is norm to norm uniformly continuous on bounded subsets of $E^*$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||x_{n} - z_n||=0. \end{aligned}$$

(3.21)

In addition, from (3.10) and (3.21), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } ||x_{n} - y_n||=0. \end{aligned}$$

(3.22)

Since T is $(k,0)-$Bregman demigeneralized and $p\in F(T)$, therefore from (4.3) and the definition of Bregman demigeneralized mapping, we have

$$\begin{aligned} \langle z_n-p,\nabla f(z_n)-\nabla f(v_n)\rangle=\,\, & \alpha _n \langle z_n-p,\nabla f(z_n)-\nabla f(Tz_n)\rangle \\\ge & \alpha _n (1-k)D_f(z_n,Tz_n). \end{aligned}$$

As $\lambda _n(1-k)>0$, so we obtain

$$\begin{aligned} D_f(z_n,Tz_n) \le \frac{1}{\lambda _n(1-k)}||z_n-p||||\nabla f(z_n)-\nabla f(v_n)||; \end{aligned}$$

from (3.19) and the fact that $\{z_n\}$ is bounded, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }D_f(z_n,Tz_n)=0 \end{aligned}$$

(3.23)

Using Lemma 2.2, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }||z_n-Tz_n||=0 \end{aligned}$$

(3.24)

Since $\{x_n\}$ is bounded, there exists a subsequence $\{x_{n_k}\} \subset \{x_n\}$, such that $x_{n_k} \rightharpoonup z$, which implies that $z_{n_k} \rightharpoonup z$ as $k \rightarrow \infty$. Using (3.24), it follows that $z \in F(T)$.

Next, we show that $z \in VI(C,A)$. Let

$$\begin{aligned} Tv= {\left\{ \begin{array}{ll} Av+N_C(v), \quad if v\in C,\\ \emptyset , \qquad \qquad \qquad if v \notin C, \end{array}\right. } \end{aligned}$$

where $N_C(v)$ is as defined in Lemma 2.8. Then, T is maximal monotone and $0 \in Tv$ if and only if $v \in VI(C,A)$. If T is maximal monotone, then $(x,x^*) \in X \times X^*$ and if $\langle x-y,x^*-y^* \rangle \ge 0, \forall (y,y^*) \in G(T),$ then $x^* \in Tx$.

Let $(v,q) \in G(T)$; it suffices to show that $\langle v-z,q \rangle \ge 0.$

Now $(v,q) \in G(T) \Rightarrow q \in Tv=Av+N_C(v) \Rightarrow q-Av \in N_C(v).$ Then

$$\begin{aligned} \langle v-y,q-Av \rangle \ge 0, \forall y\in C. \end{aligned}$$

Since $y_n = P^f_C\nabla f^*(\nabla f(x_n)-\lambda Aw_n)$ and $v \in C$, we have by Lemma 2.1 that

$$\begin{aligned} \langle y_n-v,\nabla f(x_n)-\lambda Ax_n-\nabla f(y_n)\rangle \ge 0. \end{aligned}$$

Thus

$$\begin{aligned} \Big \langle v-y_n,\frac{\nabla f(y_n)-\nabla f(w_n)}{\lambda }+Aw_n \Big \rangle \ge 0. \end{aligned}$$

As $q-Av \in N_C(v)$ and $y_n \in C$, so we have

$$\begin{aligned} \langle v-y_{n_k},q\rangle\ge & \langle v-y_{n_k},Av\rangle \\\ge & \langle v-y_{n_k},Av\rangle - \Big \langle v-y_{n_k},\frac{\nabla f(y_{n_k})-\nabla f(w_{n_k})}{\lambda }+Aw_{n_k} \Big \rangle \\=\,\, & \langle v-y_{n_k},Av-Ay_{n_k} \rangle + \langle v-y_{n_k},Ay_{n_k}-Aw_{n_k}\rangle \\&- \Big \langle v-y_{n_k},\frac{\nabla f(y_{n_k})-\nabla f(w_{n_k})}{\lambda } \Big \rangle \\\ge & \langle v-y_{n_k},Ay_{n_k}-Aw_{n_k}\rangle - \Big \langle v-y_{n_k},\frac{\nabla f(y_{n_k})-\nabla f(w_{n_k})}{\lambda } \Big \rangle . \end{aligned}$$

Using Lipschitz continuity of A, (3.10) and (3.12), we get

$$\begin{aligned} \langle v-z,q \rangle \ge 0. \end{aligned}$$

Therefore, $z\in VI(C,A).$ Hence $z\in \Omega$.

Next, we show that $\{x_n\}$ converges strongly to $p =P^f_{\Omega }u$.

Now

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_{n}-p,\nabla f(u)-\nabla f(p)\rangle=\,\, & \lim _{k \rightarrow \infty } \langle x_{n_k}-p,\nabla f(u)-\nabla f(p)\rangle \\=\,\, & \langle z-p,\nabla f(u)-\nabla f(p)\rangle . \end{aligned}$$

Using Lemma 2.1, we have

$$\begin{aligned} \langle z-p,\nabla f(u)-\nabla f(p)\rangle \le 0, \end{aligned}$$

and hence

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_{n}-p,\nabla f(u)-\nabla f(p)\rangle=\,\, & \langle z-p,\nabla f(u)-\nabla f(p)\rangle \le 0. \end{aligned}$$

(3.25)

It follows from (3.15) and (3.25) that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_{n+1}-p,\nabla f(u)-\nabla f(p)\rangle\le & 0. \end{aligned}$$

(3.26)

From (3.31), (3.5), (3.6), (3.7) and Lemma 2.6, we have

$$\begin{aligned} D_f(p,x_{n+1})\le & D_f(p, \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u)))\nonumber \\=\,\, & V_f(p, \delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u))\nonumber \\=\,\, & V_f(p, \delta _n \nabla f(x_n) + \beta _n \nabla f(v_n) + \gamma _n \nabla f(u)-\gamma _n(\nabla f(u)-\nabla f(p))) \nonumber \\&+ \gamma _n \langle x_{n+1} -p,\nabla f(u)-\nabla f(p) \rangle \nonumber \\=\,\, & \delta _n D_f(p,x_n) + \beta _n D_f(p,v_n) + \gamma _n \langle x_{n+1} -p,\nabla f(u)-\nabla f(p) \rangle \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n D_f(p,z_n) + \gamma _n \langle x_{n+1} -p,\nabla f(u)-\nabla f(p) \rangle \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n D_f(p,w_n) + \gamma _n \langle x_{n+1} -p,\nabla f(u)-\nabla f(p) \rangle \nonumber \\\le & \delta _n D_f(p,x_n) + \beta _n \big ((1-\sigma _n)D_f(p,x_n)+\sigma _nD_f(p,x_{n-1})\big )\nonumber \\&+ \gamma _n \langle x_{n+1} -p,\nabla f(u)-\nabla f(p) \rangle \nonumber \\\le & (1-\gamma _n -\beta _n \sigma _n)D_f(p,x_n)+\beta _n \sigma _nD_f(p,x_{n-1})\nonumber \\&+ \gamma _n \langle x_{n+1} -p,\nabla f(u)-\nabla f(p) \rangle . \end{aligned}$$

(3.27)

Now, by (3.26), Lemmas 2.9 and 2.2, we have $x_n \rightarrow p$.

Case 2. Assume $\{D_f(p,x_n)\}$ is non-decreasing. Set $\Gamma _n$ of Lemma 2.10, as $\Gamma _n=D_f(p,x_n)$ and let $\tau : \mathbb {N} \rightarrow \mathbb {N}$ be a mapping for all $n\ge n_0$ (for some $n_0$ large enough), defined by

$$\begin{aligned} \tau (n):=\max \{k\in \mathbb {N}:k\le n, \Gamma _k \le \Gamma _{k+1}\}. \end{aligned}$$

Then $\tau$ is non-decreasing sequence such that $\tau (n) \rightarrow \infty$ as $n \rightarrow \infty$. Thus

$$\begin{aligned} 0\le \Gamma _{\tau (n)} \le \Gamma _{\tau (n)+1},\quad \forall n\ge n_0; \end{aligned}$$

this implies

$$\begin{aligned} D_f(p,x_{\tau (n)})\le D_f(p,x_{\tau (n)+1}),\quad n\ge n_0. \end{aligned}$$

Since $\{D_f(p,x_{\tau (n)})\}$ is bounded, therefore $\lim _{n\rightarrow \infty }D_f(p,x_{\tau (n)})$ exists. Then the following estimates can be obtained, using same arguments as in Case 1 above

• 1.
  $$\begin{aligned} \lim _{n \rightarrow \infty }||y_{\tau (n)}-w_{\tau (n)}||=0, \qquad \lim _{n \rightarrow \infty }||z_{\tau (n)}-y_{\tau (n)}||=0 \end{aligned}$$
• 2.
  $$\begin{aligned} \lim _{n \rightarrow \infty }||x_{\tau (n)}-y_{\tau (n)}||=0, \qquad \lim _{n \rightarrow \infty }||x_{\tau (n)+1}-x_{\tau (n)}||=0 \end{aligned}$$
• 3.
  $$\begin{aligned} \lim _{n \rightarrow \infty }||v_{\tau (n)}-x_{\tau (n)}||=0, \qquad \lim _{n \rightarrow \infty }||z_{\tau (n)+1}-Tz_{\tau (n)}||=0 \end{aligned}$$
• 4.
  $$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_{\tau (n)+1}-p,\nabla f(u)-\nabla f(p)\rangle\le & 0. \end{aligned}$$

  (3.28)

From (3.27) and $\Gamma _{\tau (n)} \le \Gamma _{\tau (n)+1},$ we have

$$\begin{aligned} D_f(p,x_{\tau (n)})\le & (1-\gamma _{\tau (n)} -\beta _{\tau (n)} \sigma _{\tau (n)})D_f(p,x_{\tau (n)})+\beta _{\tau (n)} \sigma _nD_f(p,x_{\tau (n)-1})\\&+ \gamma _{\tau (n)} \langle x_{\tau (n)+1} -p,\nabla f(u)-\nabla f(p) \rangle \\\le & (1-\gamma _{\tau (n)})D_f(p,x_{\tau (n)+1}) + \gamma _{\tau (n)} \langle x_{\tau (n)+1} -p,\nabla f(u)-\nabla f(p) \rangle . \end{aligned}$$

Hence, we obtain

$$\begin{aligned} D_f(p,x_{\tau (n)}) \le D_f(p,x_{\tau (n)+1}) \le \langle x_{\tau (n)+1} -p,\nabla f(u)-\nabla f(p) \rangle \end{aligned}$$

(3.29)

which gives by (3.28)

$$\begin{aligned} \lim _{n \rightarrow \infty } D_f(p,x_{\tau (n)})=0. \end{aligned}$$

Therefore

$$\begin{aligned} \lim _{n \rightarrow \infty } D_f(p,x_{\tau (n)+1})=0 \end{aligned}$$

and therefore

$$\begin{aligned} \lim _{n \rightarrow \infty } \Gamma _{\tau (n)}= \lim _{n \rightarrow \infty } \Gamma _{\tau (n)+1}=0. \end{aligned}$$

(3.30)

For all $n\ge n_0$, we have that $\Gamma _{\tau (n)} \le \Gamma _{\tau (n)+1},$ if $n \ne \tau (n)$ (that is, $\tau (n)<n),$ because $\Gamma _{k+1} \le \Gamma _k$ for $\tau (n)\le k \le n$. This gives for all $n\ge n_0$

$$\begin{aligned} 0\le \Gamma _n \le \max \{\Gamma _{\tau (n)},\Gamma _{\tau (n)+1}\}=\Gamma _{\tau (n)+1}. \end{aligned}$$

This implies $\lim _{n \rightarrow \infty } \Gamma _n=0$ which gives that $\lim _{n \rightarrow \infty }D_f(p,x_n)=0$. Hence $x_n \rightarrow p=P^f_\Omega u$ as $n \rightarrow \infty$. $\square$

As an important special case of Theorem 3.3, we obtain the following result:

Corollary 3.4

Let C be a nonempty closed and convex subset of a reflexive Banach space E and $f:{E \rightarrow \mathbb {R}}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E. Let $A:C\rightarrow E$ be a monotone map and $L-$Lipschitz on E with $L>0$ and $T:C \rightarrow E \quad$ be a quasi Bregman nonexpansive mapping. Suppose that $\Omega = F(T)\cap V(C,A)\ne \emptyset$. Define a sequence $\{x_n\}_{n=1}^{\infty }$ generated by arbitrarily chosen $x_0,x_1 \in E$ and any fixed $u \in E:$

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n = \nabla f^*(\nabla f(x_n)+\sigma _n(\nabla f(x_{n-1})-\nabla f(x_n))\\ y_n = \Pi _C\nabla f^*(\nabla f(w_n)-\lambda Aw_n);\\ T_n=\{z\in E: \langle z-y_n, \nabla f(w_n)-\lambda Aw_n-\nabla f(y_n) \rangle \le 0 \};\\ z_n= \Pi _{T_n}\nabla f^*(\nabla f(w_n)-\lambda Ay_n);\\ v_n= \nabla f^*((1-\alpha _n)\nabla f(z_n) + \alpha _n \nabla f(Tz_n));\\ x_{n+1}= \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n)+\gamma _n \nabla f(u)), \quad n\ge 0 \end{array}\right. } \end{aligned}$$

(3.31)

where $\lambda \in (0,\frac{\alpha }{L}),\; \{\sigma _n\} \subset [0,\frac{1}{2}],\; \{\alpha _n\}, \{\delta _n\}, \{\beta _n\}, \{\gamma _n\}$ are sequences in (0, 1) such that $\delta _n + \beta _n + \gamma _n = 1$ and the following conditions are satisfied:

(C1):

$0<a\le \sigma _n < \beta _n \le \frac{1}{2}, \; \forall n\ge 1$,

(C2):

$\lim _{n\rightarrow \infty }\gamma _n =0$ and $\sum _{n=1}^{\infty } \gamma _n =\infty$,

(C3):

$0< \liminf _{n\rightarrow \infty }\delta _n \le \delta _n \le \limsup _{n\rightarrow \infty } \delta _n< 1.$

Then, the sequence $\{x_n\}$ generated by (3.31) converges strongly to the point $p=\Pi _{\Omega }u.$

4 Applications

In this section, using Theorem 3.3, we obtain important and new theorems that are associated with the inertial subgradient extragradient method in reflexive Banach spaces.

Theorem 4.1

Let C be a nonempty closed and convex subset of a reflexive Banach space E and $f:{E \rightarrow \mathbb {R}}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E. Let $A:C\rightarrow E$ be a monotone map and $L-$Lipschitz on E with $L>0$ and let $T:C \rightarrow E \quad$ be a quasi-Bregman strictly pseudocontractive mapping with $F(T)\ne \emptyset$. Suppose that $\Omega = F(T)\cap V(C,A)\ne \emptyset$ . Define a sequence $\{x_n\}_{n=1}^{\infty }$ generated by arbitrarily chosen $x_0,x_1 \in E$ and any fixed $u \in E:$

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n = \nabla f^*(\nabla f(x_n)+\sigma _n(\nabla f(x_{n-1})-\nabla f(x_n))\\ y_n = P_C\nabla f^*(\nabla f(w_n)-\lambda Aw_n);\\ T_n=\{z\in E: \langle z-y_n, \nabla f(w_n)-\lambda Aw_n-\nabla f(y_n) \rangle \le 0 \};\\ z_n= P_{T_n}\nabla f^*(\nabla f(w_n)-\lambda Ay_n);\\ v_n= \nabla f^*((1-\alpha _n)\nabla f(z_n) + \alpha _n \nabla f(Tz_n));\\ x_{n+1}= \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n)+\gamma _n \nabla f(u)), \quad n\ge 0 \end{array}\right. } \end{aligned}$$

(4.1)

where $\lambda \in (0,\frac{\alpha }{L}),\; \{\sigma _n\} \subset [0,\frac{1}{2}],\; \{\alpha _n\}, \{\delta _n\}, \{\beta _n\}, \{\gamma _n\}$ are sequences in (0, 1) such that $\delta _n + \beta _n + \gamma _n = 1$ and the following conditions are satisfied:

(C1):

$0<a\le \sigma _n < \beta _n \le \frac{1}{2}, \; \forall n\ge 1$,

(C2):

$\lim _{n\rightarrow \infty }\gamma _n =0$ and $\sum _{n=1}^{\infty } \gamma _n =\infty$,

(C3):

$0< \liminf _{n\rightarrow \infty }\delta _n \le \delta _n \le \limsup _{n\rightarrow \infty } \delta _n< 1.$

Then, the sequence $\{x_n\}$ generated by (4.3) converges strongly to the point $p=P_{\Omega }u.$

Proof

Since T is quasi-Bregman strictly pseudocontractive mapping with $F(T)\ne \emptyset$, then T is (k, 0)-Bregman demigeneralized mapping. Therefore the result follows from Theorem 3.3. $\square$

Theorem 4.2

Let C be a nonempty closed and convex subset of a reflexive Banach space E and $f:{E \rightarrow \mathbb {R}}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E. Let $A:C\rightarrow E$ be a monotone map and $L-$Lipschitz on E with $L>0$ and let U be maximal monotone operators of E into $E^*$. Let $Res^f_{\lambda U}$ be the resolvent of U for $\lambda >0$. Suppose that $\Omega = U^{-1}(0) \cap V(C,A)\ne \emptyset$ . Define a sequence $\{x_n\}_{n=1}^{\infty }$ generated by arbitrarily chosen $x_0,x_1 \in E$ and any fixed $u \in E:$

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n = \nabla f^*(\nabla f(x_n)+\sigma _n(\nabla f(x_{n-1})-\nabla f(x_n))\\ y_n = P_C\nabla f^*(\nabla f(w_n)-\lambda Aw_n);\\ T_n=\{z\in E: \langle z-y_n, \nabla f(w_n)-\lambda Aw_n-\nabla f(y_n) \rangle \le 0 \};\\ z_n= P_{T_n}\nabla f^*(\nabla f(w_n)-\lambda Ay_n);\\ v_n= \nabla f^*((1-\alpha _n)\nabla f(z_n) + \alpha _n \nabla f(Res^f_{\lambda U}z_n));\\ x_{n+1}= \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n)+\gamma _n \nabla f(u)), \quad n\ge 0 \end{array}\right. } \end{aligned}$$

(4.2)

where $\lambda \in (0,\frac{\alpha }{L}),\; \{\sigma _n\} \subset [0,\frac{1}{2}],\; \{\alpha _n\}, \{\delta _n\}, \{\beta _n\}, \{\gamma _n\}$ are sequences in (0, 1) such that $\delta _n + \beta _n + \gamma _n = 1$ and the following conditions are satisfied:

(C1):

$0<a\le \sigma _n < \beta _n \le \frac{1}{2}, \; \forall n\ge 1$,

(C2):

$\lim _{n\rightarrow \infty }\gamma _n =0$ and $\sum _{n=1}^{\infty } \gamma _n =\infty$,

(C3):

$0< \liminf _{n\rightarrow \infty }\delta _n \le \delta _n \le \limsup _{n\rightarrow \infty } \delta _n< 1.$

Then, the sequence $\{x_n\}$ generated by (4.3) converges strongly to the point $p=P_{\Omega }u.$

Proof

Since $Res^f_{\lambda U}$ is the resolvent of U on E, then $Res^f_{\lambda U}$ is (0, 0)-Bregman demigeneralized mapping. Therefore, the result follows from Theorem 3.3. $\square$

Theorem 4.3

Let C be a nonempty closed and convex subset of a reflexive Banach space E and $f:{E \rightarrow \mathbb {R}}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E. Let $A:C\rightarrow E$ be a monotone map and $L-$Lipschitz on E with $L>0$ and let $T:C \rightarrow E \quad$ be a quasi-Bregman nonexpansive mapping with $F(T)\ne \emptyset$. Suppose that $\Omega = F(T)\cap V(C,A)\ne \emptyset$ . Define a sequence $\{x_n\}_{n=1}^{\infty }$ generated by arbitrarily chosen $x_0,x_1 \in E$ and any fixed $u \in E:$

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n = \nabla f^*(\nabla f(x_n)+\sigma _n(\nabla f(x_{n-1})-\nabla f(x_n))\\ y_n = P_C\nabla f^*(\nabla f(w_n)-\lambda Aw_n);\\ T_n=\{z\in E: \langle z-y_n, \nabla f(w_n)-\lambda Aw_n-\nabla f(y_n) \rangle \le 0 \};\\ z_n= P_{T_n}\nabla f^*(\nabla f(w_n)-\lambda Ay_n);\\ v_n= \nabla f^*((1-\alpha _n)\nabla f(z_n) + \alpha _n \nabla f(Tz_n));\\ x_{n+1}= \nabla f^*(\delta _n \nabla f(x_n) + \beta _n \nabla f(v_n)+\gamma _n \nabla f(u)), \quad n\ge 0 \end{array}\right. } \end{aligned}$$

(4.3)

where $\lambda \in (0,\frac{\alpha }{L}),\; \{\sigma _n\} \subset [0,\frac{1}{2}],\; \{\alpha _n\}, \{\delta _n\}, \{\beta _n\}, \{\gamma _n\}$ are sequences in (0, 1) such that $\delta _n + \beta _n + \gamma _n = 1$ and the following conditions are satisfied:

(C1):

$0<a\le \sigma _n < \beta _n \le \frac{1}{2}, \; \forall n\ge 1$,

(C2):

$\lim _{n\rightarrow \infty }\gamma _n =0$ and $\sum _{n=1}^{\infty } \gamma _n =\infty$,

(C3):

$0< \liminf _{n\rightarrow \infty }\delta _n \le \delta _n \le \limsup _{n\rightarrow \infty } \delta _n< 1.$

Then, the sequence $\{x_n\}$ generated by (4.3) converges strongly to the point $p=P_{\Omega }u.$

Proof

Since T is quasi-Bregman nonexpansive mappings, then T is (0, 0)-Bregman demigeneralized mappings. Therefore the result follows from Theorem 3.3. $\square$

Remark 4.4

Every nonexpansive mapping is strictly pseudocontractive mapping and every strictly pseudocontractive is $(\eta ,0)-$ Bregman demigeneralized mapping.

5 Numerical example

Let $E=\mathbb {R}^4$ be a four-dimensional Euclidean space with the usual inner product:

$$\begin{aligned} \langle x,y \rangle = x_1y_1 + x_2y_2 + x_3y_3 + x_4y_4 \end{aligned}$$

where $x=(x_1,x_2,x_3,x_4), \quad y=(y_1,y_2,y_3,y_4) \in \mathbb {R}^4$ and let $f(x)=x_1^3+x_2^3+x_3^3+x_4^3$ for all $x=(x_1,x_2,x_3,x_4) \in \mathbb {R}^4$ and $\nabla f(x)=3(x_1^2+x_2^2+x_3^2+x_4^2)$. Let $Tx=2x,\quad f(Tx)=8(x_1^3+x_2^3+x_3^3+x_4^3)$ and $\nabla f(Tx)=24(x_1^2+x_2^2+x_3^2+x_4^2)$.

Given a half space $C=\{z\in \mathbb {R}^4: \langle u,z-w_0 \rangle \le 0 \}$ of $\mathbb {R}^4$ where $u \ne 0$ and $w_0$ are two fixed element of $\mathbb {R}^4$ then for any $x_0 \in \mathbb {R}^4$, we have

$$\begin{aligned} P_Cx_0= {\left\{ \begin{array}{ll} x_0-\frac{\langle u,x_0-w_0 \rangle }{||u||^2}u, \quad \langle u,x_0-w_0 \rangle >0;\\ x_0 \quad \quad \quad \quad \quad \quad \quad \langle u,x_0-w_0 \rangle <0. \end{array}\right. } \end{aligned}$$

Then T is $(\frac{1}{2},0)-$ Bregman demigeneralized mapping and $Ax=(-2x_3+x_2,x_4-x_1,2x_1-2x_4,-x_2+2x_3)$ is monotone and $2\sqrt{2}-$Lipschitz operator. Let $\alpha _n=\frac{2n-1}{6n}, \; \delta _n = \frac{3n+1}{6n}, \; \beta _n = \frac{2n-1}{4n}, \gamma _n = \frac{1}{12n}$ and $\sigma _n= \frac{1}{4} \; \forall n \ge 1.$ Now $\lambda \in (0, \frac{\alpha }{L})=(0,\frac{\alpha }{2\sqrt{2}}),$ for $\alpha \in (0,1),$ put $\alpha = \frac{1}{2}.$ so that we take $\lambda = \frac{1}{8}.$ All conditions of Theorem 3.3 are satisfied.

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n=\frac{1}{4}(3x_n+x_{n-1})\\ y_n=P_C(w_n-\nabla f^*(\frac{1}{8}Aw_n))\\ T_n=\{x \in \mathbb {R}^4: \langle x-y_n,\nabla f(w_n)-\frac{1}{8}Aw_n- \nabla f(y_n) \rangle \le 0 \} \\ z_n=P_{T_n}(w_n-\nabla f^*(\frac{1}{8}Aw_n))\\ v_n=\frac{8n-1}{6n}z_n \\ x_{n+1}=\frac{3n+1}{6n}x_n+\frac{2n-1}{4n}v_n+\frac{1}{12n} \quad n \ge 1. \end{array}\right. } \end{aligned}$$

The following cases are considered for a numerical experiment of our algorithm.

Case 1::

Take $x_{1}=(1,-1,2,-2)^{T}$ and $x_{0}=(2,1,-1,-2)^{T}$.

Case 2::

Take $x_{1}=(2,1,-1,-2)^{T}$ and $x_{0}=(1,-1,2,-2)^{T}$.

Case 3::

Take $x_{1}=(-1,0.3,10,-5)^{T}$ and $x_{0}=(2,-0.10,-2,-4)^{T}$.

The following tables show results of our numerical experiment based on MATLAB software (Tables 1, 2, 3; Fig. 1).

Table 1 Numerical results for CASE 1

Table 2 Numerical results for CASE 2

Table 3 Numerical results for CASE 3

Fig. 1

Errors vs number of iterations: Case 1. (up left); Case 2. (up right); Case 3. (down)