On nonlocal integral and derivative boundary value problem of nonlinear Hadamard Langevin equation with three different fractional orders

Abstract

This paper is concerned with Hadamard fractional Langevin differential equation subject to fractional integral and derivative boundary conditions and which involves three different fractional orders. By using Schaefer’s fixed point theorem and Banach contraction principle, existence and uniqueness results of solutions for the proposed equation are obtained. An example demonstrating the consistency to the theoretical findings is also presented.

1 Introduction

Fractional differential equations have attracted the attention of many researchers working in different disciplines. The existing literature on the topic not only covers its theoretical aspects, but also describes its wide range of real applications. The tools of fractional calculus, in particular, are effectively used and applied in modeling many engineering and scientific processes and phenomena; see for instance the monographs [6, 16, 26], and references therein.

Boundary value problems of fractional differential equations have been extensively studied over the last years. Many interesting results regarding the existence-uniqueness, stability and controllability of solutions have been elaborated by many researchers. However, most of the considered problems have been treated in the frame of fractional derivatives of Riemann–Liouville and Caputo types [1, 7, 9, 11, 12, 21,22,23, 27, 29]. The Hadamard derivative is another type of derivatives of non-integer order [14]. Indeed, it differs from the Riemann–Liouville and Caputo derivatives in the sense that the kernel of the integral (in the definition of Hadamard derivative) contains a logarithmic function of arbitrary exponent [8, 10]. The qualitative investigations with respect to Hadamard derivative have gained less attention compared to the analysis in terms of Riemann–Liouville and Caputo settings; see [2, 3, 13, 19, 20].

Langevin equation is an important equation of mathematical physics that is used in modeling the phenomena occurring in fluctuating environment such as Brownian motion. The classical form of this equation was derived in terms of ordinary derivatives by Paul Langevin in [17]. Langevin equation is also known as a stochastic differential equation as it governs the fast motion of microscopic variables (degrees of freedom) of the dynamical systems. Recently, fractional Langevin equations have been studied by some scholars. In [4], the authors studied a nonlinear Langevin equation involving two fractional orders in different intervals with three-point boundary conditions. The contraction mapping principle and Krasnoselskii’s fixed point theorem are applied to prove the existence of solutions for the problem. In [5], the authors developed the existence theory for a nonlinear Langevin equation involving Caputo fractional derivatives of different orders and Riemann–Liouville fractional integral supplemented with nonlocal multi-point and multi-strip boundary conditions. They make use methods of functional analysis to obtain the existence and uniqueness results for the given problem. In [18], Li et al. investigated the infinite-point boundary value problem of fractional Langevin equations. By means of the nonlinear alternative and Leray–Schauder degree theory, they obtained some existence results for the boundary value problem. Zhou and Qiao in [30], discussed a class of fractional Langevin equations with integral and anti-periodic boundary conditions by using some fixed point theorems and the Leray–Schauder degree theory. The reader is invited to consult the papers [28, 31] for further study on fractional Langevin equations. On the other hand, the study of fractional Langevin equations in frame of Hadamard derivative has comparably been seldom; see the papers [15, 25] in which the authors discussed Sturm–Liouville and Langevin equations via Hadamard fractional derivatives and systems of fractional Langevin equations of Riemann–Liouville and Hadamard types, respectively.

Inspired by the above discussion, we consider the existence and uniqueness of solutions for the following Hadamard fractional Langevin equation:

$$\begin{aligned} \left\{ \begin{array}{l} \mathcal {D}^{\beta }\left( \mathcal {D}^{\alpha }+\lambda \right) u(t)=f(t,u(t),\mathcal {D}^{\gamma }u(t)),\ t\in J=[1,T], \\ u(1)=0, \\ u(T)+\dfrac{\lambda }{\Gamma (\alpha )}\int _{1}^{T}\left( \log \frac{T}{s} \right) ^{\alpha -1}\frac{u(s)}{s}\mathrm{{d}}s=0, \\ \mathcal {D}^{\alpha }u(\xi )+\lambda u(\xi )=0,\ \ \xi \in ]1,T], \end{array} \right. \end{aligned}$$

(1.1)

where $1<\beta <2$, $\beta -1<\alpha<1, \ 0<\gamma <\beta +\alpha -2, \ \lambda >0$, $\mathcal {D}^{\nu }$ denotes the Hadamard fractional derivative of order $\nu \in \{\alpha ,\beta ,\gamma \}$ and $f:[1,T]\times \mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ is a continuous function. It is to be noted that Eq. (1.1) is subject to fractional integral and derivative boundary conditions and involves three different fractional orders defined on different intervals. Our approach is new and the current results are totally different from the ones obtained in [15, 25].

This paper is organized as follows: in Sect. 2, we present some necessary definitions and lemmas that are needed in the subsequent sections. In Sect. 3, we adopt some fixed point theorems to prove the existence of solutions for problem (1.1). An illustrative example is presented in Sect. 4.

2 Essential preliminaries

In this section, we introduce some notations and definitions of fractional calculus and present preliminary results needed in our proofs later. For more details, the reader is recommended to refer to the monograph [10].

Definition 2.1

The Hadamard fractional derivative of order $\alpha$ for a function g is defined by

$$\begin{aligned} \mathcal {D}^{\alpha }g(t)=\dfrac{1}{\Gamma (n-\alpha )}\left( t\frac{\mathrm{{d}}}{\mathrm{{d}}t}\right) ^{n}\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{n-\alpha -1}\ \frac{g(s)}{s} \mathrm{{d}}s,\quad \ n=[\alpha ]+1, \end{aligned}$$

provided the integral exists.

Definition 2.2

The Hadamard fractional integral of order $\alpha$ for a function g is defined by

$$\begin{aligned} I^{\alpha }g(t)=\dfrac{1}{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha -1}\ \frac{g(s)}{s}\mathrm{{d}}s,\quad \ \alpha >0, \end{aligned}$$

provided the integral exists.

The following two properties of the above derivative and integral operators follow.

Lemma 2.3

If $\alpha ,\beta >0$, then

$$\begin{aligned} \left( \mathcal {D}_{a}^{\alpha }\left( \log \frac{t}{a}\right) ^{\beta -1}\right) (x)= \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha )}\left( \log \frac{x}{a} \right) ^{\beta -\alpha -1}, \end{aligned}$$

and

$$\begin{aligned} \left( I_{a}^{\alpha }\left( \log \frac{t}{a}\right) ^{\beta -1}\right) (x)= \frac{\Gamma (\beta )}{\Gamma (\beta +\alpha )}\left( \log \frac{x}{a} \right) ^{\beta +\alpha -1}, \end{aligned}$$

where $a>0$ is the starting point in the interval.

Lemma 2.4

Let $\alpha >0$ and $u\in C[1,+\infty )\cap L^{1}[1,+\infty ),$ then the Hadamard fractional differential equation

$$\begin{aligned} \mathcal {D}^{\alpha }u(t)=0, \end{aligned}$$

has a solution

$$\begin{aligned} u(t)=\sum _{k=1}^{n}c_{k}(\log t)^{\alpha -k}, \end{aligned}$$

and, further, the following formulas hold

$$\begin{aligned} \mathcal {D}^{\alpha }I^{p}u(t)= & {} I^{p-\alpha }u(t),\quad \ p> \alpha , \end{aligned}$$

and

$$\begin{aligned} I^{\alpha }\mathcal {D}^{\alpha }u(t)= & {} u(t)-\sum _{k=1}^{n}c_{k}(\log t)^{\alpha -k}, \end{aligned}$$

where $c_{k}\in \mathbb {R},k=1,2,\ldots ,n$ and $n-1<\alpha <n.$

In what follows, we present the solution representation associated to problem (1.1).

Lemma 2.5

Let $1<\beta <2$, $\beta -1<\alpha <1,\ \lambda >0$, $h\in C[1,T]$ and $\frac{\log T}{\log \xi }\ne \frac{\beta +\alpha -1}{\beta -1}.$ Then the problem

$$\begin{aligned} \left\{ \begin{array}{l} \mathcal {D}^{\beta }\left( \mathcal {D}^{\alpha }+\lambda \right) u(t)=h(t), \quad t\in (1,T), \\ u(1)=0, \\ u(T)+\lambda I^{\alpha }u(T)=0, \\ \mathcal {D}^{\alpha }u(\xi )+\lambda u(\xi )=0,\quad \ \xi \in ]1,T], \end{array} \right. \end{aligned}$$

(2.1)

is equivalent to the integral equation

$$\begin{aligned} u(t)+\lambda I^{\alpha }u(t)=I^{\alpha +\beta }h(t)+\mu (t)I^{\beta }h(\xi )+\nu (t)I^{\alpha +\beta }h(T), \end{aligned}$$

(2.2)

where

$$\begin{aligned} \mu (t)=\frac{\Gamma (\beta )}{\Gamma (\beta +\alpha -1 )}\left[ \frac{\log (t/T)}{\left[ (\beta -1)\log T-(\beta +\alpha -1)\log \xi \right] }\right] \frac{( \log t)^{\beta +\alpha -2}}{ (\log \xi )^{\beta -2}}, \end{aligned}$$

and

$$\begin{aligned} \nu (t)=\frac{(\beta +\alpha -1)\log \xi -(\beta -1)\log t}{\left[ (\beta -1)\log T-(\beta +\alpha -1)\log \xi \right] }\left( \frac{\log t}{\log T} \right) ^{\beta +\alpha -2}. \end{aligned}$$

Proof

Applying the integrator operator $I^{\beta }$ to (2.1) and using the result of Lemma 2.4, we get

$$\begin{aligned} \left( \mathcal {D}^{\alpha }+\lambda \right) u(t)=c_{1}(\log t)^{\beta -1}+c_{2}(\log t)^{\beta -2}+I^{\beta }h(t), \ t\in (1,T]. \end{aligned}$$

(2.3)

We apply again the operator $I^{\alpha }$ and use the results of Lemmas 2.3 and 2.4, to get the general solution representation of problem (2.1)

$$\begin{aligned} u(t)= & {} I^{\alpha +\beta }h(t)-\lambda I^{\alpha }u(t)+c_{0}(\log t)^{\alpha -1} \nonumber \\&+\frac{c_{1}\Gamma (\beta )}{\Gamma (\beta +\alpha )}\left( \log t\right) ^{\beta +\alpha -1}+\frac{c_{2}\Gamma (\beta -1)}{\Gamma (\beta +\alpha -1)} \left( \log t\right) ^{\beta +\alpha -2}, \end{aligned}$$

(2.4)

where $c_{0},c_{1},c_{2}\in \mathbb {R}.$ By using the boundary conditions in problem (2.1) and the above equation, we observe that $c_{0}=0,$ and

$$\begin{aligned} \frac{c_{1}\Gamma (\beta )}{\Gamma (\beta +\alpha )}\left( \log T\right) ^{\beta +\alpha -1}+\frac{c_{2}\Gamma (\beta -1)}{\Gamma (\beta +\alpha -1)} \left( \log T\right) ^{\beta +\alpha -2}+I^{\alpha +\beta }h(T)=0. \end{aligned}$$

Moreover, we obtain

$$\begin{aligned} c_{1}(\log \xi )^{\beta -1}+c_{2}(\log \xi )^{\beta -2}+I^{\beta }h(\xi )=0. \end{aligned}$$

Solving the last two equations in $c_{1}$ and $c_{2},$ we end up with

$$\begin{aligned} c_{1}=\frac{(\beta +\alpha -1)\Gamma (\beta -1)\left( \log T\right) ^{\beta +\alpha -2}I^{\beta }h(\xi )-\Gamma (\beta +\alpha )(\log \xi )^{\beta -2}I^{\alpha +\beta }h(T)}{\Gamma (\beta -1)\left( \log T\right) ^{\beta +\alpha -2}(\log \xi )^{\beta -2}\left[ (\beta -1)\log T-(\beta +\alpha -1)\log \xi \right] }, \end{aligned}$$

and

$$\begin{aligned} c_{2}=\frac{\Gamma (\beta )\left( \log T\right) ^{\beta +\alpha -1}I^{\beta }h(\xi )-\Gamma (\beta +\alpha )(\log \xi )^{\beta -1}I^{\alpha +\beta }h(T) }{\Gamma (\beta -1)\left( \log T\right) ^{\beta +\alpha -2}(\log \xi )^{\beta -2}\left[ (\beta +\alpha -1)\log \xi -(\beta -1)\log T\right] }. \end{aligned}$$

Substituting $c_{1}$ and $c_{2}$ in (2.4), we get the desired solution representation (2.2). Besides and by the help of the results in Lemmas 2.3 and , one can easily figure out that Eq. (2.2) solves problem (2.1). This finishes the proof.$\square$

We will need the following properties for the functions $\mu$ and $\nu$ defined in Lemma 2.5.

Lemma 2.6

The functions $\mu$ and $\nu$ are continuous functions on J and satisfy the following properties:

• (1) $\mu _{\max }=\underset{1\le t\le T}{\max }\left| \mu (t)\right| =\frac{\Gamma (\beta )}{\Gamma (\beta +\alpha )}\frac{\left( \log T\right) ^{\beta +\alpha }}{(\log \xi )^{\beta -2}}\left| \frac{1 }{(\beta -1)\log T-(\beta +\alpha -1)\log \xi }\right| ,$

• (2) $\nu _{\max }=\underset{1\le t\le T}{\max }\left| \nu (t)\right| =\frac{(\beta +\alpha -1)\log \xi }{\left| (\beta -1)\log T-(\beta +\alpha -1)\log \xi \right| },$

• (3) $\mathcal {D}^{\gamma }\mu (t)=\frac{\Gamma (\beta )}{\Gamma (\beta +\alpha -\gamma )}\left[ \frac{(\beta +\alpha -1)\log t-(\beta +\alpha -\gamma -1)\log T}{(\beta -1)\log T-(\beta +\alpha -1)\log \xi }\right] \frac{\left( \log t\right) ^{\beta +\alpha -\gamma -2}}{(\log \xi )^{\beta -2}},$

• (4) $\mu _{\max }^{\gamma }=\underset{1\le t\le T}{\max }\left| \mathcal {D}^{\gamma }\mu (t)\right| =\frac{\Gamma (\beta )}{\Gamma (\beta +\alpha -\gamma )} \frac{\left( \log T\right) ^{\beta +\alpha -\gamma -1}}{(\log \xi )^{\beta -2}}\left| \frac{\gamma }{(\beta -1)\log T-(\beta +\alpha -1)\log \xi }\right| ,$

• (5) $\mathcal {D}^{\gamma }\nu (t)=\frac{\Gamma (\beta +\alpha )}{\Gamma (\beta +\alpha -\gamma )}\left[ \frac{(\beta +\alpha -\gamma -1)\log \xi -(\beta -1)\log t}{(\beta -1)\log T-(\beta +\alpha -1)\log \xi }\right] \frac{\left( \log t\right) ^{\beta +\alpha -\gamma -2}}{\left( \log T\right) ^{\beta +\alpha -2}},$

• (6) $\nu _{\max }^{\gamma }=\underset{1\le t\le T}{\max }\left| \mathcal {D}^{\gamma }\nu (t)\right| =\frac{\Gamma (\beta +\alpha )}{\Gamma (\beta +\alpha -\gamma )}\frac{1}{\left( \log T\right) ^{\gamma }}\left| \frac{(\beta +\alpha -\gamma -1)\log \xi }{(\beta -1)\log T-(\beta +\alpha -1)\log \xi } \right| .$

The proofs of the above statements are straightforward and can be achieved via simple computations.

3 Existence and uniqueness results

Let $\mathcal {C}:=C([1,T],\mathbb {R})$ be a Banach space of all continuous functions defined on [1, T] endowed with the usual supremum norm. Let

$$\begin{aligned} F=\{u:u\in \mathcal {C},\ D^{\gamma }u\in \mathcal {C}\}. \end{aligned}$$

Then F is a Banach space equipped with the norm

$$\begin{aligned} \left\| u\right\| _{F} =\max \left\{ \sup _{1\le t\le T}\left| u(t)\right| ,\sup _{1\le t\le T}\left| \mathcal {D}^{\gamma }u(t)\right| \right\} . \end{aligned}$$

By virtue of Lemma 2.5, we may define the operator $\Psi$ by

$$\begin{aligned} \Psi u(t)= & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) } \int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}f(s,u(s),\mathcal {D}^{\gamma }u(s))\frac{\mathrm{{d}}s}{s}\\&-\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s} \right) ^{\alpha -1}\frac{u(s)}{s}\mathrm{{d}}s \\&+\dfrac{\mu (t)}{\Gamma \left( \beta \right) }\int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}f(s,u(s),\mathcal {D}^{\gamma }u(s))\frac{\mathrm{{d}}s}{s} \\&+\dfrac{\upsilon (t)}{\Gamma \left( \alpha +\beta \right) } \int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}f(s,u(s),\mathcal {D}^{\gamma }u(s))\frac{\mathrm{{d}}s}{s}. \end{aligned}$$

It can be easily shown that

$$\begin{aligned} \mathcal {D}^{\gamma }\left( \Psi u(t)\right)= & {} \dfrac{1}{\Gamma \left( \alpha +\beta -\gamma \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -\gamma -1}f(s,u(s),\mathcal {D}^{\gamma }u(s))\frac{\mathrm{{d}}s}{s} \\&-\frac{\lambda }{\Gamma (\alpha -\gamma )}\int _{1}^{t}\left( \log \frac{t}{ s}\right) ^{\alpha -\gamma -1}\frac{u(s)}{s}\mathrm{{d}}s\\&+\dfrac{\mathcal {D}^{\gamma }\mu (t)}{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}f(s,u(s),\mathcal {D}^{\gamma }u(s))\frac{\mathrm{{d}}s}{s} \\&+\dfrac{\mathcal {D}^{\gamma }\upsilon (t)}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}f(s,u(s),\mathcal {D}^{\gamma }u(s))\frac{\mathrm{{d}}s}{s}, \end{aligned}$$

where $\mathcal {D}^{\gamma }\mu (t),$ and $\mathcal {D}^{\gamma }\nu (t)$ are described in Lemma 2.6. The continuity of the functional f would imply the continuity of $\Psi u(t)$ and $\mathcal {D}^{\gamma }\left( \Psi u(t)\right)$, for each $t\in J.$ Hence the operator $\Psi$ maps the Banach space F into itself.

In what follows, we employ fixed point theorems to prove the main results of this paper. For more details about fixed point theorems and functional analysis, the reader may refer to the book of Smart [24]. Throughout the remaining part of this paper, we assume that the following conditions hold.

• (H1) There exists a constant $L>0$ such that

  $$\begin{aligned} \left| f(t,u,v)\right| \le L,\quad \text { for any }t\in \left[ 1,T\right] ,\;\text { }u,v\in \mathbb {R}. \end{aligned}$$

• (H2) There exists a constant $N>0,$$M>0$ such that

  $$\begin{aligned} \left| f(t,u_{1},v_{1})-f(t,u_{2},v_{2})\right| \le N\left| u_{1}-u_{2}\right| +M\left| v_{1}-v_{2}\right| , \end{aligned}$$

  for any $t\in \left[ 1,T\right] ,$$u_{1},v_{1},u_{2},v_{2}\in \mathbb {R}$, and let $d=\underset{1\le t\le T}{\max }\left| f(t,0,0)\right| .$

Lemma 3.1

Let (H1) hold. Then $\Psi :F\rightarrow F$ is completely continuous operator.

Proof

We first show that $\Psi :F\rightarrow F$ is uniformly bounded: For any bounded set $U\subset F$, there exists $r>0$ such that $U=\left\{ u\in F,\left\| u\right\| \le r\right\} .$ Then for any $u\in U,$ we obtain

$$\begin{aligned} \left| \Psi u(t)\right|\le & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),D^{\gamma }u(s))\right| \frac{\mathrm{{d}}s}{s} \\&+\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s} \right) ^{\alpha -1}\left| u(s)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left| f(s,u(s),D^{\gamma }u(s))\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),D^{\gamma }u(s))\right| \frac{\mathrm{{d}}s}{s}. \end{aligned}$$

By using (H1), we get

$$\begin{aligned} \left| \Psi u(t)\right| \le \dfrac{L\left( \log t\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }+\frac{\lambda \left\| u\right\| \left( \log t\right) ^{\alpha }}{\Gamma (\alpha +1)} +\dfrac{\mu _{\max }L\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }+\dfrac{\upsilon _{\max }L\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned}&\left| \mathcal {D}^{\gamma }\left( \Psi u(t)\right) \right| \le \dfrac{ L\left( \log t\right) ^{\alpha +\beta -\gamma }}{\Gamma \left( \alpha +\beta -\gamma +1\right) }+\frac{\lambda \left\| u\right\| \left( \log t\right) ^{\alpha -\gamma }}{\Gamma (\alpha -\gamma +1)}\\&\quad +\dfrac{\mu _{\max }^{\gamma }L\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }+\dfrac{\upsilon _{\max }^{\gamma }L\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }. \end{aligned}$$

Hence, we get

$$\begin{aligned} \left\| \Psi u\right\|\le & {} L\left( \log T\right) ^{\alpha +\beta -\gamma }\max \left( \dfrac{\left( \log T\right) ^{\gamma }}{\Gamma \left( \alpha +\beta +1\right) },\dfrac{1}{\Gamma \left( \alpha +\beta -\gamma +1\right) }\right) \\&+\dfrac{L\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) } \max \left( \mu _{\max },\mu _{\max }^{\gamma }\right) +\dfrac{L\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\max \left( \upsilon _{\max },\upsilon _{\max }^{\gamma }\right) \\&+\lambda \left( \log T\right) ^{\alpha -\gamma }\max \left( \frac{1}{ \Gamma (\alpha -\gamma +1)},\frac{\left( \log T\right) ^{\gamma }}{\Gamma (\alpha +1)}\right) r, \end{aligned}$$

which implies that $\Psi (U)$ is uniformly bounded.

Next, we show that $\Psi :F\rightarrow F$ is equicontinuous: for any $t_{1},$$t_{2}$$\in \left[ 1,T\right] ,$$1\le t_{1}<t_{2}\le T$ and $u\in U,$ we deduce

$$\begin{aligned} \left| \left( \Psi u\right) (t_{2})-\left( \Psi u\right) (t_{1})\right|\le & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t_{1}}\left[ \left( \log \frac{t_{2}}{s}\right) ^{\alpha +\beta -1}\right. \\&\left. -\left( \log \frac{ t_{1}}{s}\right) ^{\alpha +\beta -1}\right] \left| f(s,u(s),\mathcal {D}^{\gamma }u(s))\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{t_{1}}^{t_{2}}\left( \log \frac{t_{2}}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))\right| \frac{\mathrm{{d}}s}{s} \\&+\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t_{1}}\left[ \left( \log \frac{ t_{2}}{s}\right) ^{\alpha -1}-\left( \log \frac{t_{1}}{s}\right) ^{\alpha -1} \right] \frac{\left| u(s)\right| }{s}\mathrm{{d}}s\\&+\frac{\lambda }{\Gamma (\alpha )}\int _{t_{1}}^{t_{2}}\left( \log \frac{ t_{2}}{s}\right) ^{\alpha -1}\frac{\left| u(s)\right| }{s}\mathrm{{d}}s \\&+\dfrac{\left| \mu (t_{2})-\mu (t_{1})\right| }{\Gamma \left( \beta \right) }\int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))\right| \mathrm{{d}}s \\&+\dfrac{\left| \upsilon (t_{2})-\upsilon (t_{1})\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))\right| \mathrm{{d}}s. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \left| \left( \Psi u\right) (t_{1})-\left( \Psi u\right) (t_{2})\right|\le & {} \dfrac{L}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t_{1}}\left[ \left( \log \frac{t_{2}}{s}\right) ^{\alpha +\beta -1}-\left( \log \frac{ t_{1}}{s}\right) ^{\alpha +\beta -1}\right] \frac{\mathrm{{d}}s}{s} \\&+\dfrac{L}{\Gamma \left( \alpha +\beta \right) }\int _{t_{1}}^{t_{2}}\left( \log \frac{t_{2}}{s}\right) ^{\alpha +\beta -1}\frac{\mathrm{{d}}s}{s} \\&+\frac{\lambda \left\| u\right\| }{\Gamma (\alpha )}\int _{1}^{t_{1}} \left[ \left( \log \frac{t_{2}}{s}\right) ^{\alpha -1}-\left( \log \frac{ t_{1}}{s}\right) ^{\alpha -1}\right] \frac{\mathrm{{d}}s}{s} \\&+\frac{\lambda \left\| u\right\| }{\Gamma (\alpha )} \int _{t_{1}}^{t_{2}}\left( \log \frac{t_{2}}{s}\right) ^{\alpha -1}\frac{\mathrm{{d}}s}{ s} \\&+\dfrac{L\left| \mu (t_{2})-\mu (t_{1})\right| }{\Gamma \left( \beta \right) }\int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1} \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t_{2})-\upsilon (t_{1})\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\frac{\mathrm{{d}}s}{s} \\\le & {} \dfrac{L}{\Gamma \left( \alpha +\beta +1\right) }\left[ \left( \log t_{2}\right) ^{\alpha +\beta }-\left( \log t_{1}\right) ^{\alpha +\beta }+2\left( \log \frac{t_{2}}{t_{1}}\right) ^{\alpha +\beta }\right] \\&+\frac{\lambda r}{\Gamma (\alpha +1)}\left[ \left( \log t_{2}\right) ^{\alpha +\beta }-\left( \log t_{1}\right) ^{\alpha +\beta }+2\left( \log \frac{t_{2}}{t_{1}}\right) ^{\alpha +\beta }\right] \\&+\dfrac{L\left| \mu (t_{2})-\mu (t_{1})\right| }{\Gamma \left( \beta +1\right) }\left( \log \xi \right) ^{\beta }+\dfrac{\left| \upsilon (t_{2})-\upsilon (t_{1})\right| }{\Gamma \left( \alpha +\beta +1\right) }\left( \log T\right) ^{\alpha +\beta }. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \left| \mathcal {D}^{\gamma }\left( \Psi u(t_{2})\right) -\mathcal {D}^{\gamma }\left( \Psi u(t_{1})\right) \right|\le & {} \dfrac{L}{\Gamma \left( \alpha +\beta -\gamma +1 \right) }\left[ \left( \log t_{2}\right) ^{\alpha +\beta -\gamma }-\left( \log t_{1}\right) ^{\alpha +\beta -\gamma }\right. \\&\left. +2\left( \log \frac{t_{2}}{t_{1}}\right) ^{\alpha +\beta -\gamma }\right] \\&+\frac{\lambda r}{\Gamma (\alpha -\gamma +1)}\left[ \left( \log t_{2}\right) ^{\alpha -\gamma }-\left( \log t_{1}\right) ^{\alpha -\gamma }+2\left( \log \frac{t_{2}}{t_{1}}\right) ^{\alpha -\gamma }\right] \\&+\dfrac{L\left| \mathcal {D}^{\gamma }\mu (t_{2})-\mathcal {D}^{\gamma }\mu (t_{1})\right| }{\Gamma \left( \beta +1\right) }\left( \log \xi \right) ^{\beta }\\&+\dfrac{\left| \mathcal {D}^{\gamma }\upsilon (t_{2}) -\mathcal {D}^{\gamma }\upsilon (t_{1})\right| }{\Gamma \left( \alpha +\beta +1\right) }\left( \log T\right) ^{\alpha +\beta }. \end{aligned}$$

From Lemma 2.6, we conclude that $\left| \mu (t_{2})-\mu (t_{1})\right| ,$ and $\left| \upsilon (t_{2})-\upsilon (t_{1})\right|$ converge to 0, as $\left| t_{2}-t_{1}\right| \rightarrow 0.$ In similar manner, $\left| \mathcal {D}^{\gamma }\mu (t_{2})-\mathcal {D}^{\gamma }\mu (t_{1})\right| \rightarrow 0,$ and $\left| \mathcal {D}^{\gamma }\upsilon (t_{2})-\mathcal {D}^{\gamma }\upsilon (t_{1})\right| \rightarrow 0$ as $\left| t_{2}-t_{1}\right| \rightarrow 0.$ Hence $\left| \left( \Psi u\right) (t_{1})-\left( \Psi u\right) (t_{2})\right|$ and $\left| \mathcal {D}^{\gamma }\left( \Psi u(t_{2})\right) -\mathcal {D}^{\gamma }\left( \Psi u(t_{1})\right) \right|$ converge to 0 as $\left| t_{2}-t_{1}\right| \rightarrow 0,$ which implies that $\Psi (U)$ is equicontinuous. Thus by the Arzela–Ascoli theorem $\Psi :F\rightarrow F$ is completely continuous. The proof is completed. $\square$

Theorem 3.2

Let ($\hbox {H}_{{1}}$) hold. If

$$\begin{aligned} \varkappa =\lambda \left( \log T\right) ^{\alpha -\gamma }\max \left( \frac{1 }{\Gamma (\alpha -\gamma +1)},\; \frac{\left( \log T\right) ^{\gamma }}{\Gamma (\alpha +1)}\right) <1, \end{aligned}$$

then problem (1.1) has at least one solution.

Proof

Lemma 3.1, we proved that the operator $\Psi :F\rightarrow F$ is completely continuous by . It remains to use Schaefer’s fixed point theorem to prove that the set

$$\begin{aligned} \Omega =\left\{ u\in F:u=\zeta \Psi u,\zeta \in [0,1]\right\} , \end{aligned}$$

is bounded. Let $u\in F$ and $t\in \left[ 1,T\right]$ such that $u(t)=\zeta \Psi u(t),$ for some $\zeta \in [0,1].$ We deduce as in the proof of Lemma 3.1 that

$$\begin{aligned} \left\| u\right\|= & {} \left\| \zeta \Psi u\right\| \le \left\| \Psi u\right\| \\\le & {} L\left( \log T\right) ^{\alpha +\beta -\gamma }\max \left( \dfrac{ \left( \log T\right) ^{\gamma }}{\Gamma \left( \alpha +\beta +1\right) }, \dfrac{1}{\Gamma \left( \alpha +\beta -\gamma +1\right) }\right) \\&+\dfrac{L\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) } \max \left( \mu _{\max },\mu _{\max }^{\gamma }\right) +\dfrac{L\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\max \left( \upsilon _{\max },\upsilon _{\max }^{\gamma }\right) \\&+\lambda \left( \log T\right) ^{\alpha -\gamma }\max \left( \frac{1}{ \Gamma (\alpha -\gamma +1)},\frac{\left( \log T\right) ^{\gamma }}{\Gamma (\alpha +1)}\right) \left\| u\right\| . \end{aligned}$$

It follows that

$$\begin{aligned} \left\| u\right\| \le \omega +\varkappa \left\| u\right\| , \end{aligned}$$

where

$$\begin{aligned} \omega= & {} L\left( \log T\right) ^{\alpha +\beta -\gamma }\max \left( \dfrac{\left( \log T\right) ^{\gamma }}{\Gamma \left( \alpha +\beta +1\right) },\dfrac{1}{\Gamma \left( \alpha +\beta -\gamma +1\right) }\right) \\&+ \dfrac{L\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) } \max \left( \mu _{\max },\mu _{\max }^{\gamma }\right) +\dfrac{L\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\max \left( \upsilon _{\max },\upsilon _{\max }^{\gamma }\right) . \end{aligned}$$

Hence, we get

$$\begin{aligned} \left\| u\right\| \le \frac{\omega }{1-\varkappa }, \end{aligned}$$

which means that $\Omega$ is bounded set in F. Therefore, by the Schaefer’s fixed point theorem, we conclude that problem (1.1) has at least one solution in F. The proof is completed.$\square$

For the sake of convenience, we set

$$\begin{aligned} \varrho _{1}= & {} \dfrac{\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }+\dfrac{\mu _{\max }\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }+\dfrac{\upsilon _{\max }\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) },\\ \varrho _{2}= & {} \dfrac{\left( \log T\right) ^{\alpha +\beta -\gamma }}{\Gamma \left( \alpha +\beta -\gamma +1\right) }+\dfrac{\mu _{\max }^{\gamma }\left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }+\dfrac{\upsilon _{\max }^{\gamma }\left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }. \end{aligned}$$

Theorem 3.3

Let (H2) hold. If

$$\begin{aligned} \varrho =\max \left\{ N\varrho _{1}+\frac{\lambda \left( \log T\right) ^{\alpha }}{\Gamma (\alpha +1)},M\varrho _{1},N\varrho _{2}+\frac{\lambda \left( \log T\right) ^{\alpha -\gamma }}{\Gamma (\alpha -\gamma +1)} ,M\varrho _{2}\right\} <1, \end{aligned}$$

then problem (1.1) has a unique solution in F.

Proof

By (H2), for any $u,v\in F$ and $t\in \left[ 1,T\right] ,$ we conclude that

$$\begin{aligned} \left| \left( \Psi u\right) (t)-\left( \Psi v\right) (t)\right|\le & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))\right. \\&\left. -f(s,v(s), \mathcal {D}^{\gamma }v(s))\right| \frac{\mathrm{{d}}s}{s} \\&+\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s} \right) ^{\alpha -1}\left| u(s)-v(s)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))-f(s,v(s),\mathcal {D}^{\gamma }v(s))\right| \frac{\mathrm{{d}}s}{s}\\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))\right. \\&\left. -f(s,v(s),\mathcal {D}^{\gamma }v(s))\right| \frac{\mathrm{{d}}s}{s}\\\le & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left( N\left| u(s)-v(s)\right| +M\left| \mathcal {D}^{\gamma }u(s)\right. \right. \\&\left. \left. -\mathcal {D}^{\gamma }v(s))\right| \right) \frac{\mathrm{{d}}s}{s} +\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha -1}\left| u(s)-v(s)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left( N\left| u(s)-v(s)\right| \right. \\&\left. +M\left| \mathcal {D}^{\gamma }u(s)-\mathcal {D}^{\gamma }v(s))\right| \right) \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left( N\left| u(s)-v(s)\right| +M\left| \mathcal {D}^{\gamma }u(s)\right. \right. \\&\left. \left. -\mathcal {D}^{\gamma }v(s))\right| \right) \frac{\mathrm{{d}}s}{s} \\\le & {} \left( \dfrac{N\left( \log t\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }+\frac{\lambda \left( \log t\right) ^{\alpha }}{ \Gamma (\alpha +1)}\right. \\&\left. +\dfrac{N\left| \mu (t)\right| \left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }+\dfrac{N\left| \upsilon (t)\right| \left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\right) \\&\times \sup _{1\le s\le T}\left| u(s)-v(s)\right| \\&+M\left( \dfrac{\left( \log t\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }+\dfrac{\left| \mu (t)\right| \left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }+\dfrac{\left| \upsilon (t)\right| \left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\right) \\&\times \sup _{1\le s\le T}\left| \mathcal {D}^{\gamma }u(s)-\mathcal {D}^{\gamma }v(s)\right| . \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \left| \mathcal {D}^{\gamma }\left( \Psi u\right) (t)-\mathcal {D}^{\gamma }\left( \Psi v\right) (t)\right|\le & {} \left( \dfrac{N\left( \log t\right) ^{\alpha +\beta -\gamma }}{\Gamma \left( \alpha +\beta -\gamma +1\right) }+\frac{\lambda \left( \log t\right) ^{\alpha -\gamma }}{\Gamma (\alpha -\gamma +1)}+\dfrac{N\left| \mathcal {D}^{\gamma }\mu (t)\right| \left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }\right. \\&\left. +\dfrac{N\left| \mathcal {D}^{\gamma }\upsilon (t)\right| \left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\right) \sup _{1\le s\le T}\left| u(s)-v(s)\right| \\&+M\left( \dfrac{\left( \log t\right) ^{\alpha +\beta -\gamma }}{\Gamma \left( \alpha +\beta -\gamma +1\right) }+\dfrac{\left| \mathcal {D}^{\gamma }\mu (t)\right| \left( \log \xi \right) ^{\beta }}{\Gamma \left( \beta +1\right) }\right. \\&\left. +\dfrac{\left| \mathcal {D}^{\gamma }\upsilon (t)\right| \left( \log T\right) ^{\alpha +\beta }}{\Gamma \left( \alpha +\beta +1\right) }\right) \\&\times \sup _{1\le s\le T}\left| \mathcal {D}^{\gamma }u(s)-\mathcal {D}^{\gamma }v(s)\right| . \end{aligned}$$

Taking the supremum of the last two estimates, and then the maximum of the four components, we deduce that

$$\begin{aligned} \left\| \Psi u-\Psi v\right\| \le \varrho \left\| u-v\right\| . \end{aligned}$$

Since $\varrho <1,$ then $\Psi$ is a contraction on F. It follows from the Banach contraction mapping theorem that $\Psi$ has a unique fixed point in F. The proof is completed.$\square$

Consider again the set $U=\left\{ u\in F:\left\| u\right\| \le r\right\} ,$ for some $r>0,$ then U is a closed ball in the Banach space F, hence it is also a Banach space. The restriction of $\Psi$ on U is still a contraction by Theorem 3.3. Then, the BVP (1.1) has a unique solution in U if $\Psi (U)\subseteq U.$

Theorem 3.4

Let $(H_{2})$ hold. If

$$\begin{aligned} \varrho =\max \left\{ N\varrho _{1}+\frac{\lambda \left( \log T\right) ^{\alpha }}{\Gamma (\alpha +1)},M\varrho _{1},N\varrho _{2}+\frac{\lambda \left( \log T\right) ^{\alpha -\gamma }}{\Gamma (\alpha -\gamma +1)} ,M\varrho _{2}\right\} <1, \end{aligned}$$

then problem (1.1) has a unique solution in U.

Proof

By (H2), for any $u\in U$ and $t\in \left[ 1,T\right] ,$ we conclude that

$$\begin{aligned} \left| \left( \Psi u\right) (t)\right|\le & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))-f(s,0,0)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left| f(s,0,0)\right| \frac{\mathrm{{d}}s }{s} \\&+\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s} \right) ^{\alpha -1}\left| u(s)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))-f(s,0,0)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left| f(s,0,0)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left| f(s,u(s),\mathcal {D}^{\gamma }u(s))-f(s,0,0)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left| f(s,0,0)\right| \frac{\mathrm{{d}}s}{s}. \end{aligned}$$

It follows that

$$\begin{aligned} \left| \left( \Psi u\right) (t)\right|\le & {} \dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left( N\left| u(s)\right| +M\left| \mathcal {D}^{\gamma }u(s))\right| \right) \frac{\mathrm{{d}}s}{s}\\&+\dfrac{1}{\Gamma \left( \alpha +\beta \right) }\int _{1}^{t}\left( \log \frac{t}{s}\right) ^{\alpha +\beta -1}\left| f(s,0,0)\right| \frac{\mathrm{{d}}s}{s}\\&+\frac{\lambda }{\Gamma (\alpha )}\int _{1}^{t}\left( \log \frac{t}{s} \right) ^{\alpha -1}\left| u(s)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left( N\left| u(s)\right| +M\left| \mathcal {D}^{\gamma }u(s))\right| \right) \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \mu (t)\right| }{\Gamma \left( \beta \right) } \int _{1}^{\xi }\left( \log \frac{\xi }{s}\right) ^{\beta -1}\left| f(s,0,0)\right| \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left( N\left| u(s)\right| +M\left| \mathcal {D}^{\gamma }u(s))\right| \right) \frac{\mathrm{{d}}s}{s} \\&+\dfrac{\left| \upsilon (t)\right| }{\Gamma \left( \alpha +\beta \right) }\int _{1}^{T}\left( \log \frac{T}{s}\right) ^{\alpha +\beta -1}\left| f(s,0,0)\right| \frac{\mathrm{{d}}s}{s}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \left| \left( \Psi u\right) (t)\right| \le \left( N\varrho _{1}+\frac{\lambda \left( \log t\right) ^{\alpha }}{ \Gamma (\alpha +1)}\right) \sup _{1\le s\le T}\left| u(s)\right| +M\varrho _{1}\sup _{1\le s\le T}\left| \mathcal {D}^{\gamma }u(s)\right| +d\varrho _{1}. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \left| \mathcal {D}^{\gamma }\left( \Psi u\right) (t)\right|\le & {} \left( N\varrho _{2}+\frac{\lambda \left( \log T\right) ^{\alpha -\gamma }}{\Gamma (\alpha -\gamma +1)}\right) \sup _{1\le s\le T}\left| u(s)\right| +M\varrho _{2}\sup _{1\le s\le T}\left| \mathcal {D}^{\gamma }u(s)\right| +d\varrho _{2}. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \left\| \Psi u\right\| \le \varrho r+d\max \{\varrho _{1},\varrho _{2}\}\le \varrho r+(1-\varrho )r=r, \end{aligned}$$

whenever $r>\frac{d\max \{\varrho _{1},\varrho _{2}\}}{1-\varrho }.$ This completes the proof.$\square$

4 An example

Consider the following Hadamard fractional Langevin equation:

$$\begin{aligned} \left\{ \begin{array}{l} \mathcal {D}^{1.5}\left( \mathcal {D}^{0.8}+\frac{1}{3}\right) u(t)=f(t,u(t),\mathcal {D}^{0.2}u(t)),\; t\in [1,e] \\ u(1)=0, \\ u(e)+\frac{1/3}{\Gamma (0.8)}\int _{1}^{e}\left( \log \frac{e}{s}\right) ^{-0.2}\frac{ u(s)}{s}\mathrm{{d}}s=0, \\ \mathcal {D}^{0.8 }u(2)+\frac{1}{3}u(2)=0, \end{array} \right. \end{aligned}$$

(4.1)

where $\beta =1.5$, $\alpha =0.8$ and $\lambda =\frac{1}{3}$. Let

$$\begin{aligned} f(t,u,v)=\frac{\log t}{2t}\frac{\left| u\right| }{2+\left| u\right| }+\frac{\left| v\right| }{10(1+t)^{2}(\left| v\right| +4)}. \end{aligned}$$

Using the given data, we observe that

$$\begin{aligned} \left| f(t,u,v)\right| \le \frac{21}{40}, \end{aligned}$$

and

$$\begin{aligned} \left| f(t,u_{1},v_{1})-f(t,u_{2},v_{2})\right| \le \frac{1}{4} \left| u_{1}-u_{2}\right| +\frac{1}{10}\left| v_{1}-v_{2}\right| , \end{aligned}$$

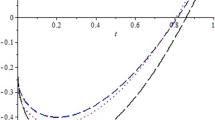
for any $t\in [1,e].$ Then f satisfies (H1) and (H2) with $L= \frac{21}{40},\ N=\frac{1}{4},$ and $M=\frac{1}{10}.$ Moreover, we find that $\varkappa \simeq 0.28<1.$ Hence, the conditions of Theorem 3.2 are satisfied; thus, we conclude that there exists at least one solution for problem (4.1) in [1, e].

On other hand, we find that $\mu _{\max }=1.6408,$$\nu _{\max }=4,$$\mu _{\max }^{\gamma }=0.86,$$\nu _{\max }^{\gamma }=3.7,$$\varrho _{1}=2.03,$ and $\varrho _{2}=2.127$. After simple computations, we get $\varrho =0.907<1.$ Therefore, all conditions of Theorem 3.3 are satisfied. Thus, problem (4.1) has a unique solution in [1, e].

5 Conclusion

The Langevin equation has been proposed to describe dynamical processes in a fractal medium in which the fractal and memory properties with a dissipative memory kernel are incorporated. However, it has been realized that the classical Langevin equation failed to describe the complex systems. Thus, the consideration of Langevin equation in frame of fractional derivatives becomes compulsory. As a result of this interest, several results have been revealed and different versions of Langevin equations have been under study. Following this trend, we considered different version of Langevin equation in frame of Hadamard derivative. We consider the main equation subject to fractional integral and derivative boundary conditions and within three different fractional orders. We claim that the results of this paper are new and have not been considered before. The main results are proved by the implementation of Schaefer’s fixed point theorem and Banach contraction principle. We present an example to demonstrate the consistency to the theoretical findings.