1 Introduction

The thermal cracking of rock is a very common phenomenon that occurs in both nature and engineering activities. Thermal cracking increases the fracture length, density and connectivity within a rock, which greatly improves its transport characteristics. In nuclear waste storage, the decay of nuclear waste produces heat and significantly increases the temperature of the surrounding rock. This temperature change results in the thermal cracking of rock, leading to radionuclide diffusion and groundwater pollution eventually. In oil development, thermal cracking increases the permeability of the reservoir and raises oil production. In the geothermal development of hot dry rock, rock contraction occurs when cold water is injected into the reservoir and influences the flow rate, outlet water temperature and heat recovery efficiency of the enhanced geothermal system (EGS).

In the past, extensive laboratory experiments have been conducted to study the thermomechanical behavior or thermal cracking of brittle material [1,2,3,4,5,6,7]. However, large expense and limitation in simple cases of such experiments led to an increased interest in using numerical methods to study thermal cracking [8,9,10,11]. For example, Fu et al. [12] and Tang et al. [13, 14] proposed a thermomechanical coupled model in a realistic failure process analysis system (RFPA) for simulating the thermal cracking of brittle material [15, 16]. Jiao et al. [17] proposed a thermomechanical coupled model in discontinuous deformation analysis method for simulating rock fracturing induced by thermal stress. Wanne and Young [18], Xia [19] and Andre et al. [20] simulated the thermal cracking of rock based on the bonded particle model (BPM). Nechnech et al. [21] presented an elastoplastic damage model for the thermomechanical analysis of concrete. Sun and Liew [22] studied the thermomechanical coupling fracture behavior of materials based on the cohesive segment model. Tenchev and Purnell [23] extended a damage constitutive model to account for the effect of high temperature on concrete.

The aforementioned numerical methods can be classified into two categories: methods based on continuous mechanics and approaches based on discontinuous mechanics. For the methods based on continuous mechanics, crack initiation, propagation and coalescence are difficult to handle, or the contact may be not explicitly considered. For the methods based on discontinuous mechanics, such as discrete element method, it is difficult to simulate the fracture of the block itself. Although it can simulate the fracture of the block through the Voronoi grain-based model [24], contact detection and contact force calculation are required for the adjacent Voronoi elements, which take a long time and cause huge calculation amount. For PFC—another method based on discontinuous mechanics, pores exist in the model despite the arrangement of spheres, which leads to nonintuitive characterization of cracks. The stress and strain in PFC are obtained indirectly by a measurement circle that is different from that in continuous mechanics. The values of the stress and strain in PFC are related to the radius of the measurement circle, and the physical meanings of stress and strain are not adequately clear. In addition, the microscopic parameters of PFC are difficult to calibrate. To overcome the drawbacks of the above methods, we attempt to construct a three-dimensional thermomechanical coupling model in the combined finite–discrete element method (FDEM) to simulate the thermal cracking of rock.

The FDEM [25,26,27] is very suitable for simulating the fracture and fragmentation of solids [28,29,30,31,32,33,34,35,36,37,38,39,40] with the following outstanding advantages: (1) the advantages of the discrete element method dealing with contact are absorbed, but the concepts of stress and strain in the continuum are also retained; (2) the initial modeling has no voids, and the crack surface consists of a series of triangular faces, which make the characterization of discontinuity (such as a crack or joint) very intuitive; (3) the contact detection and contact force calculation can be standardized because they are converted into the contact detection and contact force calculation between tetrahedral elements; (4) the input parameters of the FDEM are easier to determine than that of PFC; for example, the elastic modulus and Poisson’s ratio obtained from experiments can be directly used in the FDEM.

Therefore, if the thermomechanical coupling model can be constructed directly in this work, the defects of the existing numerical methods in simulating thermal cracking can be avoided, and the advantages of the FDEM for simulating cracking can be fully absorbed. However, the FDEM was only able to perform a purely mechanical calculation initially. Later, Yan et al. [41,42,43,44,45,46] developed several fully coupled hydromechanical models (FDEM-flow2D/3D) for simulating rock fracturing driven by fluid. Lei et al. [47] proposed a hydraulic solver to simulate fluid-driven cracks in FDEM. Ha et al. [48] modeled thermal–mechanical wellbore instability in shale formations using 2D FDEM, but the temperature field of the rock is only estimated by the analytical formula. Joulin et al. [49] presented a model based on FDEM for modeling the contact heat transfer between particles without considering thermal stress and thermal cracking.

To overcome the shortcomings of the above researches, we directly construct a three-dimensional thermomechanical coupling model (namely, FDEM-TM3D) in 3D FDEM, which considers thermal-induced deformation, stress, cracking and the evolution of the temperature field.

The paper is organized as follows: The fundamentals of the 3D FDEM are briefly introduced in Sect. 2. In Sect. 3, the three-dimensional heat conduction model, thermomechanical coupling model and the calculation procedure for the FDEM-TM3D model are presented in detail. In Sect. 4, two examples are given to verify the FDEM-TM3D model in terms of dealing with the problems of heat conduction and thermomechanical coupling. Furthermore, an example of thermal cracking is also provided in Sect. 4.

2 Fundamentals of three-dimensional combined finite–discrete element method

In 3D FDEM, the continuum is discretized into a finite element mesh (tetrahedral elements) and the six-node joint elements with zero initial thickness are inserted into the adjacent tetrahedral elements as shown in Fig. 1. Crack initiation, propagation and coalescence in the continuum can be simulated by the breaking of joint elements. The deformation of the continuum is represented by the constant strain tetrahedral element and the joint element with the bonding stress. Processing the contact between tetrahedral elements in FDEM is similar to the discrete element method (DEM), and the stress in the tetrahedral element is obtained using the finite element method (FEM). Although the meshing in FDEM is not necessarily consistent with reality, it provides convenience for cracking simulation without introducing the complex fracture mechanics theory to determine the direction and length of crack propagation. During the process of crack propagation, remeshing like the finite element method is unnecessary. Since the explicit method is used, there is no need to assemble an overall stiffness matrix and crack generation will not cause ill-conditioned solutions. In addition, for the internally adjacent tetrahedral elements connected by the unbroken joint elements, the contact detection and contact force calculation are avoided and the computational cost can be greatly reduced compared with the discrete element method. It should be noted that crack propagation has a certain degree of mesh dependence since cracks extend along the boundaries of the tetrahedral elements. However, as the mesh density increases, this mesh dependency gradually decreases [50, 51].

Fig. 1
figure 1

Connection between the tetrahedral elements and joint elements

Full size image

2.1 Governing equation of FDEM

The governing equation of the FDEM is as follows [27]

$$ {\mathbf{M\ddot{x}}} + {\mathbf{C\dot{x}}} = {\mathbf{f}}({\mathbf{x}}), $$
(1)

where \( {\mathbf{M}} \) is the mass diagonal matrix and \( {\mathbf{C}} \) is the damping diagonal matrix, which is used to consume the kinetic energy of the system since the quasi-static problems are solved using the dynamic relaxation method; \( {\mathbf{x}} \) is the nodal displacement vector; \( {\mathbf{f}}({\mathbf{x}}) \) represents the total nodal force vector, which includes the nodal force vector \( {\mathbf{F}}_{\text{c}} \) caused by contact force (Sect. 2.2), the nodal force vector \( {\mathbf{F}}_{\text{d}} \) caused by tetrahedral element deformation (Sect. 2.3), the nodal force vector \( {\mathbf{F}}_{\text{j}} \) caused by bonding stress of the joint element (Sect. 2.4), and the nodal force vector \( {\mathbf{F}}_{\text{e}} \) caused by the external load.

2.2 Contact force

Before the contact force calculation is completed, potential contact pairs are identified by the contact detection algorithm. In this work, the NBS algorithm [52] is used to find the potential contact pairs. The detection time of this algorithm is linear with the number of elements for the system having a similar element size. Later, Munjiza invented the MR contact detection algorithm [53], which has a high efficiency even for a system with a different element size. The detection time of the algorithm is also linear with the number of elements. After finding the contact pairs, the contact force can be calculated by a penalty function method [54]. The contact force in this work includes a normal contact force and tangential contact force.

As shown in Fig. 2, the contact pair contains two tetrahedral elements in contact. One of the tetrahedral elements is denoted as the contactor \( \beta_{\text{c}} \), and the other is the target \( \beta_{\text{t}} \) [27]. The normal contact force between the contact pairs is as follows [27]:

$$ \varvec{f} = \int\limits_{{V = \beta_{\text{t}} \cap \beta_{\text{c}} }} {p[{\mathbf{grad}}\varphi_{\text{c}} (P_{\text{c}} ) - {\mathbf{grad}}\varphi_{\text{t}} (P_{\text{t}} )]{\text{d}}V} . $$
(2)

where \( p \) is the normal penalty, \( P_{\text{t}} \) is a point of the target \( \beta_{\text{t}} \) in the overlapping zone \( V = \beta_{\text{t}} \cap \beta_{\text{c}} \), \( \varphi_{\text{t}} (P_{\text{t}} ) \) is the potential of the point \( P_{\text{t}} \) in the target \( \beta_{\text{t}} \), and \( \varphi_{\text{c}} (P_{\text{c}} ) \) is the potential of the point \( P_{\text{c}} \) in the contactor \( \beta_{\text{c}} \).

Fig. 2
figure 2

Contact force calculation in 3D FDEM

Full size image

According to the Gaussian formula, Eq. (2) can be rewritten as an integration over the outer surface of the overlapping zone [27]

$$ \varvec{f} = p\int\limits_{{S_{{\beta_{\text{t}} \cap \beta_{\text{c}} }} }} {\varvec{n}(\varphi_{\text{c}} (P_{\text{c}} ) - \varphi_{\text{t}} (P_{\text{t}} )){\text{d}}S} , $$
(3)

where \( \varvec{n} \) is the outer normal unit vector of the surface of the overlapping zone \( V \).

For contact forces between blocks with complex shapes, these blocks are discretized into tetrahedral elements as follows:

$$ \begin{aligned} \beta_{\text{c}} & = \beta_{{{\text{c}}_{1} }} \cup \beta_{{{\text{c}}_{2} }} \cdots \cup \beta_{{{\text{c}}_{i} }} \cdots \cup \beta_{{{\text{c}}_{n} }} \\ \beta_{\text{t}} & = \beta_{{{\text{t}}_{1} }} \cup \beta_{{{\text{t}}_{2} }} \cdots \cup \beta_{{{\text{t}}_{j} }} \cdots \cup \beta_{{{\text{t}}_{m} }} . \\ \end{aligned} $$
(4)

Thus, the total normal contact force between the blocks can be translated into the sum of the normal contact forces between a series of tetrahedral elements by using the following formula [27]:

$$ \varvec{f} = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {p\int\limits_{{S_{{\beta_{{{\text{c}}_{i} }} \cap \beta_{{{\text{t}}_{j} }} }} }} {\varvec{n}(\varphi_{{{\text{c}}_{i} }} - \varphi_{{{\text{t}}_{j} }} ){\text{d}}S} } } . $$
(5)

After obtaining the normal contact force \( \varvec{f} \) and its acting point, the tangential contact force is calculated according to the classical Coulomb friction:

$$ \varvec{f}_{\text{t}}^{t} = \varvec{f}_{\text{t}}^{t - \Delta t} - p_{\text{t}} \Delta {\mathbf{u}}_{s} S_{B} , $$
(6)

where \( \varvec{f}_{\text{t}}^{t} \) is the test value at the current time step, \( \varvec{f}_{\text{t}}^{t - \Delta t} \) is the tangential contact force at the previous time step, \( p_{\text{t}} \) is the tangential penalty and \( \Delta {\mathbf{u}}_{s} \) is the tangential relative displacement increment at the current time step, \( S_{B} \) is the area of the contact surface, which can be calculated according to Ref. [55].

If the test value \( \left| {\varvec{f}_{\text{t}}^{t} } \right| \le u\left| \varvec{f} \right| \) (\( u \) is friction coefficient) is calculated by Eq. (4), then

$$ \varvec{f}_{\text{t}} = \varvec{f}_{\text{t}}^{t} . $$
(7)

If the test value \( \left| {\varvec{f}_{\text{t}}^{t} } \right| > u\left| \varvec{f} \right| \) is calculated by Eq. (4), then

$$ \varvec{f}_{\text{t}} = \frac{{\varvec{f}_{\text{t}}^{t} }}{{\left| {\varvec{f}_{\text{t}}^{t} } \right|}}u\left| \varvec{f} \right|. $$
(8)

According to Eqs. (5) and (6), the tangential contact force is obtained.

2.3 Stress calculation of the tetrahedral element

The stress–strain relationship of the tetrahedral element satisfies [27]:

$$ {\mathbf{T}} = \frac{1}{{\left( {\left| {\det {\mathbf{F}}} \right|} \right)^{2/3} }}\left[ {\frac{E}{1 + v}{\mathbf{E}}_{d} + \frac{E}{1 - 2v}{\mathbf{E}}_{s} + 2\mu {\mathbf{D}}} \right], $$
(9)

where \( {\mathbf{T}} \) is the stress tensor, \( {\mathbf{F}} \) is the deformation gradient, \( E \) is the elastic modulus, \( v \) is Poisson’s ratio, \( {\mathbf{E}}_{d} \) is the shape-changing part of Green–St. Venant strain tensor, \( {\mathbf{E}}_{s} \) is volume-changing part of Green–St. Venant strain tensor, \( \mu \) is the damping coefficient, and \( {\mathbf{D}} \) is the strain rate tensor. The values of \( {\mathbf{F}} \), \( {\mathbf{E}}_{d} \), \( {\mathbf{E}}_{s} \) and \( {\mathbf{D}} \) can be calculated according to the initial and current coordinates, and the initial and current velocities of the four nodes of a tetrahedral element.

Since the tetrahedral element in this work is constant strain element, the equivalent nodal force of each surface caused by the deformation of the tetrahedral elements can be calculated by:

$$ {\mathbf{f}}^{(l)} = \frac{1}{3}{\mathbf{Tn}}^{(l)} S^{(l)} = \frac{1}{3}\left[ {\begin{array}{lll} {\sigma_{xx} } \hfill & {\sigma_{xy} } \hfill & {\sigma_{xz} } \hfill \\ {\sigma_{yx} } \hfill & {\sigma_{yy} } \hfill & {\sigma_{yz} } \hfill \\ {\sigma_{zx} } \hfill & {\sigma_{zy} } \hfill & {\sigma_{zz} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {n_{x}^{(l)} } \hfill \\ {n_{y}^{(l)} } \hfill \\ {n_{z}^{(l)} } \hfill \\ \end{array} } \right]S^{(l)} , $$
(10)

where \( l \) is the local number of the node in the tetrahedral element (\( l \) = 1, 2, 3, 4), \( {\mathbf{n}}^{(l)} \) is the outward normal unit vector of the triangular face opposite to node \( l \) of the tetrahedral element and \( S^{(l)} \) is area of the triangular face opposite to node \( l \) of the tetrahedral element, as shown in Fig. 3.

Fig. 3
figure 3

The number of nodes, triangular faces and their normal vectors of tetrahedral element

Full size image

2.4 Constitutive behavior of the joint element

Initially, the FDEM method can only be used to simulate two-dimensional cracking problems. Due to the contribution of Lei [56], who incorporated the 3D fracture model in Y code, FDEM can be used to simulate the three-dimensional cracking problems. Here, in the joint element, only a single integration point is used to calculate the cohesive constitutive law to improve the calculation efficiency. For more information on using more integration points to improve calculation accuracy of cohesive constitutive law, Ref. [56] is recommended.

As shown in Fig. 4, two triangular faces of the tetrahedral elements are connected by a joint element. Initially, the three vertices of the two triangular faces coincide with each other, which means \( P_{1} \) and \( P_{1}^{{\prime }} \), \( P_{2} \) and \( P_{2}^{{\prime }} \), \( P_{3} \) and \( P_{3}^{{\prime }} \) all coincide with each other. According to the relative displacements of the three vertices \( {\varvec{\updelta}}_{1} \), \( {\varvec{\updelta}}_{2} \) and \( {\varvec{\updelta}}_{3} \), the average normal opening and tangential slipping amount of the joint element are obtained by:

$$ \begin{aligned} o & = \frac{{({\varvec{\updelta}}_{1} + {\varvec{\updelta}}_{2} + {\varvec{\updelta}}_{3} ) \cdot {\mathbf{n}}}}{3} \\ s & = \frac{{({\varvec{\updelta}}_{1} + {\varvec{\updelta}}_{2} + {\varvec{\updelta}}_{3} ) \cdot {\mathbf{t}}}}{3}, \\ \end{aligned} $$
(11)

where \( {\mathbf{n}} \) and \( {\mathbf{t}} \) are the normal unit vector and tangential unit vector of the middle section, which consist of the three midpoints of the edges \( P_{1} P_{1}^{{\prime }} \), \( P_{2} P_{2}^{{\prime }} \) and \( P_{3} P_{3}^{{\prime }} \).

Fig. 4
figure 4

The opening and slipping amount of a joint element

Full size image

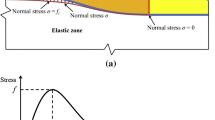
The normal opening amount and tangential slipping amount of the joint element determine the normal and tangential bonding stress of the joint element. The relationship between the opening displacement and the bonding stress is shown in Fig. 5.

Fig. 5
figure 5

The constitutive model of the joint element [51, 57]: a the relationship between the normal bonding stress and normal opening amount; b the relationship between the tangential bonding stress and tangential slipping amount of the joint element; and c the relationship between the failure type and opening displacement (where GfI and GfII are the energy release rates at Mode I and Mode II, \( o_{p} \) is the critical normal opening value and \( s_{p} \) is critical tangential slip value, \( p_{n} \) and \( p{}_{s} \) are the normal and tangential penalty parameters of the joint element, respectively). (Color figure online)

Full size image

As shown in Fig. 5a, when the normal opening amount o of the two triangular surfaces connected by the joint element reaches the critical value op (o < op, joint element is in elastic state), the normal bonding stress of the joint element is exactly equal to the tensile strength ft. If the normal opening amount o continues to increase, the normal bonding stress σ gradually reduces until the normal opening amount o reaches the maximum value or. At this time, the normal bonding stress σ is zero, i.e., the joint element breaks, and a Mode I crack is generated.

As shown in Fig. 5b, when the tangential slip s of the two triangular surfaces connected by the joint element reaches the critical value sp (s < sp, joint element is in elastic state), the tangential bonding stress of the joint element is exactly equal to the shear strength fs. If the tangential slip amount s continues to increase (joint element is in yield state), the tangential bonding stress decreases gradually until the tangential slip amount s reaches the maximum value sr. At this moment, the tangential bonding stress is zero, i.e., the joint element breaks, and a Mode II crack is generated. The shear strength \( f_{s} \) is determined according to the Mohr–Coulomb criterion, which is given by:

$$ f_{s} = c - \sigma \tan \phi , $$
(12)

where \( c \) is the cohesion of the joint element, \( \sigma \) is the normal bonding stress of the joint element, where a negative sign is in front of it because the provisions of the compressive stress for \( \sigma \) are negative, and \( \phi \) is the internal friction angle. Although the residual shear strength does not exist in the joint element, it has been considered in the tangential contact force between the two tetrahedral elements connected by the joint element, which is shown in Sect. 2.2.

Additionally, in Mode I–II, the two surfaces connected by the joint element are both in the open and slip states, but the normal opening and tangential slipping amounts are both smaller than or and sr. However, if \( \left( {\frac{{o - o_{p} }}{{o_{r} - o_{p} }}} \right)^{2} + \left( {\frac{{s - s_{p} }}{{s_{r} - s_{p} }}} \right)^{2} < 1\& \& (o > o_{p} \& \& s > s_{p} ) \), the joint element is in yielding state at this point, located in the yellow zone in Fig. 5c; if \( \left( {\frac{{o - o_{p} }}{{o_{r} - o_{p} }}} \right)^{2} + \left( {\frac{{s - s_{p} }}{{s_{r} - s_{p} }}} \right)^{2} \ge 1 \), when (o,s) is located in magenta zone of Fig. 5c, the joint element is broken and a Mode I–II crack is generated and the tensile-shear mixed failure occurs. It should be noted that the joint element with (o, s) at the left zone (o < op, sp < s < sr) is under shear yielding state (Mode I); the joint element with (o, s) at the bottom zone (s < sp, op < o < or) is tensile yield (Mode II).

The above discussion demonstrates that if the joint element yields, there is still a bonding stress acted on the two triangular faces, which are connected by the joint element. If the joint element breaks, no bonding stress acts on the two triangular faces connected by the joint element and a crack is generated.

2.5 Time integration

The contact force, action force caused by the deformation of tetrahedral element, bonding force of the joint element in Sects. 2.2–2.4, and external load are assigned to the element nodes to obtain the total nodal force vector. Then, according to Eq. (1) and the central difference integral strategy, the nodal velocity and coordinate can be updated by:

$$ \begin{aligned} v_{i}^{(t + \Delta t)} & = v_{i}^{(t)} + \sum {F_{i}^{(t)} \frac{\Delta t}{{m_{n} }}} \\ x_{i}^{(t + \Delta t)} & = x_{i}^{(t)} + v_{i}^{(t)} \Delta t, \\ \end{aligned} $$
(13)

where \( F_{i}^{(t)} \) is the total nodal force, \( \Delta t \) is the time step size and \( m_{n} \) is the nodal mass that is equal to one quarter of the mass of the tetrahedral element.

3 FDEM-TM3D model for thermal cracking

3.1 The basic concepts and assumptions of the thermomechanical coupling model

Rock expansion or shrinkage occurs when the temperature of the rock mass increases or decreases. If this shrinkage or expansion deformation is restrained, the thermal stress is produced in the rock, which means the temperature change makes the change of stress field. In turn, some mechanical energy may be transformed into heat when the external force acts on rock. However, since the loading and unloading rates for the quasi-static problem in rock mechanics are usually very slow, the heat produced has a very limited influence on the temperature field of the rock. Therefore, for the 3D thermomechanical coupling model used in this paper, the effects of the stress field on the temperature field have been neglected, while only the effect of the temperature field on the stress field is considered.

The entire thermomechanical coupling calculation is divided into two parts: (1) during the thermal cracking, the evolution of the temperature field is calculated, and (2) the temperature stress applied to the FDEM model is calculated and the mechanical calculation considering fracturing is performed. According to the two parts, the model can be applied to simulate the thermal cracking of the rock.

3.2 Heat conduction model

According to Fourier’s law, the heat flow along the i-direction can be expressed as:

$$ q_{i} = - k_{ij} \frac{\partial T}{{\partial x_{j} }}, $$
(14)

where \( k_{ij} \) is the thermal conductivity and T is the temperature.

For any given mass M, the temperature change is given by:

$$ \frac{\partial T}{\partial t} = \frac{{Q_{\text{total}} }}{{C_{p} M}}, $$
(15)

where \( Q_{\text{total}} \) is the net heat flow into the mass \( M \) per unit time and \( C_{p} \) is the specific heat.

A heat conduction model based on the unique connection between tetrahedral elements and joint elements is built as shown in Fig. 6. The temperature field of the continuum is represented by the temperature of the nodes (such as nodes 1–7 in Fig. 6). Here, the calculation of the temperature field in the continuum is presented based on the topological connection in Fig. 6.

Fig. 6
figure 6

Heat conduction calculation in FDEM-TM3D (The figure is only used to illustrate the heat conduction model. The actual calculation does not require that the tetrahedral elements are organized in the form of Fig. 6, and the shape and number of tetrahedral elements that connect to the same node allow for change)

Full size image

Taking Fig. 6 as an example, eight tetrahedral elements (T1236, T1346, T1456, T1526, T1237, T1347, T1457 and T1527) connect to node 1. Since the temperature of nodes 2, 3, 4, 5, 6 and 7 may be different from that of node 1, heat conduction may occur in these tetrahedral elements. We take the tetrahedral element T1236 as an example. If the temperature field in a tetrahedral element obeys a linear distribution, the temperature gradient in the tetrahedral element is constant and thus can be expressed as [58]:

$$ \frac{\partial T}{{\partial x_{i} }} = \frac{1}{V}\int\limits_{A} {\frac{\partial T}{{\partial x_{i} }}{\text{d}}V} . $$
(16)

According to Gaussian divergence theorem, Eq. (16) can be written as [58]:

$$ \frac{\partial T}{{\partial x_{i} }} = \frac{1}{V}\int\limits_{s} {Tn_{i} } {\text{d}}S = - \frac{1}{3V}\sum\limits_{l = 1}^{4} {T^{l} } n_{i}^{(l)} S^{(l)} , $$
(17)

where \( V \) is the volume of the tetrahedral element, \( n_{i}^{(l)} \) is the outward normal unit vector of the triangular face opposite to node \( l \) of the tetrahedral element and \( S^{(l)} \) is the area of the triangular face opposite to node l.

Substituting Eqs. (17) into (14), the heat flow along the x, y and z directions is obtained.

Thus, the heat flow QT1236 into node 1 from the tetrahedral element T1236 per unit time can be calculated by:

$$ Q_{{{\text{T}}1236}} = - \frac{{q_{i} n_{i}^{(1)} S^{(1)} }}{3}. $$
(18)

Similarly, the heat flow into node 1 from the other tetrahedral elements that directly connect to node 1 can also be obtained. Thus, the total heat flow into node 1 per unit time can be expressed as:

$$ Q_{\text{total}} = Q_{{{\text{T}}1236}} + Q_{{{\text{T}}1346}} + Q_{{{\text{T}}1456}} + Q_{{{\text{T}}1526}} + Q_{{{\text{T}}1237}} + Q_{{{\text{T}}1347}} + Q_{{{\text{T}}1457}} + Q_{{{\text{T}}1527}} . $$
(19)

After solving Eq. (15) with explicit finite difference method, the temperature of node 1 at the next time step is given by:

$$ T_{1}^{t + \Delta t} = T_{1}^{t} + \frac{{Q_{\text{total}} }}{{C_{p} M}}\Delta t. $$
(20)

Similarly, the temperatures of other nodes at the next time step can also be obtained. Thus, the evolution of the temperature field in the solution domain can be obtained.

3.3 Convection boundary condition

As shown in Fig. 7, the top boundary is a convective boundary. The temperature of the rock at the top boundary is \( T_{\text{r}} \) and the environmental temperature is \( T_{\text{e}} \). The area of the top boundary is \( A \), and the convective heat transfer coefficient between the rock and environment is \( h \). The heat from the environment into the rock per unit time is given by:

$$ Q_{e} = h(T_{\text{e}} - T_{\text{r}} )A. $$
(21)
Fig. 7
figure 7

Convection boundary diagram

Full size image

Thus, the rock temperature at the convective boundary is finally updated by:

$$ T_{1}^{t + \Delta t} = T_{1}^{t} + \frac{{Q_{\text{total}} + Q_{e} }}{{C_{p} M}}\Delta t. $$
(22)

Since the explicit algorithm is adopted in the heat conduction calculation, the time step size needs to be smaller than the critical time step size to ensure the stability of the numerical calculation. The critical time step size is given by [58]:

$$ \Delta t_{c} = \frac{1}{m}\left[ {\frac{\kappa }{{L_{\text{c}}^{2} }} + \frac{h}{{\rho C_{p} L_{\text{c}} }}} \right]^{ - 1} , $$
(23)

where \( L_{\text{c}} \) is the characteristic length (\( L_{\text{c}} = V_{T} /S_{T} \), \( V_{\text{T}} \) is the volume of a tetrahedral element and \( S_{\text{T}} \) is the surface area of the tetrahedral element, \( h \) is convection heat transfer coefficient, \( \kappa \) is the thermal diffusion coefficient (if \( k_{x} = k_{y} = k_{z} \), \( \kappa = k/\rho C_{p} \)), and m is a constant, which is larger than unity.

3.4 Thermal coupling: thermal-induced strain and stress

As already mentioned, changes in the temperature field will cause the rock to expand or contract. If the temperature change is \( \Delta T \), the deformation due to the temperature change is given by:

$$ \Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = \Delta \varepsilon_{zz} = \alpha \Delta T. $$
(24)

According to the linear elastic constitutive equation, the stress caused by temperature change can be obtained by:

$$ \Delta \sigma_{ij} = - \delta_{ij} \frac{E}{1 - 2v}\alpha \Delta T, $$
(25)

where \( \delta_{ij} \) is Kronecker delta (\( \delta_{ij} = 1 \) for i = j and 0 for i ≠ j), E is the elastic modulus, v is Poisson’s ratio and α is the thermal expansion coefficient.

Then, the thermal stress is applied to the tetrahedral element as the volume load. The equivalent nodal force of the thermal stress is given by:

$$ {\mathbf{f}}^{(l)} = - \frac{1}{3}\delta_{ij} \frac{E}{1 - 2v}\alpha \Delta Tn_{j}^{(l)} S^{(l)} , $$
(26)

where l is the local number of the node in the tetrahedral element (l = 1,2,3,4), \( n_{j}^{(l)} \) is the outward normal unit vector of the triangular face opposite to node l of the tetrahedral element and \( S^{(l)} \) is the area of the triangular face opposite to node l.

It should be noted that the thermal stress obtained by Eq. (25) does not necessarily exist in the solid but only in a load that drives the solid deformation. For example, in the case of an isotropic homogeneous solid that is uniformly heated and the boundary is unconstrained, there will be no thermal stress in the solid.

3.5 The calculation procedure

According to Sects. 3.1 and 3.2, the calculation procedure of the 3D thermomechanical coupling model is as follows: Firstly, the temperature field distribution of the problem domain is obtained by heat conduction calculation; then, the thermal stress in all tetrahedral elements is obtained according to the change of temperature field; finally, the thermal stress is applied to tetrahedral elements and the mechanical calculation is performed. Thus, one time step in thermomechanical coupling analysis is completed. The calculation procedure is shown in Fig. 8.

Fig. 8
figure 8

Calculation procedure in FDEM-TM3D model

Full size image

4 Example

4.1 Heat conduction

For a long strip with an initial temperature \( T_{i} \) = 0 °C, a sudden, constant, uniform surface heat flux is applied on the left boundary of the strip. The temperature of the strip at the left boundary is \( T_{a} \) = 200 °C. The calculation parameters are as follows: the thermal conductivity of the strip \( k \) = 4.2 W/(m °C), density \( \rho \) = 2500 kg/m3, specific heat \( C_{p} \) = 880 J/(kg °C), and heat transfer coefficient \( h \) = 1.0 W/(m2 °C).

This is a transient heat conduction problem with an analytical solution that is given [59]

$$ T(x,t) = T_{i} + (T_{a} - T_{i} )\left[ {{\text{erfc}}\left( {\frac{x}{{2\sqrt {\alpha t} }}} \right) - e^{{\left( {\frac{hx}{k} + \frac{{h^{2} \alpha t}}{{k^{2} }}} \right)}} {\text{erfc}}\left( {\frac{x}{{2\sqrt {\alpha t} }} + \frac{{h\sqrt {\alpha t} }}{k}} \right)} \right], $$
(27)

where \( x \) is the distance from the left boundary, \( t \) is time, \( {\text{erfc}} \) is the complementary error function and \( \alpha \) is the thermal diffusion rate \( \left( {\alpha = \frac{k}{{\rho C_{p} }}} \right) \).

Using the thermomechanical coupling model in this paper, we solve this problem. The mesh size used for the calculation is 0.4 m with 541 tetrahedral elements and 1250 joint elements. The time step size is 10 s. The temperature distribution in the strip is shown in Figs. 9 and 10. The numerical solution agrees well with the analytical solution, which verifies the thermomechanical coupling model when simulating the heat conduction process.

Fig. 9
figure 9

Comparison between numerical and analytical solutions of the temperature distribution in the strip at different times

Full size image
Fig. 10
figure 10

Temperature distribution in the strip at different times

Full size image

4.2 Thermal stress distribution

A cylinder with an inner diameter a = 20 mm and outer diameter b = 150 mm is shown in Fig. 11 (mesh generated by Gmsh [60]). The mesh size is 0.008 m with 17,915 tetrahedral elements and 38,423 joint elements. The initial temperature of the cylinder is 25 °C. Then, the temperature at the inner boundary of the cylinder is fixed at Ta = 100 °C, while the temperature of the outer boundary is fixed at Tb = 25 °C. For mechanical constraints of the cylinder, the top and bottom faces of this cylinder are fixed in the normal direction. The temperature and thermal stress distribution in the cylinder under a thermally stable state are determined by the 3D thermomechanical coupling model.

Fig. 11
figure 11

Model mesh

Full size image

The analytical solution of the problem is given by [61]:

$$ T = \frac{\ln (b /r)}{\ln (b /a)}T_{a} + \frac{\ln (a /r)}{\ln (a /b)}T_{b} , $$
(28)
$$ \sigma_{r} = - \frac{{E\alpha (T_{a} - T_{b} )}}{2(1 - v)}\left[ {\frac{\ln (b /r)}{\ln (b /a)} - \frac{{(b /r)^{2} - 1}}{{(b /a)^{2} - 1}}} \right], $$
(29)
$$ \sigma_{\theta } = - \frac{{E\alpha (T_{a} - T_{b} )}}{2(1 - v)}\left[ {\frac{\ln (b /r) - 1}{\ln (b /a)} + \frac{{(b /r)^{2} + 1}}{{(b /a)^{2} - 1}}} \right], $$
(30)

where \( \sigma_{\text{r}} \) is the radial stress, \( \sigma_{\theta } \) is the tangential stress, E is the elastic modulus, v is Poisson’s ratio, \( \alpha \) is the thermal expansion coefficient, a is the inner diameter of the cylinder, b is the outer diameter, \( r \) is the distance of a point to the center of the cylinder, and \( T_{a} \), \( T_{b} \) are the temperatures at the inner and outer boundaries, respectively.

The thermal conductivity k is 4.2 W/m °C, specific heat Cp is 880.0 J/kg °C, thermal expansion coefficient is 1.0 × 10−5/°C, elastic modulus E is 20 GPa, Poisson’s ratio v is 0.2, and density ρ is 2500 kg/m3. The time step size used for the calculation is 8.902862 × 10−10 s, and the damping coefficient is 8.367472 × 105 Nm.

The temperature and stress distribution calculated by this model are shown in Figs. 12 and 13. It can be seen that the numerical solution agrees well with the analytical solution, which verifies the model in terms of dealing with thermal stress calculation problem.

Fig. 12
figure 12

Temperature distribution in the cylinder at the thermally stable state

Full size image
Fig. 13
figure 13

Stress distribution in the cylinder at the thermally stable state

Full size image

4.3 Thermal cracking examples

The cylinder shown in Fig. 11 is still used in this section. The initial temperature of the model is set as 25 °C in this section. Consider the following two boundary conditions: (1) the temperature at the inner boundary Ta remains unchanged (25 °C), while the temperature Tb at the outer boundary increases with time step (i.e., Ta < Tb). The rate of temperature increase is 0.01 °C per time step, and the temperature at the outer boundary remains unchanged after increasing to 500 °C. (2) The temperature Tb at the outer boundary remains unchanged (25 °C), while the temperature Ta at the inner boundary increases with time step (i.e., Ta > Tb). The rate of temperature increase is 0.01 °C per time step, and the temperature at the inner boundary remains unchanged after increasing to 500 °C. We set up a series of monitor points on the inner and outer boundaries of the disk to analyze the stress distributions on the inner and outer boundaries before and after the crack generation, as shown in Fig. 14.

Fig. 14
figure 14

Arrangement of monitoring points on the inner and outer boundaries of the disc

Full size image

According to Eq. (30), the stress at the inner and outer boundaries of the cylinder can be given by the following:

$$ \sigma_{\theta } \left| {_{r = a} } \right. = - \frac{{E\alpha (T_{a} - T_{b} )}}{2(1 - v)}\left[ {\frac{{2b^{2} /a^{2} }}{{b^{2} /a^{2} - 1}} - \frac{1}{\ln (b /a)}} \right], $$
(31)
$$ \sigma_{\theta } \left| {_{r = b} } \right. = \frac{{E\alpha (T_{a} - T_{b} )}}{2(1 - v)}\left[ {\frac{1}{\ln (b /a)} - \frac{2}{{b^{2} /a^{2} - 1}}} \right]. $$
(32)

According to Eqs. (31) and (32), if the temperature at the inner boundary is lower than that at the outer boundary (i.e., Ta < Tb), then \( \sigma_{\theta } \left| {_{r = a} } \right. > 0 \), \( \sigma_{\theta } \left| {_{r = b} } \right. < 0 \), the tensile stress is generated at the inner boundary and the compressive stress is generated at the outer boundary. However, the absolute value of \( \sigma_{\theta } \left| {_{r = a} } \right. \) is larger than \( \sigma_{\theta } \left| {_{r = b} } \right. \). Therefore, when the stress at the inner boundary exceeds the tensile strength, tensile failure occurs. Thus, for these temperature boundary conditions, cracks are firstly generated at the inner boundary.

Similarly, if the temperature at the inner boundary is higher than that at the outer boundary (i.e., Ta > Tb), then \( \sigma_{\theta } \left| {_{r = a} } \right. < 0 \) and \( \sigma_{\theta } \left| {_{r = b} } \right. > 0 \), the compressive stress is generated at the inner boundary and tensile stress is generated at the outer boundary. Although the absolute value of \( \sigma_{\theta } \left| {_{r = b} } \right. \) is lower than \( \sigma_{\theta } \left| {_{r = a} } \right. \), the tensile strength of the rock is usually much smaller than the compressive strength. Thus, when the tensile stress at the outer boundary exceeds the tensile strength, tensile failure occurs. In this situation, cracks are firstly generated at the outer boundary.

Additionally, the cracks in the first case are generated earlier than that in the second case because in the first case we compare \( \sigma_{\theta } \left| {_{r = a} } \right. \) with the tensile strength, while in the second case we compare \( \sigma_{\theta } \left| {_{r = b} } \right. \) with the tensile strength. However, the absolute value of \( \sigma_{\theta } \left| {_{r = a} } \right. \) is larger than that of \( \sigma_{\theta } \left| {_{r = b} } \right. \).

The above part is the theoretical analysis for the problem. Then, the problem is studied by using the thermomechanical coupling model. The simulation results are compared with the theoretical analysis. The mechanical parameters are shown in Table 1. The simulation results are shown in Figs. 15, 16, 17, 18, 19 and 20, and the temperature distribution at different time steps is shown in Fig. 21.

Table 1 Parameters for three examples
Full size table
Fig. 15
figure 15

Thermal cracking morphology when Ta < Tb

Full size image
Fig. 16
figure 16figure 16

Distribution of maximum principal stress in the process of thermal cracking when Ta < Tb (Pa, positive denotes tensile stress)

Full size image
Fig. 17
figure 17

Distribution of the maximum principal stress on the inner and outer boundaries of the disc before and after crack generation (Ta < Tb). (Color figure online)

Full size image
Fig. 18
figure 18figure 18

Thermal cracking morphology when Ta > Tb

Full size image
Fig. 19
figure 19figure 19

Distribution of maximum principal stress in thermal cracking when Ta > Tb (Pa, positive denotes tensile stress). (Color figure online)

Full size image
Fig. 20
figure 20

Distribution of the maximum principal stress on the inner and outer boundaries of the disc before and after crack generation (Ta > Tb). (Color figure online)

Full size image
Fig. 21
figure 21

Temperature distribution

Full size image

As shown in Fig. 15, when the inner boundary temperature Ta of the cylinder is kept constant, while the outer boundary temperature Tb increases with time step (Ta < Tb), the cracks are firstly generated at the inner boundary of the cylinder (as shown at time step 70,000 in Fig. 15), which is consistent with the theoretical analysis. As the time step increases, cracks gradually extend from the inner boundary to the outside and radial cracks are finally formed. Although the cracks do not extend straight to the outside and instead form some bifurcation and turning, the phenomenon of crack initiation from the inner boundary and propagation from the inner boundary to the outside is obvious. These results agree well with the results in Tang [62].

As shown in Fig. 16, the inner boundary of the cylinder is in a tension state (positive denotes tensile stress) before crack initiation (see Fig. 17, red line), while the outer boundary is in a compressive stress state (see Fig. 17, green line—with very low compressive stress at the outer boundary). For example, at time step 58,000 in Fig. 16, the zone at the inner boundary is in a tensile stress state, while the zone at the outer boundary is in a compressive stress state. If the tensile stress at the inner boundary exceeds the tensile strength of the rock (see Fig. 17, red line—the maximum principal stress Smax at the inner boundary is higher than the tensile strength ft = 10 MPa), cracks will generate at the inner boundary as shown at time step 60,000 in Fig. 16. Then, the tensile stress at the start point will be released, i.e., the tensile stress at the inner boundary decreases and may be lower than the tensile strength (see Fig. 17, blue line—the maximum principal stress Smax decreases and most of them are lower than the tensile strength ft = 10 MPa). After the tensile stress at the inner boundary is completely released, no new crack is generated in the inner boundary, as shown at time steps 70,000–80,000 in Fig. 16. The tensile stress concentration zones move outward with the cracks extending, which is shown at time steps 65,000–120,000 in Fig. 16.

As shown in Fig. 18, when the temperature Tb at the outer boundary is kept constant and the temperature Ta at the inner boundary increases with time (Ta > Tb), cracks are firstly generated at the outer boundary (see time step 80,000 in Fig. 18). Those results are consistent with the theoretical analysis. As the time step increases, cracks propagate outward from the inner boundary and radial cracks are finally formed. Although cracks do not extend straight to the outside and instead extend with some bifurcation and turning, the phenomenon of crack initiation from the outer boundary and propagation from the outer boundary to the inside is obvious. These results agree well with the results in Tang [62].

As shown in Fig. 19, the outer boundary of the cylinder is in a tension state before crack initiation (see Fig. 19, green line), while the inner boundary of the cylinder is in a compressive stress state (see Fig. 19, red line—with very large compressive stress). For example, at time step 69,000 in Fig. 19, the zone at the outer boundary is in a tensile stress state, while the zone at the inner boundary is in a compressive stress state. If the tensile stress at the outer boundary exceeds the tensile strength of the rock (see Fig. 20, green line—the maximum principal stress Smax at the outer boundary is higher than the tensile strength ft = 10 MPa), cracks will generate at the outer boundary, as shown at time step 70,000 in Fig. 19. The tensile stress at the start point will be released, i.e., the tensile stress at the outer boundary decreases and may be lower than the tensile strength (see Fig. 20, black line—the maximum principal stress Smax decreases and some of them are lower than the tensile strength ft = 10 MPa). After the tensile stress in the outer boundary is completely released, no new crack is generated at the outer boundary, which is shown at time steps 80,000–90,000 in Fig. 19. The tensile stress concentration zones move inward with the cracks extending, which is shown at time steps 80,000–140,000 in Fig. 19.

In addition, as shown in Figs. 16 and 19, crack initiation occurs at time step 60,000 when Ta < Tb, but when Ta > Tb, crack initiation occurs at time step 70,000, i.e., in the first case, cracks initiate earlier than in the second case, which is also consistent with the theoretical analysis.

In short, when Ta < Tb, cracks initiate from the inner boundary and extend to the outside. When Ta > Tb, cracks initiate from the outer boundary and extend to the inside. Finally, radial cracks are formed in both cases. These results agree well with the results in Tang [62], which verifies the model FDEM-TM3D in terms of dealing with the thermal cracking problem.

5 Conclusions

Thermal cracking plays a key role in a variety of geomechanical applications, including nuclear waste storage, petroleum and geothermal development. Given the importance of this topic, the research work presented herein introduced a three-dimensional thermomechanical coupling model (FDEM-TM3D) to simulate the thermal cracking of rock. The thermomechanical coupling model can reproduce crack initiation and propagation, as well as the distributions of stress and temperature during thermal cracking. The model of this paper extends the application of FDEM so that it can be used to handle thermomechanical coupling and thermal cracking problems. Combining this model with the coupled hydromechanical models [43, 44] will enable the application of FDEM to solve rock fracturing problems under the effect of thermal–hydrological–mechanical (THM) couplings. It should be noted that crack propagation path is affected by the mesh because crack extends along the element boundary. However, as the mesh density increases, the effect of the mesh on crack propagation will gradually decrease. Since the hydromechanical model in this paper uses an explicit solution, it is time-consuming to solve large timescale problems. However, the explicit solution method is very easy to solve in parallel. With parallel computing technology, the calculation speed of the model can be increased so that the problem with large timescale can be solved in the future.