A comprehensive study of MPI parallelism in three-dimensional discrete element method (DEM) simulation of complex-shaped granular particles

Abstract

A three-dimensional (3D) DEM code for simulating complex-shaped granular particles is parallelized using message-passing interface (MPI). The concepts of link-block, ghost/border layer, and migration layer are put forward for design of the parallel algorithm, and theoretical scalability function of 3-D DEM scalability and memory usage is derived. Many performance-critical implementation details are managed optimally to achieve high performance and scalability, such as: minimizing communication overhead, maintaining dynamic load balance, handling particle migrations across block borders, transmitting C++ dynamic objects of particles between MPI processes efficiently, eliminating redundant contact information between adjacent MPI processes. The code executes on multiple US Department of Defense (DoD) supercomputers and tests up to 2048 compute nodes for simulating 10 million three-axis ellipsoidal particles. Performance analyses of the code including speedup, efficiency, scalability, and granularity across five orders of magnitude of simulation scale (number of particles) are provided, and they demonstrate high speedup and excellent scalability. It is also discovered that communication time is a decreasing function of the number of compute nodes in strong scaling measurements. The code’s capability of simulating a large number of complex-shaped particles on modern supercomputers will be of value in both laboratory studies on micromechanical properties of granular materials and many realistic engineering applications involving granular materials.

1 Motivation

The discrete element method (DEM) has been applied to study the mechanical behavior of particle assemblages for more than 30 years since its introduction in the late 1970s by Cundall and Strack [3]. However, application of 3-D DEM in simulating practical problems involving granular materials is still limited in terms of problem size (namely, number of bodies/particles). For example, most applications involving complex-shaped particles such as axisymmetric/revolution ellipsoids [23, 24] or true ellipsoids [34] constrain their number of particles to a few thousand, typically not exceeding 10,000, which implies merely $21 \times 21 \times 21$ particles in 3D space. This is mainly due to the fact that the DEM poses high computational demands characterized by CPU-intensive interparticle contact detection and a conventional explicit time integration scheme.

For many applications, the length scale and problem size of practical engineering problems cannot be circumvented even if a multi-scale model is employed. For instance, to study the influence of blast waves on gravitationally deposited coarse-grained soils in which an explosive charge is ignited, a 40 cm $\times$ 40 cm $\times$ 40 cm specimen composed of ellipsoidal sand particles is generated containing roughly 500 million 0.1–1 mm diameter particles depending on the particle shapes and size distribution. In engineering problems such as pile foundation installation, a 10-m-long precast concrete pile (modeled by the finite element method (FEM)) driven into sandy soil would involve large shear deformation along its frictional side as well as point-bearing end. Even if the thin shearing layer around the pile body and a small region at the pile end are modeled by DEM while transition to faraway zones is modeled by FEM (so-called DEM–FEM coupling [26, 34]), the number of discrete particles needed in such conditions could still be surprisingly large.

The limitation of problem size (number of particles) is a barrier to simulating realistic engineering or laboratory problems involving complex-shaped particles that are of same size as physical particles. As an example, if 2200 particles (roughly 13 $\times$ 13 $\times$ 13 particle array) in 3-D space are adopted to study the internal evolution of shear band and force chains in conventional triaxial compression test or true triaxial compression test [1], the shear band is difficult to observe: In each dimension, there are 13 particles, at least two of them on each side are needed to account for boundary effects and then only nine particles remain to investigate the internal shearing behavior. The numerical experiment would not be sufficiently convincing until an approximate 50 $\times$ 50 $\times$ 50 particle array is modeled, wherein that specimen amounts to 125k particles. Fu and Dafalias [6, 7] employed 120k particles to study the shear band evolution and anisotropic shear strength of granular materials using 2-D ployarc DEM.

It is natural to make use of modern supercomputers to perform such large-scale computational tasks. This paper presents a comprehensive study on the parallelism of a DEM code for simulating granular materials composed of complex-shaped particles, including design, implementation, optimization, theoretical analysis and practical evaluation of performance, and benchmarks.

It should be emphasized that the parallelization of a 3-D DEM code discussed in the paper is mainly developed for complex-shaped particles such as true ellipsoids [34], poly-ellipsoids [25], superellipsoids [4, 30], superquadrics [31], or asymmetrical particles constructed by non-uniform rational basis splines (NURBS) [14], rather than simple spheres. In many geotechnical and geomechanical problems, the shapes (and sizes, gradations, etc) of the discrete particles play an insurmountably important role such as for capturing interlocking and particle fracture, whereas modeling those complex-shaped particles often costs orders of magnitude more computational power than spheres. However, the parallelism is also applicable to spheres, if of interest to the modeler.

The paper contains seven sections. Section 1 has stated the motivation, mainly from the perspective of engineering applications; Sect. 2 is an introduction to the DEM method and its computational features; Sect. 3 reviews development in parallel DEM and describes new features in the paper; Sect. 4 covers numerous concepts, techniques, principles, optimizations, work-around, and programming technologies in the process of parallelization; Sect. 5 presents performance analysis using numerical experiment data collected from DoD HPC supercomputers in light of Gustafson–Barsis’s law, Karp–Flatt metric and iso-efficiency relation; Sect. 6 studies MPI profiling of the parallel code, formulates the relationships between execution time, communication time, and parallel overhead percentage with respect to number of processors and problem size, and suggests optimal computational granularity for various scales of simulation; and a summary is given in the last section.

2 Fundamentals of DEM

2.1 The DEM framework

A complete DEM system is composed of multiple essential components: particle geometry representation, interparticle mechanical models (such as Hertzian nonlinear normal contact model [11] and Mindlin’s history-dependent shear model [18, 19]), contact search and resolution algorithm, time integration scheme, damping mechanism, boundary control methods for modeling various loading conditions, etc. A typical procedure of DEM analysis consists of three major computational steps in sequence, which are integrated in time using central difference method until a simulation is completed:

• contact detection between particles, including two phases:

  • 1. neighbor search (neighbor estimate)

  • 2. contact resolution

• contact force computation for each pair of particles in contact.

• particle motion update (translations and rotations) using Newton’s second law.

The contact detection process is usually the major computational bottleneck, especially for a large number of complex-shaped particles. It is divided into two phases: the neighbor search (or spatial reasoning) phase and the contact resolution phase. Neighbor search identifies/estimates objects near the target object. It often uses an approximate geometry for the objects, such as bounding box or bounding sphere. The geometric contact resolution phase then uses a specific geometric representation of each body to resolve the contact geometry. For complex shapes such as ellipsoidal particles (three different semi-axis lengths) [34] or non-symmetric poly-ellipsoidal particles [25], the contact resolution between two particles is much more expensive than spheres, increasing the floating-point operations by several orders of magnitude due to the requirement of numerical accuracy and robustness. This is the most computationally challenging part of 3-D DEM in addition to the nonlinear and history-dependent mechanical models that describe interparticle interactions.

2.2 Neighbor search

The time complexity of a n-by-n simple search algorithm is $O(n^2)$, where n denotes the number of particles in a particle assemblage. It is acceptable to use the simple approach if n is less than several thousand. However, this simple method would become extremely inefficient as the number of particles increases significantly, for example, up to more than 50k, not to mention on the order of millions or billions of particles. Partitioning algorithms are therefore introduced, and they fall into two main classes: tree-based algorithms, which use specific data structures for storage and search and result in time complexity of $O(n\text{ log }n)$ [12, 20]; and binning algorithms whose time complexity is O(n).

The idea of binning algorithm is to place each particle into a bin using a hash on the particle’s coordinates. Once the particles are sorted into bins, one can reason about the spatial closeness based solely on the fixed relationships of the bins. Munjiza and Andrews [21] implemented a binning algorithm, which scales linearly to large numbers of particles but is limited to particles of approximately the same size. Williams et al. [32] extended the traditional binning algorithm so that objects of arbitrary shape and size in two and three dimensions can be handled by introducing an abstraction. The algorithm achieved the partitioning of n particles of arbitrary shape and size into n lists in O(n) operations, where each list consists of particles spatially near to the target object.

In molecular dynamics (MD), the link-cell (LC) method [8] is widely used for large numbers of molecules in short-range interaction with a well-defined cutoff, while Verlet’s neighbor table is used for small number of molecules. The LC method divides a computational spatial domain into equal cubic cells of size not smaller than the cutoff distance (in MD) or diameter of the largest particle (in DEM). Each particle is referenced to the cell according to the position of the particle centroid. The neighbor-searching method comprises referencing individual particles to the cells and constructing the neighbors list of particles using cells. The time complexity of LC method is O(n).

All of these nontrivial methods are based on the idea of increasing spatial locality in serial computing, namely a discrete particle does not need to check with all other particles but only needs to check its surrounding neighbors, thus lowering computational cost substantially. However, the overall computational improvement from these methods might be highly limited for complex-shaped particles because neighbor search only takes up a small fraction in floating-point operations.

Fig. 1

Ellipsoids and poly-ellipsoids represent a wide variety of shapes in DEM. a Ellipsoids with various aspect ratios, b spherical particles, c disk-like particles, d needle-like particles, e poly-ellipsoids with various aspect ratios, and f poly-ellipsoids

2.3 Contact resolution

Yan et al. [34] developed a robust contact resolution algorithm for three-axis ellipsoidal particles by constructing an extreme value problem of finding the deepest penetration of one particle into the other. Such an extreme value problem results in a sixth order polynomial equation. Conventional polynomial root finders cannot satisfy the high-precision numerical requirement in the 3-D DEM computation. For example, the elastic overlap between two particles of typical quartz sand may vary between $10^{-8}$ and $10^{-5}$ m depending on particle size, shape, and external force, and a low-precision solver can lead to numerical instability or spurious explosion of particles. Therefore, an iterative eigenvalue method, which performs QR decomposition of real Hessenberg matrices, is selected to find roots of the polynomial and determine the contact geometry. The algorithm and its implementation has been shown to be robust such that it is applicable to not only regularly bulky ellipsoidal shapes but also extreme-shaped ellipsoidal particles such as disks and needles, as shown in Fig. 1a–d.

Peters et al. [25] proposed a non-symmetric poly-ellipsoid shape, which joins eight component ellipsoids in eight different octants, respectively, to produce continuous surface coordinates, normal directions, and intersections. It is more computationally expensive than a symmetric ellipsoid but it acts as a useful extension, as shown in Fig. 1e–f.

3 State of the art of DEM parallelization

3.1 Interest and challenge in developing parallel DEM

There has been considerable interest in developing parallel DEM codes in recent years. Baugh Jr and Konduri [2] presented a distributed computing system for DEM that is designed for loosely coupled networks of workstations, where the interprocess communication is implemented using low-level BSD sockets rather than popular tools or API such as MPI, OpenMP, or PVM (parallel virtual machine). The implementation subdivides the simulation region into cube-shaped cells, and a neighbor list is constructed within a radius $R_\mathrm{c} + \Delta R$, where $R_\mathrm{c}$ is a cutoff radius and $\Delta R$ is a small value determined empirically. The implementation is used to simulate a system with as many as 200,000 spherical particles using eight processors. As an example, the speedup is close to 6 using eight processors for the computation of 120k spherical particles. The authors pointed out that a replacement of the client–server model with peer-to-peer communication would reduce communication cost.

Washington and Meegoda [29] simulated a triaxial test using an algorithm titled “TRUBAL for Parallel Machines (TPM)” and showed its benefits over the serial version DEM code, TRUBAL. The TPM assigns each processor a multiple number of contact pairs (two spheres in contact) existing within an assembly of spheres using static memory arrangement. The rubber membrane boundary is approximated and assumed to stretch between the particles. Two simulation scales are tested and compared, one with 403 spheres and the other with 1672 spheres, on Connection Machine (CM-5) with 512 nodes at the Pittsburgh Supercomputing Center. The speedup is as low as 7.9 using 512 nodes for 403 spheres. The authors found that a drastic increase in the problem size did not decrease the overall speedup. Indeed, an increase in the problem size should increase the speedup according to Amdahl effect [17].

Maknickas et al. [16] described the DEMMAT_PAR code for simulation of viscoelastic frictional granular media, which has been created in the Parallel Computing Laboratory of Vilnius Gediminas Technical University. The code adopts a static spatial domain decomposition strategy, link-cell concept, and MPI interprocessor communications. The parallel performance tests were carried out on their PC cluster VILKAS for systems consisting of 5000, 20,000, and 100,000 particles whose parameters are artificially assumed, for example, the Young’s modulus is as low as 1 MPa (compared to 29 GPa for quartz sand). The speedup is approximately 11 on 16 processors for 100,000 spherical particles.

Henty [10] chose to investigate the performance of a much smaller test code that implements precisely the same algorithm but has limited functionality rather than tackling a complete physics DEM application with all of its functionality and complexity. He implemented a hybrid parallelization of the message-passing and shared-memory models simultaneously. The superlinear speedup is observed in his tests. The author pointed out: “The results are somewhat disappointing, showing that the pure MPI code is always more efficient for a given granularity” than a hybrid scheme.

Vedachalam and Virdee [28] used LAMMPS (large-scale atomic and molecular massively parallel simulator) and LIGGGHTS (LAMMPS improved for general granular and granular heat transfer simulations) to study the motion of snow particles, wherein the snow grains are assumed to be spherical particles of 5 mm diameter. An empirical coefficient of restitution (ratio of rebound velocity to impact velocity) is adopted rather than the strict Hertzian nonlinear contact model, while Mindlin’s history-dependent shear model is not considered. With regard to the performance gain of parallelism, the authors wrote “on 480 processors for 75K particles, the speedup was 1.99, while on 960 processors for same number of particles speedup achieved was 2.52” in comparison with 120 processors, which is a relatively low performance gain.

Munjiza et al. [22] adopted parallel particle mesh (PPM) library to parallelize the DEM and used a conservative lower bound to estimate the number of time steps between two Verlet list updates. In a sand avalanche simulation, 122 million spheres were used. In the figure generated from fixed-size problems that use up to 192 processors, superlinear speedup appears to occur when the number of processors increases to a certain value.

It should be noted that the DEMs mentioned above share several weaknesses and challenges:

• 1. They only deal with spheres rather than complex-shaped particles, thus leading to several orders of magnitude less computational demand, as detailed in Sect. 3.2. For example, the CPU demand of simulating 122 million spheres is merely equivalent to that of simulating 488k poly-ellipsoids, and the CPU demand of simulating 10 million ellipsoids approaches that of 500 million spheres, when using the same interparticle contact mechanical models. Peters et al. [25] divide DEMs by two motivations: (1) prototype-scale simulations for engineering studies and (2) micromechanical studies for research of fundamental mechanics. They pointed out: “Prototype scale analyses require accurate bulk behavior of the medium, which presumably can be achieved without capturing details at the particle scale. In fact, in such studies both particle size and shape are sacrificed to obtain problem sizes suitable for practical computations. For micromechanical studies, greater fidelity to the actual particle characteristics is needed, because for simulation to be on equal footing with physical experiments, the particle-scale behavior must be correct. Simply reproducing bulk behavior is not sufficient if the intent is to develop generalizations about fundamental mechanics.” Unfortunately, the spherical DEMs mentioned above fall into the category of prototype-scale simulations.

• 2. They highly simplify the complicated interparticle contact models and can hardly capture physical properties of internal frictional granular material correctly. For example, Munjiza et al. [22] assumes constant normal and tangential elastic modulus, and LAMMPS assumes variable normal and tangential elastic modulus; however, both ignore the well-known history-dependent tangential behavior for granular particles, which needs special implementation to keep track of the complex loading-unloading-reloading path and history variables. Munjiza et al. [22] update the Verlet lists every 150 time steps; however, interparticle contacts can generate and disappear, and lasting shear contact behavior can evolve, at every time step in conventional DEM, not to mention in high-fidelity simulations like soil-buried explosion.

• 3. They do not completely disclose or implement advanced parallelism requirements such as memory consumption management, dynamic load balancing technique, tranmission of dynamically allocated objects between MPI processes, particle motion tracking mechanism across MPI processes, which set a ceiling on computational performance gain and scalability. For example, the root process may deplete compute node memory in parallel computing, if it does not implement an effective memory deallocation mechanism during the process of time integration of millions of steps; a particle could disappear in computation when it moves across dynamically adaptive compute grids, if particle migration mechanism is not implemented correctly.

• 4. They achieve poor parallel speedup and scalability. As a typical example of LAMMPS, $4\times$ number of processsors gives rise to a low speedup of 1.99, and $8\times$ number processors leads to a low speedup of 2.52, in the simulation of 75k spheres [28]. Among these parallel DEMs, the algorithmic speedup and scalability challenges mainly come from: (1) strategy of static versus dynamic spatial domain decomposition; (2) performance-critical details in design and implementation of the MPI transmission of adjacent particles from one process to another, which are described briefly in Sect. 3.2 and covered thoroughly in Sect. 4.

Fig. 2

Link-cell algorithm and serial DEM profiling, a link-cell algorithm, b CPU time components for ellipsoid and c CPU time components for Spheres

3.2 A comprehensive study of parallel 3-D DEM

This paper aims to provide a comprehensive study of parallel DEM by applying the parallel computing techniques to the mechanics research of granular materials. It includes the following novel features:

• 1. Uses Hertzian nonlinear normal contact model and especially Mindlin’s history-dependent tangential contact model, combined with Coulomb friction model and interparticle contact damping model, to describe the complicated interaction between particles. This differs from LAMMPS fundamentally because the latter uses highly simplified models and ignores the interparticle tangential behavior that determines the mechanical property of the internal frictional granular media, such as geological and geotechnical materials.

• 2. Computes true three-axis ellipsoids and non-symmetric poly-ellipsoids and allows extension to other complex-shaped particles. For complex shapes such as three-axis ellipsoidal particles [34] or non-symmetric poly-ellipsoidal particles [25], the contact resolution between two particles is several orders of magnitude more expensive than spheres. For example, contact resolution between a pair of three-axis ellipsoids is approximately 50 times as expensive as that of a pair of spheres, and contact resolution between a pair of poly-ellipsoids is nearly 260 times as expensive as that of a pair of spheres[33].

• 3. Puts forward concepts of link-block, ghost/border layer, and migration layer to optimize the parallelism and allows high flexibility and scalability in modeling from quasi-static (such as laboratory triaxial tests of soil) to dynamic problems (such as particle pluviation, buried explosion).

• 4. Derives the theoretical scalability function to predict 3-D DEM features of scalability and memory usage and analyzes performance through parallelism laws rigorously such as Gustafson–Barsis’s law, Karp–Flatt metric, and iso-efficiency relation.

• 5. Develops a dynamic load balancing technique using adaptive compute grids; optimizes memory management by minimizing global communication and avoiding large MPI memory consumption; uses migration layer to track particle motion across adjacent MPI processes; achieves efficient MPI transmission of dynamic objects and pointers using Boost C++ libraries; and eliminates redundant contact information between adjacent MPI processes using a special data structure. We emphasize such a completely optimized DEM system for complex-shaped particles; otherwise, a highly efficient and scalable parallel system for large-scale simulations cannot be achieved.

• 6. Performs extensive tests across five orders of magnitude of simulation scale (namely, the number of complex-shaped particles), evaluates the optimal computational granularity across the scales, and studies the characteristics of communication and parallel overhead with respect to number of processors and problem size across the scales.

4 MPI design and implementation

4.1 Four-step design and link-block

The paper follows the four-step paradigm proposed by Foster [5] in designing the MPI parallelization algorithm of the DEM code: partitioning, communication, agglomeration, and mapping. The computational spatial domains are divided in link-cell (LC) method into equal-sized cubic cells of length not smaller than the diameter of the largest particle, illustrated in Fig. 2a.

Figure 2b reveals the CPU time percentage of various components of 3-D DEM for simulating 2000 ellipsoidal particles, whereby it is observed the neighbor search only accounts for a small fraction (13.2%) of the overall CPU time. In comparison, the neighbor search takes up to 74.7% of CPU time for simulating 2000 spherical particles, as shown in Fig. 2c.

We upscale the link-cell (LC) to link-block (LB) technique in parallel DEM. With introduction of LB, Foster’s four-step paradigm can be readily applied in designing a parallel algorithm in DEM.

Fig. 3

Schematic of link-blocks, virtual cells, and border layers

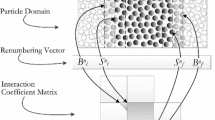
Partitioning The computational domain is divided into blocks. Each block may consist of many virtual cells. In Fig. 3, there are eight blocks numbered from 0 to 7, each containing 5 $\times$ 5 $\times$ 5 small virtual cells. The size of the virtual cells may be chosen to be the maximum diameter of the discrete particles.

Communication Each cell, as a primitive task unit, can communicate with 26 possible surrounding ones to determine contact detection. However, the communication manner may be changed after the process of agglomeration.

Agglomeration By combining 5 $\times$ 5 $\times$ 5 virtual cells into a block, communication overhead is lowered in that each block only needs to communicate with neighboring blocks through border/ghost layers, which are virtual cells marked by blue dots in Fig. 3.

Mapping There are choices of mapping a block of particles to a core, a CPU, multiCPUs within a node, or even a whole node. Very often each block is mapped to a whole compute node.

Fig. 4

Flowchart of the parallel algorithm of 3-D DEM

4.2 Flowchart of the parallel algorithm

The flowchart of the parallel code is designed as depicted in Fig. 4. It exhibits 12 flow processes or steps, among which one is sequential, two are partially parallel, and nine are fully parallel. Ten of the twelve processes are integrated in time using time increment loops until a simulation is completed. The 12 steps are not equally weighted or even have different repeatability in the time increment loops in terms of computational cost and communication overhead, and how to optimize them is discussed in subsequent sections.

In comparison with the serial algorithm, the parallel one ends up with six more steps as follows:

• 1. Step 2: 2-Root process divides and broadcasts info. This step only runs once so it does not cost much CPU time.

• 2. Step 3: 3-All processes communicate with neighbors. This interprocess communication is the most important step in the parallel algorithm.

• 3. Step 9: 9-All processes update compute grids. This step arises from consideration of computational load balance.

• 4. Step 10: 10-All processes merge and output info. This step serves the goal of snapshotting simulation states. Beware that it does not execute at each time increment; otherwise, it could cause unacceptable cost.

• 5. Step 11: 11-All processes release memory of receiving particle info. This step arises from MPI transmission mechanism and must be carefully taken care of.

• 6. Step 12: 12-All processes migrate particles. This step handles the situation when particles move across block borders.

Note steps 5 and 7 are boundary processes: Although they are partially parallel in spatial distribution (only boundary processes are running while other processes are idle), these two steps only perform 3-D operations on computational boundaries, therefore taking up a relatively small fraction of computational cost. Among the 12 steps, most of them only involve local communication, while three of them are associated with global communication.

4.3 Interblock communication

In Fig. 3, beware that a border/ghost layer is not limited to constructing a surface layer between two adjacent blocks, as there are other forms. For example, block 3 communicates with block 1 through a surface border layer, block 3 communicates with block 0 through an edge border layer, while block 3 communicates with block 4 through a vertex border layer, as shown in Fig. 3. Usually, a block needs to exchange information with its neighbors through six surface border layers, 12 edge border layers, and eight vertex border layers. It might be anticipated that communication overhead in 3D DEM is not trivial.

A “patch” test is designed using 162 ellipsoidal particles. The particle assemblage is composed of two layers of 81 particles, gravitationally deposited into a rigid container, illustrated in Fig. 5a. The container is partitioned into four blocks separated by blue dashed lines shown in Fig. 5b, which also represents the initial configuration of the randomly sized particles as shown from top view.

Each block is mapped to and computed by an individual process, so there are four processes, p0 to p3. Each process needs to communicate with other processes to determine its own boundary conditions. For example, process p3 needs to know those particles from process p1 that are enclosed by the pink rectangular box, those from process p2 enclosed by the red rectangular box, and those from process p0 enclosed by the green square box. A detailed movie records how those particles move across the borders and collide with particles from other blocks, and it reveals that each process is able to determine its boundary conditions accurately. The overall motion of the 162 particles through parallel computing is observed to be the same as that observed in serial computing.

Fig. 5

Illustration of interblock communication, a 3-D view of initial configuration, b top view of initial configuration, c top view at time t1 during simulation and d top view at time t2 during simulation

4.4 Across-border migration

Each process only knows its own space and associated particles, and a particle may enter or leave this space, which is called across-block migration. If a particle migrates across the block border, one process needs to delete this particle while another process needs to add this particle. Consider a small particle located at location 1 in process p1 at time t1 in Fig. 5c: It moves across the border of process p1 and enters the domain of process p0 at a later time t2, arriving at location 2 in Fig. 5d.

Fig. 6

Particles migrate across blocks

The algorithm to track how particles migrate across block/process borders is depicted in Fig. 6. It looks similar to that of interprocess communication; however, they are different or even the inverse of each other conceptually. In Fig. 6, those rectangular and square boxes are a spatially outward extension of process p3, not the inward inclusion of process p0, p1, p2, respectively. They are called migration layers or migration zones. For example, p3 ought to check its three spatial migration layers to see whether any of its particles move into the migration layers, and if yes, p3 should send such particles to its neighbors and delete them from its own space. The width of the migration layers is independent of the size of virtual cells, and it is actually determined by the velocities of the particles and time step used in current time increment.

4.5 Load balance and adaptive compute grids

In parallel computing, it is important to maintain load balance between processes; otherwise, some processes are busy computing while others could be hungry awaiting tasks. To this end, dynamically adaptive compute grids are developed in 3-D DEM. In a test of pouring particles into a container via gravity, it can be clearly observed from the movie that the compute grids dynamically follow motion of the particles and redistribute across the space. Three snapshots of this process are captured and shown in Fig. 7, where the 2 $\times$ 2 $\times$ 3 compute grids in x, y, z direction, respectively, are marked by green boxes (differentiated from the fixed black box of the container). Note that compute grids must be distinguished from the physical container in terms of underlying data structure because compute grids are a dynamic data structure while a container uses a fixed one.

A gravitational depositing process of 1 million polydisperse ellipsoidal particles is simulated with dynamic load balancing across 256 compute nodes, and relevant high-resolution videos are located at https://www.youtube.com/playlist?list=PL0Spd0Mtb6vVeXfGMKS6zZeikWT55l-ew.

4.6 Minimizing global communication

Parallel algorithms have two kinds of communication patterns: local and global. One of the principles in designing high-performance parallel algorithms is to minimize global communication and prefer local communication.

As pointed out in Sect. 4.2, there are three steps involving global communication. Among them, step 2 (2-Root process divides and broadcasts info) is executed once before entering time increment loops; step 9 (9-All processes update compute grids) calls a function MPI_Allreduce on a few floating-point numbers, and thus it causes minimal communication; step 10 (10-All processes merge and output info) tries to collect particles from all processes and causes high communication; however, it does not execute at each time increment. Instead, it runs on a specified interval: For instance, it only runs 100 times during 5 million time increment steps; thus, the communication overhead is still negligible.

At each time increment, two steps undergo local communication: They are step 3 (3-All processes communicate with neighbors) and step 12 (12-All processes migrate particles). In these two steps, a process exchanges particle information through border layers or migration layers with its 26 possible neighbors, which is a typical local communication.

Fig. 7

Dynamically adaptive compute grids that achieve efficient load balance. a Initial configuration of particle pluviation, b middle stage of particle pluviation and c final stage of particle pluviation

4.7 OOP/C++/STL and boost C++ libraries

The principles of object-oriented programming (OOP) [15, 27] are applied in the design and programming of the code. For instance, various classes are designed to model the practical concepts and objects that exist in a DEM simulation system: particles, interparticle contacts, assemblage of particles and boundaries, and the particle class is refactored to accommodate more particle shapes such as ellipsoidal, poly-ellipsoidal, and super-ellipsoidal particles using polymorphism. The Standard Template Library (STL) is heavily used such as vector, map, and list to ensure code robustness and performance.

In developing MPI transmission of 3-D DEM, the Boost C++ libraries are heavily relied on, such as Boost.MPI, Boost.Serialization, Boost Non-blocking communication. For instance, a process’s local communications with its 26 neighbors (six surface border layers, 12 edge border layers, and eight vertex border layers) are all accomplished in a non-blocking manner.

Boost.MPI runs on top of MPI implementations. On DoD Spirit supercomputer, we choose to use a robust combination of Intel compilers 13.0.1 and SGI MPT 2.11, based on which we build Boost C++ 1.57.

4.8 Particle–boundary interaction

Step 10 (10-All processes merge and output info) in the flowchart shown in Fig. 4 not only gathers particle information from all processes but also collects information on particle–boundary interaction from those boundary processes. As shown in Fig. 7, to obtain particle–boundary interaction information on the bottom and four sides of the top-open rigid container, relevant parallel processes must be identified, collected, and then communicated to merge the information.

4.9 Avoiding large memory consumption with MPI

Step 10 (10-All processes merge and output info) in the flowchart shown in Fig. 4 was originally coded to gather interparticle contact information from all processes. However, when a simulation of 1 million particles was tested on the Janus supercomputer (1368 compute nodes, 12 cores and 24GB RAM per node) at the University of Colorado Boulder, a severe memory management issue was discovered: On a hybrid MPI/OpenMP execution of 384 processes (1 process/12 threads per node) on 384 nodes, the memory footprint log revealed that the root process gradually depleted node memory (24GB) while other parallel processes retained nearly constant 50MB usage for running up to 40 h wall clock time.

The underlying data structure of C++ class Contact contains two pointers to the pair of in-contact particles. Boost.Serialization serializes and deserializes a pointer inside a class, that means, gathering interparticle contact information not only collects the underlying particle information implicitly, but also may collect particle information multiple times because a particle could appear in multiple interparticle contacts. This explains why the MPI transmission volume increases sharply when using MPI to gather interparticle contact information.

Our solution to the memory consumption issue can be summarized as one principle: prefer post-data processing to MPI global transmission, which covers several details:

• Separate large data operation from MPI transmission.

• Use post-processing code/script to merge or consolidate smaller pieces of data that are output from the runtime.

• Apply parallel I/O technique, or use optimized I/O libraries like HDF or NetCDF, during the process of execution.

4.10 Parallel I/O of interparticle contact information

In ParaEllip3d, a collective and shared file pointer method is selected for parallel I/O such that each process writes its interparticle contact information to a shared data file using a shared pointer, i.e., the function MPI_File_write_ordered is called. In case parallel I/O is not desired, there is a work-around implementation: Each process writes its interparticle contact information to an individual file, and then a post-processing tool is used to merge those files.

4.11 Unique interparticle contact information

Owing to the collection algorithm described in Sect. 4.10, redundant interparticle contact information exists between adjacent processes and must be removed for accurate statistics. As shown in Fig. 8, p1 and p3 each take into account the interparticle contacts at their shared border and produce obvious redundancy or overlapping.

Fig. 8

Redundant interparticle contact information between adjacent processes

During post-processing of interparticle contact statistics from the data file generated from parallel I/O, the redundancy must be eliminated. A special data structure from Boost C++ libraries, “unique hashed associative container” (called $boost::unordered\_set$) is chosen for this task. It is able to process millions of interparticle contacts quickly with automated data consolidation and optimal performance.

5 Performance analysis OF 3D DEM

5.1 Types of DEM simulations

Overall, the problems that are modeled by 3-D DEM fall into two main categories:

• Static or quasi-static problems: laboratory tests such as oedometer compression, isotropic compression, conventional or true triaxial compression, in situ cone penetration test (CPT), static load test of cast-in-place piles.

• Dynamic problems: sand pluviation or deposition with gravity, collapse of particle assemblage, landslide under gravity, explosion beneath soil, installation of precast piles by means of hammers, sand dune movement, etc.

These two types of problems exhibit different features of particle interaction in 3-D DEM simulations. The most pronounced difference is that particles come in and out of contact frequently in dynamic simulations, while there is less contact rearrangement in static or quasi-static modeling. This is mainly why granular materials are sometimes considered as the fourth state of matter (different from solids, liquids, or gases): Granular particles may transition in an instant from deforming like a solid to flowing like a fluid and vice versa.

To cover these variations, sand pluviation (“raining”) is selected as our representative test in evaluating parallel performance. Illustrated in Fig. 7, the sand particles are generated based on a specific soil gradation curve (so that they have different sizes) and “floated” in space initially without interaction; during the process of gravitational pluviation, the bottom particles start to pack up and interparticle contacts should be detected; at the end, all particles come to rest and stay in a relatively “dense” state statically under gravity. The overall pluviation process and the static packed state are both used in the performance evaluation of parallel computing.

The static/quasi-static simulations can achieve excellent load balance, whereas in dynamic simulations, such as buried explosion in sand, it is difficult to achieve good load balance because the motion and distribution of soil grains are unknown. Even though each link-block contains the same number of particles, there could still be load imbalance, because the computational cost is not determined by the number of particles but instead by the number of interparticle contacts, which is unknown before the computation is performed.

The simulations are performed on Spirit, one of the DoD HPC supercomputers (https://centers.hpc.mil/systems/unclassified.html#Spirit). Spirit is an SGI ICE X System located at the AFRL DSRC. Spirit has 4590 compute nodes each with 16 cores (73,440 total compute cores), 146.88 TBytes of memory, and is rated at 1.5 peak PFLOPS. Each compute node has two Sandy Bridge-based Intel Xeon CPU E5-2670 2.60GHz and 32 GB memory. The cluster of compute nodes is interconnected through FDR 14x InfiniBand network with enhanced LX hypercube topology.

5.2 Speedup, efficiency, and laws

In parallel computing, speedup and efficiency are defined as follows:

$$\begin{aligned} \text{ speedup }\psi (n,p)\equiv & {} \frac{\small {\text{ sequential } \text{ execution } \text{ time }}}{\small {\text{ parallel } \text{ execution } \text{ time }}}\nonumber \\\le & {} \frac{\sigma (n)+\varphi (n)}{\sigma (n)+\varphi (n)/p+\kappa (n,p)}\end{aligned}$$

(1)

$$\begin{aligned} \text{ efficiency } \varepsilon (n,p)\equiv & {} \frac{\psi (n,p)}{p} \end{aligned}$$

(2)

where n is the problem size (number of particles), p is the number of processors, $\sigma (n)$ is the inherently serial portion of computation, $\varphi (n)$ is the parallelizable portion of computation, and $\kappa$ is the overhead of parallelization (communication operations plus redundant computation).

Gustafson–Barsis’s law The maximum speedup (also called scaled speedup) $\psi$ achievable by a parallel program is

$$\begin{aligned} \psi \le p+(1-p)s, \end{aligned}$$

(3)

where $s=\sigma (n)/(\sigma (n)+\varphi (n)/p)$ denotes the fraction of time spent in the parallel computation performing inherently sequential operations.

Karp–Flatt metric Given a parallel computation exhibiting speedup $\psi$ on p processors, the experimentally determined serial fraction (EDSF) e can be computed by Eq. (4),

$$\begin{aligned} e=\frac{1/\psi -1/p}{1-1/p} =\frac{p/\psi -1}{p-1}. \end{aligned}$$

(4)

The EDSF e is defined as

$$\begin{aligned} e=\frac{\sigma (n)+\frac{p}{p-1}\kappa (n,p)}{T(n,1)}, \end{aligned}$$

(5)

where T(n, 1) denotes serial execution time using only one processor. The EDSF is useful in detecting sources of efficiency decrease.

Fig. 9

MPI performance across multiple nodes simulating 12k particles

Fig. 10

MPI performance of a large number of particles. a 150k particles and b 1 million particles

5.3 MPI performance across multiple nodes

For sand pluviation of 12k particles, 1–8 compute nodes are utilized and their wall clock time versus computational progress curves are plotted in Fig. 9; for 150k particles, 32 and 64 nodes are used to complete the simulation within 24 h and plotted in Fig. 10a; for 1 million particles, 256 nodes are requested to run within 24 h and plotted in Fig. 10b. Note that all of the times, including wall clock time and module execution times per step, are acquired using function MPI_Wtime for a high-resolution measurement, as well as the “export MPI_WTIME_IS_GLOBAL=1” option to ensure synchronization across all processes.

From all the simulations of 2.5k, 12k, 150k, and 1 million particles, it is observed that wall time versus computational progress curves using different number of compute nodes exhibit larger gaps, which is particularly clear in Fig. 10a: The 32-node and 64-node curves overlap at the earlier stage of simulation when interparticle contacts have not accumulated, but deviate and keep increasing the gap at later simulation stage when more interparticle contacts have developed.

5.3.1 Greater than 100% efficiency

Referring to Fig. 9, a dynamic simulation of 12k particles on one node runs for approximately 44 h, while a two-node simulation runs for approximately 12 h, four-node 8 h, and eight-node 6 h. From Eq. (2), efficiencies for various number of nodes are calculated precisely as follows:

$$\begin{aligned} \begin{aligned} \varepsilon (node=2)&=\frac{(44\times 60+12) \text{ min }}{2\times (11\times 60+27) \text{ min }}=193\% \\ \varepsilon (node=4)&=\frac{(44\times 60+12) \text{ min }}{4\times (8\times 60+10) \text{ min }}=135\% \\ \varepsilon (node=6)&=\frac{(44\times 60+12) \text{ min }}{6\times (6\times 60+37) \text{ min }}=111\% \\ \varepsilon (node=8)&=\frac{(44\times 60+12) \text{ min }}{8\times (5\times 60+50) \text{ min }}=95\% \end{aligned} \end{aligned}$$

(6)

Normally, $0 \le \varepsilon \le 1$ while we see higher than 100% efficiency here. It is not uncommon to achieve higher than 100% parallel efficiency for a small number of processors for some types of problems [9, 13].

Fig. 11

MPI speedup and EDSF of 12k particles. a In terms of number of processors/cores and b in terms of number of nodes

5.3.2 Constraint on performance gain

Figure 11a plots the speedup and EDSF for a static simulation of 12k particles in terms of number of processors (namely, evaluated relative to the single-processor performance). For a problem of fixed size, the speedup of a parallel computation typically increases while the efficiency typically decreases, as the number of processors increases; this is observed in Eq. (6). For the relatively small number of processors (128) used in these tests, the speedup exhibits a nonlinear relationship. MPI has achieved excellent speedup in this test; for example, it achieves a speedup of 83 using 128 cores.

The EDSF is computed using Eq. (4) and plotted as well in Fig. 11a. Firstly, it is seen that the EDSF e values are between 0.01 and 0.43%, which indicates a very low serial fraction. Recall the Gustafson–Barsis’s law presented in Sect. 5.2, $\psi \le p+(1-p)s$, in which we let $s=e$, which actually overestimates the value of s. Using the data from 128 processors, it is obtained that $\psi \le 128+(1-128)*0.43\%=127.45$, thus an excellent scaled speedup is achieved.

Secondly, it is shown that EDSF increases as the number of processors increases. This provides an important indication: The MPI performance gain is not constrained by inherently sequential code, but mostly by parallel overhead, which could be time spent in process start-up, communication, or synchronization, or it could be an architectural constraint, as stated by the book Parallel Programming in C with MPI and OpenMP [17].

5.3.3 EDSF evaluation in terms of nodes

It is worth noting that if speedup and EDSF are evaluated in terms of number of nodes (namely, relative to the single-node performance), the curves exhibit different characteristics as shown in Fig. 11b: Speedup decreases from a range of 1–80 in terms of processors to a range of 1–4 in terms of nodes; EDSF increases from a range of 0.01–0.43 to 26.5–13.7%, and it decreases as the number of compute nodes increases. These data must be interpreted with caution.

It is not uncommon that the EDSF could decrease as the number of compute processors/nodes increases. This was pointed out by Karp and Flatt [13] using the data from the work of the winners of the Gorden Bell Awards in 1987 (http://www.sc2000.org/bell/pastawrd.htm): All of the three problems (Beam Stress Analysis, Surface Wave Simulation, Unstable fluid flow model) reveal a significant reduction of the EDSF using four to 1024 processors.

The interesting discrepancy results from granularity of evaluation and can be analyzed from Eqs. (4) and (5). Firstly, let us see why the EDSF values jump up in terms of node number: From the right term of Eq. (4), $(p/\psi -1)(p-1)$, p changes from 128 (processors) to eight (nodes) as an example, while $p/\psi$ does not change much, which is shown by Fig. 12: $p/\psi = 1/\varepsilon$ according to Eq. (2), and $\varepsilon$ represents efficiency.

Fig. 12

MPI speedup and efficiency of 12k particles. a In terms of number of processors/cores and b in terms of number of nodes

Secondly, for a fixed problem size, the difference lies in the term $p/(p-1)*\kappa (n,p)$. As $\kappa (n,p)$ is a decreasing function of number of compute nodes, as pointed out later in Sect. 6.3.1, the term $p/(p-1)*\kappa (n,p)$ must decrease with an increasing number of nodes.

5.4 Iso-efficiency relation analysis of 3-D DEM

The execution time of a parallel program executing on p processors is

$$\begin{aligned} T(n,p) = \sigma (n) + \varphi (n)/p + \kappa (n,p), \end{aligned}$$

(7)

where n is the problem size (number of particles), p is the number of processors, $\sigma (n)$ is the inherently serial portion of computation, $\varphi (n)$ is the parallelizable portion of computation, and $\kappa$ is the overhead of parallelization (processor communication and synchronization, plus redundant computations). The serial program does not have any interprocessor communication or synchronization, so the execution time is

$$\begin{aligned} T(n,1) = \sigma (n) + \varphi (n). \end{aligned}$$

(8)

In order to sustain the same level of efficiency as the number of processors p increases, problem size n must increase to satisfy inequality (9),

$$\begin{aligned} T(n,1)\ge CT_o(n,p), \end{aligned}$$

(9)

where $T_o(n,p)=(p-1)\sigma (n)+p\kappa (n,p)$, and $C=\varepsilon /(1-\varepsilon )$ is a constant related to efficiency $\varepsilon$. This is called the iso-efficiency metric, which is used to determine the scalability of a parallel system.

For 3-D DEM, supposing n is the number of particles and p the number of processors used, we are able to derive the iso-efficiency metric following the analysis by Michael [17]. Yan and Regueiro [33] pointed out: In both serial and parallel computing of complex-shaped 3-D DEM, the $O(n^2)$ neighbor search algorithm is inefficient at coarse CG; however, it executes faster than the O(n) algorithm at fine CGs that are mostly employed in computational practice. The practical time complexity of 3-D DEM falls between $O(n^2)$ and O(n). Firstly, we let

$$\begin{aligned} T(n,1) = O(n^2), \end{aligned}$$

and the time needed to perform communications which are mostly through 2-D surface layers is

$$\begin{aligned} \kappa (n,p) = \left( \frac{\root 3 \of {n}}{\root 3 \of {p}}\right) ^2 = \left( \frac{n}{p}\right) ^\frac{2}{3}. \end{aligned}$$

Now Eq. (9) gives

$$\begin{aligned} n^2 \ge C p \left( \frac{\root 3 \of {n}}{\root 3 \of {p}}\right) ^2 \Longrightarrow n \ge C p^\frac{1}{4}. \end{aligned}$$

(10)

The amount of memory needed to represent a problem of size n is $M(n)=n$; then, the scalability function, which indicates how the amount of memory used per processor must increase as a function of p in order to maintain the same level of efficiency, is calculated as follows:

$$\begin{aligned} \frac{M(f(p))}{p} = \frac{C p^\frac{1}{4}}{p} = C p^{-\frac{3}{4}}. \end{aligned}$$

(11)

From Eq. (10), when the number of processors p increases from 1 to 10,000, the number of particles n only needs to increase ten times for maintaining the same efficiency; this is easily satisfied in practical computations. Equation (11) states that when the number of processors increases, the memory requirement per processor decreases.

Secondly, we let

$$\begin{aligned} T(n,1) = O(n), \end{aligned}$$

and obtain

$$\begin{aligned} \frac{M(f(p))}{p} = \frac{C p^\frac{1}{4}}{p} = C. \end{aligned}$$

(12)

Equation (12) states that when the number of processors increases, the memory requirement per processor remains constant. In both cases, a parallel system of 3-D DEM is perfectly scalable, according to Michael [17]: “ A parallel system is perfectly scalable if the same level of efficiency can be sustained as the number of processors are increased by increasing the size of the problem being solved.” Overall, the memory scalability function is a nonlinearly decreasing function of the number of processors, which is an intrinsic feature of 3-D DEM.

6 MPI profiling, overhead, and granularity of 3D DEM

6.1 MPI profiling

For each scale of number of particles (2.5k, 12k, 150k, 1M, and 10M), various numbers of compute nodes are used to test the speedup and efficiency in static simulations. In particular, an excessive number of compute nodes may be employed for the following purpose: (1) observe how the speedup and efficiency respond to the increasing number of compute nodes; (2) test whether there is an optimal computational granularity (number of particles per process) for each scale.

6.1.1 Speedup and efficiency

Figure 13 plots the speedup and efficiency of the five scales, each of which tests up to an excessive number of compute nodes. For example, the 2.5k-particle test requests up to 128 nodes, which results in nearly one particle per process, and the 150k-particle test requests up to 512 nodes, which results in nearly 18 particles per process.

Fig. 13

Speedup and efficiency across orders of magnitude of simulation scale in terms of number of particles, a 2.5k particles, b 12k particles, c 150k particles, d 1 million particles, and e 10 million particles

Of the five scales, it can be discovered that the excessive number of compute nodes leads to a decrease in speedup, although the speedup exhibits a nonlinear increase within the range of adequate number of compute nodes. As an example, the 150k-particle test achieves a speedup of 92 using 128 nodes while it achieves a speedup of 76 using 256 nodes. It implies that for each scale of simulation, there must be an optimization of computational resources, which we have defined as computational granularity, namely the number of particles per process.

With regard to efficiency, it can become very low if an excessive number of compute nodes is used. For example, in the 12k-particle test, the efficiency is 0.60 (60%) using eight nodes and 0.07 (7%) using 128 nodes. Low efficiency means low usage of computational resources and should be avoided in parallel computing.

With adequate number of compute nodes, the speedup exhibits a monotonically increasing relationship with respect to the number of compute nodes at all scales, while the efficiency exhibits a monotonically decreasing trend. On the scale of 150k, 1M and 10M particles, higher-than-1 efficiency is observed. The superlinear speedup is pronounced; for example, the efficiency goes as high as 1.97 (197%) at eight nodes in the 150k test; and 17.75 (1775%) at 32 nodes, and 7.65 (765%) at 256 nodes in the 1 million particle test. It is worth noting that for all of the one-node tests across the five scales, the memory size is sufficiently adequate to satisfy the computation and does not cause swap-out to hard drive.

As pointed out in Sect. 2.1, the DEM features a high requirement on CPU frequencies but exerts a low requirement on memory usage. In Sect. 5.4, it is theoretically proved that memory requirement per processor decreases when number of processors and problem size increase to maintain the same efficiency for 3-D DEM. Therefore, it may not be surprising that the larger the simulation scale in terms of number of particles, the more pronounced superlinear speedup may occur, because it becomes more likely that the process-partitioned data fit into CPU caches. This strong superlinear speedup for complex-shaped particle 3-D DEM could be a common thing and needs further investigation as a separate subject.

Figure 14a compiles all of the speedup data from static simulations at the five different scales. A log–log graph is plotted due to the wide range of problem size and number of processors. The Amdahl effect is pronounced: Speedup is an increasing function of the problem size for any fixed number of processors.

Fig. 14

Speedup and efficiency across orders of magnitude of simulation scale in terms of number of particles. a Speedup across orders of magnitude simulation scale and b efficiency across orders of magnitude of simulation scale

Similarly, Fig. 14b plots the efficiency across the five different scales using a log–log graph. Large-scale simulations such as 150k, 1M, and 10M particles exhibit high efficiency above 1, while smaller scale simulations such as 2.5k and 12k particles show a lower-than-1 efficiency.

Fig. 15

MPI profiling on modules for 12k and 150k particles. a 12k particles and b 150k particles

Fig. 16

MPI profiling on modules for 1 million particles. a 1 million particles and b 1 million particles, wall time in logarithmic scale

6.1.2 Module execution time and parallel overhead

Execution time of different modules is plotted with the percentage of parallel overhead using adequate number of compute nodes in Figures 15 and 16. Note that Fig. 16b uses a logarithmic scale in wall time to distinguish between the close curves shown in Fig. 16a. Each module is described here again:

• commuT: communication time in step 3 (3-All processes communicate with neighbors) of the flowchart in Fig. 4.

• migraT: migration time in step 12 (12-All processes migrate particles) of the flowchart.

• compuT: numerical computation time, which equals totalT-commuT-migraT.

• totalT: total time at each step.

• overhead%: (commuT+migraT)/totalT, i.e., the overall parallel overhead percentage.

Note that the IO cost in 3-D DEM is very limited. As a typical example, only 100 snapshots are taken for 5 million time increments of 3-D DEM simulation. The synchronization overhead is less than 0.1% of the commuT across all of the simulation scales such that it is a negligible fraction of overall parallel coverhead, of which the communication cost dominates.

Firstly, the ratio of migration time to communication time is as low as 1–6% across all simulation scales. This makes sense because there are no particles migrating across borders in static simulations, although step 12 must be executed and thus spends a very small fraction of time. Note that this ratio remains low even if it is evaluated in a dynamic simulation because use of the adaptive compute grids minimizes particle migration across borders.

Since step 3 (3-All processes communicate with neighbors) and step 12 (12-All processes migrate particles) of the flowchart employ the same design and implementation with different layer definitions, as shown in Sects. 4.3 and 4.4, it can be approximately deduced that the actual interprocess communication spends about 95% of the overall communication overhead while the additional/redundant computation needed for the communication only takes about 5%.

Secondly, as the number of compute nodes increases, both the computation time and communication time (thus the total time) decrease, and the decrease rates are high at the very beginning and slow down later for a fixed problem size. This is the goal and anticipation from parallel computing. In addition, the communication time remains a small fraction relative to the computation time. That the communication time decreases with increasing number of compute nodes is of particular interest and will be discussed in Sect. 6.3.

Thirdly, the parallel overhead consumes a low fraction of the wall time. On the scale of 12k particles, it stays as high as between 11–21% using 2–8 nodes; on the 150k particles, it ranges between 2.9–16.8% using 2–64 nodes; on the 1 million particles, it ranges between 0.2% to nearly 14% when the number of nodes increases from 2 to 256. Overall, the parallel overhead percentage is nearly 10% for static simulations when an optimal number of compute nodes is used for computation. Considering that six steps are added in order to parallelize the code, as described in Sect. 4.2, the overall parallel overhead (communication operations plus redundant computations) is low and acceptable.

Figure 17 depicts the log–log relationship between module time and parallel overhead for 1 million particles using 1–1024 compute nodes excessively. In particular, a curve fitting is performed for the total execution time per step and parallel overhead percentage. It is seen that the relationship between the total execution time per step and number of nodes can be described in the form of a negative power function,

$$\begin{aligned} T(n,p)=O(p^{-k}), \end{aligned}$$

(13)

where p is the number of nodes and k is a number greater than 1. The relationship between the parallel overhead percentage and number of nodes can be described in the form of a logarithmic function,

$$\begin{aligned} \text{ overhead }\% =O(\text{ log }p). \end{aligned}$$

(14)

T(n, p) decreases quickly and overhead% increases slowly when p increases.

Fig. 17

MPI profiling on modules for 1 million particles using excessive number of nodes

Fig. 18

Computational granularity for various scales of simulation

6.2 Computational granularity (CG) in MPI mode

Figure 18 plots the wall clock time versus number of particles per MPI process on different computational scales such that it is able to read the optimal computational granularity. Due to the wide range of number of particles and wall clock time per step, a log–log graph has to be used.

Table 1 Optimal computational granularities

Fig. 19

Computation time across orders of magnitude of simulation scale. a Logarithmic scale and b log–log scale

Overall, as the number of compute nodes increases and thus the number of particles per process decreases, the wall clock time decreases, which indicates that a smaller computational granularity leads to faster computation for a fixed problem size. However, it can be observed that the wall time starts to increase when an excessive number of compute nodes is used and thus the computational granularity becomes too small. This occurs for all of the five scales: 2.5k, 12k, 150, 1M, and 10M particles.

Although the speedup can keep increasing and thus wall clock time can keep decreasing until an extremely excessive number of compute nodes is used and thus leads to a speedup decrease and wall clock time increase eventually, the reasonable amount of computational resource (number of compute nodes) usually should not be requested too aggressively in performing practical computational tasks. For example, the 150k-particle simulation achieves a speedup of 74.6 (27.3 s per step) using 64 nodes, and 92.3 (25.3 s per step) using 128 nodes; then requesting 64 nodes may be a better choice than requesting 128 nodes.

As a guideline, the optimal computational granularity (CG), which can be estimated before submitting a job on supercomputers, is recommended in Table 1.

6.3 Communication time and parallel overhead versus number of nodes

Figure 19 depicts the computation time per step versus number of compute nodes across five orders of magnitude of simulation scale. For each fixed problem size (simulation scale), the computation time decreases with an increasing number of compute nodes; this is in response to the term $\varphi (n)/p$ in Eq. (2), wherein $\varphi (n)$ is the parallelizable portion of computation, n is the problem size, and p is the number of processors. For a larger problem size, the computation time increases.

Fig. 20

Communication time across orders of magnitude of simulation scale. a Logarithmic scale and b log–log scale

6.3.1 Communication feature of 3-D DEM

Figure 20 plots the communication time per step versus number of compute nodes across five orders of magnitude of simulation scale. For each fixed problem size (simulation scale), the communication time decreases with an increasing number of compute nodes; this is in response to the term $\kappa (n,p)$ in Eq. (2), wherein $\kappa (n,p)$ denotes the time required for parallel overhead. The communication time increases as the problem size increases.

It is interesting to see that $\kappa (n,p)$ is a decreasing function of p, the number of nodes/processors for 3-D DEM. It is known that $\kappa (n,p)$ is an increasing function of p for many problems in parallel computing. Why does the 3-D DEM exhibit such a different feature?

It can be attributed to the inherently complicated 3-D DEM model. When an ellipsoidal particle is transmitted through the border/ghost layer or migration layer of a link-block using MPI, all the information of the particle needs to be transmitted: particle ID, particle type, density, Young’s modulus, Poisson’s ratio, current and previous position, current and previous orientation, current and previous translational and rotational velocities, current and previous force and moment (note a history-dependent Mindlin’s shear model is adopted). This amounts to 624 bytes in the C++ class for each particle. As a comparison, a computational cell in a 3-D CFD (Computational Fluid Dynamics) solver for the Euler equations only needs to transmit five variables (density, three velocities, and energy), which amounts to 40 bytes in a C++ class. Put simply, the 3-D DEM inherently involves much larger MPI transmission volume than many other problems and poses a high bandwidth requirement between compute nodes.

For a problem of fixed size, the communication volume (MPI message transmission size) becomes smaller, while the communication times (how many times that MPI transmission initiates and finalizes) become larger, when the number of compute nodes increases and thus the communication granularity decreases. The parallelism of 3-D DEM enables the use of smaller communication granularity on the grounds of its large MPI transmission volume, and that is why the 3-D DEM achieves less communication time using more computational resources, as long as the latency of interconnect between compute nodes is low.

Fig. 21

Parallel overhead across orders of magnitude of simulation scale. a Linear scale and b logarithmic scale

Fig. 22

Execution time and overhead across orders of magnitude of simulation scale. a Computation time (log), b computation time (log–log), c communication time (log), d communication time (log–log), and e parallel overhead percentage

6.3.2 Percentage of parallel overhead

Figure 21 plots the parallel overhead percentage versus number of compute nodes across five orders of magnitude of simulation scale using a log–log graph. For each fixed problem size (simulation scale), the parallel overhead percentage increases with an increasing number of compute nodes. It means that computation time decreases faster than the communication time when the number of compute nodes increases and the computational granularity decreases accordingly. This makes sense because computation executes in 3-D space while communication occurs in 2-D space, referring to the link-block concept described in Sect. 4.1.

The parallel overhead percentage is

$$\begin{aligned} \text{ overhead }\% = \frac{\kappa (n,p)}{\sigma (n)+\varphi (n)/p} \approx \frac{p\kappa (n,p)}{\varphi (n)}, \end{aligned}$$

(15)

where n is a constant for a fixed problem size and $\kappa (n,p)$ is a decreasing function of p. $\sigma (n)$ is negligible in the parallel DEM, as pointed out in Sect. 5.2. Therefore, $p\kappa (n,p)$ turns out to be an increasing function of p as well as the overhead%.

As pointed out by Eq. (14), the parallel overhead percentage has a time complexity $O(\text{ log } p)$, then $\kappa (n,p)$ should have the following time complexity,

$$\begin{aligned} \kappa (n,p)=O\left( \frac{\text{ log } p}{p}\right) . \end{aligned}$$

(16)

6.4 Communication time and parallel overhead versus problem size (simulation scale)

Figure 22 plots the computation time, communication time, and parallel overhead percentage with respect to the problem size (number of particles) using various number of compute nodes. For each fixed number of compute nodes, both the computation time and communication time increase with an increasing problem size, and it can be observed that the former increases faster than the latter, which actually leads to the parallel overhead percentage decreasing with an increasing problem size. This is also attributed to the fact that computation executes in 3-D space while communication occurs in 2-D space.

Fitting these curves exhibits the following equations:

$$\begin{aligned}&\kappa (n,p)=O(n^{k1}), \quad 0<k1<1 \end{aligned}$$

(17)

$$\begin{aligned}&\varphi (n)/p=O(n^{k2}), \quad 0<k2<1 \end{aligned}$$

(18)

$$\begin{aligned}&k1<k2 \end{aligned}$$

(19)

$$\begin{aligned}&\text{ overhead }\% =O(n^{-k3}), \quad 0<k3<1 \end{aligned}$$

(20)

where n denotes the problem size.

Applying Eq. (15) again, it is obtained that

$$\begin{aligned} k1=k2-k3. \end{aligned}$$

(21)

As an example, fitting the curves for 32 compute nodes acquires the following values:

$$\begin{aligned} k1=0.42, \; k2=0.97, \;k3=0.52 \end{aligned}$$

which satisfies Eq. (21) approximately.

Table 2 Time complexity of complex-shaped 3-D DEM

In summary, the execution time, communication time, and parallel overhead percentage have time complexities with regard to the number of compute nodes p and the number of particles n as shown in Table 2.

7 Summary

Parallel computing for 3-D DEM of complex-shaped granular materials is designed and implemented in C++ following Foster’s four-step methodology, with the presentation of concepts of link-block, ghost/border layer, and migration layer. It features negligible serial fraction and low parallel overhead when executing on modern multiprocessing supercomputers.

The parallel code is heavily tested with dynamic and static DEM simulations across a wide order of magnitude of scales in terms of number of particles, on DoD HPC supercomputers, and it achieves outstanding performance gain and computational efficiency. In particular, along with the derivation of theoretical scalability function, it exhibits an inherently perfect scalability numerically and indicates a great potential for simulating large-scale DEM problems with complex-shaped particles.

The time complexity of execution time, communication time and parallel overhead percentage of complex-shaped 3-D DEM are formulated with regard to the number of compute nodes (computational resource) and the number of particles (computational scale). It is particularly important to discover that communication time is a decreasing function of the number of compute nodes. The optimal computational granularities (CG) across five orders of magnitude of simulation scale are given as a guideline for the parallel computing of complex-shaped 3-D DEM. These days, DEM researchers are still struggling in simulating a few thousand complex-shaped particles, whereas we have advanced the scale to 10 million and used them for simulations such as gravitational deposition and buried explosion in sandy soils for a DoD project successfully. All of these details and progress should be able to provide a useful guide for future complex-shaped particle 3-D DEM development and applications.