On the convergence of logit-response to (strict) Nash equilibria

Abstract

We show that the logit-response dynamics converges to a subset of (strict) Nash equilibria for any weakly acyclic, N-player normal form game. The result holds independently of whether revision opportunities arise as in asynchronous learning or in other ways, as long as the dynamics is regular. Our analysis generalizes and organizes recent convergence results in the literature. Further, it provides a simple selection criterion, because convergence to strict Nash equilibria obtains even in the presence of non-strict, pure-strategy Nash equilibria.

1 Introduction

The logit dynamics of Blume (1993, (1997) has received a great deal of attention in the game-theoretical literature. In the original specification of the dynamics, a single player is randomly selected every period to revise his or her strategy, while the other players must uphold their strategies. In this asynchronous case, the dynamics converges to a specific subset of Nash equilibria in exact potential games, namely the set of potential maximizers. Alós-Ferrer and Netzer (2010) showed that this is a knife-edge result. On the one hand, the result fails if larger classes of games are considered, e.g., it does not extend to weighted potential games, and for generalized ordinal potential games, not even convergence to Nash equilibria is guaranteed. On the other hand, the result hinges upon the assumption of asynchronous learning, and it fails even for exact potential games if more general revision processes are allowed for.

As pointed out by Alós-Ferrer and Netzer (2015), it is important to establish robust results, i.e., results which are independent of details such as the specification of revision opportunities. For instance, that work showed that the selection of potential maximizers is robust for the subclass of supermodular, symmetric binary-action games. Starting with Alós-Ferrer and Netzer (2010), a recent literature has examined the issue of convergence to the set of (pure-strategy) Nash equilibria for the logit-response dynamics with general revision processes (see also Marden and Shamma 2012; Coucheney et al 2014). This note organizes that literature by providing a simple result. Young (1993) introduced the class of weakly acyclic games, which are those where an iteration of one-sided best replies reaches a strict Nash equilibrium, starting at any possible strategy profile. We prove that for this class of games, robust convergence to the set of strict Nash equilibria obtains. Unlike previous results, ours does not require an assumption of unique best replies or strictness of all Nash equilibria. An immediate consequence is that in weakly acyclic games with both strict and non-strict Nash equilibria, the logit-response dynamics will select the former.

2 Definitions

We adopt the following notation throughout. The tuple $\Gamma =(I,(S_i,u_i)_{i\in I})$ denotes a finite normal form game. Each player $i \in I=\{1,\ldots ,N\}$ has a finite set $S_i$ of pure strategies and a payoff function $u_i: S \rightarrow \mathbb {R}$, with $S = S_1 \times \cdots \times S_N$ denoting the set of strategy profiles $s=(s_1,\ldots ,s_n)=(s_i,s_{-i})$.

Different classes of games have been characterized in the literature through properties of the best-reply correspondence, involving best-reply paths and cycles. A path is a sequence $(s^0,\ldots ,s^m)$ of strategy profiles, where for each $k=0,\ldots ,m -1$, there exists $i_k \in I$ such that $s_{i_k}^k \ne s_{i_k}^{k+1}$ and $s_{-{i_k}}^k = s_{-{i_k}}^{k+1}$, so that one and only one player changes strategy at each step. A path is a best-reply path if, additionally,

$$\begin{aligned} s_{i_k}^{k+1} \in \arg \max _{s_{i_k} \in S_{i_k}} u_{i_k}(s_{i_k},s_{-{i_k}}^k) \end{aligned}$$

holds for each $k=0,\ldots ,m -1$, so that the updating player chooses a best reply to the other players’ fixed strategies. A cycle is a path $(s^0,\ldots ,s^m)$ with $m \ge 2$ such that $s^m=s^0$. A best-reply cycle is a cycle which is a best-reply path. The class of weakly acyclic games was introduced by Young (1993, (1998).

Definition 1

$\Gamma$ is weakly acyclic if for every $s\in S$, there exists a best-reply path $(s^0,\ldots ,s^m)$ such that $s^0=s$ and $s^m$ is a strict Nash equilibrium.

The intuition is that strict Nash equilibria are the “sinks” of the best-reply correspondence, and hence weakly acyclic games ensure a basic form of stability for elementary dynamics based on best replies (Young 1993, p. 64).

We now briefly introduce the logit-response dynamics, which goes back to Blume (1993). The presentation follows Alós-Ferrer and Netzer (2010). Time is discrete. Every period, a subset of players receives the chance to revise their strategies. Players behave as myopic best-repliers, but their decisions are subject to mistakes. The probability that a revising player i chooses strategy $s_i$, given the profile $s_{-i}$, is described by the logit choice function:

$$\begin{aligned} p_i(s_i,s_{-i})=\frac{\mathrm{e}^{\beta u_i(s_i,s_{-i})}}{\sum _{s_i' \in S_i} \mathrm{e}^{\beta u_i(s_i',s_{-i})}}, \end{aligned}$$

where $0< \beta < \infty$ measures the degree of noise in best-reply behavior. This choice function converges to a (myopic) best-reply rule when $\beta \rightarrow \infty$. For any fixed $0< \beta < \infty$, players choose all strategies with strictly positive probabilities, but those that yield smaller payoffs are chosen with smaller probability. Further, as $\beta \rightarrow \infty$, the choice probability of a non-best reply goes to zero faster for a strategy that yields smaller payoffs.

Alós-Ferrer and Netzer (2010, (2015) showed that results can depend on the specification of revision opportunities. A revision process is a probability measure q on the set of all subsets of I, with the property that

$$\begin{aligned} \forall \; i\in I, \; \exists J\subseteq I \text { with } i\in J \text { and } q(J)>0. \end{aligned}$$

The interpretation is that, each period, the updating players are those in J with probability q(J), and there are no “dummy players” that never revise their strategies. We call J a revising set if $q(J)>0$, i.e., if there is a positive probability that exactly the players in J revise their strategies simultaneously. Asynchronous learning, for instance, refers to revision processes where the revising sets are the singletons $\{i\}$ for all $i\in I$ (as in Blume 1993). Independent learning refers to revision processes where all subsets $J \subseteq I$ are revising sets. A particular case thereof is independent inertia, where each player revises with a fixed, independent probability $0<p<1$ (as in Sandholm 1998, in a framework with uniform mistakes). A revision process is regular if $q(\{i\})>0$ for all $i\in I$. This minimal condition requires that each player has a positive probability of being the only one who updates. It excludes examples such as simultaneous learning, where only the complete player set I is a revising set (also discussed in Sandholm 1998).¹

The resulting stochastic process (with or without regularity) is an ergodic Markov chain on the state space S, which has a unique invariant distribution $\mu ^{\beta }$. We say that a strategy profile $s \in S$ is stochastically stable if $\lim _{\beta \rightarrow \infty } \mu ^{\beta }(s)>0$, analogously to the convergence criterion in the so-called “mistakes models” (Kandori et al 1993; Young 1993; Ellison 2000). Alós-Ferrer and Netzer (2010) established a general characterization of stochastic stability for the logit-response dynamics. Since we will provide an elementary proof of our main convergence result based on this characterization, we briefly repeat it here. Let $s, s' \in S$ be two states (strategy profiles) such that there is a revising set J that contains all players j with $s'_j\ne s_j$, so that the revision process allows for a direct transition from s to $s'$. The waste $W(s,s',J)$ of this transition with revising set J is defined as:

$$\begin{aligned} W(s,s',J)=\sum _{j \in J} \left[ \left( \max _{s_j''\in S_j} u_j (s_j'',s_{-j})\right) - u_j(s'_j,s_{-j})\right] , \end{aligned}$$

i.e., as the sum, player by player, of the difference between the payoff of a best response and the payoff of the prescribed move to $s'$. Given any $s^*\in S$, a revision $s^*$-tree is a directed tree on the set S flowing toward $s^*$ (the unique root), where all arrows $s \rightarrow s'$ must be allowed by the revision process and are labeled with an admissible revising set. The waste of such a tree is the sum of the wastes of its arrows. The stochastic potential of $s^*$ is the minimum waste among all revision $s^*$-trees. Alós-Ferrer and Netzer (2010, Theorem 1) proved that a state is stochastically stable if and only if it minimizes stochastic potential in S (in particular, stochastically stable states exist).

3 Convergence result

Theorem 1

Let $\Gamma$ be a weakly acyclic game. Then, the set of stochastically stable states of the logit-response dynamics with any regular revision process is contained in the set of strict Nash equilibria.

Proof

Fix any $s^0 \in S$ which is not a strict Nash equilibrium, and consider any revision $s^0$-tree $T^0$ with waste $W(T^0)$. Since the game is weakly acyclic, there exists a best-reply path $(s^0,\ldots ,s^m)$ ending in a strict Nash equilibrium $s^m$. Construct a revision $s^m$-tree $T^m$ by modifying $T^0$ iteratively as follows. For each $k=0,\ldots ,m-1$, add the arrow $s^k \rightarrow s^{k+1}$ with revising set $\{i_k\}$ for the unique player $i_k$ who changes strategy at this step of the best-reply path. This is possible under any regular revision process. Further, delete the arrow leaving $s^{k+1}$. The added arrows cause no waste by definition of best-reply path. The arrow deleted in the final step left the strict Nash equilibrium $s^m$, so it must have caused strictly positive waste. Hence, $W(T^m)$ is strictly smaller than $W(T^0)$, which implies that $s^0$ is not stochastically stable. Since stochastically stable states always exist, the conclusion follows. $\square$

As pointed out in Alós-Ferrer and Netzer (2015), special attention should be given to results which do not depend on the specification of revision opportunities. In this sense, the convergence result above is robust with respect to revision processes.

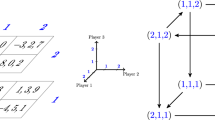
The hypothesis of weak acyclicity cannot be dispensed with. At the same time, there are games which are not weakly acyclic but in which convergence to the set of strict Nash equilibria still obtains for every regular revision process. Hence, weak acyclicity is a sufficient property for convergence, but does not lend itself to a characterization. This is not surprising. Weak acyclicity relies exclusively on the ordinal properties of the best-reply correspondence, while the characterization of stochastically stable states relies on the cardinal concept of waste. Game 1 illustrates this point. Let $0<x,y<1$. The profile (C, C) is the only strict Nash equilibrium. There is, however, a best-reply cycle $(A,A)\rightarrow (A,B) \rightarrow (B,B) \rightarrow (B,A) \rightarrow (A,A)$ among four non-strict Nash equilibria. The game is not weakly acyclic, because with $x>0$, the best-reply cycle cannot be left with a best reply, hence the states in the cycle cannot be connected to a strict Nash equilibrium. With any regular revision process, a transition involving a single revising player from the cycle to (A, C) can be achieved with a waste of $x<1$, while other transitions leaving the cycle have a waste of at least 1. All states outside the cycle can be connected to (C, C) with a single best reply, so the stochastic potential of (C, C) is exactly x. The transition $(C,C)\rightarrow (C,B)$, again involving a single revising player, has waste $y<1$, and from the latter state a best reply leads to the cycle. Hence, the stochastic potential of the states in the cycle is y. We conclude that, if $x>y$, the states in the cycle are stochastically stable for any regular dynamics, while the unique strict Nash equilibrium is not. In contrast, if $y<x$, the dynamics always converges to the unique strict Nash equilibrium.

Marden and Shamma (2012) define a game to be weakly acyclic under best replies if every strategy profile can be connected to some (not necessarily strict) Nash equilibrium by a best-reply path. They show the following (Theorem 4.1): If $\Gamma$ is a weakly acyclic game under best replies in which all pure-strategy Nash equilibria are strict, then the set of stochastically stable states of the logit-response dynamics with any regular revision process is contained in the set of Nash equilibria. This is an immediate corollary to Theorem 1 above. If all Nash equilibria are strict, then the definition of weak acyclicity under best replies coincides with the definition of weak acyclicity by Young (1993). However, the hypothesis of weak acyclicity employed in Theorem 1 does not require all Nash equilibria to be strict. Theorem 1 shows that, in the presence of both strict and non-strict Nash equilibria, all regular versions of the logit-response dynamics select the former. The result of Marden and Shamma (2012), in contrast, does not allow for non-strict Nash equilibria and, hence, is not a selection result in this sense. Consider, for instance, Game 2. Again, $(A,A)\rightarrow (A,B) \rightarrow (B,B) \rightarrow (B,A) \rightarrow (A,A)$ forms a best-reply cycle among four non-strict Nash equilibria. However, state (C, B) can be reached with a single best reply from that cycle, and then a further best reply leads to the strict Nash equilibrium (C, C). Hence, Game 2 is weakly acyclic, but due to its non-strict Nash equilibria, it is not covered by Marden and Shamma (2012).

4 Corollaries and relation to the literature

4.1 Best-response potential games

The game $\Gamma$ is a best-response potential game (Voorneveld 2000) if there do not exist best-reply cycles in which at some step the updating player experiences a strict improvement.

Marden and Shamma (2012) showed that any such game is weakly acyclic under best replies. Strictness of all Nash equilibria then additionally implies that any such game is weakly acyclic. Hence, it follows from our Theorem 1, or from Theorem 4.1 in Marden and Shamma (2012), that the set of stochastically stable states of the logit-response dynamics with any regular revision process is contained in the set of (strict) Nash equilibria, for any best-response potential game in which all pure-strategy Nash equilibria are strict. This generalizes Theorem 2 in Alós-Ferrer and Netzer (2010). We remark here that, regrettably, one hypothesis was missing in Alós-Ferrer and Netzer (2010). The result as stated there incorrectly asserts convergence for all best-response potential games. For the proof to be correct, however, the additional hypothesis of unique best replies is needed (see Coucheney et al 2014). The arguments above show that the assumption of unique best replies is in fact too strong, since robust convergence already obtains in the more general case where not all best replies are unique, but merely all pure-strategy Nash equilibria are strict.

It is easy to see that the hypothesis that all pure-strategy Nash equilibria are strict cannot be relaxed. Consider Game 3 (Example 7 in Coucheney et al 2014). This game is an exact potential game, and hence best-response potential (see Voorneveld 2000). If the regular revision process gives positive probability to the set $\{1,2\}$, the transition $(A,A)\rightarrow (B,B)$ has zero waste, and all profiles, including the non-Nash equilibrium (B, B), are stochastically stable.

4.2 Generalized ordinal potential games

An improvement path is a path $(s^0,\ldots ,s^m)$ such that at each $k=0,\ldots ,m -1$ the updating player $i_k$ improves strictly, i.e., $u_{i_k}\left( S_{i_k}^{k+1},s_{-{i_k}}^{k}\right) > u_{i_k}\left( S_{i_k}^{k},S_{-{i_k}}^k\right)$. A game has the finite improvement property if every improvement path is finite (in particular, there can be no cyclic improvement paths). Monderer and Shapley (1996) defined the class of generalized ordinal potential games and proved that a finite game belongs to this class if and only if it has the finite improvement property. Generalized ordinal potential games are neither a subset nor a superset of best-response potential games Voorneveld (2000).

We first note that any (finite) generalized ordinal potential game where all Nash equilibria are strict is weakly acyclic.² Hence, it follows from Theorem 1 that the set of stochastically stable states of the logit-response dynamics with any regular revision process is contained in the set of (strict) Nash equilibria, for any generalized ordinal potential game in which all pure-strategy Nash equilibria are strict. To the best of our knowledge, this is a new insight.

Coucheney et al (2014) pointed out that any generalized ordinal potential game is a best-response potential game under the assumption that all best replies are unique, so that already the arguments in Sect. 4.1 apply. This is not the case under our weaker assumption of strictness of all Nash equilibria. Consider the three-player Game 4, where the third player chooses tables. The game has the unique Nash equilibrium (B, B, B), which is strict. There is a best-reply cycle with a strict improvement in the left table, $(A,A,A) \rightarrow (A,B,A) \rightarrow (B,B,A) \rightarrow (B,A,A) \rightarrow (A,A,A)$, hence this is not a best-response potential game. There are no infinite improvement paths, however. Starting in the left-hand table, any such path must eventually move to the right-hand table, where it ends in the Nash equilibrium (B, B, B). Hence, this is a generalized ordinal potential game in which all equilibria are strict, but not a best-response potential game.

5 Conclusion

We have presented a simple result which organizes recent developments in the literature. For the class of weakly acyclic games, any specification of the logit-response dynamics, that is, any combination of the logit choice rule at the individual level together with a regular revision process, will converge to the set of strict Nash equilibria, in the stochastic stability sense.

The fact that the convergence result obtains for the class of weakly acyclic games is interesting in itself. Weakly acyclic games are those for which an iterative specification of a simple best-response process would converge to strict Nash equilibria. Young (1993) relied on weak acyclicity to analyze the convergence of adaptive dynamics, which is a form of truncated fictitious play where players choose best responses to a sample of observations of opponents’ play within recent memory. It seems safe to say at this point that the class of weakly acyclic games plays an important role for several, not closely-related game dynamics, and is worthy of further attention.