Optimal control of a fractional order epidemic model with carriers

Abstract

In this work, a fractional-order S–$I_{c}$–I–R epidemic model with carriers has been proposed where we have also studied the dynamics of the carrier model in the presence of treatment and vaccination. We have studied the local and global stability of the model with different criteria. The existence and uniqueness criterion along with positivity and boundedness of the solutions have also been established. An optimal control problem has been formulated and studied by the help of Pontryagin principle. Finally, we have performed numerical simulation and studied the impacts of carriers in the transmission dynamics.

1 Introduction

Today, quantitative problems in the field of epidemiology have been considered one of the most important topics in Mathematical Biology. Carriers play an significant role in the transmission of infectious disease like typhoid, hepatitis B, Epstein-Barr virus and so on. Carriers are able to transmit their illness without exhibiting any symptom. Mainly there are two type of carriers:

• 1. Genetic carriers

• 2. Infectious disease carriers

Genetic carriers carry the disease on their children’s genes [1, 2].

We have focused our study on infectious disease carriers who are asymptomatic, unwary of their conditions and hence they are able to spread the disease. Consider the case of typhoid which produces long term asymptomatic carriers by the bacteria Salmonella Typhi or Salmonella Paratyphi :

• (1) Globally approximately 12 million cases have been found where typhoid fever occurred.

• (2) In India, typhoid is a significant issue.

• (3) In a multicentric study, about 495 per 100,000 children were affected by typhoid.

• (4) World Health Organization (WHO) recommends the planned use of typhoid vaccines for controlling endemic disease.

Although in most of the cases only high risk populations are vaccinated and so the unvaccinated carriers excrete the typhoid bacteria continuously into their faeces and act as a persistent reservoir of infection [3].

Another example of infectious disease that causes long term asymptomatic carriage is Hepatitis B. It is a liver disease occurred due to Hepatitis B virus (HBV). Most HBV-affected people completely recover and develop a long term immunity to the virus. However, nearly 5–10$\%$ of adults will develop chronical HBV infection and 15–30$\%$ will grow liver disease. Control of Hepatitis B infection is one of the challenging situations due to the existence of large pool of chronic carriers responsible for transmitting this disease [2]. Inspired by the classic work of Kermack and McKendrick [4], compartmental models for epidemic spreading (e.g. SIR, SIS, SEIR, SEIS, SEIRS) have been recurrently used over the years by relying on systems of ordinary differential equations [5,6,7,8].

Fractional calculus can be considered as the generalization of integer order [9, 10]. In systematic study it has been observed that integer order model is a special case of fractional order model where solution of fractional order system must converge to the solution of integer order system as the order approaches to one [11]. There are many fields where fractional order systems are more suitable than integer order systems. Phenomena, which are connected with memory property and affected by hereditary property, cannot be expressed by integer order system [12]. It is observed that the data collected from real life phenomena fit better with fractional order system [13]. Diethelm has compared the numerical solutions of fractional order system and integer order system and concluded that the fractional order system gives more relevant interpretation than integer order system [14]. There are many systems [13, 15,16,17,18,19,20,21,22,23] which have been studied recently in fractional order framework. In epidemiology, Ebola virus model has been studied in Caputo differential equation system in 2015 [24].

Optimal control problem in fractional order system was first noticed in Agarwal’s work in 2004 [25]. In 2018, fractional order optimal control for HIV/AIDS has been studied significantly by Kheiri et al. [26] and FOCP (fractional optimal control problem) on enzyme kinetic model was proposed and analyzed numerically by Basir et al. [27]. Recently, FOCP on pathogen model in case of environmental stressors has been studied by Tugba et al. [28]. We have also recently studied a FOCP on synthetic drugs transmission [20].

Motivated by the previous works and considering the advantages of fractional derivative, we are able to construct a deterministic fractional order model for the disease transmission with carrier. As per the literature, until now no one has yet considered transmission dynamics of epidemic model with carrier with treatment and vaccination. The previous works on carrier were done in ordinary differential equations but we have formulated our model in Caputo fractional order framework. We have also studied the dynamics of the carrier model in the presence of treatment and vaccination. The controlled vaccination may be more useful and brings some interesting facts about the possible eradication of disease.

In this work, we have presented a fractional order S-$I_{c}$-I-R compartmental model using Caputo fractional differential equations. In the beginning, it is shown that the solution of the proposed system is unique and bounded. We have also discussed the feasible condition of the solutions of the system. Transfer dynamics has also been discussed by the help of reproduction number in the next section. Local and global stability of equilibrium points (both disease free and endemic) have been analyzed systematically. Then we have presented our system as optimal control problem with suitable control variables and derived optimal conditions. Finally, numerical simulations have been performed followed by some conclusions of the whole work.

2 Model formulation

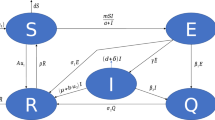
We have formulated a fractional order compartmental model along with vertical transmission of disease and carriers [29, 30]. Here S, $I_{c}$, I, R represent the respective size of susceptible population, carrier population, symptomatically infectious population and recovered population. A susceptible individual can be infected through direct contact with an infectious individual or carrier. It is assumed that newly infected individuals can become carriers with proportion q or show symptoms with proportion $(1-q)$. It is also assumed that the rate of transmission b for carrier is higher than the rate $\phi$ of symptomatically infected individuals as they (carriers) are unwary of their situation and therefore continue with their regular actions. Carriers are become symptomatic at a rate $\alpha$ and we have considered that vertical transmission of disease occurs both in carrier stage (asymptomatic) and infected (symptomatic) stages [31]. Infectious diseases, such as HBV, may have a long incubation period. Here $\alpha$ can be regarded as diagnosis rate. We also assume that a constant influx $\eta$ and $\delta _1, \delta _2, \delta _3, \delta _4$ denote the mortality rates of $S,I_{c},I$ and recovered class R respectively. The parameters are described briefly in Table 1.

$$\begin{aligned} {}^{C}_{t_0}D^{\varepsilon }_{t}S(t)&={\eta }^{\varepsilon }{-}{\delta _{1}}^{\varepsilon }S {-}S(b^{\varepsilon }I_{c}{+}{\phi }^{\varepsilon }I){-}{\theta ^{\varepsilon }S} ,S(0)=S_{0}{>}0,\nonumber \\ {}^{C}_{t_0}D^{\varepsilon }_{t}I_{c}(t)&=qS(b^{\varepsilon }I_{c}\nonumber \\&\quad +{\phi }^{\varepsilon }I) -({\delta _{2}}^{\varepsilon }+{\alpha }^{\varepsilon })I_{c} +{m_{1}}^{\varepsilon } I_{c} \nonumber \\&\quad +{m_{2}}^{\varepsilon } I,I_{c}(0)=I_{c,0}>0, \nonumber \\ {}^{C}_{t_0}D^{\varepsilon }_{t}I(t)&=(1-q)S(b^{\varepsilon }I_{c}+{\phi }^{\varepsilon }I) -({\delta _{3}}^{\varepsilon }+{\xi }^{\varepsilon })I\nonumber \\&\quad +{\alpha }^{\varepsilon }I_{c}+{m_{3}}^{\varepsilon } I_{c} +{m_{4}}^{\varepsilon } I,I(0)=I_{0}>0,\nonumber \\ {}^{C}_{t_0}D^{\varepsilon }_{t}R(t)&={\xi }^{\varepsilon }I +{\theta }^{\varepsilon }S-{\delta _{4}}^{\varepsilon }R,R(0)=R_{0}>0, \end{aligned}$$

(1)

where $0<\varepsilon < 1,\ \text {and}\ ^{C}_{t_{0}}D^{\varepsilon }_{t}$ stands for Caputo fractional derivative, $t_{0}\ge 0$ is the initial time. Equation system (1) is dimensionally consistent as both sides have dimension $(time)^{-\varepsilon }$. Next, let us consider $t_{0}=0$ and omit the superscript ${\varepsilon }$ to all parameters and redefine system (1) as follow:

$$\begin{aligned} {}^{C}_{0}D^{\varepsilon }_{t}S(t)&={\eta }-{\delta _{1}}S-S(bI_{c} +{\phi }I)-{\theta S} ,S(0)=S_{0}>0,\nonumber \\ {}^{C}_{0}D^{\varepsilon }_{t}I_{c}(t)&=qS(bI_{c} +{\phi }I)-({\delta _{2}}+{\alpha })I_{c}\nonumber \\&\quad +m_{1} I_{c}+m_{2} I,I_{c}(0)=I_{c,0}>0, \nonumber \\ {}^{C}_{0}D^{\varepsilon }_{t}I(t)&=(1-q)S(bI_{c} +{\phi }I)-({\delta _{3}}+{\xi })I\nonumber \\&\quad +{\alpha }I_{c}+m_{3} I_{c}+m_{4} I,I(0)=I_{0}>0,\nonumber \\ ^{C}_{0}D^{\varepsilon }_{t}R(t)&={\xi }I+{\theta }S-{\delta _{4}}R,R(0)=R_{0}>0 \end{aligned}$$

(2)

Table 1 Parameters in the system (2)

It is observed that the above model is different from traditional S–E–I–R models which incorporate disease latency. It is also observed that disease carriage is distinct from disease latency, because population in carrier state are infectious but those in the latent period are not infectious. In the case when $b =0$, then the class $I_c$ becomes latent and system (2) becomes a modified S–E–I–R system where new infections can be latent or infectious. We have considered our system in such a way that new infections to be either symptomatic or asymptomatic with certain proportion. This model is modified and more general than the carrier model proposed by Kemper et al. [32].

3 Preliminaries

Definition 1

[10, 33] The Caputo fractional derivative with order $\alpha >0$ for a function $f\in C^{n}([t_{0},\infty +)$, ${\mathbb {R}}$ $)$ is denoted and defined as:

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}f(t)=\left\{ \begin{array}{lll} \displaystyle \frac{1}{\Gamma (n-\alpha ) }\int ^{t}_{t_{0}} \frac{f^{(n)}(s)}{(t-s)^ {^{\alpha -n+1}}}ds,\alpha \in (n-1, n)\\ \\ \displaystyle \frac{d^n}{dt^n}f(t),\alpha =n\in {\mathbb {N}}. \end{array}\right. \end{aligned}$$

where $\Gamma (\cdot )$ is the Gamma function, $t \ge t_{0}$ and n is a positive integer. In particular, for $\alpha \in \left( 0,1\right)$:

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}f(t)= \frac{1}{\Gamma (1-\alpha )} \int ^{t}_{t_{0}}\frac{f^{'}(s)}{(t-s)^ {^{\alpha }}}ds \end{aligned}$$

Lemma 1

(Generalized Mean Value Theorem) [34] Let $0<\varepsilon \le 1,\ \phi (t)\in C\left[ a,b\right]$ and $^{C}_{0}D^{\varepsilon }_{t}\phi (t)$ is continuous in $\left( a,b\right]$. Then we have

$$\begin{aligned} \phi (x)=\phi (a)+\frac{1}{\Gamma (\varepsilon )} (x-a)^{\varepsilon }. \ {^{C}_{0}D^{\varepsilon }_{t}} \phi (\zeta ) \end{aligned}$$

where $0\le \zeta \le x$, $\forall x\in \left( a,b\right]$ .

Remark

If $^{C}_{0}D^{\varepsilon }_{t}\phi (t)\ge 0 \left( ^{C}_{0}D^{\varepsilon }_{t}\phi (t)\le 0 \right) , t\in (a,b)$ then $\phi (t)$ is a non-decreasing (non-increasing) function for $t\in \left[ a,b\right]$.

Definition 2

[9] One parametric and two parametric Mittag-Leffler functions are described as follows:

$$\begin{aligned} E_{\varepsilon }(z)= & {} \sum _{j=0}^{\infty }\frac{z^{j}}{\Gamma (\varepsilon j +1)} \ \text {and}\ E_{\varepsilon _{1},\varepsilon _{2}}(z)\\= & {} \sum _{j=0}^{\infty }\frac{z^{j}}{\Gamma (\varepsilon _{1} j +\varepsilon _{2})},\ \text {where}\ \varepsilon , \varepsilon _{1}, \varepsilon _{2} \in {\mathbb {R}}_{+}. \end{aligned}$$

Theorem 1

[35] Let $\alpha >0, n-1<\alpha <n, n\in {\mathbb {N}}$. Assume f(t) is continuously differentiable functions up to order $(n-1)$ on $\left[ t_{0},\infty \right)$ and $n^{th}$ derivative of f(t) exists with exponential order. If $^{C}_{t_{0}}D^{\alpha }_{t}f(t)$ is piecewise continuous on $\left[ t_{0},\infty \right)$, then

$$\begin{aligned} {\mathscr {L}}\left\{ ^{C}_{t_{0}}D^{\alpha }_{t}f(t)\right\} =s^{\alpha }F(s)-\sum ^{n-1}_{j=0}s^{\alpha -j-1}f^{j}(t_{0}), \end{aligned}$$

where $F(s)={\mathscr {L}}\left\{ f(t)\right\}$ denotes the Laplace transform of f(t).

Theorem 2

[36] Let C be the complex plane. For any $\alpha _{1}, \alpha _{2}\in {\mathbb {R}}_{+}$ and $B\in {\mathbb {C}}^{n\times n}$, then

$$\begin{aligned} {\mathscr {L}}\left\{ t^{\alpha _{2}-1} E_{\alpha _{1}, \alpha _{2}} (Bt^{\alpha _{1}})\right\} =\frac{s^{\alpha _{1}-\alpha _{2}}}{(s^{\alpha _{1}}-B)}, \end{aligned}$$

for ${\mathscr {R}}(s)>{\left\| B\right\| }^{\frac{1}{\alpha _{1}}}$, where ${\mathscr {R}}(s)$ represents the real part of the complex number s, and $E_{\alpha _{1}, \alpha _{2}}$ is the Mittag-Leffler function.

Theorem 3

[10] Consider the following fractional-order system:

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}X(t)= & {} \Phi \left( X\right) , X_{t_0}\\= & {} (x^{1}_{t_0},x^{2}_{t_0},\ldots ,x^{n}_{t_0}), x^{i}_{t_0} > 0, i=1,2,\ldots ,n \end{aligned}$$

with $0<\alpha \le 1$, $X(t)=(x^{1}(t),x^{2}(t),\ldots ,x^{n}(t))$ and $\Phi (X):[t_0,\infty )\rightarrow {{\mathbb {R}}}^{n\times n}.$ The equilibrium points of this system are evaluated by solving the following system of equations: $\Phi (X) = 0$. These equilibrium points are locally asymptotically stable if and only if each eigenvalue $\lambda _i$ of the Jacobian matrix $J(X)=\displaystyle \frac{\partial (\Phi _{1},\Phi _{2},\ldots , \Phi _{n})}{\partial (x^{1},x^{2},\ldots ,x^{n})}$ calculated at the equilibrium points satisfy $\left| \arg (\lambda _{i}) \right| >\frac{\alpha \pi }{2}$.

3.1 Equilibria of system (2)

The equilibria of system (2) can be obtained by solving the system:

$$\begin{aligned}&{\eta }-{\delta _{1}}S^{*}-S^{*}(bI^{*}_{c}+{\phi }I^{*})-{\theta S^{*}} =0\nonumber \\&qS^{*}(bI^{*}_{c}+{\phi }I^{*})-({\delta _{2}}+{\alpha })I^{*}_{c}+m_{1} I^{*}_{C}\nonumber \\&+m_{2} I^{*}=0 \nonumber \\&(1-q)S^{*}(bI^{*}_{c}+{\phi }I^{*})-({\delta _{3}}+{\xi })I^{*}+{\alpha }I^{*}_{c}\nonumber \\&+m_{3} I^{*}_{C}+m_{4} I^*=0\nonumber \\&{\xi }I^{*}+{\theta }S^{*}-{\delta _{4}}R^{*}=0 \end{aligned}$$

(3)

System (3) has two types of equilibrium points:

• 1. Disease-free equilibrium $E_0(S^{0},0,0,R^{0})$

• 2. Endemic equilibrium $E_1(S^*,I^*_c,I^*,R^*)$

where

$$\begin{aligned} S^0=\frac{\eta }{\theta +\delta _1}, R^0 =\frac{\theta \eta }{\delta _{4} (\theta +\delta _1)} \end{aligned}$$

and

$$\begin{aligned} S^*&=\frac{(\delta _2 +\alpha -m_{1})(\delta _3 +\xi -m_{4}) -m_{2}(m_{3}+\alpha )}{b(1-q)m_{2} -bq(m_{4}{-}\delta _{3}-\xi ) +\phi q (m_{3} +\alpha )-\phi (1-q)(m_{1}{-}\delta _{2}-\alpha )}\nonumber \\ I^*_{c}&=\{\eta -S^*(\delta _1 +\theta )\}\nonumber \\&\quad \left[ \frac{(1-q)m_{2}-q(m_{3}-\delta _{3}-\xi )}{(m_{1} -\delta _{2}-\alpha )(m_{4}-\delta _{3}-\xi )-m_{2}(m_{3}+\alpha )}\right] \nonumber \\&I^* =\{\eta -S^*(\delta _1 +\theta )\}\nonumber \\&\quad \left[ \frac{q(m_{3}+\alpha )-(1-q)(m_{1}-\delta _{2}-\alpha )}{(m_{1} -\delta _{2}-\alpha )(m_{4}-\delta _{3}-\xi )-m_{2}(m_{3}+\alpha )}\right] \nonumber \\ R^*&= \frac{\xi I^* +\theta S^*}{\delta _4} \end{aligned}$$

(4)

For $E_1$ to exist in feasible region ${\mathbb {R}}^4_+$, it is necessary and sufficient that

• $(m_{1}-\delta _{2}-\alpha )(m_{4}-\delta _{3}-\xi )-m_{2}(m_{3}+\alpha )>0$

• $(1-q)m_{2}-(m_{3}-\delta _{3}-\xi )\ge 0$

• $q(m_{3}+\alpha )-(1-q)(m_{1}-\delta _{2}-\alpha )\ge 0$

or

• $(m_{1}-\delta _{2}-\alpha )(m_{4}-\delta _{3}-\xi )-m_{2}(m_{3}+\alpha )<0$

• $(1-q)m_{2}-(m_{3}-\delta _{3}-\xi )\le 0$

• $q(m_{3}+\alpha )-(1-q)(m_{1}-\delta _{2}-\alpha )\le 0$

3.2 Existence and uniqueness

Lemma 2

[37] Consider the system

$$\begin{aligned} ^{C}_{t_{0}}D^{\varepsilon }_{t}x(t)=f(t,x), t_0> 0 \end{aligned}$$

(5)

with initial condition $x(t_{0})=x_{t_{0}}$, where $\varepsilon \in \left( 0, 1\right]$, $f:\left[ t_{0}, \infty \right) \times \Omega \rightarrow {\mathbb {R}}^{n},\Omega \in {\mathbb {R}}^{n}$, if local Lipschitz condition is satisfied by f(t, x) with respect to x, then there exists a solution of (5) on $\left[ t_{0}, \infty \right) \times \Omega \$ which is unique.

To study the existence and uniqueness of system (2), let us consider the region $\Omega \times [t_{0},\gamma ]$, where $\Omega =\{(S,I_c,I,R)\in {{\mathbb {R}}}^4:\max (\left| S\right| , \left| I_c\right| ,\left| I\right| ,\left| R\right| )\le M \}$ and $\gamma <+\infty$. Denote $X=(S,I_c,I,R)$ and $\overline{X}=(\bar{S},\bar{I_c},\bar{I},\bar{R})$. Consider a mapping $L(X)=(L_{1}(X),L_{2}(X),L_{3}(X),L_{4}(X))$, where

$$\begin{aligned} L_{1}(X)&={\eta }-{\delta _{1}}S-S(bI_{c}+{\phi }I)-{\theta S} \\ \displaystyle L_{2}(X)&=qS(bI_{c}+{\phi }I)+(m_{1}I_{c}+m_{2}I)\\&\quad -\,({\delta _{2}}+{\alpha })I_{c} \\ L_{3}(X)&=(1-q)S(bI_{c}+{\phi }I)-({\delta _{3}}+{\xi })I \\&\quad +\,{\alpha }I_{c}+(m_{3}I_{c}+m_{4}I)\\ L_{4}(X)&={\xi }I+{\theta }S-{\delta _{4}}R \end{aligned}$$

For any $X,\overline{X}\in \Omega$:

$$\begin{aligned} \left\| L(X)-L(\overline{X})\right\|&= \left| L_{1}(X)-L_{1}(\overline{X})\right| \\&\quad +\,\left| L_{2}(X)-L_{2}(\overline{X})\right| \\&\quad +\,\left| L_{3}(X){-}L_{3}(\overline{X})\right| {+}\left| L_{4}(X){-}L_{4}(\overline{X})\right| \\&= \left| \eta -\delta _{1} S-S(bI_{c}+{\phi }I)\right. \\&\quad \left. -\theta S-{\eta }+\delta _{1}\bar{S}+\bar{S}(b\bar{I_{c}} +{\phi }\bar{I})+\theta \bar{S}\right| \\&\quad +\,\left| qS(bI_{c}+{\phi }I)-({\delta _{2}}+{\alpha })I_{c} \right. \\&\quad +\,(m_{1}I_{c}+m_{2}I)-q\bar{S}(b\bar{I_{c}}\\&\quad +\,{\phi }\bar{I})+({\delta _{2}} +{\alpha })\bar{I_{c}}-(m_{1}\bar{I_{c}}+m_{2}\bar{I})| \\&\quad +\,\big |(1-q)S(bI_{c}+{\phi }I)-({\delta _{3}}+{\xi })I\\&\quad +\,{\alpha }I_{c}+(m_{3}I_{C}+m_{4}I) \\&\quad -\,(1-q)\bar{S}(b\bar{I_{c}}+{\phi }\bar{I})\\&\quad +\,({\delta _{3}}+{\xi })\bar{I}-{\alpha }\bar{I_{c}}-(m_{3}\bar{I_{C}}+m_{4}\bar{I}) \big |\\&\quad +\,\left| {\xi }I+{\theta }S-{\delta _{4}}R-{\xi }\bar{I} +{\theta }\bar{S}-{\delta _{4}}\bar{R} \right| \\&\quad \le (\delta _{1}+2\theta )\left| S-\bar{S}\right| \\&\quad +\,2b\left| SI_{c}-\bar{S}\bar{I_{c}}\right| +2\phi \left| SI-\bar{S}\bar{I}\right| \\&\quad +\,(\delta _2 {+}2\alpha )\left| I_c{-}\bar{I_c}\right| {+}(\delta _3 {+}2\xi ) \left| I{-}\bar{I}\right| \\&\quad +\,\delta _4\left| R-\bar{R}\right| \le (\delta _{1}+2\theta )\\&\quad \left| S-\bar{S}\right| +2b\left| SI_{c}-\bar{S}I_{c}+\bar{S}I_{c}-\bar{S}\bar{I_{c}}\right| \\&\quad +\,2\phi \left| SI-\bar{S}I+\bar{S}I-\bar{S}\bar{I}\right| \\&\quad +\,(m_{1}{+}m_{3})\left| I_{c}{-}\bar{I_{c}}\right| {+}(m_{2}{+}m_{4})\left| I{-}\bar{I}\right| \\&\quad +\,(\delta _2 {+}2\alpha )\left| I_c{-}\bar{I_c}\right| {+}(\delta _3 {+}2\xi ) \left| I-\bar{I}\right| \\&\quad +\,\delta _4\left| R-\bar{R}\right| \le (\delta _{1}+2\theta ) \\&\quad \left| S-\bar{S}\right| +2b\left| I_c\right| \left| S-\bar{S}\right| \\&\quad +\,2b\left| \bar{S}\right| \left| I_c-\bar{I_c}\right| +2\phi \left| I\right| \left| S-\bar{S}\right| \\&\quad +\,2\phi \left| \bar{S}\right| \left| I-\bar{I}\right| \\&\quad +\,(\delta _2 +2\alpha +m_{1}+m_{3})\left| I_c-\bar{I_c}\right| \\&\quad +\,(\delta _3 +2\xi +m_{2}+m_{4})\left| I-\bar{I}\right| +\delta _{4} \\&\quad \left| R-\bar{R}\right| \le F_1\left| S-\bar{S}\right| +F_{2}\left| I_c -\bar{I_c}\right| \\&\quad +\,F_{3}\left| I-\bar{I}\right| +F_{4}\left| R-\bar{R}\right| \\&\quad \le F\left\| X-\overline{X}\right\| , \text {where} \ F\\&=\max \{F_{1},F_{2},F_{3},F_{4}\}, \end{aligned}$$

and

$$\begin{aligned} F_1= & {} \delta _{1}+2\theta +2\phi M+2bM\\ F_{2}= & {} 2bM+\delta _2 +2\alpha +m_{1}+m_{3}\\ F_{3}= & {} 2\phi M +\delta _3 +2\xi +m_{2}+m_{4}\\ F_{4}= & {} \delta _{4} \end{aligned}$$

Hence L(X) satisfies Lipschitz’s condition with respect to X. Therefore, Lemma 2 confirms that there exists a unique solution X(t) of system (2) with initial condition $X(0)=(S_0, I_{c,0}, I_0, R_0)$. The following theorem is the consequence of this result.

Theorem 4

There exists a unique solution $X(t)\in \Omega$ of system (2) for all $t\ge 0$ with initial condition $X_{0}$ where $X(0)=(S_0, I_{c,0}, I_0, R_0) \in \Omega$.

3.3 Non-negativity and boundedness

In this section we have established the criterion for feasibility of the solution of system (2). Suppose ${\mathbb {R}}_{+}$ stands for the set of all non-negative real numbers and $\Gamma _{+}=\left\{ (S,I_c,I,R)\in {\mathbb {R}}^4_{+}\right\}$ represents the first quadrant.

Theorem 5

The solutions $X(t)=(S,I_c,I,R)$ of system (2) remain in $\Gamma _{+}$ if $X(0)=(S_0, I_{c,0}, I_0, R_0)\in \Gamma _{+}$.

Proof

$$\begin{aligned}&{}^{C}_{t_0}D^{\varepsilon }_{t}S(t)\big |_{S(t)=0}={\eta }>0 \end{aligned}$$

(6a)

$$\begin{aligned}&{}^{C}_{0}D^{\varepsilon }_{t}I_{c}(t)\big |_{I_{c}(t)=0}=qS{\phi }I+m_{2}I \end{aligned}$$

(6b)

$$\begin{aligned}&{}^{C}_{0}D^{\varepsilon }_{t}I(t)\big |_{I(t)=0}=(1-q)SbI_{c}+(m_{3}+\alpha )I_{c} \end{aligned}$$

(6c)

$$\begin{aligned}&{}^{C}_{0}D^{\varepsilon }_{t}R(t)\big |_{R(t)=0}={\xi }I+{\theta }S \end{aligned}$$

(6d)

From (6a), we have

$$\begin{aligned} ^{C}_{t_{0}}D^{\varepsilon }_{t}S(t)|_{S(t)=0} = \eta >0. \end{aligned}$$

Using remark of Lemma 1 we can say S(t) is non-decreasing at the neighbourhood of time $t=t^*(>0)$ where $S(t^*)=0$ and S(t) cannot cross the axis $S(t)=0$. Hence, $S(t)\ge 0$ for all $t\ge 0$. Now, we claim that the solution $I_{c}(t)$ starts from $\Gamma _{+}$ and remains non-negative. If not, then there exists a $\tau _c<\infty$, $0\le t< \tau _c$ such that

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {I_{c}(t)>0},\ \mathrm{for}\ 0\le t< \tau _c,\\ I_{c}(\tau _c)=0, \\ I_{c}(\tau _{c}^{+})< 0. \end{array}\right. \end{aligned}$$

If $I(\tau _c)\ge 0$, then from (6b) we have $^{C}_{0}D^{\varepsilon }_{t}I_{c}(t)\big |_{I_{c} (\tau _{c})=0}=qS{\phi }I(\tau _{c})+m_{2}I(\tau _{c})\ge 0$. From the remark of Lemma 1 it is evident that $I_{c}(t)$ is non-decreasing (remark of Lemma 1) at the neighbourhood of $t=\tau _c$ and which concludes $I_{c}(\tau ^{+}_c)=0$. Hence, we arrive at a contradiction.

If $I(\tau _c)<0$, then there exist a $\tau$ such that $0<\tau <\tau _c$.

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {I(t)>0},\ \text {for}\ 0\le t< \tau ,\\ I(\tau )=0, \\ I(\tau ^{+})< 0. \end{array}\right. \end{aligned}$$

From (6c) it is clear that

$$\displaystyle ^{C}_{0}D^{\varepsilon }_{t}I(t)\big |_{I(\tau )=0}\ge 0$$

which implies $I({\tau }^+)\nless 0$ and it opposes our assumption. Therefore, we have $I_{c}(t)\ge 0, \forall t\in [0,\infty )$. Again from (6c) we have $\displaystyle ^{C}_{0}D^{\varepsilon }_{t}I(t) \big |_{I(t)=0}\ge 0$, which means I(t) is non-decreasing (remark of Lemma 1) in the neighbourhood of time $t=t^{**} (>0)$ where $I(t^{**})=0$ and I(t) cannot cross the axis $I(t)=0$. Hence $I(t)\ge 0$ for all $t\ge 0$. Similarly from equation (6d) it is clear that $R(t)\ge 0$ for all $t\ge 0$. Hence, we can say that on each hyperplane, bounding the non-negative octant, the vector field points into $\Gamma _+$ with initial non negative conditions. Therefore, $\Gamma _+$ is positively invariant region. $\square$

Theorem 6

(Boundedness). Solutions $X(t)=(S,I_c,I,R)$ of system (2) are uniformly bounded.

Proof

From first equation of (2), it has been noted that

$$\begin{aligned} \displaystyle ^{C}_{0}D^{\varepsilon }_{t}S(t)\le \eta -{\delta _{1}}S-{\theta S} \end{aligned}$$

Taking Laplace transforms on both sides, we have

$$\begin{aligned}&s^{\varepsilon }{\mathscr {L}}\left\{ S(t)\right\} -s^{\varepsilon -1}S(0) +(\delta _{1}+\theta ) {\mathscr {L}}\left\{ S(t)\right\} \le \displaystyle \frac{\eta }{s},\\&\qquad \text {where}\ {\mathscr {L}}\{.\} \text {is the Laplace transform operator}\\&\quad \Rightarrow \displaystyle {\mathscr {L}}\left\{ S(t)\right\} \le \displaystyle \eta \frac{s^{\varepsilon -(1+\varepsilon )}}{s^{\varepsilon } +(\delta _{1}+\theta )}+S(0)\frac{s^{\varepsilon -1}}{s^{\varepsilon }+(\delta _{1}+\theta )} \end{aligned}$$

Taking inverse Laplace transforms (using Theorem 2):

$$\begin{aligned} S(t)\le S(0)E_{\varepsilon ,1 }(-(\delta _{1}+\theta ) t^{\varepsilon }) +\eta t^{\varepsilon }E_{\varepsilon ,\varepsilon +1}(-(\delta _{1}+\theta )t^{\varepsilon }) \end{aligned}$$

(7)

Let, $N(t)=S(t)+I_c (t)+I(t)+R(t)$ represents the total population, then

$$\begin{aligned} {}^{C}_{0}D^{\varepsilon }_{t}N(t)= & {} ^{C}_{0}D^{\varepsilon }_{t}S(t) +^{C}_{0}D^{\varepsilon }_{t}I_c (t)+^{C}_{0}D^{\varepsilon }_{t} I_c (t)+^{C}_{0}D^{\varepsilon }_{t}R (t)\\= & {} \eta -(\delta _{1}S(t)+\delta _{2}I_{c}(t)+\delta _{3}I(t)+\delta _{4}R(t)\\&+\,(m_{1}+m_{3})I_{C}(t)+(m_{2}+m_{4})I(t)\\\le & {} \eta -\delta N(t), \text {where}\ \delta =\min \{\delta _{1}, \delta _{2},\delta _{3},\delta _{4}\} \end{aligned}$$

Therefore,

$$\begin{aligned} \displaystyle ^{C}_{0}D^{\varepsilon }_{t}N(t)+\delta N(t)\le \eta \end{aligned}$$

Applying Laplace transformation, we have (using Theorem 1):

$$\begin{aligned}&s^{\varepsilon }F(s)-s^{\varepsilon -1}N(0)+\delta F(s)\le \frac{\eta }{s},\\&\qquad \text {where}\ F(s)={\mathscr {L}}\left\{ N(t)\right\} \\&\quad \Rightarrow \displaystyle F(s)\le \eta \frac{s^{-1}}{s^{\varepsilon } +\delta }+\frac{N(0)s^{\varepsilon -1}}{s^{\varepsilon }+\delta }\\&\quad = \frac{s^{\varepsilon -1} N(0)}{s^{\varepsilon }+\delta } +\frac{\eta s^{\varepsilon -(1+\varepsilon )}}{(s^{\varepsilon }+\delta )} \end{aligned}$$

Taking inverse Laplace transforms (using Theorem 2):

$$\begin{aligned} N(t)\le N(0)E_{\varepsilon ,1 }(-\delta t^{\varepsilon })+\eta t^{\varepsilon } E_{\varepsilon ,\varepsilon +1}(-\delta t^{\varepsilon }) \end{aligned}$$

(8)

From the properties of Mittag Leffler function [38], we have

$$\begin{aligned} \displaystyle E_{\alpha ,\beta }(z)=zE_{\alpha ,\alpha +\beta }(z) +\frac{1}{\Gamma (\beta )} \end{aligned}$$

Now, in this case

$$\begin{aligned} E_{\varepsilon ,1} (-\delta t^{\varepsilon })=(-\delta t^{\varepsilon }) E_{\varepsilon , \varepsilon +1} (-\delta t^{\varepsilon })+\frac{1}{\Gamma (1)} \end{aligned}$$

(9)

From (7), (8) and (9), we get

$$\begin{aligned} N(t)\le \Delta [E_{\varepsilon ,1 }(-\delta t^{\varepsilon }) +\delta t^{\varepsilon }E_{\varepsilon ,\varepsilon +1}(-\delta t^{\varepsilon })] = \frac{\Delta }{\Gamma (1)}=\Delta , \end{aligned}$$

where $\displaystyle \Delta =\max \left\{ \frac{\eta }{\delta }, N(0)\right\}$

Similarly,

$$\begin{aligned} S(t)\le & {} \Lambda [E_{\varepsilon ,1 }(-(\delta _{1}+\theta )t^{\varepsilon }) +(\delta _{1}+\theta ) t^{\varepsilon }E_{\varepsilon ,\varepsilon +1} (-(\delta _{1}+\theta )t^{\varepsilon })] \\= & {} \frac{\Lambda }{\Gamma (1)}=\Lambda , \end{aligned}$$

where $\Lambda =\max \left\{ \frac{\eta }{(\delta _{1}+\theta )}, S(0)\right\}$

Thus S(t), N(t) are bounded and hence the solutions $X(t) =(S(t), I_c(t) , I(t) , R(t))$ are bounded uniformly in $\Omega =\{(S,I_{c},I,R)| S+I_{c}+I+R\le \Delta ; S\le \Lambda \}$ for $t\in [0,\infty )$ $\square$

3.4 Reproduction number and local stability

The basic reproduction number is defined as the number of new infective individuals produced by a single infective individual during infectious period when contacted into susceptible compartment. Reproduction number ${\mathscr {R}}_0$ of system (2) for $\varepsilon =1$ can be computed by the next generation matrix method [39].

Since the variable R of system (2) does not appear in first three equations, in subsequent analysis we only consider the following reduced system:

$$\begin{aligned} {}^{C}_{0}D^{\varepsilon }_{t}S(t)&={\eta }-{\delta _{1}}S-S(bI_{c} +{\phi }I)-{\theta S} ,S(0)=S_{0}>0,\nonumber \\ {}^{C}_{0}D^{\varepsilon }_{t}I_{c}(t)&=qS(bI_{c} +{\phi }I)-({\delta _{2}}+{\alpha })I_{c}\nonumber \\&\quad +m_{1} I_{c}+m_{2} I,I_{c}(0)=I_{c,0}>0, \nonumber \\ {}^{C}_{0}D^{\varepsilon }_{t}I(t)&=(1-q)S(bI_{c}+{\phi }I)-({\delta _{3}}+{\xi })I\nonumber \\&\quad +{\alpha }I_{c}+m_{3} I_{c}+m_{4} I,I(0)=I_{0}>0, \end{aligned}$$

(10)

Once the dynamics of $(S,I_c,I)$ are determined, those of R can be determined by $^{C}_{0}D^{\varepsilon }_{t}R(t)={\xi }I+{\theta }S -{\delta _{4}}R$. We consider $E_0 \ \text {and} \ E_1$ as $(S^0,0,0) \ \text {and} \ (S^*,I^*_c,I^*).$ Let $u=(I_{C},I,S)^T$, then system (10) can be written as:

$$\begin{aligned} \displaystyle ^{C}_{0}D^{\varepsilon }_{t}u=\Upsilon (u)-V(u) \end{aligned}$$

where

$$\begin{aligned} \Upsilon (u)=\begin{bmatrix} q(bI_{c}+\phi I)S \\ \\ (1-q)(bI_{c}+\phi I)S\\ \\ 0\\ \\ \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} V(u)=\begin{bmatrix} -(m_{1}I_{c}+m_{2}I)+(\delta _{2}+\alpha )I_{c}\\ \\ -(m_{3}I_{c}+m_{4}I)+(\delta _{3}+\xi )I-\alpha I_{c}\\ \\ -\eta +(\delta _{1}+\theta )S+S(bI_{c}+\phi I)\\ \\ \end{bmatrix} \end{aligned}$$

The Jacobian matrix of $\Upsilon (u)$ and V(u) at disease free equilibrium $E_{0}$ are respectively.

$$\begin{aligned}&D\Upsilon (E_{0})=\begin{bmatrix} F &{}&{} 0 \\ \\ 0&{}&{}0\\ \\ \end{bmatrix} \\&DV(E_{0})=\begin{bmatrix} \nu &{}&{} 0 \\ \\ 0&{}&{}0\\ \\ \end{bmatrix}\\&F=\begin{bmatrix} \displaystyle \frac{qb\eta }{\delta _1 +\theta } &{}&{} \displaystyle \frac{q\phi \eta }{\delta _1 +\theta } \\ \\ \displaystyle \frac{(1-q)b\eta }{\delta _1 +\theta } &{}&{} \displaystyle \frac{(1-q)\phi \eta }{\delta _1 +\theta } \\ \\ \end{bmatrix}\\&\nu =\begin{bmatrix} \delta _2 +\alpha -m_1 &{}&{} -m_2 \\ \\ -\alpha -m_3&{}&{}\alpha _3+\xi -m_4\\ \\ \end{bmatrix} \end{aligned}$$

Now, ${\mathscr {R}}_0$ is the largest eigenvalue of next generation matrix $F\nu ^{-1}$.

$$\begin{aligned} {\mathscr {R}}_0= & {} \displaystyle \frac{\eta }{\delta _1 +\theta }\\&\left[ \frac{(1-q)\{bm_{2}+\phi (\delta _2+\alpha -m_1)\}}{(\delta _2 +\alpha -m_1)(\delta _3 +\xi -m_4)-m_4(m_3+\alpha )}\right] \end{aligned}$$

The endemic equilibrium $E_1(S^*,I^*_c,I^*)$ of subsystem (10) can be expressed as:

• $S^* = \displaystyle \frac{\eta }{\delta _1 +\theta }\frac{1}{{\mathscr {R}}_0}$

• $I^*=\displaystyle \eta \Bigg (1-\frac{1}{{\mathscr {R}}_0}\Bigg ) \left[ \frac{q(m_3 +\alpha )-(1-q)(m_1-\delta _2-\alpha )}{(\delta _2 +\alpha -m_1)(\delta _3 +\xi -m_4)-m_4(m_3+\alpha )}\right]$

• $I^*_c =\displaystyle \eta \Bigg (1-\frac{1}{{\mathscr {R}}_0}\Bigg ) \frac{(1-q)m_2-(m_3+\alpha )q}{(\delta _2 +\alpha -m_1)(\delta _3 +\xi -m_4)-m_4(m_3+\alpha )}$

So, ${\mathscr {R}}_0 = \displaystyle \frac{\eta }{\delta _1 +\theta }\frac{1}{S^*}$ and if ${\mathscr {R}}_0\le 1$, there is only one equilibrium point, say $E_0$. When ${\mathscr {R}}_0>1$, the system has both disease free equilibrium $E_0$ and endemic equilibrium $E_1$.

To study the local stability of the system, we need to compute Jacobian matrix at the equilibrium points $E_{0}, E_{1}$:

$$\begin{aligned} J\{(S, I_c, I)\}=\begin{bmatrix} -\delta _{1} -(bI_{c}+\phi I)-\theta &{} &{} -bS &{}&{} -\phi S \\ \\ q(bI_{c}+\phi I)&{} &{} qSb-\delta _{2} -\alpha +m_1 &{}&{} qS\phi +m_2\\ \\ (1-q)(bI_{c}+\phi I)&{} &{} (1-q)bS +\alpha +m_3 &{}&{} (1-q)\phi S-\delta _{3} - \xi +m_4\\ \end{bmatrix} \end{aligned}$$

At $E_{0}$ the Jacobian matrix is given by

$$\begin{aligned} J\{(S^0, 0, 0)\}=\begin{bmatrix} -\delta _{1} -\theta &{} &{} -bS^{0} &{}&{} -\phi S^{0} \\ \\ 0&{} &{} qS^{0} b-\delta _{2} -\alpha +m_1 &{}&{} qS^{0} \phi +m_2\\ \\ 0&{} &{} (1-q)bS^{0} +\alpha +m_3 &{}&{} (1-q)\phi S^{0}-\delta _{3}-\xi +m_4\\ \end{bmatrix} \end{aligned}$$

where

$$\begin{aligned} \displaystyle S^0=\displaystyle \frac{\eta }{\theta +\delta _1} \end{aligned}$$

The eigenvalues of the system are $\lambda _1 =-\delta _{1} -\theta$, $\lambda _2=\displaystyle \frac{qb\eta }{\theta +\delta _1}+m_1-\alpha -\delta _2$, $\lambda _3=\displaystyle \frac{(1-q)\phi \eta }{\theta +\delta _1}+m_4-\xi -\delta _3$. Therefore, $\left| \arg (\lambda _{1}) \right| =\pi >\frac{\varepsilon \pi }{2}$; $0<\varepsilon < 1$. For the other two eigenvalues, $|\arg (\lambda _{2})|=|\arg (\lambda _{3})|=\pi >\frac{\varepsilon \pi }{2}$, if the following conditions hold:

• 1. $\displaystyle \frac{qb\eta }{\theta +\delta _1}+m_1-\alpha -\delta _2<0$

• 2. $\displaystyle \frac{(1-q)\phi \eta }{\theta +\delta _1}+m_4-\xi -\delta _3<0$

The disease free equilibrium is asymptotically stable if these two conditions are fulfilled.

Jacobian matrix at $E_{1}(S^*, I_c^*, I^*)$ is given by

$$\begin{aligned} J(E_1)=\begin{bmatrix} -\delta _{1} -(bI^*_{c}+\phi I^*)-\theta &{} &{} -bS^* &{}&{} -\phi S^* \\ \\ q(bI^*_{c}+\phi I^*)&{} &{} qS^* b-\delta _{2} -\alpha +m_1 &{}&{} qS^* \phi +m_2\\ \\ (1-q)(bI^*_{c}+\phi I^*)&{} &{} (1-q)bS^* +\alpha +m_3 &{}&{} (1-q)\phi S^*-\delta _{3} - \xi +m_4\\ \end{bmatrix} \end{aligned}$$

Characteristic equation of this matrix is: $P(\lambda )\equiv \lambda ^3 +a_{1}\lambda ^2 +a_{2}\lambda +a_{3}=0$, where

$$\begin{aligned} a_{1}= & {} -(K_{1}+K_{5}+K_{3})\\ a_{2}= & {} K_{1}K_{5}+K_{1}K_{9}+K_{5}K_{9}-K_{2}K_{4}-K_{3}K_{7}-K_{6}K_{8}\\ a_{3}= & {} -K_{1}K_{5}K_{9}+K_{1}K_{6}K_{8}+K_{2}K_{4}K_{9}\\&-K_{2}K_{6}K_{7} -K_{3}K_{4}K_{8}+K_{3}K_{7}K_{5} \end{aligned}$$

and

$$\begin{aligned} K_{1}= & {} -\delta _{1} -(bI^*_{c}+\phi I^*)\\ K_{2}= & {} -bS^*\\ K_{3}= & {} -\phi S^* \\ K_{4}= & {} q(bI^*_{c}+\phi I^*)\\ K_{5}= & {} qS^* b-\delta _{2} -\alpha +m_1 \\ K_{6}= & {} qS^* \phi +m_2\\ K_{7}= & {} (1-q)(bI^*_{c}+\phi I^*)\\ K_{8}= & {} (1-q)bS^* +\alpha +m_3\\ K_{9}= & {} (1-q)\phi S^*-\delta _{3} - \xi +m_4 \end{aligned}$$

So, $\lambda _i, i=1,2,3$, can be found from this equation. Suppose $\nabla (P)=18a_{1} a_{2}a_{3}+(a_{1}a_{2})^2-4{a^2_{1}} a_{3}-4{a^2_{2}}-27{a^2_{3}}$, then by Routh-Harwitz conditions for fractional differential equation, the endemic equilibrium point $E_{1}$ is locally asymptotically stable if any of the following conditions holds good [40]:

• 1. $\nabla (P)>0, a_{1}>0, a_{3}>0$ and $a_{1}a_{2}>a_{3}$

• 2. $\nabla (P)<0, a_{1}\ge 0, a_{2}\ge 0, a_{3}>0$ and $\varepsilon <\frac{2}{3}$

• 3. $\nabla (P)<0, a_{1}>0, a_{2}>0, a_{1}a_{2}=a_{3}$ and $\varepsilon \in (0,1)$

The following theorems consequently derive from above discussions.

Theorem 7

The disease free equilibrium $E_{0}$ of system (2) is asymptotically stable if $\displaystyle \frac{qb\eta }{\theta +\delta _1}+m_1 -\alpha -\delta _2<0$ and $\displaystyle \frac{(1-q)\phi \eta }{\theta +\delta _1}+m_4-\xi -\delta _3<0$ hold.

Theorem 8

The endemic equilibrium $E_{1}$ of system (2) is asymptotically stable if any of the following condition holds.

• 1. $\nabla (P)>0, a_{1}>0, a_{3}>0$ and $a_{1}a_{2}>a_{3}$

• 2. $\nabla (P)<0, a_{1}\ge 0, a_{2}\ge 0, a_{3}>0$ and $\varepsilon <\frac{2}{3}$

• 3. $\nabla (P)<0, a_{1}>0, a_{2}>0, a_{1}a_{2}=a_{3}$ and $\varepsilon \in (0,1)$,

where $\nabla (P)=18a_{1} a_{2}a_{3}+(a_{1}a_{2})^2-4{a^2_{1}} a_{3}-4{a^2_{2}}-27{a^2_{3}}$,

$$\begin{aligned} a_{1}= & {} -(K_{1}+K_{5}+K_{3})\\ a_{2}= & {} K_{1}K_{5}+K_{1}K_{9}+K_{5}K_{9}-K_{2}K_{4}-K_{3}K_{7}-K_{6}K_{8}\\ a_{3}= & {} -K_{1}K_{5}K_{9}+K_{1}K_{6}K_{8}+K_{2}K_{4}K_{9}\\&-K_{2}K_{6}K_{7} -K_{3}K_{4}K_{8}+K_{3}K_{7}K_{5} \end{aligned}$$

and

$$\begin{aligned} K_{1}= & {} -\delta _{1} -(bI^*_{c}+\phi I^*)\\ K_{2}= & {} -bS^*\\ K_{3}= & {} -\phi S^* \\ K_{4}= & {} q(bI^*_{c}+\phi I^*)\\ K_{5}= & {} qS^* b-\delta _{2} -\alpha +m_1 \\ K_{6}= & {} qS^* \phi +m_2\\ K_{7}= & {} (1-q)(bI^*_{c}+\phi I^*)\\ K_{8}= & {} (1-q)bS^* +\alpha +m_3\\ K_{9}= & {} (1-q)\phi S^*-\delta _{3} - \xi +m_4\\ \end{aligned}$$

3.5 Global asymptotic stability

We need following useful Lemmas about Lyapunov direct method related with global stability of the equilibrium points in fractional order models.

Lemma 3

[37] Suppose $u(t)\in {\mathbb {R}}_{+}$be a continuous and differentiable function. Then, for any moment of time $t\ge t_0$, $^{C}_{t_{0}}D^{\varepsilon }_{t}\left[ u(t)-u^{*}-u^{*} \ln \frac{u(t)}{u^{*}}\right] \le \left( 1-\frac{u^{*}}{u(t)}\right) {^{C}_{t_{0}}D^{\varepsilon }_{t} u(t)},u^{*}\in {\mathbb {R}}_{+},\forall \varepsilon \in (0,1)$.

Lemma 4

[41](Uniform Asymptotic Stability Theorem) Consider the non-autonomous system

$$\begin{aligned} ^{C}_{0}D^{\varepsilon }_{t}x(t) = f(t,x),\ x \in \Omega \subseteq {\mathbb {R}}^{n} \end{aligned}$$

(15)

Let $x^{*}$ be an equilibrium point of the system ($x^{*}\in \Omega \subseteq {\mathbb {R}}^{n}$) and $\Phi (t,x(t)):\left[ 0,\infty \right) \times \Omega \rightarrow {\mathbb {R}}$ be a continuously differentiable function such that

$$\begin{aligned}&{}^{C}_{0}D^{\varepsilon }_{t}\Phi (t,x(t)) \displaystyle \le -\Theta _{3}(x),\\&\Theta _{1}(x)\le \Phi (t,x(t))\displaystyle \le \Theta _{2}(x), \forall \varepsilon \in (0,1), \forall x(t) \in \Omega \end{aligned}$$

where $\Theta _{i},\ i=1,2,3,$ are continuous positive definite functions on $\Omega$. Then the equilibrium point $x^{*}$ of system (15) is globally stable.

Theorem 9

If ${\mathscr {R}}_0\le 1$, then the disease free equilibrium $E_{0}$ of system (10) is globally asymptotically stable when

$$\begin{aligned}&m_1 \phi (\alpha +m_3)+\alpha bm_{2}+\alpha \phi (\delta _2+\alpha ) +m_{2} m_{3}b\\&\quad \le \alpha \phi m_1 +m_4 (m_{3}+\alpha )b \ \text {and } \ m_{2}\le m_4 \end{aligned}$$

Proof

We have considered a positive definite function:

$$\begin{aligned} F= & {} \left[ b(\delta _{3}+\xi -m_4)+\phi (\alpha +m_3)\right] I_{c} \\&+\left[ bm_2 +\phi (\delta _2+\alpha -m_1)\right] I. \end{aligned}$$

Clearly $F\ge 0$ and $F=0$ only at $E_{0}\Bigg (\displaystyle \frac{\eta }{ \theta +\delta _1},0,0\Bigg )$.

Taking $\varepsilon$ order Caputo derivative $^{C}_{0}D^{\varepsilon }_{t}$ of F along the solution of system (10), we have

$$\begin{aligned} {}^{C}_{0}D^{\varepsilon }_{t}F&= \left[ b(\delta _{3}+\xi -m_4) +\phi (\alpha +m_3)\right] {^{C}_{0}D^{\varepsilon }_{t}}I_{c} \\&\quad +\,\left[ bm_2 +\phi (\delta _2+\alpha -m_1)\right] {^{C}_{0}D^{\varepsilon }_{t}}I\\&=\,\left[ b(\delta _{3}+\xi -m_4)+\phi (\alpha +m_3)\right] \\&\quad [qS(bI_c +\phi I )-(\delta _2+\alpha )I_c+m_1 I_c +m_2 I] \\&\quad +\,\left[ bm_2 +\phi (\delta _2+\alpha -m_1)\right] \\&\quad [(1-q)S(bI_c+\phi I)-(\delta _3+\xi )I+m_3 I_c+m_4 I+\alpha I_c]\\&=\,[qb(\delta _3+\xi -m_4)+q\phi (\alpha +m_3)]S(b I_c+\phi I)+[(1-q)bm_2 \\&\quad +\,(1-q)\phi (\delta _2 +\alpha -m_1)]S(bI_c +\phi I)\\&\quad -\,(\delta _2 +\alpha )b(\delta _3+\xi -m_4)(m_1 I_c +m_2 I)\\&\quad +\,\phi (\alpha +m_3)(m_1 I_c +m_2 I)-(\delta _3 +\xi )\\&\quad [bm_2 +\phi (\delta _2 +\alpha -m_1)](m_3 I_c +m_4 I)\\&\quad +\,\alpha I_c [bm_2+\phi (\delta _2 +\alpha -m_1)]\\&\quad \le [(\delta _2+\alpha -m_1)(\delta _3+\xi -m_4) -m_4 (m_3 +\alpha )]\\&\quad {\mathscr {R}}_0 (bI_c +\phi I)\\&\quad -\,(\delta _3+\xi -m_4)(\delta _2+\alpha -m_1)(bI_c +\phi I)\\&\quad +\,b(\delta _3+\xi -m_4)m_2 I +\phi (\alpha +m_3)m_1 I_c\\&\quad +\,\phi (\alpha +m_3)m_2 I+b(\delta _3+\xi -m_4)m_2 I+\phi (\alpha +m_3)m_1 I_c\\&\quad +\,\phi (\alpha +m_3)m_2 I-(\delta _3 +\xi )bm_2 I\\&\quad +\,bm_2 m_3 I_c +\alpha \phi (\delta _2 +\alpha -m_1)I_c\\&\quad =\,[(\delta _2+\alpha -m_1)(\delta _3+\xi -m_4) -m_4 (m_3 +\alpha )] \\&\quad ({\mathscr {R}}_0 -1)(bI_c +\phi I)\\&\quad +\,I_c [m_1 \phi (\alpha +m_3)+ \alpha b m_2 +\alpha \phi (\delta _2+\alpha )\\&\quad \quad -\alpha \phi m_1 +bm_2 m_3-m_4(m_3+\alpha )b]\\&\quad +\,I[bm_2 (\delta _3 +\xi -m_4)+\phi m_2 (\alpha +m_3)\\&\quad \quad -(\delta _3 +\xi )b m_2 + bm_2 m_4 - m_4(m_3 +\alpha )\phi ]\\&\quad =\,[(\delta _2+\alpha -m_1)(\delta _3+\xi -m_4)\\&\quad \quad -m_4 (m_3 +\alpha )]({\mathscr {R}}_0 -1)(bI_c +\phi I)\\&\quad +\,I_c [m_1 \phi (\alpha +m_3)+ \alpha b m_2 +\alpha \phi (\delta _2+\alpha )\\&\quad \quad -\alpha \phi m_1 +bm_2 m_3-m_4(m_3+\alpha )b]\\&\quad +\,\phi (\alpha +m_3 )(m_2-m_4)I \end{aligned}$$

Hence, $^{C}_{0}D^{\varepsilon }_{t}F\le 0$ if ${\mathscr {R}}_0\le 1$ and

$$\begin{aligned}&m_1 \phi (\alpha +m_3)+\alpha bm_{2}+\alpha \phi (\delta _2+\alpha )+m_{2} m_{3}b\\&\quad \le \alpha \phi m_1 +m_4 (m_{3}+\alpha )b \ , \ m_{2}\le m_4. \end{aligned}$$

Thus $^{C}_{0}D^{\varepsilon }_{t}F$ is negative definite with respect to $E_0$ and $E_0$ is globally asymptotically stable by Lemma 4. $\square$

Theorem 10

If ${\mathscr {R}}_0>1$, then the endemic equilibrium $E_{1}(S^*, I^*_c, I^*, R^*)$ of system (2) is globally asymptotically stable.

Proof

Consider a positive definite function:

$$\begin{aligned} W&=\displaystyle k_{1}\Bigg (S-S^*-S^* \ln \frac{S}{S^*}\Bigg )\nonumber \\&\quad +k_{2}\Bigg (I_{c}-I^*_{c}-I^*_{c} \ln \frac{I_{c}}{I^*_{c}}\Bigg ) +k_{3}\Bigg (I-I^*-I^* \ln \frac{I}{I^*}\Bigg ) \end{aligned}$$

(16)

where $k_{i}, i=1,2,3$, are positive constants specified later. It is observed that $W(E_{1})=0$. Taking $\varepsilon$ order Caputo derivative $^{C}_{0}D^{\varepsilon }_{t}$ of W, $\eta =\delta _1 S^* +\theta S^* +b I^*_c S^* +\phi I^* S^*$ and Lemma 3, we have got:

$$\begin{aligned} ^{C}_{0}D^{\varepsilon }_{t}(W)\le & {} k_{1}\Bigg (1-\frac{S^*}{S}\Bigg ) {^{C}_{0}D^{\varepsilon }_{t}S}\\&+\,k_{2}\Bigg (1-\frac{I^*_{c}}{I_{c}}\Bigg ) {^{C}_{0}D^{\varepsilon }_{t}I_{c}} +k_{3}\Bigg (1-\frac{I^*}{I}\Bigg ){^{C}_{0}D^{\varepsilon }_{t}I}\\ \therefore \ ^{C}_{0}D^{\varepsilon }_{t}(W)\le & {} k_{1}\left[ \eta -(\theta +\delta _{1})S-(bI_{c}+\phi I)S\right. \\&\quad \left. -\eta \frac{S^*}{S}+(\theta +\delta _{1})S^*+(bI_{c}+\phi I)S^*\right] \\&+\,k_{2}\left[ (q(bI_{c}+\phi I)S-(\delta _{2}+\alpha )+m_1 I_{c} +m_2 I\right] \\&\left( 1-\frac{I^*_{c}}{I_c}\right) \\&+\,k_{3}\left[ (1-q)(bI_{c}+\phi I)S+\alpha I_{c}\right. \\&\quad \left. -(\delta _{3}+\xi )I+m_3 I_c +m_4 I\right] \left( 1-\frac{I^*}{I}\right) \\= & {} \,\left[ k_{1}(\delta _{1}+\theta )S^{*} \left( 2-\displaystyle \frac{S}{S^*}-\frac{S^*}{S}\right) \right] \\&+\,\left[ k_{1}(bI^*_{c}+\phi I^*)S^* +k_{2} (\delta _{2}+\alpha -m_1)I^*_{c}\right. \\&\left. +k_{3} (\delta _{3} +\xi -m_4)I^*\right] \\&+\,S(bI_c +\phi I)[-k_{1} +k_{2} q+(1-q)k_{3}]\\&+\,I_{c}[k_{1}bS^*-k_{2}(\delta _2 +\alpha -m_1)+k_{3}(m_3 +\alpha )]\\&+\,I[k_{1}\phi S^* +k_2 m_2 -k_{3}(\delta _3 +\xi -m_3)]\\&-\,\Bigg [k_1 \frac{(bI^*_c +\phi I^*){S^*}^2}{S}+k_2 qbI^*_c S\\&+\,k_2 q\phi S\frac{II^*_c}{I_c}\\&+\,k_2 m_2 \frac{I I^*_c}{I_c}+k_3 m_3 \frac{I^* I_c}{I}+k_3 (1-q)SbI_c \frac{I^*}{I}\\&\quad +\,k_3 (1-q)S\phi I^* +k_3\alpha \displaystyle \frac{I^* I_c}{I} \Bigg ] \end{aligned}$$

Let us choose $k_{1}=1$ and $k_2 , k_3$ in such a way that $k_i,i=1,2,3,$ satisfy

$$\begin{aligned}&-k_{1}+k_{2}(1-q)+k_{3}q=0\nonumber \\&k_{1}bS^*-k_{2}(\delta _{2}+\alpha -m_1)+k_{3}(m_3+\alpha )=0\nonumber \\&k_{1}\phi S^*+k_{2}m_2+k_{3}(\delta _3 +\xi -m_4)=0 \end{aligned}$$

(17)

Solving:

$$\begin{aligned} k_{2}&=\frac{(\delta _3 +\xi -m_4)+\phi S^* (m_3 +\alpha )}{(\delta _2+\alpha -m_1) (\delta _3 +\xi -m_4)-m_2 (m_3 +\alpha )}\nonumber \\ k_{3}&=\frac{b S^* m_2 +\phi S^* (\delta _2 +\alpha -m_1)}{(\delta _2+\alpha -m_1) (\delta _3 +\xi -m_4)-m_2 (m_3 +\alpha )}\nonumber \\ k_{1}&=1 \end{aligned}$$

(18)

Let us rearrange the terms of $^{C}_{0}D^{\varepsilon }_{t}(W)$ in such a way that $^{C}_{0}D^{\varepsilon }_{t}(W)=W_{1}+W_{2}+W_{3}$, where

$$\begin{aligned} W_{1}&=(\delta _{1}+\theta )S^{*} \left( 2-\frac{S}{S^*}-\frac{S^*}{S}\right) \nonumber \\ W_{2}&=k_{1}(bI^*_{c}+\phi I^*)S^* \nonumber \\&\quad +k_{2} (\delta _{2}+\alpha -m_1)I^*_{c} +k_{3} (\delta _{3} +\xi -m_4)I^*\nonumber \\ W_{3}&=-k_1 \frac{(bI^*_c +\phi I^*){S^*}^2}{S}\nonumber \\&\quad -k_2 qbI^*_c S-k_2 q\phi S\frac{II^*_c}{I_c}\nonumber \\&\quad -k_2 m_2 \frac{I I^*_c}{I_c}-k_3 m_3 \frac{I^* I_c}{I} -k_3 (1-q)SbI_c \frac{I^*}{I}\nonumber \\&\quad -k_3 (1-q)S\phi I^* -k_3\alpha \frac{I^* I_c}{I} \end{aligned}$$

(19)

It is clear that

$$\begin{aligned} W_{1}\le 0 \end{aligned}$$

(20)

from the inequality $a+\frac{1}{a}\ge 2$ for all $a>0$ and $W_{1}=0$ if and only if $S=S^*$. We have only to show that $W_{2}+W_{3}\le 0$. We can rewrite $W_{2}$ by using the relation (17), the values of $k_{i}, i=1,2,3$, mentioned in (18) and the equilibrium relation:

$$\begin{aligned}&[(1-q)(\delta _{2}+\alpha -m_1)+q(m_3+\alpha )]I^*_{c}\nonumber \\&\quad =[q(\delta _{3}+\xi -m_4)-(1-q)m_2]I^* \end{aligned}$$

(21)

as

$$\begin{aligned} W_{2}&=2k_2q\phi I^* S^*+2k_2 qb I^*_c S^*+ 2k_3(1-q)\phi I^* S^* \nonumber \\&\quad + 2(1-q)k_3 b I^*_c S^* +k_3 (m_3 +\alpha )I^*_c +k_2 m_2 I^* \end{aligned}$$

(22a)

Using $A.M.\ge G.M.$, we have

$$\begin{aligned} W_{2}&\le 2k_2q\phi I^* S^*+2k_2 qb I^*_c S^*+ 2k_3(1-q)\phi I^* S^* \nonumber \\&\quad \!+\!4[q(1\!-\!q)k_{2}k_3 b\phi I^*_c]^{\frac{1}{2}} S^* \!+\!2[k_2 k_3 m_2 (m_3 \!+\!\alpha ) I^*_c I^*]^{\frac{1}{2}} \end{aligned}$$

(22b)

Similarly,

$$\begin{aligned} W_{3}&=\left[ -k_2 q bI^*_c S -\frac{qk_2 b S*^2 I^*_c}{S}\right] \nonumber \\&\quad +\left[ -k_3 (1-q) S \phi I^* -k_3 \frac{(1-q)\phi I^* {S^*}^2}{S}\right] \nonumber \\&\quad +\left[ -k_2 q \phi \frac{S I I^*_c}{I_c}-k_2 q \phi \frac{I^* {S^*}^2}{S}\right. \nonumber \\&\quad \quad \left. -k_3 (1-q) \frac{bI^*_c {S^*}^2}{S}-k_3 (1-q)\frac{SbI_c I^*}{I}\right] \nonumber \\&\quad +\left[ -k_2 m_2 \frac{II^*_c}{I_c}-k_3(m_3 +\alpha )\frac{I^* I_c}{I}\right] \end{aligned}$$

(23)

Using the inequality $A.M.\ge G.M.$, we have got:

$$\begin{aligned} W_3&\le -2k_2q\phi I^* S^*-2k_2 qb I^*_c S^*- 2k_3(1-q)\phi I^* S^* \nonumber \\&\quad -4[q(1-q)k_{2}k_3 b\phi I^*_c]^{\frac{1}{2}} S^*\nonumber \\&\quad -2[k_2 k_3 m_2 (m_3 +\alpha ) I^*_c I^*]^{\frac{1}{2}}\le -W_{2}\nonumber \\&\Rightarrow \ W_2 +W_3 \le 0 \end{aligned}$$

(24)

From relations (20) and (24), it is clear that $^{C}_{0}D^{\varepsilon }_{t}(W)\le 0$ and thus $^{C}_{0}D^{\varepsilon }_{t}(W)$ is negative definite with respect to $E_{1}$. Hence $E_{1}$ is globally asymptotically stable by Lemma 4. $\square$

4 Fractional optimal control problem

Optimal control is an efficient tool for finding combined strategies for vaccination $(\theta )$ and treatment $(\xi )$ of the optimal control problem of an infectious disease system like Hepatitis B virus with active carrier. Our aim is to minimize the number of susceptible and infected population and the cost of implementing the control strategy. Earlier, Ding et al. [42] and Agarwal et al. [25] have contributed on optimal control theory in fractional calculus but progress in nonlinear control theory in fractional dynamics is still limited. In this section, we have used these results to solve our fractional order optimal control problem stated later.

The theory of optimal control in fractional order is based on Pontryagain’s principle [43]. The technique is quite similar to classical integer order optimal control problem. Let x be the pseudo-state vector and $u=[u^1,u^2,...,u^m]\in U\subseteq {R}^m$ is the input vector and U is the set of admissible control of the dynamical system $^{C}_{t_{0}}D^{\varepsilon }_{t} x =f(x,u,t), x(0)=x_0$. The system’s pseudo state is supposed to reach final condition $x_f$ in the unknown final time $T_f$. The control $u\in U$ must be chosen for all $t\in [0,T_f]$ to minimize the objective functional J which is denoted and defined as

$$\begin{aligned} J=\Theta (x(T_f))+ \int ^{T_f}_0 {\mathscr {F}}(x(t),u(t))dt \end{aligned}$$

The constraints on the system dynamics can be adjoined to the Lagrangian ${\mathscr {F}}$ by introducing time-varying Lagrange multiplier vector $\lambda$ , whose elements are called the co-states of the system. This motivates the construction of the Hamiltonian ${\mathscr {H}}$ defined for all $t\in [0,T_f]$.

$$\begin{aligned} {\mathscr {H}}(x(t),u(t),\lambda (t))=\lambda ^{T}(t) f(x(t),u(t))+{\mathscr {F}}(x(t),u(t)). \end{aligned}$$

Where $\lambda ^T$ stands for transpose of $\lambda$. Pontryagin’s minimum principle states that the optimal state trajectory $x^{*}$, optimal control $u^{*}$, and corresponding Lagrange multiplier vector $\lambda ^*$ must minimize the Hamiltonian ${\mathscr {H}}$ so that [44]

• 1. ${\mathscr {H}}(x^* (t),u^* (t),\lambda ^* (t))\le {\mathscr {H}}(x^* (t),u(t),\lambda ^* (t))$

• 2. $\displaystyle \frac{\partial \Theta (x)}{\partial T_f}|_{x=x(T_f)}+{\mathscr {H}}(T_f)=0$

• 3. $^{RL}_{t}D^{\varepsilon }_{T_f} \lambda ^{T} =\displaystyle \frac{\partial {\mathscr {H}}}{\partial x}|_{x=x*}$

• 4. $\displaystyle \frac{\partial {\mathscr {H}}}{\partial u}|_{u=u*}=0$ and $\displaystyle \frac{\partial ^2 {\mathscr {H}}((x^* (t),u^* (t),\lambda ^* (t)))}{\partial u^2}\le 0$,

where

$$\begin{aligned} ^{RL}_{t}D^{\varepsilon }_{T}f(t)=\displaystyle \frac{-1}{\Gamma (1-\varepsilon )} \frac{d}{d\tau }\int ^T_t (\tau -t)^{-\varepsilon } f(\tau )d\tau , \forall t\in [0,T] \end{aligned}$$

is the Right-Liouville derivative of order $\varepsilon$. These four conditions are necessary for optimal control.

We have formulated our optimal control problem as follows where the state variables $(S,I_{c},I,R)$ satisfy the proposed system of fractional order differential equations (2) depending on the control variables $u_1 (t),u_2 (t)$. Here $u_1$ is considered power of vaccination and $u_1$ can be utilized as a important factor to create a constructive outcomes on susceptible population with $0\le u_{1}\le 1$. Here 0 portrays no vaccination in certain time frame ([0,T]), while 1 is speaking to full vaccination. Likewise, $u_2 =0$ means no treatment and $u_2 =1$ is the full treatment.

We have omitted the last equation of R(t) of system (2) during the analysis since the variable R does not appear in other equations of system (2). After analyzing the reduced system, we can also acquire the knowledge of the dynamics of R. It is assumed that the control functions $u_{1} (t),u_{2} (t)$ are measurable and $0\le u_{1} (t),u_{2} (t) \le 1$. Our main objective is to minimize the given objective function J in time interval [0, T] by finding optimal control $u^*=({u^*_1},{u^*_2})$ as follows:

$$\begin{aligned} J({u^*_1} ,{u^*_2})&=J_{\min {({u_1}(t),{u_2}(t))\in U}} \end{aligned}$$

(25)

$$\begin{aligned} J(u_1,u_2)&\!=\!I_{c}(t)\!+\!\displaystyle \int _{0}^{T} \left[ \alpha _{1}S(t) \right. \nonumber \\&\left. \!+\!\alpha _{2}I_{c}(t)\!+\!\alpha _{3}I(t) \!+\!\frac{\beta _{1}}{2}{u^2 _1 (t)}\!+\!\frac{\beta _{2}}{2}{u^2 _2 (t)}\right] dt \end{aligned}$$

(26)

subject to

$$\begin{aligned} {}^{C}_{0}D^{\varepsilon }_{t}S(t)&\!=\!{\eta }\!-\!{\delta _{1}}S \!-\!S(bI_{c}\!+\!{\phi }I)\!-\!{{u_1}\theta S} ,S(0)\!=\!S_{0}>0,\nonumber \\ {}^{C}_{0}D^{\varepsilon }_{t}I_{c}(t)&=qS(bI_{c} +{\phi }I)-({\delta _{2}}+{\alpha })I_{c}\nonumber \\&\quad +m_{1} I_{c}+m_{2} I,I_{c}(0)>0,\nonumber \\ {}^{C}_{0}D^{\varepsilon }_{t}I(t)&=(1-q)S(bI_{c}+{\phi }I) -({\delta _{3}}+{u_2}{\xi })I\nonumber \\&\quad +{\alpha }I_{c}+m_{3} I_{c}+m_{4} I,I(0)=I_{0}>0, \end{aligned}$$

(26a)

where $U=\left\{ (u_1 ,u_2 )\in L^{\infty }_{1}(0,T),0\le u_1 , u_2 \le 1,t\in (0,T) \right\}$ being the control space. The existence and uniqueness of the solutions of the optimal control problem stated in (26a) can be established in a similar way as mentioned in section 3.2.

Table 2 Parametric values used in system (2)

Table 3 Parametric values used in system (2)

Fig. 1

Time series and phase portrait of system (10) corresponds to Table 2 when $E^{*}_0 (0.2856,0,0)$, In time series, Horizontal axis (time axis) $1\ \hbox {unit} = 1\hbox {day}$ ; Vertical axis $1\ \hbox {unit} = 1000\ \hbox {persons}$

Fig. 2

Time series and phase portrait of system (10) corresponds to Table 3 when $E^{*}_1 (1.042,6.635,2.174)$, In time series, Horizontal axis (time axis) $1\ \hbox {unit} =1\hbox {day}$; Vertical axis $1 \hbox {unit} = 1000\ \hbox {persons}$

Fig. 3

Time series of system (10) corresponds to Table 3 when $E^{*}_1 (1.042,6.635,2.174)$ and $\varepsilon = 0.9, 0.95, 0.99$, Horizontal axis (time axis) $1 \hbox {unit} =1\hbox {day}$; Vertical axis $1 \hbox {unit} = 1000\ \hbox {persons}$

Fig. 4

Time series of system (10) corresponds to Table 3 when $E^{*}_1 (1.042,6.635,2.174)$ and $\varepsilon = 0.5, 0.6, 0.7$, Horizontal axis (time axis) $1\ \hbox {unit} =1\hbox {day}$; Vertical axis $1\ \hbox {unit} = 1000\ \hbox {persons}$

Fig. 5

Time series of optimal state variables for the control problem (26) correspondence to Table 2 with $\varepsilon =0.8$

Fig. 6

Time series of optimal control variables for the control problem (26) correspondence to Table 2 with $\varepsilon =0.8$

The existence of optimal control $({u^*_1},{u^*_2})$ can be established in the next theorem.

Theorem 11

Let the control function $u=(u_1 ,u_2 )\in U$ be measurable on [0, T] with value of each of $u_1 ,u_2$ lies in [0,1]. Then an optimal control $u^*=(u^*_1 ,u^*_2 )$ minimizing the objective function $J(u_1 ,u_2 )$ of (26) with

$$\begin{aligned} ^{RL}_{t}D^{\varepsilon }_{T}\lambda _{1}(t)= & {} \lambda _{1}(\delta _{1}+bI_{c} +\phi I+u_1 \theta )-\lambda _{2}q(bI_{c}+\phi I)\\&-\,\lambda _{3}(1-q)(bI_{c}+\phi I)-\alpha _{1}\\ ^{RL}_{t}D^{\varepsilon }_{T}\lambda _{2}(t)= & {} \lambda _{1}(Sb)+\lambda _{2}(\delta _{2} +\alpha -qSb-m_{1})\\&-\,\lambda _{3}\{(1-q)Sb+\alpha +m_{3}\}-\alpha _{2}\\ ^{RL}_{t}D^{\varepsilon }_{T}\lambda _3(t)= & {} \lambda _{1}(S\phi ) -\lambda _{2}(q\phi S+m_{2})\\&+\,\lambda _{3}\{(\delta _{3}+u_2 \xi -m_{4})-(1-q)\phi S\}-\alpha _{3}, \end{aligned}$$

where

$$\begin{aligned}&u^*_1 =\max \{\min \{\bar{u_1},1\},0\};\nonumber \\&u^*_2=\max \{\min \{\bar{u_2},1\},0\}\nonumber \\&\bar{u_1}=\frac{\lambda _{1}S\theta }{\beta _{1}}, \bar{u_2}=\frac{\lambda _{3}I\xi }{\beta _{2}} \end{aligned}$$

(27)

and $(S,I_{c},I)$ is the corresponding solution of (26).

Proof

We have considered the Hamiltonian as follows:

$$\begin{aligned} H&=\left[ \displaystyle \alpha _{1}S(t)+\alpha _{2}I_{c}(t)+\alpha _{3}I(t) +\frac{\beta _{1}}{2}{u_1}^2+\frac{\beta _{2}}{2}{u_2}^2\right] \nonumber \\&\quad +\lambda _{1}\{{\eta }-{\delta _{1}}S-S(bI_{c}+{\phi }I)-{u_1 \theta S}\}\nonumber \\&\quad +\lambda _{2}\{qS(bI_{c}+{\phi }I)-({\delta _{2}} +{\alpha })I_{c}+m_{1} I_{c} +m_{2} I\}\nonumber \\&\quad \!+\!\lambda _{3}\{(1\!-\!q)S(bI_{c}\!+\!{\phi }I)\!-\!({\delta _{3}} \!+\!{u_2}{\xi })I\!+\!{\alpha }I_{c}\!+\!m_{3} I_{c}\!+\!m_{4} I\} \end{aligned}$$

(28)

with $(\lambda _{1},\lambda _{2},\lambda _{3})$ being the associated adjoint variables with $\lambda _{i}(T)=0 \ (i=1,2,3$), which have been written in the following canonical equations:

$$\begin{aligned} ^{RL}_{t}D^{\varepsilon }_{T}\lambda _{1}(t)&=-\frac{\partial H}{\partial S} =\lambda _{1}(\delta _{1}+bI_{c}+\phi I+u_1 \theta )\nonumber \\&\quad -\lambda _{2}q(bI_{c}+\phi I)\nonumber \\&\quad -\lambda _{3}(1-q)(bI_{c}+\phi I)-\alpha _{1}\nonumber \\ ^{RL}_{t}D^{\varepsilon }_{T}\lambda _{2}(t)&=-\frac{\partial H}{\partial I_{c}} =\lambda _{1}(Sb) +\lambda _{2}(\delta _{2}+\alpha -qSb-m_{1})\nonumber \\&\quad -\lambda _{3}\{(1-q)Sb+\alpha +m_{3}\}-\alpha _{2}\nonumber \\ ^{RL}_{t}D^{\varepsilon }_{T}\lambda _3(t)&=-\frac{\partial H}{\partial I} =\lambda _{1}(S\phi )-\lambda _{2}(q\phi S+m_{2})\nonumber \\&\quad +\lambda _{3}\{(\delta _{3} +u_2 \xi -m_{4})-(1-q)\phi S\}-\alpha _{3} \end{aligned}$$

(29)

Therefore, the problem of finding $u^*$ that minimizes J subject to (29) is converted to minimizing the Hamiltonian with respect to the control. Then by Pontryagin principle[44], we have achieved the optimal conditions:

$$\begin{aligned}&\frac{\partial H}{\partial u_2}=\beta _{2}u_{2}-\lambda _{3}I\xi =0\nonumber \\&\frac{\partial H}{\partial u_1}=\beta _{1}u_{1}-\lambda _{1}S\theta =0 \end{aligned}$$

(30)

which can be solved in terms of state and adjoint variables to give

$$\begin{aligned} \bar{u_1}=\frac{\lambda _{1}S\theta }{\beta _{1}}, \bar{u_2} =\frac{\lambda _{3}I\xi }{\beta _{2}} \end{aligned}$$

(31)

For the optimal control $u^*$, which requires considering the constrains on the control and the sign of $\displaystyle \frac{\partial H}{\partial u}$. Hence we have

$$\begin{aligned}&u^*_1=\left\{ \begin{array}{lll} \displaystyle 0 \ \text {if} \ \displaystyle \frac{\partial H}{\partial u_1 }<0\\ \\ \bar{u_1}\ \text {if} \ \displaystyle \frac{\partial H}{\partial u_1}=0\\ \\ 1 \ \text {if}\ \displaystyle \frac{\partial H}{\partial u_1}>0s \end{array}\right. \end{aligned}$$

(32a)

$$\begin{aligned}&u^*_2=\left\{ \begin{array}{lll} \displaystyle 0 \ \text {if} \ \displaystyle \frac{\partial H}{\partial u_2}<0\\ \\ \bar{u_2}\ \text {if} \ \displaystyle \frac{\partial H}{\partial u_2}=0\\ \\ 1 \ \text {if}\ \displaystyle \frac{\partial H}{\partial u_2}>0 \end{array}\right. \end{aligned}$$

(32b)

and

$$\begin{aligned} u^*_1=\max \{\min \{\bar{u_1},1\},0\};u^*_2=\max \{\min \{\bar{u_2},1\},0\} \end{aligned}$$

(33)

where $\displaystyle \bar{u_1}=\frac{\lambda _{1}S\theta }{\beta _{1}}, \bar{u_2}=\frac{\lambda _{3}I\xi }{\beta _{2}}$. Optimal state can be found by substituting $u^*$ into the system (29). $\square$

5 Numerical simulations

Analytical study is incomplete without numerical verification of the results. In this section we have presented numerical simulation of system (2). We have used FDE12 matlab function which is designed on predictor-corrector scheme based on Adams-Bashforth-Moulton algorithm introduced by Roberto Garrappa [45]. We have also used iterative scheme (Euler’s forward and backward) to develop fractional order optimal control problem.The process is briefly described below. The optimality system constitutes a two-point boundary value problem including a set of fractional-order differential equations. The state system (26a) is an initial value and adjoint system (29) is a boundary value problem.

The state system (26a) is solved using the iterative scheme below:

$$\begin{aligned} S(i)&=[{\eta }-{\delta _1}S(i-1)-S(i-1)(bI_{c}(i-1)\\&\quad +\phi I(i-1))-{u_1 \theta }S(i-1)]h^{\varepsilon }\\&\quad -\sum ^{i}_{j=1}c(j)S(i-j)\\ I_{c}(i)&=[qS(i-1)(bI_{c}(i-1)+{\phi }I(i-1))\\&\quad -({\delta _{2}}+{\alpha })I_{c}(i-1)+m_{1} I_{c}(i-1)+m_{2} I(i-1)]h^{\varepsilon }\\&\quad -\sum ^{i}_{j=1}c(j)I_{c}(i-j)\\ I(i)&=[(1-q)S(i-1)(bI_{c}(i-1)\\&\quad +{\phi }I(i-1))-({\delta _{3}}+{u_2}{\xi })I(i-1)\\&\quad +{\alpha }I_{c}(i-1)+m_{3} I_{c}(i-1)+m_{4} I](i-1)h^{\varepsilon }\\&\quad -\sum ^{i}_{j=1}c(j)I(i-j) \end{aligned}$$

Fig. 7

Optimal cost for the control problem (26) correspondence to Table 2 with $\varepsilon =0.8$

Fig. 8

Time series of optimal state variables for the control problem (26) correspondence to Table 2 with $\varepsilon =0.9$

Fig. 9

Time series of optimal control variables for the control problem (26) correspondence to Table 2 with $\varepsilon =0.9$

where $c(0)=1$ and $c(j)=(1-\frac{1+\varepsilon }{j})c(j-1), j\ge 1$ and $h^{\varepsilon }$ is the time step length (we have assumed $h=0.02$). Here S(i) is the value of S(t) at $i^{th}$ iteration. The last term of each of the above system of equations stands for memory. The adjoint system (29) is solved by backward iteration method with terminal conditions $\lambda _i (T)=0, i=1,2,3$ using the following iterative scheme:

$$\begin{aligned} \lambda _1 (i)= & {} [\lambda _{1}(i-1)(\delta _{1}+bI_{c}(i)+\phi I(i)+u_1\theta )\\&-\lambda _{2}(i-1)q(bI_{c}(i)+\phi I(i))\\&-\lambda _{3}(i-1)(1-q)(bI_{c}(i)+\phi I(i))-\alpha _{1}]h^{\varepsilon }\\&-\sum ^{i}_{j=1}c(j)\lambda _1 (i-j)\\ \lambda _2 (i)= & {} [\lambda _{1}(i)(Sb)+\lambda _{2}(i-1)(\delta _{2}+\alpha -qS(i)b-m_{1})\\&-\lambda _{3}(i-1)\{(1-q)S(i)b +\alpha +m_{3}\}-\alpha _{2}]h^{\varepsilon }\\&-\sum ^{i}_{j=1}c(j)\lambda _2 (i-j)\\ \lambda _{3} (i)= & {} [\lambda _{1}(i)(S(i)\phi )-\lambda _{2}(i)(q\phi S(i)+m_{2})\\&\!+\!\lambda _{3}(i\!-\!1)\{(\delta _{3}\!+\!u_2 \xi \!-\!m_{4})\!-\!(1\!-\!q)\phi S(i)\}\!-\!\alpha _{3}]h^{\varepsilon }\\&-\sum ^{i}_{j=1}c(j)\lambda _3 (i-j) \end{aligned}$$

The optimal control is updated by the scheme below:

$$\begin{aligned} u^*_1= & {} \max \{\min \{\bar{u_1},1\},0\},\ \text {where}\ \bar{u_1} =\frac{\lambda _{1}(i-1)S(i)\theta }{\beta _{1}}\\ u^*_2= & {} \max \{\min \{\bar{u_2},1\},0\},\ \text {where}\ \bar{u_2} =\frac{\lambda _{3}(i-1)I(i)\xi }{\beta _{2}} \end{aligned}$$

Fig. 10

Optimal cost for the control problem (26) correspondence to Table 3 with $\varepsilon =0.9$

We have assumed $t=1$ day as smallest unit in horizontal axis (time axis) and the unit in the vertical axis is person where smallest unit (1 unit) in vertical axis is 1000 persons (for $S, I_c, I$), in control diagram $u_1, u_2$ axes has no physical unit and cost axis ($J^*$) has smallest unit (1 $\hbox {unit}=1$ Euro) money. We have considered Table 2 and Table 3 where we have taken set of different parametric values. It is noticeable that natural death rate is lower than carrier class death rate and carrier class death rate is lower than infected class death rate. We have not considered recovery class in our simulations.

We first consider the case when ${\mathscr {R}}_0=0.1548<1$ using the parametric values mentioned in Table 2. Figure 1 reveals the fact that only susceptible population survives $(S=0.2856)$ and the infective population ($I_c$) in carrier stage (asymptomatic) and infective population in symptomatic stage (I) are going to extinct. It shows that disease free equilibrium is locally asymptotically stable whenever ${\mathscr {R}}_0<1$. This numerical simulations validate our analytical results derived in Theorem 7 and 8.

Next, using parametric values enlisted in Table 3, it is observed that ${\mathscr {R}}_0=2.3077>1$ and so the condition for existence of endemic equilibrium is established. It is also observed that the system is locally asymptotically stable around (1.042, 6.635, 2.174) as depicted in Fig. 2. We have also observed that for higher value of $\varepsilon$, the stability of the equilibrium reaches faster as reported in Fig. 3. When $\varepsilon$ increases, the infective population at carrier stage and the infective population at symptomatic stage also increase (Fig. 4 represents this case).

For optimal control problem, let us assume $\alpha _{i}=1,i=1,2,3$, and $\beta _1 =1,\beta _2 =10$ and all the parametric values are taken from Table 2. We have chosen $T=80$ days for final time. In each Figs. 5, 6, 7, 8, 9, 10, the dynamics of different population classes along with the implication of controls measures are demonstrated. We have studied three strategies for eradication of carrier based disease like HBV infection, typhoid etc.

Fig. 11

Time series of state variables and optimal control variables for the control problem (26) when $\alpha _1 =0, \alpha _{2}, \alpha _3 \ne 0$ correspondence to Table 2 with $\varepsilon =0.8$

Fig. 12

Time series of state variables and optimal control variables for the control problem (26) when $u_1 \ne 0,u_2 =0$ correspondence to Table 2 with $\varepsilon =0.8$

Fig. 13

Time series of state variables and optimal control variables for the control problem (26) when $u_1 =0, u_2 \ne 0$ correspondence to Table 2 with $\varepsilon =0.8$

5.1 Scenario 1: coupled control strategies

We start first the strategy by making control $u_1 \ne 0,u_2 \ne 0$ which analyze the effect of the implementation of the vaccination coupled with treatment control. The effect of vaccination and treatment controls on different population classes are shown graphically in Figs. 5, 6, 7 for $\varepsilon =0.8$ and Figs. 8, 9, 10 for $\varepsilon =0.9$. From Fig. 5, it is clear that individuals under treatment (infected class) along with carrier class decreased significantly when we have applied coupled control strategy. It is also noted that the increase in the order of derivative ($\varepsilon$) in both the infected and carrier classes is increasing, but that the susceptible classes are decreasing. In Fig. 11, we have shown the case when $\alpha _1 =0$, where we took into account the fact that there are no expenditures due to the susceptible class. It is observed that after 80 days optimal cost is higher than the previous case where $\alpha _1 =1$ and the number of population in infected and carrier class is also increased in later case ($\alpha _1 =0$).

5.2 Scenario 2: single control strategies

5.2.1 First strategy

This strategy analyze the effect of the implementation of the vaccination with no treatment ($u_1 \ne 0, u_2 =0$). Figure 12 shows the impact of this strategy and it is observed that the individuals in both infected and carrier classes are increased rapidly. So this strategy is not much effective to control the disease.

5.2.2 Second strategy

This strategy analyze the effect of the implementation of treatment with no vaccination ($u_1 =0, u_2 \ne 0$). Fig. 13 depicts the impact of this strategy. It is observed that this strategy is better than first strategy but the coupled strategy is the best among them.

6 Conclusions

It is known that treatment and vaccination of HBV infection or other carrier based infectious diseases reduce the risk of progression and so it is a desirable to implement control measures on these efforts to prevent these diseases. In this work, a deterministic fractional order model incorporating control measures on vaccination and treatment efforts is constructed to analyze the dynamic behaviors. It is observed that the disease free equilibrium is stable under suitable parametric conditions and same for endemic equilibrium. An interesting fact is observed that the solutions of the system depend on order of differentiation very much. Lowering the order of differentiation the infected and carrier population increases.

Optimal control techniques are often used in developing optimal strategy for complex biological situations. Since control combination of vaccination and treatment is important in the disease prevention and control, it is studied by classical and fractional optimal theories when these two parameters (treatment and vaccination) appear as functions of time. The aim of the proposed work is to minimize the given objective functional modulating the control variables in a time interval, which is asserted that there exists an optimal control by invoking suitable Hamiltonian. In addition to vaccination and treatment, other measures may also be important to control HBV (Hepatitis B virus) or other infectious diseases with carrier, such as the prevention of vertical transmission by vaccination and proper diagnosis. Moreover, we have illustrated three different strategies for infection minimization and observed that implementation of the vaccination and treatment control interventions at a time is useful and fruitful for the eradication of disease with carrier.

On the other hand, the actual progression of infectious diseases like HBV, typhoid and others related with carriers are complex, and the interventions in preventing these diseases are changed with time according to their responses and the administration policies. The implementation of fractional derivatives is also significant in control problems. Control acts more effectively in shorter time if we decreases fractional order ($\varepsilon$). Thus, $\varepsilon$ can be related with awareness or reception toward some policies to decrease infected and carrier population. The proposed system is not affected significantly by the vertical transmission parameters ($m_{i},i=1,2,3,4$). From numerical section it is evident that with proper control, we can reduce the infected populations and also minimize the economical burden to implement those control policies. The method of discretization and Euler’s method (both forward and backward ) have been used to solve the fractional order optimal control problem. In future works, it will be interesting to develop a good scheme for solving fractional order control problems.