1 Introduction

Autonomous underwater vehicles (AUVs) are playing a vital role in underwater exploration allowing humans to explore great depths. Trajectory tracking of an AUV along a desired path is an important task. It is difficult to develop a controller for an AUV in presence of uncertainties, disturbances and noise. Under these hardships, this paper focuses on developing a new control law for trajectory tracking for an AUV in the horizontal plane.

Sliding mode controller (SMC) is a powerful nonlinear controller to control uncertain and nonlinear systems with external disturbances, so many authors interested in the SMC method in trajectory tracking control problems and applied it to control underwater vehicles [1,2,3,4,5,6]. Pure sliding mode controller has disadvantages such as chattering and being too vulnerable against noise. Some ways to reduce chattering are reported in the literature such as Boundary Layer Control (BLC) [7, 8], Adaptive Boundary Layer method [9], Dynamic Sliding Mode Control (DSMC) [10], and High Order Sliding Mode Control (HOSMC) [11].

One other way to overcome chattering phenomenon is reaching law approach. It first was introduced by Gao and Hung [12]. In [12], three reaching law methods were proposed: (1) constant rate reaching law which consists a real, positive constant gain and a sign function, (2) constant plus proportional rate reaching law which is the constant rate reaching law plus a term of switching function with a constant gain, (3) power rate reaching law is based on a power of absolute of switching function and the sign function in which the power of absolute of switching function is between the open interval 0–1. A generalized algorithm is first researched in [13] for reaching and being boundedness of sliding variable. A new reaching law has been proposed in [14] for the discrete-time SMC in which the proposed reaching law guarantee smaller width of the quasi sliding mode domain and simultaneously it can decrease the reaching time.

Combining adaptive controller and sliding mode controller lead to adaptive sliding mode control and it has been widely used in underwater vehicles [15,16,17,18]. In [15], an adaptive non-singular integral sliding mode control is designed for trajectory tracking problem in AUVs. This controller can eliminate the singularity problem in conventional terminal SMC, and it does not require to the bound information of the lumped system uncertainty. An adaptive sliding mode control is used to control the voltage of thrusters of an underwater robot in [16]. They use an adaptive learning method based on the local recurrent neural network for unknown function item and they propose a switch gain adjust method based on exponential function to guarantee trajectory tracking error is uniformly bounded. In [17] an adaptive fuzzy sliding mode control for remotely operated underwater vehicles has been designed. This controller was used to deal with the stabilization and trajectory tracking problems in presence of disturbances which can arise in the subaquatic environment, and uncertainties in hydrodynamics coefficients of the system. An adaptive sliding mode based control allocation has been proposed for accommodating simultaneous actuator faults in [18]. The control method includes a low level module and the high level module in which the control gains for high level sliding mode control is adjusted by the adaptive scheme. Also it can reconfigure the distribution of control signals which eliminates the effect of virtual control error generated by the low-level control module.

In this paper we propose a novel controller for the trajectory tracking control of an underwater robot in the horizontal plane. We modify the reaching law and use an adaptive gain in the sliding mode control. In the presented reaching law, a continuous term is used instead of the discrete sign function. To avoid selection of big constant gain, which is one of the factors causing chattering, the gain of controller is selected adaptively. The stability analysis is survived based on a theorem as well as by another theorem it is proved that the reaching time is finite.

Main contributions of this paper are as follows:

  1. 1.

    By modifying the reaching law, the chattering problem and vulnerability to noise are eliminated.

  2. 2.

    Since the reaching law control comes into action when the variables are separated from the sliding surface, adaptive gain is used in order to select the gain in accordance with error and dynamic of error, this means that by selecting the gain of controller adaptively, the selection of the constant gain by means of trial and error method is avoided.

  3. 3.

    There is no any sign function in the control law. Therefore the chattering problem and vulnerability to noise are eliminated.

  4. 4.

    Proposed method is compared with two methods and it has better results than them.

  5. 5.

    A theorem is stated to prove the stability of proposed method, also we state another theorem to prove that the reaching time is finite.

This paper is organized as follows: In Sect. 2, the horizontal plane equations and the mathematical model of an AUV are presented. The controller design are discussed In Sect. 3. In Sect. 4 the simulation results are presented followed by a conclusion in Sect. 5.

2 A two dimensional model of an AUV

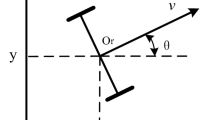
In this section, the problem of tracking of an AUV in the horizontal plane is considered. Two rudders in front and rear side of the vehicle are used as the control inputs. A schematic diagram of the system under consideration is shown in Fig. 1. According to [19, 20], the equations of motion in the horizontal plane are described as follows,

$$ \begin{aligned} \dot{v}\left[ {m - Y_{{\dot{v}}} } \right] + \dot{r}\left[ {mx_{G} - Y_{{\dot{r}}} } \right] &= Y_{{\delta_{s} }} \delta_{s} u^{2} + Y_{{\delta_{b} }} \delta_{b} u^{2} \\&\quad- d_{1} \left( {v,r} \right) + Y_{v} uv + \left( {Y_{r} - m} \right)ur, \end{aligned} $$
(1)
$$\begin{aligned} \dot{v}\left[ {mx_{G} - N_{{\dot{v}}} } \right] + \dot{r}\left[ {I_{z} - N_{{\dot{r}}} } \right] &= N_{{\delta_{s} }} \delta_{s} u^{2} + N_{{\delta_{b} }} \delta_{b} u^{2} \\&\quad- d_{2} \left( {v,r} \right) + N_{v} uv + \left( {N_{r} - mx_{G} } \right)ur,\end{aligned} $$
(2)

where \( v \) and \( r \) are relative sway and yaw velocities of the moving vehicle with respect to water. \( Y \) and \( N \) represent the total excitation sway force and yaw moment, respectively. \( x_{G} \) is the coordinate of the vehicle center of gravity in the body fixed local frame, and \( m \) and \( I_{z} \) are the vehicle mass and mass moment of inertial. Equations (1) and (2) describe the complete model of the vehicle in the horizontal plane.

Fig. 1
figure 1

Geometry and axes definition of an AUV the horizontal plane

Full size image

Remark 1

According to [21], the drag related terms \( d_{v} \left( {v,r} \right) \) and \( d_{r} \left( {v,r} \right) \) are very small, and then, these terms can be ignored. It is noticed that all values have been normalized [20].

For control purposes, (1) and (2) must be solved with respect to \( \dot{v} \) and \( \dot{r} \). On the other hand, the set of equation of motions are described as follows,

$$ \dot{v} = a_{11} uv + a_{12} ur + b_{11} u^{2} \delta_{s} + b_{12} u^{2} \delta_{b} , $$
(3)
$$ \dot{r} = a_{21} uv + a_{22} ur + b_{21} u^{2} \delta_{s} + b_{22} u^{2} \delta_{b} , $$
(4)
$$ \dot{\psi } = r, $$
(5)
$$ \dot{x} = ucos\psi - vsin\psi , $$
(6)
$$ \dot{y} = usin\psi + vcos\psi , $$
(7)

where \( a_{ij} \) and \( b_{ij} \) are the related coefficients that appear when solving (1) and (2) and they include at least two hydrodynamic coefficient, such as \( Y_{{\dot{v}}} , Y_{{\dot{r}}} , N_{{\dot{v}}} , N_{{\dot{r}}} , \ldots \)

$$ a_{ij} = \left[ {\begin{array}{*{20}c} { - 1.4776} & \quad{ - 0.3083} \\ { - 1.8673} & \quad{ - 1.2682} \\ \end{array} } \right],\quad b_{ij} = \left[ {\begin{array}{*{20}c} {0.2271} & \quad{0.1454} \\ { - 1.9159} & \quad{1.2112} \\ \end{array} } \right] $$

3 Controller design

  1. A.

    Review of Boundary layer Sliding Mode Control

Consider the following nonlinear state space equation which describes equation of motion of an AUV [8],

$$ \left\{ {\begin{array}{*{20}l} {x^{\left( n \right)} \left( t \right) = F\left( {X,t} \right) + G\left( {X,t} \right)u + d, } \hfill \\ {y = X, } \hfill \\ \end{array} } \right. $$
(8)

where

$$ X = \left[ {x, \dot{x}, \ldots , x^{{\left( {n - 1} \right)}} } \right]^{T} $$
(9)

is the state vector. Suppose that \( X_{d} = \left[ {x_{d} , \dot{x}_{d} , \ldots , x_{d}^{{\left( {n - 1} \right)}} } \right]^{T} \) is the desired state (desired trajectory), and the error vector is defined as,

$$ {\text{e}} = \left[ {{\text{e}}_{1} ,{\text{e}}_{2} , \ldots ,{\text{e}}_{n} } \right], $$
(10)

where

$$ e_{i} = x_{i} - x_{di} . $$
(11)

Sliding surface can be defined as,

$$ S\left( e \right) = \left( {\frac{d}{dt} + \lambda } \right)^{n - 1} e\quad \lambda > 0 $$
(12)

And control law is defined as,

$$ U = u_{r} + u_{eq} , $$
(13)

where \( u_{eq} \) is the equivalent control law and \( u_{r} \) is the reaching law. Then, the tracking errors are defined by,

$$ \tilde{y} = y - y_{d} , $$
(14)
$$ \tilde{\psi } = \psi - \psi_{d} $$
(15)

It should be noted that \( e_{1} = \tilde{y} \) and \( e_{2} = \tilde{\psi } \). For extracting the control law, substitution of (3) and (4) in the second time derivative of (5) and (7) results,

$$ \begin{aligned}\ddot{y} &= u\dot{\psi }cos\psi + \left( {a_{11} uv + a_{12} u\dot{\psi } + b_{11} u^{2} \delta_{s} + b_{12} u^{2} \delta_{b} } \right)cos\psi \\ &\quad-\, v\dot{\psi }sin\psi \end{aligned}$$
(16)
$$ \ddot{\psi } = a_{21} uv + a_{22} ur + b_{21} u^{2} \delta_{s} + b_{22} u^{2} \delta_{b} $$
(17)

Now (16) and (17) can be rewritten in the following vector form as in [20],

$$ \begin{aligned} \left[ {\begin{array}{c} {\ddot{y}} \\ {\ddot{\psi }} \\ \end{array} } \right] & = \left[ {\begin{array}{cc} {a_{{11}} ucos\psi - rsin\psi } \hfill & {ucos\psi + a_{{12}} ucos\psi } \hfill \\ {a_{{21}} u} \hfill & {~a_{{22}} u} \hfill \\ \end{array} } \right]\left[ {\begin{array}{c} v \\ r \\ \end{array} } \right] \\ & \qquad + \left[ {\begin{array}{cc} {b_{{11}} u^{2} cos\psi } \hfill & {b_{{12}} u^{2} cos\psi } \hfill \\ {b_{{21}} u^{2} } \hfill & {b_{{22}} u^{2} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{c} {\delta _{s} } \\ {\delta _{b} } \\ \end{array} } \right], \\ \end{aligned} $$
(18)

where \( \ddot{N} = \left[ {\ddot{y}, \ddot{\psi }} \right]^{T} \), \( X = \left[ {v, r} \right]^{T} \) and \( U = \left[ {\delta_{s} , \delta_{b} } \right]^{T} \). It is important to say that in Eq. (18). Equations (16) and (17) include nonlinear terms and are based on the acceleration terms. To obtain reaching control law, we define the following sliding surface \( s_{1} \) and \( s_{2} \),

$$ s_{1} = \dot{\tilde{y}} + \lambda_{1} \tilde{y} = 0,\quad s_{2} = \dot{\tilde{\psi }} + \lambda_{2} \tilde{\psi } = 0, $$
(19)

According to (14) and (15), we have,

$$ s_{1} = \dot{y} - \dot{y}_{r} ,\quad s_{2} = \dot{\psi } - \dot{\psi }_{r} , $$
(20)

where

$$ \dot{y}_{r} = \dot{y}_{d} - \lambda_{1} \tilde{y},\quad \dot{\psi }_{r} = \dot{\psi }_{d} - \lambda_{2} \tilde{\psi } $$
(21)

are the reference signals equations. By defining the vectors \( S = \left[ {s_{1} , s_{2} } \right]^{T} \) and \( \ddot{N}_{r} = \left[ {\ddot{y}_{r} , \ddot{\psi }_{r} } \right]^{T} \) and by differentiating with respect to time we have,

$$ \dot{S} = \ddot{N} - \ddot{N}_{r} . $$
(22)

For BLC, the following control law is derived by (13) (see [8]),

$$ \begin{aligned} U =& \left[ {\begin{array}{cc} {b_{{11}} u^{2} cos\psi }& {b_{{12}} u^{2} cos\psi } \\ {b_{{21}} u^{2} }& {b_{{22}} u^{2} } \\ \end{array} } \right]^{{ - 1}}\\ & \left( {\ddot{N}_{r} } \right. - \,\left[ {\begin{array}{cc} {a_{{11}} ucos\psi - rsin\psi } & {ucos\psi + a_{{12}} ucos\psi } \\ {a_{{21}} u} & {a_{{22}} u} \\ \end{array} } \right]\left[ {\begin{array}{c} v \\ r \\ \end{array} } \right] \\ &\left. { - \,K{\text{sat}}\left( {\frac{S}{\Phi }} \right)} \right),\quad \Phi > 0 \\ \end{aligned} $$
(23)

By defining \( u_{r} = - \left[ {\begin{array}{*{20}l} {b_{11} u^{2} cos\psi } \hfill & {b_{12} u^{2} cos\psi } \hfill \\ {b_{21} u^{2} } \hfill & { b_{22} u^{2} } \hfill \\ \end{array} } \right]^{ - 1} K{\text{sat}}\left( {\frac{S}{\Phi }} \right) \) and \( {u_{eq} = \left[ \begin{array}{*{20}l} {b_{11} u^{2} cos\psi } \hfill & {b_{12} u^{2} cos\psi } \hfill \\ {b_{21} u^{2} } \hfill & {b_{22} u^{2} } \hfill \\ \end{array} \right]^{ - 1}} \Bigg( \ddot{N}_{r} - \Bigg[ \begin{array}{*{20}l} {a_{11} ucos\psi - rsin\psi } \hfill & {ucos\psi + a_{12} ucos\psi } \hfill \\ {a_{21} u} \hfill & {a_{22} u} \hfill \\ \end{array} \Bigg] \Bigg[ \begin{array}{*{20}c} v \\ r \\ \end{array} \Bigg] \Bigg), \) the control law can be rewritten as \( U = u_{r} + u_{eq} \). where \( {\Phi } \) is the boundary layer thickness and \( K = diag\left( {k_{i} } \right), \) and \( k_{i} > 0 \) is constant. We consider \( i = \left\{ {1,2} \right\} \) for motion equation in the horizontal plane. The saturation function is defined as [8, 22],

$$ \left\{ {\begin{array}{*{20}l} {{\text{sat}}\left( y \right) = y} \hfill &\quad { {\text{if}}\quad \left| y \right| \le 1} \hfill \\ {{\text{sat}}\left( y \right) = \text{sgn} \left( y \right)} \hfill & \quad {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(24)

This method uses the high gain in the control law to reduce chattering which may cause instability in the boundary layer. In order to maintain in the attract condition in the worst case, the following inequality must be held [22]

$$ \hbox{min} \left( K \right) \ge \left\| {F - F_{0} + \left( {G - G_{0} } \right)u} \right\| + \left\| d \right\| + \eta $$
(25)

where \( F_{0} \) and \( G_{0} \) represent the nominal value of \( F \) and G in (8), respectively. In the next part the proposed adaptive control law is presented.

  1. B.

    Designing the Proposed Adaptive Sliding Mode Control

The major disadvantage of controller law (23) is chattering and massive vulnerability against the noise. In the proposed method by using a new reaching law and applying the adaptive gain in the sliding mode control, these problems are eliminated from the input signal. We use the continuous term instead of sign function in the reaching law. The proposed reaching law has the following form,

$$ u_{r} = - \frac{{K\left( {S + \varepsilon } \right)}}{{\beta + e^{ - \alpha \left\| S \right\|} }}, $$
(26)

where K is the positive gain, β and α and ε are positive constants. We use proposed reaching law (26) into (13) with \( u_{eq} \) to obtain the proposed controller as,

$$ \begin{gathered} U = \left[ {\begin{array}{cc} {b_{{11}} u^{2} \cos \psi } \hfill & {b_{{12}} u^{2} \cos \psi } \hfill \\ {b_{{21}} u^{2} ~} \hfill & {b_{{22}} u^{2} } \hfill \\ \end{array} } \right]^{{ - 1}} \hfill \\ \quad\qquad \left( {\ddot{N}_{r} - \left[ {\begin{array}{cc} {a_{{11}} u\cos \psi - r\sin \psi } \hfill & {u\cos \psi + a_{{12}} u\cos \psi } \hfill \\ {a_{{21}} u} \hfill & {a_{{22}} u} \hfill \\ \end{array} } \right]} \right. \hfill \\ \left. {\qquad\quad \left[ {\begin{array}{c} v \\ r \\ \end{array} } \right] - \frac{{K\left( {S + \varepsilon } \right)}}{{\beta + e^{{ - \alpha S}} }}} \right). \hfill \\ \end{gathered} $$
(27)

The parameter \( K \) can be found by an adaption law, so the proposed adaptive sliding mode control law is rewritten as follow,

$$ \begin{gathered} U = \left[ {\begin{array}{cc} {b_{{11}} u^{2} cos\psi } \hfill & {b_{{12}} u^{2} cos\psi } \hfill \\ {b_{{21}} u^{2} } \hfill & {b_{{22}} u^{2} } \hfill \\ \end{array} } \right]^{{ - 1}} \hfill \\ \qquad\quad \left( {\ddot{N}_{r} - \left[ {\begin{array}{cc} {a_{{11}} ucos\psi - rsin\psi } \hfill & {ucos\psi + a_{{12}} ucos\psi } \hfill \\ {a_{{21}} u} \hfill & {a_{{22}} u} \hfill \\ \end{array} } \right]} \right. \hfill \\ \left. {\quad\qquad \left[ {\begin{array}{c} v \\ r \\ \end{array} } \right] - \frac{{\hat{K}\left( {S + \varepsilon } \right)}}{{\beta + e^{{ - \alpha S}} }}~} \right), \hfill \\ \end{gathered} $$
(28)

where \( \hat{K} \) is the estimation of \( K \), and the adaptation law is,

$$ \dot{\hat{K}} = \frac{{\omega \left( {S + \varepsilon } \right)^{2} }}{{\beta + e^{ - \alpha \left\| S \right\|} }} $$
(29)

where \( \omega \) is a positive constant. Due to external disturbance, noise and uncertainties in the system dynamics, states may be separated from surface and chattering to be created, so an adaptive gain of the controller is obtained based on the states errors and the dynamics of errors. To avoid selection of a big constant gain, which is one of the factors causing chattering, the gain of controller is selected adaptively. Thus, the controller is not vulnerable to noise since there is no sign function in the proposed controller. By using a sign function in BLC, the boundary layer of sliding mode control is too vulnerable to noise and gives a very close measurement value to zero. Accordingly, chattering starts near the sliding surface using a sign function. However, the problem of vulnerability to noise is resolved in the proposed controller. The control law not only must guarantee the stability of the closed loop system, it also must guarantee that the reaching time is limited.

Theorem 1

By applying the proposed controller (28) on the system Eqs (18), closed loop control system is stable and the estimated parameter\( \hat{K} \)asymptotically converges to K.

Proof

Consider the following new Lyapunov function,

$$ V = \frac{1}{2}\left( {S + \varepsilon } \right)^{T} \left( {S + \varepsilon } \right) + \frac{1}{2\omega }\left( {\hat{K} - K} \right)^{2} . $$
(30)

Differentiating with respect to time results,

$$ \dot{V} = \left( {S + \varepsilon } \right)\dot{S} + \frac{1}{\omega }\left( {\hat{K} - K} \right)\dot{\hat{K}}. $$
(31)

According to (18) and (28),

$$ \begin{gathered} \ddot{N} = \left[ {\begin{array}{cc} {a_{{11}} u\cos \psi - r\sin \psi } \hfill {u\cos \psi + a_{{12}} u\cos \psi } \hfill \\ {a_{{21}} u} \hfill {a_{{22}} u} \hfill \\ \end{array} } \right]\left[ {\begin{array}{c} v \\ r \\ \end{array} } \right] \hfill \\ \quad \qquad + \left[ {\begin{array}{cc} {b_{{11}} u^{2} \cos \psi } \hfill {b_{{12}} u^{2} \cos \psi } \hfill \\ {b_{{21}} u^{2} } \hfill {amp;b_{{22}} u^{2} } \hfill \\ \end{array} } \right] \hfill \\ \quad\qquad \left( {\left[ {\begin{array}{cc} {b_{{11}} u^{2} \cos \psi } \hfill {b_{{12}} u^{2} \cos \psi } \hfill \\ {b_{{21}} u^{2} } \hfill {b_{{22}} u^{2} } \hfill \\ \end{array} } \right]^{{ - 1}} } \right. \hfill \\ \quad\qquad \left( {\ddot{N}_{r} - \left[ {\begin{array}{cc} {a_{{11}} u\cos \psi - r\sin \psi } \hfill {u\cos \psi + a_{{12}} u\cos \psi } \hfill \\ {a_{{21}} u} \hfill {a_{{22}} u} \hfill \\ \end{array} } \right]\left[ {\begin{array}{c} v \\ r \\ \end{array} } \right]} \right. \hfill \\ \left. {\left. {\quad\qquad - \frac{{\hat{K}\left( {S + \varepsilon } \right)}}{{\beta + e^{{ - \alpha \left\| S \right\|}} }}} \right)} \right) \hfill \\ \end{gathered} $$
(32)

According to (22),

$$ \dot{S} = - \frac{{\hat{K}\left( {S + \varepsilon } \right)}}{{\beta + e^{ - \alpha \left\| S \right\|} }} $$
(33)

Substituting (33) in (31) results,

$$ \dot{V} = - \frac{{\hat{K}\left( {S + \varepsilon } \right)^{2} }}{{\beta + e^{ - \alpha \left\| S \right\|} }} + \frac{1}{\omega }\left( {\hat{K} - K} \right)\frac{{\omega \left( {S + \varepsilon } \right)^{2} }}{{\beta + e^{ - \alpha \left\| S \right\|} }} $$
$$ \dot{V} = -\,K\frac{{\left( {S + \varepsilon } \right)^{2} }}{{\beta + e^{ - \alpha \left\| S \right\|} }} < 0 $$
(34)

It is concluded that \( \dot{V} \) is negative, so the proposed control law can stabilize the closed loop system and \( \hat{K} \) can converge to \( K \).

Theorem 2

The proposed controller (28) with adaptive gain in (29) guarantees that the reaching time (\( t_{reach} \)) is limited.

Proof

Integrating both side of (33) results,

$$ \mathop \int \nolimits_{0}^{{t_{reach} }} \dot{S} = - \mathop \int \nolimits_{0}^{{t_{reach} }} \frac{{\hat{K}\left( {S + \varepsilon } \right)}}{{\beta + e^{ - \alpha \left\| S \right\|} }} $$
$$ \mathop \int \nolimits_{0}^{{t_{reach} }} \frac{{\dot{S}\left( t \right)}}{{\left( {S\left( t \right) + \varepsilon } \right)}}dt = - \mathop \int \nolimits_{0}^{{t_{reach} }} \frac{{\hat{K}}}{{\beta + e^{ - \alpha \left\| S \right\|} }}dt $$
(35)

Since \( S\left( {t_{reach} } \right) = 0 \), then

$$ Ln\left( {\left| {\frac{S\left( 0 \right) + \varepsilon }{\varepsilon }} \right|} \right) = \frac{{\hat{K}}}{{\beta + e^{ - \alpha \left\| S \right\|} }} \cdot t_{reach} $$
$$ t_{reach} = \frac{{\beta + e^{ - \alpha \left\| S \right\|} }}{{\hat{K}}}Ln\left( {\left| {\frac{S\left( 0 \right) + \varepsilon }{\varepsilon }} \right|} \right) $$
(36)

Then it is concluded that \( t_{reach} \) is limited. It means that the proposed reaching law ensures the sliding surface \( S = 0 \) can be reached, so from Theorem 1 the states of the system move to the sliding surfaces in finite time and the tracking errors reach zero in a finite time. In the next section the proposed controller with the new reaching law is compared with the reported reaching law in [23] which is shown below,

$$ u_{r} = - \frac{{k_{1} s_{0} }}{{s_{0} + \left| S \right|}}S - k_{2} \text{sgn} \left( S \right), $$
(37)

where k1, k2 and s0 are positive constants. It is stated in [23] that the second term in (37) is added because the state convergence to the sliding surface is ensured. By combining (13) and (37) \( u_{eq} \), the sliding mode control with the reaching law in [23] is obtained as,

$$ \begin{gathered} U = \left[ {\begin{array}{cc} {b_{{11}} u^{2} cos\psi } \hfill& {b_{{12}} u^{2} cos\psi } \hfill \\ {b_{{21}} u^{2} } \hfill& {b_{{22}} u^{2} } \hfill \\ \end{array} } \right]^{{ - 1}} \hfill \\ \qquad \quad \left( {\ddot{N}_{r} - \left[ {\begin{array}{cc} {a_{{11}} ucos\psi - rsin\psi } \hfill& {ucos\psi + a_{{12}} ucos\psi } \hfill \\ {a_{{21}} u} \hfill& {a_{{22}} u} \hfill \\ \end{array} } \right]} \right. \hfill \\ \left. {\qquad \quad \left[ {\begin{array}{c} v \\ r \\ \end{array} } \right] - \frac{{k_{1} s_{0} }}{{s_{0} + \left| S \right|}}S - k_{2} {\text{sgn}}\left( S \right)} \right) \hfill \\ \end{gathered} $$
(38)

4 Simulation results

In this section the performance of the proposed controller is compared with sliding mode with the boundary layer control. Note, in the simulations, all values have been normalized. However, time has been non-dimensionalized. Thus, one second represents the time that it takes to travel one vehicle length [20]. AUV parameters are considered listed in Table 1.

Table 1 AUV parameters
Full size table

\( \lambda = 5, \omega = 3, \varepsilon = 0.05, \alpha_{1} = 0.05, \alpha_{1} = 1, \beta_{1} = 0.1,\beta_{2} = 0.2 \). In order to consider parameter alterations, it is assumed that the changes are sinusoidal with a relatively low frequency. It is assumed the parameter \( p \) varies according to [19, 20] as follows,

$$ p\left( t \right) = p + a\,sin\,\omega t, $$
(39)

where \( \omega = 0.5 \) and \( \frac{a}{p} = 50\% . \) It is assumed that the disturbance is a step wave with amplitude of 0.5, being active between 5 and 10 s. A white Gaussian noise with signal-to-noise ratio of 40 dB per sample is also considered. Assume the desired trajectories are \( \left[ {y_{d} , \psi_{d} } \right] = \left[ {2{ \sin }t,\, { \sin }t} \right] \). In the simulations, parameters of the BLC \( \Phi = 0.1 \), \( \lambda_{1} = \lambda_{2} = 5 \) and \( k_{1} = k_{2} = 8 \) are considered. The simulations are performed in the presence of parameter uncertainties and external disturbances. The initial conditions are considered to be, \( \psi \left( 0 \right) = - \pi /6 \) and \( y\left( 0 \right) = 0.8 \).

Two cases are considered for the controller based on the method which is proposed in [23]:

Case 1 :

\( k_{1} = 6, \quad k_{2} = 1,\quad s_{0} = 0.1 \)

Case 2 :

\( k_{1} = 15, \quad k_{2} = 0.2, \quad s_{0} = 1. \)

Case 2 is considered to show decreasing the amplitude of chattering in control signal and to show increasing the convergence rate to desired trajectory than the Case 1.

A comparison result of the tracking performance of the proposed controller, the controller in (38) (reported in [23]), and the BLC are shown in Figs. 2 and 3, respectively. At first, consider Case 1 for the method reported in [23]. In Fig. 2, it can be seen that the actual output in the proposed method in this paper can track the desired trajectory faster than the method in [23] (it is specified with black rectangular in Fig. 2). The sway motion \( y \) in the BLC method in Fig. 3 converges the desired trajectory faster than the method in [23] and the proposed method. The control inputs (\( \delta_{r} ,\delta_{b} \)) for the proposed controller, the controller reported in [23] and the BLC are represented in Figs. 4, 5 and 6, respectively. As can be seen in Fig. 6, a high amplitude chattering is observed (it is distinguished with red ellipse in Fig. 6) whereas there is not any chattering in the proposed adaptive sliding mode controller in the Fig. 4. As it can be seen in Fig. 5, due to a sign function shown in (38) the chattering is unavoidable.

Fig. 2
figure 2

\( {\psi }, { y} \) in the proposed controller and the method in [23] in Case 1

Full size image
Fig. 3
figure 3

\( {\psi }, { y} \) in the BLC method in the presence of disturbance and parameter variation

Full size image
Fig. 4
figure 4

Control signals, \( \varvec{ \delta }_{\varvec{b}} ,\varvec{ \delta }_{\varvec{s}} \) in the proposed controller in the presence of disturbance and parameter variation

Full size image
Fig. 5
figure 5

Control signals, \( \varvec{ \delta }_{\varvec{b}} ,\varvec{ \delta }_{\varvec{s}} \) in the controller based on [23] in Case 1

Full size image
Fig. 6
figure 6

Control signal \( \delta_{b} , \delta_{s} \) in the BLC method in the presence of disturbance and parameter variation

Full size image

Now consider Case 2 to decrease the amplitude of chattering in control signal in [23], and the relevant simulation results are shown in the Figs. 7 and 8. Comparing Figs. 2 and 7, it can be seen that the convergence rates of the sway motion \( y \) and the yaw motion \( \psi \) in [23] in the Case 2 are faster than those of in the Case 1. According to Fig. 8 the controller reported in [23] has a lower chattering amplitudes in comparison with Case 1 in Fig. 5. The simulation results for the estimation of the gains are shown in Fig. 9. As shown in Fig. 9, the gains of the proposed controller in this paper are less than the gains of BLC and the controller reported in [23].

Fig. 7
figure 7

\( \psi , y \) in the proposed controller and the controller based on [23] in Case 2 in the presence of disturbance and parameter variation

Full size image
Fig. 8
figure 8

Control signal, \( \varvec{ \delta }_{\varvec{b}} ,\varvec{ \delta }_{\varvec{s}} \) in the controller based on [23] in Case 2

Full size image
Fig. 9
figure 9

The estimation of the gains \( \left( {k_{1} ,k_{2} } \right) \) based on (32)

Full size image

Comparing the results demonstrated in Figs. 2, 3, 4, 5, 6, 7, 8, and 9, it is noticeable that the proposed method has a better performance with a less gain value than the method reported in [23] and the BLC. Finally, the performance of the three methods are compared in the presence of the output noise. As can be seen in Fig. 10, the proposed controller is superior to the other two methods and is less vulnerable to noise. The vulnerability to noise in the method reported in [23] is less than the BLC method.

Fig. 10
figure 10

Control signal, \( \varvec{ \delta }_{\varvec{b}} \) in the proposed method, the method in [23] and BLC method in the presence of disturbance and noise

Full size image

5 Conclusion

In this paper we proposed a new adaptive sliding mode controller for trajectory control of underwater robot in the horizontal plane. The proposed method has been compared with two other methods reported in the literature, BLC and the SMC with the reaching law reported in [23]. An adaptive continuous term has been proposed in this paper instead of using a sign function and an adaptive law for estimating the gain of proposed reaching law. Stability and being limit reaching time of the proposed method are proved. In comparing with the other methods, proposed controller is not vulnerable to noise because it does not have the sign function. To show efficiency of the method, parametric uncertainty, noise and external disturbance are considered in the system. In the proposed controller, the control signal has no chattering. Two cases are considered for the method in [23] and it is shown that the proposed method can lead to desired performance with the less gain value than the method in [23] and the BLC method.