1 Introduction

Chaos can be described as unconditional distraction, randomness or unpredictability. Chaotic dynamics [1] has become very interesting and attractive area for researchers. Chaotic dynamical systems are unstable and uncertain. Henri Poincare discovered a well known intrinsic property of the chaotic systems, the sensitive dependence on the initial conditions i.e. two neighbouring points in state space get isolated very quickly as they emerge in time. In general, chaos being the intrinsic property of non-linear systems has numerous applications such as in viscoelasticity [2], dielectric polarization, electromagnetic waves [3], diffusion, signal processing, mathematical biology and in many more disciplines. Different techniques are used to investigate the chaotic behaviour few of them are by plotting phase portraits, poincare section, bifurcation diagram or by finding Lyapunov exponents. The most reliable and widely used among the above technique is Lyapunov exponent spectrum. If the largest Lyapunov exponent is positive, we say that the system is chaotic and if more than one Lyapunov exponents are positive, then the system is said to be hyperchaotic.

It was the pioneering work of Pecora and Caroll who gave the concept of synchronization to control and utilize the chaos in the porper way. Synchronization means the trajectories of the coupled systems evolve with time to a usual pattern. Various techniques have been developed by researchers in this direction during last two decades. Numerous synchronization schemes have been proposed such as lag synchronization [4], complete synchronization [5], phase and anti-phase synchronization [6], anti-synchronization [7], hybrid synchronization [8], projective synchronization [9], hybrid funchtion projective synchronization [10], generalised synchronization [11], multi-switching synchronization [12] etc. To achieve synchronization different techniques have been designed some of them are adaptive feedback control,optimal control,linear and nonlinear feedback synchronization [13], active control [14], sliding mode control [15], adaptive sliding mode technique [16], time delay feedback approach [17], tracking control [18], backstepping design method [18] and so on.

In recent years, a lot of pioneering work has been done in the field of fractional calculus [19]. It was first suggested by Leibnitz and L’Hospital in 1675 and they gave the theory of integrals and derivatives of random order which combines the concept of integer order differentiation and n-fold integration. These studies describes the significant work in the real life systems and have a lot of multidisciplinary applications. As compared to integer order network the fractional order system add a degree of freedom by employing fractional derivative. Many types of fractional order chaotic and hyperchaotic systems have been introduced by researchers like Lorenz system [20], Chen system [21], Rossler system [21], Lu-system [22], Lui-system [23], Chua system [24] etc to explain the various physical processes. hlIn order to increase the complexity , researchers also introduced numerous fractional order complex chaotic systems like complex Lorenz system [25], T-sytem [26], Lu-system [27], Chen system [25] etc.

Various efforts have been made to synchronize identical and non-identical systems with different techniques. In this manuscript we have synchronized the two different fractional order complex chaotic systems by taking unknown bounded external disturbances and uncertainties. We have considered fractional order complex chaotic Lu-system as drive system and complex chaotic T-system as response system with external bounded disturbances and bounded uncertainties which has not been discussed in any literature to the best of our knowledge.The uncertainties and disturbances have a great impact on chaotic systems, dynamics and synchronization action and reduce the act of actual systems.Therefore to examine the synchronization of chaotic systems with various kind of disturbances and uncertainties, researchers have introduced different types of synchronization schemes [28, 29]. Generally sliding mode control technique [30] is an efficient approach concerning the uncertainty and disturbances. In our paper we have used adaptive sliding mode control scheme [31] to synchronize the considered systems. To decline their effect we have chosen suitable sliding surface and estimated the disturbances and uncertainties through adapting control rule.

In [27], author synchronized fractional order complex Lu-system and complex T-system by active control method. As we have taken uncertainties and disturbances into consideration, despite of that our methodology shows better results when compared with the previous work [27]. Numerical simulations have been done to validate and visualize our results in the form of plots and demonstrates that our results are in excellent agreement with the theoretical results.

2 Preliminaries

The fractional order systems is continuation to the integer order calculus. As compared to integer order network the fractional order system add a degree of freedom by employing fractional derivative. Also, fractional order derivatives show better results when modelling real life processes as compared to integer order derivatives.The fractional order derivative can be defined in various forms [19], such as Riemann–Lioville’s derivative, Gr\(\ddot{u}\)nwald Letnikov’s derivative, Caputo’s derivative etc.

The Riemann Liouville’s derivative is defined as

$$\begin{aligned} {{_{t_0} D^\alpha _t f(t)}{=}\frac{d^n}{dt^n} \left[ \frac{1}{\Gamma (n{-}\alpha )}\int _{t_0}^t\frac{f(\tau )}{(t{-}\tau )^{\alpha -n+1}}d\tau \right] ,\quad t>t_0} \end{aligned}$$

where \( \alpha \) is fractional derivative, \( n-1< \alpha < n, n\in \mathbb {N}, \Gamma (\alpha ) = \int _0^{\infty } x^{\alpha -1} e^{-x} \) is the Gamma function.

The Caputo’s derivative is defined as

$$\begin{aligned} {_{t_0} D^\alpha _t f(t)}=\frac{1}{\Gamma (n-\alpha )}\int _{t_0}^t\frac{f^{(n)} (\tau )}{(t-\tau )^{\alpha -n+1}}d\tau , \quad t>t_0 \end{aligned}$$

The Gr\(\ddot{u}\)nwald Letnikov’s derivative is defined as

$$\begin{aligned} {_{t_0} D^\alpha _t f(t)\mid _t=kh=lim_{h\rightarrow 0} \frac{1}{h^\alpha }\sum _{j=0} ^{\lfloor {\frac{t-c}{h}}\rfloor } \omega _j(\alpha ) f(kh-jh)} \end{aligned}$$

where h shows the sample time. \(\lfloor .\rfloor \) is the floor function and the coefficients

$$\begin{aligned} {\omega _j^\alpha = \frac{(-1)^j \Gamma (\alpha +1)}{\Gamma (j+1)\Gamma (\alpha -j+1)}, \quad j=0,1,2,\ldots ,k.} \end{aligned}$$

Since the Caputo’s fractional derivative of a constant is zero,in this paper we choose Caputo’s definition.

3 System description

3.1 Master system

Considering the fractional order complex Lu-system [27] given by

$$\begin{aligned} D^{\alpha }u_{1}'&= a_{1}(u_{2}'-u_{1}') \nonumber \\ D^{\alpha }u_{2}'&= a_{2}u_{2}'-u_{1}'u_{3}' \nonumber \\ D^{\alpha }u_{3}'&= \frac{1}{2}(\overline{u_{2}'}u_{2}'+u_{1}'\overline{u_{2}'})-a_{3}u_{3}' \end{aligned}$$
(1)

where \( u'=[u_{1}',u_{2}',u_{3}']^{T} \) is the state variable vector, \( u_{1}'=u_{1}+iu_{2} \), \( u_{2}'=u_{3}+iu_{4} \) are complex variables, \( u_{3}'=u_{5} \) is the real variable and \( a_{1}, a_{2}, a_{3} \) are real constant parameters.

Separating the real and imaginary parts, we obtain the system (1) as

$$\begin{aligned} D^{\alpha }u_{1}&= a_{1}(u_{3}-u_{1}) \nonumber \\ D^{\alpha }u_{2}&= a_{1}(u_{4}-u_{2}) \nonumber \\ D^{\alpha }u_{3}&= a_{2}u_{3}-u_{1}u_{5} \nonumber \\ D^{\alpha }u_{4}&= a_{2}u_{4}-u_{2}u_{5} \nonumber \\ D^{\alpha }u_{5}&= u_{1}u_{3}-u_{2}u_{4}-a_{3}u_{5} \end{aligned}$$
(2)

For the values of parameters as \( a_{1}=42, a_{2}=22, a_{3}=5 \), initial conditions as \(u(0)=[1,2,3,4,5]^T\) and \(\alpha =0.95\), the system is chaotic.

3.2 Slave system

The fractional order complex T-system [26] is

$$\begin{aligned} D^{\alpha }v_{1}'&= b_{1}(v_{2}'-u_{1}') \nonumber \\ D^{\alpha }v_{2}'&= (b_{2}-b_{1})u_{1}'-b_{1}v_{1}'v_{3}'\nonumber \\ D^{\alpha }v_{3}'&= \frac{1}{2}(\overline{v_{1}'}v_{2}'+v_{1}'\overline{v_{2}'})-b_{3}v_{3}' \end{aligned}$$
(3)

where \( y'=[v_{1}',v_{2}',v_{3}']^{T} \) is the state variable vector of the system,\( v_{1}'=v_{1}+iv_{2} \), \( v_{2}'=v_{3}+iv_{4} \) are complex variables, \( v_{3}'=v_{5} \) is the real variable and \( b_{1}, b_{2}, b_{3}\)are real constant parameters.

Separating real and imaginary parts, we have

$$\begin{aligned} D^q v_{1}&= b_{1}(v_{3}-v_{1}) \nonumber \\ D^q v_{2}&= b_{1}(v_{4}-v_{2}) \nonumber \\ D^q v_{3}&= (b_{2}-b_{1})v_{1}-b_{1}v_{1}v_{5}\nonumber \\ D^q v_{4}&= (b_{2}-b_{1})v_{2}-b_{1}v_{2}v_{5} \nonumber \\ D^q v_{5}&= v_{1}v_{3}+v_{2}v_{4}-b_{3}v_{5} \end{aligned}$$
(4)

For the values of parameters as \( b_{1}=2.1, b_{2}=30, b_{3}=0.6 \), initial conditions as \(v(0)=[8,7,5,6,10]^T\) and \(\alpha =0.95\), the system is chaotic.

4 Synchronization scheme

The fractional order complex chaotic system (2) is taken as drive system. The fractional order complex chaotic T-system (4) with uncertainty and disturbance is taken as response system given by

$$\begin{aligned} D^q v_{1}&= b_{1}(v_{3}-v_{1})+\Delta g_{1}(v_1,v_2,v_3,v_4,v_5) {+}\omega _1(t){+}\Theta _1 \nonumber \\ D^q v_{2}&= b_{1}(v_{4}-v_{2}){+}\Delta g_{2}(v_1,v_2,v_3,v_4,v_5) {+}\omega _2(t){+}\Theta _2 \nonumber \\ D^q v_{3}&= (b_{2}-b_{1})v_{1}-b_{1}v_{1}v_{5}+\Delta g_{3}(v_1,v_2,v_3,v_4,v_5)\nonumber \\&\quad +\,\omega _3(t)+\Theta _3\nonumber \\ D^q v_{4}&= (b_{2}-b_{1})v_{2}-b_{1}v_{2}v_{5}+\Delta g_{4}(v_1,v_2,v_3,v_4,v_5)\nonumber \\&\quad +\,\omega _4(t)+\Theta _4 \nonumber \\ D^q v_{5}&= v_{1}v_{3}+v_{2}v_{4}-b_{3}v_{5}+\Delta g_{5}(v_1,v_2,v_3,v_4,v_5)\nonumber \\&\quad +\,\omega _5(t)+\Theta _5 \end{aligned}$$
(5)

\( \Delta g_{i}(v_{1},v_{2},v_{3},v_{4},v_{5}) \) are bounded uncertainties, \( \omega _{i}(t) \) are bounded disturbances and \( \Theta _{i} \) are appropriate control inputs of the response system for \( i=1,2,3 \) which will be designed later.

Here we assume that \( \mid \Delta g_{i}\mid \leqslant \varpi _{i} \) and \(\mid \omega _{i}(t)\mid \leqslant \upsilon _{i} \), where \( \varpi _{i} \) and \( \upsilon _{i} \) are positive constants.Also \( \hat{\varpi }_{i} \) and \( \hat{\upsilon }_{i} \) represents the estimated values of \( \varpi _{i} \) and \( \upsilon _{i} \) respectively.

Now,the error state is defined as

$$\begin{aligned} e_{i}=v_{i}-\sigma _{i}u_{i}, i=1,2,3,4,5. \end{aligned}$$
(6)

where \(\sigma =(\sigma _{1},\sigma _{2},\ldots ,\sigma _{m})\) are scaling factors.

Definition

The drive system (2) and response system (5) are said to be in hybrid projective synchronization, if there exists suitable controller \( \Theta =(\Theta _{1},\Theta _{2},\ldots ,\Theta _{m}) \), such that

$$\begin{aligned}&\lim _{t\rightarrow \infty }\parallel e(t)\parallel \nonumber \\&\quad =\lim _{t\rightarrow \infty }\parallel v_i(t)-\sigma u_i(t)\parallel =0, i=1,2,3,4,5. \end{aligned}$$
(7)

The synchronization error is asymptotically stable between the state variables of drive system (3) and state variables of response system (2). The error dynamics is obtained as

$$\begin{aligned} D^{\alpha }e_{1}&=b_1(e_{3}-e_{1})+(b_1\sigma _{3}-a1\sigma _{1})u_{3} +\sigma _1(a1-b1)u_{1}\nonumber \\&\quad +\,\Delta g_{1}+\omega _1(t)+\Theta _1 \nonumber \\ D^{\alpha }e_{2}&=b_1(e_{4}-e_{2})+(b_1\sigma _{4}-a1\sigma _{2})u_{4} +\sigma _2(a_1-b_1)u_{2}\nonumber \\&\quad +\,\Delta g_{2}+\omega _2(t)+\Theta _2 \nonumber \\ D^{\alpha }e_{3}&=(b_{2}-b_1)e_1-b_1v_{1}v_{5}-\sigma _1(b_{2}-b_1)u_{1} -\sigma _3a_2u_{3}\nonumber \\&\quad +\,\sigma _{3}u_{1}u_{5}+\Delta g_{3}+\omega _3(t)+\Theta _3 \nonumber \\ D^{\alpha }e_{4}&=(b_{2}-b_1)e_2-b_1v_{1}v_{5}-\sigma _2(b_{2}-b_1)u_{2} -\sigma _4a_2u_{4}\nonumber \\&\quad +\,\sigma _{4}u_{2}u_{5}+\Delta g_{4}+\omega _4(t)+\Theta _4 \nonumber \\ D^{\alpha }e_{5}&=v_1v_3+v_2v_4-b_{3}e_5+b_3\sigma _{5}u_{5} -\sigma _5(u_{1}u_3+u_2u_4)\nonumber \\&\quad -\,\sigma _5a_3u_{5}+\Delta g_{5}+\omega _5(t)+\Theta _5 \end{aligned}$$
(8)

In order to minimize the error,we choose the suitable sliding surface which is as follows:

$$\begin{aligned} s_{i}(t)=D^{\alpha -1}e_{i}(t)+\phi _{i}\int _{0}^{t}e_{i}(\xi )d\xi \end{aligned}$$
(9)

To accomplish the error dynamic system (8) at chosen sliding surface (13), it is necessary that it should satisfy the following condition

$$\begin{aligned} s_{i}(t)=0, \dot{s_{i}}(t)=0, \quad i=1,2,3,4,5. \end{aligned}$$

The derivative of (9), yields the following equation

$$\begin{aligned} \dot{s_{i}}(t)=D^{\alpha }e_{i}(t)+\phi _{i}e_{i}(t), \quad i=1,2,3,4,5. \end{aligned}$$
(10)

Then, by considering the necessary condition \( \dot{s_{i}}(t)=0 \), we obtain

$$\begin{aligned} D^{\alpha }e_{i}(t)=-\phi _{i}e_{i}(t), \quad i=1,2,3,4,5. \end{aligned}$$
(11)

Hence, the system (9) is asymptotically stable by using Matignon theorem [32]. Therefore, the control laws by using (11), (8) and SMC theory are obtained as follows

$$\begin{aligned} \Theta _{1}&=-b_1(e_{3}-e_{1})-(b_1\sigma _{3}-a_1\sigma _{1})u_{3} -\sigma _1(a_1-b_1)u_{1}\nonumber \\&\quad -\,\phi _{1}e_{1}-(\hat{\varpi }_{1} +\hat{\upsilon }_{1}+\gamma _{1})signs_{1}\nonumber \\ \Theta _{2}&=-b_1(e_{4}-e_{2})-(b1\sigma _{4}-a_1\sigma _{2})u_{4} -\sigma _2(a_1-b_1)u_{2}\nonumber \\&\quad -\,\phi _{2}e_{2}-(\hat{\varpi }_{2} +\hat{\upsilon }_{2}+\gamma _{2})signs_{2} \nonumber \\ \Theta _{3}&=-(b_{2}-b_1)e_1+b_1v_{1}v_{5}+\sigma _1(b_{2}-b_1)u_{1} +\sigma _3a_2u_{3}\nonumber \\&\quad -\,\sigma _{3}u_{1}u_{5}-\phi _{3}e_{3}-(\hat{\varpi }_{3} +\hat{\upsilon }_{3}+\gamma _{3})signs_{3}\nonumber \\ \Theta _{4}&=-(b_{2}-b_1)e_2+b_1v_{2}v_{5}+\sigma _2(b_{2}-b_1)u_{2} +\sigma _4a_2u_{4}\nonumber \\&\quad -\,\sigma _{4}u_{2}u_{5}-\phi _{4}e_{4}-(\hat{\varpi }_{4} +\hat{\upsilon }_{4}+\gamma _{4})signs_{4} \nonumber \\ \Theta _{5}&=-v_1v_3-v_2v_4+b_{3}e_5-b_3\sigma _{5}u_{5}+\sigma _5(u_{1}u_3+u_2u_4)\nonumber \\&\quad +\,\sigma _5a_3u_{5}-\phi _{5}e_{5}-(\hat{\varpi }_{5}+\hat{\upsilon }_{5} +\gamma _{5})signs_{5} \end{aligned}$$
(12)

where sign(.) denotes the signum function and \( \gamma _{i} \) are positive constant parameters. The adaptive parameter update laws are

$$\begin{aligned} \dot{\hat{\varpi }}_{i}&=m_{i}\mid s_{i}\mid , i=1,2,3,4,5. \nonumber \\ \dot{\hat{\upsilon }}_{i}&=n_{i}\mid s_{i}\mid , i=1,2,3,4,5. \end{aligned}$$
(13)

where \( m_{i} \) and \(n_{i}\) are positive constants and \( \gamma _{i} \) are gain constants of the controllers for \(i=1,2,3,4,5\).

Theorem 4.1

The fractional order complex chaotic system (2) and the slave system (5) with uncertain dynamics are globally and asymptotically stable and synchronized with adaptive sliding mode control laws (12) and parameter update laws (13).

Fig. 1
figure 1

Phase portraits of fractional order complex Lu-system for fractional order \( \alpha =0.95 \)a\(u_1-u_2-u_3\)b\(u_1-u_3-u_5\)c\(u_1-u_4-u_5\)d\(u_2-u_4-u_5\)e\(u_1-u_3\)f\(u_2-u_5\)

Full size image
Fig. 2
figure 2

Phase portraits of fractional order complex T-system for fractional order \( \alpha =0.95 \)a\(v_1-v_2-v_3\)b\(v_1-v_3-v_4\)c\(v_2-v_4-v_5\)d\(v_3-v_5-v_2\)e\(v_1-v_5\)f\(v_2-v_4\)

Full size image
Fig. 3
figure 3

Synchronized state trajectories of mater system and controlled slave system a\(u_1-v_1\)b\(u_2-v_2\)c\(u_3-v_3\)d\(u_4-v_4\)e\(u_5-v_5\)

Full size image
Fig. 4
figure 4

Error converges to zero at t = 1.5 s (approx.)

Full size image
Fig. 5
figure 5

Sliding surface converges to zero at t = 1.3 s (approx.)

Full size image
Fig. 6
figure 6

Estimated values of a uncertainties bounds, b disturbances bounds

Full size image

Proof

To discuss the stability of the fractional order chaotic systems, we have used Lyapunov’s direct method [33, Ch-5]. Here our main focus is to take a positive definite function V and would show the derivative of V negative definite which would imply that our error converges asymptotically to zero. \(\square \)

Fig. 7
figure 7

Time response of controllers used to synchronization

Full size image
Fig. 8
figure 8

Ratios of the controllers and the uncontrolled slave system signal a\(\Theta _1/ v_1\)b\(\Theta _2 / u_2\)c\(\Theta _3 / u_3\)d\(\Theta _4 / u_4\)e\(\Theta _5 / u_5\)

Full size image
Fig. 9
figure 9

Ratios of the controllers and the master system signal a\(\Theta _1 / u_1\)b\(\Theta _2 / u_2\)c\(\Theta _3 / u_3\)d\(\Theta _4 / u_4\)e\(\Theta _5 / u_5\)

Full size image
Fig. 10
figure 10

Synchronization error for complex Lu-system and T-system at a\(\alpha =0.7\) , b\(\alpha =0.85 \), and c\( \alpha =1 \)

Full size image
Fig. 11
figure 11

Trajectories for secure communication based on additive encryption masking scheme a information signal \(N_T=\cos (0.5t)\)b encrypted signal \(P_E=N_T+u_1\)c decrypted signal \(P_R=P_E-v_1/\sigma _1 \)d error between decrypted signal and original signal \(P_R-N_T\)

Full size image
$$\begin{aligned} V=V_{1}+V_{2}+V_{3}+V_{4}+V_5 \end{aligned}$$
(14)

where

$$\begin{aligned} V_{1}&=\dfrac{1}{2}s_{1}^2+\dfrac{1}{m_{1}} (\hat{\varpi }_{1}-\varpi _{1})^2+\dfrac{1}{n_{1}} (\hat{\upsilon }_{1}-\upsilon _{1})^2\nonumber \\ V_{2}&=\dfrac{1}{2}s_{2}^2+\dfrac{1}{m_{2}} (\hat{\varpi }_{2}-\varpi _{2})^2+\dfrac{1}{n_{2}} (\hat{\upsilon }_{2}-\upsilon _{2})^2 \nonumber \\ V_{3}&=\dfrac{1}{2}s_{3}^2+\dfrac{1}{m_{3}} (\hat{\varpi }_{3}-\varphi _{3})^2+\dfrac{1}{n_{3}} (\hat{\upsilon }_{3}-\upsilon _{3})^2\nonumber \\ V_{4}&=\dfrac{1}{2}s_{4}^2+\dfrac{1}{m_{4}} (\hat{\varpi }_{4}-\varpi _{4})^2+\dfrac{1}{n_{4}} (\hat{\upsilon }_{4}-\upsilon _{4})^2 \nonumber \\ V_{5}&=\dfrac{1}{2}s_{5}^2+\dfrac{1}{m_{5}} (\hat{\varpi }_{5}-\varpi _{5})^2+\dfrac{1}{n_{5}} (\hat{\upsilon }_{5}-\upsilon _{5})^2 \end{aligned}$$
(15)

The dynamics of Lyapunov function is

$$\begin{aligned} \dot{V}_{1}&=s_{1}\dot{s_{1}}+\dfrac{1}{m_{1}}(\hat{\varpi }_{1} -\varpi _{1})\dot{\hat{\varpi }}_{1}+\dfrac{1}{n_{1}}(\hat{\upsilon }_{1} -\upsilon _{1})\dot{\hat{\upsilon }}_{1}\nonumber \\ \dot{V}_{2}&=s_{2}\dot{s_{2}}+\dfrac{1}{m_{2}} (\hat{\varpi }_{2}-\varpi _{2})\dot{\hat{\varpi }}_{2} +\dfrac{1}{n_{2}}(\hat{\upsilon }_{2}-\upsilon _{2}) \dot{\hat{\upsilon }}_{2} \nonumber \\ \dot{V}_{3}&=s_{3}\dot{s_{3}}+\dfrac{1}{m_{3}} (\hat{\varpi }_{3}-\varpi _{3})\dot{\hat{\varpi }}_{3} +\dfrac{1}{n_{3}}(\hat{\upsilon }_{3}-\upsilon _{3})\dot{\hat{\upsilon }}_{3}\\ \dot{V}_{4}&=s_{4}\dot{s_{4}}+\dfrac{1}{m_{4}} (\hat{\varpi }_{4}-\varpi _{4})\dot{\hat{\varpi }}_{4} +\dfrac{1}{n_{4}}(\hat{\upsilon }_{4}-\upsilon _{4})\dot{\hat{\upsilon }}_{4}\nonumber \\ \dot{V}_{5}&=s_{5}\dot{s_{5}}+\dfrac{1}{m_{5}} (\hat{\varpi }_{5}-\varpi _{5})\dot{\hat{\varpi }}_{5} +\dfrac{1}{n_{5}}(\hat{\upsilon }_{5}-\upsilon _{5}) \dot{\hat{\upsilon }}_{5}\nonumber \end{aligned}$$
(16)

Substituting the values of \( s_{i}'s \), we obtain

$$\begin{aligned} \dot{V}_{1}&=s_{1}(D^{\alpha }e_{1}+\phi _{1}e_{1})+\dfrac{1}{m_{1}} (\hat{\varpi }_{1}-\varpi _{1})\dot{\hat{\varpi }}_{1}\nonumber \\&\quad +\,\dfrac{1}{n_{1}} (\hat{\upsilon }_{1}-\upsilon _{1})\dot{\hat{\upsilon }}_{1}\nonumber \\ \dot{V}_{2}&=s_{2}(D^{\alpha }e_{2}+\phi _{2}e_{2})+\dfrac{1}{m_{2}} (\hat{\varpi }_{2}-\varpi _{2})\dot{\hat{\varpi }}_{2}\nonumber \\&\quad +\,\dfrac{1}{n_{2}} (\hat{\upsilon }_{2}-\upsilon _{2})\dot{\hat{\upsilon }}_{2} \nonumber \\ \dot{V}_{3}&=s_{3}(D^{\alpha }e_{3}+\phi _{3}e_{3})+\dfrac{1}{m_{3}} (\hat{\varpi }_{3}-\varpi _{3})\dot{\hat{\varpi }}_{3}\nonumber \\&\quad +\,\dfrac{1}{n_{3}} (\hat{\upsilon }_{3}-\upsilon _{3})\dot{\hat{\upsilon }}_{3}\nonumber \\ \dot{V}_{4}&=s_{4}(D^{\alpha }e_{4}+\phi _{4}e_{4})+\dfrac{1}{m_{4}} (\hat{\varpi }_{4}-\varpi _{4})\dot{\hat{\varpi }}_{4}\nonumber \\&\quad +\,\dfrac{1}{n_{4}} (\hat{\upsilon }_{4}-\upsilon _{4})\dot{\hat{\upsilon }}_{4}\nonumber \\ \dot{V}_{5}&=s_{5}(D^{\alpha }e_{5}+\phi _{5}e_{5})+\dfrac{1}{m_{5}} (\hat{\varpi }_{5}-\varpi _{5})\dot{\hat{\varpi }}_{5}\nonumber \\&\quad +\,\dfrac{1}{n_{5}} (\hat{\upsilon }_{5}-\upsilon _{5})\dot{\hat{\upsilon }}_{5} \end{aligned}$$
(17)

By substituting the values of \( D^{q}e_{i}\) , \(\dot{\hat{\varpi }}_{i}\) and \(\dot{\hat{\upsilon }}_{i} \) in (17) , we obtain

$$\begin{aligned} \dot{V}_{i}&=s_{1}[\Delta g_{i}+\omega _{i}-(\hat{\varpi }_{i} +\hat{\upsilon }_{i}+\gamma _{i})signs_{i}]\\&\quad +\,(\hat{\varpi }_{i} -\varpi _{i})\mid s_{i}\mid +(\hat{\upsilon }_{i}-\upsilon _{i})\mid s_{i}\mid \\&\leqslant (\mid \Delta g_{i}\mid +\mid \omega _{i}\mid ) \mid s_{i}\mid -(\hat{\varpi }_{i}+\hat{\upsilon }_{i} +\gamma _{i})\mid signs_{i}\mid \\&\quad +\,(\hat{\varpi }_{i}-\varpi _{i}) \mid s_{i}\mid +(\hat{\upsilon }_{i}-\upsilon _{i})\mid s_{i}\mid \\&< (\varpi _{i}+\upsilon _{i})\mid s_{i}\mid -(\hat{\varpi }_{i} +\hat{\upsilon }_{i}+\gamma _{i})\mid signs_{i}\mid \\&\quad +\,(\hat{\varpi }_{i} -\varpi _{i})\mid s_{i}\mid +(\hat{\upsilon }_{i} -\upsilon _{i})\mid s_{i}\mid \\&=-P_{i}\mid s_{i}\mid \end{aligned}$$

Finally, we get

$$\begin{aligned} \dot{V}&=\dot{V}_{1}+\dot{V}_{2}+\dot{V}_{3}+\dot{V}_{4}+\dot{V}_{5}\nonumber \\&<-(P_{1}\mid s_{1}\mid +P_{2}\mid s_{2}\mid +P_{3}\mid s_{3}\mid +P_{4}\mid s_{4}\mid +P_{5}\mid s_{5}\mid ) \end{aligned}$$
(18)

Thus there exist a non negative real number P such that

\((P_{1}\mid s_{1}\mid +P_{2}\mid s_{2}\mid +P_{3}\mid s_{3}\mid +P_{4}\mid s_{4}\mid +P_{5}\mid s_{5}\mid ) > P\), then (20) becomes

$$\begin{aligned} \dot{V}&< -P\sqrt{s_{1}^2+s_{2}^2+s_{3}^2+s_{4}^2+s_{5}^2}\nonumber \\&<0 \end{aligned}$$
(19)

Hence, By Lyapunov stability theory \(\parallel s_{i}\parallel \rightarrow 0 \) as \( t\rightarrow \infty \).Thus the error dynamical system (10) asymptotically converges to \( s_{i}=0 \). Therefore the trajectories of state variables of projection of master system and chaotic slave system are asymptotically and globally adjusted to desired set of points with control laws (12) and adaptive laws (13).

5 Numerical simulations

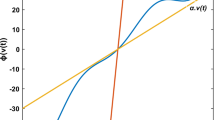
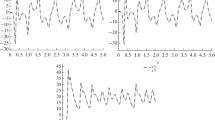
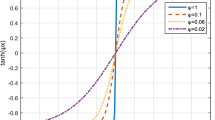
Simulations have been performed (using Matlab) to validate and visualize the effectiveness of the proposed scheme for the synchronization between master system and chaotic slave system.In simulations we have taken fractional order \(\alpha =0.95\) with step size 0.001. The parameter of master system are taken as \( a_{1}=42, a_{2}=22, a_{3}=5 \), and of slave system as \( b_{1}=2.1, b_{2}=30, b_{3}=0.6 \).Initial conditions for drive system and response system are [1,2,3,4,5], [8,7,5,6,10] respectively. Figures 1 and 2 show the Phase Portraits of respective drive and response systems.We have considered the bounded uncertainties as \( \Delta g_{1}=cos\pi v_{2}, \Delta g_{2}=cos\pi v_{2} \), \( \Delta g_{3}=0.1cos \dfrac{2}{3}\pi (v_{1}+v_5) \),\(g_{4}=0.1sin \dfrac{2}{3}\pi (v_{1}+v_5) \) and \(g_{3}=0.5cos2\pi v_{2} \), bounded disturbances as \( \omega _{1}(t)=cos \pi t, \omega _{2}(t)=sin\pi t , \omega _{3}(t)=0.5cos\dfrac{3}{2}\pi t , \omega _{4}(t)=0.5sin \dfrac{3}{2} \pi t \), and \( \omega _5=sign(cos\pi t) \) initial condition for estimating the parameters as \( \hat{\varpi }(0)=(0.1,0.1,0.1) \), \( \hat{\upsilon }(0)=(0.1,0.1,0.1) \) and designed control parameters as \( m_{1}=m_{2}=m_{3}=m_{4}=m_{5}=0.1 \), \( n_{1}=n_{2}=n_{3}=n_{4}=n_{5}=0.5 \), \( \gamma _{1}=8.5,\gamma _{2}=11,\gamma _{3}=13.5,\gamma _{4}=14.5\) and \(\gamma _{5}=18.5\) and \(\phi _1=4.5,\phi _2=6,\phi _3=7.3,\phi _4=8.5\) and \(\phi _5=9\). Figure 3 exhibits the trajectories of drive system and controlled response system behaving alike and also Fig. 4 shows that the synchronization error becomes zero as time increasing. The scaling factors are taken as \(\sigma _1=2,\sigma _2=-2, \sigma _3=-1, \sigma _4=0.5, \sigma _5=3 \) . By choosing different scaling factors, we can synchronize the given system upto desired level. Figure 5 shows that the chosen sliding surface converges to s = zero and hence stable. Figure 6 shows the estimated values for bounds of uncertainties and disturbances. Figure 7 shows the time response of controllers used for synchronization in present scheme and Figs. 8 and 9 shows the ratios of controllers with the corresponding uncontrolled slave system and master system signals respectively.

5.1 Comparison of given synchronization with previous published literature

In [27], author studies active control technique to synchronize fractional order complex Lu-system and T-system. For \( \alpha =0.7, \alpha =0.85,\) and \( \alpha =1 \) the synchronization is achieved at \( t=4\,\mathrm{s} (approx.), t=5\,\mathrm{s} (approx.)\) and \(t=6\,\mathrm{s} (approx.) \) respectively whereas in present scheme we achieve synchronization at \(t=0.3\,\mathrm{s} (approx.), t=0.9\,\mathrm{s} (approx.)\) and \(t=3.5\,\mathrm{s} (approx.) \) respectively given in Fig. 10 which is much lesser than the synchronization time of [27]. Therefore, our results are far better than the results obtained by the previous author.

5.2 Applications in secure communications

As chaos synchronization has great application in secure communication. The main reason behind the process is that, in order to transmit the original containing some secret message, we add this message into a chaotic signal which is transmitted to a prescribed receiver that would recover the original message from the chaotic signal.

In order to demonstrate our scheme, we explain it by taking a simple additive encryption masking scheme which is given below.

Here we choose periodic function \( N_T=\cos (0.5t) \)as an information signal and the chaotic carrier as \( u_1 \). The encrypted information is \(P_E=N_T+u_1\). To recover the original information, hybrid projective synchronization between master system and slave system can be attained by controller \(\Theta _1\) by using the above methodology. So, the recover signal is \(P_R=P_E-v_1/\sigma _1 \). The results are shown in Fig. 11 .

6 Conclusion

In this paper, an adaptive sliding mode technique has been consigned.Hybrid Projective synchronization has been used to synchronize different fractional order complex chaotic systems. We have chosen the suitable sliding surface and designed parameters by update laws to achieve desired synchronization and to decline the consequence of external uncertainties and disturbances and chattering problem.Since the synchronization of fractional order complex chaotic system in the presence of uncertainties and disturbances has not been examined in the prior literature, we have interrogated, and synchronized the considered fractional order complex Lu-system and complex chaotic T-systems in the presence of uncertainties and disturbances. Also we have compared our results with previous published literature results which have established that our scheme gives better synchronization time than the used technique in prior literature.Although we have taken complex system with uncertainties and disturbances but still our synchronization results are better. Also,this scheme will perform significant role to enhance security in communication. Computational methods evaluate the efficiency of the considered scheme.