Robust fault estimation controller for fractional-order delayed system using quantized measurement

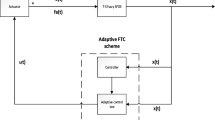
Abstract

This work is concerned with the problem of actuator fault detection for the class of linear and nonlinear fractional-order systems with differentiable time-varying delays using quantized measurement. Our observation is focused on the modelling of non-fragile fault detection controller which is constructed by using an adaptive fault estimation algorithm to ensure asymptotic stability of the considered system with suggested $H_\infty$ performance. By considering suitable Lyapunov–Krasovskii functional and using some fractional-order calculus properties for resolvability of labelled problem are derived in terms of linear matrix inequalities. Finally, the simulation studies are included to demonstrate the validity of proposed control design.

1 Introduction

The fractional-order calculus is an interesting field of mathematics, which deals with differential and integral equations under a random order, i.e. not only the order of equation must be an integer, it can be any real or even complex number. In a physical or mechanical process, the integer-order derivative denotes certain attribute at specific time, but fractional-order derivative is dealt with the whole time domain. Therefore many of the real world systems can be accurately designed by fractional-order differential equations [1,2,3]. In recent years, tremendous effect has been made on study of solving time-fractional linear and nonlinear differential equations [4], fractional coupled Burgers equations [5, 6] and time-fractional multi-dimensional diffusion equations [7]. In particular, there has been rapid growth and significant attention for fractional-order dynamical systems in various fields of engineering and biological systems (see [8, 9] and references therein). Some interesting results are developed for the stability analysis and control design of fractional-order systems(FOS) (see [10, 11]). Trigeassou et al. developed a new technique using Lyapunov stability theorem for fractional-order nonlinear systems [12]. Recently, many authors are using this technique because of its effectiveness (see [13] and references therein).

On the other hand, designing of controller plays a positive role in stabilizing the dynamical systems. In the process of designing the feedback controller, some errors(or uncertainties) may occur in gain, the non-fragile feedback controller is used to tolerate these kinds of errors. In feedback loop, suppose internet is considered as a communicative channel, which leads to face some difficulties during the analysis of closed-loop system because of its limited or less transformation capacity. The quantization effect is one of an important difficulties among them. The observer based problem of fractional-order nonlinear systems with quantized measurements reported in [14, 15] and reference therein. This problem arises frequently in data fusion and target tracking systems. Sector bounded is one of the effective methods to handle the quantization error method (see [16] and reference therein).

In general, the fractional-order control systems may meet actuator failure when the process of designing the model, variations in operating conditions and manufacturing tolerances [14]. Meanwhile, maintaining the stability of the closed-loop system is a necessary task to fractional-order control systems. Hence it is necessary to design such fault-tolerant control for the fractional-order nonlinear system. In the past few years, fault-tolerance of integer-order systems via the fault detection (FD) approach has received more attentions (see [17, 18] and reference therein). More generally, fast adaptive fault estimation algorithm is used to solve the FD problems (see [19, 20]). Recently, the FD technique for uncertain fractional-order systems with the aid of LMI is reported in [21] . Our system may meets the external disturbance during the processing time, so it is necessary to reject the external disturbance from the system. In this paper, $H_\infty$ performance (see [22, 23] reference therein) is used to reject such external disturbance. Yet, to the authors knowledge, no work is dealt with the stabilization of fractional-order nonlinear delayed system using quantized measurement based on FD approach. Motivated by this thought, in this paper, the stabilization problem for fractional-order nonlinear delayed system is discussed with the incorporation of the FD technique. The vital contributions of this work are displayed as follows:

• (1) Stabilization of fractional-order model subject to actuator fault, nonlinearities and external disturbances is considered.

• (2) The prescribed controller is designed to stabilize the fractional-order systems even in the presence of quantization effects.

• (3) Fault detection technique is utilize to derive the sufficient conditions for stabilization of fractional-order systems.

2 Problem formulation and preliminaries

This section contains the construction of the closed-loop system. Let us consider the fractional-order nonlinear system with time-varying delay of commensurate order $0< \alpha <1$ with quantized measurement,

$$\begin{aligned} D^\alpha {x}(t)&=Ax(t)+A_dx(t-d(t))+g(x(t))\nonumber \\&\quad +\,Bu(t)+B_af(t)+D\omega (t),\nonumber \\ y(t)&=Cx(t),\nonumber \\ Q(y(t))&=Q(Cx(t)), \end{aligned}$$

(1)

where state-space is denoted by $x(t)\in \mathfrak {R}^n$; control input is denoted by u(t); f(t) is actuator failure; $y(t)\in \mathfrak {R}^m$ is output; A, $A_d$, B, $B_a$ and C are system parameters with suitable dimensions; d(t) is time-varying delay satisfying $0\le d_1\le d(t)\le d_2 \text{ and } {\dot{d}}(t)\le \mu$; Q(y(t)) is quantized measurement which is defined as follows,

$$\begin{aligned} Q(y(t))={\left\{ \begin{array}{ll}c_i\varDelta _{0_i}, &{}\text{ if } \frac{c_i\varDelta _{0_i}}{1+\psi _i}<y(t)\le \frac{c_i\varDelta _{0_i}}{1-\psi _i}\\ 0,&{}\text{ if } y(t)=0\\ -Q(-y(t)),&{}\text{ if } y(t)<0 \end{array}\right. } \end{aligned}$$

(2)

where $\varDelta _{0_i}$ is density, $\psi _i=\frac{1+\varDelta _{0_i}}{1-\varDelta _{0_i}}$, $Q(y(t))=(I+\Pi \Lambda (t))y(t)$, $\Pi =diag\{\psi _1,\psi _2,\dots ,\psi _n\}$ with $\Lambda ^T(t)\Lambda (t)\le I$. The fractional-order state observer with fault estimation for the system (1) is considered as,

$$\begin{aligned} D^\alpha {{\hat{x}}}(t)&=A{\hat{x}}(t)+A_d{\hat{x}}(t-d(t))\nonumber \\&\quad +\,Bu(t)+B_a{\hat{f}}(t)+L[{\hat{y}}(t)-Q(y(t))],\nonumber \\ {\hat{y}}(t)&=C{\hat{x}}(t). \end{aligned}$$

(3)

By substituting the value of quantizer as $Q(y(t))=(I+\Pi \Lambda (t))y(t)$ into the observer system (3), we can get the following equation:

$$\begin{aligned} D^\alpha {\hat{x}}(t)&=A{\hat{x}}(t)+A_d{\hat{x}}(t-d(t))+Bu(t)+B_a{\hat{f}}(t)\nonumber \\&\quad +\,LC({\hat{x}}(t)-x(t))-L\Pi \Lambda (t)Cx(t),\nonumber \\\ {\hat{y}}(t)&=C{\hat{x}}(t), \end{aligned}$$

(4)

where ${\hat{x}}(t)$ is observer state-space; ${\hat{f}}(t)$ is estimated fault; L is observer gain; ${\hat{y}}(t)$ is output of the observer. In practical systems, gain fluctuations may arise during the designing process of controller. So, let us construct the non-fragile fault-tolerant control in the following form,

$$\begin{aligned}&u(t)=(K+\delta K(t)){\hat{x}}(t)-B^+B_a{\hat{f}}(t), \end{aligned}$$

(5)

where $B^+$ is Penrose–Moore inverse of B, K is the controller gain, the fluctuation $\delta K(t)=MF(t)N$ in which $F^T(t)F(t)\le I$. By substituting the control (5) into the system Eq. (1), we get,

$$\begin{aligned} D^\alpha x(t)&=Ax(t)+A_dx(t-d(t))+g(x(t))\nonumber \\&\quad +\,B(K+\delta {K}(t)){\hat{x}}(t)-B_a{\tilde{f}}(t)+D\omega (t),\nonumber \\ y(t)&=Cx(t), \end{aligned}$$

(6)

where ${\tilde{f}}(t)={\hat{f}}(t)-f(t)$. Let the error system be $e(t)={\hat{x}}(t)-x(t)$. Then from (4) and (6) we have,

$$\begin{aligned} D^\alpha {e}(t)&=Ae(t)+A_de(t-d(t))-g(x(t))\nonumber \\&\quad +\,LCe(t)-L\Pi \Lambda (t)Cx(t)+B_a{\tilde{f}}(t)-D\omega (t),\nonumber \\ e_y(t)&=Ce(t). \end{aligned}$$

(7)

To derive the required theoretical result, we consider the following assumptions, definition and lemmas:

Assumption 1

$D^\alpha {f}(t)$ is norm bounded. i.e. $||D^\alpha {f}(t)||\le f_1$ where $0\le f_1<\infty .$

Assumption 2

$Rank(CB_a)=r$, where r is the rank of $B_a$.

Assumption 3

Invariant zeros of $(A, B_a, C)$ lie in open left plane.

Assumption 4

(Lipchitz condition) The nonlinear function g(x(t)) satisfies the following condition $||g(x(t))||\le ||Hx(t)||$.

Definition 1

[10] An integral operator of fractional order is denoted by $D^{-\alpha }$ can be rewritten as $D^{-\alpha }f(t)=h(t)*f(t)$, where h(t) denotes impulse response of linear system with $h(t)=\frac{t^{\alpha -1}}{\Gamma \alpha }$. Let $\theta (\Omega )$ be frequency weighting function (diffusive representation) and $\Omega$ be elementary frequency then we can define h(t) as,

$$\begin{aligned} h(t)=\int _{0}^{\infty }\theta (\Omega ) e^{\Omega t} d\Omega . \end{aligned}$$

Lemma 1

[10] A nonlinear differential equation of commensurate order $\alpha$, $D^\alpha x(t)=f(x(t))$ caused by fractional integrator with continuous frequency distributed model can be written as follows,

$$\begin{aligned} \frac{\partial Z(t,\Omega )}{\partial t}&= -\Omega Z(t,\Omega )+f(x(t)),\nonumber \\ x(t)&=\int _{0}^{\infty }\theta (\Omega )Z(t,\Omega )d\Omega . \end{aligned}$$

(8)

Lemma 2

[19] Let the Assumptions 2 and 3 hold then there exist a positive definite matrix $P_2$ such that the following condition holds, $B_a^TP_2=FC$.

Lemma 3

[20] Let matrices M, N and F(t) be real matrices with appropriate dimension, with F(t) satisfying $F^T(t)F(t) \le I$, then for any scalar $\epsilon > 0$, the following inequality holds: $MF(t)N+N^TF(t)M^T \le \epsilon MM^T+ \epsilon ^{-1} N^TN.$

3 Main results

In the following theorem, a stability analysis is made on the given fractional-order system without gain fluctuations and the fault is taken as time-varying. Therefore, $D^\alpha f(t)\ne 0$, then the fractional-order derivative of ${\tilde{f}}(t)$ with respect to time is $D^\alpha {\tilde{f}}(t)= D^\alpha {\hat{f}}(t)-D^\alpha f(t)$.

Theorem 1

Let the Assumptions 1–4 hold. For the given scalars $d_1\ge 0$, $d_2>0$, $\gamma >0$, $\rho _1>0$, $\mu >0$ and given matrices F, K and $\Phi$ of appropriate dimensions, the fractional-order system (1) is asymptotically stable with prescribed $H_\infty$ performance index if there exist a positive scalar $\epsilon _1$ and positive definite matrices $P_1$, $P_2$, $Q_{11}$, $Q_{11}$, $Q_{12}$, $Q_{13}$, $Q_{21}$, $Q_{22}$, $Q_{23}$, $R_1$, $R_2$ and O such that the following condition holds:

$$\begin{aligned} \left[ \begin{matrix} \Phi _{1,1}&{}\Phi _{1,2}&{}\Phi _{1,3}&{}\dots &{}\Phi _{1,22}&{}\Phi _{1,23}\\ *&{}\Phi _{2,2}&{}\Phi _{2,3}&{}\dots &{}\Phi _{2,22}&{}\Phi _{2,23}\\ *&{}*&{}\Phi _{3,3}&{}\dots &{}\Phi _{3,22}&{}\Phi _{3,23}\\ \vdots &{}\vdots &{}\vdots &{}\dots &{}\vdots &{}\vdots \\ *&{}*&{}*&{}\dots &{}\Phi _{22,22}&{}\Phi _{22,23}\\ *&{}*&{}*&{}\dots &{}*&{}\Phi _{23,23} \end{matrix}\right] <0, \end{aligned}$$

(9)

where $\Phi _{1,1}=A^TP_{1}+P_{1}A+P_{1}BK+K^TB^TP_{1}+Q_{11}+Q_{21}+Q_{31}+(d_2-d_1)^2R_1$, $\Phi _{1,2}=P_{1}BK$, $\Phi _{1,3}=-P_{1}B_a$, $\Phi _{1,6}=P_{1}A_d$, $\Phi _{1,10}=P_1D$, $\Phi _{1,11}=P_1$, $\Phi _{1,20}=\epsilon _1C^T$, $\Phi _{1,22}=C^T$, $\Phi _{1,23}= {\sqrt{\rho _1}} L^T$, $\Phi _{2,2}=A^TP_{2}+P_{2}A+P_{2}LC+C^TL^TP_{2}+Q_{12}+Q_{22}+Q_{32} +(d_2-d_1)^2R_2$, $\Phi _{2,3}=-C^TL^TP_{2}B_a-A^TP_{2}B_a$, $\Phi _{2,7}= P_{2}A_d$, $\Phi _{2,10}=P_2D$, $\Phi _{2,11}=P_2$, $\Phi _{2,21}=P_2L\Pi$, $\Phi _{3,3}=-2B_a^TP_{2}B_a+O$, $\Phi _{3,7}=-B_a^TP_{2}A_d$, $\Phi _{3,10}=B_a^TP_2D$, $\Phi _{3,11}=B_a^T P_2$, $\Phi _{3,21}= B_a P_2L \Pi$, $\Phi _{4,4}= -Q_{11}$, $\Phi _{5,5}=-Q_{12}$, $\Phi _{6,6}=-(1-\mu )Q_{21}$, $\Phi _{7,7}=-(1-\mu ) Q_{22}$, $\Phi _{8,8}=-Q_{31}$, $\Phi _{9,9}=-Q_{32}$, $\Phi _{10,10}=-\gamma I$, $\Phi _{11,11}=-\rho _1 I$, $\Phi _{12,12}=-4R_{1}$, $\Phi _{12,18}=\frac{6}{d_2-d_1}R_1$, $\Phi _{13,13}=-4R_{2}$, $\Phi _{13,19}= \frac{6}{d_2-d_1} R_2$, $\Phi _{14,14}= -4R_{1}$, $\Phi _{14,16}= \frac{6}{d_2-d_1} R_1$, $\Phi _{15,15}= -4R_{2}$, $\Phi _{15,17}= \frac{6}{d_2-d_1} R_2$, $\Phi _{16,16}= -\frac{12}{(d_2-d_1)^2} R_1$, $\Phi _{17,17}= -\frac{12}{(d_2-d_1)^2}R_2$, $\Phi _{18,18}= -\frac{12}{(d_2-d_1)^2}R_1$, $\Phi _{19,19}= \ -\frac{12}{(d_2-d_1)^2} \ R_2$, $\Phi _{20,20}=-\epsilon _1$ , $\Phi _{21,21}=-\epsilon _1$, $\Phi _{22,22}=-I$, $\Phi _{23,23}=-I$ and remaining terms are zero. For the time-varying fault that is $D^\alpha f(t)\ne 0$, by the fractional adaptive estimation algorithm,

$$\begin{aligned} D^\alpha {\hat{f}}(t)=-P_3^{-1}F(D^\alpha e_y(t)+e_y(t)), \end{aligned}$$

(10)

where $P_3^{-1}>0$ is the learning rate, the state error e(t) and fault estimation error are bounded.

Proof

As stated in the Lemma 1, the given fractional-order equations (6), (7) and (10) can be rebuild in the backing forms:

$$\begin{aligned}&{\left\{ \begin{array}{ll} \frac{\partial Z_1(\Omega ,t)}{\partial t}= -\Omega Z_1(\Omega ,t)+Ax(t)+A_dx(t-d(t)) \\ \quad \quad \quad \quad \quad \quad +\,g(x(t))+BK{\hat{x}}(t)-B_a{\tilde{f}}(t)+D\omega (t),\\ x(t)=\int ^{\infty }_{0} \theta (\Omega )Z_1(\Omega ,t) d\Omega , \end{array}\right. } \end{aligned}$$

(11)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \frac{\partial Z_2(\Omega ,t)}{\partial t}= -\Omega Z_2(\Omega ,t)+Ae(t)+A_de(t-d(t))-g(x(t)) \\ \quad \quad \quad \quad \quad \quad +\,LCe(t)-L\Pi \Lambda (t)Cx(t)+B_a{\tilde{f}}(t)-D\omega (t),\\ e(t)=\int ^{\infty }_{0} \theta (\Omega )Z_2(\Omega ,t) d\Omega ,\end{array}\right. }\end{aligned}$$

(12)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \frac{\partial Z_3(\Omega , t)}{\partial t}= -\Omega Z_3(\Omega ,t)-P_{3}^{-1}F(D^\alpha e_y(t)\\ \quad \quad \quad \quad \quad \quad +e_y(t))-D^\alpha f(t), \\ {\tilde{f}}(t)=\int ^{\infty }_{0} \theta (\Omega )Z_3(\Omega ,t) d\Omega . \end{array}\right. }\end{aligned}$$

(13)

Initially we construct the monochromatic Lyapunov function for $Z_1$, $Z_2$ and $Z_3$,

$$\begin{aligned} v_1(t)=Z_1^T(t)P_1Z_1(t)+Z_2^T(t)P_2Z_2(t)+Z_3^T(t)P_3Z(t). \end{aligned}$$

(14)

Arising the Lyapunov function $V_1(t)$ by summing along with the weighting function $\theta (t)$,

$$\begin{aligned} V_1(t)=&\int ^{\infty }_{0} \theta (\Omega )[Z_1^T(\Omega ,t)P_{1}Z_1(\Omega ,t)]d\Omega \nonumber \\&+\int ^{\infty }_{0} \theta (\Omega )[Z_2^T(\Omega ,t)P_{2}Z_2(\Omega ,t)]d\Omega \nonumber \\&+\int ^{\infty }_{0} \theta (\Omega )[Z_3^T(\Omega ,t)P_{3}Z_3(\Omega ,t)]d\Omega . \end{aligned}$$

(15)

Let us construct required Lyapunov–Krasovskii function as follows,

$$\begin{aligned} V(t)=\sum _{i=1}^{4} V_i(t), \end{aligned}$$

(16)

where

$$\begin{aligned} V_2(t)&=\int _{t-d_2}^{t} x^T(s)Q_{11}x(s) ds+\int _{t-d(t)}^{t} x^T(s)Q_{21}x(s) ds\\&\quad +\,\int _{t-d_1}^{t} x^T(s)Q_{31}x(s) ds+\int _{t-d_2}^{t} e^T(s)Q_{12}e(s) ds\\&\quad +\,\int _{t-d(t)}^{t} e^T(s)Q_{22}e(s) ds+\int _{t-d_1}^{t} e^T(s)Q_{32}e(s) ds,\\ V_3(t)&=(d_2-d_1)\int _{t-d_2}^{t-d_1}\int _{s}^{t} x^T(u)R_1x(u) duds\\&\quad +\,(d_2-d_1)\int _{t-d_2}^{t-d_1}\int _{s}^{t} e^T(u)R_2e(u) duds. \end{aligned}$$

Taking the derivative along the solutions of Lyapunov–Krasovskii function (16) with respect to t we get,

$$\begin{aligned} {\dot{V}}(t)=&\sum _{i=1}^{4} {\dot{V}}_i(t), \end{aligned}$$

(17)

$$\begin{aligned} \dot{V_1}(t)=&-2\int _{0}^{\infty }\theta (\Omega )[Z_1^T(\Omega ,t)P_{1}Z_1(\Omega ,t)]d\Omega \nonumber \\&-\,2\int ^{\infty }_{0} \theta (\Omega )[Z_2^T(\Omega ,t)P_{2}Z_2(\Omega ,t)]d\Omega \nonumber \\&-\,2\int ^{\infty }_{0}\theta (\Omega )[Z_3^T(\Omega ,t)P_{3}Z_3(\Omega ,t)]d\Omega \nonumber \\&+\,2\int ^{\infty }_{0}\theta (\Omega )Z_1^T(\Omega ,t)P_{1}[A_dx(t-d(t))+g(x(t))\nonumber \\&+\,BK{\hat{x}}(t)-B_a{\tilde{f}}(t)+D\omega (t)]d\Omega \nonumber \\&+\,2\int ^{\infty }_{0}\theta (\Omega )Z_2^T(\Omega ,t)P_{2}[Ae(t)+A_de(t-d(t))-g(x(t))\nonumber \\&+\,LCe(t)-L\Pi \Lambda (t)Cx(t)+B_a{\tilde{f}}(t)-D\omega (t)]d\Omega (t)\nonumber \\&+\,2\int ^{\infty }_{0}\theta (\Omega )Z_3^T(\Omega ,t)P_{3}[-P_{3}^{-1} F(D^\alpha e_y(t)\nonumber \\&+\,e_y(t))-D^\alpha f(t)]d\Omega . \end{aligned}$$

(18)

From the Lemma 2 we can get,

$$\begin{aligned}&-2{\tilde{f}}^T(t)FC[D^\alpha e(t)+e(t)]=-2{\tilde{f}}^T(t)B_a^TP_{2}[D^\alpha e(t)\nonumber \\ {}&\quad +e(t)]. \end{aligned}$$

(19)

By substituting (19) and the error system $e(t)={\hat{x}}(t)-x(t)$ into (18), we obtain,

$$\begin{aligned} \dot{V_1}(t)=&-2\int _{0}^{\infty }\theta (\Omega )[Z_1^T(\Omega ,t)P_{1}Z_1(\Omega ,t)]d\Omega (t)\nonumber \\&-2\int ^{\infty }_{0} \theta (\Omega )[Z_2^T(\Omega ,t)P_{2}Z_2(\Omega ,t)]d\Omega \nonumber \\&-\,2\int ^{\infty }_{0}\theta (\Omega )[Z_3^T(\Omega ,t)P_{3}Z_3(\Omega ,t)]d\Omega \nonumber \\&+\,2x^T(t)[P_1A+P_1BK]x(t)+2x^T(t)\nonumber \\&\times [P_1BK-C^T\Lambda ^T(t)\Pi L^TP_2]e(t)\nonumber \\&+\,2x^T(t)P_1A_dx(t-d(t))-2x^T(t)P_1B_a{\tilde{f}}(t) \nonumber \\&+\,2x^T(t)P_1D\omega (t)+2x^T(t)P_1g(x(t))\nonumber \\&+\,2e^T(t)[P_2A+P_2LC]e(t)+2e^T(t)P_2\nonumber \\&\times \, A_de(t-d(t))-2e^T(t)P_2D\omega (t)\nonumber \\&-\,2e^T(t)P_2g(x(t))\nonumber \\&-\,2e^T(t)A^TP_2B_a{\tilde{f}}(t)\nonumber \\&-\,2{\tilde{f}}^T(t)B_a^TP_2A_de(t-d(t))-2{\tilde{f}}^T(t)B_a^TP_2B_a{\tilde{f}}(t)\nonumber \\&-\,2e^T(t)C^TL^TP_2B_a{\tilde{f}}(t)\nonumber \\&-\,2x^T(t)C^T\Lambda ^T(t)\Pi ^TL^T{\tilde{f}}(t)\nonumber \\&-\,2{\tilde{f}}^T(t)P_3D^\alpha f(t),\nonumber \\ \le&\, 2x^T(t)[P_1A+P_1BK]x(t)\nonumber \\&+\,2x^T(t)[P_1BK-C^T\Lambda ^T(t)\Pi L^TP_2]e(t)&\nonumber \\&+\,2x^T(t)P_1A_dx(t-d(t))\nonumber \\&-\,2x^T(t)P_1B_a{\tilde{f}}(t)\nonumber \\&+\,2x^T(t)P_1D\omega (t)+2x^T(t)P_1g(x(t))\nonumber \\&+\,2e^T(t)[P_2A+P_2LC]e(t)+2e^T(t)P_2A_de(t-d(t))\nonumber \\&-\,2e^T(t)P_2D\omega (t)&\nonumber \\&-\,2e^T(t)P_2g(x(t))-2e^T(t)A^TP_2B_a{\tilde{f}}(t)\nonumber \\&-\,2{\tilde{f}}^T(t)B_a^TP_2A_de(t-d(t))\nonumber \\&-\,2{\tilde{f}}^T(t)B_a^TP_2B_a{\tilde{f}}(t)\nonumber \\&-\,2e^T(t)C^TL^TP_2B_a{\tilde{f}}(t)-2x^T(t)C^T\Lambda ^T(t)\Pi ^TL^T{\tilde{f}}(t)\nonumber \\&-\,2{\tilde{f}}^T(t)P_3D^\alpha f(t). \end{aligned}$$

(20)

For positive definite matrix O we can rewrite the last term of the above equation as follows,

$$\begin{aligned}&-2{\tilde{f}}^T(t)P_3D^\alpha f(t)\le {\tilde{f}}^T(t)O{\tilde{f}}(t)\nonumber \\&\quad +D^\alpha f^T(t)P_3 O^{-1} P_3D^\alpha f(t). \end{aligned}$$

(21)

From (21) and Assumption 1 we obtain,

$$\begin{aligned} \dot{V_1}(t)\le&\ 2x^T(t)[P_1A+P_1BK]x(t)\nonumber \\&+2x^T(t)[P_1BK-C^T\Lambda ^T(t)\Pi L^TP_2]e(t)\nonumber \\&+2x^T(t)P_1A_dx(t-d(t)) \nonumber \\&-2x^T(t)P_1B_a{\tilde{f}}(t)+2x^T(t)P_1D\omega (t)\nonumber \\&+2x^T(t)P_2g(x(t))+2e^T(t)[P_2A+P_2LC]e(t)\nonumber \\&+2e^T(t)P_2A_de(t-d(t))-2e^T(t)A^TP_2B_a{\tilde{f}}(t)\nonumber \\&-2{\tilde{f}}^T(t)B_a^TP_2A_de(t-d(t))-2{\tilde{f}}^T(t)B_a^TP_2B_a{\tilde{f}}(t)\nonumber \\&-2e^T(t)C^TL^TP_2B_a{\tilde{f}}(t)\nonumber \\&-2x^T(t)C^T\Lambda ^T(t)\Pi ^TL^T{\tilde{f}}(t)\nonumber \\&+{\tilde{f}}^T(t)O{\tilde{f}}(t)+f_1^2\lambda _{max}(P_3O^{-1}P_3), \end{aligned}$$

(22)

$$\begin{aligned} \dot{V_2}(t)=&\ x^T(t)(Q_{11}+Q_{21}+Q_{31})x(t)\nonumber \\&-(1-\mu )x^T(t-d(t))Q_{11}x(t-d(t))\nonumber \\&-x^T(t-d_1)Q_{21}x(t-d_1)\nonumber \\&-x^T(t-d_2)Q_{31}x(t-d_2)+e^T(t)(Q_{12}+Q_{22}+Q_{32})e(t)\nonumber \\&-(1-\mu )e^T(t-d(t))Q_{12}e(t-d(t))\nonumber \\&-e^T(t-d_1)Q_{22}e(t-d_1)-e^T(t-d_2)Q_{32}e(t-d_2), \end{aligned}$$

(23)

$$\begin{aligned} \dot{V_3}(t)=&\ (d_2-d_1)^2x^T(t)R_1x(t)-(d_2-d_1)\int _{t-d_2}^{t-d_1} x^T(s)R_1x(s)ds\nonumber \\&+(d_2-d_1)^2e^T(t)R_1e(t)&\nonumber \\&-(d_2-d_1)\int _{t-d_2}^{t-d_1} e^T(s)R_2e(s)ds. \end{aligned}$$

(24)

Consider the integral terms in the above equation,

$$\begin{aligned}&-(d_2-d_1)\int _{t-d_2}^{t-d_1} x^T(s)R_1x(s)ds\nonumber \\&\quad =-(d_2-d_1)\int _{t-d_2}^{t-d(t)} x^T(s)R_1x(s)ds-(d_2-d_1)\nonumber \\&\quad \quad \times \int _{t-d(t)}^{t-d_1} x^T(s)R_1x(s)ds, \end{aligned}$$

(25)

$$\begin{aligned}&-(d_2-d_1)\int _{t-d_2}^{t-d_1} e^T(s)R_2e(s)ds\nonumber \\&\quad =-(d_2-d_1)\int _{t-d_2}^{t-d(t)} e^T(s)R_2e(s)ds-(d_2-d_1)\nonumber \\&\quad \quad \times \int _{t-d(t)}^{t-d_1} e^T(s)R_2e(s)ds \end{aligned}$$

(26)

By applying the Wirtinger inequality for the above integral terms we get,

$$\begin{aligned}&-(d_2-d_1)\int _{t-d_2}^{t-d(t)} x^T(s)R_1x(s)ds\nonumber \\&\quad \le -\left[ \int _{t-d_2}^{t-d(t)}x(s)ds\right] ^TR_1\left[ \int _{t-d_2}^{t-d(t)}x(s)ds\right] \nonumber \\&\qquad -3\left[ \int _{t-d_2}^{t-d(t)}x(s)ds-\frac{2}{d_2-d_1}\int _{t-d_2}^{t-d(t)}\int _{s}^{t-d(t)}x(u)duds\right] ^TR_1\nonumber \\&\qquad \left[ \int _{t-d_2}^{t-d(t)}x(s)ds-\frac{2}{d_2-d_1}\int _{t-d_2}^{t-d(t)}\int _{s}^{t-d(t)}x(u)duds\right] , \end{aligned}$$

(27)

$$\begin{aligned}&-(d_2-d_1)\int _{t-d_2}^{t-d(t)} e^T(s)R_2e(s)ds\nonumber \\&\quad \le -\left[ \int _{t-d_2}^{t-d(t)}e(s)ds\right] ^TR_2\left[ \int _{t-d_2}^{t-d(t)}e(s)ds\right] \nonumber \\&\qquad -3\left[ \int _{t-d_2}^{t-d(t)}e(s)ds-\frac{2}{d_2-d_1}\int _{t-d_2}^{t-d(t)}\int _{s}^{t-d(t)}e(u)duds\right] ^TR_2\nonumber \\&\qquad \times \left[ \int _{t-d_2}^{t-d(t)}e(s)ds-\frac{2}{d_2-d_1}\int _{t-d_2}^{t-d(t)}\int _{s}^{t-d(t)}e(u)duds\right] , \end{aligned}$$

(28)

$$\begin{aligned}&-(d_2-d_1)\int _{t-d(t)}^{t-d_1} x^T(s)R_1x(s)ds\nonumber \\&\quad \le -\left[ \int _{t-d(t)}^{t-d_1}x(s)ds\right] ^TR_1\left[ \int _{t-d(t)}^{t-d_1}x(s)ds\right] \nonumber \\&\qquad -3\left[ \int _{t-d(t)}^{t-d_1}x(s)ds-\frac{2}{d(t)-d_1}\int _{t-d(t)}^{t-d_1}\int _{s}^{t-d_1}x(u)duds\right] ^TR_1\nonumber \\&\qquad \times \left[ \int _{t-d(t)}^{t-d_1}x(s)ds-\frac{2}{d(t)-d_1}\int _{t-d(t)}^{t-d_1}\int _{s}^{t-d_1}x(u)duds\right] , \end{aligned}$$

(29)

$$\begin{aligned}&-(d(t)-d_1)\int _{t-d(t)}^{t-d_1} e^T(s)R_2e(s)ds\nonumber \\&\quad \le -\left[ \int _{t-d(t)}^{t-d_1}e(s)ds\right] ^TR_2\left[ \int _{t-d(t)}^{t-d_1}e(s)ds\right] \nonumber \\&\qquad -3\left[ \int _{t-d(t)}^{t-d_1}e(s)ds-\frac{2}{d(t)-d_1}\int _{t-d(t)}^{t-d_1}\int _{s}^{t-d_1}e(u)duds\right] ^TR_2\nonumber \\&\qquad \times \left[ \int _{t-d(t)}^{t-d_1}e(s)ds-\frac{2}{d(t)-d_1}\int _{t-d(t)}^{t-d_1}\int _{s}^{t-d_1}e(u)duds\right] . \end{aligned}$$

(30)

For any $\rho _1>0$ Assumption 4 becomes,

$$\begin{aligned} \rho _1x^T(t)H^THx(t)-\rho _1g^T(x(t))g(x(t)) \ge 0 . \end{aligned}$$

(31)

Let $\zeta (t)=[ x^T(t) \, \,\, \, e^T(t) \,\,\, \, {\tilde{f}}^T(t)\,\,\, \, x^T(t-d_1)\,\,\, \, e^T(t-d_1)\,\,\, \, x^T(t-d(t))\,\,\, \, e^T(t-d(t))\,\,\, \, x^T(t-d_2)\,\,\, \, e^T(t-d_2) \,\,\, \, \omega ^T(t) \,\,\, \, g(x(t)) \, \int \limits _{t-d_2}^{t-d(t)}x^T(s)ds \, \, \int \limits _{t-d_2}^{t-d(t)}e^T(s)ds \, \, \int \limits _{t-d(t)}^{t-d_1}x^T(s)ds \,\,\, \, \int \limits _{t-d(t)}^{t-d_1}e^T(s)ds \,\,\, \, \int \limits _{t-d(t)}^{t-d_1}\int _{s}^{t-d_1}x^T(u)duds\,\,\, \, \int \limits _{t-d(t)}^{t-d_1}\int \limits _{s}^{t-d_1}e^T(u)duds\,\,\, \int \limits _{t-d_2}^{t-d(t)}\int \limits _{s}^{t-d(t)}x^T(u)duds\,\,\, \, \int \limits _{t-d_2}^{t-d(t)}\int \limits _{s}^{t-d(t)}e^T(u)duds ]^T$.

From (22)–(31), Eq. (16) becomes,

$$\begin{aligned}&{\dot{V}}(t)+y^T(t)y(t)-\gamma \omega ^T(t)\omega (t)\nonumber \\&\quad \le {\dot{V}}(t)+y^T(t)y(t)\nonumber \\&\qquad -\gamma \omega ^T(t)\omega (t)+\rho _1x^T(t)x(t)\nonumber \\&\qquad -\rho _1g^T(x(t))H^THg(x(t))\nonumber \\&\le \zeta ^T(t)[{\bar{\Phi }}]_{19\times 19}\zeta (t)+\pounds , \end{aligned}$$

(32)

where ${\bar{\Phi }}_{1,1}= A^TP_{1}+P_{1}A + P_{1}BK +K^TB^TP_{1}+Q_{11} +Q_{21} +Q_{31} +(d_2-d_1)^2R_1+C^TC+\rho _1H^TH$, ${\bar{\Phi }}_{1,2}= P_{1}BK-C^T \Lambda ^T(t) \Pi ^T\ L^TP_{2}$, ${\bar{\Phi }}_{1,3}= -P_{1}B_a+ C^T\Lambda ^T(t) \Pi ^T L^TP_{2}B_a$, ${\bar{\Phi }}_{1,6}=P_{1}A_d$, ${\bar{\Phi }}_{1,10}=P_1D$, ${\bar{\Phi }}_{1,11}=P_1$, ${\bar{\Phi }}_{2,2}=A^TP_{2}+P_{2}A+P_{2}LC+C^TL^TP_{2}+Q_{12}+Q_{22}+Q_{32}+(d_2-d_1)^2R_2$, ${\bar{\Phi }}_{2,3}=-C^TL^TP_{2}B_a-A^TP_{2}B_a$, ${\bar{\Phi }}_{2,7}=P_{2}A_d$, ${\bar{\Phi }}_{2,10}=P_2D$, ${\bar{\Phi }}_{2,11}=P_2$ ,${\bar{\Phi }}_{3,3}=-2B_a^T P_{2}\ B_a+O$, ${\bar{\Phi }}_{3,7}=-B_a^T P_{2}A_d$, ${\bar{\Phi }}_{3,10}=B_a^T P_2D$, ${\bar{\Phi }}_{3,11}=B_a^T P_2$, ${\bar{\Phi }}_{4,4}= -Q_{11}$, ${\bar{\Phi }}_{5,5}=-Q_{12}$, ${\bar{\Phi }}_{6,6}=-(1-\mu )Q_{21}$,${\bar{\Phi }}_{7,7}=-(1-\mu )Q_{22}$, ${\bar{\Phi }}_{8,8}=-Q_{31}$, ${\bar{\Phi }}_{9,9}=-Q_{32}$, ${\bar{\Phi }}_{10,10}=-\gamma I$, ${\bar{\Phi }}_{11,11}=-\rho _1 I$, ${\bar{\Phi }}_{12,12}=-4R_{1}$, ${\bar{\Phi }}_{12,18}=\frac{6}{d_2-d_1}R_1$, ${\bar{\Phi }}_{13,13}=-4R_{2}$, ${\bar{\Phi }}_{13,19}= \frac{6}{d_2-d_1}R_2$,${\bar{\Phi }}_{14,14}=-4R_{1}$, ${\bar{\Phi }}_{14,16}=\frac{6}{d_2-d_1}R_1$, ${\bar{\Phi }}_{15,15}=-4R_{2}$, ${\bar{\Phi }}_{15,17}=\frac{6}{d_2-d_1}R_2$, ${\bar{\Phi }}_{16,16}=-\frac{12}{(d_2-d_1)^2}R_1$, ${\bar{\Phi }}_{17,17}=-\frac{12}{(d_2-d_1)^2}R_2$, ${\bar{\Phi }}_{18,18}=-\frac{12}{(d_2-d_1)^2}R_1$, ${\bar{\Phi }}_{19,19}=-\frac{12}{(d_2-d_1)^2}R_2$ and $\pounds =f_1^2\lambda _{max}(P_3O^{-1}P_3).$ Using the Lemma 3 for the terms involving $\Lambda (t)$, we can get ${\bar{\Phi }}\le \Phi$. From (9) we can obtain ${\bar{\Phi }}<0$. Since ${\bar{\Phi }}<0$, the eigen value of ${\bar{\Phi }}$ is negative let it be $-\epsilon$, then ${\dot{V}}(t)+y^T(t)y(t)-\gamma \omega ^T(t)\omega (t)\le -\epsilon ||\zeta (t)||^2+\pounds$. Therefore we can obtain ${\dot{V}}(t)+y^T(t)y(t)-\gamma \omega ^T(t)\omega (t)<0$ whenever $\epsilon ||\zeta (t)||^2>\pounds$, it means $\zeta (t)$ converges to a small set by Lyapunov stability theory. So, estimation error of the fault and state are uniformly bounded. Under the zero initial condition $V(0)=0$ and $V(\infty )>0$, which implies $y^T(t)y(t)\le \gamma \omega ^T(t)\omega (t)$. This completes the proof. $\square$

In the following theorem, a stability analysis made on the given fractional order system with gain fluctuation.

Remark 1

Note that it is difficult to solve and get unknowns using LMI toolbox because of the equality in Lemma 2. So we transform this equality into following LMI like optimization problem [9],

$$\begin{aligned} \left( \begin{matrix} \rho I&{}&{}B_a^TP_2-FC\\ *&{}&{}\rho I \end{matrix}\right) >0. \end{aligned}$$

(33)

Theorem 2

For the given scalars $d_1\ge 0$, $d_2>0$, $\rho _1>0$ and $\mu >0$, the fractional-order delayed system (1) with gain fluctuation and the fault is taken to be time-varying is robust asymptotically stable with $H_\infty$ performance if there exist positive definite matrices $P_1$, $P_1$, $P_3$, $Q_{11}$, $Q_{12}$, $Q_{13}$, $Q_{21}$, $Q_{22}$, $Q_{23}$, $R_1$, $R_2$, O, positive scalars $\rho _2$, $\epsilon _1$ and $\epsilon _2$ and appropriate dimensioned matrices $V_1$, $V_2$ and F such that the following conditions are satisfied,

$$\begin{aligned} \left[ \begin{matrix} \Xi _{1,1}&{}\Xi _{1,2}&{}\Xi _{1,3}&{}\dots &{}\Xi _{1,24}&{}\Xi _{1,25}\\ *&{}\Xi _{2,2}&{}\Xi _{2,3}&{}\dots &{}\Xi _{2,24}&{}\Xi _{2,25}\\ *&{}*&{}\Xi _{3,3}&{}\dots &{}\Xi _{3,24}&{}\Xi _{3,25}\\ \vdots &{}\vdots &{}\vdots &{}\dots &{}\vdots &{}\vdots \\ *&{}*&{}*&{}\dots &{}\Xi _{24,24}&{}\Xi _{24,25}\\ *&{}*&{}*&{}\dots &{}*&{}\Xi _{25,25} \end{matrix}\right] <0, \end{aligned}$$

(34)

and

$$\begin{aligned} \left( \begin{matrix} \rho _2 I_n&{}&{}B_a^TP_2-FC\\ *&{}&{}\rho _2 I_n \end{matrix}\right) >0, \end{aligned}$$

(35)

where $\Xi _{1,1}=A^TP_{1}+P_{1}A+BV_1+V_1^TB^T+Q_{11}+Q_{21}+Q_{31}+(d_2-d_1)^2R_1$, $\Xi _{1,2}=BV_1$,$\Xi _{1,3}=-P_{1}B_a$, $\Xi _{1,6}=P_{1}A_d$,$\Xi _{1,10}=P_1D$, $\Xi _{1,11}=P_1$,$\Xi _{1,20}=\epsilon _1C^T$, $\Xi _{1,22}=C^T$, $\Xi _{1,23}= {\sqrt{\rho _1}} H^T$, $\Xi _{1,24}=\epsilon _2N^T$, $\Xi _{1,25}=P_1BM$, $\Xi _{2,2}=A^TP_{2}+P_{2}A +V_2C+C^TV_2^T+Q_{12}+ Q_{22} +Q_{32} +(d_2-d_1)^2R_2$, $\Xi _{2,3} =-C^TV_2^TB_a-A^TP_{2}B_a$, $\Xi _{2,7}= P_{2}A_d$, $\Xi _{2,10}=P_2D$, $\Xi _{2,11}=P_2$,$\Xi _{2,21}=V_2\Pi$, $\Xi _{2,25}=\epsilon _2N^T$, $\Xi _{3,3} =-2B_a^TP_{2}B_a+O$, $\Xi _{3,7}=-B_a^TP_{2}A_d$,$\Xi _{3,10}=B_a^TP_2D$, $\Xi _{3,11}=B_a^T P_2$, $\Xi _{3,21}= \ B_aV_2\Pi$, $\Xi _{4,4} \ =-Q_{11}$, $\Xi _{5,5}=-Q_{12}$, $\Xi _{6,6} =-(1-\mu )Q_{21}$, $\Xi _{7,7}=-(1-\mu ) Q_{22}$, $\Xi _{8,8}=-Q_{31}$, $\Xi _{9,9}=-Q_{32}$, $\Xi _{10,10} =-\gamma I$, $\Xi _{11,11}=-\rho _1 I$, $\Xi _{12,12}=-4R_{1}$, $\Xi _{12,18}=\frac{6}{d_2-d_1} R_1$, $\Xi _{13,13}=-4R_{2}$, $\Xi _{13,19}= \frac{6}{d_2-d_1}R_2$, $\Xi _{14,14}=-4R_{1}$, $\Xi _{14,16}= \frac{6}{d_2-d_1} R_1$, $\Xi _{15,15}=-4R_{2}$, $\Xi _{15,17}=\frac{6}{d_2-d_1}R_2$, $\Xi _{16,16}=-\frac{12}{(d_2-d_1)^2}R_1$, $\Xi _{17,17}=-\frac{12}{(d_2-d_1)^2} R_2$, $\Xi _{18,18}=-\frac{12}{(d_2-d_1)^2}R_1$, $\Xi _{19,19}= -\frac{12}{(d_2-d_1)^2} R_2$, $\Xi _{20,20}=-\epsilon _1$, $\Xi _{21,21}=-\epsilon _1$, $\Xi _{22,22}=-I$, $\Xi _{23,23}=-I$, $\Xi _{24,24}=-\epsilon _2$, $\Xi _{25,25}=-\epsilon _2$ and remaining terms are zero. For the time-varying fault that is $D^\alpha f(t)\ne 0$, by the fractional adaptive estimation algorithm,

$$\begin{aligned} D^\alpha {\hat{f}}(t)=-P_3^{-1}F(D^\alpha e_y(t)+e_y(t)), \end{aligned}$$

(36)

where $P_3^{-1}$ is positive definite is the learning rate and observe that the state error e(t) and fault estimation error are bounded. Furthermore we have, $K=V_1USP_1^{-1}S^TU^T$ and $L=P_2^{-1}V_2$.

Proof

Since we take gain fluctuation in account, the gain matrix K becomes $K+\delta K(t)$ in the Theorem 1 and again applying the Lemma 3 for the term $\delta K(t)=MF(t)N$, we get   

$$\begin{aligned} \left[ \begin{matrix} \phi _{1,1}&{}\phi _{1,2}&{}\phi _{1,3}&{}\dots &{}\phi _{1,24}&{}\phi _{1,25}\\ *&{}\phi _{2,2}&{}\phi _{2,3}&{}\dots &{}\phi _{2,24}&{}\phi _{2,25}\\ *&{}*&{}\phi _{3,3}&{}\dots &{}\phi _{3,24}&{}\phi _{3,25}\\ \vdots &{}\vdots &{}\vdots &{}\dots &{}\vdots &{}\vdots \\ *&{}*&{}*&{}\dots &{}\phi _{24,24}&{}\phi _{24,25}\\ *&{}*&{}*&{}\dots &{}*&{}\phi _{25,25} \end{matrix}\right] <0, \end{aligned}$$

(37)

where $\phi _{1,1}=A^TP_{1}+P_{1}A+P_{1}BK+K^TB^TP_{1}+Q_{11}+Q_{21}+Q_{31}+(d_2-d_1)^2R_1, \phi _{1,2}=P_{1}BK,\phi _{1,3}=-P_{1}B_a, \, \phi _{1,6}=P_{1}A_d, \ \phi _{1,10}=P_1D, \ \phi _{1,11}=P_1, \ \phi _{1,20}=\epsilon _1C^T, \ \phi _{1,22}=C^T , \ \phi _{1,23}= \ {\sqrt{\rho _1}} \ H^T,\ \phi _{1,24}=\epsilon _2N^T, \, \phi _{1,25}=P_1BM, \ \phi _{2,2}=A^TP_{2}+P_{2}A +P_{2}LC+C^TL^TP_{2}+Q_{12}+ \ Q_{22} \ +Q_{32} +(d_2-d_1)^2R_2, \, \phi _{2,3}=-C^TL^TP_{2}B_a-A^TP_{2}B_a, \ \phi _{2,7}= \ P_{2}A_d, \ \phi _{2,10}=P_2D, \ \phi _{2,11}=P_2, \ \phi _{2,21}=P_2L\Pi ,\ \phi _{2,25}=\epsilon _2N^T, \, \phi _{3,3}=-2B_a^TP_{2}B_a+O, \ \phi _{3,7}=-B_a^TP_{2}A_d, \ \phi _{3,10}=B_a^TP_2D, \phi _{3,11}=B_a^T \ P_2, \ \phi _{3,21}= \ B_aP_2L\Pi , \, \phi _{4,4}=-Q_{11}, \ \phi _{5,5}=\ Q_{12}, \ \phi _{6,6}\ =-(1-\mu )Q_{21}, \ \phi _{7,7}=-(1-\mu ) \ Q_{22}, \ \phi _{8,8}=-Q_{31},\ \phi _{9,9}=-Q_{32}, \, \phi _{10,10}=-\gamma I,\ \phi _{11,11}=-\rho _1 I, \phi _{12,12}=-4R_{1},\ \phi _{12,18}=\frac{6}{d_2-d_1}\ R_1,\ \phi _{13,13}=-4R_{2}, \phi _{13,19}= \ \frac{6}{d_2-d_1}R_2, \, \phi _{14,14}=-4R_{1}, \ \phi _{14,16}= \ \frac{6}{d_2-d_1} \ R_1, \phi _{15,15}=-4R_{2},\ \phi _{15,17}=\frac{6}{d_2-d_1}R_2, \ \phi _{16,16}=-\frac{12}{(d_2-d_1)^2}R_1, \phi _{17,17}=-\frac{12}{(d_2-d_1)^2} R_2, \ \phi _{18,18}=-\frac{12}{(d_2-d_1)^2}R_1, \phi _{19,19}= -\frac{12}{(d_2-d_1)^2} R_2,\ \phi _{20,20}=-\epsilon _1 , \ \phi _{21,21}=-\epsilon _1, \, \phi _{22,22}=-I, \ \phi _{23,23}=-I,\phi _{24,24}=-\epsilon _2 \text{ and } \phi _{25,25}=-\epsilon _2$ By applying SVD lemma for $P_1B$ and letting $B{\bar{P}}_1=P_1B$, $V_1={\bar{P}}_1K$ and $V_2=P_2L$, we can obtain that $[\phi ]_{25\times 25}= [\Xi ]_{25\times 25}$. Then it is obvious that the given fractional-order system is stable by the Theorem 1. $\square$

In the following corollary an analysis of stability done for linear systems. By taking the nonlinear term g(x(t)) as zero, we can linearise the nonlinear system (1) as follows,

$$\begin{aligned} D^\alpha {x}(t)&=Ax(t)+A_dx(t-d(t))+Bu(t)+B_af(t)\nonumber \\ {}&\quad +D\omega (t). \end{aligned}$$

(38)

Corollary 1

Let Assumptions 1–3 hold . For the given scalars $d_1\ge 0$, $d_2>0$, $\mu >0$, the fractional order delayed system (38) with gain fluctuation and the fault is taken to be time-varying, is robust asymptotically stable with $H_\infty$ performance if there exist matrices $V_1$, $V_2$ and F of appropriate dimensions, positive definite matrices $P_1$, $P_1$, $P_3$, $Q_{11}$, $Q_{12}$, $Q_{13}$, $Q_{21}$, $Q_{22}$, $Q_{23}$, $R_1$, $R_2$, O and positive scalars $\rho _2$, $\epsilon _1$, $\epsilon _2$ such that the following condition are satisfied,

$$\begin{aligned} \left[ \begin{matrix} {\bar{\Xi }}_{1,1}&{}{\bar{\Xi }}_{1,2}&{}{\bar{\Xi }}_{1,3}&{}\dots &{}{\bar{\Xi }}_{1,22}&{}{\bar{\Xi }}_{1,23}\\ *&{}{\bar{\Xi }}_{2,2}&{}{\bar{\Xi }}_{2,3}&{}\dots &{}{\bar{\Xi }}_{2,22}&{}{\bar{\Xi }}_{2,23}\\ *&{}*&{}{\bar{\Xi }}_{3,3}&{}\dots &{}{\bar{\Xi }}_{3,22}&{}{\bar{\Xi }}_{3,23}\\ \vdots &{}\vdots &{}\vdots &{}\dots &{}\vdots &{}\vdots \\ *&{}*&{}*&{}\dots &{}{\bar{\Xi }}_{22,22}&{}{\bar{\Xi }}_{23,23}\\ *&{}*&{}*&{}\dots &{}*&{}{\bar{\Xi }}_{23,23} \end{matrix}\right] <0, \end{aligned}$$

(39)

and

$$\begin{aligned} \left( \begin{matrix} \rho _2 I_n&{}&{}B_a^TP_2-FC\\ *&{}&{}\rho _2 I_n \end{matrix}\right) >0, \end{aligned}$$

(40)

where ${\bar{\Xi }}_{1,1}=A^TP_{1}+P_{1}A+BV_1+V_1^TB^T+Q_{11}+Q_{21}+Q_{31}+(d_2-d_1)^2R_1$, ${\bar{\Xi }}_{1,2}=BV_1$,${\bar{\Xi }}_{1,3}=-P_{1}B_a$, ${\bar{\Xi }}_{1,6}=P_{1}A_d$,${\bar{\Xi }}_{1,10}=P_1D$, ${\bar{\Xi }}_{1,19}=\epsilon _1C^T$, ${\bar{\Xi }}_{1,22}=C^T$, ${\bar{\Xi }}_{1,22}=\epsilon _2N^T$, ${\bar{\Xi }}_{1,23}=P_1BM$, ${\bar{\Xi }}_{2,2}=A^TP_{2}+P_{2}A +V_2C+C^TV_2^T+Q_{12}+ Q_{22} +Q_{32} +(d_2-d_1)^2R_2$, ${\bar{\Xi }}_{2,3} =-C^TV_2^TB_a-A^TP_{2}B_a$, ${\bar{\Xi }}_{2,7}= P_{2}A_d$, ${\bar{\Xi }}_{2,10}=P_2D$, ${\bar{\Xi }}_{2,20}=V_2\Pi$, ${\bar{\Xi }}_{2,23}=\epsilon _2N^T$, ${\bar{\Xi }}_{3,3} =-2B_a^TP_{2}B_a+O$, ${\bar{\Xi }}_{3,7}=-B_a^TP_{2}A_d$, ${\bar{\Xi }}_{3,10}=B_a^TP_2D$, ${\bar{\Xi }}_{3,20}= B_aV_2\Pi$, ${\bar{\Xi }}_{4,4} =-Q_{11}$, ${\bar{\Xi }}_{5,5}=Q_{12}$, ${\bar{\Xi }}_{6,6} =-(1-\mu )Q_{21}$, ${\bar{\Xi }}_{7,7}=-(1-\mu ) Q_{22}$, ${\bar{\Xi }}_{8,8}=-Q_{31}$, ${\bar{\Xi }}_{9,9}=-Q_{32}$, ${\bar{\Xi }}_{10,10} =-\gamma I$, ${\bar{\Xi }}_{11,11}=-4R_{1}$, ${\bar{\Xi }}_{11,17}=\frac{6}{d_2-d_1}\ R_1$, ${\bar{\Xi }}_{12,12}=-4R_{2}$, ${\bar{\Xi }}_{12,18}= \frac{6}{d_2-d_1}R_2$, ${\bar{\Xi }}_{13,13}=-4R_{1}$, ${\bar{\Xi }}_{13,15}= \frac{6}{d_2-d_1} R_1$, ${\bar{\Xi }}_{14,14}=-4R_{2}$, ${\bar{\Xi }}_{14,16}=\frac{6}{d_2-d_1}R_2$, ${\bar{\Xi }}_{15,15}=-\frac{12}{(d_2-d_1)^2}R_1$, ${\bar{\Xi }}_{16,16}=-\frac{12}{(d_2-d_1)^2} R_2$, ${\bar{\Xi }}_{17,17}=-\frac{12}{(d_2-d_1)^2}R_1$, ${\bar{\Xi }}_{18,18}= -\frac{12}{(d_2-d_1)^2} R_2$, ${\bar{\Xi }}_{19,19}=-\epsilon _1$, ${\bar{\Xi }}_{20,20}=-\epsilon _1$, ${\bar{\Xi }}_{21,21}=-I$, ${\bar{\Xi }}_{22,22}=-\epsilon _2$, ${\bar{\Xi }}_{23,23}=-\epsilon _2,$ and remaining terms are zero. For the time-varying fault that is $D^\alpha f(t)\ne 0$, by the fractional adaptive estimation algorithm,

$$\begin{aligned} D^\alpha {\hat{f}}(t)=-P_3^{-1}F(D^\alpha e_y(t)+e_y(t)), \end{aligned}$$

(41)

where $P_3^{-1}$ is positive definite is the learning rate and observe that the state error e(t) and fault estimation error are bounded. Furthermore we have, $K=V_1USP_1^{-1}S^TU^T$ and $L=P^{-1}V_2$.

Proof

By taking g(x(t)) as zero in the Theorem 2 we can obtain the LMIs (39) and (40). Hence from the Theorem 2 the linear system (38) is robust asymptotically stable. $\square$

4 Simulation verifications

In this section we dispense two examples to exhibit the accomplishment of suggested non-fragile fault-tolerance control. First example is used to show the effectiveness of suggested controller for nonlinear fractional-order system. A practical model of a vertical take-off and landing aircraft in the vertical plane is given to display the effectiveness of suggested controller for linearised fractional-order system.

Example 1

Consider the following fractional-order system of order $\alpha =0.5$,

$$\begin{aligned} D^{0.5} x(t)=&\left[ \begin{matrix}-3&{}6\\ 8&{}-1\end{matrix}\right] x(t)+\left[ \begin{matrix}-0.1&{}-0.02\\ 0.01&{}0.01\end{matrix}\right] x(t-d(t))\nonumber \\&+\left[ \begin{matrix}5\\ 3\end{matrix}\right] u(t)+\left[ \begin{matrix}0.1\\ 0.2\end{matrix}\right] \omega (t)+g(x(t)), \nonumber \\y(t)=&\left[ \begin{matrix}1&1\end{matrix}\right] x(t). \end{aligned}$$

Fig. 1

State response for open-loop system

Fig. 2

State response for closed-loop system

Fig. 3

State estimation of the system based on the prescribed controller

It is obvious that the above system is equivalent to the system (1). Consider the fault as $f(t) = 0.5\sin {\pi t}+0.3\cos {15t}$, the disturbance as $\omega (t) = 0.2[\sin {2t}-0.4\cos {0.5t}]$ and nonlinear term as $g(x(t)) = \left[ \begin{matrix}0.6&{}0\\ 0&{}0.8\end{matrix}\right] sin(0.2x(t))$. The fluctuation in the gain taken as $\delta K=M\cos {t}I_2N$, where $M=[0.3 \ 0.01]$ and $N=0.01I_2.$ In the quantizer, the density of the quantizer considered as $\Pi =\frac{1-0.8}{1+0.8}$ and $\Lambda (t)=\sin {t}.$ The Lipchitz’s constant $H=2*I_2$ and $\rho _1=6$. The minimum $\rho _2$ and minimum $\gamma$ are given by 0.1 and 0.1016 respectively. Then we solve the LMIs given in the Theorem 2 using MATLAB LMI toolbox, we can get the following gains $K=[-1.2126 -0.7276]$, $L=\left[ \begin{matrix}-0.6095 \\ -5.4518\end{matrix}\right]$ and $F=[22.8026]$.

Fig. 4

Fault signal and its estimation under prescribed controller

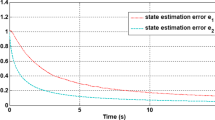
The figure of open-loop system (i.e. Fig. 1) shows the divergence of the state trajectories. Since $rank(CB_a)=1=rank(B_a)$ and the open-loop system is unstable, the fault estimation control design is suitable for given example. From the Fig. 2 we can conclude that the suggested controller make the system stable within short time duration. It reveals and proved the effectiveness of suggested controller. Fig. 3 exhibits the estimation of state trajectories with the observer trajectories. Fig. 4 shows the estimation of system fault with estimated fault. Fig. 5 reveals the estimation error of fault of the integer-order system has less conservative compare to the error provided by the fractional-order system. Fig. 6 shows the tracking of the output y(t) with the quantizer Q(y(t)).

Example 2

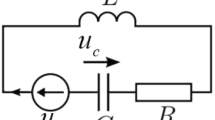
In this Example, a linearised dynamic model of a vertical take-off and landing aircraft in the vertical plane [17] is considered as follows:

$$\begin{aligned} D^\alpha x(t)=&\left[ \begin{matrix}0.0336&{}0.0271&{}0.0188&{}0.4555\\ 0.0482 &{} 1.0100 &{} 0.0024 &{} 4.0208\\ 0.1002 &{} 0.3681 &{} 0.7070 &{} 1.4200\\ 0.0000 &{} 0.0000 &{} 1.0000 &{} 0.0000\end{matrix} \right] x(t)\\&+\left[ \begin{matrix}0.4422 &{} 0.1761\\ 3.5446 &{} 7.5922\\ 5.5200 &{} 4.4900\\ 0.0000 &{} 0.0000\end{matrix}\right] u(t),\\ y(t)&=\left[ \begin{matrix}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1\end{matrix}\right] x(t), \end{aligned}$$

where $x(t)=[V_h\ V_v\ q\ \theta ]^T$ and $u(t) = [\delta _c\ \delta _l ]^T$; $V_h$ and $V_v$ represents horizontal velocity and vertical velocity, respectively; q denotes pitch rate; $\theta$ is pitch angle; $\delta _c$ and $\delta _1$ represents collective pitch control and longitudinal cyclic pitch control, respectively. Let us consider actuator faults in this system. These type of faults generally occur in the input vectors, so we assume that the coefficient of fault in the system (38) as $B_a = B$. Assume that the disturbance distribution matrix as $D = 0.01[1\ 1\ 1\ 1\ ]^T$. Since $rank(CB_a)=1$, we can use the fault detection control for the given system. Consider the learning rate as $P_3^{-1}=75$ and using LMI tool box in MATLAB, we can obtain the following unknown matrices:

Fig. 5

Estimation error of actuator fault under fractional-order and integer-order

Fig. 6

Output signal and its quantified output signal under quantized measurement approach

Fig. 7

State response of the closed-loop system

Fig. 8

Fault signal and its estimation under prescribed controller

Fig. 9

Estimation error of actuator fault under fractional-order and integer-order

Fig. 10

Output signal and its quantified output signal under quantized measurement approach

$$\begin{aligned} K= & {} \left[ \begin{matrix} -0.0036&{}-0.1361&{}-0.0180&{}0\\ -0.0084&{}-0.0185&{}-0.1170&{}0\end{matrix}\right] ,\\ L= & {} 10^3\left[ \begin{matrix} -0.0538&{}0.2387\\ -0.1561&{} 0.7135\\ 0.3301&{}-1.4658\\ 0.3445&{}-1.5758 \end{matrix}\right] \hbox { and }\\ F= & {} \left[ \begin{matrix}16.1861&{}0.4183\\ 10.0093&{}-1.4735\end{matrix}\right] \end{aligned}$$

Assume that an actuator fault is created as $f(t)=[f_1(t) f_2(t)]^T$ where

$f_1(t)={\left\{ \begin{array}{ll}0 &{}\quad if\ 0\le t<3\\ 7\sin {2*t}-4\cos {1.5(t-1)} &{}\quad otherwise\end{array}\right. }$, $f_2(t)=0$, $\Lambda (t)=\sin (0.1t)$ and the disturbance signal is assumed as $\omega (t)=0.2\sin {0.2t}$.

Figure 7 describes the effectiveness of the proposed controller which shows that the stability of the given linearised system occur within 10 s. From the Fig. 8 it is revealed that within few seconds the fault estimation is quite accurately achieved by the proposed controller. Further, the error of actuator fault and its estimation is presented in Fig. 9, which shows that the fault estimation error based on fractional-order system is smaller than the integer-order system. Furthermore, Fig. 10 and its sub figures highlight that the accuracy of estimation of output with quantized output based on fractional-order system is better than the integer-order system. The simulation result discloses the potential and efficiency of the proposed observer based non-fragile fault-tolerant controller based on quantized measurement for delayed fractional-order linear systems in the presence external disturbances.

5 Conclusion

In this paper the problem of FD for the class of nonlinear and linear fractional-order systems with differentiable time-varying delays using quantized measurement is dealt. By using adaptive fault estimation algorithm, a non-fragile FD controller is designed to ensure the control error system is asymptotically stable with a prescribed $H_\infty$ performance attenuation level. By choosing proper Lyapunov–Krasovskii functional along with some properties of fractional-order calculus, a new set of sufficient conditions are derived in terms of linear matrix inequalities for the stabilization of the labelled problem. Finally, two examples provided to show the effectiveness of the prescribed controller.