Identification and control design for a class of non-minimum phase dead-time systems based on fractional-order Smith predictor and genetic algorithm technique

Abstract

The design of Smith predictor (SP) controllers has been largely investigated in the literature to solve fractional-order dead-time systems control problems; this is due to its robustness in presence of modeling uncertainties and measurement noises. In this paper, a new SP control strategy is proposed for a special class of non-minimum phase dead-time systems. This controller can be designed only by imposing a new fractional-order model and new robust controller in the modeling and synthesis stages. A fractional multi-low-order dead-time (FMLODT) model is accordingly proposed in the SP modeling stage, where an actual process behavior is well ensured by high model accuracy. The proposed fractional model parameters are identified by an adequate optimization tool based genetic algorithm. Furthermore, a robust fractional order controller based FMLODT model is synthesized, its structure is analytically determined through a three terms fractional-order reference (TTFOR) model. The proposed fractional controller parameters are tuned according to some guidelines available in the literature. Thus, two main contributions are proposed in this work: the first one consists of introducing a general framework for the SP modeling scheme. This is ensured by the proposed FMLODT model, which enhances significantly the modeling accuracy compared to the existing models in the literature. The second innovation consists of proposing a general framework for the controller design step in the SP scheme. This is guaranteed by the proposed TTFOR model, which improves significantly the trade-off between the two contradictory goals: performance and robustness. To highlight the proposed strategy of good performances, both the new fractional order model and the classical controller are applied on the minimum phase dead-time systems. The obtained simulation results illustrate the performance and improvement of the proposed model comparatively to preceding works.

1 Introduction

Identification and control of the delays systems have attracted several researchers in the last decades. Many control methods have been suggested so far to ensure a good closed-loop process performance. In practice, one can notice that in major approaches the desired performances are constrained by two basic stages: a modeling stage including identification, to obtain an adequate model describing the system behavior as precisely as possible and a controller synthesis stage to ensure a robust stability for the controlled plant.

To achieve this objective, fractional calculus [1,2,3] has been successfully used with satisfactory results to model and control processes with complicated dynamical behavior. Fractional-order system identification is among the application domain of fractional calculus [4,5,6]. In general, most of the existing modeling methods can be classified into time-domain and frequency-domain techniques from which several researchers have developed fractional-order models.

Among them, Poinot and Trigeassou [7] proposed a fractional-order model based time-domain approach using the state-space representation, they successfully designed the dynamical model of a heat transfer system. Cois et al. [8] modeled non-integer systems using the non-integer state-space representation, modal coefficients, differentiation order, eigenvalues and Marquardt algorithm. Lin et al. [9] proposed a fractional-order model, their parameters were identified by the least squares method using the frequency response identification approach, whereas Peng et al. [10] combined the harmony research with the least squares method to solve the frequency-domain identification problem of fractional order time delay systems.

A similar approach using an identification model defined by a generalized ARX structure was proposed by Djouambi et al. [11]. Valério and Costa [12] demonstrated the fractional transfer function approximation based on phase characteristics in the frequency domain. Amairi et al. [13] proposed a frequency-domain identification of fractional order systems, in which the estimated parameters (coefficients and differential orders) are expressed as intervals.

In the same way, other researchers proposed identification techniques by combining both time-domain and frequency domain responses. Rahmani and Farrokhi [14] used a neuro-fractional-order Hammerstein model with a systematic identification algorithm for identifying unknown nonlinear dynamic systems.

Through the detailed analysis of these studies, it could be observed that the time domain identification proposed by Poinot and Trigeassou [7] and Cois et al. [8] could approximate most system parameters including the fractional order, but the solution of the derivation and inverse matrix is difficult and requires heavy computation. In comparison to the time-domain method, the identification methods derived by Lin et al. [9] and Valério and Costa [12] require simple calculation, but the fractional order cannot be solved directly. The major drawback of these methods appears when the delay is important.

The control strategy based on SP principle [15,16,17] presents an alternative solution often used to solve this problem. It offers a good robustness margin against modeling uncertainties, sensor noise effects and nonlinear dynamic neglected in high frequencies. The interest of SP based technique is the possibility of canceling the time delay effect from the closed-loop system [18]. In comparison with conventional feedback control techniques, therefore, the analysis and design issues for dead-time systems can be facilitated using SP schemes. This fact has encouraged many researchers to investigate in this methodology for fractional-order control design.

Wang et al. [19] introduced SP systems while using deliberately mismatched model to enhance performance by means of a simple primary controller. They reduced the closed-loop (CL) system into one by involving second order dynamics. Recently, Djabri et al. [20] proposed a fractional-order controller synthesis method based on SP scheme, in which the modeling stage is performed by a fractional-order model. Both the fractional controller and model parameters are designed through solving two proposed constraint optimization problems by the particle swarm optimization (PSO) meta-heuristic algorithm. Safaei and Tavakoli [21] used the SP structure to design a fractional-order controller for time-delay integer-order systems based on time-domain specifications. In this paper, two original contributions are proposed in modeling and synthesis controller stages of SP configuration for a class of time-delay non-minimum phase systems. The first contribution consists of proposing the new FMLODT model where the system identification is performed in the frequency domain by the GA optimization technique. Firstly, the effective fitness function based on output-error is put forward in the frequency domain, and then the parameters identification is converted into parameters optimization using GA [22, 23]. The second contribution consists of proposing the new fractional controller structure which systematically designed through the adaptive control principle based on the TTFOR model. The tuning controller parameters are ensured by satisfying some criteria to enhance the controlled plant behavior.

It is worth to mention here that to the best of the authors’ knowledge, the free parts of existing plants’ models have never been proposed in SP schemes as a fractional-order model including the particular non-integer power $\gamma _m$. Indeed, the novelty lies in this last power, leading to a more general FMLODT model than the ones available in the literature. As a result, the proposed FMLODT model presents a new mathematical formulation, including a set of widely used mathematical models such as: first-order plus time delay (FOPTD) model (obtained when $\gamma _m=1$ and $\beta _m=1$), second-order plus time delay (SOPTD) model (obtained when $\gamma _m=2$ and $\beta _m=1$), fractional low-order dead-time FLODT model (obtained when $\gamma _m=1$ and $\beta _m \ne 1$)... etc.. In addition, the controller synthesis step based on TTFOR model is also a novelty based on the model reference adaptive control (MRAC) principal. Indeed, in comparison with the existing similar conventional model, the TTFOR model has never been proposed before in all previous works. It includes a set of widely reference models such as: reference model based on the Bode’s ideal transfer function (provided when $\xi =0$), reference model based on the standard second-order transfer function (provided when $m=1$)... etc.

The organization of this paper is as follows: in Sect. 2, basic definitions related to fractional-order systems and problem statement are introduced. In Sect. 3, the proposed design procedure for the controller based on SP scheme is detailed, while simulation results and discussions are presented in Sect. 4. Finally, conclusions are given in Sect. 5.

2 Fundamental definitions and tools

2.1 Fractional-order operators and systems

The major developments of fractional calculus theory happened more than a century ago. Recent (but already classical) books [24] offer a very nice documentation on the state of art of this problematic. It is worth to notice that researchers in the field of control and analysis of dynamical processes began more recently to consider fractional order operators and systems in their design and studies [25].

The physical phenomenon of di-electrical relaxation in certain liquids was discovered in the early 1951 by Davidson and Cole. They modeled it under the form of an equation with a pole of fractional order power (FPP):

$$\begin{aligned} X(s) = \frac{1}{\left( 1 + s \tau \right) ^{\alpha }} \end{aligned}$$

(1)

The slope of its Bode diagram was found between 0.550 and 0.666.

2.1.1 Definitions

The non-integer order fundamental operators, generalizations of the classical ones, are commonly symbolized by $_{t_{0}}D^{\nu }_{t}$ such that $t_{0}$ and t are the limits and $\nu (\nu \in \mathfrak {R})$ the order of operation.

Various definitions have proposed in literature [24, 26]. The frequently used definition of the fractional-order integro-differential operator is the Riemann–Liouville (RL) definition [22, 27]:

$$\begin{aligned} _{t_{0}}D^{\nu }_{t}h(t) = \frac{1}{\varGamma (n-\nu )}\frac{d^{n}}{dt^{n}}\int ^{t}_{t_{0}}(t-\zeta )^{n-1-\nu }h(\zeta )d(\zeta ) \end{aligned}$$

(2)

where $(t_{0},t)\in \mathbb {R}^{2}$ with $t_{0}<t$, the fractional order $\nu$ is such that $n-1< \nu < n$ with $n\in \aleph ^{*}$ and $\varGamma (\cdot )$ is the Gamma function.

The Laplace transform of the Riemann–Liouville fractional operator (2) under null initial conditions is

$$\begin{aligned} L\left\{ _{t_{0}}D^{\pm \nu }_{t}h(t);s\right\} = s^{\pm \nu } H(s) \end{aligned}$$

(3)

We can express a SISO system with fractional orders using the transfer function,

$$\begin{aligned} H(s)=\frac{b_{m}s^{\eta _{m}}+ b_{m-1}s^{\eta _{m-1}}+ \cdots +b_{0}s^{\eta _{0}}}{a_{n}s^{\lambda _{n}}+ a_{n-1}s^{\lambda _{n-1}}+ \cdots + a_{0}s^{\lambda _{0}}} \end{aligned}$$

(4)

with $\lambda _{i}, \eta _{j} \in \mathfrak {R}$ are real numbers verifying,

$$\begin{aligned} \left\{ \begin{array}{c} 0\le \lambda _{0}<\lambda _{1}< \cdots<\lambda _{n}\\ 0\le \eta _{0}<\eta _{1}< \cdots <\eta _{m}\end{array}\right. \end{aligned}$$

(5)

and s is Laplace operator.

2.1.2 Approximation methods

In general, the transfer function in the implementation stage of fractional model and fractional controller needs to be approximated into rational one. To reach this goal, many approximation methods have been proposed in literature such as the singularity function method [28], Oustaloup’s method [25] and optimization based techniques [29].

In this paper we use a Matlab Simulink Toolbox for fractional order controllers developed by Valério et al. [30].

2.2 Genetic algorithms optimization technique

Genetic algorithms are among the most popular optimization techniques [22]. A computation system is constructed around a representative population of candidate solutions that converge to the best solution for the optimization problem. The GA principle can be summarized as follows.

Once the genetic representation and the fitness function are defined, the GA proceeds to initialize a population of solutions randomly. Then a process of repetitive application of mutation, crossover and selection operators allows the improvement of obtained results.

In general, a randomly generated population of individuals is used to start the computation. In each generation, the fitness of every individual in the population is evaluated and several individuals are selected arbitrarily from the current population and modified to form a new population. The next iteration of the algorithm will use this new population. The process ends when either the maximum number of generations N is produced, or a satisfactory fitness level has been reached. Using a fitness-based scheme, individual solutions are selected (evaluated by a fitness function).

Furthermore, the procedure of GA follows four stages:

• 1. Initial population is chosen,

• 2. The fitness of each individual in the population is evaluated,

• 3. Repeat

  • (a) Select best-ranking individuals for the reproduction,

  • (b) Breed new generation through crossover and mutation and give birth to offspring,

  • (c) Evaluate the fitness of the offspring individuals,

  • (d) Replace the worst ranked part of population with offspring,

• 4. Termination (maximum number of generations N is produced, or a satisfactory fitness level has been reached).

3 Proposed design procedure for SP scheme

In this section, the proposed method will be applied on delayed processes, especially a class of non-minimal phase process plus dead-time. This class presents a real challenge for the fractional control problems. This is due to delays between the inputs and outputs of the system to be controlled. They are very common in industrial processes, engineering systems, economical, and biological systems mainly caused by transportation and measurement lags, analysis times, computation and communication lags,... etc.

Besides, the modeling and control of non-minimal phase systems (due to unstable zero) presents another major challenge because of their faulty behavior at the beginning of the response, often providing a relatively slow response.

3.1 Parameters identification of the proposed FMLODT model

In the modeling stage, the desired FMLODT model should describe as closely as possible the actual process behavior. This can be achieved through the following stages. First, the frequency response data FRD should be properly measured through the real process. Second, the mean square error (MSE) criterion is formulated from the discrepancy value generated at each frequency point between both FRD of actual process and proposed FMLODT model.

Finally, the evolutionary optimization technique based on GA is used to minimize the MSE criterion yielding therefore the optimal FMLODT model parameters. Figure 1 presents the standard configuration used in the parameters’ identification of the proposed FMLODT model, this is by using the output error method.

Fig. 1

Standard output error method configuration for the parameters’ identification of the proposed FMLODT model

3.1.1 Parameter identification of the proposed FMLODT model

In general, the block diagram of the conventional SP control is shown in Fig. 2.

Fig. 2

Closed loop system based on Smith predictor scheme

Fig. 3

Closed loop system using the modified Smith predictor scheme

Fig. 4

Design of adequate controller structure using MRAC-TTFOR principle

Where $G_r (s)$ and $G_m (s)=G_{m_0} (s)\; e^{-\theta _m s}$ are strictly stable proper transfer functions that characterize the actual process and the proposed FMLODT model respectively. $G_{m_0} (s)$ is the dead-time free part of the proposed model and $G_c (s)$ is the transfer function of the desired controller. $r_{ref}$, $d_u$ and u correspond to the set-point reference, disturbance input and manipulated variable respectively. $y_r$, $y_m$ and $\xi _m$ are the process output, model output and modeling error where $\xi _m = y_r-y_m$. The transfer functions of the proposed FMLODT model is expressed by:

$$\begin{aligned} G_m(s) = \frac{K_m e^{-\theta _m s}}{(1+\alpha _m s^{\beta _m})^{\gamma _m}} \end{aligned}$$

(6)

where $K_m$, $\alpha _m$ and $\theta _m$ are the static gain, time constant and dead-time model respectively. Moreover, $\gamma _m$ ($\gamma _m>1$) is the order of $G_m (s)$ and $\beta _m$ ($0<\beta _m<1)$) is the fractional order carried out the Laplace operators. It should be noted that the dead-time free part of $G_m (s)$ can be factored as:

$$\begin{aligned} G_{m_0}(s)=G_{m_{01}}(s) G_{m_{02}}(s) \end{aligned}$$

(7)

where $G_{m_{01}} (s)$ is a stable fractional-order transfer function that is inverted by the robust fractional controller. It is expressed by,

$$\begin{aligned} G_{m_{01}}(s) = \frac{K_m}{1+\alpha _m s^{\beta _m}} \end{aligned}$$

(8)

Moreover, $G_{m_{02}} (s)$ is the fractional portion that the robust controller does not attempt to invert. This portion contains any unstable poles or zero and must have a steady-state gain equal to one. It is expressed as follow:

$$\begin{aligned} G_{m_{02}}(s) = \frac{1}{(1+\alpha _m s^{\beta _m})^{\gamma _m - 1}} \end{aligned}$$

(9)

The proposed factorization for $G_{m_{0}} (s)$ facilitates the design procedure of $G_c (s)$ where the controller synthesis stage is performed using the modified SP scheme of Fig. 3.

The design problem of the proposed FMLODT model can be formulated by a constrained optimization problem given by

$$\begin{aligned} \underbrace{\min _{x_m}\left\{ J_m(x_m,\omega _i)\right\} {=} \min _{x_m}\left\{ \frac{1}{n} \sum _{i=1}^n \left| G_n (\omega _i)-G_m (x_m, \omega _i) \right| ^2 \right\} }_{subject \ to \ \ \ x_{m_{min}} \le x_m \le x_{m_{max}}} \end{aligned}$$

(10)

where the suitable FMLODT model depends on the optimization set of the parameters constituting the vector $x_m$ given by:

$$\begin{aligned} x_m=[K_m, \alpha _m, \beta _m, \gamma _m, \theta _m]^T. \end{aligned}$$

(11)

3.2 Design of the robust fractional-order controller

In the modified SP scheme, several controller structures have been proposed to simultaneously ensure a good trade-off between the tracking dynamic of the set-point reference and a good dynamic attenuation of the system load disturbances. The controller design, when set with adequate structure for a class of non-minimum phase dead-time systems presents a real challenge in controller synthesis stage. In this paper, the TTFOR model based adaptive control principal is applied to determine systematically the desired structure of the robust fractional controller.

3.2.1 Controller synthesis stage based on TTFOR model

When the proposed FMLODT model matches closely to the actual process (i.e. $\xi _m=0$), the outer loop is approximately open. The controller design is therefore performed through the time-delay free part $G_{m_{01}} (s)$ regardless of the troublesome time-delay (see Fig. 4).

In general, the best performance tracking dynamic of the set-point reference can be guaranteed when a conventional model reference adaptive control (MRAC) principal is applied on the inner loop of the modified SP scheme. Usually, a standard integer second-order reference (ISOR) model is used in the tuning of the controller parameters. The corresponding closed-loop transfer function is commonly expressed by:

$$\begin{aligned} G_{{ CL}0}^{{ ref}} (s)= \frac{\omega ^2_n}{s^\frac{2}{m} + 2\xi \omega _n s^\frac{1}{m} + \omega ^2_n} \end{aligned}$$

(12)

where $\omega _n$ and $\xi$ are respectively, damping ratio and natural frequency.

In this paper, the following closed-loop transfer function of the TTFOR model is used in the MRAC principal, enhancing therefore the trade-off between performance and robustness of the modified SP:

$$\begin{aligned} G_{{ CL}}^{{ ref}} (s)= \frac{\omega ^2_n}{s^\frac{2}{m} + 2\xi \omega _n s^\frac{1}{m} + \omega ^2_n} \end{aligned}$$

(13)

where $m \in R^+ (m>1)$, and $\omega _n \in R^+$ is used. Other reasons for substituting the standard ISOR model by the TTFOR one is to ensure a wider stability region system to satisfy a higher number of both time-domain and frequency-domain specifications. Furthermore, the suitable controller structure is systematically derived when the following equality condition is satisfied:

$$\begin{aligned} G_{{ OL}}^{{ ref}} (s)= G_{01}(s) G_{c}(s) \end{aligned}$$

(14)

where $G_{{ OL}}^{{ ref}} (s)$ is the open-loop transfer function of $G_{{ CL}}^{{ ref}} (s)$ given by:

$$\begin{aligned} G_{{ OL}}^{{ ref}} (s)= \frac{\omega ^2_n}{s^\frac{1}{m} \left( s^\frac{1}{m} + 2\xi \omega _n \right) }. \end{aligned}$$

(15)

Based on Eqs. (8), (14) and (15), the desired controller structure can be derived as follow:

$$\begin{aligned} G_{c_{{ Frac}}}(s) = \left( \frac{1}{2\xi K_m}\right) \left( \frac{\omega _n}{s^\frac{1}{m}}\right) \left( \frac{1+\alpha _m s^{\beta _m}}{1+\frac{1}{2\xi \omega _n}s^\frac{1}{m}}\right) \end{aligned}$$

(16)

where the stability region is ensured when $\xi$ is chosen by:

$$\begin{aligned} \cos \left( \frac{\pi }{2 m} \right)< \xi < -\cos \left( \frac{\pi }{m} \right) \end{aligned}$$

(17)

Figure 5 shows the stability region limited by the upper bound $\xi _{max}$ and the lower bound $\xi _{min}$ for different values of m

Fig. 5

Stability region ensured by the TTFOR model

Moreover, the obtained dynamic tracking of the set-point reference is accordingly characterized by the settling time $t_{S_{5\%}}$, defined according to Ref. [31] by:

$$\begin{aligned} t_{S_{5\%}} = \left( \frac{2 \left| \xi \right| \sin \left( \frac{\pi }{m}\right) \varGamma \left( \frac{1+m}{m}\right) }{p \pi \omega _n} \right) ^{\frac{1+m}{m}} \end{aligned}$$

(18)

where $\varGamma (\cdot )$ is the gamma function that is available in Matlab environment. p is a positive friction chosen commonly equal to 0.02.

Figure 6 shows the 3D view of various $t_{S_{5\%}}$ for $\cos \left( \frac{\pi }{2 m} \right)< \xi < -\cos \left( \frac{\pi }{m} \right)$ and $1<\xi <30$ at fixed value $m=2$.

Fig. 6

3D curves of $t_{S_{5\%}}=f(\xi ,\omega _n)$ for the constant value $m=2$

Now, for the mismatched FMLODT model case, (i.e. $\xi _m \ne 0$), the robustness analysis of the closed-loop system is established using the standard configuration, presented by Fig. 7.

Fig. 7

Standard configuration based mismatched FMLODT model used for robustness analysis

According to Fig. 7, the transfer function from the load disturbance input $d_u$ to the process output $y_r$ is given by the following sensitivity plant:

$$\begin{aligned} T_{d_u \rightarrow y_r} = \frac{G_r(s)}{1 + Q_c(s) G_r(s)} \end{aligned}$$

(19)

where $Q_c$ is the parameterized controller, given by the following transfer function:

$$\begin{aligned} Q_c(s) = \frac{G_c}{1 + G_r G_{m_{01}}(1 - G_{m_{02}} e^{-\theta _m s})}. \end{aligned}$$

(20)

According to Eq. (19), a good robustness against a load disturbance input is provided when the peak value of $\left| T_{d_u \rightarrow y_r}\right|$, called also $\left\| T_{d_u \rightarrow y_r}(\omega )\right\| _\infty$,is well attenuated within the frequency range $\omega \in [\omega _{min}, \omega _{max}]$. This goal can be reached by satisfying the following robustness condition:

$$\begin{aligned} \left\| W_{{ GS}} T_{d_u \rightarrow y_r}\right\| \le 1 \end{aligned}$$

(21)

where $W_{{ GS}}$ is a performance specification chosen previously by the user. Its transfer function is usually chosen as follow:

$$\begin{aligned} W_{{ GS}} = \frac{\frac{s}{M_{{ GS}}}+\omega _B}{s+\omega _B \varepsilon _{{ GS}}} \end{aligned}$$

(22)

where $M_{{ GS}}$ is the desired peak value chosen to limit the overshoot of $\left| T_{d_u \rightarrow y_r}\right|$ (i.e., $M_{{ GS}}=\left\| T_{d_u \rightarrow y_r}(\omega )\right\| _\infty$). This last is usually chosen less than $1.5 (3\,\mathrm{dB})$ to ensure a good robustness margin. $\omega _B$ is the desired bandwidth chosen for $\left| T_{d_u \rightarrow y_r}\right|$. Generally, a high value of $\omega _B$ providing often a fast rejection dynamic of the load disturbance input. $\varepsilon _{{ GS}}$ is a positive value chosen often close to zero (i.e., $\varepsilon _{{ GS}} \approx 0$). Figure 8 shows the inverse function of $W_{{ GS}}$ limiting some sensitivity plants.

Fig. 8

Perfect template limiting the plant sensitivity $\left| T_{d_u \rightarrow y_r}\right|$

In this paper, the TTFOR model parameters will be chosen from a 3D view of various $\left\| T_{d_u \rightarrow y_r}(\omega )\right\| _\infty$ plotted within the frequency range $\omega \in [\omega _{min}, \omega _{max}]$ where $\cos (\pi /2m)< \xi < -\cos (\pi /m)$ and $1<\xi <30$.

It should be noted that the robustness margin of the sensitivity plant can be ensured by a high margin. This can considerably deteriorate, in contrast, the closed-loop performance. The last opposite is also true.

4 Simulation results and discussion

In order to highlight the good performance of the proposed modified SP scheme based two stages: modeling based FMLODT model and controller synthesis based MRAC-TTFOR strategy, the performances given through modeling and controlling a class of non-minimum phase process with dead-time are discussed. This process was previously studied by Wang et al. [19] where its actual behavior was presented by the following typical plant:

$$\begin{aligned} Gr(s) = \frac{(1 - s)e^{-2 s}}{(1+ s)^{5}}. \end{aligned}$$

(23)

Accordingly, their corresponding FRD are extracted within the frequency range $\omega \in [10^{-5}, 10^{+5}]$ radians per seconds using 1000 logarithmically equally spaced points. Figure 9 shows the obtained FRD, presented in Nyquist plot.

Fig. 9

The FRD describing the actual process behavior presented in Nyquist plot

Fig. 10

Best fitness plots of the MSE criterion

Table 1 The obtained model performances provided by the proposed FMLODT model and Wang’s model

4.1 Modeling stage based on GA optimization

In the optimization mechanism based on GA, the two used sets of lower and upper bounds are:

$$\begin{aligned} \left[ \begin{array}{l} 0.1000\\ 0.1000\\ 0.0001\\ 0.5000 \\ 1.0000 \end{array} \right] \le \left[ \begin{array}{l} K_m\\ \alpha _m\\ \beta _m\\ \gamma _m \\ \theta _m \end{array} \right] \le \left[ \begin{array}{l} 3.0000\\ 3.0000\\ 0.9999\\ 10.500 \\ 5.0000 \end{array} \right] . \end{aligned}$$

(24)

Due to the probabilistic behavior of the GA, the optimization process is run several times using the following setting parameters:

• Generation number = 27

• ${ TolFun} = 1 \times 10^{-4}$

• Population size = 27

• ${ PlotFcns@gaplotbestfun}$.

Figure 10 shows the best height fitness curves ensuring the best minimization of the MSE criterion.

It should be noted that the actual process behavior was previously described by Wang’s model, expressed by:

$$\begin{aligned} G_{0_{{ Wang}}}(s) = \frac{e^{-5.07 s}}{(1.46 s + 0.999)^{2}}. \end{aligned}$$

(25)

Table 1 summarizes the obtained optimal FMLODT model parameters and determines therefore, the best eight models: the better results are mentioned in bold.

Table 1 presents also the obtained model accuracy $\varepsilon _{{{ MSE}}_i}$ corresponding to $G_{m_i}(s)$. It also gives the relative ratio $\varepsilon _{{{ MSE}}_\%}$ presenting the improvement rate in comparison with Wang’s model. This ratio can be determined by:

$$\begin{aligned} \varepsilon _{{{ MSE}}_\%} = 100 \times \left( \frac{\varepsilon _{{{ MSE}}_W}-\varepsilon _{{{ MSE}}_i}}{\varepsilon _{{{ MSE}}_W}} \right) _{i=1,2, \ldots , 8}. \end{aligned}$$

(26)

Among the obtained eight FMLODT models, the controller synthesis stage is carried out using best one ensuring a better model accuracy. Its transfer function is given as below:

$$\begin{aligned} G_m(s) = \frac{1.0013 e^{-4.2325 s}}{(1+ 1.5156 s^{1.0261})^{2.5267}}. \end{aligned}$$

(27)

Figure 11 compares the Nyquist plots of actual process and the corresponding FMLODT model.

Fig. 11

Nyquist plots of actual process and proposed FMLODT model

According to Eq. (27), the dead-time free part of the proposed FMLODT model is factored in two parts. It yields:

$$\begin{aligned} \left\{ \begin{array}{l} G_{m_{01}}(s) = \frac{1.0013}{1+ 1.5156 s^{1.0261}} \\ G_{m_{02}}(s) = \frac{1}{(1+ 1.5156 s^{1.0261})^{1.5267}} \end{array} \right. \end{aligned}$$

(28)

In the implementation stage of the proposed FMLODT model, the Simulink block of $G_{m_{02}}(s)$ is unfortunately nonexistent in Simulink library browser, therefore a very heavy computing task is required. To overcome this drawback, the corresponding integer model, called also $\hat{G}_{m_{02}}(s)$, should be predetermined. Their FRD should closely match those provided by $G_{m_{02}}(s)$.

This can be done by the two following steps. The FRD of $G_{m_{02}}(s)$ are firstly extracted in the entire frequency range $\omega \in [10^{-5}, 10^{+5}]$ radians per seconds.

A state-space representation of $\hat{G}_{m_{02}}(s)$, with a state-dimension $N_{\hat{G}}$ is then computed using the Matlab function Fitfrd. Accordingly, by choosing $N_{\hat{G}}=5$, this ensures a best fit, providing therefore the following stable integer transfer function:

$$\begin{aligned} \hat{G}_{m_{02}}(s) = \frac{-9.529\; 10^{-5}\; s^5 + 0.04145\; s^4 + 1.841\; s^3 + 7.462\; s^2 + 5.001\; s + 0.3193}{s^5+ 10.52\; s^4 + 23.66\; s^3+ 18.81\; s^2 + 5.663\; s + 0.3192}. \end{aligned}$$

(29)

This may be confirmed by presenting both FRD, extracted from $\hat{G}_{m_{02}}(s)$ and $G_{m_{02}}(s)$, in Nyquist plot, giving therefore Fig. 12.

Fig. 12

Nyquist plots of both FRD extracted from $G_{m_{02}}(s)$ and $\hat{G}_{m_{02}}(s)$

All fractional transfer functions, used in this work, are been established using the extra Simulink blocks, which are available in the free website [30].

Figure 13 shows the Simulink block presenting the free dead-time part $G_{m_{02}}(s)$.

Fig. 13

Simulink block presenting he free dead-time part $G_{m_{01}}(s)$

4.2 Controller synthesis stage based on MRAC-TTFOR principle

According to Ref. [19], the Wang’s controller was synthesized through the integer model given by Eq. (25) where the MRAC based ISOR principal was used. The corresponding transfer function is given by:

$$\begin{aligned} G_{C_{{ Wang}}}(s) = \frac{5.85\, s + 4}{s^2 + 2.83\, s}. \end{aligned}$$

(30)

In the next section, the choice of TTFOR model parameters ensuring a good trade-off is performed after several trails. Accordingly, a good closed-loop performance may be reached by optimal TTFOR model parameters using both Figs. 5 and 6.

On the other hand, a good robustness, in the presence of load disturbance input, may be reached using Fig. 14.

Fig. 14

3D curves of $\left\| T_{d_u \rightarrow y_r}(\omega )\right\| _\infty$ satisfying a good dynamic attenuation of the load disturbance input

This last presents the 3D curves of $\left\| T_{d_u \rightarrow y_r}(\omega )\right\| _\infty$ in the frequency range $\omega \in [\omega _{{ min}}, \omega _{{ max}}]$, where m is kept at a constant value $m=2$, $\xi$ and $\omega _n$ varied within $]-\cos (\frac{\pi }{2 m}), -\cos (\frac{\pi }{m}) [$ and ]1, 30[ respectively. As a result, the common choice of TTFOR model parameters leads to a desired trade-off.

Table 2 summarizes the obtained optimal controller parameters, this table shows the best four robust fractional-order controllers. The best trade-off in term of better settling time, the largest robustness margin is mentioned in bold. Table 2 summarizes also the relative improvement ratio $\varepsilon _{t_{{S5}_\%}}$ ensured by the proposed modified SP scheme compared to the one provided by modified SP scheme based Wang method. It can be determined by:

$$\begin{aligned} \varepsilon _{t_{{S5}_\%}} = 100 \times \left( \frac{\varepsilon _{t_{{S5\%}_W}}-\varepsilon _{t_{{S5\%}_i}}}{\varepsilon _{t_{{S5\%}_W}}}\right) _{i = 1, 2, \ldots 8} \end{aligned}$$

(31)

The robustness margin $\varDelta \varphi$ is the distance in modulus between $\left\| T_{d_u \rightarrow y_r}(\omega )\right\| _{\omega =\omega _{min}}$ and the abscissa $0\,\mathrm{dB}$.

Table 2 Performance assessments in term of trade-off robustness ensured by the proposed robust fractional-order controller and Wang’s controller

Figure 15 presents a comparison of $\left| T_{d_u \rightarrow y_r}(\omega )\right|$ curves, provided by Wang’s controller and the four robust fractional ones.

Fig. 15

Robustness analysis based sensitivity plant, provided by Wang’s controller and the four proposed robust fractional-order controllers

In robust control theory, it can be mentioned that a better robustness margin is given when $\left| T_{d_u \rightarrow y_r}(\omega )\right|$ is small as much as possible at low frequencies. Consequently, all proposed controllers, especially the 4th proposed one, allow ensuring the biggest robustness margin, compared to the one given by the Wang’s controller. This can be explained, in time domain, by a quick time needed to reject the disturbance input. To confirm the above results in time domain, the closed-loop system based Simulink blocks, given by Fig. 16, is used.

Fig. 16

Closed-loop configuration used for time-domain analysis

According to Fig. 16, the closed-loop systems based on Wang’s controller and our proposed controller, they are excited using two exogenous inputs. The first input presents the set-point reference that is assumed as a unit-step function. The second input is the load disturbance that is carried-out on the input of the process. It is assumed as a unit-step function with a gain equals to $-\,0.25$ (i.e., 25% overshoot), with start-time $t =40$ s.

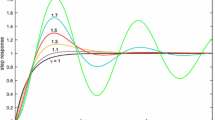
Figure 17 shows the obtained time responses given by the proposed four controllers and Wang’s controller while the obtained dynamic tracking of the set-point reference input is enlarged in Fig. 18 and the obtained dynamic attenuation of the load disturbance input is enlarged in Fig. 19.

Fig. 17

Process outputs provided by Wang’s controller and the proposed four controllers

Fig. 18

Tracking dynamic of the set-point reference, input ensured by Wang’s controller and the proposed four controllers

According to Fig. 17, the obtained process outputs by the proposed four controllers are significantly better than the one provided by Wang’s controller.This is explained by the better dynamic tracking obtained, it is characterized by a faster output response and a better settling time. This dynamic is enlarged in the time range of $0\le t \le 11.76$ s (see Fig. 18). Also, it is explained by the good dynamic attenuation obtained when using the load disturbances, it is also characterized by the quick time to cancel the load disturbance effect. This dynamic is enlarged in the time range of $46\le t\le 165$ s (see Fig. 19).

Fig. 19

Rejection dynamic of the load disturbance, input ensured by Wang’s controller and the proposed four controllers

As a result, according to both obtained frequency- and time-responses, it is easy to confirm that the proposed modified SP scheme attains our main goal, which is the enhancement of the trade-off robustness of the conventional SP scheme based on either integer model or integer controller.

5 Conclusion

In this paper, a new design procedure of the modified SP scheme based fractional model and fractional controller for a class of non-minimum phase delay systems is proposed. The FMLODT model and the appropriate fractional order controller based on the TTFOR model are proposed to replace the conventional models and controllers, they are introduced in the modeling and synthesis steps of the new design procedure. The model parameters are identified using the GA optimization. Whereas, the controller parameters are graphically determined using two 3-Dimensional curves. The latter leads to achieving good trade-off robustness between tracking dynamic of set-point input and the dynamic attenuation of the load disturbance input.

The simulation results show that there is noticeable improvement of the modified SP scheme acquired. Indeed, the proposed model enhances significantly the plant modeling accuracy, which allows a better control design in performance and robustness and ensures good analysis and diagnosis of the actual system during its operating state. However, it is also clear that further improvements in the proposed design procedure can be obtained, particularly in its synthesis controller stage, this will require systematic tuning to well optimize the TTFOR model parameters using an optimization tool.