Keywords

1 Introduction

PID controllers family is still used in most process industries, though many advanced control strategies emerged. The reason behind this is due to the PID’s easy tuning, industry convenient design and structure, fewer tunable controller parameters, prominently adopted history, etc. [1, 2]. While using them in the noisy and disturbance scenarios, they fail to produce effective control signals due to the aggregation of error in the control loop. In those conditions, the plant response will be more oscillatory and lead to the control valve stiction issues and even may lead to damage to the actuator as well [3]. For amending these problems, many variants like fractional-order PI, set-point weighted PI, fuzzy-PI, predictive PI (PPI), and nonlinear PI have been proposed by different researchers [4, 5].

Further developments for handling the dead-time processes were also carried out by combining the PID controllers family with the dead-time compensators (DTC-PI), model predictive controller-PI, fuzzy adaptive set-point weighted PI, fractional-order PPI (FOPPI), and internal model controller-PI [6, 7]. Even after these developments, a stand-alone controller to remove the noise and disturbance from the control and process signal is impossible because of the standard way of designing and developing the new controllers. Thus, combining external filters with the controllers in the closed-loop process is one of the fast, effective ways to deal with this issue.

In the related development, Hassan et al. successfully designed and implemented a stand-alone filtered PPI controller to handle the stochastic noise and external disturbance in the processes characterized by long dead time [8]. But, they faced sluggish response and destabilization of the closed-loop control system in the higher-order processes. To reduce the output oscillations (offset) and the peak overshoot, the introduction noise filter and set-point filter in the process feedback loop and after set-point signal give satisfactory results in the processes characterized by stochastic noise and external disturbances [9].

Different types of filters are available to remove and reduce the stochastic noise, external disturbance, and peak overshoot, but choosing them for the implementation depends on the end process. Initial research on set-point filtering is carried out by Vijayan and Panda for the two tank-level process [10]. Their initial design used more complex approaches to calculate the filter time constant from the process overshoot. To make the filters more robust and effective against the noise, the researchers introduced the process dynamics parameters like process gain in their design. Such improvement is proposed by Padhan et al. for the dead-time processes where the phase lag causes a more sluggish response [11]. While using the system dynamics in their design, they approximated them during the implementation in the actual process. A set-point filter designed mainly for the fractional control system is proposed by the researchers in [12]. Their successful design structure is limited to fractional-order systems alone, caused them not adaptable for regular processes. However, the researchers themselves agreed on the difficulty of their proposed approach in the industrial-scale implementation. In all the above techniques, calculation of the filter time constant used more assumption parameters which led to the frequent tuning of the filter, and its realization is more complex. Also, the effectiveness of minimizing the peak overshoot and reducing the noise is very minimal while comparing with the actual process.

Application of the fractional-order filters along with the Smith predictor is carried out by the researchers in [7]. Due to the uncertainties in the reference model, obtaining effective control is much reduced in this design. In contradiction with all the above methods, researchers in [1, 13,14,15] used the combination of conventional first- and second-order low pass filters with the associated controller in their design. Their results indicated the possibility of obtaining the effective noise and overshoot removed original process signal. Thus, it is not essentially higher-order filters needed to achieve good performance with the incorporated controller in the closed-loop processes. Hence, in this paper, the conventional first-order filter structure is utilized with a new method of calculating the filter time constant.

The remaining sections of the paper are organized as follows: A comprehensive discussion of the PI controllers family evolution, their structural design, and the set-point and noise filters strategies are presented in Sect. 2. Simulation results of the real-time processes transfer functions are given in Sect. 3 with detailed numerical and performance comparisons. Simulation outcomes, conclusions, and future directions of the current work are given in Sect. 4.

2 Methodology

In the initial part of the section, the selection of dead-time compensating controllers from the PI controller family is explained, followed by the designing and developing noise and set-point filters.

2.1 Controller Selection

The classical PI control signal U(s) in a closed-loop system from reference R(s) to the output Y(s) can be given as:

$$\begin{aligned} U(s)= K_\text {p}\bigg (1+\frac{1}{T_{i}s}\bigg )E(s), \quad E(s)=R(s)-Y(s). \end{aligned}$$
(1)

Introduction of the fractional-order integrator (\(\lambda \)) in the above control signal yields to the control action of the FOPI controller, which provides additional frequency-based controlling options. Thus, the FOPI control signal equation can be achieved as,

$$\begin{aligned} U(s)=K_\text {p}\bigg (1+\frac{1}{T_{i}s^\lambda }\bigg )E(s), \quad 0<\lambda <1. \end{aligned}$$
(2)

Smith predictor design is the widely acclaimed dead-time compensator with industry-accepted and straightforward structure with no additional tuning requirements [16, 17]. To overcome the time delay effects in the processes, hybridizing of dead-time compensators (DTC’s) with the conventional controller’s structure is essential [18]. Such a combination of the Smith predictor and PI controller yields the PPI controller. The control action of the PPI control signal is given as,

$$\begin{aligned} U(s)=K_\text {p} \bigg (1+\frac{1}{T_{i}s}\bigg )E(s)-\frac{1}{T_{i}s}(1-\text {e}^{-sL_\text {p}})U(s). \end{aligned}$$
(3)

For achieving better frequency-domain controls, robust performance against the dead time, peak overshoot, and external disturbance, designing of FOPPI controller from PPI by the fractional-order integrator is adopted. The FOPPI control signal is given as,

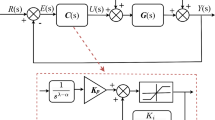
$$\begin{aligned} U(s)=K_\text {p} \bigg (1+\frac{1}{T_{i}s^\lambda }\bigg )E(s)-\frac{1}{T_{i}s^\lambda }(1-\text {e}^{-sL_\text {p}})U(s), \quad 0<\lambda <1. \end{aligned}$$
(4)

The closed-loop block diagram of the dead-time process plant with the FOPPI controller in (4) is shown in Fig. 1. The selection of the FOPPI controller is based on our earlier work reported in [19].

Fig. 1
figure 1

Closed-loop block diagram of the dead-time process plant with the FOPPI controller and external filters

Full size image

2.2 Filtering

Processes facing the undesired stochastic noises will always produce an oscillatory response, which is due to the higher error present in the processed signal fed to the controller [20]. This, in turn, affects the final control elements of the control valve and causes the closed loop to become unstable, which even further escalated to the worst catastrophe due to the process dead time [21]. These issues can be settled down by placing the filters in the appropriate places on the closed-loop process. Thus, placement of set-point and noise filters with time constants \(\tau _{\text {fs}}\) and \(\tau _{\text {fn}}\) in the closed-loop is shown in Fig. 1. The process input signal R(s) is sent to the controller only after passing through the set-point filter \(F_{\text {s}}\), which performs the function of isolating the variations in the load disturbances from the actual input signal R(s). This reduces the peak overshoot oscillations and high-frequency noise changes, which ultimately yields faster settling and rise time.

On the other hand, the noise filter performs the function of nullifying the external disturbance and noise signal from the process feedback signal Y(s) using the roll-off. This roll-off technique is proved to be an effective noise reduction method while operating with the PI and PID controllers [22]. Combining both filters will result in a more significant improvement error signal fed to the controller \(G_\text {c}(s)\), which produces the noise-free control signal U(s) for effectively controlling the process.

The literature works show that adequate performance of the process can also be achieved with lower-order filters. Therefore, the classical first-order filter is combined with the FOPPI controller for the simulation analysis in this paper. Here, the structure of the filter remains unchanged, but the method of finding the filter time constant (\(\tau _\text {f}\)) is changed by utilizing the system dynamics of the process under consideration. The transfer function of the filter is given as,

$$\begin{aligned} F(s)=\frac{1}{1+\tau _\text {f}{s}^\alpha }, \end{aligned}$$
(5)

where \(\tau _\text {f}\) is filter time constant and \(\alpha \) is the fractional integrator.

As mentioned earlier, the proposed method for calculating the \(\tau _\text {f}\) includes both process gain (K) and the process model dead time (\(L_\text {p}\)). Thus, the filter time constant can be calculated as: \(\tau _\text {f}=\frac{K}{L_\text {p}}\). Since the external disturbances and noises arise from the environment where the controller is interfaced with the real-time process, this implementation idea can remove the noise with maximum efficiency since the filter possesses all the system dynamics. For demonstrating the capability of the proposed method, a comparison study is made with the integer-order filter structure used in [19]. During the simulation, constant values were used for both set-point and noise filters and the same fractional integrator value from the FOPPI controller design.

3 Results and Discussion

In this section, a detailed analysis of the real-time processes simulation is discussed with the different filters incorporated over the FOPPI controller.

3.1 Process Model Selection

In this article, the first-order plus dead-time (FOPDT) process model of the process plant as reported in [23] and the real-time second-order plus dead-time (SOPDT) process model reported in [10] are considered for the analysis. The transfer functions of the systems are given as follows:

Fig. 2
figure 2

White noise signal used for the simulation

Full size image
$$\begin{aligned} G_{\text {p}1}(s)=\frac{K}{1+Ts}\text {e}^{-sL_\text {p}}=\frac{0.866}{1+1.365s}\text {e}^{-s}, \end{aligned}$$
(6)
$$\begin{aligned} G_{\text {p}2}(s)=\frac{K}{1+2T\zeta +T^2s^2}\text {e}^{-sL_\text {p}}=\frac{2}{1+15s+50s^2}\text {e}^{-5s}. \end{aligned}$$
(7)

During the simulation analysis, a white noise signal with a magnitude of 0.01 is injected in the process feedback loop to mimic the real-time scenario of the industrial processes. The profile of the white noise signal used is shown in Fig. 2. For all the considered process plants, a 30% disturbance is injected at 500 s of the control signal to analyze the disturbance rejection of the FOPPI controller. Since the FOPPI controller is designed empirically based on the FOPDT system, the first-order process controller parameters are obtained directly (refer to [19]). However, for the second-order process, the controller parameters are obtained using the MATLAB-SISO toolbox.

Thus, the optimized controller parameters for the FOPDT model are \(K_\text {p}=1.15\) and \(K_\text {i}=0.84\). Further, the parameters of SOPDT are \(K_\text {p}=0.789\) and \(K_\text {i}=0.101\). For both the plants, the fractional integrator is \(\lambda =0.98\). For implementing the fractional integrator, the Oustaloup approximation has been used as reported in [19]. For all fractional filters, the \(\alpha \) value is also kept the same as 0.98.

3.2 FOPDT Process Model

In this section, the industrial process model shown in (6) is used for the performance evaluation of the filters and the FOPPI controller. The comparative analysis is carried out in terms of rise time (\(t_\text {r}\)), settling time (\(t_\text {s}\)), and peak overshoot (%OS) that are given in Table 1.

Table 1 Numerical analysis of FOPDT model with various filters in the presence of external noise
Full size table

The performance analysis of the integer-order and fractional-order set-point filters is shown in Fig. 3, and its detailed numerical analysis is given in Table 1. From the results shown in Table 1, the proposed fractional set-point filter initially lagged in rising time and settling time (\(t_{\text {s}1}\)) before disturbance with 4.9149 s and 496.0599 s, respectively. But, it produced the most negligible overshoot value of 4.7103% than the integer-order set-point filter (5.0512%) and the actual process (7.5712%). Thus, the proposed filter effectively reduces the initial load disturbance, minimizing the overshoot and making the process settle faster. This performance led to the proposed set-point filter settling faster at 995.2130 s, followed by integer order with 996.3493 s and the actual process 997.3462 s. Furthermore, the dotted sections of A and B are enhanced and shown in the exact figure, which contains the detailed view of process output and control signal.

Fig. 3
figure 3

Performance comparison of FOPDT for disturbance rejection with various set-point filters

Full size image

The integer-order and fractional-order noise filters performance comparison is shown in Fig. 4 with zoomed-in regions of A and B. Because of the improved noise-free signal from the feedback loop, both the filters produced a faster rise time of 2.1384 s and 2.0851 s for fractional-order and integer-order noise filters, respectively. This situation helped the filters settle faster than the actual process at 997.6322 s for integer order and 994.3601 s for fractional-order noise filter. In contradiction with the set-point filter, the stand-alone noise filter fails to reduce the load variations, which caused the overshoot to increase than the actual process at 12.7284 and 9.5354% for integer order and fractional order.

Fig. 4
figure 4

Performance comparison of FOPDT for disturbance rejection with various noise filters

Full size image

The combined set-point and noise filter simulation results in the closed-loop are illustrated in Fig. 5. From the numerical analysis shown in Table 1, the proposed fractional filter combination had a faster rise time than its comparators with 2.5315 s followed by an integer-order combination (2.6647 s) and the actual process (4.2074 s). This more rapid rise time helped the proposed fractional filter combination to settle faster than all the filters before and after the disturbance. The integer-order filter combination settled slightly slower than the actual process combination at 997.6315 s due to the lack of additional frequency-based tuning parameters. In terms of overshoot performance, the proposed filtering combination takes the lead of minimizing them with the value of 6.0703%, followed by an integer-order combination with 8.0742%.

Fig. 5
figure 5

Performance comparison of FOPDT for disturbance rejection with combined set-point and noise filters

Full size image

3.3 SOPDT Process Model

Similarly, the simulation results of the process plant given in (7) are discussed in this section. The comparative results of second-order system with various set-point filters in the presence of the external noise are shown in Fig. 6, and its corresponding numerical analysis is tabulated in Table 2.

Fig. 6
figure 6

Performance comparison of SOPDT for disturbance rejection with various set-point filters

Full size image
Table 2 Numerical analysis of SOPDT model with various filters in the presence of external noise
Full size table

The numerical analysis has shown the same trend that happened in the FOPDT model. There is an initial slowdown in the rise time for the proposed set-point filter with 10.6541 s. But, this does not affect the capability of the proposed fractional filter to settle faster at 364.4879 s followed by integer-order filter (366.2489 s) and actual process (368.3541 s) during the initial period. After the disturbance rejection also, the proposed filter topped with a faster settling time (683.9720 s) and significantly less peak overshoot (31.6825%) than others. Different noise filter analysis of the second-order system is given in Fig. 7.

Fig. 7
figure 7

Performance comparison of SOPDT for disturbance rejection with various noise filters

Full size image

On the contrary with the FOPDT model, both noise filters used in the SOPDT system settled faster than the actual process before and after the disturbance. But, the peak overshoot problem is continued in this system as well. The integer-order noise filter produced the maximum peak overshoot value of 43.4283%, which is 5.8988% and 5.3601% higher than the actual process and fractional-noise filter, respectively. While noticing the performance of the combined filters shown in Fig. 8, the proposed filter settled faster during both instances. The proposed filter is settled at 683.5698 s, which is 106.92 s faster than the actual process and 69.3771 s faster than the integer-order filters. In all the results and discussion figures, it is worth mentioning that the proposed fractional-order filters produced a smooth control signal than all the different combination filters and the actual process.

Fig. 8
figure 8

Performance comparison of SOPDT for disturbance rejection with combined set-point and noise filters

Full size image

4 Conclusion

This article proposed a new fractional-order filter design for both the set-point and noise filter under the combination of FOPPI controller for the processes with longer dead time. The performance analysis has shown that the proposed filters are more effective than the conventional integer-order filter without any filters in overshoot minimization and faster settling. This new proposed filter design incorporates the essential system dynamics in its structure, which is advantageous for the new design widely accepted in industrial processes. In the future, the proposed method will be evaluated over the real-time actual process plant along with the optimized parameters using any optimization techniques.