1 Introduction

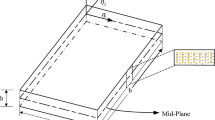
An increase in demand for high-performance lightweight aircraft structures with high strength has developed a new class of composite materials such as fiber-metal laminate (FML) [1]. A layer-by-layer arrangement of a thin aluminum sheet metal and fiber layer forms FML [2] configuration as shown in Fig. 1. It shows enhanced fatigue, fire retardant, high static and cracks resistant properties than conventional polymer composites. First, FML was successfully designed and developed using thin sheet metals and fiber-based epoxy laminate by Prof. Vogelesang, Delft University of Technology, Netherland. Further, he tested various combinations of FML structures and proved that the Kevlar-based FML shown better heat-resistant properties than others. However, its compressive strength and fatigue life behaviors are low when compared to other FML. To overcome such disadvantages, a new type of FML (GLARE) was developed by Vlot and Gunnink [3]. Much work has been carried out by many authors on GLARE to understand the impact load behavior, energy absorption, tensile load strength, and fatigue strength through various experimental, numerical, and theoretical approaches. Among them, Holleman [4] has given an overview of selection criteria of aluminum, fiber, adhesive and design guidelines for GLARE composites. After the initial development of FML composites, many researchers have shown key interest in fabricating GLARE panels with various combinations for enhanced mechanical and impact strength.

Sinke [5] has discussed and compared various processes involved in manufacturing and machining of GLARE composite with the conventional sheet metal works. Botelho et al. [6] made a comprehensive study on GLARE composite and how the strength has changed with respect to different types of fibers and their grades. Table 1 shows the different grades and configurations of GLARE panels used in the market are available for commercial purposes. Wu and Yang [7] critically reviewed and listed recent developments in GLARE by considering tensile, compressive, shear, fracture resistance, notched residual strength, impact and environmental durability as key parameters and also pointed out the need for further investigation on GLARE by considering the combined effect of temperature and moisture to understand the damage mechanism and durability and the author also focused on optimizing the material constituents based on the volume fractions of adhesive (Epoxy) with different glass fibers such as R-glass and S-glass from GLARE-1 to GLARE-6 grades. Wilk and Sliwa [8] tested mechanical strength of the GLARE panel by changing the stacking configuration with aluminum 2024, 6061 and 7075 alloys. Based on the literature review, it is evident that the different material grades and layups were used for the fabrication of GLARE panels and impact strength was studied by many researchers.

Table 1 Standard GLARE grades Botelho et al. [6]
Full size table

Alemi-Ardakani and Ghazavi [9] examined glass-fiber-reinforced aluminum to study the effect of bonding adhesion on resistance under low-velocity impact. Sadighi et al. [10] studied various FMLs with different thicknesses and materials for low-velocity impact behavior. In this work, a nonlinear transient finite element analysis was carried out to study the influence of elements on impact strength. Further, the study discusses the selection of finite elements had much more influence than the selection of failure criterion on impact strength results. Hinz et al. [11] analyzed inter-laminar shear strength of a composite plate with glass fiber using a representative volume finite element and experimental approaches and developed a new model to simulate de-bonding at the fiber-matrix interface of the interlaminar transverse composite ply. Further, the consequences of de-bonding after interlaminar shear load are also studied in detail.

Material properties extraction plays a significant role in numerical studies. Chen and Cheng [12] investigated the overall elastic behavior of the composite material and thermal expansion coefficients based on a micromechanical approach and compared the results with an experimental study. Chen and Cheng [13] extracted the orthotropic properties of short and continuous glass fiber composite material using an experimental approach. Chen and Sun [14] extracted elastic and plastic properties of an Aramid-reinforced aluminum laminate (ARALL) using a macro-mechanical approach. In this work, researchers used both orthotropic plasticity and laminated plate theories to get the elasto-plastic model. In the first case, a three-parameter plastic potential functions to model the ARALL laminate as a whole and in the second case, distinct linearly elastic and elasto-plastic models were used for aluminum and Kevlar layers. They found that the orthotropic model gave reasonable accurate results up to a total strain of 1.2 percent when compared to the experimental studies. Wang [15] analyzed micromechanics of the fibrous composite materials and developed an analytical model to describe the mechanics of material under external load. Upadhyay and Lyons [16] used a micromechanics-based three-phase model to examine the effective elastic properties of three-phase composites. Further, the effect of inter-phase coating on elastic constants was examined and found the degree of degradation plays a significant role in mechanical properties. Soltani et al. [17] proposed a numerical model to predict the nonlinear behavior of GLARE laminates by using a finite element approach. Tensile properties of reinforced polypropylene-based FML sandwich panels were investigated by Lee et al. [18] using ASTM D-3039 test standards.

Based on the conducted survey, most of the research carried out is focused on the development and testing of the elastic properties of GLARE. Very few discussed their structural behavior under external static and dynamic loads. Harras [19] investigated the vibration amplitudes of all side clamped (CCCC) GLARE-3 panels by using a nonlinear model and found that the amplitude depends upon the first nonlinear mode shape. They examined the free vibration characteristics such as natural frequencies and bending mode shapes of the GLARE-3 panel using experimental and numerical approaches. Botelho et al. [20] examined free vibration characteristics of FMLs by experimental testing and compared the results with micromechanics-based theoretical calculations. Calculated damping behavior such as storage modulus and loss factors was used to estimate the visco-elastic behavior of hybrid FML. Rahimi et al. [21] examined the effect of boundary conditions and layup directions on free vibration characteristics of an FML annular plate.. In vibration testing, modal assurance criterion (MAC) plays a major role in calculating the correlation coefficient between experimental and numerical modal vectors Heylen and Janter [22]. Allemang [23] reviewed the development of the MAC with other related assurance criteria proposed over the last twenty years and demonstrated how a statistical concept is used in structural dynamics application problems. The above works were concentrated only on vibration characteristics of the GLARE panel. However, much works have been carried on the determination of acoustical characteristics (sound radiation, sound transmission loss (STL) and radiation efficiency (RE)) of isotropic, composite and functionally grades material (FGM) panels using experimental, analytical and numerical approaches.

Rayleigh [24] is the pioneer to develop an analytical method to find the acoustic properties of the flat panels resting with baffled conditions. Li and Li [25] studied the effect of mass loading on sound radiation behavior of a plate located at air and water medium. Significant changes were observed in the sound radiation behavior of a mass-loaded panel under air than water. Chandra et al. [26] used analytical methods to study the vibro-acoustic behavior of functionally graded plates. Sharma et al. [27] investigated the vibro-acoustic behavior of shear deformable laminated composite flat panel using boundary element method (BEM) and the higher-order shear deformation theory (HSDT). Arunkumar et al. [28] developed an equivalent model to examine vibro-acoustic characteristics of honeycomb sandwich panel. In their work, ANSYS software and Rayleigh integral approaches were used to get forced vibration response and sound radiation characteristics. Further, Arunkumar et al. [29] extended their approach to study the vibro-acoustic behavior of sandwich panels with truss core filled with foam. In all most of the above works, first-order shear deformation theory (FSDT)-based models were used to study both static and dynamic characteristics of GLARE and composite panels. Doong et al. [30] examined the vibration and stability of pre-stressed cross-ply laminated composite plates using HSDT. Khoa and Thinh [31] used Reddy’s higher-order shear deformation theory based on 4-noded finite elements with seven degrees of freedom to analyze the dynamic behavior of composite panels. Sharma et al. [32] investigated the vibro-acoustic characteristics of the multilayered composite doubly curved shell panel using nine-noded iso-parametric Lagrangian elements with nine degrees of freedom per node.

Sufficient works related to FML were concentrated only on the extraction of mechanical properties, energy absorption, impact and static structural behavior by an experimental and numerical approach. Further, minimal researchers worked with experimental studies to extract the natural frequencies of hybrid FML. However, in this work, the vibro-acoustic behavior of GLARE, such as free, forced vibration characteristics, sound power level, sound transmission loss and radiations efficiency have been examined, along with the effect of boundary conditions (all side clamped-CCCC, all side simply supported-SSSS), aspect ratio (a/b = 0.5, 1, 1.5, 2), thickness ratio (a/h = 5, 30, 50, 83.33) and material percentage variation from 100 % aluminum to 100 % composite panels using experimental and finite element approaches (HSDT).

2 Problem description and methodology

A rectangular GLARE-5 hybrid panel as shown in Fig. 1 with \(\big [\mathbf{Al }/0^\circ /90^\circ /90^\circ /0^\circ /\mathbf{Al }\big ]_{s}\) multilayered configuration is considered for the detailed investigation. It is assumed that the layers of the GLARE panel are perfectly bonded. The complete overview of the methodology followed for the above investigation is given in Fig. 2.

Fig. 1
figure 1

GLARE-5 Composite panel

Full size image

2.1 Manufacturing of GLARE-5 composite panel

Traditional hand layup techniques were used to manufacture the GLARE-5 multilayered composite laminate having dimensions of \(300 \,\hbox {mm} \times 215 \,\hbox {mm} \times 3.58 \,\hbox {mm}\) with stacking sequence as shown in Fig. 3a. A commercially available aluminum sheet with 0.18 mm thickness was used for this purpose. The properties of the glass fiber and epoxy resin materials used to make the samples are given in Tables 2 and 3. The aluminum sheet roll is cut into uniform pieces with dimensions equal to the panel’s length and width. Similarly, the glass fibers in the form of unidirectional glass fiber were cut according to the panel’s length. 92 \(\%\) of thermosetting polymer epoxy and 8 \(\%\) of amine-based hardener (curing agent) were mixed in a beaker and uniform stirring is applied with the mechanical stirrer. Hardener addition helps to speed up the curing period of the composite material.

Fig. 2
figure 2

Methodology

Full size image
Fig. 3
figure 3

a Stacking sequence of GLARE-5 composite material, b and c hand layup technique

Full size image
Table 2 Properties of Epoxy resin
Full size table
Table 3 Properties of unidirectional glass fiber
Full size table

Initially, the flat surface is cleaned and polished with the release gel or wax to avoid composite sticking. Next, the aluminum sheet metal is placed over the flat surface and the prepared resin matrix is poured on the surface of the aluminum sheet metal. After ensuring the poured resins spread uniformly throughout the surface, the glass fiber layer is placed on the top of the aluminum sheet and resin. As part of the fabrication process of the composite panel, the unidirectional glass fiber is quenched with epoxy to reduce voids and porosity. [33]. The roller is applied over the glass fiber layer to remove shrinks and excess resins from the surface layer. The same process is continued for all the stacked configurations shown in Fig. 3a. After completing all the layers, a flat plate is placed over the top surface, and a uniform pressure load is applied over the GLARE-5 composite panel by a universal compression machine as shown in Fig. 4 to decrease the geometry imperfection and to achieve uniform thickness over the cross section of the panel. After a standard curing period of 48-hours at room temperature for epoxy-based polymers, the specimens are used for further studies. The calculated material percentage of aluminum and composite of the fabricated sample were used for further numerical investigation. GLARE-5 panel is prepared with aluminum layers of thickness 0.18 mm and glass/epoxy laminates with \([ 0^{\circ }\)/\(90^{\circ }\)/\(90^{\circ }\)/\(0^{\circ } ]\) layup scheme having a thickness of 1.52 mm (each layer 0.38 mm). The manufactured GLARE panel using the above manufacturing process and microscopic view in thickness directions are shown in Fig. 5a and b.

Fig. 4
figure 4

Compression machine for uniform pressure

Full size image
Fig. 5
figure 5

Manufactured GLARE panel and microscopic view in the thickness direction at 2 mm

Full size image

2.2 Evaluation of material properties

Finite element modeling of GLARE-5 laminate requires transverse isotropic properties such as \(\hbox {E}_x\), \(\hbox {E}_y\), \(\hbox {E}_z\), \(\hbox {G}_{{xy}}\), \(\hbox {G}_{{yz}}\), \(\hbox {G}_{{xx}}\), \(\gamma _{xy}\), \(\gamma _{yz}\), \(\gamma _{xz}\) [34]. In this study, all elastic properties of the composite material are evaluated using the rule of mixture methods [35, 36]. Table 4 shows the calculated elastic properties using the rule of mixture method.

Table 4 Elastic properties of a GLARE-5 composite material
Full size table

In addition, the obtained Young’s modulus (\(\hbox {E}_x\)) in fiber direction is verified by performing a standard tensile test using a Universal testing machine. For this purpose, the tensile specimens are individually cut from the manufactured composite plate as per the size mentioned in ASTM D-3039 standard [32] with a length 250 mm, width 25 mm, thickness 3.58 mm, gauge length 150 mm and 50 mm fixing at each end. The test is performed using a universal testing machine INSTRON 8800 under 0.2 mm/min load rate with humidity of 60% and the ambient temperature of \(35^\circ \hbox {C}\) with the clamping pressure of about 10 bar on each side of the test specimen.

2.3 Modeling of GLARE-5 laminate using layer wise Reddy’s higher-order shear deformation theory (HSDT)

GLARE-5 panel is modeled using Reddy’s layer-wise higher-order shear deformation theory [37] and discretized with 4-noded iso-parametric conforming finite element having eight degrees of freedom per node, namely \(\bar{{\bar{u}}}_0\), \(\bar{{\bar{v}}}_0\), \(\bar{{\bar{w}}}_0\), \({{\hat{\phi }}}_x\), \({{\hat{\phi }}}_y\) \(\frac{\partial {\bar{{\bar{w}}}_{0}}}{\partial {x}}\), \(\frac{\partial \bar{\bar{w_{0}}}}{\partial {y}}\), \(\frac{\partial ^2{\bar{{\bar{w}}}_{0}}}{\partial {x}\partial {y}}\).

Figure 6 shows the layer-wise model of the GLARE-5 composite laminate used for the detailed vibro-acoustic behavior investigation. Figure 7 shows the four-noded iso-parametric elements which are used to discretize the geometry in physical coordinates. The displacement field of the GLARE-5 laminated composite panel is given as follows [37]:

$$\begin{aligned} u=\, & {} \bar{{\bar{u}}}_{0}+z {\hat{\phi }}_{x}-\dfrac{4}{3h^{2}}z^{3} \Big ({\hat{\phi }}_{x}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}}\Big ) \end{aligned}$$
(1)
$$\begin{aligned} v=\, & {} \bar{{\bar{v}}}_{0}+z {\hat{\phi }}_{y}-\dfrac{4}{3h^{2}}z^{3} \Big ({\hat{\phi }}_{y}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\Big ) \end{aligned}$$
(2)
$$\begin{aligned} w=\, & {} \bar{{\bar{w}}}_{0} \end{aligned}$$
(3)
Fig. 6
figure 6

Geometry layup of a GLARE-5 panel

Full size image
Fig. 7
figure 7

Transformation from physical to natural coordinates

Full size image

From Eq. 1, 2 and 3, \(\bar{{\bar{u}}}_{0}=u_{m}(x,y,z_{0},t)\), \(\bar{{\bar{v}}}_{0}=v_{m}(x,y,z_{0},t)\), \(\bar{{\bar{w}}}_{0}=w_{m}(x,y,z_{0},t)\), \({\hat{\phi }}_{x}=\left( \frac{\partial {u}}{\partial {x}} \right) _{z=0}\) and \({\hat{\phi }}_{y}= \left( \frac{\partial {v}}{\partial {y}} \right) _{z=0}\) are the mid-plane displacements and rotations.

The obtained strain vector using the above displacement is given by,

$$\begin{aligned} \left\{ \begin{array}{c} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \gamma _{xy}\\ \gamma _{yz}\\ \gamma _{xz} \end{array}\right\}&= \left\{ \begin{array}{c} \dfrac{\partial \bar{{\bar{u}}}_{0}}{\partial {x}}\\ \dfrac{\partial \bar{{\bar{v}}}_{0}}{\partial {y}}\\ \dfrac{\partial \bar{{\bar{u}}}_{0}}{\partial {y}}+\dfrac{\partial \bar{{\bar{v}}}_{0}}{\partial {x}}\\ \phi _{y}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\\ \phi _{x}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}} \end{array}\right\} +z \left\{ \begin{array}{c} \dfrac{\partial {{{\hat{\phi }}}}_{x}}{\partial {x}}\\ \dfrac{\partial {{{\hat{\phi }}}}_{y}}{\partial {y}}\\ \dfrac{\partial {{{\hat{\phi }}}}_{x}}{\partial {y}}+\dfrac{\partial {{{\hat{\phi }}}}_{y}}{\partial {x}}\\ 0\\ 0 \end{array}\right\} \\&\quad +z^2 \left\{ \begin{array}{c} 0\\ 0\\ 0\\ \dfrac{-4}{h^{2}}\Big ({{\hat{\phi }}}_{y}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\Big )\\ \dfrac{-4}{h^{2}}\Big ({{\hat{\phi }}}_{x}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}}\Big ) \end{array}\right\} \\&\quad +z^3 \left\{ \begin{array}{c} \dfrac{-4}{3h^{2}}\Big (\dfrac{\partial {{{\hat{\phi }}}}_{x}}{\partial {x}}+\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}^2}\Big )\\ \dfrac{-4}{3h^{2}}\Big (\dfrac{\partial {{{\hat{\phi }}}}_{y}}{\partial {y}}+\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {y}^2}\Big )\\ \dfrac{-4}{3h^{2}}\Big (\dfrac{\partial {{{\hat{\phi }}}}_{x}}{\partial {y}}+\dfrac{\partial {{{\hat{\phi }}}}_{y}}{\partial {x}}+2\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}}\Big )\\ 0\\ 0 \end{array}\right\} \end{aligned}$$
(4)

The generalized strain vector \(\big \{\varepsilon \big \}\) of the above equation is given by the relation, Reddy [37],

$$\begin{aligned} \big \{\varepsilon \big \} = \big \{\varepsilon ^{0}\big \}+z\big \{\varepsilon ^{1} \big \}+z^{2}\big \{\varepsilon ^{2} \big \}+z^{3}\big \{\varepsilon ^{3} \big \} \end{aligned}$$
(5)

where \(-\gamma _{y}={{\hat{\phi }}}_{y}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\Rightarrow {{\hat{\phi }}}_{y}=-\gamma _{y}-\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\), \(-\gamma _{x}={{\hat{\phi }}}_{x}+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}} \Rightarrow {{\hat{\phi }}}_{x}=-\gamma _{x}-\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}}\), \(\dfrac{\partial {{\hat{\phi }}}_{x}}{\partial {x}}=-\dfrac{\partial \gamma _{x}}{\partial {x}}-\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x^{2}}}\), \(\dfrac{\partial {{\hat{\phi }}}_{y}}{\partial {y}}=-\dfrac{\partial \gamma _{y}}{\partial {y}}-\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {y^{2}}}\)

From the above relation,

$$\begin{aligned}&\dfrac{\partial {{\hat{\phi }}}_{x}}{\partial {y}} +\dfrac{\partial {{\hat{\phi }}}_{y}}{\partial {x}} =-\dfrac{\partial \gamma _{x}}{\partial {y}}-\dfrac{\partial ^{2} \bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}} -\dfrac{\partial \gamma _{y}}{\partial {x}}-\dfrac{\partial ^{2} \bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}} \end{aligned}$$
(6)
$$\begin{aligned}&z \left\{ \begin{array}{c} \dfrac{\partial {{\hat{\phi }}}_{x}}{\partial {x}}\\ \dfrac{\partial {{\hat{\phi }}}_{y}}{\partial {y}}\\ \dfrac{\partial {{\hat{\phi }}}_{x}}{\partial {y}}+\dfrac{\partial {{\hat{\phi }}}_{y}}{\partial {x}} \\ 0\\ 0 \end{array}\right\} =z \left\{ \begin{array}{c} -\Big (\dfrac{\partial \gamma _{x}}{\partial {x}}+\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x^{2}}}\Big ) \\ -\Big (\dfrac{\partial \gamma _{y}}{\partial {y}}+\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {y^{2}}}\Big )\\ -\Big (\dfrac{\partial \gamma _{x}}{\partial {y}}+\dfrac{\partial \gamma _{y}}{\partial {x}}+\dfrac{2\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}}\Big )\\ 0\\ 0 \end{array}\right\} \end{aligned}$$
(7)
$$\begin{aligned}&z^2 \left\{ \begin{array}{c} 0\\ 0\\ 0\\ -\dfrac{4}{h^2}\Big ({{\hat{\phi }}}_y+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\Big )\\ -\dfrac{4}{h^2}\Big ({{\hat{\phi }}}_x+\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}}\Big ) \end{array}\right\} =z^2 \left\{ \begin{array}{c} 0\\ 0\\ 0\\ \dfrac{4}{h^2}\gamma _y\\ \dfrac{4}{h^2}\gamma _x\\ \end{array}\right\} \end{aligned}$$
(8)
$$\begin{aligned}&z^{3}\dfrac{4}{3h^{2}} \left\{ \begin{array}{c} -\Big (-\dfrac{\partial {\gamma }_{x}}{\partial {x}}-\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}^2}+\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}^2}\Big )\\ -\Big (-\dfrac{\partial {\gamma }_{y}}{\partial {y}}-\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {y}^2}+\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {y}^2}\Big )\\ -\Big (-\dfrac{\partial {\gamma }_{x}}{\partial {y}}-\dfrac{\partial {\gamma }_{y}}{\partial {x}}-2\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}}+2\dfrac{\partial ^{2}\bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}}\Big )\\ 0\\ 0 \end{array}\right\} \\&\quad =z^3\left\{ \begin{array}{c} \dfrac{4}{3h^2}\dfrac{\partial {\gamma }_{x}}{\partial {x}}\\ \dfrac{4}{3h^2}\dfrac{\partial {\gamma }_{y}}{\partial {y}}\\ \dfrac{4}{3h^2}\Big (\dfrac{\partial {\gamma }_{x}}{\partial {y}}+\dfrac{\partial {\gamma }_{y}}{\partial {x}}\Big )\\ 0\\ 0 \end{array}\right\} \end{aligned}$$
(9)

The constitutive equation of the kth layer is given by

$$\begin{aligned} \left[ \begin{array}{c} \sigma _{x}\\ \sigma _{y}\\ \sigma _{xy}\\ \sigma _{yz}\\ \sigma _{xz} \end{array}\right] _{k}=\left[ \begin{array}{ccccc} \tilde{{\tilde{C}}}_{11}&{} \tilde{{\tilde{C}}}_{12} &{} \tilde{{\tilde{C}}}_{16} &{} 0 &{} 0\\ \tilde{{\tilde{C}}}_{12}&{} \tilde{{\tilde{C}}}_{22} &{} \tilde{{\tilde{C}}}_{26} &{} 0 &{} 0\\ \tilde{{\tilde{C}}}_{16}&{} \tilde{{\tilde{C}}}_{26} &{} \tilde{{\tilde{C}}}_{66} &{} 0 &{} 0\\ 0&{}0 &{} 0 &{} \tilde{{\tilde{C}}}_{44} &{} \tilde{{\tilde{C}}}_{45}\\ 0&{}0 &{}0 &{} \tilde{{\tilde{C}}}_{45} &{} \tilde{{\tilde{C}}}_{55} \end{array}\right] _k\left[ \begin{array}{c} \varepsilon _{x} \\ \varepsilon _{y}\\ \gamma _{xy}\\ \gamma _{yz}\\ \gamma _{xz} \end{array}\right] _k \end{aligned}$$
(10)

Elastic constants \([\tilde{{\tilde{C}}}_{11}]\), \([\tilde{{\tilde{C}}}_{12}]\), \([\tilde{{\tilde{C}}}_{16}]\), \([\tilde{{\tilde{C}}}_{22}]\), \([\tilde{{\tilde{C}}}_{26}]\), \([\tilde{{\tilde{C}}}_{66}]\), \([\tilde{{\tilde{C}}}_{44}]\), \([\tilde{{\tilde{C}}}_{45}]\), \([\tilde{{\tilde{C}}}_{55}]\) can be calculated using the material properties (\(E_{x},E_{y},E_{z},G_{xy},G_{yz},G_{zx},\gamma _{xy},\gamma _{xz},\gamma _{yz}\)). For more details, the reader may refer to Reddy [37].

By integrating the stress through the plate thickness, we obtain the generalized force–strain relation by,

$$\begin{aligned} \left[ \begin{array}{c} \hat{N^{\circ }}\\ \hat{M^{\circ }}\\ \hat{P^{\circ }}\\ \hat{Q^{\circ }}\\ \hat{W^{\circ }} \end{array}\right] =\left[ \begin{array}{ccccc} \hat{A^{\circ }} &{} \hat{B^{\circ }} &{} \hat{E^{\circ }} &{} 0 &{} 0\\ \hat{B^{\circ }} &{} \hat{D^{\circ }} &{} \hat{F^{\circ }} &{} 0 &{} 0\\ \hat{E^{\circ }} &{} \hat{F^{\circ }} &{} \hat{H^{\circ }} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \hat{{A}'} &{}\hat{{D}'} \\ 0 &{} 0 &{} 0 &{} \hat{{D}'} &{}\hat{{F}'} \end{array}\right] =\left[ \begin{array}{c} \epsilon ^{0}\\ \kappa \\ \eta \\ \gamma ^{0}\\ \xi \end{array}\right] \end{aligned}$$
(11)

The different quantities of the rigidity matrix in Eq. (11) can be derived as follows:

$$\begin{aligned}&\bigl (\begin{array}{cccccc} \hat{A^{\circ }}_{ij}&\hat{B^{\circ }}_{ij}&\hat{D^{\circ }}_{ij}&\hat{E^{\circ }}_{ij}&\hat{F^{\circ }}_{ij}&\hat{H^{\circ }}_{ij} \end{array}\bigr ) \\&\quad =\sum _{k=1}^{n}\int _{h_{k-1}}^{h_k}(\tilde{{\tilde{C}}}_{ij})_{k}\bigl (\begin{array}{cccccc} 1&z&z^2&z^3&z^4&z^6 \end{array}\bigr )dz, i,j = 1,2,6 \end{aligned}$$
(12)
$$\begin{aligned}&\bigl (\begin{array}{ccc} \hat{{A}'}_{ij}&\hat{{D}'}_{ij}&\hat{{F}'}_{ij} \end{array}\bigr ) \\&\quad =\sum _{k=1}^{n}\int _{h_{k-1}}^{h_k}(\tilde{{\tilde{C}}}_{ij}t)_{k}\bigl (\begin{array}{ccc} 1&z^2&z^4 \end{array}\bigr )dz, i,j = 4,5 \end{aligned}$$
(13)

2.4 Finite element formulation for GLARE-5 panel

The Hamilton’s principle of virtual displacement of a typical GLARE-5 panel finite element is given by weak form of the HSDT-based governing equations [37] as follows:

$$\begin{aligned} \begin{aligned}&\int _{\Omega ^{e}}{} \{N_{xx}\delta u_{0,x}+N_{xy}(\delta u_{0,y}+\delta v_{0,x})\\&\quad +N_{yy}\delta v_{0,y}+(Q_{x}-c_2 R_x)\delta w_{0,x}\\&\quad +(Q_y-c_2 R_y)\delta w_{0,y}\\&\quad -c_1(P_x \delta w_{0,xx}+P_y\delta w_{0,yy} +2P_{xy}\delta w_{0,xy})-q\delta w_0\\&\quad +(Q_x-c_2 R_x)\delta \phi _x +(M_x-c_1 P_x)\delta \phi _{x,x}\\&\quad +(M_{xy} -c_1P_{xy})\delta \phi _{x,y}\\&\quad +(Q_y-c_2 R_y)\delta \phi _y + (M_{xy}-c_1 P_{xy})\delta \phi _{y,x}\\&\quad +(M_{yy}-c_1 P_y)\delta \phi _{y,y}\\&\quad +(I_0 \ddot{u_0}+J_1\ddot{\phi _x}-c_1I_3 \ddot{w_{0,x}})\delta u_0\\&\quad +(I_0 \ddot{v_0}+J_1\ddot{\phi _y}-c_1I_3 \ddot{w_{0,y}})\delta v_0\\&\quad +(J_1\ddot{u_0}+K_2\ddot{\phi _x}-c_1J_4\ddot{w}_{0,x})\delta \phi _x\\&\quad +(J_1\ddot{v_0}+K_2\ddot{\phi _y}-c_1J_4\ddot{w}_{0,y})\delta \phi _y +I_0\ddot{w_0}\delta w_0\\&\quad +c_1(-I_3\ddot{u_0}-J_4\ddot{\phi _x}+c_1I_6\ddot{w_{0,x}}) \delta w_{0,x}\\&\quad +c_1(-I_3\ddot{v_0}-J_4\ddot{\phi _y}+c_1I_6\ddot{w_{0,y}})\delta w_{0,y}\\&\quad +(\hat{N_{xx}w_{0,x}}+\hat{N_{xy}w_{0,y}})\delta w_{0,y}\\&\quad +(\hat{N_{xy}w_{0,x}}+\hat{N_{yy}w_{0,y}})\delta w_{0,y}{\mathrm{d}}x{\mathrm{d}}y \}\\&\quad -\oint _{\Gamma ^e}(N_n\delta u_n +N_{nx}\delta u_{ns}){\mathrm{d}}s\\&\quad -\oint _{\Gamma ^e}({\bar{V}}_n\delta w_0 +P_{nn}\delta w_{0,n}){\mathrm{d}}s\\&\quad -\oint _{\Gamma ^e}(M_n\delta \phi _n +M_{n s}\delta \phi _{ns}){\mathrm{d}}s=0 \end{aligned} \end{aligned}$$
(14)

A comma followed by subscripts denotes differentiation with respect to the subscripts. \((N_{xx}, N_{yy}, N_{xy})\) denotes the force resultant, \((M_{xx}, M_{yy}, M_{xy} )\) represent the moment resultants, \((Q_{x} \; and \; Q_{y} )\) are the transverse shear force resultants, \(\delta u_{0}, \delta v_{0}, \delta w_{0}\) are the generalized displacements, \(I_{i}\) represent mass moment of inertia and it is given by Eqs. 15 and 16, whereas two points above a variable mean the second derivative with respect to time.

$$\begin{aligned} I_i=\, & {} \sum _{k=1}^{N}\int _{zk}^{zk+1}\rho ^{(k)}(z)^i dz (i=0,1,2.....,6) \end{aligned}$$
(15)
$$\begin{aligned} c_1=\, & {} \frac{4}{3h^2},c_2=\frac{4}{h^2},J_i=I_i-c_1I_{i+2}, \\ K_2=\, & {} I_2-2c_1I4 +c_1^2I_6 \end{aligned}$$
(16)

The generalized displacement is approximated over an element \(\Omega ^e\) by the expressions [37].

$$\begin{aligned} \begin{aligned} u_0(x,y,t)&=\sum _{i=1}^{N}[N_i(x,y)]u_i(t)\\ v_0(x,y,t)&=\sum _{i=1}^{N}[N_i(x,y)]v_i(t)\\ w_0(x,y,t)&=\sum _{i=1}^{N}[\bar{{\bar{\Delta }}}_i(x,y)]\bar{\varphi _i}(t)\\ \hat{\phi _x}(x,y,t)&=\sum _{i=1}^{N}[N_i(x,y)]\hat{\phi _x}_i(t)\\ \hat{\phi _y}(x,y,t)&=\sum _{i=1}^{N}[N_i(x,y)]\hat{\phi _y}_i(t) \end{aligned} \end{aligned}$$
(17)

The constants, \(\bar{{\bar{\Delta }}}_i =w_0\), \(\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {x}}\), \(\dfrac{\partial \bar{{\bar{w}}}_{0}}{\partial {y}}\), \(\dfrac{\partial ^2 \bar{{\bar{w}}}_{0}}{\partial {x}\partial {y}}\), \(N_i\) and \(\bar{{\bar{\Delta }}}_i\) denote Lagrangian and Hermite interpolation functions. The weak form of equations are discretized using the 4-noded iso-parametric finite element with 8 DOF per node.

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}c} {[{\bar{K}}^{11}]} &{} {[{\bar{K}}^{12}]} &{} {[{\bar{K}}^{13}]} &{} {[{\bar{K}}^{14}]} &{} {[{\bar{K}}^{15}]} \\ {[{\bar{K}}^{12}]^{\mathrm{T}}} &{} {[{\bar{K}}^{22}]} &{} {[{\bar{K}}^{23}]} &{} {[{\bar{K}}^{24}]} &{} {[{\bar{K}}^{25}]} \\ {[{\bar{K}}^{13}]^{\mathrm{T}}} &{} {[{\bar{K}}^{23}]^{\mathrm{T}}} &{} {[{\bar{K}}^{33}]} &{} {[{\bar{K}}^{34}]} &{} {[{\bar{K}}^{35}]} \\ {[{\bar{K}}^{14}]^{\mathrm{T}}} &{} {[{\bar{K}}^{24}]^{\mathrm{T}}} &{} {[{\bar{K}}^{34}]^{\mathrm{T}}} &{} {[{\bar{K}}^{44}]} &{} {[{\bar{K}}^{45}]} \\ {[{\bar{K}}^{15}]^{\mathrm{T}}} &{} {[{\bar{K}}^{25}]^{\mathrm{T}}} &{} {[{\bar{K}}^{35}]^{\mathrm{T}}} &{} {[{\bar{K}}^{45}]^{\mathrm{T}}} &{} {[{\bar{K}}^{55}]} \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {u^i} \\ {v^i} \\ {\varphi ^i} \\ {{\hat{\phi }}_x^i} \\ {{\hat{\phi }}_y^i} \\ \end{array} } \right\} \\&\quad \quad + \left[ {\begin{array}{*{20}c} {[{\bar{M}}^{11}]} &{} {[{\bar{M}}^{12}]} &{} {[{\bar{M}}^{13}]} &{} {[{\bar{M}}^{14}] } &{} {[{\bar{M}}^{15}]} \\ {[{\bar{M}}^{12}]} &{} {[{\bar{M}}^{22}]} &{} {[{\bar{M}}^{23}]} &{} {[{\bar{M}}^{24}]} &{} {[{\bar{M}}^{25}]} \\ {[{\bar{M}}^{13}]^{\mathrm{T}}} &{} {[{\bar{M}}^{23}]^{\mathrm{T}}} &{} {[{\bar{M}}^{33}]} &{} {[{\bar{M}}^{34}]} &{} {[{\bar{M}}^{35}]} \\ {[{\bar{M}}^{14}]^{\mathrm{T}}} &{} {[{\bar{M}}^{24}]} &{} {[{\bar{M}}^{34}]^{\mathrm{T}}} &{} {[{\bar{M}}^{44}]} &{} {[{\bar{M}}^{45}]} \\ {[{\bar{M}}^{15}]} &{} {[{\bar{M}}^{25}]^{\mathrm{T}} } &{} {[{\bar{M}}^{35}]^{\mathrm{T}}} &{} {[{\bar{M}}^{45}] } &{} {[{\bar{M}}^{55}]} \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\ddot{u^i}} \\ {\ddot{v^i}} \\ {\ddot{\varphi ^i}} \\ {\ddot{\phi _x^i}} \\ {\ddot{\phi _y^i}} \\ \end{array} } \right\} \\&\quad = \left\{ {\begin{array}{*{20}c} {{\bar{F}}^1} \\ {{\bar{F}}^2} \\ {{\bar{F}}^3} \\ {{\bar{F}}^4} \\ {{\bar{F}}^5} \\ \end{array} } \right\} \\ \end{aligned} \end{aligned}$$
(18)

The functions can be determined using \(\alpha =1,2,3,4,5;\,\Delta _j^1=u_j\); \(\hbox {i}=1\) to n\(\alpha\). The complete details of stiffness and mass matrices elements are given in “Appendix”.

2.5 Free vibration analysis: numerical approach

Transversely isotropic properties obtained from the micromechanics approach in Sect. 2.2 are used to get the stiffness and mass matrices from Eq. (18) with harmonic time dependence assumption. Then, the standard eigenvalue problem is formulated as given in Eq. (19) and solved using MATLAB to get the natural frequencies and mode shapes

$$\begin{aligned} ([{\bar{K}}] - \omega ^2 [{\bar{M}}]){X} = {0} \end{aligned}$$
(19)

as per the above equation [\({\bar{K}}\)] & [\({\bar{M}}\)] is given as the global assembled stiffness and mass matrices of the GLARE panel.

2.6 Free vibration analysis: experimental method

Experimental modal analysis is carried out to get the natural frequencies and mode shapes of the panel. A simple laboratory-scale experiment was developed for this purpose using the available vibration fixture and impact hammer test setup. A GLARE-5 panel is fabricated as per the fabrication process specified in Sect. 2.1 with dimensions specified in Fig. 5a. The GLARE-5 panel is clamped over all four sides to arrest all the degrees of freedom using lock nuts with uniform pressure as shown in Fig. 8.

Fig. 8
figure 8

Experimental test setup for free vibration of GLARE-5 panel for all side clamped boundary condition

Full size image

The GLARE-5 panel is excited using Dytron make impulse hammer and the response is measured using a uniaxial accelerometer. The sensitivities of the impact hammer and accelerometer are 10.29 mV/lbf and 104.11 mV/g. In order to avoid nodal locations, the accelerometer is fixed at one by fourth locations of the plate. The accelerometer is mounted on the panel’s top surface using a thermo-set adhesive and connected to the M+P VibPilot 8-channel data acquisition system. During the multipoint modal test, one can perform the test by moving the impact hammer or accelerometer between measurement points. But there are some difficulties in moving the accelerometer when making measurements such as changing the position of the accelerometer at the measurement points. Instead, roving the impact hammer to the measuring points will help to overcome the above difficulties. In addition, roving the accelerometer also alters the mass distribution of the structure, which affect the system natural frequencies. The time taken for a roving hammer is also very less compared to the rowing accelerometer. Hence, the roving hammer technique is widely preferable than moving the accelerometer. For the above reasons, the roving hammer technique is used in this work to obtain the natural frequencies and mode shapes of the GLARE-5 panel and the schematic diagram for position of the accelerometer and position of the impact hammer is also shown in Fig. 9. The entire GLARE-5 panel is discretized with 11 \(\times\) 8 mesh size and excited by the roving hammer method shown in Fig. 9b. The output response is recorded using M+P international software. The recorded time-domain signal is converted into the frequency domain using Fast Fourier Transform (FFT) and operating deflection shape (ODS) analysis is also carried out. Figure 8 shows the GLARE-5 panel, specimen holder and vibration measurement instruments used for free vibration testing.

Fig. 9
figure 9

Schematic diagram for roving accelerometer and roving impact hammer

Full size image

2.7 Modal assurance criterion (MAC)

Modal assurance criterion (MAC) plays an important role in pairing the obtained data from experimental and numerical approaches. This allows us to compare the measured vibration mode shape with the finite element results. The degree of similarity between the two different displacement vectors is expressed in Eq. (20). In general, MAC varies from zero to one (0 to 1) and the MAC value close to zero represents significant variation between the displacement vectors and the MAC value close to one represents identical shape correlation between displacement vectors. Achieving MAC value exactly equal to one is difficult for most of the cases and the MAC value will always be \(< 1\) [38].

$$\begin{aligned} {\mathrm{MAC}}(r,q)= \frac{| \big \{{\tilde{\psi }}_A\big \}_{r}^{\mathrm{T}} \big \{{\tilde{\psi }}_X\big \}_{q}^{*}|^2}{\big (\big \{{\tilde{\psi }}_A\big \}_{r}^{\mathrm{T}} \big \{{\tilde{\psi }}_A\big \}_{r}^{*} \big \{{\tilde{\psi }}_X\big \}_{q}^{\mathrm{T}} \big \{{\tilde{\psi }}_X\big \}_{q}^{*}\big )} \end{aligned}$$
(20)

as per the equation for any, \(\big \{{\tilde{\psi }}_A\big \}_{r}\) is the displacement vector of solution \(\hbox {A}_{{r}}\), \(\big \{{\tilde{\psi }}_A\big \}_{r}^{\mathrm{T}}\) is the transpose displacement vector\(\big \{{\tilde{\psi }}_A\big \}_{r}\), \(\big \{{\tilde{\psi }}_X\big \}_{q}^{*}\) is the complex conjugate of \(\big \{{\tilde{\psi }}_X\big \}_{q}\), \(\big \{{\tilde{\psi }}_X\big \}_{q}^{\mathrm{T}}\) is the transpose displacement vector \(\big \{{\tilde{\psi }}_X\big \}_{q}\) and \(\big \{{\tilde{\psi }}_A\big \}_{r}^{*}\) is the complex conjugate of \(\big \{{\tilde{\psi }}_A\big \}_{r}\).

2.8 Forced vibration analysis using finite element approach

The modal superposition method (MSP) is implemented to estimate the forced vibration response analysis of a GLARE-5 multilayered composite panel [39] by applying a harmonic point load with a magnitude of 1N at the locations 0.5 X, 0.5 Y and 0.75 X, 0.75 Y along in z-direction. The MSP is a unique method for obtaining stable dynamic responses under dynamic loading conditions with high-performance computing efficiencies and low calculation time. The eigenvalues and eigenvectors obtained by solving the standard eigenvalue Eq. (19) were used to perform the forced vibration response of the GLARE-5 panel [40]. The governing equation of motion for a dynamic system acted on by external load is expressed as follows:

$$\begin{aligned} \left[ {\bar{M}}_{ij} \right] \left\{ {\ddot{X}} \right\} +\left[ \tilde{{\tilde{C}}}_{ij} \right] \left\{ {\dot{X}} \right\} +\left[ {\bar{K}}_{ij} \right] \left\{ X \right\} ={\bar{F}}(t) \end{aligned}$$
(21)

The function, \({\bar{F}}(t)\) is the time-dependent applied force vector and \(\left\{ {X} \right\}\) is the displacement vector. The displacement vector in terms of modal coordinates is given by

$$\begin{aligned} \left\{ {X} \right\} =\sum _{k=1}^{n}\left[ {\bar{\phi }} \right] Z_{k} \end{aligned}$$
(22)

Thus, the constant, \({\bar{\phi }}\) is the ortho-normalized eigenvector as given by the following equation,

$$\begin{aligned} {\bar{\phi }} = \frac{1}{\sqrt{\phi _{i}^{\mathrm{T}}{\bar{M}}_{ij}\phi _{i}}}\phi _{i} \end{aligned}$$
(23)

i.e., \(\phi _{i}\) is the eigenvector and \({\bar{M}}_{ij}\) is the mass matrix

$$\begin{aligned} \left[ {\bar{M}}_{ij}\right] \left[ {\bar{\phi }} \right] \left\{ {\ddot{Z}} \right\} +\left[ \tilde{{\tilde{C}}}_{ij}\right] \left[ {\bar{\phi }} \right] \left\{ {\dot{Z}} \right\} +\left[ {\bar{K}}_{ij}\right] \left[ {\bar{\phi }} \right] \left\{ Z \right\} ={\bar{F}}(t) \end{aligned}$$
(24)

Pre-multiplying Eq. (24) by \(\left[ {{\bar{\phi }}} \right] ^{\mathrm{T}}\) and considering orthogonality condition, the uncoupled equation in modal coordinate is given by

$$\begin{aligned} {\ddot{Z}}_k+2\zeta \omega _{n}{\dot{Z}}_k+\omega ^2_kZ_k={\bar{F}}_k \end{aligned}$$
(25)

for, \(\hbox {k} = 1,2,\ldots \hbox {n}\) (represents mode). For harmonic oscillation, the above equation given by

$$\begin{aligned} \left\{ Z \right\} _k=\frac{{\bar{F}}_{k}}{\left( \omega ^2_k-\Omega ^2 \right) +2\zeta \omega _k\Omega } \end{aligned}$$
(26)

and the actual displacement vector is calculated using Eq. (22)

The surface normal velocity of the GLARE panel is calculated from the vibration displacement response using the following relation

$$\begin{aligned} {\dot{w}} =j \omega \left\{ X\right\} \end{aligned}$$
(27)

In the above equation, \({\dot{w}}\) denotes the surface normal velocity, \(\omega\) represents excitation frequency, and \(\left\{ X\right\}\) indicates the displacement vector. Then, the average RMS velocity of the GLARE panel is calculated for each frequency using the relation given below

$$\begin{aligned} V_{{\mathrm{RMS}}}=\sqrt{\frac{1}{N}\sum _{n=1}^{N}\left| {\dot{w}} \right| ^2} \end{aligned}$$
(28)

2.9 Acoustic studies of GLARE-5 panel

Acoustic characteristics such as sound power level (SPL), sound transmission loss (STL), radiation efficiency and sound directivity pattern are obtained from the surface normal velocity of the GLARE panel using the methodology described below.

  1. 1.

    The complex sound pressure at any point can be obtained in terms of the plate surface normal velocity using the Rayleigh integral as given below

    $$\begin{aligned}&{\text {Complex pressure amplitude}}\;{\bar{p}}({\bar{r}}) \\&\quad = \frac{j\rho ck}{2\pi }\int _{S} {\dot{w}}\big ( r_{S} \big )\frac{e^{-jk |{\bar{r}}-{\bar{r}}_{S}|}}{|{\bar{r}}-{\bar{r}}_{S}|} {\mathrm{d}}s \end{aligned}$$
    (29)

    The constant, \(\rho\) is the density of the air medium, c is the velocity of sound, S is the surface area of the plate, \({\bar{r}}_{S}\) is the point located on the surface S,\({\bar{r}}\) is the field point, \({\dot{w}}\big ( {\bar{r}}_{S}\big )\) is the surface normal velocity, \(|{\bar{r}}-{\bar{r}}_{S}|\) is the distance between a surface point and the field point, k is the wave number \(( k = \omega /c )\) and \(\omega\) is the circular frequency. Figure 10 shows the geometric interpretation of the sound pressure calculation at any point above the vibrating panel.

    $$\begin{aligned} {\bar{W}}=\dfrac{1}{2} Re \left( \oint {\bar{p}}({\bar{r}}){\dot{w}}^{*}({\bar{r}}) \right) {\mathrm{d}}s \end{aligned}$$
    (30)

    where \({\bar{W}}\) is the sound power, \({\bar{p}}({\bar{r}})\) is the complex pressure amplitude, and \({\dot{w}}^{*}({\bar{r}})\) is the complex conjugate of the acoustic particle velocity. Then, the sound power level can be calculated using the equation as follows:

    $$\begin{aligned} {\text {Sound power level (SPWL)}} = 10\;{\mathrm{log}} \dfrac{{\bar{W}}}{{\hat{W}}_{\mathrm{ref}}} \end{aligned}$$
    (31)

    where \({\hat{W}}_{\mathrm{ref}}\) represents the reference power \(\left( {\hat{W}}_{\mathrm{ref}} = 1 \times 10^{-12} Watts \right)\)

  2. 2.

    Radiation efficiency of the vibrating panel can be calculated using equation

    $$\begin{aligned} \sigma = \dfrac{{\bar{W}}}{\rho \;c\;S\;V^2 } \end{aligned}$$
    (32)

    From the above equation, \(V^2={\dot{V}}_n^H N {\dot{V}}_n\), V is the spatial time averaged normal velocity, \(\mathbf{N }=(1/2N)\mathbf{I }\), N is the number of elements used in the discretization, I is the identity matrix and \({\bar{W}}\) is the sound power taken from the Eq. (30)

  3. 3.

    Using the Rayleigh integral approach, the sound pressure at a field point is given in terms of surface velocity by the following equation,

    $$\begin{aligned} {{\bar{{\mathrm{p}}}}({\bar{r}},\theta )}= \frac{j\rho \omega }{2\pi } \int _{-L/2}^{L/2}\int _{-W/2}^{W/2}{\dot{w}}\big ( x,y \big )\frac{e^{-jk |{\bar{r}}-{\bar{r}}_{S}|}}{|{\bar{r}}-{\bar{r}}_{S}|} {\mathrm{d}}x{\mathrm{d}}y \end{aligned}$$
    (33)

    In the above equation, \(|{\bar{r}}-{\bar{r}}_{S}|\) is the distance between a surface point and the field point, \({\dot{w}}\big ( x,y \big )\)is the acoustic particle velocity, \({\bar{r}}\) is the field point, \({\bar{r}}_{S}\) is the point located on the surface S.

    Sound pressure at a distance of 1m from the center of the panel is calculated using the above relation by varying the angles from \(0^\circ\) to \(180^\circ\) and it is shown in Fig. 11.

    Then, the sound pressure level is calculated at field points by the equation given below

    $$\begin{aligned} {\mathrm{SPL}}=20{\mathrm{log}}\frac{{\bar{p}}}{{\bar{p}}_{\mathrm{ref}}} \end{aligned}$$
    (34)
  4. 4.

    Transmission loss is defined as the ratio of incoming and transmitted sound power. The sound transmission loss of the GLARE-5 panel in decibel is given by Eq. (35)

    $$\begin{aligned} {\mathrm{STL}}=10\;{\mathrm{log}}_{10}\dfrac{1}{\tau } \end{aligned}$$
    (35)

    The function \(\tau\) represents the transmission ratio which is defined as the ratio of transmitted power (\({\bar{W}}\)) and incident power (\(W_{i}\)) and it is given by,

    $$\begin{aligned} \tau = \dfrac{{\bar{W}}}{W_{i}} \end{aligned}$$
    (36)

    The constant, transmitted sound power (\({\bar{W}}\)) is calculated from Eq. 30 and incident sound power \(\left( W_{i} = {p_{i}^{2}\cos \theta L W}/{2 \rho c} \right)\), \(p_{i}\) is incident pressure assumed to be a real constant \(\left( 1 N/m^2 \right)\), \(\theta\) is normal incidence angle \(\left( \theta = 0^{\circ } \right)\) in radian, L is the length, W refers to width of the GLARE-5 panel, respectively, and the reader may also refer to [26, 41] for further details.

Fig. 10
figure 10

Geometric interpretation of the panel

Full size image
Fig. 11
figure 11

A baffled rectangular panel with the main geometrical parameters and defined coordinate systems

Full size image

3 Validation studies

3.1 Validation of Reddy’s higher-order shear deformation theory

In order to verify the developed finite element model, a simply supported square 4-layered laminated composite plate [\(0^{\circ }\)/\(90^{\circ }\)/\(90^{\circ }\)/\(0^{\circ }\)] was analyzed by Peng [42] is considered for validation. The material properties of the composite layer are given by Peng [42] as \(E_1= 175 \times 10^9\) Pa, \(E_2 = 7 \times 10^9\,\hbox {Pa}\), \(G_{12} = G_{13} = 3.5 \times 10^9\,\hbox {Pa}\), \(G_{23} = 1.4 \times 10^9\,\hbox {Pa}\), \(\gamma _{12} = \gamma _{13} = 0.25\).

Table 5 shows the results of proposed model and Peng [42] for bending deflection and stress variations. It shows good agreement between the two and the present HSDT-based finite element model predicts the bending deflection more accurately.

Table 5 Non-dimensionalized deflection and stresses in simply supported condition for symmetric cross-ply squared laminates
Full size table

3.2 Validation of sound power level

Similarly to verify the developed Rayleigh integral code, a simply supported rectangular isotropic plate with the dimensions of \(0.445\, \hbox {m}\ \times 0.379 \,\hbox {m} \times 0.003 \,\hbox {m}\), was analyzed by Li and Li [25] for radiated sound power level which is considered for the material properties of the isotropic plate given [25] as density \(\rho = 7850 \,\hbox {kg}/{\mathrm{m}}^{3}\), Young’s modulus \(\hbox {E} = 2.1 \times 10^{11}\,\hbox {N}/{m^2}\), and Poisson’s ratio \(\gamma = 0.3\), is taken for validation. The plate is assumed to be vibrating in air medium with density and sound speed of about \(\rho = 1.21\, \hbox {kg}/{\mathrm{m}}^{3}\), \(\hbox {c} = 343 \,\hbox {m/s}\). The isotropic plate is modeled using Reddy’s HSDT theory and discretized with a 4-noded finite element. The sound power level of the vibrating surface is computed by exciting the isotropic plate by a harmonic load with 1N magnitude \((Fe^{j\omega t})\) along normal to the thickness. Figure 12 shows the comparison of radiated sound power level and good agreement between the two.

Fig. 12
figure 12

Present study of sound power level with Li and Li [25]

Full size image

4 Results and discussion

GLARE-5 hybrid multilayered composite plate having dimensions of 0.3 m and 0.215 m along length and width directions is considered for the detailed investigation of vibro-acoustic behavior using experimental and HSDT based finite element methods. The influence of aspect ratio, boundary conditions, thickness ratio and material percentage variation on vibro-acoustic behavior of GLARE-5 composite plate is examined in detail. The material properties of aluminum and glass fiber/epoxy used for the detailed investigation are given in Table 4. The thickness of aluminum and glass/epoxy laminates with \([ 0^{\circ }\)/\(90^{\circ }\)/\(90^{\circ }\)/\(0^{\circ } ]\) layup is 0.18 mm and 1.52 mm. It is assumed that the plate is vibrating in air medium and discretized using a 4-noded HSDT-based finite element with eight degrees of freedom (DOF) per node. The detailed convergence study has been carried out for the highest natural frequency considered for the analysis, and the results are compared with the experimental natural frequencies.

Next, the vibration displacement response of the plate is obtained by applying a harmonic point load at a distance of about 0.75 length and 0.75 width from the origin of the panel. Then, the Rayleigh integral is used to obtain the acoustic response using the obtained displacement response for each frequency. Vibro-acoustic quantities such as displacement, velocity and root mean square (RMS) acceleration at the driving point, radiated sound power, sound pressure level, overall sound power level and sound transmission loss are computed using Eqs. (29)–(35).

4.1 Modal analysis

Modal analysis is carried out on the GLARE-5 panel using HSDT-based finite element method and experimental methods as shown in Fig. 8 and described in Sects. 2.5 and 2.6. A converged finite element mesh size of \(11 \times 11\) is used to obtain the natural frequencies and eigenvectors by solving Eq. (19). Extracted natural frequencies from the experimental modal analysis are compared with the finite element results. Table 6 shows the comparison of the first five natural frequencies extracted from experimental and finite element methods along with the percentage of error. From Table 6, it is clear that the obtained natural frequencies using the experimental method are closely matching with numerical results for the selected modes with less percentage of errors.

Table 6 Natural frequencies of GLARE-5 panel by experimental and present finite element approach (HSDT)
Full size table

The extracted experimental natural frequencies were verified with numerical results by MAC analysis according to the procedure described in Sect. 2.7. For this purpose, an in-house MATLAB code has been developed to compare the displacements extracted from the ODS analysis with the numerical results for each frequency. Calculated MAC values are listed in Table 7, and it clearly shows that the diagonal values are nearly equal to one and the mode shapes are perfectly matched to each other. The compared MAC values are plotted with the help of a confusion matrix plot in 3-D as shown in Fig. 13.

Table 7 Modal assurance criterion (MAC) for CCCC boundary condition
Full size table
Fig. 13
figure 13

MAC comparison between experimental and numerical results

Full size image

4.2 Influence of load location on vibro-acoustic behavior

To examine, how the modes have been shifted based on the loading condition, a GLARE-5 panel with dimensions specified in Sect. 2.1 is considered for detailed investigation on vibro-acoustic behavior due to excitation locations. For this purpose, a harmonic load is applied at center and offset locations with 1N magnitude in the frequency range from 1 Hz to 2500 Hz. The forced vibration response and RMS velocity of the GLARE-5 panel are calculated using the modal superposition method as specified in Sect. 2.8 and the radiated sound power level of the panel is calculated as specified in Sect. 2.9. Figures 14 and 15 show the results of sound power level and average RMS velocity due to center and offset locations.

Fig. 14
figure 14

Effect of sound power level and RMS velocity for load acting at center

Full size image
Fig. 15
figure 15

Effect of sound power level and RMS velocity for load acting at offset distance

Full size image

From Fig. 14, it is clear that when the load is acting at the center of the panel, few modes were not excited due to the position of excitation location nearer to panels nodal positions corresponds to the particular mode. The entire modes between the selected frequency range are observed when the load is shifted from center to offset location as seen in Fig. 15. Both average RMS velocity and sound power level are overlaid for the load acting at the center and offset locations on a single plot to show how the peak amplitude matches each other at natural frequencies.

4.3 Influence of aspect ratio and boundary conditions on vibro-acoustic behavior

The influence of aspect ratio (a/b) on vibro-acoustic characteristics of GLARE panel is analyzed for all side clamped (CCCC) and simply supported (SSSS) boundary conditions. Table 8 shows the extracted natural frequencies for different aspect ratios using the finite element method. The results show that the natural frequencies increase as the aspect ratio increases for all sides clamped and simply supported conditions. Figure 16a and b shows the influence of aspect ratio on average RMS velocity of the GLARE panel for CCCC and SSSS boundary conditions. The results indicate that irrespective of boundary conditions, the curves monotonically have a similar pattern while changing the aspect ratio.

Fig. 16
figure 16

Effect of average RMS velocity for different aspect ratio and boundary conditions

Full size image
Table 8 Modal frequencies for different aspect ratio and boundary condition
Full size table

Figure 17a and b shows the results of sound radiation efficiency for CCCC and SSSS boundary conditions. The results indicate that there is no significant variation in radiation efficiency for all cases except the aspect ratio a/b = 2, which also applies only to CCCC boundary conditions.

Fig. 17
figure 17

Effect of radiation efficiency for different aspect ratio and boundary conditions

Full size image

The influence of aspect ratio and boundary conditions on radiated sound power level is shown in Fig. 18a and b. It is clear from the figures that at resonant frequencies the radiated sound power level is high, although it is difficult to distinguish the radiated sound power level by just looking at the plot.

Fig. 18
figure 18

Effect of sound power level for different aspect ratio and boundary conditions

Full size image

The overall sound power level is therefore calculated at 1/3rd Octave band frequency and is useful for differentiating the radiated power for different aspect ratios, as shown in Fig. 15. One can see from Fig. 19a and b that the overall sound power level decreases at 1/3rd octave band frequencies as the aspect ratio of the GLARE panel increases. However, the overall sound power level increases at some octave frequencies for a/b = 1 compared to a/b = 0.5, which may be due to an increase in natural frequencies as the ratio increases.

The effect of boundary conditions on overall sound power level at 1/3rd Octave band frequencies are plotted as shown in Fig. 19a and b. Figures show that the sound power level decreases while increasing the aspect ratio for all side clamped boundary conditions. However, a similar trend has not been observed for SSSS conditions, as shown in Fig. 19b.

Fig. 19
figure 19

Effect of aspect ratio and boundary conditions on overall sound power level at 1/3rd octave band frequency

Full size image

The radiated sound pressure level is calculated by Eq. (34). Figure 20a and  b shows the variations in sound directivity pattern due to the change in aspect ratio and boundary conditions for 500 Hz. Figures clearly indicate that the radiated sound pressure level increases as increase in aspect ratio for all side clamped boundary conditions. However, the simply supported boundary conditions do not show much variation for a higher aspect ratio. Figure  21a and b shows the variations in sound directivity pattern due to the change in aspect ratio and boundary conditions for 1000 Hz. The radiated sound pressure level for the CCCC boundary condition shows a definite pattern and represents modes close to 1000 Hz. From Fig. 21a, it is clear that the radiated sound pressure level is not uniform and shows significant variation when increasing the aspect ratio for all side clamped boundary conditions. Irrespective of aspect ratio similar trend has been observed for simply supported boundary conditions as well and the results are shown in Fig. 21b.

Fig. 20
figure 20

Effect of sound pressure level at 500 Hz for different aspect ratio with different boundary conditions

Full size image
Fig. 21
figure 21

Effect of sound pressure level at 1000 Hz for different aspect ratio with different boundary conditions

Full size image

Next, the effect of boundary conditions on transmission loss of GLARE-5 panel is examined as specified in Sect. 2.9. A plane acoustic wave with amplitude \(1\,{\mathrm {N/m}}^{2}\) and \(0^\circ\) incident angle is considered for analyzing sound transmission loss of the GLARE panel. Figure 22a and b shows the sound transmission loss of all side clamped and simply supported GALRE-5 panel for thickness aspect ratio a/h = 83.33. From the figures, it is clear that irrespective of boundary conditions, the STL of the panel increases with an increase in aspect ratio.

Fig. 22
figure 22

Effect of sound transmission loss for different aspect ratio with different boundary conditions

Full size image

4.4 Influence of thickness ratio

Vibro-acoustic behavior of the GLARE panel is investigated by varying a/h ratio for different a/b ratios. All side clamped boundary conditions with symmetric cross-ply \(\big [\mathbf{Al }/0^\circ /90^\circ /90^\circ /0^\circ /\mathbf{Al }\big ]_{s}\) laminate is considered for the detailed investigation. In this analysis, the thickness is maintained based on the manufactured GLARE-5 composite material with \(15\%\) of aluminum metal and \(85\%\) of composite material. This study’s focus is to see how vibration and acoustic characteristics behavior change according to the thickness parameter variation. The fundamental modal frequencies for different thickness ratios along with different aspect ratios are given in Table 9, and it shows that the frequency decreases with an increase in thickness ratio and increases with a decrease in thickness ratio.

Table 9 Modal frequencies for different thickness ratio with CCCC boundary condition
Full size table

Figure 23a and b shows the effect of thickness aspect ratio on average RMS velocity and radiation efficiency of GLARE panel with a/b =1. As expected, the modal density is higher for larger thickness aspect ratio and lower for smaller thickness aspect ratio. It is also observed that the radiation efficiency decreases with increase in thickness aspect ratio as shown in Fig. 23b. Similar trends have been observed for a/b = 1.5 and 2 as shown in Figs. 24a, b, 25a and b.

Fig. 23
figure 23

Effect of average RMS velocity and radiation efficiency for \({a/b} = 1\) with different thickness ratios

Full size image
Fig. 24
figure 24

Effect of average RMS velocity and radiation efficiency for \({a/b} = 1.5\) with different thickness ratios

Full size image
Fig. 25
figure 25

Effect of average RMS velocity and radiation efficiency for a/b = 2 with different thickness ratios

Full size image

Next, the acoustic response due to the change in aspect ratio is computed using the Rayleigh integral from each nodal velocities corresponding to each excitation frequency. Figure 26a and b shows the radiated sound power level and the overall sound power level of all side clamped GLARE panel at Octave frequencies for a/b ratio = 1. The variation in sound power level is very similar to the RMS velocity, as expected. The overall sound power level increases as the thickness aspect ratio decrease at a few Octave 1/3rd frequencies except at 500 Hz, 800 Hz and 100 Hz center frequencies for a/h = 83.33. This may be due to the increase in modal density at that Octave band region. Similar trends are observed for thickness aspect ratios 1.5 and 2 as shown in Figs. 27a, b, 28a and b.

Fig. 26
figure 26

Effect of sound power level and overall sound power level based on 1/3rd octave band frequency for a/b = 1 with different thickness ratios

Full size image
Fig. 27
figure 27

Effect of sound power level and overall sound power level based on 1/3rd octave band frequency for a/b = 1.5 with different thickness ratios

Full size image
Fig. 28
figure 28

Effect of sound power level and overall sound power level based on 1/3rd octave band frequency for a/b = 2 with different thickness ratios

Full size image

The effect of thickness aspect ratio on radiated sound directivity pattern of all side clamped GLARE panel for different aspect ratio at 1500 Hz is shown in Fig. 29a–c. From the figures, it is clear that the radiated sound pressure level increases with an increase in thickness aspect ratio. The variations in sound transmission loss due to the change in thickness aspect ratio for 1500 Hz are shown in Fig. 30a–c. Unlike the aspect ratio a/b = 83.333, the sound transmission loss of a/b = 1, 1.5 and 2 significantly increased for the decrease in thickness aspect ratio. This may be due to the increase in thickness of the GLARE panel.

Fig. 29
figure 29

Effect of sound pressure level at 1500 Hz for different thickness ratios

Full size image
Fig. 30
figure 30

Effect of sound transmission loss for different thickness ratios

Full size image

4.5 Influence of material percentage variation

The influence of various percentage combinations of aluminum and GFRC on vibration and acoustic characteristics is studied by considering symmetric cross-ply layup of the all-side clamped GLARE-5 panel. Table 10 shows the free vibration results of the GLARE panel and clearly indicates that the natural frequencies are increasing by adding aluminum with composite material. Therefore, one can select the appropriate Al and GFRC material percentages to fabricate a hybrid multilayered GLARE-5 panel to obtain enhanced vibro-acoustic properties.

Figure 31a and b shows the average RMS velocity of the GLARE panel for different material percentage variation along with different thickness ratio a/h = 83.33 and a/h = 5. The natural frequencies of 100 \(\%\) GFRC from Fig. 31a are less than 100 \(\%\) Al and are between GFRC and Al for other configurations. A similar trend is observed for the thick panel as seen in Fig. 31b. Figure 32a and b shows the radiation efficiency of the GALRE panel for different material percentage variation. As shown in the figures, the radiation efficiency shows a significant variation for the thin plate and no variation for the thick plate. The radiated sound power level for different material configurations is shown in Fig. 33a and b. Figures indicate that the radiated sound power level at natural frequencies and show significant variation with respect to the percentage of GFRC and aluminum. Further, the trend for thin and thick GLARE panels does not seem to be different.

Table 10 Material percentage variation from composite to aluminum
Full size table
Fig. 31
figure 31

Effect of average RMS velocity for various material \(\%\) variation

Full size image
Fig. 32
figure 32

Effect of radiation efficiency for various material \(\%\) variation

Full size image
Fig. 33
figure 33

Effect of sound power level for different material \(\%\) variation

Full size image

Figure 34a and b shows the STL due to change in material percentage variation for thin and thick panels, 100 \(\%\) Al shows better transmission loss than 100 \(\%\) GFRC and values for other configurations lie in between them. However, STL for the thin panel does not show much variation if its GFRC percentage is more than 50 \(\%\). Therefore, the percentage of GFRC should be kept as low as possible for high STL and at the same time, the percentage should be more than 50 \(\%\). This helps to reduce the weight of the GLARE for thin panels without compromising acoustic characteristics.

Fig. 34
figure 34

Effect of sound transmission loss for different material \(\%\) variation

Full size image

4.6 Influence of GLARE grades on acoustic characteristics

GLARE panels of different grades are considered to examine sound properties given in Table 1. The radiated sound power level and STL are examined for thin and thick plates with a/b ratios of 1 and 1.5. Figure 35a and b shows the radiated sound power level for square and rectangular thin plates. They indicate that the radiated sound power level does not vary much at the fundamental frequency and show significant variations for higher natural frequencies. Figure  36a and b shows the results of sound transmission loss of various GLARE grades panels. GLARE-4 and GLARE-5 grades exhibit low transmission loss than other grades for both square and rectangular panels. However, the trend does not differ significantly for all other grades.

Fig. 35
figure 35

Effect of sound power level for GLARE grades variation

Full size image
Fig. 36
figure 36

Effect of sound transmission loss for GLARE grades variation

Full size image

Similarly, thick GLARE panels with different grades are examined for acoustic characteristics. Figure 37a and b shows the radiated sound power level for square and rectangular thick panels. Unlike thin plates, all thick GLARE grades except GLARE-6 exhibit the same amount of radiated sound power at many resonant frequencies, regardless of the aspect ratio variations. Figure  38a and b shows similar trends in sound transmission loss for square and rectangular thick panels with all grades other than GLARE-4 and GLARE-5. This may be due to the high number of layers associated with GLARE-4 and GLARE-5 when compared to other GLARE grades.

Fig. 37
figure 37

Effect of sound power level for GLARE grades variation

Full size image
Fig. 38
figure 38

Effect of sound transmission loss for GLARE grades variation

Full size image

5 Conclusion

In this work, vibro-acoustic characteristic of a hybrid multilayer GLARE-5 composite panel is investigated using experimental and numerical approaches. GLARE-5 panel with aluminum and unidirectional glass fiber composite are fabricated using the hand layup process. A micromechanics approach was employed to determine the material properties. The free vibration characteristics of the panel are extracted using experimental modal analysis and the results are verified numerically using the finite element approach. Reddy’s higher-order shear deformation theory based non-confirming finite element was used for this purpose. MAC analysis was carried out to quantify the correlation between experimental and numerical results.

Modal superposition is a method of using the fundamental natural frequencies and mode shapes of the structure from the modal analysis to characterize the dynamic response characteristic of a structure with a steady harmonic excitation. The Rayleigh integral method is used to get the acoustic properties of the GLARE-5 panel. Vibro-acoustic behavior of GLARE-5 is investigated for different aspect ratios (a/b), boundary conditions (CCCC & SSSS), thickness aspect ratio (a/h), material percentage and GLARE grade variations. Results reveal that irrespective of aspect ratio combination of the low percentage of GFRC with Al exhibits enhanced vibration and acoustic characteristics than 100 \(\%\) of GFRC.

The below-mentioned observations were made with respect to vibration and sound response characteristics of GLARE panels:

  • Radiated sound power level of thin GLARE panel for CCCC and SSSS boundary conditions shows similar patterns for all aspect ratios. It is clear that the natural frequencies of the GLARE panel shifted to a higher level as the percentage of Al increases, and radiated sound power level showed distinct peaks irrespective of aspect ratios and boundary conditions.

  • Irrespective of different aspect ratios, the radiation efficiency of the GLARE panel decreases with an increase in thickness. The radiation efficiency of the thin GLARE panel not varied much for all aspect ratios except all side clamped panel with an aspect ratio (a/b) 2. In the same manner, the material percentage variations of all GLARE grades did not show considerable effects on radiation efficiency.

  • Thin and thick panels exhibited the same transmission loss for all the GLARE grade variations of GLARE except GLARE-4 and GLARE-5. It was also observed that GLARE-4 and GLARE-5 grades exhibit low transmission loss when compared to other grades for thin/thick square/rectangular panels. However, the trend does not differ significantly for all other grades. Further, it was found that the transmission loss of the GLARE panel not only depends on thickness but also on the number of composite layers used.

  • Irrespective of aspect ratio, combination of the low percentage of GFRC with Al exhibits enhanced vibration and acoustic characteristics than 100 percentage GFRC. Design guidelines for selecting Al and GFRC percentages are provided to obtain enhanced vibro-acoustic properties in hybrid multilayer GLARE panels.