Numerical analysis of steady-state performance of misaligned journal bearings with turbulent effect

Abstract

A theoretical analysis has been carried out to investigate into the effect of turbulence and journal misalignment on the steady-state characteristics of hydrodynamic journal bearings lubricated with micropolar fluid. The governing non-dimensional Reynolds equation applicable to turbulent micropolar lubrication has been solved numerically to obtain the film pressure distribution which was then used to determine the load carrying capacity, attitude angle, misalignment moment, end flow rate and frictional parameter. The turbulent shear coefficients have been computed by using the turbulent model proposed by Ng and Pan. The results suggest that the effect of turbulence is to increase the load carrying capacity and misalignment moment of the misaligned journal bearings, and this effect is more pronounced for micropolar fluid as compared to Newtonian fluid.

1 Introduction

Turbulence in journal bearings is very common phenomena nowadays in the applications of large turbomachinery operating at relatively high speed with large diameters and in machines using process fluids of low viscosity. In the field of turbulent lubrication, Prandtl’s mixing length concept was used by Constantinescu [1, 2] and Reichardt’s eddy diffusivity concept was used by Ng and Pan [3] for the analysis of bearings operating in turbulent regime. Among these two turbulent models, application of Ng–Pan model of turbulent lubrication was suggested by Taylor et al. [4] for better and more accurate results.

In the literatures mentioned so far, the lubricants have been considered as Newtonian fluid. But in practice, most of the lubricants are blended with additives to improve the lubricating effectiveness. Moreover, after few cycles of operations, the lubricants often get contaminated with suspended particles or dirt. These makes the lubricant to behave as non-Newtonian fluid, and hydrodynamic lubrication theories developed for Newtonian fluids yield erroneous results for such lubricants. Therefore, to analyze the lubrication problem of such fluids, the theory of micropolar fluids [5] which are characterized by the presence of suspended rigid microstructure particles has been applied. The investigation on the lubrication theory of micropolar fluids was initiated by Allen and Kline [6]. Later on, many research works [7,8,9,10,11] had been carried out using the micropolar theory of lubrication to find out the effect of non-Newtonian lubricants on the bearing performances. So far, extensive works [12,13,14,15,16,17] have been carried out to analyze the steady-state characteristics on misaligned hydrodynamic journal bearings lubricated with non-Newtonian fluid. An analytical model was developed by Nikolakopoulos and Papadopoulos [18] to formulate a relationship between wear depth, misalignment angle and frictional force in case of journal bearing operating under severe lubricating conditions. Enhancement in friction coefficient and power loss was observed with increase in wear depth. A theoretical investigation on water-lubricated misaligned journal bearing with rigid bush materials has been carried out by Zhang et al. [19] to determine the load carrying capacity. In a recent work, Lv et al. [20] made an attempt to provide an efficient method in order to analyze equivalent supporting point location and load capacity of journal bearing with misalignment in vertical direction without using numerical simulation.

Until last century, the applications of turbulent lubrication theories were limited to the analysis of problems where the lubricants were assumed to be Newtonian. Early of this century, in a very interesting work, micropolar fluid theory has been combined with Constantinescu’s turbulent model by Faralli et al. [21] to obtain the modified Reynolds equation applicable to turbulent micropolar lubrication and analyze the steady-state characteristics of worn spherical bearings. Recently, the effect of turbulence on the static performance of misaligned hydrodynamic journal bearings lubricated with coupled stress fluids has been studied by Shenoy et al. [15]. In this work, an improvement of load capacity with reduced friction and end leakage flow has been observed for turbulent flow of lubricant. Following similar methodology, as suggested by Faralli et al. [21], the modified Reynolds equation applicable to turbulent micropolar lubrication has been derived by Das et al. [22] to analyze the steady-state performance characteristics of finite hydrodynamic journal bearings. However, no such literature is available up to date which analyzes the steady-state characteristics of misaligned journal bearings lubricated with micropolar fluid operating in turbulent regime. Hence, in this paper, an attempt has been made to extend the turbulent lubrication theory applicable to micropolar lubricants to predict the steady-state characteristics of misaligned finite journal bearings in terms of load carrying capacity, attitude angle, misalignment moment, end flow rate and frictional parameter.

2 Analysis

2.1 Modified Reynolds equation

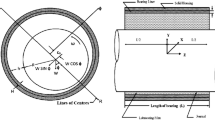
A schematic diagram of a misaligned hydrodynamic journal bearing used in the analysis is shown in Fig. 1. It is considered that the journal rotates with an angular velocity of Ω rad/s about its axis. The governing modified steady-state Reynolds equation for misaligned journal bearing operating under micropolar lubrication in turbulent regime is given by [21]

Fig. 1

Configuration of the misaligned journal bearing geometry

$$ \frac{\partial }{\partial x}\left[ {\Phi _{x} \left( {h,\Lambda ,N} \right)\frac{\partial p}{\partial x}} \right] + \frac{\partial }{\partial z}\left[ {\Phi _{z} \left( {h,\Lambda ,N} \right)\frac{\partial p}{\partial z}} \right] = \frac{1}{2}\mu U\frac{\partial h}{\partial x} $$

(1)

where $\Phi _{x,z} \left( {h,\varLambda ,N} \right) = \frac{{h^{3} }}{{k_{x,z} }} +\Lambda ^{2} h - \frac{{N\varLambda h^{2} }}{2}\coth \left( {\frac{Nh}{2\varLambda }} \right)$

$$ N = \left( {\frac{\chi }{2\mu + \chi }} \right)^{{\frac{1}{2}}} ,\;\Lambda = \left( {\frac{\gamma }{4\mu }} \right)^{{\frac{1}{2}}} ,\;\mu_{v} = \mu + \frac{1}{2}\chi $$

Using the following substitutions:

$$ \theta = \frac{x}{R};\quad \bar{z} = \frac{z}{L};\quad \bar{h} = \frac{h}{C};\quad \bar{p} = \frac{{pC^{2} }}{{\mu\Omega R^{2} }};\quad l_{m} = \frac{C}{\Lambda }. $$

Equation (1) can be written in the as follows:

$$ \frac{\partial }{\partial \theta }\left[ {\Phi _{\theta } \left( {\bar{h},l_{m} ,N} \right)\frac{{\partial \bar{p}}}{\partial \theta }} \right] + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \frac{\partial }{{\partial \bar{z}}}\left[ {\Phi _{{\overline{z} }} \left( {\bar{h},l_{m} ,N} \right)\frac{{\partial \bar{p}}}{{\partial \overline{z} }}} \right] = \frac{1}{2}\frac{{\partial \bar{h}}}{\partial \theta } $$

(2)

where

$$ \Phi _{{\theta ,\overline{z} }} \left( {\overline{h} ,l_{m} ,N} \right) = \frac{{\overline{h}^{3} }}{{k_{{\theta ,\overline{z} }} }} + \frac{{\overline{h} }}{{l_{m}^{2} }} - \frac{1}{2}\frac{{\overline{h}^{2} N}}{{l_{m} }}\coth \left( {\frac{{\overline{h} \cdot l_{m} \cdot N}}{2}} \right); $$

$$ k_{\theta } = 12 + A_{\theta } \left( {Re\bar{h}} \right)^{{B_{\theta } }} \quad {\text{and}}\quad k_{{\bar{z}}} = 12 + C_{{\bar{z}}} \left( {Re\bar{h}} \right)^{{D_{{\bar{z}}} }} $$

The values of the turbulent shear constants (A_θ, B_θ, $\, C_{{\bar{z}}}$ and $\, D_{{\bar{z}}}$) have been obtained from the work of Ng et al. [3].

As the film thickness $\overline{h}$ is a function of $\theta {\text{ and }}\bar{z}$, $\Phi _{{\theta ,\bar{z}}} \left( {\bar{h}_{0} ,l_{m} ,N} \right)$ are also functions of $\theta {\text{ and }}\bar{z}$.

In case of journal misalignment inside the bearing as shown in Fig. 1, the expression for non-dimensional film thickness is expressed as

$$ \overline{h} = 1 + \varepsilon_{0} \cos (\theta - \alpha_{0} ) + \varepsilon^{\prime } \, \bar{z}\cos (\theta - \alpha_{0} - \psi ) $$

(3)

where, $\varepsilon^{\prime } ,\varepsilon_{\hbox{max} }^{\prime } ,\alpha_{0}$ and ψ are already defined by Das et al. [14].

$$ \varepsilon^{\prime } = D_{m} \varepsilon_{\hbox{max} }^{\prime } $$

(4)

where, D_m is known as degree of misalignment as defined below

$$ D_{m} = \frac{{\xi_{e} }}{{\xi_{m} }}. $$

2.2 Boundary conditions

The following boundary conditions are used to solve Eq. (2) to obtain the steady-state film pressure distribution.

$$ \begin{aligned} & ( {\text{i) }}\bar{p}\left( {\theta , { 0}} \right) = \bar{p}\left( {\theta , { 1}} \right) = 0\quad ( {\text{Ambient presssure at both bearing ends)}} \\ & ( {\text{ii) }}\frac{{\partial \bar{p}\left( {\theta_{c} , \, \bar{z}} \right)}}{\partial \theta } = 0 , { }\bar{p}\left( {\theta , { }\overline{z} } \right) = 0\quad {\text{for}}\quad \theta \ge \theta_{\text{c}} \quad ( {\text{Cavitation condition)}} \\ \end{aligned} $$

(5)

where θ_c represents the angular coordinate at which film cavitations occur.

2.3 Numerical procedure

Equation (2) is discretized into the finite central difference form with rectangular mesh size of $\left( {\Delta \theta \times \Delta \bar{z}} \right)$ and solved by the Gauss–Seidel iterative procedure using the successive over-relaxation scheme, satisfying the boundary conditions as given in (5).

Equation (2) is discretized into finite difference form as follows:

$$ \frac{\partial }{\partial \theta }\left[ {\Phi _{\theta } \left( {\bar{h},l_{m} ,N} \right)\frac{{\partial \bar{p}}}{\partial \theta }} \right] + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \frac{\partial }{{\partial \bar{z}}}\left[ {\Phi _{{\bar{z}}} \left( {\bar{h},l_{m} ,N} \right)\frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right] = \frac{1}{2}\frac{{\partial \bar{h}}}{\partial \theta } $$

$$ {\text{or}},\;\frac{{\partial\Phi _{\theta } }}{\partial \theta } \cdot \frac{{\partial \bar{p}}}{\partial \theta } +\Phi _{\theta } \frac{{\partial^{2} \bar{p}}}{{\partial \theta^{2} }} + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \frac{{\partial\Phi _{{\bar{z}}} }}{{\partial \bar{z}}} \cdot \frac{{\partial \bar{p}}}{{\partial \bar{z}}} + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2}\Phi _{{\bar{z}}} \frac{{\partial^{2} \bar{p}}}{{\partial \bar{z}^{2} }} = \frac{1}{2}\frac{{\partial \overline{h} }}{\partial \theta } $$

$$ \begin{aligned} {\text{or}},\; &\Phi _{1}^{\prime } \left[ {\frac{{\left( {\bar{p}} \right)_{i + 1,j} - \left( {\bar{p}} \right)_{i - 1,j} }}{2\Delta \theta }} \right] +\Phi _{\theta } \left[ {\frac{{\left( {\bar{p}} \right)_{i + 1,j} - 2\left( {\bar{p}} \right)_{i,j} + \left( {\bar{p}} \right)_{i - 1,j} }}{{\Delta \theta^{2} }}} \right] \\ & \quad + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} .\Phi _{2}^{\prime } \left[ {\frac{{\left( {\bar{p}} \right)_{i,j + 1} - \left( {\bar{p}} \right)_{i,j - 1} }}{2\Delta \theta }} \right] + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2}\Phi _{{\bar{z}}} \left[ {\frac{{\left( {\bar{p}} \right)_{i,j + 1} - 2\left( {\bar{p}} \right)_{i,j} + \left( {\bar{p}} \right)_{i,j - 1} }}{{\Delta \bar{z}^{2} }}} \right] \\ & = \frac{1}{2}\left\{ { - \varepsilon_{0} \sin (\theta - \alpha_{0} ) - \varepsilon^{\prime } \bar{z}\sin (\theta - \alpha_{0} - \psi )} \right\} \\ \end{aligned} $$

$$ \begin{aligned} {\text{or}},\; & 2\left[ {\frac{1}{{\left( {\Delta \theta } \right)^{2} }} + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \left( {\frac{{\Phi _{{\bar{z}}} }}{{\Phi _{\theta } }}} \right)\frac{1}{{\left( {\Delta \bar{z}} \right)^{2} }}} \right]\left( {\bar{p}} \right)_{i,j} = \left[ {\frac{1}{{\left( {\Delta \theta } \right)^{2} }} + \frac{1}{2}\left( {\frac{{\Phi _{1}^{\prime } }}{{\Phi _{\theta } }}} \right)\frac{1}{\Delta \theta }} \right]\left( {\bar{p}} \right)_{i + 1,j} \\ & \quad + \left[ {\frac{1}{{\left( {\Delta \theta } \right)^{2} }} - \frac{1}{2}\left( {\frac{{\Phi _{1}^{\prime } }}{{\Phi _{\theta } }}} \right)\frac{1}{\Delta \theta }} \right]\left( {\bar{p}} \right)_{i - 1,j} + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \left[ {\left( {\frac{{\Phi _{{\bar{z}}} }}{{\Phi _{\theta } }}} \right)\frac{1}{{\left( {\Delta \bar{z}} \right)^{2} }} + \frac{1}{2}\left( {\frac{{\Phi _{2}^{\prime } }}{{\Phi _{\theta } }}} \right)\frac{1}{{\Delta \bar{z}}}} \right]\left( {\bar{p}} \right)_{i,j + 1} \\ & \quad + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \left[ {\left( {\frac{{\Phi _{{\bar{z}}} }}{{\Phi _{\theta } }}} \right)\frac{1}{{\left( {\Delta \bar{z}} \right)^{2} }} - \frac{1}{2}\left( {\frac{{\Phi _{2}^{\prime } }}{{\Phi _{\theta } }}} \right)\frac{1}{{\Delta \bar{z}}}} \right]\left( {\bar{p}} \right)_{i,j - 1} = \frac{1}{2}\left\{ { - \varepsilon_{0} \sin (\theta - \alpha_{0} ) - \varepsilon^{\prime } \bar{z}\sin (\theta - \varepsilon_{0} - \psi )} \right\} \\ \end{aligned} $$

(6)

where

$$ \begin{aligned}\Phi _{1}^{\prime } & = \frac{{\partial \varPhi_{\theta } }}{\partial \theta } = \frac{{\partial \varPhi_{\theta } }}{{\partial \overline{h} }} \cdot \frac{{\partial \overline{h} }}{\partial \theta } \\ & = \left[ {\frac{{\bar{h}^{2} }}{{k_{\theta } }}} \right.\left\{ {3 - \frac{{a_{\theta } b_{\theta } \left( {Re\bar{h}} \right)^{{b_{\theta } }} }}{{k_{\theta } }}} \right\} + \frac{1}{{l_{m}^{2} }} - \frac{{\bar{h}N}}{{l_{m} }}\coth \left( {\frac{{\bar{h} \cdot l_{m} \cdot N}}{2}} \right) \\ & \quad + \frac{{N^{2} \bar{h}^{2} }}{4}\left. {{\text{cosech}}^{ 2} \left( {\frac{{\bar{h} \cdot l_{m} \cdot N}}{2}} \right)} \right] \, \times \left\{ { - \varepsilon_{0} \sin (\theta - \alpha_{0} ) - \varepsilon^{\prime } \bar{z}\sin (\theta - \alpha_{0} - \psi )} \right\} \, \\ & =\Phi _{\theta }^{\prime } \cdot \left\{ {\varepsilon_{0} \sin (\theta - \alpha_{0} ) + \varepsilon^{\prime } \bar{z}\sin (\theta - \alpha_{0} - \psi )} \right\} \\ \end{aligned} $$

$$ {\text{and}},\;\Phi _{2}^{\prime } = \frac{{\partial\Phi _{{\bar{z}}} }}{{\partial \bar{z}}} = \frac{{\partial\Phi _{{\bar{z}}} }}{{\partial \bar{h}}} \cdot \frac{{\partial \bar{h}}}{{\partial \bar{z}}} $$

$$ \begin{aligned}\Phi _{2}^{\prime } & = \left[ {\frac{{\bar{h}^{2} }}{{k_{{\bar{z}}} }}} \right.\left\{ {3 - \frac{{c_{{\overline{z} }} d_{{\overline{z} }} \left( {Re\bar{h}} \right)^{{d_{{\overline{z} }} }} }}{{k_{{\bar{z}}} }}} \right\} + \frac{1}{{l_{m}^{2} }} - \frac{{\bar{h}.N}}{{l_{m} }}\coth \left( {\frac{{\bar{h} \cdot l_{m} \cdot N}}{2}} \right) \\ & \quad + \frac{{N^{2} \bar{h}^{2} }}{4}\left. {{\text{cosech}}^{ 2} \left( {\frac{{\bar{h} \cdot l_{m} \cdot N}}{2}} \right)} \right] \, \times \left\{ {\varepsilon^{\prime } \cos (\theta - \alpha_{0} - \psi )} \right\} \, \\ & =\Phi _{{\bar{z}}}^{\prime } \cdot \left\{ {\varepsilon^{\prime } \cos (\theta - \alpha_{0} - \psi )} \right\} \\ \end{aligned} $$

Now, Eq. (6) is written in the following form:

$$ \left( {\bar{p}} \right)_{i,j} = C_{1} \left( {\bar{p}} \right)_{i + 1,j} + C_{2} \left( {\bar{p}} \right)_{i - 1,j} + C_{3} \left( {\bar{p}} \right)_{i,j + 1} + C_{4} \left( {\bar{p}} \right)_{i,j - 1} + C_{5} $$

(7)

where,

$$ \begin{aligned} C_{0} & = 2\left[ {\frac{1}{{\left( {\Delta \theta } \right)^{2} }} + \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \left( {\frac{{\Phi _{{\bar{z}}} }}{{\Phi _{\theta } }}} \right)\frac{1}{{\left( {\Delta \bar{z}} \right)^{2} }}} \right];\quad C_{1} = \frac{1}{{C_{0} \cdot \left( {\Delta \theta } \right)^{2} }}\left[ {1 + \frac{1}{2}\left( {\frac{{\Phi _{1}^{\prime } }}{{\Phi _{\theta } }}} \right).\Delta \theta } \right]; \, \\ C_{2} & = \frac{1}{{C_{0} \cdot \left( {\Delta \theta } \right)^{2} }}\left[ {1 - \frac{1}{2}\left( {\frac{{\Phi _{1}^{\prime } }}{{\Phi _{\theta } }}} \right).\Delta \theta } \right];\quad C_{3} = \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \frac{1}{{C_{0} \cdot \left( {\Delta \bar{z}} \right)^{2} }}\left[ {\left( {\frac{{\Phi _{{\bar{z}}} }}{{\Phi _{\theta } }}} \right) + \frac{1}{2}\left( {\frac{{\Phi _{2}^{\prime } }}{{\Phi _{\theta } }}} \right).\Delta \bar{z}} \right] \\ C_{4} & = \frac{1}{4}\left( {\frac{D}{L}} \right)^{2} \frac{1}{{C_{0} \cdot \left( {\Delta \bar{z}} \right)^{2} }}\left[ {\left( {\frac{{\Phi _{{\bar{z}}} }}{{\Phi _{\theta } }}} \right) - \frac{1}{2}\left( {\frac{{\Phi _{2}^{\prime } }}{{\Phi _{\theta } }}} \right).\Delta \bar{z}} \right];\quad C_{5} = \frac{{ - \varepsilon_{0} \sin (\theta - \alpha_{0} ) - \varepsilon^{\prime } \bar{z}\sin (\theta - \alpha_{0} - \psi )}}{{2C_{0} .\varPhi_{\theta } }} \\ \end{aligned} $$

To implement the above numerical procedure, a uniform grid size is adopted in the circumferential (120 divisions) and axial direction (20 divisions). Iteration is started considering initial pressures at all mesh points as zeros, and the computed grid pressures are modified through successive over-relaxation scheme. For calculating film pressure at each set of input parameters, the following convergence criterion is adopted.

$$ \left| {1{ - }\frac{{\sum {\bar{p}_{\text{old}} } }}{{\sum {\overline{p}_{\text{new}} } }} \, } \right| \le 0. 0 0 0 1 $$

With the computed values of the pressures, the steady-state performance characteristics of the misaligned journal bearings are calculated.

3 Steady-state bearing performance characteristics

3.1 Load carrying capacity and attitude Angle

The steady-state load components along the line of centers and perpendicular to the line of centers in non-dimensional form are given by

$$ \bar{W}_{r} = - \int\limits_{0}^{1} {\int\limits_{0}^{{\theta_{c} }} {\bar{p}.\cos \theta .{\text{d}}\theta .} {\text{d}}\bar{z}} $$

(8a)

$$ \bar{W}_{\phi } = - \int\limits_{0}^{1} {\int\limits_{0}^{{\theta_{c} }} {\bar{p}.\sin \theta .{\text{d}}\theta .} {\text{d}}\bar{z}} $$

(8b)

Utilizing the above non-dimensional load components, the non-dimensional steady-state load carrying capacity and attitude angle are computed as follows:

$$ \bar{W} = \sqrt {\left( {\bar{W}_{r} } \right)^{2} + \left( {\bar{W}_{\phi } } \right)^{2} } $$

(9)

$$ \phi_{0} = \tan^{ - 1} \left\{ {\frac{{\bar{W}_{\phi } }}{{\bar{W}_{r} }}} \right\} $$

(10)

3.2 Misalignment moment

For steady-state operating conditions, the misalignment moments are calculated directly from the steady-state pressure distributions. The radial and tangential components of misalignment moment in non-dimensional form are expressed as

$$ \bar{M}_{r} = - \int\limits_{0}^{1} {\int\limits_{0}^{{\theta_{c} }} {\bar{p}.\cos \theta .\bar{z}.{\text{d}}\theta .} {\text{d}}\bar{z}} $$

(11a)

$$ \bar{M}_{\phi } = - \int\limits_{0}^{1} {\int\limits_{0}^{{\theta_{c} }} {\bar{p}.\sin \theta .\bar{z}.{\text{d}}\theta .} {\text{d}}\bar{z}} $$

(11b)

Total misalignment moment in dimensionless form is thus obtained as follows:

$$ \bar{M} = \sqrt {\left( {\bar{M}_{r} } \right)^{2} + \left( {\bar{M}_{\phi } } \right)^{2} } $$

(11c)

3.3 End flow rate

The volume flow rate in dimensionless form along the z-axis form the bearing rear end, front end and as a whole is expressed by

$$ \bar{Q}_{\text{RearEnd}} = - \int\limits_{0}^{{\theta_{c} }} {\Phi _{{\bar{z}}} \left( {l_{m} ,N,\overline{h} } \right)\left( {\frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right)_{{\bar{z} = 0}} {\text{d}}\theta } $$

(12a)

$$ \bar{Q}_{\text{FrontEnd}} = - \int\limits_{0}^{{\theta_{c} }} {\Phi _{{\bar{z}}} \left( {l_{m} ,N,\bar{h}} \right)\left( {\frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right)_{{\bar{z} = + 1}} {\text{d}}\theta } $$

(12b)

$$ \bar{Q}_{z} = \bar{Q}_{\text{RearEnd}} + \bar{Q}_{\text{FrontEnd}} $$

(12c)

The non-dimensional end flow rate is thus obtained first by finding numerically $\left[ {\frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right]_{{\bar{z} = + 1}}$ following backward difference formula of order $\left[ {\left( {\Delta \bar{z}^{2} } \right)} \right]$ and then by numerical integration using Simpson’s one-third formula.

3.4 Frictional parameter

The non-dimensional frictional force is given by [14]

$$ \bar{F} = \int\limits_{0}^{1} {\int\limits_{0}^{{\theta_{c} }} {A.{\text{d}}\theta .} {\text{d}}\bar{z} + } \int\limits_{0}^{1} {\int\limits_{0}^{{\theta_{c} }} {A.\frac{{\left( {\bar{h}} \right)_{\text{cav}} }}{{\bar{h}}}.{\text{d}}\theta .} {\text{d}}\bar{z}} $$

(13)

where, $\left( {\bar{h}} \right)_{\text{cav}} = 1 + \varepsilon_{0} \cos \theta_{c}$

$$ A = \frac{{\bar{\tau }_{c} }}{{\bar{h} - \frac{2N}{{l_{m} }}\tanh \left( {\frac{{Nl_{m} \bar{h}}}{2}} \right)}} + \frac{{\bar{h}}}{2}.\frac{{\partial \bar{p}}}{\partial \theta } $$

The non-dimensional surface shear stress, $\bar{\tau }_{c}$ is obtained by considering the following expression as suggested by Taylor et al. [4] for dominant Couette flow

$\bar{\tau }_{c} = 1 + 0.00099\left( {Re_{h} } \right)^{0.96}$ where, $\bar{\tau }_{c} = \frac{{\tau_{c} h}}{{\mu\Omega R}}$

The frictional parameter is consequently obtained as follows:

$$ f\left( {{R \mathord{\left/ {\vphantom {R C}} \right. \kern-0pt} C}} \right) = \frac{{\bar{F}}}{{\bar{W}}} $$

(14)

4 Results and discussions

It is evident from Eq. (1) that the film pressure distribution and consequently the load carrying capacity, misalignment moment, end flow rate and frictional parameter depend on the parameters viz. the slenderness ratio (L/D), eccentricity ratio (ɛ₀), micropolar characteristic length (l_m), coupling number (N), degree of misalignment (D_m) and average Reynolds number (Re). A theoretical study has been carried out to analyze the steady-state performance of misaligned journal bearing under micropolar lubrication operating in turbulent flow regime.

4.1 Validation of results

As there is no available literature that gives the experimental data on this kind of analysis, the results of the present work have been validated by comparing the data obtained from the work of Elsharkawy [23] for laminar flow of Newtonian lubricant and presented in Figs. 2 and 3. Figure 2 presents the comparison of load capacity obtained in the present study and that obtained by Elsharkawy [23] for different values of degrees of misalignment. Figure 3 shows the comparison of values of frictional parameter obtained from the aforesaid two analyses.

Fig. 2

Comparison of values of load capacity obtained in the present study and by Elsharkawy [23]

Fig. 3

Comparison of values of frictional parameter obtained in the present study and by Elsharkawy [23]

The results of the present study have also been compared with those obtained by Das et al. [14] for laminar flow of micropolar lubricants and presented in Fig. 4. The comparison shows that the values obtained for load carrying capacity and frictional parameter vary marginally with those obtained by Das et al. [14]. Also in both the analysis, similar trend of variation of load carrying capacity and frictional parameters has been observed.

Fig. 4

Comparison of results obtained in the present study and by Das et al. [14]

4.2 Steady-state pressure profile

Pressure profiles for micropolar fluid lubricated misaligned journal bearing with l_m = 15.0, N² = 0.3 and D_m = 0.6 at L/D = 1.0,ɛ₀ = 0.4 are plotted and presented in Fig. 5a for laminar flow and in Fig. 5b for turbulent flow. It is observed that the pressure developed in case of turbulent flow is higher than that obtained in case of laminar flow of lubricant. With enhancement in Reynolds number, the turbulent shear coefficients k_θ and $k_{{\bar{z}}}$ increase, resulting in reduction in the values of the film thickness terms $\frac{{\bar{h}^{3} }}{{k_{\theta } }}$ and $\frac{{\bar{h}^{3} }}{{k_{{\bar{z}}} }}$. This causes an enhancement in pressure in the fluid film. Hence, higher film pressure is observed when the lubricant flow in the bearing is turbulent in nature.

Fig. 5

a Pressure profile of micropolar fluid at laminar flow, b Pressure profile of micropolar fluid at turbulent flow

4.3 Load carrying capacity and attitude Angle

The effect of D_m on dimensionless load carrying capacity and attitude angle as a function of l_m is shown in Fig. 6. It is seen that $\bar{W}$ decreases with an increase in D_m up to D_m = 0.5 and $\bar{W}$ increases considerably with further increase in D_m. This trend is reversed in case of attitude angle. Further, it is observed that for any value of D_m, load carrying capacity decreases as l_m → ∞. This is because of the fact that as l_m → ∞, the micropolar effect vanishes and the fluid converts to a Newtonian fluid. On the other hand, the micropolar effect becomes significant with decrease in the value of l_m, as the microrotational effect of the substructure present in the fluid imparts an additional spin viscosity to the lubricant. Hence, there is an increase in the effective viscosity of the micropolar fluid resulting in higher film pressure which in turn increases the load carrying capacity of the lubricant.

Fig. 6

Variation of $\bar{W}$ and $\phi_{0}$ with l_m for different values of D_m

Figure 7 shows the effect turbulence characterized by the average Reynolds number on $\bar{W}{\text{ and }}\varphi_{ 0}$ as a function of l_m. It is observed that for all values of l_m, the load carrying capacity and attitude angle increase with an increase in Re, and this effect is more pronounced at lower range of l_m. Also, the values of $\bar{W}$ gradually decreases with an increase in l_m and attains a steady value as l_m → ∞. This increase in $\bar{W}$ is due to the enhancement of film pressure with increase in Re, whereas, the attitude angle does not vary significantly with l_m.

Fig. 7

Variation of $\bar{W}$ and $\phi_{0}$ with l_m for different values of Re

4.4 Misalignment moment

Variation of misalignment moment, $\bar{M}$ with respect to l_m, is presented in Figs. 8 and 9 for different values of D_m and Re, respectively. The results show similar variation of misalignment moment as observed in case of load carrying capacity. This is because of the dependence of misalignment moment on film pressure only.

Fig. 8

Variation of $\bar{M}$ with l_m for different values of D_m

Fig. 9

Variation of $\bar{M}$ with l_m for different values of Re

4.5 End flow rate

Variation of end flow rate, $\bar{Q}_{z}$ with respect to l_m, is presented in Fig. 10 for various values of D_m. It can be noted that the effect of misalignment is to increase the end flow rate. Also, the characteristic length of micropolar fluid has negligible effect on end leakage flow when all other parameters are unchanged.

Fig. 10

Variation of $\bar{Q}_{z}$ with l_m for different values of D_m

It can be noted from the expressions that increase in Reynolds number results in increase in the value of turbulent shear coefficients and consequently decreasing the value of micropolar fluid functions. Also as the end flow rate depends on the micropolar function, the value of the end flow rate decreases with increase in Re. This phenomenon has been shown in Fig. 11.

Fig. 11

Variation of $\bar{Q}_{z}$ with l_m for different values of Re

4.6 Frictional parameter

The frictional parameter, f(R/C) is plotted as a function of l_m for various degrees of misalignment and presented in Fig. 12. It is observed that the effect of misalignment is to increase f(R/C) for all values of l_m. Further, f(R/C) increases with increase in l_m, indicating that the frictional parameter is maximum for the Newtonian fluids.

Fig. 12

Variation of f(R/C) with l_m for different values of D_m

Figure 13 shows the effect of Re on f(R/C) as a function of l_m. The results reveal that in general, the frictional parameter increases with l_m for a particular value of Re. The effect of Re is to reduce the frictional parameter up to around l_m = 25. Similar observations have been reported by Shenoy et al. [15] for non-Newtonian couple stress fluid. However, the trend gets reversed beyond l_m = 25, where the fluid gradually transforms to Newtonian fluid. The value of frictional parameter is found to be the lowest for laminar flow conditions at higher values of l_m(> 15).

Fig. 13

Variation of f(R/C) with l_m for different values of Re

5 Conclusions

From the above parametric analysis of turbulence, the following conclusions can be drawn:

• 1. For a misaligned journal bearing lubricated with micropolar fluid, the effect of turbulence is to increase film pressure, load carrying capacity, attitude angle and misalignment moment.

• 2. Turbulence reduces the end flow rate of misaligned journal bearings.

• 3. In turbulent flow regime, the frictional parameter is found to reduce with increase in Reynolds number at lower values of l_m, i.e., when the effect of micropolarity is high.

• 4. The effect of the degree of misalignment is to decrease the load carrying capacity and misalignment moment at lower misalignment. But when the misalignment is large, this trend gets reversed.

• 5. The effect of misalignment is to increase the end leakage flow and friction factor.