Keywords

1 Introduction

Hydrodynamic journal bearing is generally used for supporting radial load acting on rotating machines [1, 2] such as turbines, pumps, compressors, etc. In such bearings, the mating surfaces are separated by a thin film of lubricant. The film pressure required to support external load is generated by churning of lubricant in narrow passage between the bearing surfaces. Therefore, converging passage, viscous media and sufficient operating speed are prerequisite for safe and reliable operation of hydrodynamic journal bearings [2].

Since the first use of journal bearing [3], numerous theoretical/experimental investigations were carried out to examine and improve the performance of such bearing system. The performance of journal bearing significantly depends upon the geometry of bearing and lubricant employed during its service. Initial design of journal bearing system is mostly confined with circular shape of shaft and bearing. However, ever rising demands of higher production rate made the machines to operate under extremely heavy load and high speed. Under such stringent conditions, the conventional circular bearings are unable to produce desirable performance. Therefore, with the advancement in manufacturing technologies, non-circular bearings were more frequently produced and employed in turbo-machine applications. These non-circular bearing such as pressure dam bearing [4], elliptical bearings [5], multi-lobe bearings [6], titling pads bearings [7], etc. provides better rotor-dynamic performance and stability as compared to conventional circular bearings.

Recently, laser surface texturing [8, 9] is establishing as a new way of improving the tribo-performance of hydrodynamic bearings. In these techniques, micro-dimple and grooves patterns are generated over the bearing surface. These dimples act as numerous micro-bearings [8] and has the ability to enhance the performance level of tribo-pairs operating in different lubrication regimes. Many studies [8,9,10,11,12,13,14] have been reported examining the performance of textured surface fluid film bearing. Majorities of these studies reported a marked increase in the load carrying capacity [8, 11, 14] and reduction in coefficient of friction [8,9,10, 12], provided optimization of texture attributes under given operating conditions. Once the journal bearing is manufactured and employed in engineering applications, its performance can be effectively managed by an appropriate selection of type and quantity of lubricant. In most engineering applications, certain additives such viscosity improver agents, anti-friction, anti-wear agents, rust inhibitors, etc. [1, 2] are added to the base stock oil. This is done to impart specific characteristics to the lubricant. As a results of this, the lubricant during its intended use exhibits nonlinear behavior for shear-stress versus strain rate. Some experimental studies have been reported examining the effect of additives on coefficient of friction between tribo-pairs such as journal bearings [15, 16], sliding surface [17] and friction clutch [18]. Experimental and theoretical study from Wada and Hayashi [15] recommended that cubic shear-stress fluid model satisfactorily describes the non-Newtonian characters of lubricants blended with viscosity index improvers. However, then many theoretical investigations [19,20,21,22,23,24,25,26] have been reported investigating the effect of nonlinear behavior of lubricant on performance of fluid film bearings. The nonlinear behavior of lubricant in these studies has been characterized using theories/law such as couple-stress theory [19,20,21,22,23,24], micropolar theory [25], power law [26], cubic shear-stress law [15], etc. The couple-stress and micropolar theories are mainly concerned with effect of size of additives [18,19,20,21,22,23,24] on the performance of fluid film bearing systems, operating with non-Newtonian lubricant. It has been reported that an increase in characteristic length of additives and coupling number can enhance the load carrying capacity, increase minimum film thickness and decrease lubricant flow rate through the journal bearing system. Other theories such as power law, cubic shear-stress law, etc., define nonlinear relationship between shear-stress and strain rate. Numerical investigations [15, 24] have been reported on journal bearing operating with shear-thinning and shear-thickening lubricants, as described by cubic shear-stress law and power law fluid model.

The available published literature discussed above indicates that the non-Newtonian lubricants are commonly employed to enhance the performance of hydrodynamic journal bearing. It was reported that cubic shear-stress fluid model [15] satisfactorily approximates the shear-thinning behavior of commercial lubricants, containing long-chain polymer additives as viscosity index improvers. Some studies [15, 19, 23,24,25] are reported examining the steady-state performance of journal bearing, operating with non-Newtonian lubricants. To the best of author knowledge, very few studies are available dealing with influence of shear-thinning lubricant on dynamic performance of hydrodynamic journal bearing. In view of above, this study has been planned to examine the effect of shear-thinning nature of lubricant on the rotor-dynamic coefficient of hydrodynamic journal bearing system.

2 Mathematical Formulation

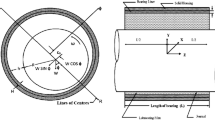
Figure 1 depicts the configuration of hydrodynamic journal bearing system under consideration. The non-Newtonian lubricant exhibiting shear-thinning behavior is supplied from a supply hole located at top of the bearing. The lubricant flow condition between journal and bearing is considered laminar, incompressible and iso-viscous. In steady-state operation, the flow of lubricant inside the clearance space is governed by generalized Reynolds equation described as flows:

$$\frac{\partial }{{\partial \overline{x}}}\left( {\overline{h}^{3} \overline{F}_{2} \frac{{\partial \overline{p}}}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{h}^{3} \overline{F}_{2} \frac{{\partial \overline{p}}}{{\partial \overline{z}}}} \right) = {\Omega }\frac{\partial }{{\partial \overline{x}}}\left[ {\left( {1 - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right)\overline{h}} \right] + \frac{{\partial \overline{h}}}{{\partial \overline{t}}}$$
(1)
$$\overline{x} = \frac{x}{{r_{j} }};\overline{z} = \frac{z}{{r_{j} }};\overline{h} = \frac{h}{{c_{r} }};\overline{r} = \frac{r}{{r_{j} }};\overline{p} = \frac{{p - p_{a} }}{{p_{r} }};\overline{\mu } = \frac{\mu }{{\mu_{r} }};p_{r} = \frac{{\mu_{r} \omega r_{j}^{2} }}{{c_{r}^{2} }};\overline{t} = t\omega$$
Fig. 1
figure 1

Journal bearing system and unwrapped bearing surface

Full size image

where \(\overline{F}_{o} ,\overline{F}_{1}\) and \(\overline{F}_{2}\) represent viscosity integrals of lubricant and describe as follows:

$$\overline{F}_{0} = \mathop \int \limits_{0}^{1} \frac{1}{{\overline{\mu }}}{\text{d}}\overline{z};\quad \overline{F}_{1} = \mathop \int \limits_{0}^{1} \frac{{\overline{z} }}{{\overline{\mu }}}{\text{d}}\overline{z};\quad \overline{F}_{2} = \mathop \int \limits_{0}^{1} \frac{{\overline{z} }}{{\overline{\mu }}}\left( {\overline{z} - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right){\text{d}}\overline{z}$$

The film thickness expression for journal bearing configuration is described as follows:

$$\overline{h} = 1 - \overline{x}*\cos \left( \alpha \right) - \overline{z}*\sin \left( \alpha \right)$$
(2)

The shear-stress versus strain rate relationship for lubricant is governed by Rabinowitsch fluid model.

$$\overline{\tau } + n\overline{\tau }^{3} = \overline{\gamma }$$
(3)
$$\overline{{\dot{\gamma }}} = \sqrt {\left[ {\frac{{\overline{h}}}{{\overline{\mu }}}\frac{{\partial \overline{p}}}{{\partial \overline{x}}}\left( {\overline{z} - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right) + \frac{{{\Omega } }}{{\overline{\mu }\overline{h}\overline{F}_{0} }}} \right]^{2} + \left[ {\frac{{\overline{h}}}{{\overline{\mu }}}\frac{{\partial \overline{p}}}{{\partial \overline{y}}}\left( {\overline{z} - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right)} \right]^{2} }$$
(4)

where n is known as fluid nonlinearity index.

In present work, finite element approach is used to solve Eq. 1 for computing film pressure distribution. The bearing surface is divided into sub-domains using 2D quadrilateral elements. The pressure within an element is assumed to be distributed linear along x- and z-direction.

$$\overline{p} = \mathop \sum \limits_{j = 1}^{4} \left[ {N_{j} \overline{p}_{j} } \right];\quad N_{j} = \frac{1}{4}\left( {1 + \xi_{i} \xi } \right)\left( {1 + \eta_{i} \eta } \right)$$
(5)

The weak form of Eq. 1 has been obtained using weighted residual approach. The shape function of primary variable is taken as weights.

$$\begin{aligned} & \mathop {\iint }\limits_{A}^{ } \left( {\frac{\partial }{{\partial \overline{x}}}\left( {\frac{{\overline{h}^{3} }}{{\overline{\mu }}}\overline{\varphi }\frac{\partial }{{\partial \overline{x}}}\left\{ {\mathop \sum \limits_{j = 1}^{4} \left( {\overline{p}_{j} N_{j} } \right)} \right\}} \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\frac{{\overline{h}^{3} }}{{\overline{\mu }}}\overline{\varphi }\frac{\partial }{{\partial \overline{z}}}\left\{ {\mathop \sum \limits_{j = 1}^{4} \left( {\overline{p}_{j} N_{j} } \right)} \right\}} \right)} \right. \\ & \quad \left. { - {\Omega } \frac{\partial }{{\partial \overline{x}}}\left[ {\left( {1 - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right)\overline{h}} \right] - \frac{{\partial \overline{h}}}{{\partial \overline{t}}}} \right)d\overline{x}d\overline{z} = 0 \\ \end{aligned}$$
(6)

The simplification of above Eq. 6 yields set of algebraic equations, and these elemental equations can be assembled in matrix form as described below.

$$\left[ {\overline{F} } \right]\left\{ {\overline{p}} \right\} = \left[ {\overline{Q} } \right] + {\Omega }\left[ {\overline{H} } \right] + \overline{{\dot{x}}}_{j} \left[ {\overline{S}_{j} } \right] + \overline{{\dot{z}}}_{j} \left[ {\overline{S}_{j} } \right]$$
(7)

The above equation depicts assembly of fluidity matrix, pressure vector, flow term, hydrodynamic term and squeeze terms along x- and z-direction, respectively.

Boundary condition:

  1. 1.

    At axial boundary:\(z = \pm L/2; p = p_{a}\)

  2. 2.

    At lubricant supply location:\(x = 0;2\pi r_{j} ; \overline{p} = p_{a} { }\)

  3. 3.

    Gaseous cavitation (Reynolds boundary condition) [26]: \(x = x_{c}\); \(\overline{p} = 0;\frac{\partial p}{{\partial x}} = 0\).

The solution of Eq. 7 under steady-state operation \(\left( {\overline{{\dot{x}}}_{j} = \overline{{\dot{z}}}_{j} = 0} \right)\) provides film pressure distribution on bearing surface. The integration of film pressure values on bearing area provides fluid film reaction.

$${\text{Film reaction:}}\quad \overline{F} = \left[ {\left( {\overline{F}_{x} } \right)^{2} + \left( {\overline{F}_{z} } \right)^{2} } \right]^{1/2} ;$$
(8)
$$\overline{F}_{x} = \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{0}^{2\pi } \overline{p}\cos \alpha {\text{d}}\overline{x}{\text{d}}\overline{z};\quad \overline{F}_{z} = \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{0}^{2\pi } \overline{p}\sin \alpha {\text{d}}\overline{x}{\text{d}}\overline{z};$$
$${\text{Frictional Torque:}}\quad \overline{T}_{f} = \mathop \int \limits_{ - 1}^{ + 1} \mathop \int \limits_{0}^{2\pi } \left( {\overline{h}\frac{{\partial \overline{p}}}{{\partial \overline{x}}}\left( {\overline{z} - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right) + \frac{{{\Omega } }}{{\overline{h}\overline{F}_{0} }}} \right){\text{d}}\overline{x}{\text{d}}\overline{z}$$
(9)

Newton–Raphson method is used to obtain dynamic state \(\left( {\overline{{\dot{x}}}_{j} \ne 0;\overline{{\dot{z}}}_{j} \ne 0} \right)\) solution of Eq. 7. This will provide fluid film pressure gradient along x- and z-direction, which can be used to describe film stiffness and damping coefficients.

$$\overline{k}_{ij} = - \frac{{\partial \overline{F}_{i} }}{{\partial \overline{x}_{j} }} \Rightarrow \overline{K} = - \left[ {\begin{array}{*{20}c} {\overline{k}_{11} } & {\overline{k}_{12} } \\ {\overline{k}_{21} } & {\overline{k}_{22} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\frac{{\partial \overline{F}_{x} }}{{\partial \overline{x}}}} & {\frac{{\partial \overline{F}_{x} }}{{\partial \overline{z}}}} \\ {\frac{{\partial \overline{F}_{z} }}{{\partial \overline{x}}}} & {\frac{{\partial \overline{F}_{z} }}{{\partial \overline{z}}}} \\ \end{array} } \right]$$
(10)
$$\overline{D}_{ij} = \frac{{\partial { }\overline{F}_{i} }}{{\partial \overline{{\dot{x}}}_{j} }} \Rightarrow \overline{D} = \left[ {\begin{array}{*{20}c} {\overline{D}_{11} } & {\overline{D}_{12} } \\ {\overline{D}_{21} } & {\overline{D}_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial \overline{F}_{x} }}{{\partial \overline{{\dot{x}}} }}} & {\frac{{\partial \overline{F}_{x} }}{{\partial \overline{{\dot{z}}} }}} \\ {\frac{{\partial \overline{F}_{z} }}{{\partial \overline{{\dot{x}}} }}} & {\frac{{\partial \overline{F}_{z} }}{{\partial \overline{{\dot{z}}} }}} \\ \end{array} } \right]$$
(11)

The dynamic coefficients of bearing system are used to compute the threshold speed \((\omega_{t} )\) margin of journal bearing.

$$\omega_{t} = \left[ {\frac{{\overline{m}_{{\text{c}}} }}{F}} \right]^{1/2}$$
(12)

where \(\overline{m}_{{\text{c}}}\) is critical mass of journal, whose value depend upon the film direct and cross-couple stiffness and damping coefficients. The system becomes stable if mass of journal becomes lesser than the critical mass of the bearing system.

3 Solution Procedure

The analysis presented in preceding section has been used to simulate hydrodynamic journal bearing. The analytical solution of Reynolds equation (Eq. 1) is a cumbersome process due to nonlinear nature of partial differential equation. Therefore, finite element numerical technique is used to obtain solution of problem. The bearing input parameters are listed in Table 1. Bearing surface is divided into discrete regions using 4-node quad elements, and film pressure has been computed iteratively, using Newton–Raphson’s method. A grid size of 50*.

Table 1 Bearing geometric and operating condition
Full size table

A total of 20 nodes have been taken to generate mesh-free numerical results. The solution scheme adopted to perform finite element simulation of bearing is presented in Fig. 2. The convergence of iterative scheme is based on eccentricity of the bearing. A convergence (Eq. 13) of order of 10−05 is defined on eccentricity between successive iteration. Once the convergence criteria are satisfied, film pressure and performance indices mentioned in previous section of the manuscript will be computed.

$$\left| {\frac{{\left[ {\left( {\Delta \overline{x}_{j}^{i} } \right)^{2} + \left( {\Delta \overline{z}_{j}^{i} } \right)^{2} } \right]^{1/2} }}{{\left[ {\left( {\overline{x}_{j}^{i} } \right)^{2} + \left( {\overline{z}_{j}^{i} } \right)^{2} } \right]^{1/2} }}} \right| \le 10^{ - 05}$$
(13)
Fig. 2
figure 2

Solution scheme

Full size image

Figure 3 depicts validation of mathematical model/numerical solution scheme with available published [23] results for hydrodynamic journal bearings. The finite element method based solution scheme depicted in Fig. 2 has been used to reproduce the numerical results of reference study [23]. Figure 3 shows variation in load supporting capacity of finite journal bearing with respect to eccentricity ratio. It can be clear seen that result from two schemes are in good agreement with each other. This justifies the accuracy of solution scheme to numerically simulate hydrodynamic journal bearing.

Fig. 3
figure 3

Load supporting capacity versus eccentricity ratio [23]

Full size image

4 Results and Discussion

In this section, numerical results are discussed, obtained following numerical simulation of hydrodynamic journal bearings. Influence of external load and shear-thinning (n) behavior of lubricant is examined on the performance indicators of the hydrodynamic journal bearing. With a value of fluid nonlinearity index (n) approaching to zero, the lubricant is going to exhibit Newtonian character. The performance of bearing is examined in terms of physical quantitates such as film pressure, min. film thickness, film frictional torque and film rotor-dynamic coefficient.

Figure 4 depicts influence of lubricant nonlinearity index (n) on fluid film pressure distribution for bearing operating under varying external load. It can be seen that for a given external load, an increase in nonlinearity has very little effect on maximum value of fluid as well as pressure distribution. However, an increase in external load value significantly affects peak value of film pressure and its distribution in bearing domain. This might be due to that fact that to sustain heavy low, the fluid has to generate higher magnitude of fluid film pressure values on the bearing surface. The effect of lubricant nonlinearity index (n) and external load on minimum film thickness is depicted in Fig. 5. A continuous reduction has been observed with respect to increase in the external load imposed on bearing system. Also, as lubricant nonlinearity index is increased, a significant reduction in min. film thickness has been reported. This is because an increase in n leads to a reduction in the apparent viscosity of lubricant. The reduction in min. film thickness with respect to n is noticed to be lying in the range of −22.83 to −31.88%, as the non-dimensional external load is increased from 1.5 to 2.2 (Fig. 5).

Fig. 4
figure 4

Pressure distribution in bearing for Newtonian and shear-thinning lubricant as a function of external load

Full size image
Fig. 5
figure 5

Min. film thickness versus load

Full size image
Fig. 6
figure 6

Frictional torque \((\overline{{\varvec{T}}}_{{\varvec{f}}} )\) versus load

Full size image

Figure 6 presents the influence of external load and shear thinning behavior of lubricant on film frictional torque. It has been found that by increasing the external load, the frictional torque of system continuously increases. Further, it was observed that with an increase in shear-thinning coefficient/fluid nonlinearity index (n), the frictional torque in the system reduces significantly. This can be accounted for the reduction in the apparent viscosity of the lubricant for an increase in n. Although the use of non-Newtonian lubricant (n = 0.5, 1) reduces friction torque in the bearing system, maximum percentage increase in frictional torque w.r.t external load is noticed to be maximum for non-Newtonian lubricant (31.8, 32.5%) as compared to Newtonian lubricant (+20.4%).

The numerical results for direct film stiffness coefficient \((\overline{K}_{xx} \;{\text{and}}\;\overline{K}_{zz} )\user2{ }\) are presented in Figs. 7 and 8. It has been observed that an increase in external load leads to a reduction the stiffness coefficient \(\overline{K}_{xx}\). The shear-thinning nature of lubricant is reporting to enhancing the value of \(\overline{K}_{xx}\). On the contrary, the stiffness coefficient \((\overline{K}_{zz} )\) is noticed to be enhanced with an increase in external load. Also, the shear-thinning behavior of lubricant is noticed to reduce the direct stiffness coefficient \(\overline{K}_{zz}\). However, this effect is found to be diminished progressively with an increase in external load. Figures 9 and 10 depicts the influence of fluid nonlinearity index on direct film damping coefficient \((\overline{D}_{xx} \;{\text{and}}\;\overline{D}_{zz} )\user2{ }\) of the bearing system operating under a wide range of external load. It has been found that increase in external load tends to increase the damping coefficients of journal bearing. Further, the shear-thinning behavior (n = 0.5, 1) of lubricant is also noticed to be enhance the damping coefficients. The effect of n on damping coefficient is noticed to profound at higher values of external load acting on the system. The \(\overline{D}_{xx}\) is reported to gradually increase from 1.8% to 4.5%, with an increase in external load from 1.5 to 2.2. A substantially higher gain (6.7–18.7%) has been observed in \(\overline{D}_{zz}\) by the use of shear-thinning lubricant (n = 1), when external load has been increased from 1.5 to 2.2.

Fig. 7
figure 7

Stiffness coefficient \((\overline{{\varvec{K}}}_{{{\varvec{xx}}}} )\) versus load

Full size image
Fig. 8
figure 8

Stiffness coefficient \((\overline{{\varvec{K}}}_{{{\varvec{zz}}}} )\) vs load

Full size image
Fig. 9
figure 9

Damping coefficient \((\overline{{\varvec{D}}}_{{{\varvec{xx}}}} )\) versus load

Full size image
Fig. 10
figure 10

Damping coefficient \((\overline{{\varvec{D}}}_{{{\varvec{zz}}}} )\) versus load

Full size image

Figure 11 depicts variations in the threshold speed margin of bearing for an increase in external load acting on the system. The threshold speed margin depends upon direct and cross-coupled stiffness and damping coefficients. It can be seen that threshold speed margin of bearing system almost decreases linearly with a gradual increase in the external load. Further, it has been found that shear-thinning behavior of lubricant slightly reduces (−0.3 to −0.38%) the threshold speed of the hydrodynamic journal bearing system.

Fig. 11
figure 11

Threshold speed margin \(\left( {{\varvec{\omega}}_{{\varvec{t}}} } \right)\) versus load

Full size image

5 Conclusions

Following conclusion can be drawn from the numerical simulation of hydrodynamic journal bearing operating with shear-thinning lubricant.

  • The shear-thinning of lubricant has minimal effect on maximum film pressure but significantly reduces (−31.88%) the min. fluid film thickness of journal bearing system under given operating conditions.

  • The film frictional torque significantly reduces (−18.5 to −5.8%) owing to the use of shear-thinning lubricant. The reduction in frictional torque is noticed to be larger at lower values of external load acting on the system.

  • The shear-thinning of lubricant and external load is noticed to be beneficial in enhancing the film rotor-dynamic coefficients stiffness \((\overline{K}_{zz} ,\overline{D}_{xx} \;{\text{and}}\;D_{zz} )\) of the hydrodynamic journal bearing.

  • An increase in external load is reported to significantly reduces the threshold speed margin of the journal bearing; however, threshold speed margin is noticed to be almost invariant to shear-thinning of lubricant.