On three-dimensional MHD Oldroyd-B fluid flow with nonlinear thermal radiation and homogeneous–heterogeneous reaction

Abstract

This exploration studies a new mathematical model that highlights the impact of homogeneous–heterogeneous reactions on the flow of three-dimensional Oldroyd-B fluid past a bidirectional stretched surface. Here, homogeneous reaction is described by cubic autocatalysis and heterogeneous reaction is indicated by first-order process. Additional impacts of nonlinear thermal radiation and variable thermal conductivity are also taken into account. Flow analysis is materialized in attendance of magnetohydrodynamic, heat generation/absorption and free convection. Convective heat boundary condition is also engaged in the present problem. Homotopy analysis method is betrothed to elucidate the nonlinear system of partial differential equations. A comparison to a previously done study is also added to substantiate existing results; hence, dependable results are being exhibited. Graphs of important parameters versus all distributions are also given to elucidate their physical aspects. It is reported that temperature profile is an increasing function of Biot number. It is further noted that impact of strength of homogeneous and heterogeneous reactions on concentration profile are conflicting.

1 Introduction

Non-Newtonian fluids have diverse engineering and industrial applications like paper production, biomechanics, oil drilling and plastic production. Many examples of non-Newtonian fluid may be quoted like applesauce, suspension and colloidal solutions, tomato ketchup, sugar solution, exotic lubricants, condensed milk, soaps, cosmetic products and clay coatings. No single constitutive relation can exhibit varied physical structures of these fluids. In general, non-Newtonian fluids [1,2,3,4,5,6,7,8,9,10] are categorized into three leading groups: the integral type; the differential type; and the rate type. A good number of attempts in case of differential type fluids can be quoted because mathematical modeling of such fluids is much simpler in comparison with rate type fluids. Differential type fluids describe shear stress in the form of velocity components. However, very few attempts may be found in the recent literature’s survey discussing rate type fluids. Maxwell fluid is a rate type fluid that only provides information about relaxation time but no information regarding retardation time. Nevertheless, Oldroyd-B fluid [11] has the ability to provide information about both relaxation and retardation times. This fluid model shows viscoelastic physiognomies of dilute polymeric solutions with normal flow conditions. Some latest attempts discussing Oldroyd-B fluid flows include a study by Hayat et al. [12]. They examined the impact of homogeneous and heterogeneous (h–h) reactions on two-dimensional MHD Oldroyd-B fluid in the presence of Cattaneo–Christov heat flux model. Then, Shehzad et al. [13] analyzed analytical solution of 3D Oldroyd-B fluid flow in attendance of Cattaneo–Christov heat flux. This was followed by an exploration by Mahanthesh et al. [14] who computed numerical solution of 3D Oldroyd-B fluid flow with heat generation/absorption and nonlinear thermal radiation past a surface which is stretched in a nonlinear way. Afterward, Sandeep and Reddy [15] analyzed numerically MHD flow of Oldroyd-B fluid across a horizontal surface in attendance of thermal and solutal stratification and cross-diffusion. Then, Mustafa [16] obtained analytical solution of mixed convective Oldroyd-B fluid with non-Fourier heat flux approach. Recently, Hayat et al. [17] discussed analytical solution of time-dependent 2D Oldroyd- B fluid flow past a non-porous stretched surface with impacts of nonlinear thermal radiation and Joule heating. Effects of heat generation/absorption with viscous dissipation with zero mass flux at the surface and convective heat conditions are also considered.

There are several chemical reacting systems which involve a number of h–h reactions occurring simultaneously. Fewer reactions proceed very sluggishly or even not at all unless a catalyst is present there. Since the h–h reactions interact in the system, therefore, the rate of product formation and reactant species’ consumption varies with time. These reactions may include crops damage via freezing, hydrometallurgical industry, fog formation and dispersion, chemical processing equipment design and chemical processing equipment design. Recently, great interest in this thought-provoking idea is seen by researchers and scientists. Among these, Ramzan et al. [18] studied numerical solution of 2D magnetohydrodynamic flow of Williamson fluid near stagnation point in attendance of h–h reactions and Cattaneo–Christov heat flux with convective conditions at the boundary. Then, Hayat et al. [19] examined the series solution of the flow of second-grade fluid past a stretched cylinder in the presence of h–h reactions, Joule heating and viscous dissipation. Later, Yasmeen et al. [20] elaborated the flow of ferrofluid with effects of h–h reactions and magnetic dipole over a linearly stretching surface. This was followed by a study by Maria et al. [21] who discussed series solution of Jeffrey fluid with h–h reactions in attendance of convective boundary condition and applied magnetic field and many therein [22,23,24,25,26].

It is noted that most of the literature available on the subject deals with influence of homogeneous–heterogeneous reactions in varied scenarios in two-dimensional flows. Fewer explorations are also available discussing impact of h–h reactions in 3D. But no study so far has been carried out taking into account simultaneous effects of both homogeneous heterogeneous reactions and nonlinear thermal radiation in the three-dimensional Oldroyd-B fluid flow in the presence of heat generation/absorption. Additional effects of variable thermal conductivity and magnetohydrodynamic with convective boundary condition are also taken into consideration. This study may be the first in its own capacity. Homotopy analysis method (HAM) [27,28,29,30,31] is employed to solve highly nonlinear system of equations. The behavior of different sundry parameters on velocity, temperature and concentration fields is highlighted with graphical illustrations. Comparison to a previous study in limiting case is also made to corroborate our results.

2 Mathematical formulation

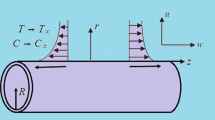
We assume 3D flow of MHD Oldroyd-B fluid with simultaneous effects of h–h reactions and nonlinear thermal radiative heat flux occupying the region $z\ge 0,$ past a surface stretched along x and $y$directions with velocities $u=ax$ and $v=by$, respectively. It is further assumed that temperature far away from the surface $T_{\infty }$ is much smaller as compared to the temperature at the surface $T_\mathrm{w}$. Along z-axis, fluid is taken electrically conducting in attendance of constant magnetic field Bo as shown in Fig. 1. Because of our supposition of small Reynolds number, induced magnetic field is overlooked. A nonlinear thermal diffusivity and the effect of heat generation absorption are considered during the formulation of energy equation. Modified Fourier’s law known as Cattaneo–Christov heat flux model is used to see the behavior of thermal relaxation time during non-Newtonian fluid flow. It is further assumed that the temperature of the bidirectional stretching sheet is maintained constant by considering the convective boundary condition. An investigation of two chemical species A and B with h–h reactions is performed. For cubic autocatalysis, the homogeneous reaction is given by [8]

Fig. 1

Geometry of the problem

$$\begin{aligned} A+2B\rightarrow 3B,{\text{ rate }}=k_{c}ab^{2}. \end{aligned}$$

(1)

However, on the catalyst surface there is only heterogeneous reaction represented by:

$$\begin{aligned} A\rightarrow B,{\text{ rate }}=k_{s}a, \end{aligned}$$

(2)

where $k_{c},k_{s}$ and a, b are rate constants and concentrations of the chemical species A and B, respectively. The constitutive equations of Oldroyd-B fluid (incompressible) model are appended by

$$\begin{aligned} \mathrm{div} \mathbf {V}= 0, \end{aligned}$$

(3)

$$\begin{aligned} \rho \frac{{\rm d}\mathbf {V}}{\mathrm{d}t}= \mathrm{div}\mathbf {T.} \end{aligned}$$

(4)

Here, extra stress tensor $\mathbf {S}$ and the Cauchy stress tensor $\mathbf { T}$ are defined as

$$\begin{aligned} \mathbf {T}= & {} -p\mathbf {I}+\mathbf {S}, \end{aligned}$$

(5)

$$\begin{aligned} \mathbf {S}= & {} \lambda _{1}\frac{D\mathbf {S}}{Dt}=\mu \left( A_{1}+\lambda _{2} \frac{DA_{1}}{Dt}\right) , \end{aligned}$$

(6)

with D / Dt is the covariant differentiation and fluid relaxation and retardation time is represented by $\mathbf {\lambda }_{1}$ and $\lambda _{2}$, respectively. The first Rivlin–Ericksen tensor $A_{1}$ is defined as

$$\begin{aligned} A_{1}=\mathrm{grad}\mathbf {V+}\left( \mathrm{grad}\mathbf {V}\right) ^{\prime }, \end{aligned}$$

(7)

where $\prime$ specifies the matrix transpose and the velocity field $\mathbf {V}$ is represented by

$$\begin{aligned} \mathbf {V=}\left[ u\left( x,y,z\right) ,v\left( x,y,z\right) ,w\left( x,y,z\right) \right] , \end{aligned}$$

(8)

The derivative D / Dt is [32] given by

$$\begin{aligned} \frac{Da_{i}}{Dt}=\frac{\partial a_{i}}{\partial t} +u_{r}a_{i,r}-u_{i,r}a_{r}. \end{aligned}$$

(9)

the energy and the species equations in the vector form are defined as

$$\begin{aligned} \rho C_{p}\left( V.\nabla T\right) =\nabla .q-\nabla q_{r}+Q^{*}\left( T-T_{\infty }\right) \end{aligned}$$

(10)

with q is heat flux and is defined by the Cattaneo–Christov model as

$$\begin{aligned} q+\lambda _{3}\left[ \frac{\partial q}{\partial t}+V.\nabla q-q.\nabla V+\left( \nabla .V\right) q\right] =\nabla \left( kT\right) \end{aligned}$$

(11)

The species concentration equations in the vector form are defined as

$$\begin{aligned} V.\nabla a&= D_{A}^{2}\nabla a-k_{c}ab^{2} \end{aligned}$$

(12)

$$\begin{aligned} V.\nabla b&= D_{B}^{2}\nabla b+k_{c}ab^{2} \end{aligned}$$

(13)

Following the instructions given in [32] and then adopting the boundary layer postulations [33], we have [14, 34]:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial \upsilon }{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(14)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+\upsilon \frac{\partial u}{\partial y}+w\frac{ \partial u}{\partial z}+\lambda _{1}\left( \begin{array}{c} u^{2}\frac{\partial ^{2}u}{\partial x^{2}}+\upsilon ^{2}\frac{\partial ^{2}u }{\partial y^{2}}+w^{2}\frac{\partial ^{2}u}{\partial z^{2}}+ \\ 2u\upsilon \frac{\partial ^{2}u}{\partial x\partial y}+2\upsilon w\frac{ \partial ^{2}u}{\partial y\partial z}+2uw\frac{\partial ^{2}u}{\partial x\partial z} \end{array} \right) \nonumber \\&=\nu \left( \frac{\partial ^{2}u}{\partial z^{2}}+\lambda _{2}\left( \begin{array}{c} u\frac{\partial ^{3}u}{\partial x\partial z^{2}}+\upsilon \frac{\partial ^{3}u}{\partial y\partial z^{2}}+w\frac{\partial ^{3}u}{\partial z^{3}}- \\ \frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial z^{2}}-\frac{ \partial u}{\partial y}\frac{\partial ^{2}\upsilon }{\partial z^{2}}-\frac{ \partial u}{\partial z}\frac{\partial ^{2}w}{\partial z^{2}} \end{array} \right) \right) -\frac{\sigma B_{o}^{2}}{\rho }\left( u+\lambda _{1}w\frac{ \partial u}{\partial z}\right) +g\beta \left( T-T_{\infty }\right) , \end{aligned}$$

(15)

$$\begin{aligned}&u\frac{\partial \upsilon }{\partial x}+v\frac{\partial \upsilon }{\partial y} +w\frac{\partial \upsilon }{\partial z}+\lambda _{1}\left( \begin{array}{c} u^{2}\frac{\partial ^{2}\upsilon }{\partial x^{2}}+v^{2}\frac{\partial ^{2}\upsilon }{\partial y^{2}}+w^{2}\frac{\partial ^{2}\upsilon }{\partial z^{2}}+ \\ 2uv\frac{\partial ^{2}\upsilon }{\partial x\partial y}+2vw\frac{\partial ^{2}\upsilon }{\partial y\partial z}+2uw\frac{\partial ^{2}\upsilon }{ \partial x\partial z} \end{array} \right) \nonumber \\&=\nu \left( \frac{\partial ^{2}\upsilon }{\partial z^{2}}+\lambda _{2}\left( \begin{array}{c} u\frac{\partial ^{3}\upsilon }{\partial x\partial z^{2}}+v\frac{\partial ^{3}\upsilon }{\partial y\partial z^{2}}+w\frac{\partial ^{3}\upsilon }{ \partial z^{3}}- \\ \frac{\partial \upsilon }{\partial x}\frac{\partial ^{2}\upsilon }{\partial z^{2}}-\frac{\partial \upsilon }{\partial y}\frac{\partial ^{2}\upsilon }{ \partial z^{2}}-\frac{\partial \upsilon }{\partial z}\frac{\partial ^{2}w}{ \partial z^{2}} \end{array} \right) \right) -\frac{\sigma B_{o}^{2}}{\rho }\left( v+\lambda _{1}w\frac{ \partial \upsilon }{\partial z}\right) , \end{aligned}$$

(16)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+\upsilon \frac{\partial T}{\partial y}++w \frac{\partial T}{\partial z}=\frac{1}{\rho C_{P}}\frac{\partial }{\partial z }\left( \alpha \frac{\partial T}{\partial z}\right) \nonumber \\&-\lambda _{3}\left( \begin{array}{c} u^{2}\frac{\partial ^{2}T}{\partial x^{2}}+\upsilon ^{2}\frac{\partial ^{2}T }{\partial y^{2}}+w^{2}\frac{\partial ^{2}T}{\partial z^{2}}+2u\upsilon \frac{\partial ^{2}T}{\partial x\partial y} \\ +2\upsilon w\frac{\partial ^{2}T}{\partial y\partial z}+2uw\frac{\partial ^{2}T}{\partial x\partial z}+\left( u\frac{\partial u}{\partial x}+\upsilon \frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right) \frac{ \partial T}{\partial x}+ \\ \left( u\frac{\partial \upsilon }{\partial x}+\upsilon \frac{\partial \upsilon }{\partial y}+w\frac{\partial \upsilon }{\partial z}\right) \frac{ \partial T}{\partial y}+\left( u\frac{\partial w}{\partial x}+\upsilon \frac{ \partial w}{\partial y}+w\frac{\partial w}{\partial z}\right) \frac{\partial T}{\partial z} \end{array} \right) -\frac{1}{\rho C_{p}}\frac{\partial q_{r}}{\partial z}+\frac{Q^{*}}{\rho C_{P}}\left( T-T_{\infty }\right) , \end{aligned}$$

(17)

$$\begin{aligned}&u\frac{\partial a}{\partial x}+v\frac{\partial a}{\partial y}+w\frac{ \partial a}{\partial z}=D_{A}\frac{\partial ^{2}a}{\partial z^{2}} -k_{c}ab^{2}, \end{aligned}$$

(18)

$$\begin{aligned}&u\frac{\partial b}{\partial x}+v\frac{\partial b}{\partial y}+w\frac{ \partial b}{\partial w}=D_{B}\frac{\partial ^{2}b}{\partial z^{2}} +k_{c}ab^{2}, \end{aligned}$$

(19)

with u, v and w are the velocities along x-,  y- and $z-\mathrm{axes}$, respectively. Here, $\nu ,\sigma ,B_{0}, T,C_{p},\rho , D_{A}, D_{B}, \lambda _{3}, \alpha$ and $\lambda _{1}$ denote kinematic viscosity, electrical conductivity, uniform magnetic field, temperature, specific heat, fluid density, diffusion coefficients, thermal relaxation time, variable thermal conductivity and retardation time, respectively. Equations (10–15) are supported by the boundary conditions given below

$$\begin{aligned} \left. \begin{aligned}&u=cx,\ \upsilon =dy,~w=0,\ -k_{h}\frac{\partial T}{\partial z}=h_{f}\left( T_\mathrm{w}-T\right) ,\\&D_{A}\frac{\partial a}{\partial z}=k_{s}a,\ D_{B}\frac{\partial b}{\partial z }=-k_{s}a,~{\text{at}}\ z=0, \\&u\rightarrow 0,\upsilon \rightarrow 0,\ a\rightarrow a_{o},\ b\rightarrow 0, \ T\rightarrow T_{\infty }\ {\text{as}}\,z\rightarrow \infty , \end{aligned}\right\} \end{aligned}$$

(20)

where $h_{f}$ and $~k_{h}$ are heat transfer coefficient and thermal conductivity with a, b and $a_{0}$ are positive-dimensional constants. Using the following transformations [35]

$$\begin{aligned} \left. \begin{aligned}&u=U_{w}(x)=cxf^{\prime }\left( \eta \right) ,~\upsilon =V_{w}(y)=cyg^{\prime }\left( \eta \right) ,~w=-\sqrt{c\nu }\left( f\left( \eta \right) +g\left( \eta \right) \right) , \\&\theta \left( \eta \right) =\frac{T-T_{\infty }}{T_{w}-T_{\infty }},~\eta = \sqrt{\frac{c}{\nu }}z,~b=a_{0}h\left( \eta \right) ,~a=a_{0}\phi \left( \eta \right) . \end{aligned}\right\} \end{aligned}$$

(21)

The variable thermal conductivity [35] is given by $~\epsilon =\frac{ k_{w}-k_{\infty }}{k_{\infty }}$ with $k_{\infty }$ and $k_{w}~$ are the fluid-free stream conductivity and the thermal conductivity at wall, respectively, also in Eq. $T=T_{\infty }\left( \left( \theta _{w}-1\right) \theta \left( \eta \right) +1\right) ,$ with $\theta _{w}=\frac{T_\mathrm{w}}{ T_{\infty }}.$ Using above transformations, requirement of Eq. (10) is fulfilled spontaneously, nevertheless, Eqs. (11–16) take the form

$$\begin{aligned}&f^{\prime \prime \prime }+\left( M^{2}\beta _{1}+1\right) \left( f+g\right) f^{\prime \prime }-f^{\prime 2}-M^{2}f^{\prime }+\beta _{1}\left( 2\left( f+g\right) f^{\prime }f^{\prime \prime }-\left( f+g\right) ^{2}f^{\prime \prime \prime }\right) + \nonumber \\&\beta _{2}\left( \left( f^{\prime \prime }+g^{\prime \prime }\right) f^{\prime \prime }-\left( f+g\right) f^{\prime \prime \prime \prime }\right) +Gr_{x}\theta =0, \end{aligned}$$

(22)

$$\begin{aligned}&g^{\prime \prime \prime }+\left( M^{2}\beta _{1}+1\right) \left( f+g\right) g^{\prime \prime }-g^{\prime 2}-M^{2}g^{\prime }+\beta _{1}\left( 2\left( f+g\right) g^{\prime }g^{\prime \prime }-\left( f+g\right) ^{2}g^{\prime \prime \prime }\right) + \nonumber \\&\beta _{2}\left( \left( f^{\prime \prime }+g^{\prime \prime }\right) g^{\prime \prime }-\left( f+g\right) g^{\prime \prime \prime \prime }\right) =0, \end{aligned}$$

(23)

$$\begin{aligned}&\left( 1+\epsilon \theta \right) \theta ^{\prime \prime }+\epsilon \theta ^{\prime 2}+Pr\left( f+g\right) \theta ^{\prime }-PrS\left( \left( f+g\right) ^{2}\theta ^{\prime \prime }+\left( f+g\right) \left( f^{\prime }+g^{\prime }\right) \theta ^{\prime }\right) \nonumber \\&+\Pr Q\theta +\frac{4}{3}Rd\left( \left( \theta _{w}-1\right) \theta +1\right) ^{3}\theta ^{\prime \prime }+4Rd\left( \theta _{w}-1\right) \left( \left( \theta _{w}-1\right) \theta +1\right) ^{2}\theta ^{\prime 2}=0, \end{aligned}$$

(24)

$$\begin{aligned}&\phi ^{\prime \prime }+Sc\left( f+g\right) \phi ^{\prime }-Sc\gamma _{1}\phi h^{2}=0, \end{aligned}$$

(25)

$$\begin{aligned}&\zeta h^{\prime \prime }+Sc\left( f+g\right) h^{\prime }+Sc\gamma _{1}\phi h^{2}=0, \end{aligned}$$

(26)

$$\begin{aligned} \left. \begin{aligned}&f(0)=0,\ f^{\prime }(0)=1,~g(0)=0, g^{\prime }(0)=\lambda ,~\phi ^{\prime }\left( 0\right) =\gamma _{2}~\phi \left( 0\right) ,\\&\theta ^{\prime }\left( 0\right) =-\delta \left( 1-\theta \left( 0\right) \right) ,~\zeta h^{\prime }\left( 0\right) =-\gamma _{2}~\phi \left( 0\right) ,\\&f^{\prime }(\infty )\rightarrow 0,\ f^{\prime \prime }(\infty )\rightarrow 0,~g^{\prime }\left( \infty \right) \rightarrow 0,~g^{\prime \prime }\left( \infty \right) \rightarrow 0, \\&\phi \left( \infty \right) \rightarrow 1,\ h\left( \infty \right) \rightarrow 0,~\theta \left( \infty \right) \rightarrow 0, \end{aligned}\right\} \end{aligned}$$

(27)

where$\ Pr,~Gr_{x},~M,~\theta _{w},~\epsilon ,~\delta ,~Q,~\beta _{1}~$ and $\beta _{2},~Sc,~Rd,~\lambda ,\gamma _{1}~$ and$~\ \gamma _{2},~\zeta ~$ and S  are the Prandtl number, local Grashof number, magnetic field strength, temperature ratio parameter, thermal conductivity parameter, Biot number, heat generation/absorption parameter, Deborah numbers in terms of relaxation and retardation time, Schmidt number, thermal radiation parameter, ratio of stretching rate, measure of strength of homogenous and heterogeneous reactions, ratio of diffusion coefficient and Deborah number w.r.t relaxation time of heat flux. The values of these parameters are given below:

$$\begin{aligned} \left. \begin{aligned}&Pr = \frac{\mu C_{p}}{k},\ M^{2}=\frac{\sigma B_{o}^{2}}{\rho c},~\delta = \frac{h_{f}}{k}\sqrt{\frac{\nu }{c}},~\beta _{1}=\lambda _{1}a,\ \beta _{2}=\lambda _{2}a,~\theta _{w}=\frac{T_{w}}{T_{\infty }}, \\&Rd = \frac{4\sigma ^{*}T_{\infty }^{3}}{kk^{*}},~{Re}_{x}=\frac{u_{w}x}{\nu },~Q=\frac{Q^{*}}{c\rho C_{P}},~Gr_{x}=\frac{g\beta \left( T_{w}-T_{\infty }\right) }{c^{2}x}, \\&Sc = \frac{\nu }{D_{A}},\ \lambda =\frac{d}{c},~\gamma _{1}=\frac{k_{c}a_{0}^{2}}{c},~\gamma _{2}=\frac{k}{D_{A}}\ \sqrt{\frac{\nu }{c}},\ \zeta =\frac{D_{B}}{D_{A}},~S=\lambda _{3}a. \end{aligned}\right\} \end{aligned}$$

(28)

The result that $D_{A}$ and $D_{B}$ are same, i.e.,  $\zeta =1~$ is because of our supposition that diffusion coefficients related to chemical species A and B are having the same size. That is why we have

$$\begin{aligned} \phi \left( \eta \right) +h\left( \eta \right) =1. \end{aligned}$$

(29)

Now, Eqs. (21) and (22) yield

$$\begin{aligned} \phi ^{\prime \prime }+Sc\left( f+g\right) \phi ^{\prime }-Sc\gamma _{1}\phi \left( 1-\phi \right) ^{2}=0, \end{aligned}$$

(30)

with boundary conditions

$$\begin{aligned} \phi ^{\prime }(0)=\gamma _{2}\phi (0),\ \phi (\infty )=1. \end{aligned}$$

(31)

The local Nusselt number in dimensional form is given by

$$\begin{aligned} Nu_{x}=\frac{xq_{w}}{k(T_{w}-T_{\infty })}, \end{aligned}$$

(32)

where

$$\begin{aligned} q_{w}=\left. -k\left( \frac{\partial T}{\partial z}\right) +q_{r}\right| _{z=0}. \end{aligned}$$

(33)

Dimensionless form of Nusselt number is

$$\begin{aligned} Nu_{_{x}}{Re}_{x}^{-1/2}=-\left( 1+\frac{4}{3}Rd\left( \left( \theta _{w}-1\right) \theta \left( 0\right) +1\right) ^{3}\right) \theta ^{\prime }\left( 0\right) . \end{aligned}$$

(34)

3 Homotopic solutions

There are many numerical and analytical techniques which can be used to solve the system of Eqs. (22–26). Among these, the most commons are finite difference method [36] shooting method [37, 38] Fehlberg–Runge–Kutta integration [39] Successive linearization method [40]. The choice of Homotopy analysis method (HAM) is because of its edge on the other contemporary techniques. The HAM is a powerful analytical method, suggested by Liao [41] in 1992, has following advantages in comparison with the other techniques;

• It is independent of the choice of small or large parameter.

• The convergence in case of HAM is guaranteed.

• An ample choice to select the initial guess estimates and the respective operators.

The preliminary guess estimates $\left( f_{0},g_{0},\theta _{0},\phi _{0}\right)$ and linear operators $\left( \mathcal {L}_{f},\mathcal {L}_{g}, \mathcal {L}_{\theta },\mathcal {L}_{\phi }\right)$ required for Homotopy analysis method are defined as:

$$\begin{aligned} \left. \begin{aligned}&f_{0}\left( \eta \right) =\left( 1-\exp \left( -\eta \right) \right) , { }g_{0}\left( \eta \right) =\lambda \left( 1-\exp \left( -\eta \right) \right) , \\&\theta _{0}\left( \eta \right) =\frac{\delta \exp \left( -\eta \right) }{1+\delta },~\phi _{0}\left( \eta \right) =1-\frac{1}{2}\exp \left( -\gamma _{2}\eta \right) , \end{aligned}\right\} \end{aligned}$$

(35)

and

$$\begin{aligned} \mathcal {L}_{f}\left( \eta \right) &=\frac{d^{3}f}{d\eta ^{3}}-\frac{df}{ d\eta },\,\mathcal {L}_{g}\left( \eta \right) =\frac{d^{3}g}{d\eta ^{3}}-\frac{ dg}{d\eta },\,\mathcal {L}_{\theta }\left( \eta \right) =\frac{ d^{2}\theta }{d\eta ^{2}}\\&\quad-\theta ,~\mathcal {L}_{\phi }\left( \eta \right) = \frac{d^{2}\phi }{d\eta ^{2}}-\phi . \end{aligned}$$

(36)

with the following properties

$$\begin{aligned} \left. \begin{aligned}&\mathcal {L}_{f}\left[ C_{1}+C_{2}\exp (\eta )+C_{3}\exp (-\eta )\right] =0, \\&\mathcal {L}_{g}\left[ C_{4}+C_{5}\exp (\eta )+C_{6}\exp (-\eta )\right] =0, \\&\mathcal {L}_{\phi }\left[ C_{7}\exp (\eta )+C_{8}\exp (-\eta )\right] =0, \\&\mathcal {L}_{\theta }\left[ C_{9}\exp (\eta )+C_{10}\exp (-\eta )\right] =0, \end{aligned}\right\} \end{aligned}$$

(37)

where $C_{i}$ $\left( i=1-10\right)$, the arbitrary constants. The values of these constants using given boundary conditions are

$$\begin{aligned} \left. \begin{aligned}&C_{2} = C_{5}=C_{7}=C_{9}=0, \qquad C_{3}=\left. \frac{\partial f_{m}^{\star }\left( \eta \right) }{\partial \eta }\right| _{\eta =0}, \\&C_{1} = -C_{3}-f_{m}^{\star }\left( 0\right) \qquad C_{6}=\left. \frac{\partial g_{m}^{\star }\left( \eta \right) }{\partial \eta } \right| _{\eta =0}, \\&C_{4}= -C_{6}-g_{m}^{\star }\left( 0\right) \qquad C_{8}=\frac{1}{1+\delta }\left( \left. \frac{\partial \theta _{m}^{*}\left( \eta \right) }{\partial \eta }\right| _{\eta =0}-\delta \theta _{m}^{*}\left( 0\right) \right) , \\&C_{10} = \frac{1}{1+\gamma _{2}}\left( \left. \frac{\partial \phi _{m}^{*}\left( \eta \right) }{\partial \eta }\right| _{\eta =0}-\gamma _{2}\phi _{m}^{*}\left( 0\right) \right) . \end{aligned}\right\} \end{aligned}$$

(38)

3.1 Convergence analysis

To determine the region of convergence for series solutions, the importance of auxiliary parameters $(\hslash _{f},~\hslash _{g},$ $\hslash _{\theta },~\hslash _{\phi })~$ cannot be denied. In Fig. 2, illustration for $\hslash -$ curves is presented to identify the same region. Tolerable ranges of parameters $\hslash _{f},~\hslash _{g},$ $\hslash _{\theta }~$ and $~\hslash _{\phi }$ are $-1.7\le \hslash _{f}\le -0.5,$ $-1.6\le \hslash _{g}\le -0.4,~-1.6\le \hslash _{\theta }\le -0.4~$ and $-2.0\le \hslash _{\phi }\le -0.4~$, respectively. The values of these parameters are in complete alignment to those numerical values found in Table 1.

Table 1 Convergence table for varied values of approximations when $\ \beta _{1}=0.2,\,\beta _{2}=0.2,\,M=0.4,\,\epsilon =0.3,\,\lambda =0.3,\,\delta =0.3,\,\Pr =2.0,\,Rd=0.3,\,Q=0.2,$ $\Psi =0.1,\,\theta _{w}=1.3,\,S=0.2,\,\gamma _{1}=0.4,\,\gamma _{2}=0.6,\,\mathrm{Sc}=0.7$

4 Results and discussion

Figures (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16) depict the behavior of emerging parameters on velocity, temperature and concentration distributions. All the computation is carried out for the following ranges of physical parameters [42] $\beta _{1}(0.0 \le \beta _{1} \le 1.0), \beta _{2}(0.0 \le \beta _{2} \le 1.0), Pr (\le 0.0 Pr \le 6.0), \epsilon (0.0 \le \epsilon \le 3.0), \gamma _{1} (0.0 \le \gamma _{1} \le 3.0), \gamma _{2} (0.1 \le \gamma _{2} \le 0.9), \delta (0.2 \le \delta \le 1.0), M (0.0 \le M \le 1.5), Rd (0.2 \le Rd \le 1.0), Q (0.2 \le Q \le 0.8), Gr (0.0 \le Gr \le 3.0), \theta _{w} (1.0 \le \theta _{w} \le 2.0), S (0.1 \le S \le 3.0)$ From Fig. 3, it is witnessed that the fluid velocity along the $x-$axis, i.e.,  $f^{\prime }(\eta )$ is a decreasing function of “Deborah number for relaxation time” $\beta _{1}$. Since, relaxation time and Deborah number have a direct relation. That is why higher relaxation time results in larger Deborah number which resist the flow of the fluid and ultimately lowers the fluid velocity distributions. In comparison, it is observed that both $\beta _{1}$ and $\beta _{2}$ have an opposite effect on velocity distribution. $\beta _{2}$ namely known as “Deborah number for retardation time” have an increasing trend for the velocity profile. As by the definition of $\beta _{2}$, it is directly related with the retardation time which is defined as the delay response to an applied force or simply the “delay of the elasticity.” It is observed from Fig. 4 that velocity of the fluid increases for the higher values of Deborah number $\beta _{2}$. Influence of Deborah number $\beta _{1}$ depending on relaxation time is displayed in Fig. 5. Temperature has a direct proportion to relaxation time. That is why higher values of $\beta _{1}$ corresponds to an increase in the temperature and hence its thermal boundary layer thickness.

Fig. 2

$\hbar$ for the function $f,~g,~\theta ,~\phi$

Fig. 3

Graph of $\beta _{1}$ versus $f^{\prime }(\eta )$

Fig. 4

Graph of $\beta _{2}$ versus $f^{\prime }(\eta )$

Fig. 5

Graph of $\beta _{1}$ versus $\theta (\eta )$

Fig. 6

Graph of Pr versus $\theta (\eta )$

Fig. 7

Graph of $\epsilon$ versus $\theta$

Fig. 8

Graph of $\gamma _{1}$ versus $\phi (\eta )$

Fig. 9

Graph of $\gamma _{2}$ versus $\phi (\eta )$

Figure 6 displays the impact of Prandtl number on the temperature profile. Thermal diffusivity has a reverse relation with Prandtl number. Hence, the conduction reduces for higher value of Pr which causes the reduction in temperature of the fluid. It is further observed that the large value of Pr resultantly lower the thermal boundary layer thickness. Figure 7 shows the impacts of thermal conductivity parameter $\epsilon$ on temperature field. Since, we know that liquids with higher thermal conductivity have increased temperature. The same effect may be visualized in Fig. 7. The reactants are expanded during the homogeneous reaction which triggers the reduction in concentration profile. This impact of strength of homogeneous reaction $\gamma _{1}$ on concentration distribution is depicted in Fig. 8. An opposite behavior in case of increasing values of strength of heterogeneous reaction $\gamma _{2}$ on concentration field is shown in Fig. 9. Here, concentration boosts because of less diffused particles. The impact of Biot number $\delta$ on the thermal boundary layer is elucidated in Fig. 10. As anticipated, the larger surface temperature is observed due to sturdier convection, instigating the thermal effect penetrating deeper into the fluid.

Fig. 10

Graph of $\delta$ versus $\theta (\eta )$

Fig. 11

Graph of M versus $f^{\prime }(\eta )$

Fig. 12

Graph of Rd versus $\theta (\eta )$

Fig. 13

Graph of Q versus $\theta (\eta )$

Fig. 14

Graph of Gr versus $f^{\prime }(\eta )$

Fig. 15

Graph of $\theta _{w}$ versus $\theta (\eta )$

Fig. 16

Graph of Pr and S versus $Nu_{x}Re_{x}^{-\frac{1}{2}}$

Figure 11 illustrates that velocity distribution function is diminishing function of magnetic field parameter M. Lorentz force generated by the applied magnetic transverse field will oppose the flow of the fluid and eventually a decrease in the velocity function is observed. Figure 12 shows the effect of radiation parameter Rd on temperature distribution. The rise in the fluid temperature is experimented because of increase in values of Rd. Actually, more heat transferred to the fluid because of high values of radiation parameter. Effect of heat generation/absorption parameter Q on the temperature field is portrayed in Fig. 13. It is perceived that temperature distribution is escalating function of Q. Fluid’s temperature is on rise because of growing values of Q that eventually boosts the temperature field. Figure 14 illustrates the influence of Grashof number Gr on velocity profile. As Grashof number Gr is the quotient of buoyancy to viscous force. Higher values of Gr mean stronger buoyancy force in comparison with viscous force. This act accelerates the fluid flow and enhanced fluid’s velocity is perceived.

Fig. 17

Streamline graph in 2D view

Fig. 18

3D view of streamlines for various values of $\beta _{2}$

Fig. 19

Graphical comparison with [34] for varied values of $\beta _{1}$ and $\lambda$

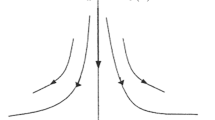
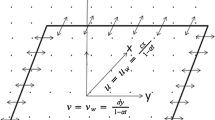
In Fig. 15, fluid’s temperature rise is observed versus increasing values of temperature ratio parameter $\theta _{w}.$ In fact, enhanced wall temperature is the core cause to boosts the temperature of the fluid by increasing values of $\theta _{w}$. In Fig. 16, effects of both Prandtl number Pr and Deborah number with respect to relaxation time of heat flux S are presented on Nusselt number. It is witnessed that Nusselt number escalates with increasing values of Pr. However, an opposite behavior is observed for growing values of S. Streamlines are basically the path traced out by the fluid particles within the flow. The graphs of streamlines with 2D and 3D views for various values of $\beta _{2}$ are portrayed in Figs. 17 and 18, respectively. Excellent alignment in both figures is found. Figure 19 gives a comparison of $-\theta ^{\prime }(0)$ for various values of $\beta _{1}$ and $\lambda$ by fixing other parameters for the first three values of Table 2 of [35]. An excellent agreement is seen in both numerical and graphical results.

Table 2 Local Nusselt number $-\,\theta ^{\prime }\left( 0\right)$ in the absence of homogeneous heterogeneous reactions, variable thermal conductivity, magnetohydrodynamic, heat generation and nonlinear thermal radiation when compared with Hayat et al. [34] for $\beta =0.5$

5 Conclusions

In this study, simultaneous effects of h–h reactions with nonlinear radiative heat flux on the flow of 3D Oldroyd fluid past a linearly bidirectional stretched surface are pondered. Impacts of magnetohydrodynamic with heat generation/absorption in the presence of variable thermal conductivity and free convection are also considered. The important points highlighted in this investigation are appended as follows:

• Nusselt number escalates and decreases for growing values of Prandtl number and Deborah number with respect to relaxation time of heat flux , respectively.

• Effects of strength of homogeneous–heterogeneous (h–h) reactions on concentration profile are opposite, as it decreases for the strength of homogenous reaction and increases for the heterogeneous reaction.

• Thermal boundary layer escalates with increasing values of Biot number.

• Larger values of magnetic field parameter cause an enhancement in velocity field.

• Temperature filed is mounting function of thermal conductivity and thermal radiation parameters.

• For larger values of local Grashof number, velocity profile also increases.

• Temperature distribution with its associated thermal boundary layer thickness is boosted for the larger values of temperature ratio parameter.