1 Introduction

There has been interest to study swirling flow for last many decades. The swirling flow occurs in various flow devices: ranging from centrifuges used for particle separation and collection of vortex tubes used for cooling to furnaces and combustion chambers. Vortex breakdown is beneficial in vortex reactors and burners, [12], as in these devices Vortex breakdown bubble acts as a flame holder and hence provides efficient mixing and stable combustion. In vortex suction devices, vortex breakdown also helps to collect hazardous emissions Shtern and Hussain [26].

A fundamental basis for vortex breakdown control is yet to be fully understood and developed. In general, the prediction and control of vortex breakdown are difficult because of involvement of many parameters, e.g., swirls-to-axial velocity ratio, external axial pressure gradient, flow divergence angle, and upstream flow profile. Any changes in these parameters or the presence of external disturbances strongly influence the vortex breakdown. Hence, for a basic research aimed at developing a vortex breakdown control strategy, it is desirable to have a well-defined and well-controlled flow. This requirement motivated present research to choose a confined flow that is free of any types of external disturbances.

A well-studied swirling flow problem is confined flow in a cylindrical container or cavity and the swirl is due to the end rotating wall or lid. It is commonly referred as lid-driven swirling flow. The appearances of vortex breakdowns (one, two, or three vortex breakdowns) depend upon the aspect ratio (AR = height/radius) of the cavity and Reynolds number (Re) which has been experimentally investigated and established first time by Escudier [8]. Escudier represented his experimental data in the Reynolds number (Re) and Aspect ratio (AR) plane clearly showing the stability boundaries for single, double, and triple breakdowns zones and boundary between oscillatory and steady flows. There are several advantages of studying the vortex breakdown in a confined flow. First, the role of control parameters can easily be established in the absence of unknown or unpredictable ambient disturbances. Second, the flow boundary conditions are well defined and hence allowing meaningful comparisons of experimental data Escudier [8] and numerical results Lopez [20]. Once the flow physics and the means of VB control are understood, one can extend this knowledge to practical problems of confined or unconfined flows. Lopez 20] carried out a detailed numerical study with an aim to develop a more detailed understanding of the physics of the flow and to clarify features that were not readily resolved from the experimental visualizations.

Velocity measurements of vortex breakdown in an enclosed cylinder were carried out experimentally by Fujimura et al. [10]. In their study, detailed flow patterns near the rotating disk are constructed by using the experimental data. Confined swirling flows of aqueous surfactant solutions due to a rotating disk in a cylindrical casing have been investigated by Tamano et al. [28]. They clarified the effects of the Reynolds number, elasticity number, and aspect ratio on the velocity profiles in their study. A region of rigid body rotation was found at the higher Reynolds number tested for C14TASal 0.4 wt%. Presence of axial temperature gradient greatly influences lid-driven swirling flow and appearance of vortex breakdowns at given combination of values of AR and Re. Such swirling flows under the influence of the axial temperature gradient has been investigated using CFD techniques by various researchers Lugt and Abboud [22], Kim and Hyun [18], Lee and Hyun [19] and Iwatsu [16]. Presence of axial magnetic field on lid-driven swilling flow also influences the vortex breakdown and stability of the flow and has been studied by various authors Bessaı¨h et al. [2], Bessaı¨h et al. [3] and Gelfgat and Gelfgat [11].

The effects of partial heating of top rotating lid with axial temperature gradient on vortex breakdown, in case of axisymmetric stratified lid-driven swirling flow, have been investigated by Dash and Singh [6]. In this study, the effect of partially heating the top rotating lid on the vortex breakdown size, shape, and location have been investigated.

Husain et al. [14] have experimentally visualized the vortex breakdown behavior for lid-driven swirls flow in a cylindrical cavity with the presence of thin axial stationary or rotating rod (i.e., in the cylindrical annulus region with its inner wall as surface of stationary or rotating rods). JØrgensen et al. [17] through their numerical simulation have shown the effects of thin axial rod on vortex breakdown. The presence of rotating rod, rotating in same or opposite direction with respect to the direction of rotation top lid, greatly influences the vortex breakdown. [Jørgensen et al. [17] have investigated the control of vortex breakdown in a closed cylindrical cavity with a rotating lid along with thin rotating or stationary rod positioned along the axis. They carried out numerical simulations using various parameter values to study the effects of a thin rotating rod and also to analyze the influence of local vorticity sources. Their results show that the vortex breakdown bubbles in the steady axisymmetric flow can be affected dramatically, i.e., fully suppressed or significantly enhanced, by rotating the rod and confirm the experimental observations of Husain et al. [14].

Dash and Singh [5, 7] have analyzed the lid-driven swirling flow in a closed cylindrical cavity under the effects of an axial Magnetic field and thin axial rod inserted in the middle. The study involved solution of Navier–Stokes equation in cylindrical coordinates with appropriate Lorentz force components due to magnetic field. It was observed that a co-rotation of axial thin rod has similar effects as those due to the presence of magnetic field, i.e., both have the stabilizing effects on the swirling flow.

Mununga et al. [23] have investigated the control of confined vortex breakdown with partial rotating lids. Their study describes large changes to the interior flow structure induced by localized flow modification at the rotating boundary. In a very recent study, subcritical instability of finite circular Couette flow with stationary inner cylinder has been studied by Lopez [21]. He found that at sufficiently high Reynolds numbers, due to non-dimensional rotation rate of the outer cylinder, the sidewall boundary layer has concentrated shear, the pressure gradient in the azimuthal direction and its thickness remains constant.

Pereira and Sousa [24] have modified the experimental arrangement to include a conical rotating end wall. Also, Escudier et al. [9] has investigated flow produced in a conical container by a rotating end wall. In all these above studies, hardly any study has been conducted to find the zones and boundaries of vortex breakdowns due to the presence of rotation or stationary axial rod. Aspect ratio and Reynolds number effects on vortex breakdown and steady/unsteady flow in the presence of axial rod (cylindrical annulus) are hardly ever discussed.

Present study involves a systematic analysis of effects of the presence of thin axial rod, stationary or rotating in either direction, on lid-driven swirling flow. Presence of rotating axial rod imparts angular momentum is in near flow field and hence influences the vortex breakdowns along the axis. The results with various rotational speeds of co-rotating rod are represented in terms of modification of zones and boundaries of one-vortex and two-vortex breakdowns on the AR–Re plane. The range of aspect ratio (AR) of the cavity considered is to be from 1.0 to 2.5. However, Reynolds number (Re) value, for a given AR, ranges from 1000 to any value till the topmost point on the boundary of steady vortex breakdown zone is achieved. The radius of the axial rod for all the cases is taken to be 10% of the radius of the cavity. The presence of rotating axial rod, rotating in same or opposite direction with respect to the direction of rotation of the top lid, greatly influences the vortex breakdown as the rotating rod imparts angular momentum in the surrounding flow field.

In this present study, the zones and boundaries of vortex breakdowns for steady and unsteady flow in Aspect ratio and Reynolds number plane have been investigated due to the presence of axial rotating or stationary rod. The radius of axial rod is kept constant (r = 0.1) to find the effect of stationary or rotating condition of axial rod on swirling flow. Present numerical simulation of the swirling flow is based on solution of incompressible Navier–Stokes equations expressed in primitive variables. The flow under the conditions considered in the present study is assumed to remain axisymmetric. The present code has been developed, using finite difference method, on staggered grids and using pressure correction technique. The velocity components \( u_{r} \), \( u_{\theta } \), \( u_{y} \), are in r, θ, y directions, respectively, in cylindrical coordinate systems.

2 Mathematical formulations and method of solution

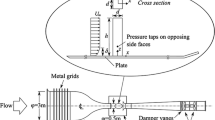
The flow domain consists of a vertical cylindrical annulus cavity of radius R and height H, one end with a fixed wall and other end with a rotating lid, is filled with incompressible viscous Newtonian fluid, Fig. 1. Without axial rod the flow domain is simply that of a cylindrical cavity. The basic swirling motion is generated by rotating the top/bottom disk with constant angular velocity. As the lid rotates with some angular velocity, it imparts angular momentum and the fluid inside the cylindrical cavity also rotates. The resulting fluid flow developed inside the cavity has three velocity components; radial \( u_{r} \), azimuthal \( u_{\theta } \) and axial \( u_{y} \). A schematic of the flow domain is shown in Fig. 1. The bottom end wall of the cylinder is fixed, whereas the top lid is rotated with a steady angular velocity (\( \varOmega \)) about the cylindrical axis. The fluid adjacent to the top lid acquires angular momentum and is pushed radially outward; when it reaches the cylindrical sidewall, the fluid is constrained to flow downward. The swirling fluid reaches the stationary bottom and moves radially inward along the bottom end wall. In the vicinity of the axis, the swirling fluid flows upward toward the top end wall, thus completing the circuit in the meridional plane. The flow structure is known to depend upon two key parameters, namely; aspect ratio AR = H/R, and rotational Reynolds number \( Re = \frac{{R^{2} \varOmega }}{\nu } \) where H and R are the height and radius of the cylinder, respectively, and \( \nu \) the kinematic viscosity of the fluid. Previous investigations by Escudier [8], Vogel [29], and Lopez [20] have confirmed that, at certain combinations of these two parameters (AR & Re), a recirculation region forms along the axis of the cylinder; such a recirculation region is referred as vortex breakdown or vortex breakdown bubble. The zones and boundaries for single, double, and triple breakdowns, and boundary between unsteady and steady flow zones, in the Reynolds number (Re) and aspect ratio (AR) plane, has been obtained experimentally by Escudier [8].

Fig. 1
figure 1

Schematic of lid-driven swirling flow in cylindrical cavity of aspect ratio H/R with an axial rod

Full size image

2.1 Governing equations

The Navier–Stokes equations in cylindrical coordinate for axisymmetric case can be obtained by dropping all the terms having partial derivatives with respect to \( \theta \).

Continuity Equation

$$ \frac{1}{r}\frac{{\partial (ru_{r} )}}{\partial r} + \frac{{\partial u_{z} }}{\partial z} = 0. $$
(1)

Momentum equation in radial direction

$$ \frac{{\partial u_{r} }}{\partial t} + \frac{1}{r}\frac{{\partial (ru_{r} u_{r} )}}{\partial r} + \frac{{\partial (u_{r} u_{z} )}}{\partial z} - \frac{{u^{2}_{\theta } }}{r} = - \frac{\partial p}{\partial r} + \frac{1}{Re}\left[ {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial ru_{r} }}{\partial r}} \right) + \frac{{\partial^{2} u_{r} }}{{\partial z^{2} }}} \right]. $$
(2)

Momentum equation in axial direction

$$ \frac{{\partial u_{y} }}{\partial t} + \frac{1}{r}\frac{{\partial (ru_{r} u_{z} )}}{\partial r} + \frac{{\partial (u_{z} u_{z} )}}{\partial z} = - \frac{\partial p}{\partial z} + \frac{1}{Re}\left[ {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial ru_{z} }}{\partial r}} \right) + \frac{{\partial^{2} u_{z} }}{{\partial z^{2} }}} \right]. $$
(3)

Momentum equation in azimuthal direction

$$ \frac{{\partial u_{\theta } }}{\partial t} + \frac{1}{r}\frac{{\partial (ru_{r} u_{\theta } )}}{\partial r} + \frac{{\partial (u_{z} u_{\theta } )}}{\partial z} + \frac{{u_{r} u_{\theta } }}{r} = \frac{1}{Re}\left[ {\frac{\partial }{\partial r}\left( {r\frac{{\partial ru_{\theta } }}{\partial r}} \right) + \frac{{\partial^{2} u_{\theta } }}{{\partial z^{2} }}} \right] $$
(4)

where the reference scale for length, time, velocity and pressure are \( R \), \( \varOmega^{ - 1} \), \( R\varOmega \), and [\( \rho R^{2} \varOmega^{2} \)], respectively. To obtain non-dimensional equations these scaling systems are used. The physical parameters which govern the fluid motion and are used in the present study are defined as: aspect ratio: [AR = H/R], H = height and R = radius of cylindrical cavity and Reynolds number = [\( Re = \frac{{R^{2} \varOmega }}{\nu } \)].

2.1.1 Boundary condition

On the surface of vertical side wall

$$ r = 1,0 \le z \le H/R,u_{r} = 0,u_{z} = 0,u_{\theta } = 0. $$
(5-a)

On the bottom stationary wall

$$ z = 0,0 \le r \le 1,u_{r} = 0,u_{z} = 0,u_{\theta } = 0. $$
(5-b)

On the top rotating wall

$$ z = 0,0 \le r \le 1,u_{r} = 0,u_{z} = 0,u_{\theta } = r\varOmega . $$
(5-c)

On axis of the cavity: (without axial rod)

$$ r = 0,0 \le z \le H/R,u_{r} = 0,\quad \frac{{\partial u_{z} }}{\partial r} = 0,u_{\theta } = 0. $$
(5-d)

On the surface of axial rod of radius \( r_{\text{rod}} \) (with axial rod having angular velocity \( \varOmega_{\text{rod}} \))

$$ r = r_{\text{rod}} ,\quad 0 \le z \le H/R,\quad u_{r} = 0,u_{z} = 0,\quad u_{\theta } = \lambda \times \varOmega_{\text{rod}} \times r_{\text{rod}} . $$
(5e)

where are \( \varOmega \) and \( \varOmega_{\text{rod}} \) rotational velocity of the lid and the rod, respectively, (radian/sec) and \( \lambda = \frac{{\varOmega_{\text{rod}} }}{\varOmega } \). The numerical solution to the problem is obtained using finite difference scheme on a staggered grid arrangement to solve the set of equations, i.e., Eqs. (1)–(4) subjected to the boundary equation Eq. (5).

2.2 Numerical technique and solution procedure

For incompressible flow problem, numerical solution of Eqs. (1)–(4) is obtained on a staggered grid.

In the staggered grid arrangement, various physical quantities are stored at different locations of a cell.

In the present scheme, the scalar quantity (p) is stored at the center of the cell, whereas the velocity components \( u_{r} ,u_{z} \) are stored on the midpoints of the cell faces. However, for axisymmetric case velocity component \( u_{\theta } \) is effectively stored at the cell center only as shown in Fig. 2b. It may be noted that in present numerical scheme the convective terms in the momentum equations are discretized by central/upwind differencing whereas the viscous and the pressure terms are always approximated by second-order central differencing.

Fig. 2
figure 2

a Grid in meridional plane with dummy cells, b velocities and pressure on staggered grid arrangement

Full size image

Knowing the solution at nth time level \( u_{r} ,u_{\theta } ,u_{z} \), p, the aim is to obtain the solution at next time level. The procedure of solving radial and axial momentum equations is based on pressure correction technique, and subsequently finite difference solution of angular momentum equation is obtained. While advancing solution from nth time level to \( (n + 1){\text{th}} \) time level explicitly, one get velocity field which may or may not satisfy the continuity equation. This problem is resolved by using pressure correction technique where the pressure and velocity components for each cell are corrected iteratively in such a way that for the final pressure field the velocity divergence in each cell vanishes.

The typical features of pressure correction technique, also referred as modified MAC method, are available in detail in a paper by Chorin [1] and Peyret and Taylor [25] for the solution of incompressible Navier Stoke equation in rectangular Cartesian coordinate system. After obtaining the corrected radial and axial velocity field using the above pressure correction technique, these velocity components are used to solve the azimuthal momentum equation explicitly to get the \( u_{\theta } \) at the (n + 1)th time level.

A brief outline of the procedure for the governing equations (Eqs. (1)–(4) in cylindrical coordinate for axisymmetric case is presented here.

The solution procedure is summarized as:

  1. 1.

    The momentum equations along radial and axial directions are solved following the pressure correction technique.

  2. 2.

    After the corrected radial and axial velocities components are known, momentum equation for azimuthal direction is solved to obtain \( u_{\theta } \).

  3. 3.

    Steps (1) to (2) are repeated until convergence for the case where the steady state exists or for a required time for unsteady flow calculations.

3 Results and discussion

A few grid independency tests have been conducted for lid-driven swirling flow without any axial rod. Effects of the time step size on the accuracy of the solution and the convergence history of the solution have also been investigated for a test case. Present code has been validated for a number of test cases by comparing the present numerical solution with both the numerical results as well as the experimental data available in open literature. A systematic study has been conducted to investigate the behavior of confine lid-driven swirling in the annuals region with stationary or rotating inner wall.

3.1 Grid resolution and time-step size effects

A grid independency test has been conducted for the case of a AR = 2.0 cavity with top rotating lid at Re = 2000 and time step dt = 0.001. Numerical solutions for the case with equal spacing grids 101 × 201, 201 × 401, and 301 × 601 on the meridional plane have been obtained and compared in Fig. 3. It can be observed from the time history of \( \hbox{max} \left| {{\text{Del}}_{i,j} } \right| \) (i.e., the maximum value of the mod of the divergence of velocity field \( {\text{Del}}_{i,j} \)) that for all the grids the convergence is quite good and the convergence becomes slower with the fineness of the grid Fig. 3a. However, the final converged solution is almost identical as can be seen from axial velocity profile along the axis of the cavity, Fig. 3b.

Fig. 3
figure 3

Grid resolution effects on a time history residual, b axial velocity. Profile at r = 0

Full size image

To observe any influence of the time-step size on the final solution the above case was re-evaluated with three time steps; dt = 0.0005, 0.001 and 0.005. The time history of \( \hbox{max} \left| {{\text{Del}}_{i,j} } \right| \) for these time steps shows that the convergence rate increase with increase in the time-step size and the final converged solutions are identical as can be seen from Fig. 4.

Fig. 4
figure 4

Effect of time step (dt) on a time history of residual, b axial velocity profile at r = 0.0

Full size image

For the same case of swirling flow in AR = 2.0 cavity with Re = 2000, 101 × 201 grid and dt = 0.005, Fig. 5 shows that the time histories of \( \hbox{max} \left| {\frac{{\partial u_{ri,j} }}{\partial t}} \right| \), \( \hbox{max} \left| {\frac{{\partial u_{yi,j} }}{\partial t}} \right| \) and \( \hbox{max} \left| {\frac{{\partial u_{\theta i,j} }}{\partial t}} \right| \) (residues of radial, axial, and azimuthal momentum equations, respectively) are almost identical indicating a good convergence. The time history of \( \hbox{max} \left| {{\text{Del}}_{i,j} } \right| \) is also included in the figure. Hence, it may be concluded that vanishing of \( {\text{Del}}_{i,j} \) in each cell, i.e., a divergence-free velocity field along with the associated pressure field ensures that all the three momentum equations are also satisfied.

Fig. 5
figure 5

Comparison of time histories of different residuals with 101 × 201 grids

Full size image

Another case of swirling flow in AR = 2.5 cavity with Re = 2000 has been selected for grid independency study. This case was selected because of the presence of two-vortex breakdowns and hence more challenging one. Axial/radial profiles of radial, axial, and azimuthal velocity components of the swirling flow obtained by the bottom rotating lid are shown in Fig. 6. It can be seen that there is no difference in the solutions obtained with the finer 201 × 501 and 301 × 751 grids. Solution with 101 × 251 grid shows some small localized deviations in the regions close to the vortex breakdowns. The same can also be observed from the stream contours with the three grids, Fig. 7.

Fig. 6
figure 6

Effect of grid resolution on a axial velocity profile at r = 0, b radial profiles at of axial, radial, and azimuthal velocity at y/h = 0.5

Full size image
Fig. 7
figure 7

Comparison of stream contours at three different grids 101 × 251, 201 × 601 and 301 × 751

Full size image

3.2 Code validation

Present code is validated against both the experimental as well as the numerical results available in open literature. The first case of lid-driven confined swirling flow for AR = 2.0 cavity with Re = 1000, 2000 and 2300 is considered and validated against the experimental data by Sancho et al. [27]. The comparison of the present axial velocity profiles with the experimental data is good for all the three Reynolds numbers as shown in Fig. 8. The steam contours for each Reynolds number are included in Fig. 9 which show the flow structure in the meridional plane which is consistent with the regions and boundary diagram due to Escudier [8]. For Re = 1000 case, stream lines near the axis of symmetry are parallel, indicating no sign of vortex breakdown for the case. With Re = 2000 there are two distinct vortex breakdown along the axis and the collapse into one-vortex breakdown as the Reynolds number is further increased to Re = 2300.

Fig. 8
figure 8

(I) Comparison of axial velocity profiles for AR = 2.0 cavity at a Re = 1000, b Re = 2000, c Re = 2300

Full size image
Fig. 9
figure 9

Stream contours at different Reynolds number for AR = 2.0 cavity

Full size image

In another validation, the axial velocity profiles along the axis of symmetry, for three cases; AR = 1.5 with Re = 990 &1290 and AR = 2.5 with Re = 1010, have been obtained and compared with number of other numerical solutions due to Guo et al. [24], Wang et al. [25] and Bhaumic et al. [26] in Fig. 10. For all the three cases, present solution in each case matches well with those due to Guo et al. [13] and Wang et al. [30], but the solutions due to Bhaumik and Laksmisha [4] show some small local deviations. However, the overall comparison of all the numerical solutions is quite good.

Fig. 10
figure 10

Comparison of axial velocity profiles at r = 0.0 with available numerical solutions for a Re = 990, AR = 1.5, b Re = 1290, AR = 1.5, c Re = 1010, AR = 2.5

Full size image

3.3 Effect of time step size on unsteady flows

A comparative study for unsteady swirling flow calculations has been carried out for the case of AR = 2.5 cavity with Re = 2765. The case is a known to be a one with unsteady flow and the point AR-Re plane lies in the unsteady zone Escuder [8]. Figure 11 shows the comparison of the time history of stream function at (r = R/3, y = 2H/3) at sufficiently large time t = 3000.

Fig. 11
figure 11

Instantaneous time history of stream contours at r = 0.2, y = 0.8 and Re = 2765, AR = 2.5

Full size image

The effect of time step size on the unsteady flow calculations is presented in the form of time history of the stream function at the same selected point with various time step size as shown in Fig. 11. There are differences with time step from dt = 0.005 to dt = 0.0005 but further decrease in time step to dt = 0.0001 makes no difference as compared to the one with dt = 0.0005. Hence, for the present case the time step dt = 0.0005 looks adequate. After approximately 2750 revolutions of the lid (i.e., t = 2750) the flow settles down to a periodic state.

3.4 Vortex breakdown in cylindrical cavity with axial thin rod of radius \( r_{\text{rod}} \)

The behavior of vortex breakdown in case of confined lid-driven swirling flow can be controlled by inserting a thin (rotating/stationary) rod along the axis. The boundary condition along the axis of symmetry is replaced with no-slip condition on the surface of the rod as is given in Eq. 5(e) and rewritten as \( r = r_{\text{rod}} ,\;0 \le y \le h,\;u_{r} = 0,\;u_{y} = 0,\;u_{\theta } = \lambda \times \varOmega_{\text{rod}} \times r_{\text{rod}}, \)where \( \varOmega \) and \( \varOmega_{\text{rod}} \) are the rotational velocities (rad/sec) of the top lid and the rod, respectively, and \( \lambda = \frac{{\varOmega_{\text{rod}} }}{\varOmega } \).

All other boundary conditions remain same as in case of lid-driven swirling flow without rod along its axis. Depending on the selected value of \( \lambda \), different cases can be studied. For stationary rod, \( \lambda = 0 \), co-rotating rod, i.e., the rod and the lid rotate in the same direction \( \lambda = + ve \) and for counter-rotating rod \( \lambda = - ve \). Here, \( Re_{\text{rod}} = \frac{{\varOmega_{\text{rod}} r_{\text{rod}}^{2} }}{\nu } \) is Reynolds number due to axial rod rotation.

3.4.1 Validation in the presence of axial rod

The present result is validated with the experimental result of Husain et al. [14] and the numerical result of Herrada and Shtern [15] at Re = 2720, AR = 3. 25. The axial (stationary/rotating) thin rod (radius of rod (rrod)/radius of lid (rlid) = 0. 04). Figure 12a–c shows flow patterns for Re = 2720, AR = 3. 25 at \( Re_{\text{rod}} = 0.0 \) where the rod is at rest. The streamline contours of present calculation shown in Fig. 12b middle is validated with flow visualization of Husain et al. [14] in Fig. 12a left and streamline contour Fig. 12c of Herrada and Shtern [15] Fig. 12c right; where the rod is at rest, \( Re_{\text{rod}} = 0.0 \).

Fig. 12
figure 12

Comparison of experimental Husain et al. [14] left, numerical results at present middle, numerical Herrada and Shtern [15], at Re = 2720, and Ri = 0.04, for different axial rod speed: a–c Rei = 0, d–f-Rei = 21, g–i Rei = − 12

Full size image

The presently calculated streamline contour is consistent with the results of Husain et al. [14] Fig. 12a left and Herrada and Shtern [15] Fig. 12c right; where three vortex breakdowns are existing along the axis. The marking of vortex number (i, ii, iii) by Husain et al. [14] in Fig. 12a left can be seen in the present streamline contours.

In case of co-rotating rod condition for Re = 2720, AR = 3. 25 at Rerod = 21, the present stream contours Fig. 12e middle has been well matched with the flow visualization of Husain et al. [14] Fig. 12d left and calculated stream contours of Herrada and Shtern [15] Fig. 12f right. In this condition, vortex numbers (ii, iii) are completely suppressed. Regardless of minor differences, the present numerical result is well agreed concerning the main effect suppression of vortex breakdown even by a weak co-rotation of the rod.

The rotating flow with the counter-rotation of the axial rod, at a critical steady flow condition, Rerod = −12, for Re = 2720, AR = 3. 25 the present stream contours Fig. 12h middle has been validated with the flow visualization of Husain et al. [14] in Fig. 12g left and calculated stream contours of Herrada and Shtern [15] Fig. 12i right. The present result is in excellent agreement, both showing that the counter-rotation (a) significantly enlarges the vortex ring (iii), shifts the vortex ring (iii) downstream, and the flow is still steady at this Rerod = −12. Also, for these above corresponding cases, quantitative comparison of present numerical results with that due to Herrada and Shtern [15] at Re = 2720, AR = 3.2, and rrod = 0.04, are shown in Table 1. The magnitude of maximum and minimum of stream function of the present result are well agreed with Herrada and Shtern [15].

Table 1 Comparison of present numerical results with that due to Herrada and Shtern [15], at Re = 2720, and Ri = 0.04, for different axial rod speed
Full size table

3.4.2 For unsteady flow condition

Flow visualization of Husain et al. [14] is investigated by present code with help of the time history of vortex breakdown bubbles and stream contours for counter-rotating of the axial rod at Rer = −16.5. Re = 2720, AR = 3.25. Figure 13 shows the time history of radial, axial and circulation for Rei = −16.5. The flow becomes weakly non-periodic and unsteady which confirms the validity of the present code with the experimental result of Husain et al. [14].

Fig. 13
figure 13

Time-periodic oscillation in the flow with the counter-rotating rod at Rei = 16.5. (AR = 3.25, Re = 2720). Value at r = 0.4, y = 1.9. a Radial component of velocity, b Axial component of velocity (c) circulation

Full size image

The upstream vortex ring i also become strongly unsteady and the number of vortex rings increases. As the entire array of vortex rings i through iv moves downstream, the downstream vortex iv approaches the disk. At this stage, a satisfactory comparison of present result can be visualized with the help of stream contours in Fig. 14a at a non-dimensional time t = 2980. After the elongation, ring transforms into Ni to Niv where N denotes new rings. At a non-dimensional time, t = 2990 the matching of present stream contour can be seen in Fig. 14b.

Fig. 14
figure 14

Comparison of flow visualization of the time evolution of vortex breakdown bubbles for counter-rotating disk and central rod at Rer = 16.5. (AR = 3.25, Re = 2720). a Husain et al. [14] Present at t = 2980, b Husain et al. [14] Present t = 2990

Full size image

3.4.3 Case-I: AR = 2.5 Cylindrical cavity with axial stationary/rotating rod at Re = 2400

To investigate the effects of presence of stationary or rotating rod, a rod with \( r_{\text{rod}} = 0.1r \), has been inserted along the axis. Stream contours for cases with the rod being stationary \( \lambda = 0 \), co-rotating rod with \( \lambda = 1\& 2 \) have been compared with the one without any rod as shown in Fig. 15. By introducing thin stationary rod some changes have been observed from stream function contours in terms of size, shape and location of vortex breakdowns as can be seen in Fig. 15a, b. These changes are expected due to; (i) the drastically different no-slip condition as compared to the symmetric boundary condition and (ii) because of a slight increase of the aspect ratio of the cavity. Co-rotating rod imparts angular momentum in the same direction as the rotating disk that delays or completely avoids bubble-type vortex formation along the axis. For the co-rotating rod with \( \lambda = 1 \), the vortex breakdown still exists and its size and shape is very similar to the case of flow with stationary rod, Fig. 15b, c. This indicates that co-rotating rod with same speed as the lid does not impart sufficient axial momentum to remove the vortex breakdown completely. When the speed of the co-rotating rod is further increases to \( \lambda = 2 \) the vortex breakdown completely varnishes, Fig. 15d.

Fig. 15
figure 15

Streamline contours without and with rod (rrod = 0.1r) for AR = 2.5 cavity at Re = 2400

Full size image

The azimuthal velocity profiles at y/h = 0.5 for the cases of stationary and co-rotating rod has been compared with the one without rod Fig. 16a. It can be observed that the azimuthal velocity for stationary rod near its surface is lower than the one without any rod. This is expected because of the application of no-slip condition on the surface of the stationary rod. The effect of co-rotation of the rod, \( \lambda = 1 \& 2 \), on the lid-driven swirling flow is manifested in the form of increase in the azimuthal velocity; the increase is maximum near the rotating rod, start decreasing with r, and almost diminishes beyond r = 0.8.

Fig. 16
figure 16

Effect of thin axial rod on a azimuthal velocity profile at y/h = 0.5, b axial velocity profile at r = 0.15 for AR = 2.5 cavity at Re = 2400

Full size image

The axial velocity profiles at r = 0.15, a location 0.05r away from the surface of the wall, for all the cases of stationary and co-rotating axial rod have been compared with axial profiles at r = 0.0 and r = 0.15 for the case without the axial rod, 16(b). The profile along the axis for the case without any rod shows the size and axial location of two-vortex breakdowns. It can be observed that there is no vortex breakdown for \( \lambda = 2 \) case and there is only single vortex breakdown for each of the cases with \( \lambda = 0.0 \& 1.0 \). However, the vortex with \( \lambda = 1 \) gets stretched in axial direction and also slightly shifts upward as compared to the one with stationary rod.

For the counter-rotating rod,\( \lambda = - ve \), the angular momentum imparted by the rod is in opposite direction to the one imparted by the rotating lid, and this may lead to unsteady flow. When the rotation speed is \( \lambda = - 1 \), the flow still remains steady, as shown in Fig. 17, but two distinct vortex breakdown bubbles appear along the axis: lower one is smaller in size and is similar to the one with stationary rod but the other one is bigger in size and is situated close to the top rotating lid. When the speed of the counter-rotating rod is increased to \( \lambda = - 2 \), it makes the flow highly unsteady as can be seen from Fig. 18. Time histories of the residual of axial momentum equation, \( \hbox{max} \left| {\frac{{\partial u_{ri,j} }}{\partial t}} \right| \), and \( \hbox{max} \left| {{\text{Del}}_{i,j} } \right| \) for the swirling flow without rod and with rod for the cases with \( \lambda = - 2, - 1,0, + 1 \& + 2 \) is included in Fig. 19.

Fig. 17
figure 17

Flow pattern in meridional plane at different time for AR = 2.5 cavity at Re = 2400 with rod speed \( \lambda = - 1 \). a t = 2800, b t = 2840, c t = 2880

Full size image
Fig. 18
figure 18

Flow pattern in meridional plane at different time for AR = 2.5 cavity at Re = 2400 with rod speed \( \lambda = - 2 \). a t = 3500, b t = 3520, c t = 3540

Full size image
Fig. 19
figure 19

Effect of axial rod on the time history of residuals of a continuity equation, b radial momentum equation for AR = 2.5 cavity at Re = 2400

Full size image

For all the cases considered here, both time histories show similar trends. It may be observed that for the counter-rotating rod with \( \lambda = - 2 \), the residuals do not fall with time indicating the flow remains oscillatory. Swirling flow with co-rotating rod, \( \lambda = 2 \), results in a converged vortex breakdown free steady solution although the convergence is much slower than the reaming cases included Fig. 19.

The vortex breakdown zones and boundaries, in AR-Re plane for lid-driven swirling flow in cylindrical cavity with thin axial stationary or co-rotating rod (i.e., with \( \lambda = 0, + 1 \& + 2 \)) have been generated. This is achieved by extensive study of these flows with varying values of AR and Re to obtain the zones and boundaries in each case. These boundaries and zones of vortex breakdowns for different cases are shown in Figs. 20 and 21.

Fig. 20
figure 20

Zones and boundaries of one-breakdown and two-breakdowns in AR–Re plane; a present results with stationary axial rod \( (\lambda = 0) \), b comparison with the case without rod due to Escudier [8]

Full size image
Fig. 21
figure 21

Time history of radial component of velocity at point, r = 0.15 y = 0.2, with Re = 2550 and a AR = 1.5, b AR = 1.7, c AR = 2.0, d AR = 2.5 for the case with stationary rod \( (\lambda = 0) \)

Full size image

3.4.4 Case-II Zones and boundaries of vortex breakdowns in AR–Re plane for the lid-driven swirling flow with axial stationary rod. [\( \lambda = 0 \)]

Figure 20a shows the regions and boundaries of one-vortex breakdown and two-vortex breakdown zones, as obtained by the present code, for the case of rotating lid in the presence of thin axial stationary rod. The two-vortex breakdown zone, within the range of AR = 2.5, is indicated here by a curve-BQP and part of the boundary of one-vortex breakdown zone is indicated by curve-ASM. The curve-OQP is obtained as the boundary between the single- and the double-vortex breakdown zones. The curve-AOB separates the unsteady zone from steady vortex breakdown zones. To have an idea how these zones and boundaries are affected due to the presence of a stationary rod these have been compared, in Fig. 20b, with the zones and boundaries of vortex breakdowns for lid-driven cylindrical cavity flow as obtained experimentally by Escudier [8].

The corresponding boundaries and zones of vortex breakdowns as obtained by Escudier [8] consist of curve-CKN as the boundary for one-vortex breakdown zone, curve-HG as the boundary between the one-breakdown and two-vortex breakdown zones and curve-CD as the boundary between steady and unsteady zones as shown in Fig. 20b. It may be observed from the comparison shown in Fig. 20b that the effects of presence of stationary axial rod are; the one-vortex breakdown zone is shifted toward left with upper boundary sifting more than the lower boundary and the horizontal width of the zone increases, the two-vortex breakdown zone reduces in size and the boundary between steady vortex breakdown zones and unsteady zone get stretched as well as shifts downward.

To capture the boundary curve-AOB between steady and unsteady zones a large number of computations have been performed. For example, for given aspect ratio (AR), one has to find flow at increasing Reynolds number in small steps and keep checking if the flow is steady or unsteady. To establish the steady/unsteady nature of the swirling flow corresponding to any point on the AR–Re plane, the variation of three components velocity at nine selected locations, in the flow field in meridional plane, is studied. If at all the selected locations on meridional plane each velocity component show the steady behavior then the flow corresponding to pair of values of Re and AR (i.e., a point on the Re–AR plane) is assumed to be steady.

Figure 21 shows, e.g., the variation of radial component of the velocities with time at a location (r = 0.15, y = 0.2) on the meridional plane corresponding to three selected points lying just above the unsteady boundary in the AR–Re plane, i.e., the curve-AOB in Fig. 20. All these points lying just above the unsteady boundary have Reynolds number Re = 2550. After initial transient, the amplitudes of fluctuation of radial velocity for AR = 1.5 case remains more or less constant Fig. 21a. Similar trends for AR = 2.0 case can be observed from Fig. 21c. However, the amplitude of fluctuation for AR = 1.7 keeps increasing with time, Fig. 21b, which is expected as this point is relatively farther from the unsteady boundary (Fig. 20). This indicates that flow corresponding to each of these three points, lying on AR–Re plane, is unsteady and hence these points lie in the unsteady zone.

3.4.5 Case III Zones and boundaries of vortex breakdowns in AR–Re plane for lid-driven swirling flow with co-rotating axial rod [\( \lambda = 1 \)]

The effects upon vortex breakdown zones and boundaries due to the presence of a thin axial co-rotating rod with \( \lambda = 1 \) have been investigated and the results are presented in Fig. 22a. This study has been carried out for AR range from 1 to 2.5 only. It may be noted that for the rage of AR up to 2.5, the two-vortex breakdown zone disappears completely and that the boundary between steady and unsteady zones (i.e., curve-AOB) shifts downwards.

Fig. 22
figure 22

Zones and boundaries of one-breakdown and two-breakdowns on the AR–Re plane; a present results with co-rotating axial rod \( (\lambda = 1) \), b comparison with the case without rod due to Escudier [8]

Full size image

In Fig. 22b, a comparison of zones and boundaries of present case with rotating axial rod has been made with those due to Escudier [8] for lid-driven swirling flow in a cavity. It may be noted that for this case of co-rotating rod the double-vortex breakdown zone disappears completely. This is due to an additional angular momentum imparted to the surrounding fluid by the rotating axial rod in the same direction as by the top rotating lid. The shifting of single-vortex breakdown zone, with its boundary curve-ASM Fig. 22b, is relatively smaller in comparison with the case of lid-driven swirling flow with stationary rod Fig. 20b. Also shifting of the unsteady zone downwards, boundary AOB in Fig. 22a, is larger as compared to the case with stationary axial rod boundary curve-AOB Fig. 20.

3.4.6 Case IV zones and boundaries of vortex breakdown in AR–Re plane for lid-driven swirling flow with co-rotating axial rod [\( \lambda = 2 \)]

To understand the effects of increasing the rotational speed of co-rotating rod, a case with [\( \lambda \) = 2] has been investigated. This study also has been carried out for AR = 1 to 2.5 only. It may be noted from Fig. 23a that for the given range of AR up to 2.5, there is no vortex breakdown developed for any combination of values of AR and Re corresponding to any point lying throughout the zone of steady flow in Re–AR plane.

Fig. 23
figure 23

Zones and boundaries of one-breakdown and two-breakdowns on the AR–Re plane; a present results with co-rotating axial rod \( (\lambda = 2) \), b comparison with the case without rod due to Escudier [8]

Full size image

Reason for having no vortex breakdowns is due to larger additional angular momentum (angular speed of the rod is twice that of the lid) imparted to the fluid by the rotating axial rod. The present case has been compared with that due to Escudier [8] curve in Fig. 23b. However, like previous cases the zone of the unsteady flow shifts downward as compared to the one due to Escudier [8] for the case without any axial rod.

4 Conclusions

The present numerical solutions provide a clear picture of the flow topology of lid-driven swirling flow especially of the structure of the multiple recirculation zones, represented on AR–Re plane, and how these zones and boundaries are influenced by the presence of axial stationary/rotating rod. An addition of swirl, by inserting a rotating axial rod, near the axis of a lid-driven swirling flow is an effective means to either suppress or enhance vortex breakdown. The flow appears to be very sensitive to the direction of rotation of the axial rod; co-rotating rod retains a steady flow, suppresses vortex breakdown bubbles, whereas counter-rotating rod tends to create unsteadiness. Similar observations are also made by Husain et al. [14] and JØrgensen et al. (2003).

One can use the counter-rotating (\( \lambda = - ve \)) thin axial rod to achieve considerable oscillations even at much lower Reynolds numbers, thereby subjecting, e.g., the biological material to lower damaging stress levels. The vortex breakdown zones and boundaries, in AR–Re plane for lid-driven swirling flow in cylindrical cavity with thin axial stationary or co-rotating rod (i.e., with \( \lambda = 0, + 1\& + 2 \)) have been generated. In addition for each case, the boundary between unsteady and steady zones has also been obtained. The zones and boundaries of the vortex breakdowns in the AR–Re plane are greatly affected by swirl number \( \lambda \) as shown in Figs. 18, 20 and 21 for various values of \( \lambda \).