1 Introduction

Due to their light weight and powerful capabilities in terms of energy absorption, polymeric foams have gained a large deal of attention in recent years. Being very useful in terms of energy absorption, these materials have been used as energy absorbers in such applications as car bumpers, helmets, drawing chairs, etc. Determination of materials’ mechanical properties is a significant step towards designing new products. Numerical simulation is a basic principle in engineering applications, because it contributes to optimize different components based on the analysis of stress field under various loading conditions, geometries, or with replaced materials. Whenever the simulation results are in good agreement with experimental data, the simulation process will be able to describe mechanical behavior of the material at a good level of accuracy.

In recent years, numerous researches have done on the analysis of mechanical behavior exhibited by similar materials.

Arriga et al. [1] studied the convergence of three-point bending test on specimens of polypropylene. For the sake of simulation, they used a linear elastic model which exhibits plastic behavior beyond the yield point. The results of tests on polyamide specimens indicated that the materials’ responses may not be modeled as a linear relation between stress and strain.

In Izod impact test, Tvergaard et al. [2] analyzed the effects of thickness on stress and strain fields for specimens of polycarbonate.

In his research, Viot showed that, in spite of uniaxial compression is the most common mechanical test used, but the results from this test alone are insufficient to characterise the foam response to three-dimensional stress states. Therefore, he proposed a new device for hydrostatic stress tests. Hydrostatic compression tests carried out, on polypropylene foams, both quasi statically and at high strain rates. The data obtained from hydrostatic compression test finally used for modelling purposes [3].

Avalle et al. [4] experimentally evaluated mechanical properties of three polymeric foams, namely expanded polypropylene (EPP), expanded polyurethane (PUR), and polyphenylene oxide/polystyrene (PPO/PS), at ambient temperature under two different loading conditions, namely static loading and impact loading. Using energy-absorption diagrams and efficiency curves, the energy absorption properties of foams were investigated.

The performance of expanded polypropylene (EPP) foams has to be studied as a function of several parameters including the foam density, microstructure, and the strain rate imposed during dynamic loading. Bouix et al. [5] investigated compressive strain–stress behavior of polymeric foams over a wide range of engineering strain rates (from 0.01 to 1500 s−1) to study the effects of foam density and strain rate on the initial collapse stress and the hardening modulus in the post-yield plateau region. They used a flywheel for intermediate rates of strain (about 200 s−1); however, for higher strain rates (about 1500 s−1) used a viscoelastic Split Hopkinson Pressure Bar (SHPB) with nylon bars. A range of foam densities (34–150 kg m−3) were considered and microstructural characteristics were investigated using two specific foam types.

Chen et al. [6] investigated, both experimentally and theoretically, nonlinear behavior of bumper foams under cycling loading. To study compressible materials, Chen et al. modified the incompressible viscoelastic model proposed by Rajagopal and Srinivasa [7] and expressed it as a function of the principle stretches. The modified model was first used to describe bumper foams. They also proposed a new compressible viscoelastic model to better predict the nonlinear process underwent by bumper foams (under cyclic loading). The new model was expressed separately as the invariants of stretches and the principle stretches. The compressible viscoelastic model and the compressible viscoelastic model were used to describe bumper foams’ response to cyclic loadings of constant amplitude and variable amplitude, respectively. Experimental results illustrates that both the compressible viscoelastic and the viscoelastic models can be seen as suitable models to describe bumper foam response to cyclic loading; the compressible viscoelastic model was proved, however, to provide better results when it came to description of deformation at the end of each cycle.

For large-strain deformation of porous hyperelastic materials, Danielsson et al. [8] proposed a micromechanical structure to develop continuum-level constructive models. They showed that strain-energy density function depends on incompressible hyperelastic matrix material, initial level of porosity, and macroscopic deformation. Taking the first derivative of the strain-energy density function with respect to deformation, they came to an expression for stress–strain behavior of the porous hyperelastic material. To predict the stress–strain behavior of the porous matrix a constructive model expressed as a function of the initial porosity and macroscopic loading conditions.

Demiray et al. [9] determined the macroscopic stress–strain relationships by means of a strain energy based homogenization procedure from the behavior of the cellular structure at the mesoscopic level. Also, they adopted spatially periodic 2-D and 3-D lattices for representing open-cell foams.

Colloca et al. [10] studied the mechanical behavior of hollow glass microballoon–epoxy matrix syntactic foams reinforced with carbon nanofibers (CNFs). They showed that the presence of CNFs leads to increased values of strength and modulus in syntactic foams containing 50 vol.% microballoons compared to unreinforced syntactic foams. Also, they used a homogenization technique based on the so-called differential scheme that accounts for particle size and wall thickness polydispersivity along with entrapped matrix voids to interpret experimental results.

Othman et al. [11] described the performance of polyurethane (PU) foam as an internally-reinforced filler material on pultruded composite square cross-section tubes made of E-glass/polyester resin. They applied various loads to different angle cross-head platens to assess their energy absorption capacity based on quasi-static load–displacement curves. In addition, the interaction properties of the composite and the foam core sheets during the loadings were discussed. Experimental results indicated that the crashworthy structure of the polyurethane (PU) foam-filled specimen enhanced the specific and quasi-static absorbed energies more than the empty composite tubes.

Composite sandwich panels comprising fibre reinforced polymer (FRP) skins and lightweight material cores are being increasingly used in civil engineering. Garrido et al. [12] presented experimental and analytical investigations about the effects of elevated temperature on the shear response of polyethylene terephthalate (PET) and polyurethane (PUR) foams used in composite sandwich panels. Their results showed that with increasing temperature, the shear responses of PET and PUR foams become more markedly nonlinear. In addition, the shear moduli of these foams suffer considerable reductions, particularly for the PET foam; although at ambient temperature (20 °C) the PET foam is three times stiffer than the PUR foam, at 80 °C their shear moduli become similar, being, respectively, 24 and 66 % of those at ambient temperature.

Gover et al. [13] studied polymeric foam efficacy in portable water filled barriers. They found that extruded polystyrene foam functioned well, with a greater thickness of the foam panel significantly reducing the impacting body velocity as the barrier began to translate.

Dynamic stress–strain response of rigid closed-cell polymeric foams by subjecting high toughness polyurethane foam specimens to direct impact with different projectile velocities and quantifying their deformation response with high speed stereo-photography together with 3D digital image correlation investigated by Koohbor et al. [14]. By obtaining the full-field acceleration and density distributions, the inertia stresses at each point in the specimen are determined through a nonparametric analysis and superimposed on the stress magnitudes measured at specimen ends to obtain the full-field stress distribution.

Heat insulating properties of polymeric foams at ambient temperature using the model of coupled heat transfer by conduction and radiation through computer-reconstructed domains investigated by Ferkl et al. [15]. The developed model was validated using experimental data and compared with other approaches, including state-of-the-art homogeneous phase approach (HPA). The model predicts that the radiative heat flux can account for more than one third of the total heat flux in high porosity expanded polystyrene (EPS) or polyethylene (PE) foams and that the equivalent conductivity of polymeric foam can be significantly reduced by the careful balancing of porosity, cell size, wall thickness and strut content.

The aim of this study is numerical modelling of mechanical properties of specimens of EPP polymeric foam using macroscopic method implemented in Abaqus FEA software. The modelling process is performed on the basis of the results obtained from laboratory tests including stress–strain data from uniaxial tensile tests. The results of the proposed model for the naturally disordered polymeric foams indicate the best match with the mechanical properties of the actual material. Since the mechanical behavior of EPP polymeric foams follow the theory of hyperelasticity, the hyperelastic material model was used to investigate the behavior of these kinds of materials in Abaqus FEA software. Considering the nonlinear nature of hyperelastic materials, it is very difficult and even impossible, in some cases, to numerically model these materials. There are several strain-energy density functions proposed for modelling these materials: Ogden, Polynomial, Marlow, Van der Waals, etc. [16–18].

The specimens were produced via mixing molten technique in an extruder (Aslanian Extruder/EM 80/IRAN) and injection molding process performed on specimens according to the corresponding standards of tensile test, three-point bending test, and Izod impact test. The prepared specimens were then subjected to three different tests including uniaxial tensile test, three-point bending test, and Izod impact test.

2 Uniaxial tensile test

2.1 Nanocomposites preparation

Before preparation of nanocomposites samples, polypropylene granules and their compatibilizer were dried in 80 °C for 48 h in a vacuum furnace. Polypropylene granules and polypropylene compatibilizer (PP-GMA) which used for better dispersing of nanoparticles in polypropylene matrix and linking of matrix/reinforcement interface were blended. These nanoparticles were mixed in an internal mixer. This mixer (HAC/HBI 90) included a pair of roller-rotors with high cutting force. Rotating speed of 120 rpm and chamber temperature of 180 °C were applied, and mixing process was continued for 10 min. The resulting compositions were formed with a milling device and three samples were injected. Holder pressure and injection speed were 115 bar and 45 rpm, respectively. Injection mold temperature in extrusion was among 200–220 °C.

2.2 Morphological properties

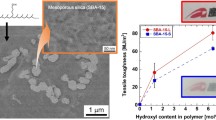
Image of Mesoporous silica-hydroxyapatite particles in a polypropylene matrix is shown in Fig. 1. The hollow circular cross-sections represent silica-hydroxyapatite particles. As seen in image, these particles have good and homogeneous dispersion. Figure 2 presents image of Mesoporous silica-hydroxyapatite particles in which cylinders are hydroxyapatite and porous particles are mesoporous silica.

Fig. 1
figure 1

Image of mesoporous silica-hydroxyapatite particles in a polypropylene matrix

Full size image
Fig. 2
figure 2

Hydroxyapatite and mesoporous silica

Full size image

The specimens were composed of the following components: polypropylene (PP), polypropylene glycol methacrylate (PP-GMA), mesoporous (MCM-41) and hydroxyapatite (HA) with the following composition percentages:

According the three different kinds of material, five specimens for each kind of material were prepared (Table 1).

Table 1 The weight percent of components in each specimen
Full size table

2.3 Experimental results

Uniaxial tensile test was performed at ambient temperature of 21 °C on three dog-bone specimens on a Santam’s universal tensile testing machine (according to ISO 527-2 [19]) (Figs. 3, 4).

Fig. 3
figure 3

Santam’s universal tensile testing machine (uniaxial tensile test)

Full size image
Fig. 4
figure 4

A schematic of uniaxial tensile test setup

Full size image

Tensile force was gradually applied to the specimens at the constant continuous rate of 5 mm per min, so as they underwent plastic deformation with an ultimate failure. The force and the strain values were recorded by a load cell and a strain gauge extensometer, respectively.

The stress and strain were calculated according to ISO 527-1.

The obtained values of tensile test were converted into nominal stress and nominal strain values using Eqs. (1) and (2), respectively. By the converted values we can draw nominal stress-nominal strain curve.

$$\sigma = \frac{F}{{A_{0} }}$$
(1)
$$\varepsilon = \frac{{L_{i} - L_{0} }}{{L_{0} }}$$
(2)

where \(L_{0} = 50{\text{ mm}}\) and \(A_{0} = 42{\text{ mm}}^{2}\).

2.4 Simulation of test

Abaqus FEA software provides simulations of tensile tests. According to Fig. 5, the selected elements are three-dimensional hexahedrons with one node at each vertex (each element possess a total of eight nodes) via structure technique. Linear elements geometry is of C3D8R type. This numerical model has 3692 nodes and 2430 elements with the average element size of 1.6 mm.

Fig. 5
figure 5

The gridding of the model

Full size image

Hyperelastic model with different strain-energy density functions was used for all simulations. These functions are generally expressed in form of polynomials [20]. We have:

$$U(\varepsilon ) = \sum\limits_{i + j = 1}^{N} {C_{ij} (\bar{I}_{1} } - 3)^{i} (\bar{I}_{2} - 3)^{j} + \sum\limits_{i = 1}^{N} {\frac{1}{{D_{i} }}} (J_{\text{el}} - 1)^{2i}$$
(3)

where U(ε) denotes strain-energy density function, \(J_{\text{el}}\) is elastic volume ratio, \(\bar{I}_{1}\) and \(\bar{I}_{2}\) represent measures of distortion in the material’s deviant strain, and N, C ij , and D i are functions of temperature which express material properties.

Three types of strain-energy density functions (i.e., three types of models) are used in the performed simulations. These three models include:

  1. a)

    Van der Waals model also known as Kilian model. This model has its name after a similar model used in equations of state describing real gas behavior. The corresponding strain-energy density function can be expressed as follows:

    $$U(\varepsilon ) = \mu \left\{ { - (\lambda_{m}^{2} - 3)[\ln (1 - \eta ) + \eta ] - \frac{2}{3}a\left( {\frac{{\tilde{I} - 3}}{2}} \right)^{{\frac{2}{3}}} } \right\} + \frac{1}{D}\left( {\frac{{J_{\text{el}}^{2} - 1}}{2} - \ln J_{\text{el}} } \right)$$
    (4)

    where \(\tilde{I} = (1 - \beta )\bar{I}_{1} + \beta \bar{I}_{2}\) and \(\eta = \sqrt {\frac{{\tilde{I} - 3}}{{\lambda_{m}^{2} - 3}}}\) \(\mu\) is the initial shear modulus; \(\lambda_{m}\) is the locking stretch; a is the global interaction parameter; \(\beta\) is an invariant mixture parameter and D governs the compressibility. These parameters can be temperature-dependent. \(\bar{I}_{1}\) and \(\bar{I}_{2}\) are the first and second deviatoric strain invariants defined as \(\bar{I}_{1} = \bar{\lambda }_{1}^{2} + \bar{\lambda }_{2}^{2} + \bar{\lambda }_{3}^{2}\) and \(\bar{I}_{2} = \bar{\lambda }_{1}^{( - 2)} + \bar{\lambda }_{2}^{( - 2)} + \bar{\lambda }_{3}^{( - 2)}\).

  2. b)

    Ogden model wherein strain-energy density function is expressed as function of principle stretches; it is expressed as the following equation [18]:

    $$U = \sum\limits_{i = 1}^{N} {\frac{{2\mu_{i} }}{{\alpha_{i}^{2} }}(} \lambda_{1}^{ - \alpha i} + \lambda_{2}^{ - \alpha i} + \lambda_{3}^{ - \alpha i} - 3) + \sum\limits_{i = 1}^{N} {\frac{1}{{D_{i} }}} (J_{\text{el}} - 1)^{\alpha i}$$
    (5)

    where N is the material parameter and \(\mu_{i} ,\,\alpha_{i} ,\,D_{i}\) are temperature dependent parameters. Furthermore, \(J_{\text{el}}\) denotes the material’s elastic volume ratio and \(\lambda_{i}\) s are the principle expansions (stretches).

  3. c)

    Marlow model strain-energy density function which is solved based on the test data [21]. It is a function of I (the first invariant deviant strain) obtained from the following equation:

    $$U = U_{\text{dev}} (\bar{I}_{1} ,\bar{I}_{2} ) + U_{\text{vol}} (J_{\text{el}} )$$
    (6)

    where \(U_{\text{dev}}\) and \(U_{\text{vol}}\) are deviatoric and volumetric parts of strain-energy density function; \(\bar{I}_{1}\) is the first deviatoric strain invariant defined as \(\bar{I}_{1} = \lambda_{1}^{2} + \lambda_{2}^{2} + \lambda_{3}^{2}\).

For modelling hyperelastic materials, there are two main approaches to declare material properties in FEA software:

  1. 1.

    By directly declaring the material coefficients.

  2. 2.

    By the use of test data.

In the second approach, the software estimates the coefficients of strain-energy density function according to the data obtained from test; the material coefficients of the hyperelastic models can be calibrated by Abaqus from experimental stress–strain data. In the case of the Marlow model, the test data directly characterize the strain energy potential (there are no material coefficients for this model). This study follows the second approach. Abaqus minimizes the relative error rather than an absolute error measure since this provides a better fit at lower strains. This method is available for all strain energy potentials and any order of N except for the polynomial form, where a maximum of N = 2 is allowed. The Ogden and Van der Waals potentials are nonlinear in some of their coefficients, thus necessitating the use of a nonlinear least-squares procedure. The estimated coefficients of Ogden and Van der Waals models are provided in Tables 2 and 3. For material calibration, Abaqus requires the Kirchhoff stress versus true strain as input. The Kirchhoff stress accounts for compressibility through the Jacobian (determinant of the deformation gradient). For incompressible materials, the Kirchhoff stress is equal to the true stress. However, for compressible materials (such as foams), they will differ. These simulations are based on incompressibility assumption.

Table 2 The estimated coefficients of Ogden model by Abaqus FEA
Full size table
Table 3 The estimated coefficients of Van der Waals model by Abaqus FEA
Full size table

Once finished with simulating the tensile test in Abaqus software, the corresponding data to actual stress and actual strain was extracted for all three models (Van der Waals, Ogden, and Marlow models). To compare the stress–strain curves obtained from these three models with those of tests, we should convert simulation results into engineering stress and engineering strain via the following equations:

$$\varepsilon_{\text{true}} = \ln (1 + \varepsilon_{e} ) \to \varepsilon_{e} = e^{{\varepsilon_{\text{true}} }} - 1$$
(7)

and,

$$\sigma_{\text{true}} = \sigma_{e} (1 + \varepsilon_{e} ) \to \sigma_{e} = \frac{{\sigma_{\text{true}} }}{{1 + \varepsilon_{e} }}$$
(8)

where \(\sigma_{\text{true}}\), \(\varepsilon_{\text{true}}\), \(\sigma_{e}\) and \(\varepsilon_{e}\) denote actual stress, actual strain, engineering stress and engineering strain, respectively.

Figures 6, 7, 8 demonstrate the stress–strain curves obtained from uniaxial tensile test together with different models for each of the three specimens.

Fig. 6
figure 6

Stress–strain curves obtained from uniaxial tensile test together with different models: specimen 1

Full size image
Fig. 7
figure 7

Stress–strain curves obtained from uniaxial tensile test together with different models: specimen 2

Full size image
Fig. 8
figure 8

Stress–strain curves obtained from uniaxial tensile test together with different models: specimen 3

Full size image

According to the Figs. 6, 7 and 8, in specimens 1 and 3, Marlow model has the highest agreement with the test data. In the following elasticity modulus percentage error, yield strength, and ultimate strength corresponding are compared to the three models for the specimen 1.

2.5 Elasticity modulus, yield strength, and ultimate strength percentage errors

Elasticity modulus (E) (according to ISO 527-1), yield strength \((\sigma_{\text{Y}} )\), and ultimate strength \((\sigma_{\text{u}} )\) percentage errors can be obtained via the following equations:

$$\begin{aligned} E_{\text{experimental}} = \frac{{\left( {\sigma_{\text{Y}} } \right)_{\text{experimental}} }}{{\left( {\varepsilon_{\text{Y}} } \right)_{\text{experimental}} }}, \, E_{x} = \frac{{\left( {\sigma_{\text{Y}} } \right)_{x} }}{{\left( {\varepsilon_{\text{Y}} } \right)_{x} }} \hfill \\ E_{\text{percent of error}} = \frac{{E_{x} - E_{\text{experimental}} }}{{E_{\text{experimental}} }} \times 100 \hfill \\ \sigma_{\text{Y percent of error}} = \frac{{\left( {\sigma_{\text{Y}} } \right)_{x} - \left( {\sigma_{\text{Y}} } \right)_{\text{experimental}} }}{{\left( {\sigma_{\text{Y}} } \right)_{\text{experimental}} }} \times 100 \hfill \\ \sigma_{\text{u percent of error}} = \frac{{\left( {\sigma_{\text{u}} } \right)_{x} - \left( {\sigma_{\text{u}} } \right)_{\text{experimental}} }}{{\left( {\sigma_{\text{u}} } \right)_{\text{experimental}} }} \times 100 \hfill \\ \end{aligned}$$
(9)

where \(\varepsilon_{\text{Y}}\) and \(\varepsilon_{\text{u}}\) are yield strain and ultimate strain, respectively. Tables 4, 5, 6 report the values of stress, strain, and elasticity modulus (for both the model and test) corresponding to the specimens 1, 2, and 3.

Table 4 The values of stress, strain, and elasticity modulus (for both the model and test) corresponding to the specimen 1
Full size table
Table 5 The values of stress, strain, and elasticity modulus (for both the model and test) corresponding to the specimen 2
Full size table
Table 6 The values of stress, strain, and elasticity modulus (for both the model and test) corresponding to the specimen 3
Full size table

It is observed that in all simulations the Marlow model has acceptable adaptation with experimental parameters. Also, it is obvious that adding nanoparticles (MCM-41 and PP-GMA) to polypropylene improve the mechanical properties of specimens such as yield stress and ultimate stress.

Figures 9, 10, 11 demonstrate the bar charts of elasticity modulus (E), yield strength \((\sigma_{\text{Y}} )\) [MPa], and ultimate strength \((\sigma_{\text{u}} )\) [MPa] percentage errors corresponding to the specimen 1.

Fig. 9
figure 9

Bar chart of elasticity modulus percentage error, specimen 1

Full size image
Fig. 10
figure 10

Bar chart of yield strength percentage error, specimen 1

Full size image
Fig. 11
figure 11

Bar chart of ultimate strength percentage error, specimen 1

Full size image

The Figs. 9, 10, 11 illustrate that the Marlow model has the lowest error among the other models in numerical simulation.

3 Three-point bending test

3.1 Experimental results

According to ASTM D790-03 [22], three-point bending test was conducted on the specimens of 150 × 10 × 4.2 mm dimensions. Figures 12 and 13 show the three-point bending test machine along with the test setup. Specimens were placed on supporting pins of 64 mm distance from one another. The loading pin’s downward movement speed was set to 1.7 mm min−1. The loading rate in bending tests is normally fluctuating within 0.1–10 mm min−1. Force-related data was recorded by a load cell unit.

Fig. 12
figure 12

Three-point bending test machine

Full size image
Fig. 13
figure 13

Three point bending test setup

Full size image

3.2 Simulation of three-point bending test

Abaqus FEA software was utilized to simulate bending test. In the part section, R3D4 rigid shell element was used to model constraints corresponding to the loading pin and supporting pins. In the property section, the Marlow form was selected for the hyperelastic material. Furthermore, in the step section, the dynamic implicit solution was selected to solve the problem. In the interaction phase, surface-to-surface command across different surfaces was used to define the contact surface with a friction coefficient of 0.25. In the load section, the two underneath shells were constrained on all sides with the upper shell moving downward at 0.02833 mm s−1.

Two different meshing approaches are followed here (Figs. 14, 15):

Fig. 14
figure 14

Linear meshing

Full size image
Fig. 15
figure 15

Second order meshing

Full size image
  1. a)

    C3D4H (linear)

  2. b)

    C3D10H (quadratic)

The rigid components had 1560 nodes and 1443 elements with the average element size of 0.8 mm. The models had 18,666 nodes and 11,304 elements with the average element size of 1.8 mm.

In the linear meshing approach, a considerable amount of dispersion was observed within the results which represent unacceptable convergence (the convergence criterion is defined as the closeness of the resultant curve from simulation to the curve obtained from test data; with linear meshing, a while after starting to run the simulation in the software, we dealt with an error message) across the results. (Because with a little data available due to errors encountered during the simulation process, we may not achieve an acceptable curve). Therefore, first order elements seem not to be adequate for bending simulations. Second order meshing, however, gave acceptable convergence. Although the second order meshing, took much longer time, compared to that of the linear meshing, but it returned better results. Figure 16 shows the specimens deformation in three-point bending test simulation.

Fig. 16
figure 16

Model deformation in the course of bending simulation

Full size image

Figures 17, 18, 19 present the force–displacement curves corresponding to the three specimens and have them compared with the experimental values.

Fig. 17
figure 17

Force–displacement curves obtained from test data and simulation results, specimen 1

Full size image
Fig. 18
figure 18

Force–displacement curves obtained from test data and simulation results, specimen 2

Full size image
Fig. 19
figure 19

Force–displacement curves obtained from test data and simulation results, specimen 3

Full size image

In Figs. 20 and 21 the results of force–displacement simulation curves for the specimens 1 and 3 at three different friction coefficients (μ = 0, 0.25, and 0.5) are compared to those obtained from test. The figures show that the lower the friction coefficient, the closer will be the simulation-derived force–displacement curve to that obtained from test data. This is because the lower the friction coefficient, the lower force is required by the upper shell to impose deformations into the specimen. In the case of bending simulations, the imposed friction coefficient influences the results only after the specimens start to slip between the supports. The simulations overestimate the reaction forces regardless of the friction coefficient. It is worth mentioning that, in the course of bending simulation, the center of the upper shell was taken as the point from which the force-related values were measured; it is commonly referred to as the reference point.

Fig. 20
figure 20

Contribution of friction coefficient into the force–displacement curve, specimen 1

Full size image
Fig. 21
figure 21

Contribution of friction coefficient into the force–displacement curve, specimen 3

Full size image

4 Izod impact test

4.1 Experimental results

Izod impact test is often used to measure the strength of a material against impact loading. In this test, notched specimens of specified dimensions were prepared and then the Izod impact test was done on them using the Izod impact test machine according to ASTM D246. Figures 22 and 23 represent the impact test machine and test setup, respectively. Notched specimens were vertically placed between the supports and then the pendulum was released from an initial position at 150°, so that it hit the free end of the specimen at 3.46 m s−1. The screen displayed the absorbed energy immediately after the specimen was fractured. The test was undertaken at 21 °C.

Fig. 22
figure 22

Izod impact test machine

Full size image
Fig. 23
figure 23

A schematic view of Izod impact test setup

Full size image

To achieve more accurate results, the Izod impact test was repeated 3–5 times for each specimen. The average of the achieved results was chosen as the absorbed energy for each specimen (Table 7). As we see in Table 7 the absorbed energy results show high dispersion. One of the reasons is the quality of specimens during the mixing and injection processes. Because after the end of Izod impact test for each specimen, it was shown that there are hollows in some of them which could impress the results of the test. For this reason five repetitions were done for each specimen.

Table 7 The results of Izod impact test
Full size table

4.2 Simulation of Izod impact test

The specimens were modeled in the software according to ASTM D256. In the part section, R3D4 rigid shell element was used to model the pendulum. To apply boundary conditions onto the model, Encastre command was used to fully constraint the model up to the notch. In the load section, the two underneath shells were constrained on all sides with the upper shell moving downward at 0.02833 mm s−1. In mesh part, a three-dimensional hexahedron element with one node at each vertex was chosen with linear geometry (Fig. 24). The rigid shell element had 255 nodes and 238 elements with the average element size of 0.4 mm. The model had 56,265 nodes and 49,200 elements with the average element size of 0.4 mm.

Fig. 24
figure 24

Model deformation across the notched area in the course of impact test simulation

Full size image

In Fig. 25 the impact energy corresponding to each specimen at different instances versus time was plotted. In contrary, to the tests where specimens actually break under the impact, we cannot observe such a breakage in the software; therefore, it is not possible to indicate the absorbed energy at the moment of failure in terms of a specific value. This is why the results are illustrated as a plot of absorbed energy versus time. Since no fracture criteria were integrated in the constitutive models, the Izod impact simulation results present little relevance. As shown in the figures, the value of impact energy within 0–0.5 s is observed to be zero; this time interval represents the time before the pendulum collide to the specimen.

Fig. 25
figure 25

Energy-time plot, specimens 1, 2, and 3

Full size image

With a low percentage error, the results of simulation were found to be close to test data.

5 Conclusion

In this study, finite element simulation was utilized to obtain mechanical properties of porous polymeric nanocomposites before undertaking corresponding tests; this approach may help reducing the cost of sample preparation and save the time of performing actual tests. As mentioned, the specimens were produced by mixing molten in an extruder before being injection molded according to the corresponding standards to tensile loading tests, three-point bending test, and Izod impact test. Once finished with performing the tests, Abaqus FEA software was utilized to simulate tensile test, three-point bending test, and Izod impact test. In the undertaken simulations, different models of a hyperelastic material were considered. After plotting the stress–strain curves which obtained from the tensile test and those of simulation of the tensile test with different models, the percentage errors of elasticity modulus, yield strength, and ultimate strength with the corresponding bar charts were drawn. Comparing the results, the best convergence to the data obtained from tensile test, three-point bending test, and Izod impact test was observed to be those with Marlow model without plasticity. The observations released that in all simulations the Marlow model had acceptable adaptation with experimental parameters. Also, adding nanoparticles (MCM-41 and PP-GMA) to polypropylene improved the mechanical properties of specimens such as yield stress and ultimate stress. Although using the second order elements, rather than linear elements, considerably increased the time to have simulation runs performed, but it was observed that for the sake of bending, torsion, and other complex loading regimes, the second order elements are the only alternatives which lead to relatively acceptable results. Due to considerable dispersion observed with linear meshing, the corresponding results would not exhibit an acceptable convergence; this is while with the second order meshing, the desired convergence was achieved. Investigation of the effect of friction coefficient on the force–displacement curve corresponding to three-point bending test revealed that the lower the friction coefficient, the smaller will be the area under force–displacement curve. The results further demonstrated that we can improve the mechanical properties of specimens, particularly in the course of three-point bending test and Izod impact test, by introducing nanoparticles, particularly a mix of mesoporous silica/hydroxyapatite, into them.