Nonlinear Vibration of Functionally Graded Porous-Cellular Timoshenko Beam Subjected to In-Plane Periodic Loading

Abstract

The present study deals with an open cell shear deformable functionally graded porous beam subjected to in-plane periodic loading to analyze its nonlinear vibration behaviour. The porous beam in this study is modelled based on Timoshenko beam theory i.e., first-order shear deformation theory (FSDT). The porosities are dispersed throughout the thickness of the beam considering uniform and non-uniform symmetric distribution models. For the two distribution systems, the mass density and elasticity moduli of porous beams are considered to vary in the thickness direction. Using Hamilton’s principle, the partial differential equations (PDEs) governing the behaviour of porous beams are derived for the simply supported boundary condition. Then, Galerkin’s method is employed to convert the PDEs to nonlinear ordinary differential equations (ODEs). Further to trace the non-linear vibration behaviour (frequency-amplitude curve) of the porous beam, these ODEs are solved by Incremental Harmonic Balance (IHB) method. A parametric study is presented to assess the influence of porosity, static and dynamic load factors on the vibrational characteristics of the porous beams. As anticipated, the porous beam with non-uniformly symmetric distribution exhibited a higher critical buckling load compared to the uniform distribution of porosity.

1 Introduction

In recent times, assessing a structure with the knowledge of material properties and increasing just the load-carrying capacity as such is not enough. The structure's stability and responsiveness are extremely important in determining the structure's longevity and serviceability. Porous structures possess a high degree of designability and can have refined porosity dependent properties which may influence the dynamic and static behaviours of structures by tailoring their architecture as well as mechanical properties. A porous beam is like a sandwich beam with smooth top and bottom surfaces (i.e., without pores) and its interior is comprised of varying degrees of porosity in the transverse direction according to Magnucki and Stasiewicz (2004). The material exhibit homogeneity in characteristics. As discussed by Xue et al. (2019), porous materials offer more advantages than the normal laminated composite materials like reducing the weight of the structure, removing stress concentration and eliminating energy absorption.

Many investigations are reported in the available literature on the porous beam and its ability by several scientists and researchers. Magnucki and Stasiewicz (2004) reported the findings of their investigation on the porous beam that was analytically solved to give an explicit equation for critical load and then validated using the finite element method based software (through COSMOS). Chen et al. (2015) conducted a study on elastic buckling and static bending based on Timoshenko beam theory or FSDT on non-uniformly distributed porous beams (symmetric and unsymmetric) by varying porosity coefficient and slenderness ratio under different boundary conditions and solved using the Ritz method. It was found that non-uniform symmetrical porosity showed better resistance to buckling and bending. Later, Chen et al. (2016) research was channelised to analyse the porous beams for free and forced vibration under impulsive load, harmonic point load and moving load using the Ritz method in conjunction with Newmark-$\beta$ scheme and it was found that symmetric porosity distribution offered higher stiffness (higher fundamental frequency) and lower dynamic deflection. Barati et al. (2017a, b) used a nonlinear higher order refined beam model to investigate the post-buckling behaviour of porous nanocomposite beams reinforced with graphene nanoplatelets. They found that post-buckling loads of porous nanocomposite beams are heavily influenced by the porosity coefficient, graphene platelets (GPLs) distribution and the type of porosity.

Apart from porosity, analysis of a beam is also done for different parameters which influence the strength and stiffness of the structure. In addition to improving the strength and stiffness of a plate or beam, it is important to integrate nonlinear vibration analysis of porous beams in the design. From this viewpoint, a parametric study on free vibration and elastic buckling to improve the behaviour of beam were done by Kitipornchai et al. (2017) in which GPL was introduced into functionally graded metal foam beams to determine the best combination of GPL and porosity distribution for attaining the effective beam stiffness. However, using the hierarchical finite element method (HFEM) and the harmonic balancing approach, Ribeiro and Petyt (1999) and Houmat (2012) examined the nonlinear free vibration of a simply supported composite plate using HBM. For free vibration response, a moderately thick, unsymmetrically laminated composite plate was modelled using FSDT and solved using FEM (Singh et al. 1995). Cheung et al. (1990) investigated the efficacy of the incremental harmonic balance method (IHBM) and Hsu's techniques in cubic nonlinear systems, which control numerous engineering applications such as large-amplitude beam and plate vibration. Darabi and Ganesan (2017) used Galerkin’s technique to investigate the nonlinear vibration of an internally thickness tapered plate under parametric excitation.

From the literature survey of the available works, it is observed that a vast investigation in vibration and buckling characteristics of porous beams and/or plates are in progress. However, the detailed research on the parametric influence with different porosity distribution as such is limited and often overlooked. So, in this study, functionally graded porous beam simply supported at both ends with rectangular cross-section subjected to in-plane periodic loading is studied based on Timoshenko beam theory for its non-linear vibration response. Mechanical properties of the material varying through the thickness of the unidirectional porous beam model considering symmetric porosity distribution patterns in uniform and non-uniform is studied throughout. For non-uniformly distributed beams, Young's modulus is minimum on the axis of the beam and assumed to be highest at the bottom and top surfaces. Effect of porosity, static and dynamic load factors are studied in detail for the non-linear vibration of the porous beams.

2 Formulation

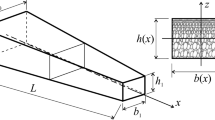
Consider a porous beam of length L, width b and height h along x-, y-, and z-coordinates respectively as shown in Fig. 1. The two types of porosity distributions considered are uniform distribution and non-uniform symmetric distribution. In the non-uniform symmetric porous beams, the mass density and elastic moduli are observed to be highest at the top and bottom surfaces and the lowest values at the mid-plane due to the presence of larger size pores.

Fig. 1

An open-cell porous beam's geometry and coordinate system

$$E(z) ={E}_{1}[1-e \cdot X(z)]$$

(1)

$$G(z) = \frac{E(z)}{2(1+\vartheta)}$$

(2)

$$\rho (z)={\rho }_{1}[1-{e}_{m} \cdot X(z)]$$

(3)

where X(z) = $\frac{1}{e} - \frac{1}{e}{\left(\frac{2}{\pi }\sqrt{1-e} - \frac{2}{\pi } + 1\right)}^{2}$ for uniform distribution of porosity (see Fig. 2).

Fig. 2

Uniform porosity distribution (Type 1) through the thickness of the beam

= $\mathrm{cos}\left(\frac{\pi z}{L}\right)$ for non-uniform symmetric distribution of porosity (see Fig. 3).

Fig. 3

Non-uniform symmetric porosity distribution (Type 2) through the thickness of the beam

Here ${E}_{1}$ and ${E}_{0}$ denote the maximum and minimum value of Young’s modulus through the thickness of the porous cellular beam, respectively (vide Fig. 3). ${\rho}_{1}$ and ${\rho}_{0}$ denote the maximum and minimum value of mass density through the thickness of the porous cellular beam, respectively (vide Fig. 3). The relationship between the porosity coefficient ‘${e}_{0}$’ and the porosity coefficient for mass density ‘${e}_{m}$’ for open-cell cellular solid can be expressed as:

$${e}_{m} = 1 - \sqrt{1-e}$$

(4)

2.1 Assumptions and Limitations

The current problem has some assumptions and limitations, based on that the entire semi-analytical study is conducted. The assumptions are as follows: the laminate stiffness is computed using the equivalent single layer theory. The unloaded beam is considered stress-free. The beam is studied for simply supported boundary conditions. The plate kinematics is assumed to be modelled based on the Timoshenko beam theory. The limitations are as follows: the nonlinear vibration is studied under only uniform in-plane loading. The formulation is applicable to flat beams only. Only symmetric porosity distribution through the thickness is considered in the model.

2.2 Displacement and Strains

Let u and w denote the displacement functions in the x and z directions respectively. The displacement functions as per FSDT are as follows:

$$u\left( {x,t} \right) = u_{0} \left( {x,t} \right) + z\emptyset_{x} \left( {x,t} \right)$$

(5)

$$w(x,t) = w_{0} (x,t)$$

(6)

where ${u}_{0}$ and ${w}_{0}$ stand for the displacement of a point that lies on the mid-plane of the beam. ‘${\mathrm{\varnothing }}_{\mathrm{x}}$’ is the rotation of transverse normal in the x-axis. ‘t’ represents the time. The strain components of the FSDT-based strain–displacement relations are expressed as follows:

$$E_{xx} = E^{{\text{o}}}_{xx} + zk_{xx}$$

(7)

where E_xx$^\circ$ = $\frac{\partial {u}_{0}}{\partial x}$ $+ \frac{1}{2}{\left(\frac{\partial {w}_{0}}{\partial x} \right)}^{2}$ and k_xx = $\frac{\partial {\varnothing }_{x}}{\partial x}$

$$\gamma_{xz} = \frac{du}{{dz}} + \frac{dw}{{dx}} = \emptyset_{x} + \frac{{dw_{o} }}{dx}$$

(8)

The stress–strain relationship of a beam is represented as follows by Hooke's law:

$$\sigma_{xx} = \frac{E\left( z \right)}{{1 - \vartheta^{2} }}E_{xx} = \theta_{11} \left( z \right)E_{xx} \,\,\,\,\,\left( {{\text{where}}\,\theta_{11} \left( z \right) = \frac{E\left( z \right)}{{1 - \vartheta^{2} }}} \right)$$

(9)

$${\sigma }_{xz} ( {\tau }_{xz }) =\frac{E(z)}{2 (1+ \vartheta )}{\gamma }_{xz}$$

(10)

2.3 Equations of Motions

Using Hamilton’s principle considering $\delta U$ (virtual strain energy), $\delta V$ (virtual work done by different forces) and $\delta K$ (virtual kinetic energy), we can write (Kitipornchai et al. 2017)

$$\int\limits_{0}^{T}( \delta U+\delta V - \delta K )dt = 0$$

(11)

The functionally graded porous beam's governing differential equations are as follows:

$$\delta {u}_{0}{:}\, \frac{\partial {N}_{xx}}{\partial x} = {I}_{0}{\ddot{u} }_{0}+ {I}_{1}\ddot{{\varnothing }_{x}}$$

(12)

$$\delta {w}_{0}{:}\, \frac{\partial {Q}_{xz}}{\partial x}+{\frac{\partial }{\partial x}((N}_{xx}-{n}_{xx})\frac{\partial {w}_{0}}{\partial x}) = {I}_{0}\ddot{{w}_{0}}$$

(13)

$$\delta {\varnothing }_{x}{:}\,\frac{\partial {M}_{xx}}{\partial x}- {Q}_{xz} = {I}_{1}{\ddot{u} }_{0}+ {I}_{2}\ddot{{\varnothing }_{x}}$$

(14)

Here, ${n}_{xx}$ is the internal stress resultants due to applied in-plane loading. ${N}_{xx}$ is the in-plane normal intensity, ${M}_{xx}$ is the bending intensity and ${Q}_{xz}$ is the shear intensity expressed in terms of laminate coefficients and displacement components (${u}_{0}, {w}_{0}\mathrm{ and }{\varnothing }_{x})$ are:

$${N}_{xx} = {A}_{11}\left[\frac{\partial {u}_{0}}{\partial x}+ \frac{1}{2}{\left(\frac{\partial {w}_{0}}{\partial x} \right)}^{2}\right] +{B}_{11}\frac{\partial {\varnothing }_{x}}{\partial x}$$

(15)

where ${A}_{11} = b {\int }_{-0.5h}^{0.5h}\frac{E(z)}{1-{\vartheta }^{2}}dz$ and ${B}_{11} = b {\int }_{-0.5h}^{0.5h}\frac{zE(z)}{1-{\vartheta }^{2}}dz$

$${M}_{xx} = {B}_{11}\left[\frac{\partial {u}_{0}}{\partial x}+ \frac{1}{2}{\left(\frac{\partial {w}_{0}}{\partial x} \right)}^{2}\right] +{D}_{11}\frac{\partial {\varnothing }_{x}}{\partial x}$$

(16)

where ${D}_{11} = b {\int }_{-0.5h}^{0.5h}\frac{{z}^{2}E(z)}{1-{\vartheta }^{2}}dz$

$${Q}_{xz }= k{A}_{55} \left[\frac{\partial {w}_{0}}{\partial x}+{\varnothing }_{x}\right] (\mathrm{Since }{\gamma }_{xz }= \frac{\partial {w}_{0}}{\partial x}+{\varnothing }_{x} )$$

(17)

where k (=5/6) is the shear correction factor and ${A}_{55} = b {\int }_{-0.5h}^{0.5h}\frac{E(z)}{2(1+\vartheta )}dz$

${I}_{0}, \,{I}_{1}\,and \,{I}_{2}$ are the mass moment of inertia which can be calculated as:

$$\left\{ {\begin{array}{*{20}c} {I_{0} } \\ {I_{1} } \\ {I_{2} } \\ \end{array} } \right\} = \int\limits_{{ - 0.5h}}^{{0.5h}} {\left\{ {\begin{array}{*{20}c} 1 \\ z \\ {z^{2} } \\ \end{array} } \right\}} b\,p\left( z \right) \cdot dz$$

(18)

Finally, the displacements (${u}_{0}, {w}_{0}\mathrm{ and }{\varnothing }_{x})$ in Eqs. (12)–(14) can be written as:

$${A}_{11}\left[\frac{{\partial }^{2}{u}_{0}}{\partial {x}^{2}} +\frac{1}{2}\frac{\partial }{\partial x}{\left(\frac{\partial {w}_{0}}{\partial x}\right)}^{2}\right] +{B}_{11}\frac{{\partial }^{2}{\varnothing }_{x}}{\partial {x}^{2}} = {I}_{0}{\ddot{u} }_{0}+ {I}_{1}\ddot{{\varnothing }_{x}}$$

(19)

$$\begin{aligned} k{A}_{55} &\left[\frac{{d}^{2}{w}_{0}}{d{x}^{2}} +\frac{\partial {\varnothing }_{x}}{\partial x}\right]+\frac{\partial }{\partial x} (({A}_{11}\left[\frac{\partial {u}_{0}}{\partial x}+ \frac{1}{2}{\left(\frac{\partial {w}_{0}}{\partial x} \right)}^{2}\right] +{B}_{11}\frac{\partial {\varnothing }_{x}}{\partial x}-{n}_{xx})\frac{\partial {w}_{0}}{\partial x}) \\ &= {I}_{0}\ddot{{w}_{0}} \end{aligned}$$

(20)

$${B}_{11}\left[\frac{{\partial }^{2}{u}_{0}}{\partial {x}^{2}} +\frac{1}{2}\frac{\partial }{\partial x}{\left(\frac{\partial {w}_{0}}{\partial x}\right)}^{2}\right] +{D}_{11}\frac{{d}^{2}{\varnothing }_{x}}{d{x}^{2}} - k{A}_{55} \left[\frac{\partial {w}_{0}}{\partial x}+{\varnothing }_{x}\right] = {I}_{1}{\ddot{u} }_{0}+ {I}_{2}\ddot{{\varnothing }_{x}}$$

(21)

2.4 Boundary Condition and Displacement Fields

In the current study, simply supported boundary conditions used are as follows.

$${N}_{xx} = {w}_{0} = {M}_{xx} = 0\, \mathrm{ at }\, x = 0\, \mathrm{ and }\, L$$

(22)

The aforementioned boundary conditions have been met by the assumed displacements of the form:

$${u}_{0} (x,t) = \sum_{m=1}^{\propto }{u}_{m }(t) s{f}_{u}$$

(23)

$${w}_{0} (x,t) = \sum_{m=1}^{\propto }{w}_{m }(t) s{f}_{w}$$

(24)

$${\varnothing }_{x} (x,t) = \sum_{m=1}^{\propto }{\varnothing }_{m} (t) s{f}_{{\varnothing }_{x}}$$

(25)

where $s{f}_{u} = \mathrm{cos}\frac{m\pi }{L}x$ (Shape function/basis function to satisfy the in-plane displacement in x-direction)

$s{f}_{w} = \mathrm{sin}\frac{m\pi }{L}x w$ (Basis function to satisfy the out-of-plane displacement in w-direction)

$s{f}_{{\varnothing }_{x} }= \mathrm{cos}\frac{m\pi }{L}x$ (Basis function to satisfy the rotation).

2.5 Solution Methodology

The in-plane periodic loading can be mathematically represented as, ${N}_{x}={N}_{s}+{N}_{t}\mathrm{cos}(pt)$. After the projection of Galerkin’s method, the above nonlinear PDEs (Eqs. 19–21) transformed into nonlinear ODEs and can be represented in matrix–vector form as (Kumar et al 2016; Singh et al. 2021a, b):

$$\mathbf{M}\ddot{{\varvec{\updelta}}}+\left({\mathbf{K}}_{\mathrm{L}}+{\mathbf{K}}_{\mathrm{NL}}-\left({N}_{S}+{N}_{t}\mathrm{cos}pt\right){\mathbf{K}}_{\mathrm{G}}\right){\varvec{\updelta}}=0$$

(26)

In the above equation, $\mathbf{M}$ stands for mass matrix, ${\mathbf{K}}_{\mathrm{L}}$ stands for linear stiffness matrix, ${\mathbf{K}}_{\mathrm{NL}}$ stands for non-linear stiffness matrix and ${\mathbf{K}}_{\mathrm{G}}$ stands for the geometric stiffness matrix of the beam. In Eq. (26), the nonlinear stiffness (${\mathbf{K}}_{\mathrm{NL}}$) is expressed into two parts: quadratic nonlinear stiffness (${\mathbf{K}}_{\mathrm{NL}2}$) and cubic nonlinear stiffness matrix (${\mathbf{K}}_{\mathrm{NL}3}$). Finally, the resulting nonlinear ODEs are expressed as (Kumar et al. 2019; Singh et al. 2021c, 2021d):

$$\mathbf{M}\ddot{{\varvec{\updelta}}}+\left({\mathbf{K}}_{\mathrm{L}}+{\mathbf{K}}_{\mathrm{NL}2}+{\mathbf{K}}_{\mathrm{NL}3}-\left({N}_{S}+{N}_{t}\mathrm{cos}pt\right){\mathbf{K}}_{\mathrm{G}}\right){\varvec{\updelta}}=0$$

(27)

In this present study, the IHB method by Cheung et al. (1990) is adopted to sketch the nonlinear forced vibration response (frequency-amplitude curve) of the functionally graded porous-cellular Timoshenko beam. Where ${\varvec{\updelta}}$ is considered as the periodic solution (Singh et al. 2021b).

3 Results and Discussion

In this section, uniform and non-uniform symmetric distribution of open-cell porous functionally graded beam subjected to in-plane periodic loading are considered for non-linear vibration analysis. Validation for the current approach and the parametric influences on the non-linear vibration behaviour of the beam are evaluated and presented in the next subsection. The response plotted between dimensionless amplitude (w/h) against dimensionless excitation frequency ($\Omega)$ represents the non-linear vibration behaviour (i.e., frequency-amplitude curve) of the porous beam. For simply supported functionally graded porous beam subjected to periodic in-plane loading, the following properties Length (L) = 1 m, width (b) = height (h) = 0.1 m, maximum Young’s modulus (E₁) = 200 GPa, maximum mass density (${\rho }_{1}$) = 7850 kg/m³, Poisson’s ratio ($\vartheta$) = 0.3, porosity coefficient (e) = 0.5, dynamic load factor ($\beta )$ = 0.5 and static load factor $\left(\alpha \right)$ = 0 are considered in the current study until and otherwise mentioned. With the current formulation and properties, critical buckling load (N_cr) for uniformly and non-uniformly distributed porous beams are obtained as 1.163e7 kN and 1.432e7 kN respectively.

3.1 Validation Study

Validation studies are presented with data available from the published papers to verify the appropriateness of the semi-analytically formulation presented and used in the current study. Table 1 represents the results of a non-porous functionally graded beam under in-plane loading with simply supported boundary condition and it is found that the results of the presented semi-analytical approach are matched well with the study by Rahul and Datta (2013), which is obtained using the method of multiple scales. Non-dimensional free-vibration frequency $\left(\omega {b}^{2}\sqrt{\frac{\rho }{D}}\right)$ and non-dimensional buckling load $\left(\frac{{N}_{cr} \cdot {b}^{2}}{D}\right)$ where N_cr is the critical buckling load, $\omega$ is the natural frequency and D = Eh³ /12(1-$\vartheta$²) for beam having properties as L/b = 10, b/h = 100 (L = 1000 mm, b = 100 mm, h = 1 mm), E = 70 GPa, $\vartheta$ = 0.3 and ρ = 7800 kg/m³ are considered.

Table 1 Comparison of non-dimensional frequency and buckling load of the simply supported non-porous beam

Table 2 shows the non-dimensional buckling load of a simply supported porous beam with non-uniform porosity distribution having non-dimensional buckling load (N_cr $\times$ b $\times$ 1000) where N_cr is the critical buckling load, b is the width (b = 0.001 m) and material properties as E₁ = 205 GPa, $e$ = 0.99, $\vartheta$ = 0.3 and ρ₁ = 7850 kg/m³. When the results of the current approach are compared to those of Kitipornchai et al. (2017), which is obtained using the Lagrange equation method in conjunction with Ritz trial functions, they are found to be in good agreement.

Table 2 Comparison of the critical buckling load of the simply supported porous beam

Table 3 represents the results reported by Chen et al. (2016) of the dimensionless fundamental frequencies for the non-uniformly distributed porous beam with simply supported boundary conditions, which is obtained using the Ritz method. The material properties and dimensions are given as E₁ = 200 GPa, $\mu$ =1/3, ρ₁ = 7850 kg/m³, b = 0.1 m, h = 0.1 m and $e$ = 0.5. The results obtained from the present study were in good agreement with the published one, where dimensionless frequency obtained by $\omega = \Omega L\sqrt{\frac{{I}_{10}}{{A}_{110}}}$ where $\Omega$ is the natural frequency, L is the length, A₁₁₀ and I₁₀ are the values of extension stiffness and inertia term of the beam with $e$ = 0 (in the study, A₁₁₀ = 22.49e8 and I₁₀ = 78.5).

Table 3 Comparison of dimensionless fundamental frequencies with varying aspect ratios (L/h)

3.2 Effect of Porosity Coefficient and Porosity Distribution

Figure 4 represents the frequency-amplitude curve of the functionally graded beam acted by uniform in-plane loading with the two types of porosity distributions (TYPE 1 and TYPE 2) with porosity coefficient, $e$ = 0.5. It is observed that the frequency-amplitude curves of the beam with non-uniform symmetric porosity distribution (TYPE 2) have shifted to the right compared to the frequency-amplitude curves of the beam with uniform porosity distribution (TYPE 1). It implies that porosity distribution TYPE-2 in the porous beam shows more hardening in nature because the reduction in stiffness of beam with porosity distribution TYPE-2 is less compared to porosity distribution TYPE-1. Thus, non-uniform distribution of pores as considered in the study can enhance the stiffness of the beam and thus relatively better mechanical performance can be achieved.

Fig. 4

Influence of porosity distribution on non-linear vibration response of simply supported functionally graded porous beam at e₀ = 0.5

The porosity coefficients have been varied for a simply supported functionally graded open-cell uniformly distributed porous beam as represented in Fig. 5. As the porosity coefficient (e) increases, the fundamental natural frequency of the beam decreases. Porosity coefficient increment (e) causes the reduction in stiffness of beam but the rate of reduction in stiffness is more for a beam with uniform porosity distribution (TYPE 1). Right tilting in the frequency-amplitude curve implies the stiffening of the beam. The frequency for the origin of the nonlinear vibration curve lowers as the porosity coefficient (e) increases, as seen in the graph. Moreover, the curves representing nonlinear vibration responses shows less hardening nature for e = 0.75, while the plots for e = 0.25 shows more hardening nature. This implies that when the porosity coefficient (e) increases, the beam's stiffness decreases, and it becomes more prone to deformation.

Fig. 5

Influence of porosity coefficient on non-linear vibration response of simply supported functionally graded uniform porous beam (TYPE 1)

3.3 Effect of Static and Dynamic Load

Figure 6 illustrates the plot of dimensionless amplitude (w/h) versus dimensionless excitation frequency ($\Omega$) of the non-uniform functionally graded porous beam for different static load factors ($\alpha )$ which are −0.4, 0 and 0.4 at a constant dynamic load factor ($\beta =0.5)$. The sum of static and dynamic load factors must not exceed unity (i.e., $\alpha + \beta$ ≯ 1).

Fig. 6

Influence of static load factor ($\alpha)$ on non-linear vibration response at $\beta$ = 0.5

Owing to the tensile nature of the pre-loading effect on the beam, the overall stiffness (K = ${\mathbf{K}}_{\mathrm{L}}+{\mathbf{K}}_{\mathrm{NL}}-\left({N}_{S}+{N}_{t}\,\mathrm{cos}\,pt\right){\mathbf{K}}_{\mathrm{G}}$) rises with a drop in static load factor ($\alpha = {N}_{S}/{N}_{cr})$ from 0 to −0.4, whereas the stiffness decreases with an increase in static load factor from ($\alpha$) 0 to 0.4 due to the compressive nature of the pre-loading effect on the beam. As a result, the frequency–amplitude curves traced for $\alpha$ = 0.4 and $\alpha$ =  −0.4 shift towards the left and right respectively about curves at $\alpha$ = 0.

Figure 7 depicts the non-linear vibration response of the non-uniform functionally graded porous beam comprising of 6 curves (i.e., left and right curves) corresponding to dynamic load factor ($\beta)$ = 0.33, 0.66 and 0.99 for a constant null static load factor (i.e., $\alpha$ = 0). The difference between upper and lower dimensionless excitation frequencies (Ω) grows when the dynamic load factor ($\beta = {N}_{t}/{N}_{cr})$ increases for a fixed value of dimensionless amplitude (w/h) and when accompanied with an increase in w/h, the difference between them decreases owing to overall beam stiffness (K = ${\mathbf{K}}_{\mathrm{L}}+{\mathbf{K}}_{\mathrm{NL}}-\left({N}_{S}+{N}_{t}\mathrm{cos}pt\right){\mathbf{K}}_{\mathrm{G}}$) reduction.

Fig. 7

Influence of dynamic load factor on non-linear vibration response at $\alpha$ = 0

4 Conclusion

In the paper, a parametric study on nonlinear vibration behaviour (frequency-amplitude curve) of an open-cell porous beam acted by in-plane periodic loading has been conducted and the parameters discussed include the influence of porosity (uniform and non-uniform), static and dynamic load factors on the behaviour of the simply supported porous beams. The following are the conclusions drawn:

• The smallest critical buckling load is observed for uniformly distributed porous functionally graded beams. TYPE 2 (non-uniform) porous beam exhibits relatively better buckling resistance. Hence porosity distribution plays a vital role in assessing the stability of beams.

• With a rise in porosity coefficient, the degree of hardening of the porous beam decreases thereby significantly decreasing the stiffness of the beam and resistance to deformation.

• Irrespective of the porosity distribution, as the dynamic load factor increases, the non-linear curve is observed to shift to the right showing an increase in the degree of hardening which in turn enhances the stiffness of the porous beams whereas the shift of the curve towards the left implies the greater rate of deformation at lower frequencies due to loss of stiffness of the beams.

• The stiffness of the porous beam increases when the static load factor is negative due to the tensile pre-loading effect on the beam, shifting the curve to the right, whereas when the static load factor is positive, the curve shifts to the left due to compressive pre-loading effect on the beam, lowering the stiffness of the porous beams.