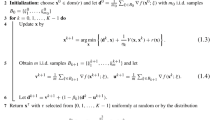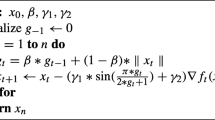1 Introduction

The learning capacities of the human brain, which is made up of neurons connected by synapses, provide the inspiration for Artificial Neural Networks (ANN) (Singh et al. 2015). In fact, they can learn any given mapping up to arbitrary accuracy (Stutz 2014), at least theoretically. They also make it simple to incorporate past task information into the network design. As a consequence, LeCun et al. (1989) proposed Convolutional Neural Networks (CNN) for computer vision including image classification and Natural Language Processing (NLP) including text classification and text generation.

We can find the major real-world applications of image classification in autonomous vehicles (Bojarski et al. 2016), face recognition (Xinhua and Qian 2015), medical diagnosis (Singh et al. 2015), and satellite image (Pelletier et al. 2019).

When discussing the learning of feature hierarchies, we are usually talking about deep learning, that is training deep neural networks (DNN) (Huang et al. 2019). Here, DNN usually refers to neural networks with more than 3 layers. To date, deep learning is still considered challenging (Bengio 2009).

Due to the constrained architecture of CNN,Footnote 1 they allow to train deep architectures with traditional methods,Footnote 2 in 2020 El Mouatasim improved gradient algorithm (El Mouatasim 2020) via Nesterov step for softmax classifier without using any activation function ReLu ( Rectified Linear Units) and activation function tanh, see Sect. 3.

This allows a CNN to learn feature hierarchies, that means that the CNN is used to learn a hierarchy of task-specific features which can then be used for classification using traditional multilayer perceptrons.Footnote 3 This property is a huge advantage of CNN over fully-connected multilayer perceptrons where learning deep architectures is considered difficult (Bengio 2009).

However, when using a popular and applicable activation function ReLU (nonsmooth) or tanh (nonconvex) in the architecture of Deep Neural Networks (DNN) model (Konstantin and Johannes 2019), the training of DNN is a hard problem, since it is a nonsmooth nonconvex optimization problem; therefore, the local minimum can not be a global minimum. To find the parameters updated by the Stochastic Gradient Descent (SGD) algorithm (Tuyen and Hang-Tuan 2021) and its variants including Nesterov accelerated gradient (NAG) algorithm (Botev et al. 2017), Adagrad (Duchi et al. 2011) and Adam (Kingma and Ba 2015) are easy to converge into the local minimum of loss function slowly. The theory and numerical results show that the SGD algorithm and its variants need more improvements for nonsmooth global optimization DNN.

Therefore, the learning rate of optimization algorithm can be improved, the parameters update, such as learning rate annulling (Nakamura et al. 2021), cyclical learning rate [35] and (Liu and Liu 2019). We propose in this paper a fast iterative algorithm with a control learning rate called stochastic perturbation of subgradient algorithm (SPSA) for solving a nonsmooth nonconvex DNN including image classification.

We analyze the propose algorithm SPSA and offer some encouraging findings from numerical tests using the MNIST dataset (LeCun and Cortes 2010), demonstrating that the proposed classification method SPSA is more accurate and anti-overfitting than previous image classification methods such as SGD and its variants.

Although neural networks can be used to solve computer vision problems, previous knowledge should be incorporated into the network architecture to improve generalization performance (LeCun 1989). The goal of CNN is to exploit spatial information between image pixels. As a result, they rely on discrete convolution. We explore the essential components of CNN in Sect. 3.7, as reported in Jarrett et al. (2009) and LeCun et al. (2010).

This work is organized as follows: after the introduction, Sect. 2 presents notation and assumptions. Section 3 gives a brief view of deep neural network modeling. Section 4: considers the optimization of a DNN, including SPSA. Finally, in Sect. 5, the numerical results are examined, and Sect. 6 presents the conclusions and perspectives.

2 Notations and assumptions

We denote by \(\mathbb {R}\) the set of the real numbers \((-\infty ,+\infty )\), \(\mathbb {R}^{+}\) the set of positive real numbers \([0,+\infty )\), \(\mathbb {E}=\mathbb {R}^{n} \), the n-dimensional real Euclidean space. For \(\textbf{w} =(w_{1},w_{2},\ldots ,w_{n})^{t}\in \mathbb {E}\), \(\textbf{w}^{t}\) denotes the transpose of \(\ \mathbf {w.}\) We denote by \(\left\| \text { }\textbf{w} \text { }\right\| =\sqrt{\textbf{w}^{t}\textbf{w}} =(w_{1}^{2}+\cdots +w_{n}^{2})^{1/2} \) the Euclidean norm of \(\textbf{w}\) and by \(\left( {\ }\textbf{w}{,}\textbf{y}\right) =\textbf{w}^{t}\textbf{y}\) the scalar product on \(\mathbb {E}\).

We shall denote \(\textbf{Id}\) the \(n\times n\) Identity matrix.

Training a DNN implies the solution of an optimization problem of the kind:

$$\begin{aligned} Find~\textbf{w}^*\in \mathbb {E}~such~that~G(\textbf{w}^*)=G^*= \min \limits _{\textbf{w}\in \mathbb {E}} G(\textbf{w}), \end{aligned}$$
(1)

\(\textbf{w}^*\) is said to be a global minimum solution of of problem (1) and \(G^*\) is the corresponding global minimal value. In the context of DNN, the objective function \(G: \mathbb {E}\longrightarrow \mathbb {R}\) is referred as loss function and \(\textbf{w}\) is a vector of weights. In general, the weights of a network form a list of vectors \(\textbf{w} = \left( \textbf{w}^{1)}, \ldots , \textbf{w}^{(K)}\right) \), where K is the number of layers in the DNN (see Sect. 3) and \(\textbf{w}^{(\ell )}\in \mathbb {R}^{\eta _\ell }\), where \(\eta _\ell \) is the number of units in the layer no. \(\ell \), \(1\le \ell \le K\). The list of vectors is brought to a vector \(\textbf{w}\) (see Sect. 3).

The problem (1) is unconstrained, since the admissible set is \( \mathbb {E}= \mathbb {R}^n\). Typical loss functions are bounded from below on \(\mathbb {E}\):

$$\begin{aligned} \exists m\in \mathbb {R}~such~that~G(\textbf{w})\ge m, \forall \textbf{w}\in \mathbb {E}\text { }. \end{aligned}$$
(2)

Such an asumption is verified if, for instance, G continuous and coercive, i.e.,

$$\begin{aligned} G~{\text {is}}~{\text {continuous}}~{\text {on}}~\mathbb {E}~{\text {and}}~\lim \limits _{\Vert \textbf{w}\Vert \rightarrow +\infty }G(\textbf{w})=+\infty . \end{aligned}$$

Under these asumptions, there exists a solution \(\textbf{w}^*\in \mathbb {E}\) and \(G^*=G(\textbf{w}^*)\). Let us introduce \(\ S_{\alpha }=\{\textbf{w} \in \mathbb {E}\, \ \ G(\textbf{w})\le \alpha \}\). We assume also that

$$\begin{aligned} \forall \alpha> m:~S_{\alpha }\ \hbox {is not empty, closed and bounded, }{\text {meas}}\left( S_{\alpha }\right) >0 \end{aligned}$$
(3)

where \(\ {\text {meas}}\left( \text { }S_{\alpha }\text { }\right) \) is the Lebesgue measure of \(S_{\alpha }\). Notice that these asumptions eliminate the trivial situation where G is constant on \(\mathbb {E}\) (in such a situation, Problem (1) is trivial: any point of \(\mathbb {E}\) is a global minimum). Equation (3) is verified when G is continuous and coercive.

Finally, we assume that G is uniformly Lipschitz continuous, i.e.,

$$\begin{aligned} \exists L\in \mathbb {R}~~\text {such that }~~ \forall (\textbf{w},\textbf{y}) \in \mathbb {E}\times \mathbb {E}~~~~ \vert G(\textbf{w}) - G(\textbf{y})\vert \le L\Vert \textbf{w} - \textbf{y} \Vert _2, \end{aligned}$$

In this work, we consider the determination of these global minima by subgradient methods involving stochastic perturbations. These methods have shown to be efficient and robust for nonconvex nonsmooth problems (El Mouatasim et al. 2006, 2011).

Subgradient methods are descent methods, id est, methods that generate a sequence \(\{\textbf{w}_{(n)}: n\in \mathbb {N}\}\), from a given initial vector \(\textbf{w}_{(0)} \in \mathbb {E}\), using iterations:

$$\begin{aligned} \textbf{w}_{(k+1)} = \textbf{Q}\left( \textbf{w}_{(k)}, \textbf{d}_{(k)},\rho _{(k)}\right) =\textbf{w}_{(k)} + \rho _{(k)} \textbf{d}_{(k)}~,~ \forall k\ge 0~. \end{aligned}$$
(4)

In the framework of descent methods, \(\textbf{d}_{(k)}\) is the descent direction and \(\rho _{(k)}\) is the step, referred as learning rate in the context of DNN. For subgradient methods, the descent direction is given by (notice the sign minus preceding \(\textbf{d}_{(k)}\)):

$$\begin{aligned} {}-\textbf{d}_{(k)} \in \partial G(\textbf{w}_{(k)}). \end{aligned}$$
(5)

where \(\partial G(\textbf{w})\) is the Clarke’s subdifferential at point \(\textbf{w} \in \mathbb {E}\), see for instance (Bagirov et al. 2013).

To simplify the analysis, we assume that there is a constant \(M\in \mathbb {R}^{+}\), such that

$$\begin{aligned} \left\| \text { }\textbf{d}_{(k)}\text { }\right\| \le M\text {.} \end{aligned}$$
(6)

The determination of the step \(\rho _{(k)}\ge 0\) involves often one-dimensional search with a previously established maximal step \( \rho _{\max }\). For instance, the optimal step is determined by

$$\begin{aligned} \rho _{(k)}=\arg {\min }\text { }\left\{ f(\rho ) =G\left( \textbf{w}_{(k)}+\rho \textbf{d}_{(k)}\right) \text { : } 0\le \rho \le \rho _{\max }\right\} \end{aligned}$$
(7)

So, the step is given by a function \(\rho : \mathbb {E}\times \mathbb {E}\rightarrow \mathbb {R}\) and reads as

$$\begin{aligned} \rho _{(k)}=\rho \left( \textbf{w}_{(k)}\text {, }\textbf{d}_{(k)}\right) \text {; }0\le \rho \left( \textbf{w}_{(k)}\text {, } \textbf{d}_{(k)}\right) \le \rho _{\max }\text {. } \end{aligned}$$
(8)

Stochastic perturbations are introduced to prevent from convergence to local minima and the difficulties. They consist of a controlled random search (see, for instance El Mouatasim et al. 2006, 2011, 2014 and El Mouatasim (2018)). In such an approach, \(\left\{ \textbf{w}_{(k)}: k\in \mathbb {N}\right\} \) becomes a sequence of random vectors \(\left\{ \textbf{W}_{(k)}: k\in \mathbb {N}\right\} \), with \(\textbf{W}_{(0)}=\textbf{w}_{(0)}\) and the iterations (4) modified as follows (again, notice the sign minus preceding \(\textbf{D}_{(k)}\)):

$$\begin{aligned} \textbf{W}_{(k+1)}=\textbf{Q}\left( \textbf{W}_{(k)}, \textbf{D}_{(k)},\rho _{(k)}\right) +\textbf{P}_{(k)},~,~{}-\textbf{D}_{(k)}\in \partial G(\textbf{W}_{(k)})~. \end{aligned}$$
(9)

Here, \(\left\{ \textbf{P}_{(k)}: k\in \mathbb {N}^*\right\} \) is a suitable sequence of random vectors—the stochastic perturbations. A convenient choice of \(\{\textbf{P}_{(k)}: k\in \mathbb {N}^*\}\) ensures the convergence of \( \textbf{W}_{(k)}\) to \(\textbf{w}^{\star } \) almost surely. The step (or learning rate) is given by

$$\begin{aligned} \rho _{(k)}=\rho \left( \textbf{W}_{(k)}\text {, }\textbf{D}_{(k)}\right) ~;~0\le \rho \left( \textbf{W}_{k}\text {, } \textbf{D}_{(k)}\right) \le \rho _{\max }~. \end{aligned}$$
(10)

The practical implementation of (9)–(10) involves finite samples of \(\textbf{P}_{(k)} \) (see Sect. 5).

3 Deep neural network modeling

The goal of this section is to present briefly the mathematical modeling of DNN including the graph of DNN, activation functions, loss function, forward evaluation, backpropagation and regularization. The contents of this section are classical in the literature and our presentation is largely based on Bishop (1995), Stutz (2014) and Haykin (2005).

The basic element of an ANN is a unit usually referred as neuron, perceptron or unit. Indeed, at the origins of ANN, the units were intended to represent a neuron and simulate its activity (Marvin 1954). Later, perceptrons were designed to simulate the behavior of the eye (Rosenblatt 1958). Nowadays, the terminology unit is often preferred since it is neutral and does not imply analogies with the human organism.

Indeed, the basic element is a processing unity that computes an output y, using given a vector of n input values \(\textbf{e} = (e_1,\ldots ,e_n)^t\). Usually, the output is determined as a function of unknown parameters brought to a row vector \(\textbf{w} = (w_0, w_1, \ldots , w_n)\):

$$\begin{aligned} y = \delta (a) ~,~a = \alpha (\textbf{e}, \textbf{w})~. \end{aligned}$$
(11)

The unknown parameters \(\textbf{w}\) must be determined from available observed data given in a dataset \(\mathcal {D} =\{ (\textbf{e}_s, y_s)\), \(1\le s\le n_s\}\)—observations that form a sample from the \((\textbf{e}, y)\). The determination of the unknown values \(\textbf{w}\) is called training. It is usually carried by dividing \(\mathcal {D}\) is divided in three parts: a training set T, a validation set V and a test set S. training usually consists in minimizing the gap between the predictions of the ANN and the observations on T, with verifications on V. After the training, the performance of the ANN is evaluated on S. In the framework of ANN, \(w_0\) is usually referred as bias—it can be seen as an external element, independent from the inputs; \((w_1, \ldots , w_n)^t\) are the weights; \(\delta \) is the activation function and \(\alpha \) is a weighted sum of the input values (Haykin 2005):

$$\begin{aligned} \alpha (\textbf{e}, \textbf{w}) = w_0 + w_1 e_1 + \cdots + w_n e_n~. \end{aligned}$$
(12)

It is usual to introduce a dummy input \(e_0 = 1\), so that the bias can be treated as a weight (see Fig. 1):

$$\begin{aligned} \alpha (\textbf{e}, \textbf{w}) = \textbf{w}^t \textbf{e} = \sum _{i = 0} ^{n} {w_i e_i}~. \end{aligned}$$
(13)
Fig. 1
figure 1

Basic unit of a neural net. The basic unit transforms the inputs \(\textbf{e} = (e_1, \ldots , e_n)^t\) into a value a by aggregation involving weights \(\textbf{w} = (w_0, w_1, \ldots , w_n)^t\): \(a=w_0 + w_1 e_1 +\cdots + w_n e_n \) (\(w_0\) is the bias). Using a dummy input \(e_0 = 1\), we have \(a = \alpha (\textbf{e},\textbf{w}) = \textbf{w}^t\textbf{e}\). The value of a is modified by an activation function \(\delta \) to produce the output \(y = \delta (a)\)

Full size image

To generate an ANN, different units are interconnected, so that the output of a unit becomes one of the inputs of another unit (Bishop 1995). The units are organized according to a directed graphFootnote 4—the network graph—where each unit becomes a node (generally labeled according to its output) and the directed edges represent the information flow in the network: an arrow from a first unit to a second one, indicates that the output of the first unit is used as input for the second unity (see Figs. 2, 3)

Fig. 2
figure 2

Using a directed graph to generate an ANN. Each \(\blacksquare \) is an unity. Arrows show the flow of information

Full size image

3.1 Multilayer perceptrons

The units of an ANN are generally organized in layers—i. e., in subsets of units receiving the same inputs and producing different outputs each, which will form the inputs of the next layer. Each subset is visualized as a stack of units (see Fig. 3) and referred by indexes \((\ell , k)\) indicating their positions (stack \(\ell \), position k from the top). The first layer receives the input and the last layer furnishes the output of the ANN—these layers are particularly referred as being the input layer and the output layer. The other intermediating layers are called hidden layers and are generally invisible to the user.

Fig. 3
figure 3

DNN graph of a K-layer perceptron. The \(\ell ^{\text {th}}\) hidden layer contains \(\eta _{\ell }\) hidden units. As usual in this kind of diagram, the bias is not represented

Full size image

When there are more than three hidden layers, we refer to the multilayer perceptron as a Deep Neural Network (DNN). Training a DNN—or Deep Learning—is considered as challenging (Bengio 2009).

Let us consider a multilayer perceptronFootnote 5 formed by the input layer (numbered as 0) and K other layers, where K is a strictly positive integer. Layers \(1,\ldots , K-1\) are hidden ones, layer K is the output layer. Layer number \(\ell \) contains \(\eta _\ell \) units and produces outputs \(h_i^{(\ell )}\), \(1\le i\le \eta _\ell \), as shown in Fig. 3. The input layer performs the identity: \(h^{(0)}_i = x_i\). With these notations,the net receives \(\eta _0\) inputs and generates \(\eta _K\) outputs.

Let us denote, for \(\ell \ge 0\), \(\textbf{h}^{(\ell )}=\left( h_1^{(\ell )},\ldots , h_{\eta _{\ell }}^{(\ell )}\right) ^t\). The vector \(\textbf{h}^{(\ell )}\) contains the outputs of the layer \(\ell \) which are the inputs of the layer \(\ell +1\). Analogously, let us introduce, for \(\ell > 0\), \(\mathbf {w_i}^{(\ell )} = (w_{i,0}^{(\ell )},\ldots ,w_{i,\ell -1}^{(\ell )})\): \(\mathbf {w_i}^{(\ell )}\) is a row vector containing the weigths for the unit \((\ell , i)\)—id est, \(w_{i,k}^{(\ell )}\) is the weight corresponding to the oriented edge going from unit \((\ell -1, k)\) to unit \((\ell , i)\) (from the \(k^{\text {th}}\) unit in layer \((\ell - 1)\) to the \(i^{\text {th}}\) unit in layer \(\ell \)), and \(w_{i,0}^{(\ell )}\) is the bias. We have (see Eq. (12) )

$$\begin{aligned} h_i^{(\ell )} = \delta _i^{(\ell )}(a_i^{(\ell )} )~,~a_i^{(\ell )} = \alpha _i^{(\ell )}(\textbf{h}^{(\ell -1)}, \mathbf {w_i}^{(\ell )})~, 1\le i \le \eta _\ell ~, 1\le \ell \le K ; \end{aligned}$$
(14)

with (see Eq. (13) )

$$\begin{aligned} \alpha _i^{(\ell )}(\textbf{h}^{(\ell -1)}, \mathbf {w_i}^{(\ell )})=\mathbf {w_i}^{(\ell )}\textbf{h}^{(\ell -1)}~, 1\le \ell \le K~. \end{aligned}$$
(15)

Let us introduce \(\textbf{w}^{(\ell )} = \left( w_{i,k}^{(\ell )}: 1\le i\le \eta _\ell , 0\le k\le \eta _{\ell -1}\right) \)—a matrix containg the weights of layer \(\ell \); \(\varvec{\alpha }^{(\ell )} \left( \textbf{h}^{(\ell -1)}, \textbf{w}^{(\ell )}\right) = \left( \alpha _1^{(\ell )}\left( \textbf{h}^{(\ell -1)}, \mathbf {w_1}^{(\ell )}\right) , \ldots , \alpha _{\eta _\ell }^{(\ell )}\left( \textbf{h}^{(\ell -1)}, \textbf{w}_{\eta _\ell }^{(\ell )}\right) \right) \), \(\textbf{a}^{(\ell )}= \left( a_1^{(\ell )},\ldots , a_{\eta _\ell }^{(\ell )}\right) ^t\)—vectors containing all the agregations of layer \(\ell \); and \(\varvec{\delta }^{(\ell )}(\textbf{a}) = \left( \delta _1^{(\ell )}(a_1^{(\ell )}), \ldots , \delta _{\eta _\ell }^{(\ell )}(a_{\eta _\ell }^{(\ell )})\right) \)—a vector containing all the activations of layer \(\ell \). Then, Eqs. (14)-(15) can be written in a concise form

$$\begin{aligned} \textbf{h}^{(\ell )}=\varvec{\delta }^{(\ell )}(\textbf{a}) ~,~\textbf{a}^{(\ell )}=\varvec{\alpha }^{(\ell )}(\textbf{h}^{(\ell -1)}, \textbf{w}^{(\ell )})=\textbf{w}^{(\ell )}\textbf{h}^{(\ell -1)}~1\le \ell \le K~. \end{aligned}$$
(16)

Let \(\textbf{x}=\left( x_1, \ldots , x_{\eta _0}\right) \) be the vector of inputs, and \(\textbf{w}= \left( \textbf{w}^{(\ell )}: 1\le \ell \le K\right) \) represent the list of all weights in the network: \(\textbf{w}\) is brought to a vector \(\textbf{w}\):

$$\begin{aligned} \textbf{w} = \left( v^{(1)},\ldots , v^{(K)}\right) \end{aligned}$$

where

$$\begin{aligned} v^{(i)} = \left( w^{(i)}_{1,0},\ldots ,w^{(i)}_{1,\eta _{i-1}},\ldots , w^{(i)}_{\eta _i,0},\ldots ,w^{(i)}_{\eta _i \eta _{i-1}}\right) . \end{aligned}$$

Then

$$\begin{aligned} \textbf{h}^{(K)}=\varvec{\tau }(\textbf{x},\textbf{w}) ~,~ \end{aligned}$$
(17)

where

$$\begin{aligned} \varvec{\tau }(\textbf{x},\textbf{w}) = \varvec{\delta }^{(K)}\left( \varvec{\delta }^{(K-1)}\left( \varvec{\delta }^{(K-2)}\left( \ldots , \textbf{w}^{(K-2)}\right) , \textbf{w}^{(K-1)}\right) , \textbf{w}^{(K)}\right) ~,~ \end{aligned}$$
(18)

and the multilayer perceptron can be considered as a function

$$\begin{aligned} \textbf{ h}(\bullet ,\textbf{w}) : \mathbb {R}^{\eta _0} \rightarrow \mathbb {R}^{\eta _K}, \textbf{x} \mapsto \textbf{ h}(\textbf{x},\textbf{w}), \end{aligned}$$
(19)

associating to the inputs \(\textbf{x} \) the outputs \(\textbf{ h}(\textbf{x},\textbf{w}) = \left( h_1^{(K)}, \ldots , h_{\eta _K}^{(K)}\right) \).

From the standpoint of mathematical modeling, the training of a DNN summarizes as

  1. (a)

    Data: a set of observations \(\mathcal {D} = \left\{ (\textbf{x}_s, \textbf{y}_s)~, ~1\le s\le n_s\right\} \subset \mathbb {R}^{\eta _0}\times \mathbb {R}^{\eta _K}\) is given. A loss function \(\mathcal {L}: \mathbb {R}^{\eta _k}\times \mathbb {R}^{\eta _K}\mapsto \mathbb {R}^+\) is given to measure the gap between two elements from \(\mathbb {R}^{\eta _K}\) (for instance, a distance or a pseudo-distance). Examples of standard loss functions are given in 3.3.

  2. (b)

    The decision variables are the weights and bias, grouped in \(\textbf{w}\)—these are the model parameters to be determined.

  3. (c)

    The performance of a given set of model parameters \(\textbf{w}\) is evaluated by the aggregation of the values of the gaps between the outputs \(\varvec{\tau }(\textbf{x}_s, \textbf{w})\) and the observed values \(\textbf{y}_s\), for \(1\le s\le n_s\). The aggregation is performed by a function \(\mathcal {A}:\mathbb {R}^{n_s}\mapsto \mathbb {R}^+\), transforming the vector of distances \(\textbf{d}(\textbf{w}) = \left( \mathcal {L} (\varvec{\tau }(\textbf{x}_1,\textbf{w}),\textbf{y}_1),\ldots , \mathcal {L} (\varvec{\tau }(\textbf{x}_{n_s},\textbf{w}),\textbf{y}_{n_s})\right) \) into a non-negative real number. The global loss function to be minimized is

    $$\begin{aligned} G\left( \textbf{w}\right) = \mathcal {A}\left( \textbf{d}(\textbf{w}) \right) ~. \end{aligned}$$
    (20)

    For instance, we can use the arithmetic mean of the gaps:

    $$\begin{aligned} \mathcal {A}\left( \textbf{d}(\textbf{w}) \right) =\frac{1}{n}\sum \limits _{s=1}^{n_s} d_s(\textbf{w}) = \frac{1}{n}\sum \limits _{s=1}^{n_s} \mathcal {L} (\varvec{\tau }(\textbf{x}_{s}),\textbf{y}_{s}) ~. \end{aligned}$$
    (21)
  4. (d)

    Find the model parameters that minimize the global loss function f, id est, find

    $$\begin{aligned} \varvec{\mathbb {w}^*}=\arg {\min {\{ G\left( \textbf{w}\right) : \textbf{w}\} }}~. \end{aligned}$$
    (22)

In the sequel, we use this model for the training of a DNN on a daset of images \(\textbf{X}\) and labels Y: \(\mathcal {D} = \left\{ \left( \textbf{X}_s, Y_s\right) , i = 1, \ldots n_s\right\} \).

3.2 Activation functions

Although the activation functions are, in principle, specific to each unit—as indicated in the preceding—it is usual to consider a single activation function for all the hidden layers: \(\delta _i^{(\ell )} = \delta \), for \(1\le i\le \eta _\ell \) and \(1\le \ell \le K-1\). Often, a distinct activation function is used for the output layer: \(\delta _i^{(K)} =\overline{ \delta }\), for \(1\le i\le \eta _K\), with a choice adapted to the problem under consideration. The choice of \(\delta \) and \(\overline{\delta }\) is considered as important, since it modifies the behavior of the network. Today, the choice for \(\delta \) is mostly dictated by experience and trial (Feng and Lu 2019; Szandała yyy), while the choice of \(\overline{\delta }\) results from the characteristics of the expected output (binary, discrete, bounde, unbounded). Concerning the hidden layers, a popular choice is a family of Rectified Linear Units—activation functions usually referred as ReLU:

$$\begin{aligned} \delta (z) = {\text {ReLU}}(z) = \max (0,z). \end{aligned}$$
(23)

Notice that \({\text {ReLU}}(\mathbb {R}) = (0, +\infty )\), so that the outputs are positive but unbounded (Stutz 2014), (Krizhevsky et al. 2012). A variant of \({\text {ReLU}}\) is \({\text {PReLU}}\) or \({\text {Leaky}}{\text {ReLU}}\) (El Jaafari et al. 2021), given by (\(a > 0\) is a parameter to be chosen by the user):

$$\begin{aligned} \delta (z) = {\text {PReLU}}(z) = \max (0,z) + a~\min (0,z)~~~(a > 0). \end{aligned}$$
(24)

\({\text {PReLU}}(\mathbb {R}) = (-\infty , +\infty )\), so that the outputs are unbounded, and can take negative values.

For the output layer, a popular family of activation functions is the sigmoid family. For instance, the logistic sigmoid, given by

$$\begin{aligned} \overline{\delta }(z) = \sigma (z) = \frac{1}{1 + \exp (-z)}, ~~ z\in \mathbb {R}. \end{aligned}$$
(25)

This function has a bounded range: we have \(\sigma (\mathbb {R}) = (0,1)\). From the same family, the hyperbolic tangent \(\overline{\delta }(z) = th(z) =\tanh (z)\) takes negative values, since \(th(\mathbb {R}) = [-1,1]\), so that th can be used if the user desires bounded outputs including negative values (Stutz 2014), (Duda et al. 2001). These sigmoid family is often used when we are interested in binary outputs. However, according to Stutz (2014), Glorot and Bengio (2010) both the logistic sigmoid and the hyperbolic tangent perform badly in deep learning. These authors recommend the use of the softsign activation function:

$$\begin{aligned} \overline{\delta }(z) = s(z) = \frac{1}{1+ \vert z \vert }. \end{aligned}$$
(26)

Nevertheless, some works tend to show that the combination of the family ReLU with the hyperbolic tangent activation produces good results (Jarrett et al. 2009).

When considering classification in \(\eta _K\) classes with neural networks,Footnote 6 the user to choose a most relevant output among \(\textbf{h}^{(K)} = (h_1^{(K)}, \ldots , h_{\eta _K}^{(K)})\).

Thus, we can design a DNN destined to classify data \(\textbf{X}\) in one among \(\eta _K\) classes, by producing an output that can be interpreted in terms of probability: the class i, \(1\le i\le \eta _K\) corresponds to the unit (K, i) in the output layer and \(p_i = h_i^{(K)}\) is a prediction of the probability of the event “ \(\textbf{X}\in \) class i” (id est, “ \(\textbf{X}\) is member of class i ”). Let us denote by Y the class number: \(Y\in \{1,\ldots ,\eta _K\}\): we look for a DNN such that

$$\begin{aligned} p_i = P(Y = i\vert \textbf{X}) \Rightarrow \textbf{p} = (p_1, \ldots , p_{\eta _K})^t \in \mathbb {R}^{\eta _K} : \sum \limits _{i=1}^{\eta _K}p_i = 1, \end{aligned}$$
(27)

where \(P(\bullet \vert \bullet )\) denotes the conditional probability.

In this case, a popular choice is the softmax activation functions, whose outputs can be interpreted as probabilities:

$$\begin{aligned} \delta _i^{(K)}(\textbf{a}^{(K)}) = {\text {softmax}}(\textbf{a}^{(K)},i) = \frac{\exp (a_i^{(K)})}{\sum _{j = 1} ^{\eta _K} \exp (a_j^{(K)})}. \end{aligned}$$
(28)

Indeed, \(p_i = \delta _i^{(K)}(\textbf{a}^{(K)})\) verifies \(p_i > 0\) and \(\sum _{j = 1} ^{\eta _K} p_i = 1\), so that the outputs \(p_i = h_i^{(K)}\), \(1 \le i \le \eta _K\), can be interpreted as probabilities (Bishop 2006).

3.3 Loss functions for classification

Let be given \(\textbf{X}\) belonging to the class Y: we have as exact probability \(p_Y^*= 1\), so that the exact vector of probabilities is \(\mathbf {p^*}(Y) = (p_1, \ldots , p_{\eta _K})\) such that \(p_Y^*= 1\) and \(p_i^*= 0\), if \(i\ne Y\)—it is a one-hot vector.Footnote 7

The gap between the probabilities of the classes furnished by \(\textbf{p} = \varvec{\tau }(\textbf{X},\textbf{w}) \) and the exact probabilities \(\mathbf {p^*}\) can be evaluated by the cross-entropy loss function

$$\begin{aligned} \mathcal {L} \left( \textbf{p},\mathbf {p^*}(Y))\right) = {}-\sum \limits _{j=0}^{\eta _K-1}p^*_j(Y)\log (p_j) . \end{aligned}$$
(29)

We can consider this loss function under the form

$$\begin{aligned} \mathcal {L} \left( \textbf{p},Y)\right) = {}-\sum \limits _{j=1}^{\eta _K}\textbf{1}_{Y=j}\log (p_j) ~, \end{aligned}$$
(30)

where

$$\begin{aligned} \textbf{1}_{Y=j}=\left\{ \begin{array}{ll} 1 &{} \hbox {if } Y = j\\ 0 &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

The global loss function becomes

$$\begin{aligned} G\left( \textbf{w}\right) = \frac{1}{n_s}\sum \limits _{s=1}^{n_s}\mathcal {L} (\varvec{\tau }\left( \textbf{X}_s,\textbf{w}) ,Y_s)\right) , \end{aligned}$$
(31)

id est,

$$\begin{aligned} G\left( \textbf{w}\right) = {}-\frac{1}{n_s}\sum \limits _{s=1}^{n_s}\sum \limits _{j=1}^{\eta _K}\textbf{1}_{Y_s=j}\log (\tau _j(\textbf{X}_s,\textbf{w}) ), \end{aligned}$$
(32)

with \(h_j ^{(K)} = \tau _j(\textbf{X},\textbf{w}) \).

3.4 Forward evaluation

The evaluation of the objective function f requests the determination of the global outputs \(\textbf{h}^{(K)}_s = \varvec{\tau }\left( \textbf{X}_s,\textbf{w}\right) \), for \(1\le s\le n_s\). As usual in the framework of DNN, such a determination is carried by forward propagation, which consists in the successive determination of the outputs \(\textbf{h}^{(\ell )}\), for \(0\le \ell \le K\). Forward propagation implements the evaluation of \(\varvec{\tau }\left( \textbf{X},\textbf{w}\right) \), by generating the finite sequence \(\varvec{h}^{(1)}, \ldots , \varvec{h}^{(K)}\), defined by Eqs. (14)–(15), with the initial data \(\varvec{h}^{(0)}= \textbf{X}\). For the classification of a image, \(\textbf{X}\) is a \(\eta \times \eta \) square matrix containing values of the pixels—for a black-and-white image, the pixels take either the value 0 either the value 1, so that \(\textbf{X}\in \{0,1\}^{\eta \times \eta }\). The final outputs of the net are the probabilities of membership, as described in the preceding section: we have \(0\le h_j ^{(K)}\le 1 \), so that \(\varvec{\tau }\left( \textbf{X},\textbf{w}\right) \in [0,1]^{\eta _k}\) and the forward propagation implements a map

$$\begin{aligned} \varvec{\tau }_{\textbf{w}} : {\{0,1\}}^{\eta \times \eta }\mapsto {[0,1]}^{\eta _k}~,~ \varvec{\tau }_{\textbf{w}}\left( \textbf{X}\right) = \varvec{\tau }\left( \textbf{X},\textbf{w}\right) ~. \end{aligned}$$
(33)

3.5 Backpropagation

To implement the optimization methods described in Sect. 2, we need to evaluate the gradient of the global loss function f with respect to the weigths \(\textbf{w}\). In the framework of DNN, such an evaluation is performed by backpropagation., which corresponds to the successive application of the chain rule for the derivation of the composition of functions. The rule is successively applied from the last layer to the first one, to generate \(\partial _{\textbf{w}} G = \partial G \bigm / \partial {\textbf{w}}\), id est, the derivatives \(\partial _{ w^{(\ell )}_{ij}} G= \partial G / \partial w^{(\ell )}_{ij}\), corresponding to each weight \(w^{(\ell )}_{ij}\) of the net: \(0\le \ j\le \eta _{\ell -1}\), \(1\le i\le \eta _\ell \), \(1\le \ell \le K\). As previously observed, the global loss functions are defined by Eqs. (20), (21), (31) and involves a loss function \(\mathcal {L}\) destined to evaluate the gap between the prediction \(\varvec{\tau }_{\textbf{w}}\left( \textbf{X}\right) \) and the real value \(\mathbf {p^*}(Y)\). From Eq. (31):

$$\begin{aligned} \partial _{\textbf{w}} G = \frac{1}{n_s}\sum \limits _{s=1}^{n_s}\partial _{\textbf{w}} \mathcal {L} (\varvec{\tau }\left( \textbf{X}_s,\textbf{w}) ,Y_s)\right) ~~, \end{aligned}$$
(34)

Thus, we must evaluate the derivatives \(\partial _{\textbf{w}} \mathcal {L}\), id est, \(\partial _{ w^{(\ell )}_{ij}} \mathcal {L}\), for \(0\le \ j\le \eta _{\ell -1}\), \(1\le i\le \eta _\ell \), \(1\le \ell \le K\). The derivatives can be evaluated by recurrence, using Eqs. (14)–(15) or Eq. (16). Indeed, we observe that

$$\begin{aligned} \partial _{ h_{s}^{(\ell -1)}} h^{(\ell )}_t = D^{(\ell )}_{t} w_{ts}^{(\ell )}~ ,~D^{(\ell )}_{t} = \left( \delta ^{(\ell )}_t\right) '(a_t^{(\ell )}). \end{aligned}$$
(35)

Moreover,

$$\begin{aligned} \partial _{ w^{(\ell )}_{ij}} h^{(\ell )}_t = D^{(\ell )}_{t}\; \partial _{ w^{(\ell )}_{ij}} a_t^{(\ell )} =\sum _{s=0}^{\eta _{\ell -1}} D^{(\ell )}_{t} w_{ts}^{(\ell )}\partial _{ w^{(\ell )}_{ij}} h^{(\ell -1)}_s~~ , \end{aligned}$$
(36)

so that

$$\begin{aligned} \partial _{ w^{(\ell )}_{ij}} h^{(\ell )}_t =\sum _{s=0}^{\eta _{\ell -1}}\partial _{ h_{s}^{(\ell -1)}} h^{(\ell )}_t \partial _{ w^{(\ell )}_{ij}} h^{(\ell -1)}_s ~~ , \end{aligned}$$
(37)

and

$$\begin{aligned} \partial _{ w^{(\ell )}_{ij}} \textbf{h}^{(\ell )}_t =\partial _{ \textbf{h}^{(\ell -1)}} \textbf{h}^{(\ell )} \partial _{ w^{(\ell )}_{ij}} \textbf{h}^{(\ell -1)}~~. \end{aligned}$$
(38)

Thus,

$$\begin{aligned} \partial _{\textbf{w}} \textbf{h}^{(\ell )}_t =\partial _{ \textbf{h}^{(\ell -1)}} \textbf{h}^{(\ell )} \partial _{\textbf{w}} \textbf{h}^{(\ell -1)}~~. \end{aligned}$$
(39)

We have

$$\begin{aligned} \partial _{\textbf{w}} \mathcal {L}(\varvec{\tau }_{\textbf{w}}(\textbf{X}), Y) = \partial _{\varvec{\tau }_{\textbf{w}}} \mathcal {L}(\varvec{\tau }_{\textbf{w}} (\textbf{X}), Y) \; \partial _{\textbf{w}} \varvec{\tau }_{\textbf{w}}(\textbf{X}) ~~, \end{aligned}$$
(40)

id est,

$$\begin{aligned} \partial _{\textbf{w}} \mathcal {L}(\varvec{\tau }_{\textbf{w}}(\textbf{X}), Y) = \partial _{\varvec{\tau }_{\textbf{w}}} \mathcal {L}(\varvec{\tau }_{\textbf{w}}(\textbf{X}), Y) \; \partial _{\textbf{w}} \textbf{h}^{(K)} . \end{aligned}$$
(41)

Thus, Eq. (39) yields that, for \(0 \le \ell \le K-1\)

$$\begin{aligned} \partial _{\textbf{w}} \mathcal {L}(\varvec{\tau }_{\textbf{w}}(\textbf{X}), Y) = \partial _{\textbf{h}^{(K)}} \mathcal {L}(\textbf{h}^{(K)}, Y) \left[ \; \prod _{i=0}^{K-\ell -1} \partial _{\textbf{h}^{(K-i-1)}} \textbf{h}^{(K-i)} \right] \partial _{\textbf{w}} \textbf{h}^{(\ell )}~. \end{aligned}$$
(42)

Equations (35) and (42) furnish \(\partial _{\textbf{w}} \mathcal {L}\). Then, Eq. (34) furnishes \(\partial _{\textbf{w}} G\). Practical implementation is made by the algorithms of backpropagation, such as:

figure a

3.6 Regularization

Multilayer perceptrons with at least one hidden layer have been shown to approximate any target mapping to arbitrary precision. As a result, the training data may be overfitted, with a low training error on the training set but a large training error on unknown data (Bengio 2009). Regularization is the job of avoiding overfitting to improve generalization performance, which means that the trained network should also perform well on unknown data (Haykin 2005). As a result, the training set is frequently divided into two parts: real training and validation. The neural network is subsequently trained with the new training set, and its generalization performance is assessed using the validation set (Duda et al. 2001).

Regularization can be done in a variety of ways. The training set is frequently supplemented to include particular invariances that the network is supposed to learn (Krizhevsky et al. 2012). Other methods include a regularization component in the error measure to manage the solution’s complexity and form (Bishop 1995)—the objective function to be minimized is modified by the adjonction of a penalty term:

$$\begin{aligned} G_\lambda (\textbf{w}) = G(\textbf{w}) + \lambda \varphi (\textbf{w}), \end{aligned}$$
(43)

where \(\varphi (\textbf{w})\) affects the solution’s shape and \(\lambda \) is a balancing parameter. A popular \(\varphi \) is the \(\ell _2\)-regularizationFootnote 8

$$\begin{aligned} \varphi (\textbf{w}) = \Vert \textbf{w}\Vert _2^2 = \sum _{\ell = 1}^{K} \sum _{i=1}^{\eta _\ell }\sum _{j=1}^{\eta _{\ell -1}}{(w_{ij}^{(\ell )})}^2. \end{aligned}$$

The goal is to punish big weights because they are associated with overfitting (Bishop 1995). More generally, we can consider \(\ell _p\)-regularization. For instance, for \(p = 1\), \(\ell _1\)-regularizationFootnote 9 is used in El Mouatasim (2015, 2019) to enforce sparsity of the weights, that is many of the weights should vanish.

3.6.1 Early stopping

While the error on the training set tends to decrease with the number of iterations, once the network starts to overfit the training set, the error on the validation set usually starts to climb again. To minimize overfitting, training should be halted as soon as the error on the validation set reaches a minimum, i.e. before the error on the validation set rises again (Bishop 1995). This technique is known as early stopping.

3.6.2 Dropout

Another regularization strategy based on human brain observation is proposed in Hinton et al. (2012). Each hidden unit is skipped with probability \(P=\frac{1}{2}\) whenever the neural network is given a training sample (Hinton et al. 2012). This method can be interpreted in a variety of ways. Units cannot, for starters, rely on the presence of other units. Second, this strategy allows for the simultaneous training of numerous distinct networks. As a result, dropout can be equated to model averaging.Footnote 10

In this situation, nearly half of the neurons are inactive and are not regarded to be part of the neural network. As you can see, the neural network grows more basic.

Overfitting can be reduced by using a simpler version of the neural network with less complexity. At each forward propagation and weight update step, neurons with a particular probability P are deactivated.

3.7 Convolutional neural networks

The mathematical modeling of CNN including convolution, convolutional layer, non-linearity layer, local contrast normalization layer, fully connected layer and architectures is given in Stutz (2014).

We look at the architecture employed in Krizhevsky et al. (2012) as an example of a modern CNN that performs well on the ImageNet Dataset (Zeiler and Fergus 2013). Five convolutional layers are followed by a rectified linear unit non-linearity layer, brightness normalization, and overlapping pooling in the architecture. Three additional fully-connected layers are used for classification. Krizhevsky et al. (2012) employs dropout as a regularization strategy to avoid overfitting.

The authors of Ciresan et al. (2012) integrate many deep CNN with comparable architectures and average their classification/prediction results. The multi-column deep CNN is the name for this architecture.

We summarized the description of the CNNs by the flow diagram in Fig. 4.

Fig. 4
figure 4

Flow diagram of deep CNN (Figure from Izaak (2022), under licence CC BY-SA 4.0)

Full size image

4 Optimization DNN

The goal of this section is given the mathematical modeling of optimization DNN including analysis of the optimization problem, SGD, Subgradient algorithm, control learning rate and SPSA.

4.1 Nonconvex optimization DNN problem

Piecewise affine activation functions provide a dilemma since the resultant mathematical issue is a multicomposite optimization problem with associated nonconvexity and non differentiability. The variable linear transformation from one layer to the next, where the transformation matrix is multiplied by the variable input of that layer, which is determined from the previous layer, causes the nonconvexity. By gradually aggregating the resultant bilinearity over all layers, a highly nonconvex composite objective function may be reduced. This property of linked nonconvexity and nondifferentiability poses significant hurdles for solving the optimization issue using a mathematically rigorous approach with a proved guarantee of convergence to some form of stable solution. Indeed, there is no known solution that can achieve the latter stated aim as a stand-alone deterministic optimization problem (Cui et al. 2020). In particular, usually SGD algorithms converges to suitable local minimum even though the problem itself is highly nonconvex optimization, for more about analysis of the optimization error, see for instance (Kutyniok 2022).

4.2 Stochastic gradient descent (SGD)

SGD techniques are prominent strategies for estimating the parameters \(\textbf{w}\) of DNN.

  1. (I)

    Forward: Let \(\textbf{w}_{(k)}\) be the current weights. For \(\ell = 1\) to K

    • Calculate the predicted values \((\varvec{\tau }_{\textbf{w}}(\textbf{X}_s)\), \(s = 1, \ldots , n_s\).

    • Calculate the corresponding values of \((\textbf{a}^{(\ell )}_s, \textbf{h}^{(\ell )}_s)\), \(s = 1, \ldots , n_s\).

  2. (II)

    Backpropagation:

    • Calculate the gradient of the output

      $$\begin{aligned} \nabla _{a^{(K)}(x)}\mathcal {L}(\varvec{\tau }_{\textbf{w}}(\textbf{X}_s), Y_s) =\varvec{\tau }_{\textbf{w}}(\textbf{X}_s) - \textbf{p}^*(Y_s), \end{aligned}$$

      where \(\textbf{p}^*(Y_s) \in \mathbb {R}^{\eta _K}\) is a one-hot vector such that \(p^*_{Y_s} = 1\), id est, \(p^*_i =\textbf{1}_{i=Y_s}\), \(1\le \i \le \eta _K\).

    • For \(\ell = K\) to 1 - Calculate the gradient at hidden layer \(\ell \) using Eqs. (35), (42) and (34)

  3. (III)

    Mini-Batch: The technique employed in SGD algorithms is to replace the Eq. (31) of classification error with

    $$\begin{aligned} f(\textbf{w}, s)= \frac{-1}{\vert M_s\vert }\sum \limits _{i: z_i\in M_s}\sum \limits _{j=1}^{\eta _K}\textbf{1}_{Y_s=j}\log (\varvec{\tau }_{\textbf{w}}(\textbf{X}_s) ), \end{aligned}$$
    (44)

    for each iteration s, where \(M_s\) is mini-batch and \(\vert M_s\vert \) is mini-batch size. Then

    $$\begin{aligned} \textbf{E}[G(\textbf{w},s)] = G(\textbf{w}), \end{aligned}$$

    where \(\textbf{E}[.]\) is mathematical expectation, and

    $$\begin{aligned} \textbf{E}[\nabla _{\textbf{w}} G(\textbf{w},t)] = \nabla _{\textbf{w}} G(\textbf{w}). \end{aligned}$$

    are satisfied by Eq. (44).

However, prior to testing, the sample is randomly mixed, sorted into batches of a defined size, and each batch is used one at a time until all of the samples have been gathered. This is then repeated in the same order as the previous batch. Then, starting with the first batch and finishing with the last, each epoch is made up of sequential batches that encompass all of the training data.

figure b

4.3 Subgradient algorithm

To determine the global optimum, the DNN algorithm employs an optimization strategy. The SGD algorithm, a well-referenced artificial intelligence function to model a first-order optimization technique that helps us identify a local minimum, was employed in the neural network algorithm.

A subgradient algorithm is an unconstrained minimization method that’s used to reduce the size of a function, in this case the loss function. In this section, the loss function (43) can be presented the objective function of the nonconvex nonsmooth optimization problem 1.

The goal was to find a \(\textbf{w}\) value that produced the least amount of error and allowed the loss function to attain a local minimum. In this strategy, each iteration seeks to find a new \(\textbf{w}\) value that gives a somewhat smaller error than the preceding iteration.

Typically, (1) computational methods rely on the usage of subgradient iteration algorithms, which supply information at any point \(\textbf{w}\), the value of the loss function \(G(\textbf{w})\), as well as a subgradient \(\textbf{g}\) from the subdifferential set \(\partial G(\textbf{w})\).

Remember that every vector \(\textbf{g}\) that fulfills the inequality

$$\begin{aligned} G(\textbf{y})\ge G(\textbf{w}) + \textbf{g}^t\mathbf {(y-w)}~~~~ \forall \textbf{y} \in \mathbb {R}^n, \end{aligned}$$
(45)

is a subgradient of \(G(\textbf{w})\) at \(\textbf{w}\).

Since the subgradient algorithm with learning rate \(\rho \) starts with some initial \(\textbf{w}_{(0)}\) and updates it repeatedly:

$$\begin{aligned} \textbf{w}_{(k+1)}=\textbf{w}^k-\rho ^k \textbf{g}^k,~~\textbf{g}^k\in \partial G(\textbf{w}^k),~~~~k=0,1,\ldots \end{aligned}$$
(46)

which have been the subject of extensive research since the 1960s.

A convex function is known to be subdifferentiable at all points in its domain. The subdifferential is also a non-empty convex, closed, and bounded set (Dem’vanov and Vasil’ev 1985). At all locations in its domain, a convex function isn’t necessarily differentiable. If a convex function is differentiable at a point \(\textbf{w}\), then \(\nabla G(\textbf{w})\) is a subgradient of G at \(\textbf{w}\). Also we have

$$\begin{aligned} \partial G(\textbf{w}) = \{\nabla G(\textbf{w})\}. \end{aligned}$$

Subgradient can be thought of as a generalized gradient of a convex function in this context.

For nonconvex function \(\partial G(\textbf{w})\) is Clarke subdifferential at point \(\textbf{w} \in \mathbb {E}\) (Bagirov et al. 2013). A learning rate is also employed to govern the size of the downward step we take throughout each iteration. For learning rate \(\rho _{(k)}\) meeting the "divergence series" criterion, it was proven that (46) converges under relatively mild conditions:

$$\begin{aligned} \rho _{(k)}\xrightarrow {k\rightarrow \infty } 0+{},~~~~\sum _k\rho _{(k)}=\infty . \end{aligned}$$
(47)

Theorem 1

Let G satisfy the asumptions on the objective function of optimization problem 1. Let the sequence \(\{ \textbf{w}_{(k)}: k\in \mathbb {N}\}\) given by the formula (46) and the learning rate \(\rho _{(k)}\) satisfy the conditions (47). Then \(G(\textbf{w}_{(k)})\rightarrow G^*\).

Proof

To demonstrate the theorem, we must show that

$$\begin{aligned} \forall \epsilon > 0, \exists n_k\in \mathbb {N}\text { such that } k \ge n_k \Rightarrow G\left( \textbf{w}_{(k)}\right) - G\left( \textbf{w}^*\right) < \epsilon . \end{aligned}$$

Let us proof it by reductio ad absurdum: assume that \(\exists \epsilon > 0\) such that

$$\begin{aligned} \forall k \in \mathbb {N}:~~~~ G(\textbf{w}_{(\sigma _k)}) -G(\textbf{w}^*)\ge \epsilon , \end{aligned}$$
(48)

where \(G(\textbf{w}_{(\sigma _k)})\) is a subsequence of \(G(\textbf{w}_{(k)})\).

Let \(\textbf{w} = \textbf{w}_{(\sigma _k)}, y = \textbf{w}^*\) in (45) then:

$$\begin{aligned} G(\textbf{w}^*)\ge G(\textbf{w}_{(\sigma _k)}) + \textbf{g}_{(\sigma _k)}^t\left( \mathbf {w^*}-\textbf{w}_{(\sigma _k)}\right) , \end{aligned}$$
(49)

from (48) and (49) we have:

$$\begin{aligned} \textbf{g}_{(\sigma _k)}^t\left( \textbf{w}_{(\sigma _k)}-\textbf{w}^*\right) \ge \epsilon . \end{aligned}$$
(50)

Since \(\rho _{(\sigma _k)} > 0\), multiplying (50) by \(-2\rho _{(\sigma _k)}\) yields

$$\begin{aligned} -2\rho _{(\sigma _k)}\textbf{g}_{(\sigma _k)}^t\left( \textbf{w}_{(\sigma _k)}-w^*\right) \le -2\rho _{(\sigma _k)}\epsilon . \end{aligned}$$

As a consequence, Eq. (46) is used in the estimations that follow:

$$\begin{aligned} \begin{array}{rl} \Vert \textbf{w}_{(\sigma _k + 1)} - \mathbf {w^*}\Vert ^2 &{} = \Vert \textbf{w}_{(\sigma _k)}-\rho _{(\sigma _k)}\textbf{g}_{(\sigma _k)}-\mathbf {w^*}\Vert ^2\\ &{} = \Vert \textbf{w}_{(\sigma _k)}-\mathbf {w^*}\Vert ^2 + (\rho _{(\sigma _k)})^2\Vert \textbf{g}_{(\sigma _k)}\Vert ^2\\ &{} ~~- 2\rho _{(\sigma _k)}\textbf{g}_{(\sigma _k)}^t\left( \textbf{w}_{(\sigma _k)}-\mathbf {w^*}\right) \\ &{} \le \Vert \textbf{w}_{(\sigma _k)} - \mathbf {w^*}\Vert ^2 + (\rho _{(\sigma _k)})^2\Vert \textbf{g}_{(\sigma _k)}\Vert ^2 - 2\rho _{(\sigma _k)}\epsilon . \end{array} \end{aligned}$$

Since \(\partial G(\textbf{w}_{(\sigma _k)})\) is a bounded set (Dem’vanov and Vasil’ev 1985), then \(\exists M > 0\) such that \(\Vert \textbf{g}_{(\sigma _k)}\Vert ^2 \le M\).

Using the first condition of (47) \(\exists n_k \in \mathbb {N}\) such that

$$\begin{aligned} \forall k \ge n_k:~~~~\rho _{(\sigma _k)} \le \dfrac{\epsilon }{M} \Leftrightarrow \rho _{(\sigma _k)} M \le \epsilon . \end{aligned}$$

Then we have:

$$\begin{aligned} \begin{array}{rl} \forall k\ge n_k:~\Vert \textbf{w}_{(\sigma _k)}-\mathbf {w^*}\Vert ^2 &{} \le \Vert \textbf{w}_{(\sigma _k)}-\mathbf {w^*}\Vert ^2 + \rho _{(\sigma _k)}(\rho _{(\sigma _k)} M -2\epsilon )\\ &{} \le \Vert \textbf{w}_{(\sigma _k)}-\mathbf {w^*}\Vert ^2 -\rho _{(\sigma _k)}\epsilon . \end{array} \end{aligned}$$

Recursively expressed, this last inequality produces for every arbitrary integer \(n> n_k\):

$$\begin{aligned} \Vert \textbf{w}_{(n+1)}-\mathbf {w^*}\Vert ^2 \le \Vert \textbf{w}_{(n_k)}-\mathbf {w^*}\Vert ^2 -\epsilon \sum \limits _{k=n_k}^n\rho _{(\sigma _k)}. \end{aligned}$$
(51)

Using the second condition of (47), the right side of (51) tends to \(-\infty \), so that a contradiction with \(0 \le \Vert \mathbf {w^{n+1}-w^*}\Vert ^2\le {}-\infty \), what is a contradiction. Thus, we conclude that the theorem is true. \(\square \)

4.4 Control learning rate

However, numerical experimentation and theoretical research revealed that this learning rate rule leads to delayed convergence as a rule, and future development followed in the footsteps of the subgradient technique (El Mouatasim 2015).

Let \(\Psi (\rho )=G(\textbf{w}-\rho \textbf{g}),~~\textbf{g}G\in \partial G(\textbf{w})\). Let us consider \(\psi \) a smooth quadratic approximation of \(\Psi \), verifying the following conditions: \(\Psi (0)=\psi (0),~~\Psi (\rho )=\psi (\rho )\) and \(\psi ^{'}(0) \in \partial \Psi (0)\), where \(\psi ^{'}(\textbf{w})\) is the derivative of \(\psi \) at point \(\textbf{w}\). For instance, \(\psi \) can be defined as follows:

$$\begin{aligned} \psi (h)= G(\textbf{w}) - \Vert \textbf{g}G\Vert ^2h + \nu _\rho \dfrac{\Vert \textbf{g}\Vert ^2}{\rho }h^2, \end{aligned}$$

where \(\nu _\rho = \dfrac{\Psi (\rho )-(G(\textbf{w})-\rho \Vert \textbf{g}\Vert ^2)}{\rho \Vert \textbf{g}\Vert ^2}.\) Then

$$\begin{aligned} \psi ^{'}(\rho )= - \Vert \textbf{g}\Vert ^2 + 2\nu _\rho \dfrac{\Vert \textbf{g}\Vert ^2}{\rho }\rho = \Vert \textbf{g}\Vert ^2(2\nu _\rho - 1). \end{aligned}$$

This suggests that if \(\nu _\rho \le 0.5\); the derivative of function \(\psi \) at point \(\rho \) is negative, we should increasing the learning rate to reduce loss function G. If, on the other hand, \(\nu _\rho \ge 0.5\); the derivative of function \(\psi \) at point \(\rho \) is positive, and so the learning rate should be decreasing to reduce loss function G (Wójcik1 et al. 2018).

Let us suppose a learning rate of \(\rho _{(k)}\) was used at iteration k and let us identify at \(\textbf{w}_{(k+1)}\) relation between \(\rho _{(k)}\) and the learning rate providing minimization of G in the direction \(-\textbf{g}^{k}\) (El Mouatasim 2020; Uryas’ev 1991).

In this paper, we propose this control learning rate:

$$\begin{aligned} \rho _{(k+1)}=\left\{ \begin{array}{rll} \rho _\textrm{incr}\rho _{(k)},&{}\hbox {if}&{}\nu _\rho \le 0.5,\\ \rho _\textrm{decr}\rho _{(k)},&{}\hbox {if}&{}\nu _\rho \ge 0.5, \end{array} \right. \end{aligned}$$
(52)

where:

  • \(\rho _{(0)}0\) is starting learning rate,

  • \( \rho _\textrm{incr} > 1\) is a increasing coefficient,

  • \(\rho _\textrm{decr}=\dfrac{1}{\rho _\textrm{incr}} < 1\) is a decreasing coefficient.

Theorem 2

If the sequence \(\{\textbf{w}_{(k)}: k\in \mathbb {N}\}\) given by the formula (46) and the learning rate \(\rho _{(k)}\) given by (52), then \(G(\textbf{w}_{(k)})\rightarrow G^*\).

Proof

Let \(\left\{ \rho _{(k_j)} \vert \rho _{(k_j)}=\rho _{(0)}\rho _\textrm{incr}^{k_j} \right\} \) be a subsequence of a sequence \(\{\rho _{(k)}: k \in \mathbb {N}\}\), since \( \rho _{incr} > 1\), we have \(\sum \nolimits _{j=1}^\infty \rho _{(k_j)} = +\infty \). The problem (1) is nonconvex and we assume \(\exists M >0\) such that \(\rho ^{k} \le M \rho _\textrm{decr}^{k}\). Since \(\rho _\textrm{decr} < 1\) then \(\rho _\textrm{decr}^k\rightarrow +0\). Thus, we have also

$$\begin{aligned} \rho _{(k)}\xrightarrow {k\rightarrow \infty } +0. \end{aligned}$$
(53)

The conditions of (47) are satisfied by (53). So we can apply the Theorem 1. \(\square \)

4.5 Stochastic perturbation of subgradient algorithm (SPSA)

The main difficulty remains the lack of convexity: if G is nonconvex, the Kuhn–Tucker points may not correspond to global minimum (El Mouatasim et al. 2006, 2011). In the sequel, we shall improve this point by using an appropriate random perturbation: as previously observed, the real quantities are replaced by random variables (Eqs. (9)–(10)). Since

$$\begin{aligned} \textbf{Q}\left( \textbf{W}_{(k)},\textbf{D}_{(k)},\rho _{(k)}\right) +\textbf{P} _{(k)}=\textbf{Q}\left( \textbf{W}_{(k)},\textbf{D}_{(k)}+\textbf{P}_{(k)}/\rho _{k},\rho _{k}\right) , \end{aligned}$$
(54)

the stochastic iterations may be considered as perturbations of the descent direction \(\textbf{D}_{(k)}\). In the sequel, we describe the general properties of these elements leading to convenient sequences and we show that sequences of Gaussian vectors may be used.

A simple way for the generation of a convenient sequence of perturbations \(\left\{ \textbf{P}_{(k)}: k\in _N\right\} \) is

$$\begin{aligned} \textbf{P}_{(k)}=\xi _{(k)}\textbf{Z}_{(k)}, \end{aligned}$$

where

  1. 1.

    \(\left\{ \xi _{(k)}:k\in \mathbb {N}\right\} \) is a nonincreasing sequence of strictly positive real numbers converging to zero and such that \(\xi _{(0)}\le 1\).

  2. 2.

    \(\left\{ \textbf{Z}_{(k)}: k\in \mathbb {N}\right\} \) is a sequence of random vectors taking their values on E.

Let us introduce \(U_{(k)}=G(\textbf{W}_{(k)})\). Since, at each iteration number \(k\ge 0\), the step \(\rho _{(k)}\) is determined into a way that reduces the value of the objective function (Eq. (7)), the sequence \(\left\{ \text { }U_{(k)}: k \in \mathbb {N}\right\} \) is decreasing by construction. Moreover, it has a lower bound given by \(G^*\).

$$\begin{aligned} \forall k\ge 0 ~:~G^*\le U_{(k+1)}\le U_{(k)}. \end{aligned}$$
(55)

Thus, \(\left\{ U_{(k)}: k\in \mathbb {N}\right\} \) is nonincreasing and bounded from below by m: there exists \(U\ge m\) such that \( U_{(k)}\rightarrow U\ \) for \(\ k\rightarrow +\infty \). The aim is to establish that \(U=G^{*}\).

Theorem 3

Let \(\textbf{Z}_{(k)}\) \(=\textbf{Z}\), where \(\textbf{Z}\) is a random variable following \(N\left( \text { }\textbf{0},\text { }\sigma \textbf{ Id}\right) \), \(\left( \text { }\sigma >0\right) \) and let

$$\begin{aligned} \xi _{(k)}=\sqrt{\,\frac{a}{\log \left( k+d\right) }}, \end{aligned}$$
(56)

where \(a>0\), \(d>0\) and k is the iteration number. Then, for a large enough, \(U=l^{*}\) almost surely.

Proof

See, for instance, Pogu and Souza de Cursi (1994) and El Mouatasim et al. (2006). \(\square \)

5 Computational experiment

All of the tests were run on a personal PC with an HP i5 CPU processor running at 1.20GHz, 4 GB of RAM, and Python 3.9 for Windows 10 installed.

In this paper, we implement CNN (LeNet-5) using PyTorch3, an open source Python library for deep learning classification.

5.1 Algorithm of SPSA

The pseudocode of SPSA is given as follows:

figure c

The pytorch implementation of SPSA algorithm is available in public repository https://github.com/el-mouatasim/SPSA.

5.2 MNIST dataset

MNIST dataset (LeCun and Cortes 2010), consisting 70,000 images \(28\times 28\) grayscale of handwritten digits in the range of 0 to 9, for a total of 10 classes, which includes 60,000 training and validation, and 10,000 test, Fig. 5.

Fig. 5
figure 5

Samples from the MNIST dataset (Figure from Steppan (2022), under licence CC BY-SA 4.0)

Full size image

We present digits from the 54,000 MNIST training set to the network LeNet5 to train it, 6000 images for the validation set and 10,000 for test set. A 32 mini-batch size was used.

5.3 LeNet-5 model

Deep learning models might have a lot of hyperparameters that need to be adjusted. The number of layers to add, the number of filters to apply to each layer, whether to subsample, kernel size, stride, padding, dropout, learning rate, momentum, batch size, and so on are all options. Because the number of possible choices for these variables is unlimited, using cross-validation to estimate any of these hyperparameters without specialist GPU technology to expedite the process is extremely challenging.

As a result, we suggest a model the LeNet-5 model (Fig. 6). The LeNet architecture pad the input image with to make it \(32\times 32\) pixels, then convolution and subsampling with \(\tanh \) activation in two layers. The next two layers are completely connected linear layers with tanh activation, followed by a layer of Gaussian connections, which are fully connected nodes that use mean squared-error as the loss function.

Fig. 6
figure 6

Architect of the LeNet model

Full size image

5.4 Comparing results

We start learning rate of SPSA by \(lr=1e-2\) and the coffecient of update \(\rho _\textrm{incr}=1.05\) are applied, We used \(K_{\max } = 20\) epochs and additional \(K_\textrm{sto} = 5\) stochastic perturbation epochs applied to the best epoch with minimal train loss of subgradient algorithms with control learning rate. also we comparing with popular algorithms such as Adam Kingma and Ba (2015) (with initial learning rate \(lr=1e-3\)), SGD (with initial learning rate \(lr=1e-2\)) and Adagrad. Table 1 give the results of the algorithms in 25 training epochs. Figures 7, 8, 9, 10 exhibit the results of comparing approaches: training loss, training accuracy, validation loss, and validation accuracy, respectively.

Table 1 LeNet-5 model: comparison between SPSA, Adam, Adagrad and SGD in terms of accuracy and loss
Full size table
Fig. 7
figure 7

LeNet-5 model. Comparing training losses results of SPSA, Adam, Adagrad and SGD

Full size image
Fig. 8
figure 8

LeNet-5 model. Comparing training accuracy results of SPSA, Adam, Adagrad and SGD

Full size image
Fig. 9
figure 9

LeNet-5 model. Comparing evaluation losses results of SPSA, Adam, Adagrad and SGD

Full size image
Fig. 10
figure 10

LeNet-5 model. Comparing evaluation accuracy results of SPSA, Adam, Adagrad and SGD

Full size image

The network’s classification accuracy was then measured using the class-assigned neuron response in the 10,000 MNIST test set and SPSA for LeNet-5 model. Figure 11 for confusion matrix show how to determine the estimated number by multiplying each neuron’s responses by class and then choosing the class with the largest average frequency; also the classification report in Table 2, and Fig. 12 give the predict of random sample in test set.

Fig. 11
figure 11

Average confusion matrix of the testing results was calculated over ten presentations of the MNIST test set digits, using the SPSA for LeNet-5 model

Full size image
Table 2 LeNet-5 model: classification report for classifier SPSA
Full size table
Fig. 12
figure 12

Predict sample in MNIST test set, using the SPSA for LeNet-5 model

Full size image

6 Concluding remarks

We considered the training of DNN including multilayer perceptrons (MP), and CNN for image classification with tanh activation function, ReLU activation function or \(\ell _1\) regularization. In such a context, training leads to a nonsmooth nonconvex optimization problem, which has been solved by subgradient techniques—SGD with with controlled learning rate, using locally optimal conditions. The results were improved when compared with the literature.

Additional stochastic perturbation epochs are applied to find a global solution for nonconvex CNN cases. The convergence theorem of the stochastic perturbation subgradient algorithm with control learning rate (SPSA) was established, and numerical results of SPSA compared to the SGD and its variant algorithms in the dataset MNIST for LeNet-5 model revealed that SPSA is more robust and faster than other approaches when a large number of stochastic perturbations was used.

In future work, we shall consider Hilbert networks (Khalij 2021).