1 Introduction

Singular integral equations (SIE) with a Cauchy or Hilbert kernel have been developed by famous mathematicians such as (Gakhov 1990; Lifanov 1996; Muskhelisvili 1968; Pogorzelski 1996; Ladopoulos 2013) and others. Since it is hard to track down scientific arrangements of particular indispensable equations for Cauchy kernels, lots of scientists have prepared various numerical techniques for solving this equation, similar to what (Abdou and Nasr 2003) presented in their Legendre polynomial procedure for solving singular integral equations of the second sort. Mohamed (2022) used the Lerch matrix procedure for solving singular integral equations of the first sort. Mandal and Bhattacharya (2007) applied Bernstein polynomials for solving classes of integral equations. Kumar and Singh (2010) presented a homotopy perturbation procedure for the solution of the Abel integral equation. Seifi (2020) used a collocation system to solve the Cauchy singular integral. Seifi et al. (2017) used a collocation procedure for the solution of singular integral equations. Kumar et al. (2011) used the Homotopy perturbation technique for the solution scheme of general Abel’s integral equations. Dezhbord et al. (2016) used a reproducing kernel for a solution singular integral equation of the first sort. Abdulkawi and Moayad (2015) used a differential transform technique to solve first-order singular integral equations. Mennouni and Guedjiba (2011) use iterations for the solution of singular integral equations. Karczmarek et al. (2006) introduced the Jacobi polynomials technique for the solution of singular integral equations with a Cauchy kernel. Jen and Srivastas (1981) presented the Cubic spline technique to approximate the solution of singular integral equations. Yaghobifar et al. (2010) applied rational functions to obtain approximation solutions of characteristic singular integral equations. Eshkuvatov et al. (2009) used a Chebyshev polynomial technique to approximate the solution of singular integral equations. For the purpose of solving Cauchy singular integral equations, De Bonisand invented the Nystr”om technique with a negative index in De Bonis and Laurita (2009). Abdou and Ezz-Eldin (1994) used Krein’s method to get the solution of the FIE of the first type.

The type generic of Cauchy singular integral the equation has presented in Gakhov (1990), Golberg (1990):

$$\begin{aligned} \nu \int ^1_{-1}\frac{\varphi (x)}{x-z}\textrm{d}x+\int ^1_{-1} k(x,z) \varphi (x) \textrm{d}x=g(z), ~~~~~-1<z<1, \end{aligned}$$
(1.1)

where g(z) and k(x, z) have presented continuous real-valued functions, \(\varphi (z)\) has the undefined function. At \(k(x,z)=0\) in (1.1) simplified to the following formula:

$$\begin{aligned} \nu \int ^1_{-1}\frac{\varphi (x)}{x-z}\textrm{d}x=g(z), ~~~~~~~~~~~~~~~~~-1<z<1. \end{aligned}$$
(1.2)

In physical phenomena, if the function \(\varphi (z)\) is considered to be a ”flux” then the kernel \(k(x,z)=(x-z)^{-1},\) is called ordinary Cauchy singularity (Cauchy kernel). While, if the unknown function represents a ”potential”, then \(k(x,z)=(x-z)^{-2},\) called strong singular kernel.

The authors must note that when using Eq. (1.2) in physical mathematics problems or nuclear reaction problems we must consider the next conditions:

$$\begin{aligned} \varphi (1)=\varphi (-1)=0. \end{aligned}$$
(1.3)

But in the communication (contact) problems in the theory of elasticity or mixed problems in dynamic systems, condition (1.3) is replaced by the following pressure condition:

$$\begin{aligned} \int _{-1}^1\varphi (x)\textrm{d}x=P. \end{aligned}$$
(1.4)

The complete analytic solution of Eq. (1.2), after using the Cauchy method, see Muskhelisvili (1968), leads to discuss the following four cases:

Case (I) The response has bounded at the end point \(z=\pm 1\), where

$$\begin{aligned} \pi \nu \varphi (z)= \int _{-1}^1 k_1(x,z)g(z) \textrm{d}z,~~~~~k_1(x,z)=\frac{\sqrt{(1-z^2)}}{(\sqrt{(1-x^2)}(x-z))}. \end{aligned}$$
(1.5)

Case (II) The response has unbounded at the all end points \(z=\pm 1.\) In this case, we adapt Eq. (1.2) to take the following form

$$\begin{aligned} \pi \nu \varphi (z)=\left\{ \int _{-1}^1 k_2(x,z)g(z) \textrm{d}z +\frac{C}{\sqrt{1-z^2}}\right\} ,~~~~k_2(x,z)= \frac{\sqrt{(1-x^2)}}{(\sqrt{(1-z^2)}(x-z))}. \end{aligned}$$
(1.6)

In mathematical physics phenomena, the value of the constant C,  which depending upon the interval of integration, is very important to determine. Therefore, we go to determine it at \(z=-1.\) So, multiplying (1.6) by \(\sqrt{1-z^2}\) and then following up by evaluating the result form at \(z=-1,\) we have

$$\begin{aligned} C=\frac{1}{\pi } \int _{-1}^1\sqrt{\frac{1-z}{1+z}}g(z)\textrm{d}z. \end{aligned}$$
(1.7)

Case (III): The response has bounded at the end point \(z=1\) and unbounded at \(z=-1,\) where

$$\begin{aligned} \pi \nu \varphi (z)= \int _{-1}^1 k_3(x,z)g(z) \textrm{d}z,~~~~~k_3(x,z)= \sqrt{\frac{(((1-z)(1+x))}{((1+z)(1-x)))}}~ \frac{1}{((x-z))}. \end{aligned}$$
(1.8)

Case (IV): The response has bounded at the end point \(z=-1\) and unbounded at \(z=1\) In this case, the formula (1.2) yields

$$\begin{aligned} \pi \nu \varphi (z)\!=\! \int _{-1}^1 \left\{ k_4(x,z)g(z) \textrm{d}z\!+\!\frac{C_1}{\sqrt{(1-z^2)}}\right\} ,~~~ k_4(x,z)\!=\!\sqrt{\frac{(((1\!+\!z)(1\!-\!x))}{((1\!-\!z)(1\!+\!x)))}}\frac{1}{((x-z))}.\nonumber \\ \end{aligned}$$
(1.9)

To discuss the value of the constant \(C_1\) at \(z=1\), multiplying both sides of Eq. (1.9) by \(\sqrt{1-z^2}\) and evaluating the result at \(z=1\), we have another expression for the value of \(C_1\) in the form

$$\begin{aligned} C_1=\frac{1}{\pi }\int _{-1}^1 \sqrt{\frac{1+z}{1-z}} g(z) \textrm{d}z. \end{aligned}$$
(1.10)

     In this paper, the Lucas polynomial technique is developed to resolve singular Cauchy integral equations of the first type of the form (1.2).

Such researchers like (Abd-Elhameed and Youssri 2017; Abd-elhameed and Youssri 2016) used these polynomials to solve fractional differential equations. Cetin et al. (2015) studied a system of higher order differential equations utilizing the Lucas polynomial technique. For delay differential equations, Baykus and Sezer (2017) used the hybrid Taylor–Lucas collocation approach. Lucas series was used by Nadir (2017) to solve an integro-differential problem. By combining Lucas and Fibonacci polynomials, Haq and Ali (2021) investigate the approximate solution of the two-dimensional Sobolev equation. Chelyshkov polynomials were introduced by Mahdy et al. (2022) for the first class of two-dimensional integral equations.

In the remainder of this paper. In Sect. 2, Lucas polynomial method and some properties are presented. In Sect. 3, transformation of Eq. (1.2) is presented to remove the singularity. In Sect. 4, we study the numerical solution by Lucas polynomial method. In Sect. 5, Error evaluation is presented. In Sect. 6, a few numerical examples are provided to show how the technique works and comparison between other methods are presented.

2 Lucas polynomials

Definition 2.1

Koshy (2001) By the recurrence relation, the Lucas polynomials are obtained

$$\begin{aligned} L_{n+2}(z)=z L_{n+1}(z)+L_{n}(z),~~~~~n\ge 0, \end{aligned}$$
(2.1)

with \(L_{0}(z)=2\) and \(L_{1}(z)=z.\)

These polynomials have the following explicit form:

$$\begin{aligned} L_{n}(z)=\frac{(z+\sqrt{z^2+4})^n+(z-\sqrt{z^2+4})^n}{2^n}, \end{aligned}$$
(2.2)

and also have the following explicit power form representation

$$\begin{aligned} L_{n}(z)=\sum _{k=0}^{\lceil \frac{n}{2}\rceil } \frac{n}{n-k}~{{n-k} \atopwithdelims ()k}z^{n-2k},~~~~~~~n \ge 1, \end{aligned}$$
(2.3)

where

$$\begin{aligned} {\left\lceil \frac{n}{2}\right\rceil }=\left\{ \begin{array}{ll} \frac{n}{2}, ~~~~~~~~~~~~~~~~~~~~~~~~~n~ \textrm{even}, \\ \\ \frac{n-1}{2},~~~~~~~~~~~~~~~~~~~~~n ~\textrm{odd}. \end{array}~~ \right. \end{aligned}$$

The first several Lucas polynomials are shown here, along with a variety of their coefficients in Table 1.

Table 1 The array contains the first few coefficients for the Lucas polynomials
Full size table

Definition 2.2

(Rodrigues’s formula) The Rodrigues formula provided by can be used to obtain the Lucas polynomials \(L_n(z)\)

$$\begin{aligned} L_{n}(z)=2 \frac{n!}{(2n)!} (z^2+4)^{1/2}~\frac{\textrm{d}^n}{\textrm{d}z^n}\left\{ (z^2+4)^{n-\frac{1}{2}}\right\} . \end{aligned}$$
(2.4)

Proposition 2.1

Lucas polynomials’ generating function is described as

$$\begin{aligned} G(z,t)=\sum _{n=0}^\infty L_{n}(z) t^n=\frac{1+t^2}{1-t^2-zt}=1+zt+(z^2+2)t^2+(z^3+3z)t^3+\cdots . \end{aligned}$$

3 Changing the Eq. (1.2)

TThe accompanying structure can be used to address the peculiar function \(\varphi (z)\) in Eq. (1.2):

$$\begin{aligned} \varphi ^{(i)}(z)=\frac{\psi ^{(i)}(z)~\Phi ^{(i)}(z)}{\sqrt{1-z^2}},~~~~~~~~~~~i=1,2,3,4, \end{aligned}$$
(3.1)

a well-behaved function of z in \([-1,1]\) called \(\psi ^{(i)}(z)\), and

$$\begin{aligned} \left\{ \begin{array}{cccc} \Phi ^{(1)}(z)=1-z^2,~~~~~~~~~~~~~~~~~~~~~ {\text {for Case (I)}}, \\ \\ \\ \Phi ^{(2)}(z)=1,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~{\text {for Case (II)}},\\ \\ \\ \Psi ^{(3)}(z)=1-z,~~~~~~~~~~~~~~~~~~~~~~~~{\text {for Case (III)}},\\ \\ \\ \Phi ^{(4)}(z)=1+z,~~~~~~~~~~~~~~~~~~~~~~~~{\text {for Case (IV)}}.\end{array}~~ \right. \end{aligned}$$
(3.2)

Now, we must independently transform Eq. (1.2) into each case’s corresponding transformation to eliminate the singular term at \(x=z\).

Case (I): In the structure, the weird function \(\varphi ^{(1)}(z)\) can be handled by utilizing (3.1) and (3.2):

$$\begin{aligned} \varphi ^{(1)}(z)=\sqrt{1-z^2}~\psi ^{(1)}(z),~~~~~~~~~~~~~~ -1\le z\le 1. \end{aligned}$$
(3.3)

By changing (3.3) to (1.2), we obtain

$$\begin{aligned} \int ^1_{-1}\frac{\sqrt{1-x^2}}{x-z}~\psi ^{(1)}(x) \textrm{d}x=g(z),~~~~~~~~~~-1\le z\le 1. \end{aligned}$$
(3.4)

Therefore,

$$\begin{aligned}{} & {} \int ^1_{-1}\frac{\sqrt{1-x^2}}{x-z}~\psi ^{(1)}(x) \textrm{d}x\nonumber \\{} & {} \qquad =\int ^1_{-1}\sqrt{1-x^2}~\frac{\psi ^{(1)}(x)-\psi ^{(1)}(z)}{x-z}~\textrm{d}x+ \int ^1_{-1}\sqrt{1-x^2}~\frac{\psi ^{(1)}(z)}{x-z}~\textrm{d}x.\nonumber \\ \end{aligned}$$
(3.5)

The Cauchy principle value in its intended sense,

$$\begin{aligned} \int ^1_{-1}\sqrt{1-x^2}~\frac{1}{x-z}~\textrm{d}x=-\pi z,~~~~~~~~-1\le z \le 1. \end{aligned}$$
(3.6)

Equation (3.4) can therefore be transformed into

$$\begin{aligned} -\pi z~\psi ^{(1)}(z)+\int ^1_{-1}\sqrt{1-x^2}~\frac{\psi ^{(1)}(x)-\psi ^{(1)}(x)}{x-z}~\textrm{d}x=g(z),~~~~~~-1\le z \le 1. \end{aligned}$$
(3.7)

Case (II): The unknown function \(\varphi ^{(2)}(z)\) in Eq. (1.2) can be handled in the structure using (3.1) and (3.2):

$$\begin{aligned} \varphi ^{(2)}(z)=\frac{1}{\sqrt{1-z^2}}~\psi ^{(2)}(z),~~~~~~~~~~~~~~ -1< z <1. \end{aligned}$$
(3.8)

When we change (3.8) to (1.2), we get

$$\begin{aligned} \int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{\psi ^{(2)}(x)}{x-z}~\textrm{d}x=g(z),~~~~~~~~~~-1< z < 1. \end{aligned}$$
(3.9)

Therefore,

$$\begin{aligned}{} & {} \int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{\psi ^{(2)}(x)}{x-z}~\textrm{d}x\nonumber \\{} & {} \qquad =\int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{\psi ^{(2)}(x)-\psi ^{(2)}(z)}{x-z}~\textrm{d}x +\psi ^{(2)}(z)\int ^1_{-1}\frac{1}{\sqrt{1-x^2}(x-z)}~\textrm{d}x.\nonumber \\ \end{aligned}$$
(3.10)

Cauchy principle value is a concept that

$$\begin{aligned} \int ^1_{-1}\frac{1}{\sqrt{1-x^2}(x-z)}~\textrm{d}x=0. \end{aligned}$$
(3.11)

Equation (3.9) can therefore be transformed into

$$\begin{aligned} \int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{\psi ^{(2)}(x)-\psi ^{(2)}(z)}{x-z}~\textrm{d}x=g(z),~~~~~~-1<z<1. \end{aligned}$$
(3.12)

Case (III): It is possible to address the structure of the unknown function \(\varphi ^{(3)}(z)\) of Eq. (1.2) from (3.1) and (3.2):

$$\begin{aligned} \varphi ^{(3)}(z)=\sqrt{\frac{1-z}{1+z}}~\psi ^{(3)}(z),~~~~~~~~~~~~~~ -1 < z \le 1. \end{aligned}$$
(3.13)

By changing (3.13) to (1.2), we obtain

$$\begin{aligned} \int ^1_{-1}\sqrt{\frac{1-x}{1+x}}~\frac{\psi ^{(3)}(x)}{x-z}~\textrm{d}x=g(z),~~~~~~~~~~-1< z \le 1. \end{aligned}$$
(3.14)

Therefore,

$$\begin{aligned}{} & {} \int ^1_{-1}\sqrt{\frac{1-x}{1+x}}~\frac{\psi ^{(3)}(x)}{x-z} \textrm{d}t=\int ^1_{-1}\frac{\sqrt{1-x^2}}{1+x}~\frac{\psi ^{(3)}(x)}{x-z}~\textrm{d}x\\{} & {} \quad =\int ^1_{-1}\frac{\sqrt{1-x^2}}{x-z}~\left( \frac{\psi ^{(3)}(x)}{1+x}-\frac{\psi ^{(3)}(z)}{1+z}+\frac{\psi ^{(3)}(z)}{1+z}\right) ~\textrm{d}x\\{} & {} \quad =\int ^1_{-1}\frac{\sqrt{1-x^2}}{x-z}~\left( \frac{\psi ^{(3)}(x)}{1+x}-\frac{\psi ^{(3)}(z)}{1+z}\right) ~\textrm{d}x+\frac{\psi ^{(3)}(z)}{1+z} \int ^1_{-1}\frac{\sqrt{1-x^2}}{x-z}~\textrm{d}x\\{} & {} \quad =\frac{1}{1+z}\left( \int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(3)}(x)-\psi ^{(3)}(z)}{x-z}~\textrm{d}x-\int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(3)}(x)}{1+x}~\textrm{d}x\right) \\{} & {} \qquad - \frac{\pi z \psi ^{(3)}(z)}{1+z }, \end{aligned}$$

and Eq. (3.14) can be converted into

$$\begin{aligned}{} & {} \frac{1}{1+z}\left( \int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(3)}(x)-\psi _3(z)}{x-z}~\textrm{d}x-\int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(3)}(x)}{1+x}~\textrm{d}x\right) \nonumber \\{} & {} \quad - \frac{1}{1+z}\pi z \psi ^{(3)}(z)=g(z)~,-1 < z \le 1. \end{aligned}$$
(3.15)

Case (IV): It is possible to address the structure of the unknown function \(\varphi ^{(4)}(x)\) of Eq. (1.2) from (3.1) and (3.2):

$$\begin{aligned} \varphi ^{(4)}(z)=\sqrt{\frac{1+z}{1-z}}~\psi ^{(4)}(z),~~~~~~~~~~~~~~ -1 \le z < 1. \end{aligned}$$
(3.16)

Represent from (3.16) into (1.2), we obtain

$$\begin{aligned} \int ^1_{-1}\sqrt{\frac{1+x}{1-x}}~\frac{\psi ^{(4)}(x)}{x-z}~\textrm{d}x=g(z),~~~~~~~~~~-1 \le z < 1. \end{aligned}$$
(3.17)

In a same manner, Eq. (3.17) can be changed into

$$\begin{aligned}{} & {} \frac{1}{1-z}\left( \int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(4)}(x)-\psi ^{(4)}(z)}{x-z}~\textrm{d}x+\int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(4)}(x)}{1-x} \textrm{d}x\right) \nonumber \\{} & {} \quad - \frac{1}{1-z}\pi z \psi ^{(4)}(z)=g(z),-1 \le z < 1. \end{aligned}$$
(3.18)

In Eqs. (3.7), (3.12), (3.15) and (3.18), \(\frac{\psi (x)-\psi (z)}{x-z}=\psi '(z)\) if \(x=z,\) then \(\frac{\psi (x)-\psi (z)}{x-z}\in C([-1,1]\times [-1,1])\) for each event, the singularity of (1.2) has taken out.

4 The approach to the problem

According to the truncated Lucas series structure, the approximate solution of Eqs. (3.7), (3.12), (3.15) and (3.18) is as follows:

$$\begin{aligned} \psi ^{(j)}(z)\cong \psi ^{(j)}_N(z)=\sum ^N_{n=0}a_n^{(j)}~L_n(z),~~~~~~~j=1,2,3,4, \end{aligned}$$
(4.1)

while \(j=1,2,3,4\) for examples I, II, III, and IV individually, \(a_n^{(j)}\) stands for the undetermined Lucas coefficients for \(n=0,1,\ldots , N,\) and \(L_n(x)\) stands for the Lucas polynomials, that are described by (2.3).

The following form is used to rewrite Eqs. (3.7), (3.12), (3.15), and (3.18):

$$\begin{aligned} F^{(j)}(z)+G^{(j)}(z)=f(z),~~~~~~~~j=1,2,3,4, \end{aligned}$$
(4.2)

where

$$\begin{aligned}{} & {} F^{(1)}(z)=\int ^1_{-1}\sqrt{1-x^2}~\frac{\psi ^{(1)}(x)-\psi ^{(1)}(z)}{x-z}~\textrm{d}t, \nonumber \\{} & {} G^{(1)}(z)=-\pi x \psi ^{(1)}(z),~~~~~~~~~~~~~~ {\text {for case (I)}}, \end{aligned}$$
(4.3)
$$\begin{aligned}{} & {} F^{(2)}(z)=\int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{\psi ^{(2)}(x)-\psi ^{(2)}(z)}{x-z} \textrm{d}t, \nonumber \\{} & {} G^{(2)}(z)=0,~~~~~~~~~~~~~~ {\text {for case (II)}}, \end{aligned}$$
(4.4)
$$\begin{aligned}{} & {} F^{(3)}(z)=\frac{1}{1+z}\left( \int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(3)}(x)-\psi ^{(3)}(z)}{x-z}~\textrm{d}t-\int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(3)}(x)}{1+x}~\textrm{d}x\right) , \nonumber \\{} & {} G^{(3)}(z)=-\frac{\pi z \psi ^{(3)}(z)}{1+z}, ~~~~~~~~~~~{\text {for case (III)}}, \end{aligned}$$
(4.5)
$$\begin{aligned}{} & {} F^{(4)}(z)=\frac{1}{1-z}\left( \int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(4)}(x)-\psi ^{(4)}(z)}{x-z}~\textrm{d}t+\int ^1_{-1} \sqrt{1-x^2}~\frac{\psi ^{(4)}(x)}{1-x}~\textrm{d}x\right) , \nonumber \\{} & {} G^{(4)}(z)=-\frac{\pi z \psi ^{(4)}(z)}{1-z}, ~~~~~~~~~~~{\text {for case (IV)}}. \end{aligned}$$
(4.6)

By using the collocation points

$$\begin{aligned} z_l=-1+\frac{2}{N}~l,~~~~~~~~~~l=0,1,\ldots ,N, \end{aligned}$$
(4.7)

into Eq. (4.2), we get

$$\begin{aligned} F^{(j)}(z_l)+G^{(j)}(z_l)=f(z_l),~~~~~~~~j=1,2,3,4,~~~~~~l=0,1,\ldots ,N. \end{aligned}$$
(4.8)

When we change (4.1) to (4.3), (4.4), (4.5), and (4.6), we get

$$\begin{aligned}{} & {} F^{(1)}(z_l)\simeq \sum ^N_{n=0}a_n^{(1)}\int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)-L_n(z_l)}{x-z_l}~\textrm{d}t,~~~~~~{\text {for case (I)}}, \nonumber \\{} & {} F^{(2)}(z_l)\simeq \sum ^N_{n=0}a_n^{(2)}\int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{L_n(x)-L_n(z_l)}{x-z_l}~\textrm{d}x, ~~~~~~~~{\text {for case (II)}}, \end{aligned}$$
(4.9)
$$\begin{aligned}{} & {} F^{(3)}(z_l)\simeq \frac{1}{1+x_l}\left[ \sum ^N_{n=0}a_n^{(3)}\int ^1_{-1} \sqrt{1-x^2}~\frac{L_n(x)-L_n(z_l)}{x-z_l}~\textrm{d}t \right. \\{} & {} \quad \left. -\sum ^N_{n=0}a_n^{(3)}\int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)}{1+x}~\textrm{d}x\right] ,~{\text {for case (III)}}, \\{} & {} F^{(4)}(z_l)\simeq \frac{1}{1-x_l}\Bigg [\sum ^N_{n=0}a_n^{(4)}\int ^1_{-1} \sqrt{1-x^2}~\frac{L_n(x)-L_n(z_l)}{x-z_l}~\textrm{d}x \\{} & {} \quad +\sum ^N_{n=0}a_n^{(4)}\int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)}{1-x}~\textrm{d}x \Bigg ],~{\text {for case (IV)}}, \end{aligned}$$

and

$$\begin{aligned}{} & {} G^{(1)}(z_l)\simeq -\pi z_l~\sum ^N_{n=0}a_n^{(1)}L_n(z_l),~~~~~~~~~~~~~~ {\text {for case (I)}}, \nonumber \\{} & {} G^{(2)}(z_l)=0,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ {\text {for case (II)}}, \end{aligned}$$
(4.10)
$$\begin{aligned}{} & {} G^{(3)}(z_l)\simeq -\frac{\pi z_l}{1+z_l}~\sum ^N_{n=0}a_n^{(3)}L_n(z_l),~~~~~~~~~~~~~~ {\text {for case (III)}}, \\{} & {} G^{(4)}(z_l)\simeq -\frac{\pi z_l}{1-z_l}~\sum ^N_{n=0}a_n^{(4)}L_n(z_l),~~~~~~~~~~~~~~ {\text {for case (IV)}}. \end{aligned}$$

Substituting from (4.9) and (4.10) into (4.8) we get

$$\begin{aligned}{} & {} \sum ^N_{n=0}a_n^{(1)}~\left[ \int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(z)-L_n(z_l)}{x-z_l}~\textrm{d}t-\pi z_l~L_n(z_l)\right] =f(z_l),~~~~{\text {for case (I)}}, \nonumber \\{} & {} \sum ^N_{n=0}a_n^{(2)}~\left[ \int ^1_{-1}\frac{1}{\sqrt{1-x^2}}~\frac{L_n(x)-L_n(z_l)}{x-z_l}~\textrm{d}x\right] =f(z_l), ~~~~~~~~~~~~~~~~{\text {for case (II)}}, \end{aligned}$$
(4.11)
$$\begin{aligned}{} & {} \sum ^N_{n=0}a_n^{(3)}~\frac{1}{1+z_l}\left[ \int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)-L_n(z_l)}{t-z_l}~\textrm{d}x-\int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)}{1+x}~\textrm{d}t \right. \\{} & {} \quad \left. - \pi z_l~L_n(z_l)\right] =f(x_l),~~~~{\text {for case (III)}}, \\{} & {} \sum ^N_{n=0}a_n^{(4)}~\frac{1}{1-z_l}\left[ \int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)-L_n(z_l)}{t-x_l}~\textrm{d}t-\int ^1_{-1}\sqrt{1-x^2}~\frac{L_n(x)}{1-x}~\textrm{d}t \right. \\{} & {} \quad \left. - \pi z_l~L_n(z_l)\right] =f(z_l),~~~~{\text {for case (IV)}}. \end{aligned}$$

Equation (4.11) can be expressed as follows:

$$\begin{aligned} \sum ^N_{n=0}a_n^{(j)}[{\textbf {F}}^{(j)}(z_l)+{\textbf {G}}^{(j)}(z_l)]=f(z_l),~~~~~~~~~~~j=1,2,3,4. \end{aligned}$$
(4.12)

As a result, the following matrix form (4.12) may be formed, which is equivalent to each condition of Eq. (1.2)

$$\begin{aligned} A_j~X_j=F,~~~~~~~~j=1,2,3,4, \end{aligned}$$
(4.13)

which

$$\begin{aligned}{}[A_j]= & {} {\textbf {F}}^{(j)}(z_l)+{\textbf {G}}^{(j)}(z_l),~~~~~~j=1,2,3,4, \\ X_j= & {} \left[ a^{(j)}_0,~~~a^{(j)}_1,~~~a^{(j)}_2,~~~\ldots ,~~~a^{(j)}_N\right] ^T,~~~~~j=1,2,3,4 \end{aligned}$$

and

$$\begin{aligned} F=[f(z_0),~~~f(z_1),~~~\ldots ,~~~f(z_N)]^T.~~~~~~~~~~ \end{aligned}$$

Once the unusual coefficients \(a_n^{(j)}\) have been solved for in Eq. (4.13) for conditions I through (iv), convergent solutions to (3.3), (3.8), (3.13) and (3.16) using Eq. (4.1) are provided by

$$\begin{aligned} \varphi ^{(1)}_N (z)=\sqrt{1-z^2}~\sum ^N_{n=0}a_n^{(1)}~L_n(z),~~~~~~~~{\text {for case I}}, \nonumber \\ \varphi ^{(2)}_N (z)=\frac{1}{\sqrt{1-z^2}}~\sum ^N_{n=0}a_n^{(2)}~L_n(z),~~~~~~~~{\text {for case II}}, \nonumber \\ \varphi ^{(3)}_N (z)=\sqrt{\frac{1-z}{1+z}}~\sum ^N_{n=0}a_n^{(3)}~L_n(z),~~~~~~~~{\text {for case III}}, \nonumber \\ \varphi ^{(4)}_N (z)=\sqrt{\frac{1+z}{1-z}}~\sum ^N_{n=0}a_n^{(4)}~L_n(z),~~~~~~~~{\text {for case IV}}. \end{aligned}$$
(4.14)

5 Error evaluation

For the convergent solutions of equation, we permit an error evaluation in this section (1.2). Let the approximation for all situations be \(\varphi m(z)\). For all situations I, II, III, IV, \(e_m(z)=\varphi (z)-\varphi _m(z)\) is the error function connected to \(\varphi _m(z)\), where \(\varphi (z)\) is the precise solution of (1.2). Since it satisfies, \(\varphi _m(z)\) is the approximate answer.

$$\begin{aligned} \int ^1_{-1}\frac{\varphi _m(x)}{x-z}\textrm{d}x=g(z)+H_m(z)~~~~~~~~~~~~~~~~-1<z<1, \end{aligned}$$
(5.1)

where \(H_m(z)\) is a perturbation term and it is obtained from:

$$\begin{aligned} H_m(z)=\int ^1_{-1}\frac{\varphi _m(z)}{x-z}\textrm{d}x-g(z). \end{aligned}$$
(5.2)

Subtracting (1.2) from (5.2), we obtain

$$\begin{aligned} \int ^1_{-1}\frac{e_m(x)}{x-z}\textrm{d}x=H_m(z), \end{aligned}$$
(5.3)

for the \(e_m(z)\) error function. We will solve (5.3) using the same techniques we used for finding an approximation of \(\hat{e}(z)\) to \(e_m(z)\) (1.2). In this scenario, the perturbation term \(H_m(z)\) must only affect the function g(z).

6 Illustrative data

A few mathematical examples are presented in this section to demonstrate the viability and dependability of the Lucas polynomial strategy. Our method was used to solve these models with \(N=5\), and Maple 18 was used for all numerical computations.

Example 1

The first kind Cauchy integral equation shown below is (Mohamed 2022; Seifi et al. 2017; Dezhbord et al. 2016; Eshkuvatov et al. 2009):

$$\begin{aligned} \int ^1_{-1} \frac{\varphi (x)}{x-z} \textrm{d}x=z^4+5z^3+2z^2+z-\frac{11}{8},~~~~~-1<x<1. \end{aligned}$$
(6.1)

Equation (6.1)’s accurate response in every situation is provided by:

$$\begin{aligned} {\textbf {Case (I)}}:~~~~~~~~~~~ \varphi (z)= & {} -\frac{1}{\pi } \sqrt{1-z^2}\left( z^3+5z^2+\frac{5}{2}z+\frac{7}{2}\right) . \end{aligned}$$
(6.2)
$$\begin{aligned} {\textbf {Case (II)}}:~~~~~~~~~~~ \varphi (z)= & {} \frac{1}{\pi ~\sqrt{1-z^2}} \left( z^5+5z^4+\frac{3}{2}z^3-\frac{3}{2}z^2-\frac{5}{2}z-\frac{7}{2}\right) . \end{aligned}$$
(6.3)
$$\begin{aligned} {\textbf {Case (III)}}:~~~~~~~~~~~ \varphi (z)= & {} -\frac{1}{\pi } ~\sqrt{\frac{1-z}{1+z}}\left( z^4+6z^3+\frac{15}{2}z^2+6z+\frac{7}{2}\right) . \end{aligned}$$
(6.4)
$$\begin{aligned} {\textbf {Case (IV)}}:~~~~~~~~~~~ \varphi (z)= & {} \frac{1}{\pi } ~\sqrt{\frac{1+z}{1-z}}\left( z^4+4z^3-\frac{5}{2}z^2+z-\frac{7}{2}\right) . \end{aligned}$$
(6.5)

Utilizing the collocation points (4.7) and the Lucas polynomial approach for Eq. (6.1), where \(N=5.\)

For case (I): Using the matrix equation shown below, we can:

$$\begin{aligned} ~\left( \begin{array}{cccccc} 2 \pi ~~~~&{} -\frac{1}{2}\pi ~~~~&{} \frac{5}{2}\pi ~~~~&{} -\frac{15}{8}\pi ~~~~&{} \frac{35}{8}\pi ~~~~&{} -\frac{75}{16}\pi \\ \\ \\ \frac{6}{5} \pi ~~~~&{} \frac{7}{50}\pi ~~~~&{} \frac{279}{250}\pi ~~~~&{} \frac{2977}{5000}\pi ~~~~&{} \frac{18969}{250000}\pi ~~~~&{} \frac{425661}{250000}\pi \\ \\ \\ \frac{2}{5}\pi ~~~~&{} \frac{23}{50}\pi ~~~~&{} -\frac{77}{250}\pi ~~~~&{} \frac{7617}{5000}\pi ~~~~&{} \frac{83}{25000}\pi ~~~~&{} \frac{771309}{250000}\pi \\ \\ \\ - \frac{2}{5} \pi ~~~~&{} \frac{23}{50}\pi ~~~~&{} -\frac{77}{250}\pi ~~~~&{} \frac{7617}{5000}\pi ~~~~&{}- \frac{83}{25000}\pi ~~~~&{} \frac{771309}{50000}\pi \\ \\ \\ - \frac{6}{5}\pi ~~~~&{} \frac{7}{50}\pi ~~~~&{} -\frac{279}{250}\pi ~~~~&{} \frac{2977}{5000}\pi ~~~~&{}- \frac{18969}{25000}\pi ~~~~&{} \frac{425661}{250000}\pi \\ \\ \\ -2\pi ~~~~&{} -\frac{1}{2}\pi ~~~~&{}- \frac{5}{2}\pi ~~~~&{} -\frac{15}{8}\pi ~~~~&{} -\frac{35}{8}\pi ~~~~&{} -\frac{75}{16}\pi \\ \\ \\ \end{array} \right) ~\left( \begin{array}{c} a^{(1)}_0 \\ \\ \\ a^{(1)}_1\\ \\ \\ a^{(1)}_2 \\ \\ \\ a^{(1)}_3 \\ \\ \\ a^{(1)}_4\\ \\ \\ a^{(1)}_5 \\ \\ \\ \end{array} \right) =\left( \begin{array}{c} - \frac{35}{8} \\ \\ \\ -\frac{11027}{5000} \\ \\ \\ -\frac{7667}{5000} \\ \\ \\ - \frac{5267}{5000} \\ \\ \\ \frac{5773}{5000} \\ \\ \\ \frac{61}{8} \\ \\ \\ \end{array} \right) . \end{aligned}$$

We can find the values of the constants as follows by solving the matrix problem above:

$$\begin{aligned} \left[ a^{(1)}_0=\frac{13}{4\pi },~~~~a^{(1)}_1=\frac{1}{2\pi },~~~~a^{(1)}_2=-\frac{5}{\pi },~~~~a^{(1)}_3 =-\frac{1}{\pi },~~~~~a^{(1)}_4=a^{(1)}_5=0\right] . \end{aligned}$$

These constants can be substituted into (4.14) to obtain the approximate solution, which is the same as the exact result (6.2). A comparison between our method and the methods of Seifi et al. (2017); Dezhbord et al. (2016); Eshkuvatov et al. (2009) for case I are shown in Table 2.

Table 2 Numerical outcomes of Example 1 for case (I) and Seifi et al. (2017), Dezhbord et al. (2016), Eshkuvatov et al. (2009)
Full size table

For case (II): Using the matrix equation shown below, we can:

$$\begin{aligned} ~\left( \begin{array}{cccccc} 0 ~~~~&{} \pi ~~~~&{} -\pi ~~~~&{} \frac{9}{2}\pi ~~~~&{} -\frac{11}{2}\pi ~~~~&{} \frac{115}{8}\pi \\ \\ \\ 0 ~~~~&{} \pi ~~~~&{} -\frac{3}{5}\pi ~~~~&{} \frac{193}{50}\pi ~~~~&{} -\frac{729}{250}\pi ~~~~&{} \frac{49923}{5000}\pi \\ \\ \\ 0 ~~~~&{} \pi ~~~~&{} -\frac{1}{5}\pi ~~~~&{} \frac{177}{50}\pi ~~~~&{} -\frac{227}{250}\pi ~~~~&{} \frac{40483}{5000}\pi \\ \\ \\ 0 ~~~~&{} \pi ~~~~&{} \frac{1}{5}\pi ~~~~&{} \frac{177}{50}\pi ~~~~&{} \frac{227}{250}\pi ~~~~&{} \frac{40483}{5000}\pi \\ \\ \\ 0 ~~~~&{} \pi ~~~~&{} \frac{3}{5}\pi ~~~~&{} \frac{193}{50}\pi ~~~~&{} \frac{729}{250}\pi ~~~~&{} \frac{49923}{5000}\pi \\ \\ \\ 0 ~~~~&{} \pi ~~~~&{} \pi ~~~~&{} \frac{9}{2}\pi ~~~~&{} -\frac{11}{2}\pi ~~~~&{} \frac{115}{8}\pi \\ \\ \\ \end{array} \right) ~\left( \begin{array}{c} a^{(2)}_0 \\ \\ \\ a^{(2)}_1\\ \\ \\ a^{(2)}_2 \\ \\ \\ a^{(2)}_3 \\ \\ \\ a^{(2)}_4\\ \\ \\ a^{(2)}_5 \\ \\ \\ \end{array} \right) =\left( \begin{array}{c} - \frac{35}{8} \\ \\ \\ -\frac{11027}{5000} \\ \\ \\ -\frac{7667}{5000} \\ \\ \\ - \frac{5267}{5000} \\ \\ \\ \frac{5773}{5000} \\ \\ \\ \frac{61}{8} \\ \\ \\ \end{array} \right) . \end{aligned}$$

We can find the values of the constants as follows by solving the matrix problem above:

$$\begin{aligned} \left[ a^{(2)}_0 \textrm{arbitrary},~~~~a^{(2)}_1=\frac{3}{\pi },~~~~a^{(2)}_2=\frac{-43}{2\pi },~~~~a^{(2)}_3=-\frac{7}{2\pi },~~~~~a^{(2)}_4 =\frac{5}{\pi },~~~~ a^{(2)}_5=\frac{1}{\pi }\right] . \end{aligned}$$

As a result of these constants being substituted into (4.14), the following approximate solution is obtained:

$$\begin{aligned} \varphi ^{(2)}_5(z)=\frac{1}{\pi \sqrt{1-z^2}}(z^5+5z^4+\frac{3}{2}z^3- \frac{3}{2}z^2-\frac{5}{2}z)-\frac{33}{\pi \sqrt{1-z^2}}+\frac{2a^{(2)}_0}{\sqrt{1-z^2}}. \end{aligned}$$
(6.6)

If we use \(a^{(2)}_0=\frac{33}{2\pi },\) it is clear from comparing the precise and approximate solutions (6.3 and 6.6) that the approximate answer is equivalent to the accurate solution.

A comparison between our method and the methods of Seifi et al. (2017), Dezhbord et al. (2016), Eshkuvatov et al. (2009) for case II are shown in Table 3.

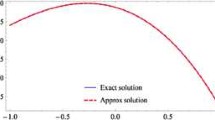
Table 3 Numerical outcomes of Example 1 for case (II) and Seifi et al. (2017), Dezhbord et al. (2016), Eshkuvatov et al. (2009)
Full size table

The outcomes of Example 1 for case (III) are shown in Table 4 and Fig. 1, just as they were for cases (I) and (II), respectively.

Table 4 Numerical outcomes of Example 1 case III and Seifi et al. (2017), Dezhbord et al. (2016), Eshkuvatov et al. (2009)
Full size table
Fig. 1
figure 1

Error of example 1 case III

Full size image

Similarly, the outcomes of Example 1 for case (IV) are presented in Table 5 and Fig. 2.

Table 5 Numerical outcomes of Example 1 case IV and Seifi et al. (2017), Dezhbord et al. (2016), Eshkuvatov et al. (2009)
Full size table
Fig. 2
figure 2

Error of example 1 case IV

Full size image

Example 2

Define the first sort’s next Cauchy integral equation as Mohamed (2022), Seifi et al. (2017).

$$\begin{aligned} \int ^1_{-1} \frac{\varphi (t)}{x-z} \textrm{d}x=-z^4+\frac{3}{2}z^2-\frac{3}{8},-1<z<1. \end{aligned}$$
(6.7)

The accurate response of Eq. (6.7) each case has provided by:

$$\begin{aligned} {\textbf {Case (I)}}:~~~~~~~~~~~\varphi (z)= & {} -\frac{1}{\pi } \sqrt{1-z^2}(z-z^3). \end{aligned}$$
(6.8)
$$\begin{aligned} {\textbf {Case (II)}}:~~~~~~~~~~~\varphi (z)= & {} \frac{1}{\pi \sqrt{1-z^2}} (-z+2z^3-z^5) \end{aligned}$$
(6.9)
$$\begin{aligned} {\textbf {Case (III)}}:~~~~~~~~~~~\varphi (z)= & {} -\frac{1}{\pi } \sqrt{\frac{1-z}{1+z}}(z+z^2-z^3-z^4). \end{aligned}$$
(6.10)
$$\begin{aligned} {\textbf {Case (IV)}}:~~~~~~~~~~~\varphi (z)= & {} -\frac{1}{\pi } \sqrt{\frac{1+z}{1-z}}(z-z^2-z^3+z^4). \end{aligned}$$
(6.11)

Equation (6.7) is solved using the Lucas polynomial technique, and collocation points (4.7) are used at \(N=5\).

For case (I) We arrive at the subsequent matrix equation.:

$$\begin{aligned} \left( \begin{array}{cccccc} 2 \pi &{} -\frac{1}{2}\pi &{} \frac{5}{2}\pi &{} -\frac{15}{8}\pi &{} \frac{35}{8}\pi &{} -\frac{75}{16}\pi \\ \\ \\ \frac{6}{5} \pi &{} \frac{7}{50}\pi &{} \frac{279}{250}\pi &{} \frac{2977}{5000}\pi &{} \frac{18969}{250000}\pi &{} \frac{425661}{250000}\pi \\ \\ \\ \frac{2}{5}\pi &{} \frac{23}{50}\pi &{} -\frac{77}{250}\pi &{} \frac{7617}{5000}\pi &{} \frac{83}{25000}\pi &{} \frac{771309}{250000}\pi \\ \\ \\ - \frac{2}{5} \pi &{} \frac{23}{50}\pi &{} -\frac{77}{250}\pi &{} \frac{7617}{5000}\pi &{}- \frac{83}{25000}\pi &{} \frac{771309}{50000}\pi \\ \\ \\ - \frac{6}{5}\pi &{} \frac{7}{50}\pi &{} -\frac{279}{250}\pi &{} \frac{2977}{5000}\pi &{}- \frac{18969}{25000}\pi &{} \frac{425661}{250000}\pi \\ \\ \\ -2\pi &{} -\frac{1}{2}\pi &{}- \frac{5}{2}\pi &{} -\frac{15}{8}\pi &{} -\frac{35}{8}\pi &{} -\frac{75}{16}\pi \\ \\ \\ \end{array} \right) \left( \begin{array}{c} a^{(1)}_0 \\ \\ \\ a^{(1)}_1\\ \\ \\ a^{(1)}_2 \\ \\ \\ a^{(1)}_3 \\ \\ \\ a^{(1)}_4\\ \\ \\ a^{(1)}_5 \\ \\ \\ \end{array} \right) =\left( \begin{array}{c} \frac{1}{8} \\ \\ \\ \frac{177}{5000} \\ \\ \\ -\frac{1583}{5000} \\ \\ \\ -\frac{1583}{5000} \\ \\ \\ \frac{177}{5000} \\ \\ \\ \frac{1}{8} \\ \\ \\ \end{array} \right) . \end{aligned}$$
(6.12)

We arrive at the constant values by solving the matrix problem (6.12) as follows:

$$\begin{aligned} \left[ a^{(1)}_0=0,a^{(1)}_1=-\frac{4}{\pi },a^{(1)}_2=0,a^{(1)}_3=\frac{1}{\pi },a^{(1)}_4=a^{(1)}_5=0\right] . \end{aligned}$$

By replacing these constants in (4.14), we achieve the approximate solution, which is equivalent to the correct solution (6.8).

A comparison between our method and the method of Seifi et al. (2017) for case I are shown in Table 6.

Table 6 Numerical outcomes of Example 2 for case (I) and Seifi et al. (2017)
Full size table

For case (II): The constant values are obtained in a manner similar to case (I) as follows:

$$\begin{aligned} \left[ a^{(2)}_0 \textrm{arbitrary},a^{(2)}_1=-\frac{17}{\pi },a^{(2)}_2=0,a^{(2)}_3=\frac{7}{\pi },a^{(2)}_4=0, a^{(2)}_5=-\frac{1}{\pi }\right] . \end{aligned}$$

As a result of these constants being substituted into (4.14), the following approximate solution is obtained:

$$\begin{aligned} \varphi ^{(2)}_5(z)=\frac{1}{\pi \sqrt{1-z^2}}(-z+2z^3-z^5)+\frac{2 a^{(2)}_0}{\sqrt{1-z^2}}. \end{aligned}$$
(6.13)

If we accept \(a^{(2)}_0=0\), then it is obvious from comparing the exact answer (6.9) with the approximate solution (6.13), that they are identical.

A comparison between our method and the method of Seifi et al. (2017) for case II are shown in Table 7.

Table 7 Numerical outcomes of Example 2 for case (II) and Seifi et al. (2017)
Full size table
Table 8 Numerical outcomes of Example 2 case III and Seifi et al. (2017)
Full size table

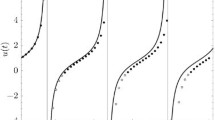
The outcomes of Example 2 for case (III) are presented in Table 8 and Fig. 3. The outcomes of Example 2 for case (IV) are presented in Table 9 and Fig. 4.

Fig. 3
figure 3

Error of example 2 case III

Full size image
Table 9 Numerical outcomes of Example 2 case IV and Seifi et al. (2017)
Full size table
Fig. 4
figure 4

Error of example 2 case IV

Full size image

7 Conclusion

This study develops the Lucas polynomial approach for resolving a variety of first-class Cauchy integral equation problems. Implementing smooth transforms significantly eliminates the singularity of Eq. (1.2). Numerical illustrates are presented to illustrate the method comparison between the Lucas polynomial method at \(N=5\) and the Chebyshev polynomial method (Eshkuvatov et al. 2009) at \(N=20\). Reproducing the kernel method (Dezhbord et al. 2016) at \(N=200\) and the Bernstein polynomials method (Seifi et al. 2017) at \(N=4\) are presented in Tables 2, 3, 4 and 5 for Example 1. A comparison between the Lucas polynomial method and the Bernstein polynomial method is presented in Tables 6, 7, 8, and 9, for Example 2. Also by comparing the results of our method with the results of Mohamed (2022) we note that the method used in Mohamed (2022) gives exact solution in special case \(\lambda =1\) but if \(\lambda \ne 1\) the approximate solution different the exact solution. It is clear the accuracy of our method is very high. Future Work:

We will consider the following potential function

$$\begin{aligned} \mu \Phi (x,t)-\lambda \int _0^t \int _{-1}^1 F(t,\tau ) \frac{1}{(x-y)^2}\Phi (y,t) \textrm{d}y \textrm{d}\tau =f(x,t). \end{aligned}$$

The importance of this integral equation appears in mathematical physics problems especially, in nuclear reactions when its boundary conditions are applied.

It also shows its importance, when studying the forces of internal and external stress on a longitudinal crack in ceramics. It also shows its importance in treating cracks in linear and nonlinear elastic materials.