Efficient alternating direction implicit numerical approaches for multi-dimensional distributed-order fractional integro differential problems

Abstract

This paper proposes the alternating direction implicit (ADI) numerical approaches for computing the solution of multi-dimensional distributed-order fractional integrodifferential problems. The proposed method discretizes the unknown solution in two stages. First, the Riemann–Liouville fractional integral term and the distributed-order time-fractional derivative are discretized with the help of the second-order convolution quadrature and the weighted and shifted Grünwald formula, respectively. Second, the spatial discretization is obtained by the general centered finite difference (FD) technique. At the same time, the ADI algorithms are devised for reducing the computational burden. Additionally, the convergence analysis of proposed ADI FD schemes is analyzed in detail through the energy method. Finally, two numerical examples highlight the accuracy of the proposed method and verify the theoretical formulations.

1 Introduction

This paper considers the distributed-order fractional integrodifferential equation in two/three dimensions

$$\begin{aligned} \begin{aligned} \mathbb {D}^{\omega }_{t}u({\textbf {x}},t)&- \mu \varDelta u({\textbf {x}},t) - I^{(\beta )}\varDelta u({\textbf {x}},t)= f({\textbf {x}},t),\quad 0< \beta < 1, \quad ({\textbf {x}},\, t) \in \varOmega \times (0, T]. \end{aligned} \end{aligned}$$

(1)

The initial condition and the boundary condition (IC and BC, respectively) are prescribed as

$$\begin{aligned} u({\textbf {x}},0)&=\kappa ({\textbf {x}}), \qquad {\textbf {x}}\in \varOmega , \end{aligned}$$

(2)

$$\begin{aligned} u({\textbf {x}},t)&=0, \quad ({\textbf {x}},\, t) \in \partial \varOmega \times [0, T], \end{aligned}$$

(3)

and the distributed-order integral is defined as

$$\begin{aligned} \begin{array}{ll} \mathbb {D}_{t}^{\omega }u({\textbf {x}},t) = \int \limits ^{1}_{0}\omega (\alpha ) D_{t}^{\alpha }u({\textbf {x}},t)\mathrm{d}\alpha . \end{array} \end{aligned}$$

(4)

Following Podlubny (1999), the Caputo fractional derivative (CFD) and the Riemann–Liouville fractional integral (RLFI) are respectively defined in

$$\begin{aligned} D_{t}^{\alpha }u({\textbf {x}},t) = {\left\{ \begin{array}{ll} \frac{1}{\varGamma (1-\alpha )} \int \limits _{0}^{t}(t-s)^{-\alpha }\frac{\partial u}{\partial s}({\textbf {x}},s)\mathrm{d}s, \quad 0< \alpha <1, \\ \frac{\partial u}{\partial t}({\textbf {x}},t), \quad \alpha = 1, \end{array}\right. } \end{aligned}$$

(5)

and

$$\begin{aligned} \begin{array}{ll} I^{(\vartheta )}\phi (t) = \int \limits _{0}^{t}\beta (t-s)\phi (s)\mathrm{d}s := \frac{1}{\varGamma (\vartheta )}\int \limits _{0}^{t}(t-s)^{\vartheta -1}\phi (s)\mathrm{d}s,\\ \qquad \qquad \qquad \vartheta \in (0,1),\qquad t\in (0,\infty ), \end{array} \end{aligned}$$

(6)

in which $\omega (\alpha )\ge 0$ with $\int \nolimits _{0}^{1}\omega (\alpha )\mathrm{d}\alpha =c_0>0$, $\varOmega =\mathbb {R}^2$ or $\mathbb {R}^3$, $\varGamma (\vartheta )$ = $\int \nolimits _{0}^{+\infty }$ $\xi ^{\vartheta -1}$ $\exp {(-\xi )}\mathrm{d}\xi$ and $f({\textbf {x}},t)$ represent the weight function, spatial domain, the Euler’s Gamma function, and forcing term, respectively. Without loss of generality, we can take a zero initial value $u({\textbf {x}},0)$. If $u({\textbf {x}},0) = \varpi ({\textbf {x}})$, then we can consider a transform $w({\textbf {x}},t)=u({\textbf {x}},t)-\varpi ({\textbf {x}})$. Theory of fractional calculus (FC) generalizes the integer order derivative to arbitrary order, which can be achieved in space and time with a power law memory kernel of the nonlocal problems (Tarasov 2021a, b; Kumar and Saha Ray 2021; Behera and Ray 2022; Moghaddam et al. 2019; Abdelkawy et al. 2022; Lopes and Machado 2021). With the increasing popularity of FC, fractional differential equations (FDEs) have become an important key for describing and modeling various phenomena phenomena in scopes of engineering and sciences (Podlubny 1999; Hilfer 2000; Akram et al. 2021; Alia et al. 2021). Nakhushev (1998, 2003) discussed the importance of studies on the positivity of continuous and discrete differentiation and integration operators in the theory of mixed type equations and FC and proposed that fractional integrals (FIs) of uniformly distributed order can be expressed in terms of the so-called continual FIs. Then, Pskhu (2004, 2005) suggested the fractional operators which are the opposite of the continual FIs and presented the theory about the continual integro-differentiation operator. Their research has had a significant impact on the study of FC. Furthermore, many scholars have proposed different numerical methods for solving FDEs, including finite difference (FD) (Qiu et al. 2019; Yn et al. 2011), finite element (FE) (Liu et al. 2015), two-grid methods (Liu et al. 2015; Qiu et al. 2020, mehless method (Nikan et al. 2021b, a; Nikan and Avazzadeh 2021) and etc. In recent decades, distributed-order partial differential equations (DOPDEs) have a wide range of applications in mathematical physics and engineering (Bagley and Torvik 2000; Caputo 2001), and can be used to describe the dynamics of anomalous diffusion and relaxation phenomena. Distributed order derivatives are fractional derivatives that have integrated the order of the derivative over a certain range. On the one hand, the distributed order fractional problem can be extended to a general integer order problem. On the other hand, the distributed order problem can be discretized into a multi-term time fractional order problem. In the past few years, more and more researchers have studied distributed-order differential equations. Naber (2004) obtained the solution for the fractional subdiffusion equations with the distributed-order by means of Laplace transform and variable separation. Kochubei (2008) studied the distributed order derivative and integral. Atanackovic et al. (2009) investigated the Cauchy problem of the time distributed-order diffusion wave problem. Meerschaert et al. (2011) analyzed explicit strong and random analogs solutions. Katsikadelis (2014) adopted a new numerical approach to approximate distributed order FDEs of a general formulation in an integration domain. Morgado and Rebelo (2015) explored an implicit approach for solution of the distributed-order time-fractional nonlinear reaction-diffusion problem. Chen et al. (2016) studied the spectral scheme and pseudo-spectral scheme in a domain of semi-infinite space. Du et al. (2016) analyzed and proposed the higher-order FD techniques having smooth solutions in 1D and 2D spaces. Jin et al. (2016) developed two fully discrete approaches including error analysis to discretize the distributed-order time fractional diffusion problem including nonsmooth initial of data. Abbaszadeh and Dehghan (2017) subsequently presented an improved meshfree technique with error estimation. Gao et al. (2017) developed an interpolation-based approximation for the temporal second order difference scheme to approximate multi-term distributed order time FDEs. Yang et al. (2018) formulated an orthogonal spline collocation (OSC) technique. Qiu et al. (2020) advanced the Galerkin FE technique for the time fractional mobile-immobile model with the distributed-order. Gao et al. (2020) investigated the nonhomogeneous 2D distributed-order time-fractional cable equations by unstructured grids of Galerkin FE. Zhang et al. (2022) presented an ADI Legendre–Laguerre spectral scheme for the 2D time distributed-order diffusion-wave problem on a semi-infinite domain. Jian et al. (2021) established fast numerical algorithms to solve the Riesz space fractional diffusion-wave problem with time distributed-order.

It is well known that the ADI methods have the advantage of reducing the computational burden using decomposing a multidimensional problem into several independent one-dimensional problems Huang et al. (2021). Some fractional order problems have been studied so far by the ADI methods. Chen et al. (2016) and Qiao et al. (2021) proposed the ADI FD technique for fractional order Volterra equation and the 3D nonlocal evolution equation. Pani et al. (2010) implemented ADI OSC method for the single-order time FDEs. Gao and Zz (2016b, 2016a) adopted the ADI FD approach to the distributed-order time-diffusion equations, while Li et al. (2013) used the ADI FE scheme for the investigation of single-order temporal/spatial FDEs. However, the problem (1)–(3) in two/three dimensions has not been studied. In the following, we will discuss and analyze this issue.

For large problems, the ADI method can reduce the storage requirements and computational complexities. In addition, although the implicit method has good stability, it requires a large amount of CPU run time if the number of unknowns is large. Therefore, we construct an ADI FD scheme, which deals with two- and three-dimensional problems by solving a series of smaller, independent one-dimensional problems. The main objective of current work is to develop the efficient ADI numerical approaches for distributed-order integrodifferential equations for the case of two/three dimensions. The time discretization is obtained based on the second-order CQ rule and the weighted and shifted Grünwald formula for the RLFI and the distributed-order time-fractional derivative, respectively. Then, we adopt the central FD technique to establish the fully discrete scheme. Meanwhile, the fully-discrete ADI difference approaches in two/three dimensions are obtained with corresponding ADI algorithms. The numerical results show that our schemes in two/three dimensional cases are convergent, with time convergence of order 2, spatial convergence of order 2, and distributed-order convergence of order 2, respectively.

This paper includes five sections as follows. Section 2 gives the necessary notations, some useful lemmas and derivation of ADI difference approaches and performs the convergence analysis of the two-dimensional distributed order problem. Section 3 constructs the ADI approach of the three-dimensional problem by adding a tiny term, and studies the convergence analysis of the ADI approach by means of the energy method. Section 4 presents two test problems to confirm the theoretical prediction and show effectiveness of the method. Finally, Section 5 summarizes the main concluding remarks.

2 Numerical description and theoretical analysis for the two-dimensional case

2.1 Preliminary

In the following numerical method analysis, we assume that two-dimensional problems (1)–(3) have a sufficiently smooth and unique solution on the domain $\varOmega$ = $(0, L_1)\times (0, L_2)$ and its boundary $\partial \varOmega$. We will give some useful symbols and significant lemmas, which can help us in the subsequent discussions. First of all, let us define the necessary notations of time and distributed order. For convenience, we consider a temporal step size which is selected as the nodes $\tau =\frac{T}{N}$ and $t_n = n\tau$, $0 \le n \le N$, where N and T are the total number of time steps and a finite time, respectively. For positive integers N and J, we separate [0, 1] into 2J-subintervals $\alpha _l = l\triangle \alpha , ~~0\le l \le 2J$, so that distributed-order step size $\triangle \alpha =\frac{1}{2J}\cdot$ For $n=1,2,\ldots ,N$, let us introduce $\delta _tv^{n-\frac{1}{2}} = \frac{1}{\tau }(v^{n}-v^{n-1})\cdot$ In what follows, we mention the composite trapezoid formulation for discretizing the distributed-order integral.

Lemma 1

(Gao and Zz 2016b) For $\sigma (\alpha ) \in C^2[0,1]$, we have

$$\begin{aligned} \begin{array}{ll} \int \limits _{0}^{1}\sigma (\alpha )\mathrm{d}\alpha = \triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\sigma (\alpha _l) - \frac{\sigma ''(\xi )}{12}(\triangle \alpha )^2, \quad \xi \in (0,1), \end{array} \end{aligned}$$

in which

$$\begin{aligned} c_l= {\left\{ \begin{array}{ll} \frac{1}{2}, \qquad l = 0,\, 2J, \\ 1, \qquad l = 1, 2, \ldots , 2J-1. \end{array}\right. } \end{aligned}$$

Next, we describe the process of discretization for the distributed-order CFD. Now, let us introduce

$$\begin{aligned} \begin{array}{ll} \Im ^{\alpha +s}(\mathbb {R}) = \Big \{ \varphi \big | \varphi \in L^1(\mathbb {R}); \int \limits _{-\infty }^{+\infty }(1+|\xi |)^{\alpha +s}|\hat{\varphi }(\xi )|\mathrm{d}\xi < \infty \Big \}, \qquad s \ge 1, \end{array} \end{aligned}$$

where $\hat{\varphi }(\xi )=\mathcal {F}[\varphi ](\xi )=\int \nolimits _{-\infty }^{+\infty }e^{i\xi t}\varphi (t)\mathrm{d}t$ illustrates the Fourier transformation for the function $\varphi (t)$.

Lemma 2

(Pskhu 2004; Meerschaert and Tadjeran 2004) For $\varphi \in \Im ^{\alpha +1}(\mathbb {R})$, the RL fractional derivative can be stated as

$$\begin{aligned} \begin{array}{ll} _{-\infty }D_{t}^{\alpha }\varphi (t) = \frac{1}{\varGamma (1-\alpha )}\frac{\mathrm{d}}{\mathrm{d}t}\int \limits _{-\infty }^{t}(t-\theta )^{-\alpha }\varphi (\theta )\mathrm{d}\theta \end{array} \end{aligned}$$

(7)

and

$$\begin{aligned} \begin{array}{ll} B_{\tau ,m}^{\alpha }\varphi (t) = \tau ^{-\alpha } \sum \limits _{k=0}^{\infty } g_{k}^{(\alpha )} \varphi \big ( t-(k-m)\tau \big ), \end{array} \end{aligned}$$

(8)

in which $g_{k}^{(\alpha )} = (-1)^k\left( {\begin{array}{c}\alpha \\ k\end{array}}\right)$ are the coefficients for $\alpha \in (0,1]$ and m is an integer. Then, we have

$$\begin{aligned} \begin{array}{ll} B_{\tau ,m}^{\alpha }\varphi (t) = _{-\infty }D_{t}^{\alpha }\varphi (t) + \mathcal {O}(\tau ), \end{array} \end{aligned}$$

uniformly satisfies in $t\in \mathbb {R}$ when $\tau \rightarrow 0$.

Furthermore, in the case of $0<\alpha \le 1$, the coefficients $g_{k}^{(\alpha )}$ introduced in (8) satisfy the following properties

$$\begin{aligned} \begin{array}{ll} g_{0}^{(\alpha )} = 1, \quad g_{1}^{(\alpha )}=-\alpha <0,\\ g_{2}^{(\alpha )} \le g_{3}^{(\alpha )} \le g_{4}^{(\alpha )} \le \cdots \le 0, \qquad \\ \sum \limits _{k=0}^{\infty } g_{k}^{(\alpha )} = 0, \quad \sum \limits _{k=0}^{n} g_{k}^{(\alpha )} \ge 0, \quad n\ge 1. \end{array} \end{aligned}$$

(9)

For carrying out a theoretical analysis, we require the following lemma.

Lemma 3

(Tian et al. 2015) Assume that $\varphi \in \Im ^{\alpha +2}(\mathbb {R})$. Then, we have

$$\begin{aligned} \begin{array}{ll} (1+\frac{\alpha }{2})B_{\tau ,0}^{\alpha }\varphi (t) - \frac{\alpha }{2}B_{\tau ,-1}^{\alpha }\varphi (t) = \tau ^{-\alpha } \sum \limits _{k=0}^{\infty } \lambda _{k}^{(\alpha )} \varphi (t-k\tau ) \\ = _{-\infty }D_{t}^{\alpha }\varphi (t) + \mathcal {O}(\tau ^2), \end{array} \end{aligned}$$

uniformly holds for $t\in \mathbb {R}$ when $\tau \rightarrow 0$, and the coefficients $\lambda _{k}^{(\alpha )}$ can be evaluated as follows

$$\begin{aligned} \begin{array}{ll} \lambda _0^{(\alpha )} = (1+\frac{\alpha }{2})g_{0}^{(\alpha )}, \qquad \lambda _k^{(\alpha )} = (1+\frac{\alpha }{2})g_{k}^{(\alpha )} - \frac{\alpha }{2}g_{k-1}^{(\alpha )}, \qquad k\ge 1. \end{array} \end{aligned}$$

(10)

Actually, it can be checked for $0\le \alpha \le 1$ that

$$\begin{aligned} \begin{array}{ll} \lambda _0^{(\alpha )} = 1+\frac{\alpha }{2}> 0, \qquad \lambda _1^{(\alpha )} = -\frac{\alpha (3+\alpha )}{2} \le 0, \end{array}\\ \lambda _2^{(\alpha )} = \frac{1}{4}\alpha (\alpha ^2+3\alpha -2) = {\left\{ \begin{array}{ll} \le 0, \qquad \alpha \in [0,\frac{\sqrt{17}-3}{2}], \\ > 0, \qquad \alpha \in (\frac{\sqrt{17}-3}{2},1], \end{array}\right. }\\ \begin{array}{ll} \lambda _k^{(\alpha )} = \big [ (1+\frac{\alpha }{2})(\frac{k-\alpha -1}{k}) - \frac{\alpha }{2} \big ] g_{k-1}^{(\alpha )} \le 0, \qquad k \ge 3. \end{array} \end{aligned}$$

From Wang and Vong (2014a), we can obtain the following non-negative properties.

Lemma 4

(Wang and Vong 2014a) Let the coefficients $\big \{\lambda _{k}^{(\alpha )}\big \}^{\infty }_{k=0}$ are introduced in (10). For any mesh series $\big ({\mathcal {W}}^1,\ldots ,{\mathcal {W}}^m\big )^\mathrm{T}\in \mathbb {R}^{m}$, we have

$$\begin{aligned} \sum \limits _{n=1}^m \Big (\sum \limits _{k=0}^{n-1}\lambda _{k}^{(\alpha )}{\mathcal {W}}^{n-k}\Big ){\mathcal {W}}^n \ge 0. \end{aligned}$$

According to the aforesaid lemma, we can conclude the lemma as follows.

Lemma 5

(Gao and Zz 2016a, b) Assume that the coefficients$\big \{\lambda _{k}^{(\alpha )}\big \}^{\infty }_{k=0}$ are introduced in Eq. (10). Then, for any mesh series $\big ({\mathcal {W}}^0,\ldots ,{\mathcal {W}}^m\big )^\mathrm{T}\in \mathbb {R}^{m+1}$, it follows that

$$\begin{aligned} \sum \limits _{n=0}^m \left( \sum \limits _{k=0}^{n}\lambda _{k}^{(\alpha )}{\mathcal {W}}^{n-k}\right) {\mathcal {W}}^n \ge 0. \end{aligned}$$

Afterwards, we define the following notation

$$\begin{aligned} \begin{array}{ll} \mu _1 := \Big [ \triangle \alpha \sum \limits _{l=0}^{2J}c_l \omega (\alpha _l)\tau ^{-\alpha _l} \lambda _{0}^{(\alpha _l)} \Big ] . \end{array} \end{aligned}$$

(11)

Then, we get the estimate as follows.

Lemma 6

(Gao and Zz 2016b) Let $\mu _1$ be defined in the relation (11). Then, we get $\mu _1 = \mathcal {O}\Big ((\tau |\ln \tau |)^{-1}\Big )$.

Secondly, we take two positive integers $M_1$ and $M_2$. Let $h_1$ = $L_1$/$M_1$, $h_2$ = $L_2$/$M_2$, $h=\max \{h_1, h_2\}$. Define the nodal points $x_i$ = $ih_1$, $0\le i \le M_1$, $y_j$ = $jh_2$, $0\le j \le M_2$, $\chi = \{1\le i \le M_1-1, 1\le j \le M_2-1\}$, $\gamma$ = {$(i,j)|(x_i,y_j)\in \partial \varOmega$}. Also, we introduce ${\overline{\varOmega }_h}$ = {($x_i$,$y_j$)| $0 \le i \le M_1, 0 \le j \le M_2$}, $\mathring{\varOmega }_h$ = {$w| w\in \varOmega _h; w_{ij} = 0, {~\mathrm{when}~} (i,j)\in \gamma$}, $\varOmega _h$ = ${\overline{\varOmega }_h}$ $\cap$ $\varOmega$ and $\partial \varOmega _h$ = $\varOmega _h$ $\cap$ $\partial \varOmega$.

In order to facilitate the analysis, suppose that the symbols $u^{n}_{ij}$ and $f^{n}_{ij}$ represent the values of functions u(x, y, t) and f(x, y, t) at nodal point $(x_i, y_j, t_n)$, respectively. We define some necessary notations for any grid function w = {$w_{ij} | 0 \le i \le M_1, 0 \le j \le M_2$} over ${\overline{\varOmega }_h}$,

$$\begin{aligned} \delta _xw_{ij}^n:= & {} \frac{1}{h_1}(w_{ij}^n-w_{i-1,j}^n),\qquad \delta _yw_{ij}^n := \frac{1}{h_2}(w_{ij}^n-w_{i,j-1}^n),\\ \delta _x^2w_{ij}^n:= & {} \frac{1}{h_1}(\delta _xw_{ij}^n-\delta _xw_{i-1,j}^n),\qquad \delta _y^2w_{ij}^n := \frac{1}{h_2}(\delta _yw_{ij}^n-\delta _yw_{i,j-1}^n),\\ \varDelta _hw_{ij}^n:= & {} \delta _x^2w_{ij}^n + \delta _y^2w_{ij}^n, \quad 1 \le i \le M_1-1,\quad 1 \le j \le M_2-1,\quad 1 \le n \le N. \end{aligned}$$

Let us define the discrete inner product and the associated norms for $w,v\in \mathring{\varOmega }_h$ by

$$\begin{aligned} \begin{array}{ll} (w, v) := h_1h_2\sum \limits _{i=1}^{M_1-1}\sum \limits _{j=1}^{M_2-1}w_{ij}v_{ij}, \qquad \Vert v\Vert = \sqrt{(v,v)}, \qquad \Vert v\Vert _\infty = \max \limits _{\tiny \begin{array}{c}1 \le i \le M_1-1 \\ 1 \le j \le M_2-1\end{array}}|v_{ij}|. \end{array} \end{aligned}$$

Here, we present the associated discrete method and some lemmas to construct the ADI difference approach. First, we introduce the second-order CQ strategy (cf. Lubich 1986, 1988) for discretizing the RLFI $I^{(\beta )}\phi (t_n)$ as

$$\begin{aligned} \begin{array}{ll} Q^{(\beta )}_n(\phi ) = \tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\phi ^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\phi ^0, \qquad 0\le \beta \le 1, \end{array} \end{aligned}$$

(12)

where the CQ weights $\omega _s^{(\beta )}$ can be derived by

$$\begin{aligned} \begin{array}{ll} (\delta (\nu ))^{-\beta } = \sum \limits _{s=0}^{\infty }\omega ^{(\beta )}_s\nu ^s, \end{array} \end{aligned}$$

in which $\delta (\nu )$ denotes the generating function Lubich (1988). For the CQ with second-order accuracy, we get

$$\begin{aligned} \begin{array}{ll} \delta (\nu ) = \sum \limits _{s=1}^{2}\frac{1}{s}(1-\nu )^s. \end{array} \end{aligned}$$

Therefore, we can get the quadrature weights $\omega ^{(\beta )}_s$ via

$$\begin{aligned} \begin{array}{ll} c^{(\beta )}_s = (-1)^s\genfrac(){0.0pt}0{-\beta }{s} = (-1)^n\frac{\varGamma (1-\beta )}{\varGamma (1+n)\varGamma (1-\beta -n)}> 0, \\ \omega _s^{(\beta )} = (\frac{2}{3})^\alpha \sum \limits _{i=0}^s\frac{c^{(\beta )}_{s-i}c^{(\beta )}_i}{3^i},\qquad s\ge 0. \end{array} \end{aligned}$$

We can present the correction weights $\tilde{\omega }{_n^{(\beta )}}$ introduced in (12) for discretizing the integral term with second-order accuracy in the time dimension. When $\phi = 1$, we have

$$\begin{aligned} \begin{array}{ll} Q^{(\beta )}_n(1) = \frac{1}{\varGamma (\beta )}\int \limits _{0}^{t_n}(t_n-s)^{\beta -1}\mathrm{d}s = \frac{(t_n)^\beta }{\varGamma (1+\beta )}. \end{array} \end{aligned}$$

(13)

Thus, we arrive at

$$\begin{aligned} \begin{array}{ll} \tilde{\omega }^{(\beta )}_n = \frac{n^{\beta }}{\varGamma (1+\beta )}-\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}. \end{array} \end{aligned}$$

Now, we analyze the quadrature error.

Lemma 7

(Chen et al. 2016; Xu 1997) Suppose that the function $\psi (t)$ is continuously differentiable over (0, T] and real, $\psi _{tt}(t)$ is integrable and continuous on (0, T]. Then, the quadrature error can be obtained using

$$\begin{aligned} \begin{array}{ll} |I^{(\beta )}\psi (t_n)-Q^{(\beta )}_n(\psi )|\le C\Big [\tau ^2t_n^{\beta -1}|\psi _t(0)| + \tau ^2\int \limits _{0}^{t_{n-1}}(t_n-\xi )^{\beta -1}|\psi _{tt}(\xi )|\mathrm{d}\xi \\ \qquad \qquad \qquad \qquad \quad + \tau ^{1+\beta }\int \limits _{t_{n-1}}^{t_n}|\psi _{tt}(\xi )|\mathrm{d}\xi \Big ], \qquad 0<\beta <1, \end{array} \end{aligned}$$

in which $Q^{(\beta )}_n(\psi )$ is presented by (12), and $0<t_n<T<\infty$.

Remark 1

Throughout the article, C represents a generic positive constant which is independent of the space and time step sizes. In addition, it is not necessarily same in different occurrences.

Remark 2

Through the above-mentioned Lemma, the quadrature error of the CQ is $\mathcal {O}({\tau ^{1+\beta }})$. However, the quadrature error of second-order CQ is $\mathcal {O}({\tau ^2})$ when $|\psi _{tt}(t)|\le C$, $t \in [0, T]$.

In the following, we list some useful lemmas based on the Taylor formula with integral remainder.

Lemma 8

(Yn et al. 2011) Supposing that $u(x,y,\cdot )\in C^{4,4}_{x,y}\big ([0, L_1]\times [0, L_2]\big )$. Then, we get

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\partial ^2u}{\partial x^2}(x_i,y_j,t_n) = \delta _x^2U_{ij}^n \\ \displaystyle \quad -\frac{h_1^2}{6}\int \limits _{0}^{1}\Big [\frac{\partial ^4u}{\partial x^4}(x_i+\xi h_1,y_j,t_n)+\frac{\partial ^4u}{\partial x^4}(x_i-\xi h_1,y_j,t_n)\Big ](1-\xi )^3\mathrm{d}\xi , \end{array} \end{aligned}$$

(14)

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\partial ^2u}{\partial y^2}(x_i,y_j,t_n) = \delta _y^2U_{ij}^n \\ \displaystyle \quad -\frac{h_2^2}{6}\int \limits _{0}^{1}\Big [\frac{\partial ^4u}{\partial y^4}(x_i,y_j+\xi h_2,t_n)+\frac{\partial ^4u}{\partial y^4}(x_i,y_j-\xi h_2,t_n)\Big ](1-\xi )^3\mathrm{d}\xi . \end{array} \end{aligned}$$

(15)

Now, we can obtain the bound of $I^{(\beta )}u_{xx}(x_i,y_j,t_n)-Q_n^{(\beta )}(\delta _x^2U_{ij})$.

Lemma 9

Assume that $u(x,y,t)\in C^{4,4,2}_{x,y,t}\big ([0, L_1]\times [0, L_2]\times [0,T]\big )$. Then, for $n=1, \ldots , N$ and $(i, j)\in \chi$, we get

$$\begin{aligned} \begin{array}{ll} \big |(R_1)^n_{ij}\big | = \big |I^{(\beta )}\varDelta u(x_i,y_j,t_n)-Q_n^{(\beta )}(\varDelta _hU_{ij})\big |\le C(\tau ^2 + h_1^2+h_2^2). \end{array} \end{aligned}$$

(16)

Proof

Using the triangle inequality, we have

$$\begin{aligned} \begin{array}{ll} &{} \big |I^{(\beta )}u_{xx}(x_i,y_j,t_n)-Q_n^{(\beta )}(\delta _x^2U_{ij})\big | \\ &{}\le \big |I^{(\beta )}u_{xx}(x_i,y_j,t_n)-Q_n^{(\beta )}\big (u_{xx}(x_i,y_j,\cdot )\big )\big | + \big |Q_n^{(\beta )}\big (u_{xx}(x_i,y_j,\cdot )\big )-Q_n^{(\beta )}(\delta _x^2U_{ij})\big |. \end{array} \end{aligned}$$

In other hand, for the estimate of $\big |Q_n^{(\beta )}\big (u_{xx}(x_i,y_j,\cdot )\big )-Q_n^{(\beta )}(\delta _x^2U_{ij})\big |$, we use Lemma 8 and (formula (2.4), Qiao et al. 2022) to get

$$\begin{aligned} \begin{array}{ll} &{}\big |Q_n^{(\beta )}\big (u_{xx}(x_i,y_j,\cdot )\big )-Q_n^{(\beta )}(\delta _x^2U_{ij})\big |\\ &{}\le C\Big (\tau ^\beta \sum \limits _{p=1}^n|\omega _{n-p}^{(\beta )}|\Big )h_1^2+C\tau ^\beta |\omega _n^{(\beta )}|h_1^2\\ &{}\le C\Big (\int \limits _{0}^{t_n}s^{\beta -1}\mathrm{d}s\Big )h_1^2+C\tau ^\beta \frac{\tau t_n^{\beta -1}}{\tau ^\beta }h_1^2\\ &{}\le Ct_n^\beta h_1^2+t_n^\beta n^{-1}h_1^2\\ &{}\le C(T)h_1^2. \end{array} \end{aligned}$$

Regarding Lemma 7 and Remark 2, we get

$$\begin{aligned} \begin{array}{ll} \big |I^{(\beta )}u_{xx}(x_i,y_j,t_n)-Q_n^{(\beta )}(\delta _x^2U_{ij})\big | &{}\le \big |I^{(\beta )}u_{xx}(x_i,y_j,t_n)-Q_n^{(\beta )}\big (u_{xx}(x_i,y_j,\cdot )\big )\big |+Ch_1^2\\ &{}\le C\big (\tau ^2+h_1^2 \big ). \end{array} \end{aligned}$$

In the same way, we can prove $\big |I^{(\beta )}u_{yy}(x_i,y_j,t_n)-Q_n^{(\beta )}(\delta _y^2U_{ij})\big |\le C(\tau ^2 + h_2^2)$. To sum up, the proof is completed. $\square$

2.2 The derivation of the ADI difference approach in two dimensions

Firstly, we can establish the ADI difference approach for Eqs. (1)–(3). Considering Eq. (1) at the nodal point $(x_i,y_j,t_n)$ for $(i, j)\in \chi$, $n=1, \ldots , N$, we have

$$\begin{aligned} \begin{array}{ll} \mathbb {D}^{\omega }_{t}u(x_i,y_j,t_n) - \mu \varDelta u(x_i,y_j,t_n) - I^{(\beta )}\varDelta u(x_i,y_j,t_n)= f(x_i,y_j,t_n), \\ \qquad \qquad \qquad \qquad (x,y)\in \varOmega , \qquad n=1, \ldots , N. \end{array} \end{aligned}$$

(17)

From Lemma 1, we can get

$$\begin{aligned} \begin{array}{ll} \mathbb {D}^{\omega }_{t}u_{ij}^n = \int \limits _{0}^{1}\omega (\alpha ) D_{t}^{\alpha }u_{ij}^n\mathrm{d}\alpha = \triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)D_{t}^{\alpha _l}u_{ij}^n + \mathcal {O}(\triangle \alpha ^2). \end{array} \end{aligned}$$

Observing the equivalence of the CFD $D_{t}^{\alpha }\varphi (t)$ and the RLFD $_{-\infty }D_{t}^{\alpha }\varphi (t)$ with $\varphi (t)=0$ at $t\le 0$ and employing Lemma 3 as well as the above formula, we can obtain

$$\begin{aligned} \begin{array}{ll} \mathbb {D}^{\omega }_{t}u_{ij}^n = \triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} u_{ij}^{n-k} + \mathcal {O}(\tau ^2 + \triangle \alpha ^2). \end{array} \end{aligned}$$

(18)

From Lemmas 8 and 9 leads to

$$\begin{aligned} \begin{array}{ll} I^{(\beta )}\varDelta u(x_i,y_j,t_n) = Q_n^{(\beta )}(\varDelta _h u_{ij})+(R_1)^n_{ij}, \quad (i, j)\in \chi ,\quad n=1, \ldots , N. \end{array} \end{aligned}$$

(19)

Inserting relations (14), (15), (18) and (19) in (17) yields that

$$\begin{aligned} \begin{array}{ll} \triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} u_{ij}^{n-k} - \mu \varDelta _hu_{ij}^n-(\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _hu_{ij}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hu_{ij}^0)\\ \quad =f_{ij}^n + (R_1)_{ij}^n, \qquad (i, j)\in \chi ,\quad n=1, \ldots , N, \end{array} \end{aligned}$$

(20)

in which

$$\begin{aligned} \begin{array}{ll} \big |(R_1)_{ij}^n\big |\le C\Big (\tau ^2+h_1^2+h_2^2+\triangle \alpha ^2\Big ). \end{array} \end{aligned}$$

(21)

Then adding the small term $\tau \mu _1\mu _2^2\delta _x^2\delta _y^2\delta _tu_{ij}^{n-\frac{1}{2}} = (R_2)_{ij}^n$ to both sides of Eq. (20), we can get

$$\begin{aligned} \begin{array}{ll} \triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _p)} u_{ij}^{n-k} - \mu \varDelta _hu_{ij}^n-(\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _hu_{ij}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hu_{ij}^0)\\ \quad +\tau \mu _1\mu _2^2\delta _x^2\delta _y^2\delta _tu_{ij}^{n-\frac{1}{2}} = f_{ij}^n + R_{ij}^n , \qquad (i, j)\in \chi ,\quad n=1, \ldots , N, \end{array} \end{aligned}$$

(22)

in which

$$\begin{aligned} \begin{array}{ll} \big |R_{ij}^n\big | = \big |(R_1)_{ij}^n + (R_2)_{ij}^n\big |\le C\Big (\tau ^2+h_1^2+h_2^2+\triangle \alpha ^2\Big ), \end{array} \end{aligned}$$

from which, if $u\in C_{x,y,t}^{4,4,2}\big ([0,L_1]\times [0,L_2]\times [0,T]\big )$ with $\tau \mu _1\mu _2^2=\mathcal {O}(\tau ^2|\ln \tau |)$, then $|(R_2)_{ij}^n|\le C\tau ^2$. Noting the IC and BC in (2)–(3), we obtain

$$\begin{aligned} \begin{array}{ll} u_{ij}^0 = \kappa (x_i,y_j), \qquad (i, j)\in \chi , \quad u_{ij}^n = 0, \quad (i, j)\in \gamma , \quad n=1, \ldots , N. \end{array} \end{aligned}$$

(23)

Ignoring the truncation error $R_{ij}^n$ and using the substitution of $U_{ij}^n$ instead of $u_{ij}^n$ in Eqs. (22)–(23), we can provide the ADI difference approach for Eqs. (1)–(3) as

$$\begin{aligned}&\begin{array}{ll} \triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _p)} U_{ij}^{n-k} - \mu \varDelta _hU_{ij}^n-(\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _hU_{ij}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\\ \qquad \varDelta _hU_{ij}^0)+\tau \mu _1\mu _2^2\delta _x^2\delta _y^2\delta _tU_{ij}^{n-\frac{1}{2}} = f_{ij}^n , \qquad (i, j)\in \chi ,\quad n=0,\,1, \ldots , N, \\ \end{array} \end{aligned}$$

(24)

$$\begin{aligned}&\begin{array}{ll} U_{ij}^0 = \kappa (x_i,y_j), \qquad (i, j)\in \chi , \\ U_{ij}^n = 0, \qquad (i, j)\in \gamma , \quad n=0,\,1, \ldots , N. \end{array} \end{aligned}$$

(25)

Let us introduce $\mu _2 = \mu _1^{-1}(\mu +\tau ^\beta \omega _0^{(\beta )})$, where $\mu _1$ is defined in (11). It is not hard to get that $\mu _2 = \mathcal {O}(\tau |\ln \tau |)$. At the same time, we notice that (24) can be restated as

$$\begin{aligned} \begin{array}{ll} \mu _1U_{ij}^n-(\mu +\tau \omega _0^{(\beta )})\varDelta _hU_{ij}^n +\tau \mu _1\mu _2^2\delta _x^2\delta _y^2\delta _tU_{ij}^{n-\frac{1}{2}} = {\mathcal {F}}_{ij}^n, \end{array} \end{aligned}$$

(26)

where

$$\begin{aligned} \begin{array}{ll} {\mathcal {F}}_{ij}^n = -\triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=1}^{n} \lambda _{k}^{(\alpha _p)} U_{ij}^{n-k} + \tau ^\beta \sum \limits _{p=1}^{n-1}\omega _{n-p}^{(\beta )}\varDelta _hU_{ij}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hU_{ij}^0 + f_{ij}^n. \end{array} \end{aligned}$$

Denoting the notation $E^n = U^n-U^{n-1}$, after simplification, we can obtain the following ADI scheme

$$\begin{aligned} \begin{array}{ll} ({\mathcal {I}} - \mu _2\delta _x^2)({\mathcal {I}} - \mu _2\delta _y^2)E_{ij}^n = \tilde{\mathcal {F}}_{ij}^n, \end{array} \end{aligned}$$

(27)

where ${\mathcal {I}}$ is an identity operator, $\tilde{\mathcal {F}}_{ij}^n$ is given as follows

$$\begin{aligned} \begin{aligned} \tilde{\mathcal {F}}_{ij}^n&= -U_{ij}^{n-1} + \mu _2\varDelta _hU_{ij}^{n-1} -\mu _1^{-1}\triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=1}^{n} \lambda _{k}^{(\alpha _l)} U_{ij}^{n-k} \\&\quad + \mu _1^{-1}\tau ^\beta \sum \limits _{p=1}^{n-1}\omega _{n-p}^{(\beta )}\varDelta _hU_{ij}^p + \mu _1^{-1}\tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hU_{ij}^0 + \mu _1^{-1}f_{ij}^n. \end{aligned} \end{aligned}$$

Solving two sets of independent 1D problem, we can determine ${U_{ij}^n}$. Let us define

$$\begin{aligned} \begin{array}{ll} E_{ij}^{n-\frac{1}{2}} = \big ({\mathcal {I}} - \mu _2\delta _y^2\big )E_{ij}^n,\qquad (x_i, y_j)\in \varOmega _h, \quad n=1, \ldots , N. \end{array} \end{aligned}$$

Therefore, we give the following computational steps:

$\mathbf {Step~{1}}$ Firstly, for fixed $j\in \{1, 2, \ldots , M_2-1\}$ we solve the following system to calculate $\{E_{ij}^{n-\frac{1}{2}}\}$:

$$\begin{aligned} \begin{array}{ll} {\left\{ \begin{array}{ll} \big ({\mathcal {I}}-\mu _2\delta _x^2\big )E_{ij}^{n-\frac{1}{2}} = \tilde{\mathcal {F}}_{ij}^n ,\quad 1\le i\le M_1-1, \quad n=1, \ldots , N,\\ E_{0,j}^{n-\frac{1}{2}} = E_{M_1,j}^{n-\frac{1}{2}} = 0. \end{array}\right. } \end{array} \end{aligned}$$

(28)

$\mathbf {Step~{2}}$ Once $\{E_{ij}^{n-\frac{1}{2}}\}$ is available, fixed $i\in \{1, 2, \ldots , M_1-1\}$, we can solve the system as follows:

$$\begin{aligned} \begin{array}{ll} {\left\{ \begin{array}{ll} \big ({\mathcal {I}}-\mu _2\delta _y^2\big )E_{ij}^n = E_{ij}^{n-\frac{1}{2}} ,\quad 1\le j\le M_2-1, \quad n=1, \ldots , N,\\ E_{i,0}^n = E_{i,M_2}^n = 0 \end{array}\right. } \end{array} \end{aligned}$$

(29)

to compute $\{E_{ij}^n\}$, and we can get the desired solution $\{U_{ij}^n\}$ further.

2.3 Analysis of the ADI difference approach

This subsection only examines the convergence analysis of the proposed algorithm (24)–(25). In what follows, we introduce some useful lemmas.

Lemma 10

(Xu 1997) For $t\in \{t\in \mathbb C, \mathbf {Re}(t)>0\}$, $\beta (t)\in L^{1,loc}(0,\infty )$ denote a positive value if and only if $\mathbf {Re}\big (\hat{\beta }(t)\big )\ge 0$, in which $\hat{\beta }(\xi ) = \int \nolimits _{-\infty }^{+\infty }e^{i\xi t}\beta (t)\mathrm{d}t$ indicates the Laplace transform of $\beta (t)$ introduced in (6), and $\mathbf {Re}(\cdot )$ represents the real part.

Lemma 11

(Lopez-Marcos 1990; Xu 1997) Suppose that a real-valued sequence $\{a_0, a_1, \ldots , a_s, \ldots \}$ satisfies: for any vector $(L^1, L^2, \ldots , L^N)\in \mathbb R^N,$ positive integer N,  and $\,\hat{a}(z) = \sum \nolimits _{s=0}^{\infty }a_sz^s$ is analytic in ${\mathcal {S}} = \{z\in \mathbb C: |z|\le 1\}$, for $z \in {\mathcal {S}}$, it follows that

$$\begin{aligned} \begin{array}{ll} \sum \limits _{n=1}^N \big (\sum \limits _{p=1}^na_{n-p}L^p\big )L^n \ge 0, \end{array} \end{aligned}$$

if and only if $\mathbf {Re}\big (\hat{a}(z)\big )\ge 0$.

Lemma 12

(Chen et al. 2016; Lopez-Marcos 1990) The functions $w, v\in \mathring{\varOmega }_h$ have the following properties:

$$\begin{aligned} \begin{array}{ll} (i) |(\delta _x^2w, v)| \le \frac{4}{h_1^2}\Vert w\Vert \Vert v\Vert , \\ (ii) (\delta _x^2w, v) = -h_1\sum \limits _{j=0}^{M_1-1}(\delta _xw_{j+1})(\delta _xv_{j+1}). \end{array} \end{aligned}$$

In the same way, we can denote the notation $(\delta _y^2w, v)$ and so on.

Define

$$\begin{aligned} \begin{array}{ll} e_{ij}^n := u(x_i,y_j,t_n)-U_{ij}^n = u_{ij}^n-U_{ij}^n,\quad (i, j)\in \chi ,\quad n=0,\,1, \ldots , N. \end{array} \end{aligned}$$

Subtracting (24)–(25) from (22)–(23), respectively, and denoting the notation $\triangle \alpha \sum \nolimits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} = \varPhi _{l,J}$, we can compute the error system of equations as follows

$$\begin{aligned} \begin{array}{ll} \varPhi _{l,J} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} e_{ij}^{n-k} - \mu \varDelta _he_{ij}^n-(\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _he_{ij}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _he_{ij}^0)\\ +\tau \mu _1\mu _2^2\delta _x^2\delta _y^2\delta _te_{ij}^{n-\frac{1}{2}} = R_{ij}^n , \qquad (i, j)\in \chi ,\quad n=1, \ldots , N, \end{array} \end{aligned}$$

(30)

$$\begin{aligned} \begin{array}{ll} e_{ij}^0 = 0, \qquad (i, j)\in \chi , \\ e_{ij}^n = 0, \qquad (i, j)\in \gamma , \quad n=0,\,1, \ldots , N. \end{array} \end{aligned}$$

(31)

Theorem 1

(Convergence). Suppose that $\{u^n\}_{n=0}^{N}$ and $\{U^n\}_{n=0}^{N}$ are the solutions of (1)–(3) and (24)–(25), respectively. Let $u(x,y,t)\in C^{4,4,2}_{x,y,t}\big ([0, L_1]\times [0, L_2]\times [0,T]\big )$. Then, we obtain

$$\begin{aligned} \begin{aligned} \sqrt{\tau \sum \limits _{n=1}^{N}\left\| e^n \right\| ^2} \le C(T) \Big (\tau ^2+h^2+\triangle \alpha ^2 \Big ). \end{aligned} \end{aligned}$$

Proof

We establish the following weak formulation by taking the inner product of (30) by $\tau e^n$, summing from $n=1$ to N, adding small term $\tau \mu _1(e^0, e^0)$ to the both sides of (30) and denoting $\tilde{\varepsilon } = \tau \mu _1$ as

$$\begin{aligned} \begin{array}{ll} \tau \varPhi _{l,J} \sum \limits _{n=0}^N\sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} (e^{n-k},e^n)-\mu \tau \sum \limits _{n=1}^N(\varDelta _he^n,e^n)-\tau ^{1+\beta }\sum \limits _{n=1}^N\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}(\varDelta _he^p,e^n) \\ \quad - \tau ^{1+\beta }\sum \limits _{n=1}^N\tilde{\omega }{_n^{(\beta )}}(\varDelta _he^0, e^n)+ \tau \sum \limits _{n=1}^N\tau \mu _1\mu _2^2(\delta _x^2\delta _y^2\delta _te^{n-\frac{1}{2}},e^n) = \tau \sum \limits _{n=1}^{N}(R^n, e^n) + \tilde{\varepsilon }\Vert e^0\Vert ^2. \end{array} \end{aligned}$$

(32)

Each term in (32) will be analyzed below. Firstly, based on the Lemma 5, we have

$$\begin{aligned} \begin{array}{ll} \tau \varPhi _{l,J} \sum \limits _{n=0}^N\sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} (e^{n-k},e^n)\ge 0. \end{array} \end{aligned}$$

(33)

Secondly, we can get

$$\begin{aligned} \begin{aligned} -(\varDelta _he^n,e^n)&= -(\delta _x^2e^n+\delta _y^2e^n,e^n)\\&= (\delta _xe^n,\delta _xe^n) +(\delta _ye^n,\delta _ye^n)\\&= \Vert \delta _xe^n\Vert ^2 + \Vert \delta _ye^n\Vert ^2\\ :&= \Vert \nabla _h e^n\Vert ^2. \end{aligned} \end{aligned}$$

(34)

Thirdly, from Lemmas 10–12, we get

$$\begin{aligned} \begin{aligned} -\sum \limits _{n=1}^N\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}(\varDelta _he^p,e^n)&= \sum \limits _{n=1}^N\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\big [(\delta _xe^p,\delta _xe^n)+(\delta _ye^p,\delta _ye^n)\big ]\\&\ge 0. \end{aligned} \end{aligned}$$

(35)

Fourthly, applying Lemma 12 (i), we arrive at

$$\begin{aligned} \begin{aligned} \tau ^{1+\beta }\sum \limits _{n=1}^N\tilde{\omega }{_n^{(\beta )}}(\varDelta _he^0, e^n)&\le \tau ^{1+\beta }\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|(\varDelta _he^0, e^n)\\&\le \tau ^{1+\beta }\Big [\frac{4\big \Vert e^0\big \Vert \Vert e^n\Vert }{h_1^2}+\frac{4\big \Vert e^0\big \Vert \Vert e^n\Vert }{h_2^2}\Big ]\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|\\&= 4\tau ^{1+\beta }\big (\frac{1}{h_1^2}+\frac{1}{h_2^2}\big )\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|\big \Vert e^0\big \Vert \Vert e^n\Vert . \end{aligned} \end{aligned}$$

(36)

Moreover, we have

$$\begin{aligned} \begin{aligned} \tau ^2\mu _1\mu _2^2\sum \limits _{n=1}^N(\delta _x^2\delta _y^2\delta _te^{n-\frac{1}{2}},e^n)&= \tau ^2\mu _1\mu _2^2\sum \limits _{n=1}^N\Big (\delta _x^2\delta _y^2\frac{e^n-e^{n-1}}{\tau },e^n\Big )\\&= \tau ^2\mu _1\mu _2^2\sum \limits _{n=1}^N\Big (\delta _x\delta _y\frac{e^n-e^{n-1}}{\tau },\delta _x\delta _ye^n\Big )\\&= \tau ^2\mu _1\mu _2^2\sum \limits _{n=1}^N\Big (\delta _x\delta _y\frac{e^n-e^{n-1}}{\tau },\delta _x\delta _y\frac{e^n-e^{n-1}+e^{n-1}+e^n}{2}\Big )\\&\ge \tau ^2\mu _1\mu _2^2\sum \limits _{n=1}^N\Big (\delta _x\delta _y\frac{e^n-e^{n-1}}{\tau },\delta _x\delta _y\frac{e^n-e^{n-1}+e^{n-1}+e^n}{2}\Big )\\&\ge \frac{\tau \mu _1\mu _2^2}{2}\big (\Vert \delta _x\delta _ye^N\Vert ^2-\Vert \delta _x\delta _ye^0\Vert ^2\big ). \end{aligned} \end{aligned}$$

(37)

Finally, employing the Cauchy–Schwarz inequality arrives at

$$\begin{aligned} \begin{aligned} \tau \sum \limits _{n=1}^{N}(R^n, e^n)\le \tau \sum \limits _{n=1}^{N}\big \Vert R^n\big \Vert \Vert e^n\Vert . \end{aligned} \end{aligned}$$

(38)

Inserting (33)–(38) in (32), we have

$$\begin{aligned} \begin{aligned} \tau \mu \sum \limits _{n=1}^N\Vert \nabla _h e^n\Vert ^2 + \frac{\tau \mu _1\mu _2^2}{2}\Vert \delta _x\delta _ye^N\Vert ^2\le \frac{\tau \mu _1\mu _2^2}{2}\Vert \delta _x\delta _ye^0\Vert ^2 + \tilde{\varepsilon }\Vert e^0\Vert ^2 \\ + 4\tau ^{1+\beta }\big (\frac{1}{h_1^2}+\frac{1}{h_2^2}\big )\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|\big \Vert e^0\big \Vert \Vert e^n\Vert + \tau \sum \limits _{n=1}^N\big \Vert R^n\big \Vert \Vert e^n\Vert . \end{aligned} \end{aligned}$$

(39)

Next, using the Young inequality $ab\le \varepsilon a^2+\frac{1}{4\varepsilon }b^2 (a,b\in \mathbb R,\varepsilon >0)$ and Poincaré inequality $\Vert e^n\Vert \le C_0\Vert \nabla e^n\Vert$ to get

$$\begin{aligned} \begin{aligned} \frac{\mu \tau }{C^2}\sum \limits _{n=1}^N\Vert e^n\Vert ^2&+ \frac{\tau \mu _1\mu _2^2}{2}\Vert \delta _x\delta _ye^N\Vert ^2\le \frac{\tau \mu _1\mu _2^2}{2}\Vert \delta _x\delta _ye^0\Vert ^2 + \tilde{\varepsilon }\Vert e^0\Vert ^2 \\&+ 4\tau ^{1+\beta }\big (\frac{1}{h_1^2}+\frac{1}{h_2^2}\big )\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|\big \Vert e^0\big \Vert \Vert e^n\Vert + \frac{\tau C^2}{\mu }\sum \limits _{n=1}^N\Vert R^n\Vert ^2 + \frac{\mu \tau }{4C^2}\sum \limits _{n=1}^N\Vert e^n\Vert ^2 . \end{aligned} \end{aligned}$$

(40)

Then, because of $e^0 = 0$, we have

$$\begin{aligned} \begin{aligned} \frac{3\mu \tau }{4C^2}\sum \limits _{n=1}^N\Vert e^n\Vert ^2 \le \frac{\tau C^2}{\mu }\sum \limits _{n=1}^N\Vert R^n\Vert ^2. \end{aligned} \end{aligned}$$

(41)

Finally, we obtain the convergence results as

$$\begin{aligned} \begin{aligned} \tau \sum \limits _{n=1}^N\Vert e^n\Vert ^2&\le C \tau \sum \limits _{n=1}^N\Vert R^n\Vert ^2\\&\le C(T)\Big (\tau ^2+h_1^2+h_2^2+\triangle \alpha ^2\Big )^2. \end{aligned} \end{aligned}$$

(42)

This completes the proof $\square$

3 Numerical method and error analysis for the three-dimensional case

This section presents the numerical scheme and analysis of the three-dimensional problem (1)–(3) with $\varOmega = (0,L_1)\times (0,L_2)\times (0,L_3)$. Except for special definitions, other signs are the same as the two-dimensional case.

3.1 The derivation of the ADI difference scheme in three dimensions

Let $h_1 = \frac{L_1}{M_1}, h_2 = \frac{L_2}{M_2}, h_3 = \frac{L_3}{M_3}, h = \max \{h_1,h_2,h_3\}$, where $M_1, M_2, M_3$ are the number of divisions in the x, y and z dimensions, respectively. The nodal points $x_i=ih_1, y_j=jh_2, z_m=mh_3, \varrho =\{1\le i\le M_1-1, 1\le j\le M_2-1, 1\le m\le M_3-1\}, \iota =\{(i,j,m)|(x_i,y_j,z_m)\in \partial \varOmega \}, \overline{\varOmega }_h=\{(x_i,y_j,z_m)|0\le i\le M_1, 0\le j\le M_2, 0\le m\le M_3\}, \mathring{\varOmega }=\{w|w\in \varOmega _h, w_{ijm}=0, when (i,j,m) \in \iota \}, \varOmega _h= \overline{\varOmega }_h \cap \varOmega$ and $\partial \varOmega _h=\varOmega _h\cap \partial \varOmega$. Let us introduce the following grid functions

$$\begin{aligned} \begin{array}{ll} u_{ijm}^n := u(x_i,y_j,z_m,t_n),\quad f_{ijm}^n:=f(x_i,y_j,z_m,t_n), \quad (x_i,y_j,z_m)\in \varOmega _h,\quad n=0,\,1, \ldots , N. \end{array} \end{aligned}$$

For any grid function $w= \{w_{ijm}|0\le i\le M_1, 0\le j\le M_2, 0\le m\le M_3\}$ over $\overline{\varOmega }_h$, we define

$$\begin{aligned}&\delta _xw_{ijm}^n := \frac{1}{h_1}(w_{ijm}^n-w_{i-1,j,m}^n),\\&\delta _x^2w_{ijm}^n := \frac{1}{h_1}(\delta _xw_{ijm}^n-\delta _xw_{i-1,j,m}^n),\\&\varDelta _hw_{ijm}^n := \delta _x^2w_{ijm}^n + \delta _y^2w_{ijm}^n + \delta _z^2w_{ijm}^n . \end{aligned}$$

In like manner, we define other symbols, e.g., $\delta _yw_{ijm}^n, \delta _zw_{ijm}^n, \delta _y^2w_{ijm}^n, \delta _z^2w_{ijm}^n,$ etc.

In addition, for grid functions $w= \{w_{ijm}|0\le i\le M_1, 0\le j\le M_2, 0\le m\le M_3\}$ and $v= \{v_{ijm}|0\le i\le M_1, 0\le j\le M_2, 0\le m\le M_3\}$, let us introduce the inner product and norms as

$$\begin{aligned}&\begin{array}{ll} (w, v) := h_1h_2h_3\sum \limits _{i=1}^{M_1-1}\sum \limits _{j=1}^{M_2-1}\sum \limits _{m=1}^{M_3-1}w_{ijm}v_{ijm}, \quad \Vert v\Vert = \sqrt{(v,v)}, \end{array}\\&\Vert v\Vert _\infty = \max \limits _{\tiny \begin{array}{c}1 \le i \le M_1-1 \\ 1 \le j \le M_2-1\\ 1 \le m \le M_3-1 \end{array}}|v_{ijm}|. \end{aligned}$$

We obtain the following expression by considering (1) at the nodal point $(x_i, y_j, z_m, t_n)$ for $(i, j ,m)\in \varrho , n=1, \ldots , N$, as

$$\begin{aligned} \begin{array}{ll} \mathbb {D}^{\omega }_{t}u(x_i,y_j,z_m,t_n) - \mu \varDelta u(x_i,y_j,z_m,t_n) - I^{(\beta )}\varDelta u(x_i,y_j,z_m,t_n)= f(x_i,y_j,z_m,t_n), \\ \qquad \qquad \qquad \qquad (x,y,z)\in \varOmega , \qquad n=1, \ldots , N. \end{array} \end{aligned}$$

(43)

Similarly to what was considered in Sect. 2, from Lemmas 1 and 3, we can obtain

$$\begin{aligned} \begin{array}{ll} \mathbb {D}^{\omega }_{t}u_{ijm}^n = \varPhi _{l,J} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} u_{ijm}^{n-k} + \mathcal {O}(\tau ^2 + \triangle \alpha ^2). \end{array} \end{aligned}$$

(44)

Meanwhile, in virtue of Lemmas 8 and 9, we have

$$\begin{aligned} \begin{array}{ll} I^{(\beta )}\varDelta u(x_i,y_j,z_m,t_n) = Q_n^{(\beta )}(\varDelta _h u_{ijm})+(R_3)^n_{ijm}, \qquad (i, j, m)\in \varrho ,\quad n=1, \ldots , N. \end{array} \end{aligned}$$

(45)

Bring (44)–(45) into (43) and according to Lemma 8, we can get

$$\begin{aligned} \begin{array}{ll} \varPhi _{l,J} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} u_{ijm}^{n-k} - \mu \varDelta _hu_{ijm}^n-(\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _hu_{ijm}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hu_{ijm}^0)\\ =f_{ijm}^n + (R_3)_{ijm}^n, \qquad (i, j, m)\in \varrho ,\quad n=1, \ldots , N, \end{array} \end{aligned}$$

(46)

where

$$\begin{aligned} \begin{array}{ll} \big |(R_3)_{ijm}^n\big |\le C\Big (\tau ^2+h_1^2+h_2^2+h_3^2+\triangle \alpha ^2\Big ). \end{array} \end{aligned}$$

Adding the small term $\mathcal LU_{ijm}^{n-\frac{1}{2}}=\tau \mu _1\mu _2^2(\delta _x^2\delta _y^2+\delta _x^2\delta _z^2+\delta _y^2\delta _z^2)\delta _tU_{ijm}^{n-\frac{1}{2}}-\tau \mu _1\mu _3^3\delta _x^2\delta _y^2\delta _z^2\delta _tU_{ijm}^{n-\frac{1}{2}}=(R_4)_{ijm}^n$ to both sides of (46), we can get

$$\begin{aligned} \begin{array}{ll} \varPhi _{l,J} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} u_{ijm}^{n-k} - \mu \varDelta _hu_{ijm}^n-\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _hu_{ijm}^p +\mathcal Lu_{ijm}^{n-\frac{1}{2}}\\ = \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hu_{ijm}^0+f_{ijm}^n + (\hat{R})_{ijm}^n, \qquad (i, j, m)\in \varrho ,\quad n=1, \ldots , N, \end{array} \end{aligned}$$

(47)

where

$$\begin{aligned} \begin{array}{ll} |(\hat{R})_{ijm}^n|=|(R_3)_{ijm}^n+(R_4)_{ijm}^n|\le C\Big (\tau ^2+h_1^2+h_2^2+h_3^2+\triangle \alpha ^2\Big ), \end{array} \end{aligned}$$

with the IC and BC as follow

$$\begin{aligned} \begin{array}{ll} u_{ijm}^0 = \kappa (x_i,y_j,z_m), \qquad (i, j, m)\in \varrho , \\ u_{ijm}^n = 0, \qquad (i, j, m)\in \iota , \quad n=1, \ldots , N. \end{array} \end{aligned}$$

(48)

Dropping the truncation errors $(\hat{R})_{ijm}^n$, with $U_{ijm}^n$ instead of $u_{ijm}^n$ in (47)–(48), we obtain the difference scheme as follow

$$\begin{aligned}&\begin{array}{ll} \varPhi _{l,J} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} U_{ijm}^{n-k} - \mu \varDelta _hU_{ijm}^n-\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _hU_{ijm}^p +\mathcal LU_{ijm}^{n-\frac{1}{2}}\\ \qquad = \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hU_{ijm}^0+f_{ijm}^n , \qquad (i, j, m)\in \varrho ,\quad n=1, \ldots , N. \end{array} \end{aligned}$$

(49)

$$\begin{aligned}&\begin{array}{ll} U_{ijm}^0 = \kappa (x_i,y_j,z_m), \qquad (i, j, m)\in \varrho , \\ U_{ijm}^n = 0, \qquad (i, j, m)\in \iota , \quad n=1, \ldots , N. \end{array} \end{aligned}$$

(50)

This moment, by observing that (49) can rewritten as

$$\begin{aligned} \begin{array}{ll} \mu _1U_{ijm}^n-(\mu +\tau \omega _0^{(\beta )})\varDelta _hU_{ijm}^n +\mathcal LU_{ijm}^{n-\frac{1}{2}}= \bar{\mathcal {F}}_{ijm}^n, \end{array} \end{aligned}$$

(51)

in which

$$\begin{aligned} \begin{array}{ll} \bar{\mathcal {F}}_{ijm}^n = -\triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=1}^{n} \lambda _{k}^{(\alpha _p)} U_{ijm}^{n-k}+ \tau ^\beta \sum \limits _{p=1}^{n-1}\omega _{n-p}^{(\beta )}\varDelta _hU_{ijm}^p + \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hU_{ijm}^0 + f_{ijm}^n. \end{array} \end{aligned}$$

Let the notation $E^n$ is defined in front. After simplification, we get the following ADI difference scheme

$$\begin{aligned} \begin{array}{ll} ({\mathcal {I}} - \mu _2\delta _x^2)({\mathcal {I}} - \mu _2\delta _y^2)({\mathcal {I}} - \mu _2\delta _z^2)E_{ijm}^n = \hat{\mathcal {F}}_{ijm}^n, \end{array} \end{aligned}$$

(52)

where ${\mathcal {I}}$ is an identity operator, and $\hat{\mathcal {F}}_{ijm}^n$ is presented as follows

$$\begin{aligned} \begin{aligned} \hat{\mathcal {F}}_{ijm}^n&= -U_{ijm}^{n-1} + \mu _2\varDelta _hU_{ijm}^{n-1} -\mu _1^{-1}\triangle \alpha \sum \limits _{l=0}^{2J}c_{l}\omega (\alpha _l)\tau ^{-\alpha _l} \sum \limits _{k=1}^{n} \lambda _{k}^{(\alpha _l)} U_{ijm}^{n-k} \\&\quad + \mu _1^{-1}\tau ^\beta \sum \limits _{p=1}^{n-1}\omega _{n-p}^{(\beta )}\varDelta _hU_{ijm}^p + \mu _1^{-1}\tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _hU_{ijm}^0 + \mu _1^{-1}f_{ijm}^n. \end{aligned} \end{aligned}$$

Next, we present several intermediate variables to determine at $U_{ijm}^n$:

$$\begin{aligned} \begin{array}{ll} E_{ijm}^{n-\frac{1}{3}} = \big ({\mathcal {I}} - \mu _2\delta _z^2\big )E_{ijm}^n,\quad 0\le i\le M_1,\quad 0\le j\le M_2, \quad 0\le m\le M_3-1, \quad n=1, \ldots , N \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} E_{ijm}^{n-\frac{2}{3}} = \big ({\mathcal {I}} - \mu _2\delta _y^2\big )E_{ijm}^{n-\frac{1}{3}},\quad 0\le i\le M_1,\quad 1\le j\le M_2-1, \quad 0\le m\le M_3, \quad n=1, \ldots , N. \end{array} \end{aligned}$$

From the above formulae, we can calculate the $E_{ijm}^n$ through the following three steps.

$\mathbf {Step~{1}}$ Firstly, solve the following system to compute $\{E_{ijm}^{n-\frac{2}{3}}\}$ in the x-dimension by fixing $m\in \{1, 2, \ldots , M_3-1\}$ and $j\in \{1, 2, \ldots , M_2-1\}$ as

$$\begin{aligned} \begin{array}{ll} {\left\{ \begin{array}{ll} \big ({\mathcal {I}}-\mu _2\delta _x^2\big )E_{ijm}^{n-\frac{2}{3}} = \hat{\mathcal {F}}_{ijm}^n ,\quad 1\le i\le M_1-1,\quad n=1, \ldots , N, \\ E_{0jm}^{n-\frac{2}{3}} = ({\mathcal {I}}-\mu _2\delta _y^2)E_{0jm}^{n-\frac{1}{3}} = ({\mathcal {I}}-\mu _2\delta _y^2)({\mathcal {I}}-\mu _2\delta _z^2)E_{0jm}^n,\\ E_{M_1jm}^{n-\frac{2}{3}}=({\mathcal {I}}-\mu _2\delta _y^2)E_{M_1jm}^{n-\frac{1}{3}} = ({\mathcal {I}}-\mu _2\delta _y^2)({\mathcal {I}}-\mu _2\delta _z^2)E_{M_1jm}^n. \end{array}\right. } \end{array} \end{aligned}$$

(53)

$\mathbf {Step~{2}}$ Solve the following system in the y-dimension by fixing $m\in \{1, 2, \ldots , M_3-1\}$ and $i\in \{1, 2, \ldots , M_1-1\}$ , we can

$$\begin{aligned} \begin{array}{ll} {\left\{ \begin{array}{ll} \big ({\mathcal {I}}-\mu _2\delta _y^2\big )E_{ijm}^{n-\frac{1}{3}} = E_{ijm}^{n-\frac{2}{3}} ,\quad 1\le j\le M_2-1,\quad n=1, \ldots , N, \\ E_{i0m}^{n-\frac{1}{3}} = ({\mathcal {I}}-\mu _2\delta _z^2)E_{i0m}^n,\\ E_{iM_2m}^{n-\frac{1}{3}} = ({\mathcal {I}}-\mu _2\delta _z^2)E_{iM_2m}^n. \end{array}\right. } \end{array} \end{aligned}$$

(54)

$\mathbf {Step~{3}}$ Solve the following system in the z-dimension when once $\{E_{ijm}^{n-\frac{2}{3}}\}$ and $\{E_{ijm}^{n-\frac{1}{3}}\}$ are determined by fixing $j\in \{1, 2, \ldots , M_2-1\}$ and $i\in \{1, 2, \ldots , M_1-1\}$ as

$$\begin{aligned} \begin{array}{ll} {\left\{ \begin{array}{ll} \big ({\mathcal {I}}-\mu _2\delta _z^2\big )E_{ijm}^n = E_{ijm}^{n-\frac{1}{3}} ,\quad 1\le m\le M_3-1,\quad n=1, \ldots , N, \\ E_{ij0}^n = 0, E_{ijM_3}^n = 0. \end{array}\right. } \end{array} \end{aligned}$$

(55)

3.2 Analysis of the ADI difference approach in three case

Following a similar process used in the 2D case, we only consider the convergence analysis of the proposed scheme (49)–(50). To begin with, we present the following significant lemmas.

Lemma 13

(Sun 2009; Wang and Vong 2014b) Assume that $w, v\in \mathring{\varOmega }$ and w, v are grid functions. Then it holds that

$$\begin{aligned} \begin{array}{ll} (\delta _x^2\delta _y^2w, v) = (\delta _x\delta _yw, \delta _x\delta _yv), \end{array}\\ \begin{array}{ll} (\delta _x^2\delta _z^2w, v) = (\delta _x\delta _zw, \delta _x\delta _zv), \end{array}\\ \begin{array}{ll} (\delta _y^2\delta _z^2w, v) = (\delta _y\delta _zw, \delta _y\delta _zv). \end{array} \end{aligned}$$

Lemma 14

(Sun 2009) Let us define grid functions $w, v\in \mathring{\varOmega }$. We obtain

$$\begin{aligned} \begin{array}{ll} (\delta _x^2\delta _y^2\delta _z^2w, v) = -(\delta _x\delta _y\delta _zw, \delta _x\delta _y\delta _zv). \end{array} \end{aligned}$$

At first, define

$$\begin{aligned} \begin{array}{ll} e_{ijm}^n := u(x_i,y_j,z_m,t_n)-U_{ijm}^n = u_{ijm}^n-U_{ijm}^n,\quad (i, j, m)\in \varrho ,\quad n=0,\,1, \ldots , N. \end{array} \end{aligned}$$

Now, we obtain the error system of equations by subtracting (49)–(50) from (47) and (48), respectively, as

$$\begin{aligned}&\begin{array}{ll} \varPhi _{l,J} \sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} e_{ijm}^{n-k} - \mu \varDelta _he_{ijm}^n-\tau ^\beta \sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\varDelta _he_{ijm}^p +\mathcal Le_{ijm}^{n-\frac{1}{2}}\\ \quad = \tau ^\beta \tilde{\omega }{_n^{(\beta )}}\varDelta _he_{ijm}^0+f_{ijm}^n + (\hat{R})_{ijm}^n, \qquad (i, j, m)\in \varrho ,\quad n=1, \ldots , N, \end{array} \end{aligned}$$

(56)

$$\begin{aligned}&\begin{array}{ll} e_{ijm}^0 = 0, \qquad (i, j, m)\in \varrho , \\ e_{ijm}^n = 0, \qquad (i, j, m)\in \iota , \quad n=0,\,1, \ldots , N. \end{array} \end{aligned}$$

(57)

Theorem 2

(Convergence). Assume that $\{u^n\}_{n=0}^{N}$ and $\{U^n\}_{n=0}^{N}$ represent the solutions of (1)–(3) and (49)–(50), respectively. If $u(x,y,z,t)\in C^{4,4,4,2}_{x,y,z,t}\big ([0, L_1]\times [0, L_2]\times [0, L_3]\times [0,T]\big )$, then we can arrive at

$$\begin{aligned} \begin{aligned} \sqrt{\tau \sum \limits _{n=1}^{N}\left\| e^n \right\| ^2} \le C(T) \Big (\tau ^2+h^2+\triangle \alpha ^2 \Big ). \end{aligned} \end{aligned}$$

Proof

We can obtain the following weak formulation employing the inner product of (56) by $\tau e^n$ and the summing from $n = 1$ to $k = M$ as well as adding small term $\tau \mu _1(e^0, e^0)$ to the both sides of (56) as

$$\begin{aligned} \begin{array}{ll} \tau \varPhi _{l,J} \sum \limits _{n=0}^N\sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} (e^{n-k},e^n)-\mu \tau \sum \limits _{n=1}^N(\varDelta _he^n,e^n)-\tau ^{1+\beta }\sum \limits _{n=1}^N\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}(\varDelta _he^p,e^n) \\ \quad - \tau ^{1+\beta }\sum \limits _{n=1}^N\tilde{\omega }{_n^{(\beta )}}(\varDelta _he^0, e^n)+ \tau (\mathcal Le_{ijm}^{n-\frac{1}{2}}, e^n) := \sum \limits _{s=1}^5\Xi _s = \tau \sum \limits _{n=1}^{N}(\hat{R}^n, e^n) + \tilde{\varepsilon }\Vert e^0\Vert ^2. \end{array} \end{aligned}$$

(58)

Below we shall estimate the terms in (58). For the first term $\Xi _1$, according to Lemma 5, we have

$$\begin{aligned} \begin{array}{ll} \tau \varPhi _{l,J} \sum \limits _{n=0}^N\sum \limits _{k=0}^{n} \lambda _{k}^{(\alpha _l)} (e^{n-k},e^n)\ge 0. \end{array} \end{aligned}$$

(59)

Then for $\Xi _2$, utilizing Poincaré inequality $\tilde{\lambda }\Vert e^n\Vert \le \Vert \nabla e^n\Vert$, we yield

$$\begin{aligned} \begin{aligned} -(\varDelta _he^n,e^n)&= -\Big ((\delta _x^2+\delta _2^2+\delta _z^2)e^n, e^n\Big )\\&= (\delta _xe^n,\delta _xe^n) +(\delta _ye^n,\delta _ye^n)+(\delta _ze^n,\delta _ze^n)\\&= \Vert \delta _xe^n\Vert ^2 + \Vert \delta _ye^n\Vert ^2+ \Vert \delta _ze^n\Vert ^2\\ :&= \Vert \nabla _h e^n\Vert ^2\ge \tilde{\lambda }^2\Vert e^n\Vert ^2 . \end{aligned} \end{aligned}$$

(60)

For $\Xi _3$, from Lemmas 10–12, we have

$$\begin{aligned} \begin{aligned} -\sum \limits _{n=1}^N\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}(\varDelta _he^p,e^n)&= \sum \limits _{n=1}^N\sum \limits _{p=1}^{n}\omega _{n-p}^{(\beta )}\big [(\delta _xe^p,\delta _xe^n)+(\delta _ye^p,\delta _ye^n)+(\delta _ze^p,\delta _ze^n)\big ]\\&\ge 0. \end{aligned} \end{aligned}$$

(61)

Next for $\Xi _4$, applying Lemma 12 (i), we arrive at

$$\begin{aligned} \begin{aligned} \tau ^{1+\beta }\sum \limits _{n=1}^N\tilde{\omega }{_n^{(\beta )}}(\varDelta _he^0, e^n)&\le \tau ^{1+\beta }\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|(\varDelta _he^0, e^n)\\&\le \tau ^{1+\beta }\Big [\frac{4\big \Vert e^0\big \Vert \Vert e^n\Vert }{h_1^2}+\frac{4\big \Vert e^0\big \Vert \Vert e^n\Vert }{h_2^2}+\frac{4\big \Vert e^0\big \Vert \Vert e^n\Vert }{h_3^2}\Big ]\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|\\&= 4\tau ^{1+\beta }\big (\frac{1}{h_1^2}+\frac{1}{h_2^2}+\frac{1}{h_3^2}\big )\sum \limits _{n=1}^N|\tilde{\omega }{_n^{(\beta )}}|\big \Vert e^0\big \Vert \Vert e^n\Vert . \end{aligned} \end{aligned}$$

(62)

Moreover, for $\Xi _5$, in view of Lemmas 13–14, we have

$$\begin{aligned} \begin{aligned} 2\tau (\delta _x^2\delta _y^2\delta _te^n,e^n)&\ge \Vert \delta _x\delta _ye^n\Vert ^2-\Vert \delta _x\delta _ye^{n-1}\Vert ^2,\\ 2\tau (\delta _x^2\delta _z^2\delta _te^n,e^n)&\ge \Vert \delta _x\delta _ze^n\Vert ^2-\Vert \delta _x\delta _ze^{n-1}\Vert ^2,\\ 2\tau (\delta _y^2\delta _z^2\delta _te^n,e^n)&\ge \Vert \delta _y\delta _ze^n\Vert ^2-\Vert \delta _y\delta _ze^{n-1}\Vert ^2,\\ -2\tau (\delta _x^2\delta _y^2\delta _z^2\delta _te^n,e^n)&\ge \Vert \delta _x\delta _y\delta _ze^n\Vert ^2-\Vert \delta _x\delta _y\delta _ze^{n-1}\Vert ^2. \end{aligned} \end{aligned}$$

(63)

Let us denote $\tau \mu _1\mu _2^2:=\mu _3=\mathcal {O}(\tau ^2|\ln \tau |), \tau \mu _1\mu _2^3:=\mu _4=\mathcal {O}(\tau ^3|\ln \tau |^2)$, then we obtain

$$\begin{aligned} \tau \sum \limits _{n=1}^N(\mathcal Le_{ijm}^{n-\frac{1}{2}}, e^n)&= \tau \mu _3\sum \limits _{n=1}^N\Big ((\delta _x^2\delta _y^2+\delta _x^2\delta _z^2+\delta _y^2\delta _z^2)\delta _te^{n-\frac{1}{2}},e^n\Big )\nonumber \\&\quad -\tau \mu _4\sum \limits _{n=1}^N(\delta _x^2\delta _y^2\delta _z^2\delta _te^{n-\frac{1}{2}},e^n)\nonumber \\&= \mu _3\sum \limits _{n=1}^N\Big ((\delta _x^2\delta _y^2+\delta _x^2\delta _z^2+\delta _y^2\delta _z^2)(e^n-e^{n-1}),e^n\Big )\nonumber \\&\quad - \mu _4\sum \limits _{n=1}^N\Big (\delta _x^2\delta _y^2\delta _z^2(e^n-e^{n-1}),e^n\Big )\nonumber \\&= \mu _3\sum \limits _{n=1}^N\Big ((\delta _x^2\delta _y^2+\delta _x^2\delta _z^2+\delta _y^2\delta _z^2)(e^n-e^{n-1}), \frac{e^n-e^{n-1}+e^{n-1}+e^n}{2}\Big )\nonumber \\&\quad -\mu _4\sum \limits _{n=1}^N\Big (\delta _x^2\delta _y^2\delta _z^2(e^n-e^{n-1}),\frac{e^n-e^{n-1}+e^{n-1}+e^n}{2}\Big )\nonumber \\&\ge \frac{\mu _3}{2}\Big [\Vert \delta _x\delta _ye^N\Vert ^2-\Vert \delta _x\delta _ye^0\Vert ^2+\Vert \delta _x\delta _ze^N\Vert ^2-\Vert \delta _x\delta _ze^0\Vert ^2+\Vert \delta _y\delta _ze^N\Vert ^2\nonumber \\&\quad -\Vert \delta _y\delta _ze^0\Vert ^2\Big ]+\frac{\mu _4}{2}\Big [\Vert \delta _x\delta _y\delta _ze^N\Vert ^2-\Vert \delta _x\delta _y\delta _ze^0\Vert ^2\Big ]. \end{aligned}$$

(64)

Finally, employing Cauchy–Schwarz inequality and Young inequality $ab\le \varepsilon a^2+\frac{1}{4\varepsilon }b^2 (a,b\in \mathbb R,\varepsilon >0)$, we arrive at

$$\begin{aligned} \begin{aligned} \tau \sum \limits _{n=1}^{N}(R^n, e^n)\le \tau \sum \limits _{n=1}^{N}\big \Vert R^n\big \Vert \Vert e^n\Vert \le \frac{\mu \tilde{\lambda }^2}{3}\sum \limits _{n=1}^N\Vert e^n\Vert ^2+\frac{3}{4\mu \tilde{\lambda }^2}\sum \limits _{n=1}^N\Vert R^n\Vert ^2 . \end{aligned} \end{aligned}$$

(65)

Substituting (59)–(65) into (58) and noticing $e^0 = 0$, we can obtain

$$\begin{aligned} \begin{aligned} \tilde{\lambda }^2\tau \mu \sum \limits _{n=1}^N\Vert e^n\Vert ^2 \le \frac{\tau \mu \tilde{\lambda }^2}{3}\sum \limits _{n=1}^N\Vert e^n\Vert ^2+\frac{3\tau }{4\mu \tilde{\lambda }^2}\sum \limits _{n=1}^N\Vert R^n\Vert ^2 . \end{aligned} \end{aligned}$$

(66)

After simplification, we can get

$$\begin{aligned} \begin{aligned} \frac{2\mu \tilde{\lambda }^2}{3}\tau \sum \limits _{n=1}^N\Vert e^n\Vert ^2 \le \frac{3}{4\mu \tilde{\lambda }^2}\tau \sum \limits _{n=1}^N\Vert R^n\Vert ^2. \end{aligned} \end{aligned}$$

(67)

Thus, we obtain

$$\begin{aligned} \begin{aligned} \tau \sum \limits _{n=1}^N\Vert e^n\Vert ^2&\le C \tau \sum \limits _{n=1}^N\Vert R^n\Vert ^2\\&\le C(T)\Big (\tau ^2+h_1^2+h_2^2+h_3^2+\triangle \alpha ^2\Big )^2, \end{aligned} \end{aligned}$$

(68)

which finishes the proof. $\square$

Table 1 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated time convergence orders $\mathrm{Order}^1_\tau$ and CPU run times (in s) by c $h=\frac{1}{64}$, $\triangle \alpha =\frac{1}{128}$ and $q= 2$

Table 2 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated time convergence orders $\mathrm{Order}^1_\tau$ and CPU run times (in s) by taking $h=\frac{1}{64}$, $\triangle \alpha =\frac{1}{128}$ and $q = 3$

4 Numerical results and discussion

This section presents two test problems to show the accuracy and computational efficiency of the proposed algorithm. Here, the ADI schemes (24)–(25) and (49)–(50) are adopted to approximate the problem (1)–(3). Let $M_1=M_2=M_3=M=\frac{L}{h}$ with $L=1$ , $T=0.5$ and $\mu =0.5$. For this aim, we calculate the maximum error and associated convergence orders as

$$\begin{aligned} \begin{array}{cc} E(\tau ,h,\varDelta \alpha ):= \max \limits _{1\le n \le N}\Vert u^n-U^n \Vert _{\infty }, \qquad ~ \mathrm{Order}^1_\tau :=\log _2\Big (\frac{E(\tau ,h,\varDelta \alpha )}{E(\tau /2,h,\varDelta \alpha )}\Big ),\\ \mathrm{Order} ^2_h:=\log _2\Big (\frac{E(\tau ,h,\varDelta \alpha )}{E(\tau ,h/2,\varDelta \alpha )}\Big ),\qquad ~~~~~~~~~\mathrm{Order}^3_{\varDelta \alpha }:=\log _2\Big (\frac{E(\tau ,h,\varDelta \alpha )}{E(\tau ,h,\varDelta \alpha /2)}\Big ). \end{array} \end{aligned}$$

Numerical computations have been done in Matlab environment with a desktop computer with Windows 10 and RAM 16 GB.

Example 1

Let us consider the two-dimensional problem (1)–(3) including an analytic solution

$$\begin{aligned} u(x,y,t)= t^q \sin (\pi x) \sin (\pi y), \end{aligned}$$

such that the weight function and the source term are

$$\begin{aligned} \omega (\alpha )=\varGamma (1+q-\alpha ),\\ \begin{array}{ll} f(x,y,t)= t^{q-1} \Big (\varGamma (q+1)(1-t)(\ln (\frac{1}{t}))^{-1}+2\mu t\pi ^{2}+\frac{2t^{1+\beta }\varGamma (q+1)\pi ^{2}}{\varGamma (1+\beta +q)} \Big ) \sin (\pi x) \sin (\pi y), \end{array} \end{aligned}$$

respectively.

We solve this example with various values of parameters at total time T based on the proposed method in the temporal and spatial dimensions. Tables 1 and 2 report the maximum absolute errors, associated time convergence orders and CPU run times (in s) when the space and distribution step sizes are fixed. It is seen that the proposed algorithm (49)–(50) is second-order convergent in the time direction. Tables 3 and 4 list the maximum absolute errors, associated time convergence orders and CPU run times (in s) when the time and distributed-order step sizes are fixed. We observe that the proposed method (49)–(50) is second-order convergent in the spatial direction. Table 5 displays the maximum absolute errors, distributed orders and CPU run times (s) and reflects the second order in distributed-order. Looking at Tables 1, 2, 3, 4 and 5 as a whole, we see that the proposed method has less time-consuming in the case of the two-dimensional problem. Figure 2 depicts the temporal convergence order when $h=\frac{1}{64}$, $\triangle \alpha =\frac{1}{128}$ and $q = 2$, while Fig. 3 represents the spatial convergence order when fixed $\tau =\frac{1}{256}$ and $\triangle \alpha =\frac{1}{256}$. Finally, Fig. 4 demonstrates the distributed convergence order for fixed $\tau =\frac{1}{380}$, $h=\frac{1}{55}$ and $q = 3$.

Table 3 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated space convergence orders $\mathrm{Order}^2_h$ and CPU run times (in s) by choosing $\tau =\frac{1}{256}$, $\triangle \alpha =\frac{1}{256}$ and $q = 2$

Table 4 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated space convergence orders $\mathrm{Order}^2_h$ and CPU run times (in s) by considering $\tau =\frac{1}{256}$, $\triangle \alpha =\frac{1}{256}$ and $q = 3$

Table 5 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, distributed orders $\mathrm{Order}^3_{\triangle \alpha }$ and CPU run times (in s) with $\tau =\frac{1}{380}$, $h=\frac{1}{55}$ and $q = 3$

Fig. 1

The CPU run times with $\tau =\frac{1}{400}$, $\triangle \alpha =\frac{1}{32}$, $\mu =0.1$ and $q = 2$ for the ADI FD scheme and the SFD scheme

Fig. 2

The time convergence order with $h=\frac{1}{64}$, $\triangle \alpha =\frac{1}{128}$ and $q = 2$

Fig. 3

The space convergence order with $\tau =\frac{1}{256}$, $\triangle \alpha =\frac{1}{256}$ and $q = 2$

Fig. 4

The distributed convergence order when $\tau =\frac{1}{380}$, $h=\frac{1}{55}$ and $q = 3$

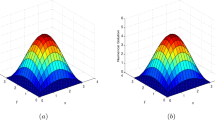
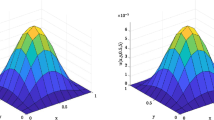
To show the efficiency of the ADI algorithm, we show the maximum errors, spatial convergence orders and CPU run times for the ADI FD scheme and the standard finite difference (SFD) scheme in Table 6. From Table 6 we can see that the errors do not have much difference between the two methods, at the same time, our ADI method has a better spatial convergence order and a shorter running time. Then we present Fig. 1, which intuitively illustrate the efficiency of the proposed method. In summary, these demonstrate the competitiveness of the ADI algorithm (Figs. 2, 3, 4).

Table 6 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, the corresponding spatial orders $\mathrm{Order}^2_{h}$ and CPU run times (in s) with $\tau =\frac{1}{400}$, $\triangle \alpha =\frac{1}{32}$, $q = 2$ and $\mu = 0.1$ for the ADI FD scheme and the SFD scheme

Example 2

Consider the three-dimensional problem (1)–(3) including an analytic solution $u(x,y,z,t)= t^q \sin (\pi x) \sin (\pi y) \sin (\pi z)$ such that the weight function and the source term are

$$\begin{aligned} \omega (\alpha )=\varGamma (1+q-\alpha ) \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} f(x,y,z,t) &{}= t^{q-1} \Big (\varGamma (q+1)(1-t)(\ln (\frac{1}{t}))^{-1}+3\mu t\pi ^{2}+\frac{3t^{1+\beta }\varGamma (q+1)\pi ^{2}}{\varGamma (1+\beta +q)} \Big ) \\ &{}\quad \sin (\pi x) \sin (\pi y) \sin (\pi z), \end{array} \end{aligned}$$

respectively.

We simulate this example with different values of parameters at total time T based on the proposed method in the temporal and spatial dimensions. Tables 7 and 8 extract the maximum absolute errors, associated time convergence orders and CPU run times (in s) when the space and distribution step sizes are fixed. It is observed that the proposed method (49)–(50) is second-order convergent in the time direction. Tables 9 and 10 report the maximum absolute errors, associated time convergence orders and CPU run times (in s) when the time and distributed-order step sizes are fixed. It is seen that the proposed method (49)–(50) is second-order convergent in the space direction. Table 11 shows the maximum absolute errors, distributed orders and CPU run times (s) and reflects the second order in distributed-order. Looking at Tables 7, 8, 9, 10 and 11 as a whole, we observe that the proposed method has less time-consuming in the case of the three-dimensional problem.

Table 7 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated time convergence orders $\mathrm{Order}^1_\tau$ and CPU run times (in s) when $h=\frac{1}{50}$, $\triangle \alpha =\frac{1}{64}$ and $q = 2$

Table 8 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated time convergence orders $\mathrm{Order}^1_\tau$ and CPU run times (in s) by considering $h=\frac{1}{50}$, $\triangle \alpha =\frac{1}{64}$ and $q = 3$

Table 9 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated space convergence orders $\mathrm{Order}^2_h$ and CPU run times (in s) by taking $\tau =\frac{1}{420}$, $\triangle \alpha =\frac{1}{64}$ and $q = 2$

Table 10 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, associated space convergence orders $\mathrm{Order}^2_h$ and CPU run times (in s) with $\tau =\frac{1}{420}$, $\triangle \alpha =\frac{1}{64}$ and $q = 3$

Table 11 Maximum absolute errors $E(\tau ,h,\varDelta \alpha )$, distributed orders $\mathrm{Order}^3_{\triangle \alpha }$ and CPU run times (in s) by choosing $\tau =\frac{1}{502}$, $h=\frac{1}{52}$ and $q = 3$

5 Concluding remarks

This paper analyzed and constructed the ADI difference approaches in two/three dimensions for distributed-order integrodifferential equations. The proposed method computed the unknown solution in two parts. First, the distributed-order time-fractional derivative and the RLFI term were approximated by using the weighted and shifted Grünwald–Letnikov expansion and second-order CQ, respectively. Second, the spatial discretization was obtained by the general centered FD method. The convergence of the ADI difference approaches was thoroughly proven and verified numerically. Numerical experiments highlighted the validity of the method and supported the theoretical predictions.