Numerical solutions of time-fractional coupled viscous Burgers’ equations using meshfree spectral method

Abstract

In this article, we compute numerical solutions of time-fractional coupled viscous Burgers’ equations using meshfree spectral method. Radial basis functions (RBFs) and spectral collocation approach are used for approximation of the spatial part. Temporal fractional part is approximated via finite differences and quadrature rule. Approximation quality and efficiency of the method are assessed using discrete $E_{2}$, $E_{\infty }$ and $E_{\text {rms}}$ error norms. Varying the number of nodal points M and time step-size $\Delta t$, convergence in space and time is numerically studied. The stability of the current method is also discussed, which is an important part of this paper.

1 Introduction

Fractional partial differential equations (FPDEs) can model various dynamical systems effectively as contrary to integer order PDEs, because fractional derivatives have memory (non-local) property (West et al. 2003; Hilfer 1995; Podlubny 1999; Mainardi 1997). The importance of investigating FPDEs having time-fractional derivatives lies in their infinitesimal generating nature of time evolution processes when considering long time scale limit. Enhancements in various concepts, such as equilibrium, stability states and evolution in long time limit, have been observed with the notion of time-fractional PDEs (Hilfer 1995, 2000; Fujita 1990). As FPDEs appear always as a challenging task in terms of finding analytical solutions, numerical methods are needed for obtaining their approximate solutions. Various methods in literature have been proposed for solutions of FPDEs. For example, Adomian decomposition method (ADM) (Chen 2008), generalized differential transform method (gDTM) (Liu and Huo 2011) and homotopy perturbation transform method (HPTM) (Hayat et al. 2013) have been used for approximate solutions of fractional Burgers’ equations. RBFs-based approximation methods were used to solve fractional Black–Scholes models (Haq and Hussain 2018), fractional KdV equations (Hussain et al. 2019) and fractional diffusion equations (Chen et al. 2010). In Mardani et al. (2018), the authors proposed moving least square approximation method for solution of fractional advection–diffusion equation with variable coefficients.

In this paper, we propose an efficient and accurate meshfree method using radial basis functions (RBFs) and spectral collocation approach for numerical solutions of the following time-fractional coupled viscous Burgers’ equations of fractional order $0<\alpha \le 1$ [taken from Hayat et al. (2013)]:

$$\begin{aligned}&\frac{\partial ^{\alpha } Y_{1}}{\partial t^{\alpha }}-\frac{\partial ^{2} Y_{1}}{\partial s^{2}} -\varepsilon Y_{1}\frac{\partial Y_{1}}{\partial s}+ \varepsilon _{1}\frac{\partial \left( Y_{1}Y_{2}\right) }{\partial s}=Z_{1}(s,t), \end{aligned}$$

(1.1)

$$\begin{aligned}&\frac{\partial ^{\alpha } Y_{2}}{\partial t^{\alpha }}-\frac{\partial ^{2} Y_{2}}{\partial s^{2}} -\varepsilon Y_{2}\frac{\partial Y_{2}}{\partial s} +\varepsilon _{2}\frac{\partial \left( Y_{1}Y_{2}\right) }{\partial s}=Z_{2}(s,t), \end{aligned}$$

(1.2)

with initial conditions

$$\begin{aligned} Y_{1}(s,0)=\phi _{1}(s),\quad Y_{2}(s,0)=\phi _{2}(s), \quad s\in \left[ \gamma _{1},\gamma _{2}\right] , \end{aligned}$$

(1.3)

and boundary conditions

$$\begin{aligned}&Y_{1}(\gamma _{1},t)=\chi _{1}(t),\ Y_{1}(\gamma _{2},t)=\chi _{2}(t),\quad \text {and} \quad Y_{2}(\gamma _{1},t)=\chi _{3}(t),\nonumber \\&Y_{2}(\gamma _{2},t)=\chi _{4}(t), \quad t\in \left( 0,t_{\max }\right] . \end{aligned}$$

(1.4)

Here, the fractional derivative is considered in Caputo sense due to its good nature of modeling a real-world phenomenon and treatment of initial conditions in the formulation of the problem-like integer case (Mainardi 1997; Caputo 1967). In the above equations, $Y_{r}=Y_{r}(s,t), \quad (r=1,2)$, s and t represent space and time variables, $t_{\max }$ is final time and $Z_{r}(s,t)$ are known functions. The constants $\varepsilon ,\ \varepsilon _{1},\ \text {and}\ \varepsilon _{2}$ represent system parameters such as Peclet number, Stokes velocity of particles due to gravity and the Brownian diffusivity (Nee and Duan 1998).

Coupled Burgers’ equations have applications in many areas of engineering and physical sciences. For instance, they have been used to model sedimentation or evolution of scaled volume concentrations of two kinds of particles in fluid suspensions or colloids under the gravitational effect (Esipov 1995). Burgers’ equations attracted attention of many researchers due to its applications in gas dynamics, heat conduction, elasticity, shock waves, shallow water waves, wave propagation in acoustics and most importantly as a test problem in validation of various numerical methods. Coupled Burgers’ equations of integer order have been solved using Haar wavelet collocation method (Kumar and Pandit 2014) and recently by fourth-order finite difference method (Bhatt and Khaliq 2016).

Various numerical methods are available in literature for solution of PDEs, such as finite difference method, finite element method and finite volume method. These methods were the pioneer, but due to high computational cost of mesh generation their use became limited. To cope with this cost, RBFs-based meshfree methods gain importance over the aforementioned methods because of their meshfree nature, simplicity in understanding, ease of implementation and spectral accuracy. Meshfree methods work for arbitrary provided scattered nodes that represent (but not discretizing) the interior and boundary of the problem domain. RBFs approximated method was developed by Kansa (1990) in solutions of various PDEs and later on used by researchers to solve other engineering and physical science problems, see e.g., (Karkowski 2013; Golbabai et al. 2014; Liew et al. 2017; Haq and Hussain 2018; Hussain et al. 2019; Chen et al. 2010).

However, high condition number of the system matrix arising from collocation creates severe issue which limits its use in practical applications. To deal with this issue and high cost of numerical integration in local form, a new technique based on point interpolation and spectral collocation approach was introduced (Liu and Gu 2005; Shivanian 2015). This approach utilized spectral method to construct differentiation matrices explicitly. For these matrices, meshfree shape functions were used, so named as meshfree spectral point interpolation method (MSRPIM). The shape functions were obtained via RBFs and point interpolation. These functions also possess Kronecker delta function property which makes implementation of the essential boundary conditions easy. This approach is quite different from the Kansa and provides accurate results with a well-conditioned system matrix (Shivanian 2015; Hussain et al. 2019).

In this study, our aim is to apply MSRPIM to numerically solve time-fractional coupled viscous Burgers’ equations. Rest of the paper is arranged as follows. in Sect. 2, we describe the proposed solution methodology for the considered problem. Section 3 is devoted to the current method’s stability. Convergence of the technique is given in Sect. 4, whereas numerical results are presented in Sect. 5. Finally the paper ends with a concise conclusion in Sect. 6.

2 Proposed solution methodology

In this part, a brief outline of the proposed meshfree method is considered. Let $Y_{r}^{n}(s)=Y_{r}(s,t_{n}),~ (r=1,2),$ where $\left\{ t_{n}=n \times \Delta t \right\} _{n=0}^{N}$ and $\Delta t=t_{\max }/N \ (N\in {\mathbb {N}})$ is time-step length. We approximate the temporal part at the $(n+1)^{th}$ time level by the formula (Chen et al. 2010):

$$\begin{aligned} \frac{\partial ^{\alpha }Y^{n+1}_{r}(s)}{ \partial t^{\alpha }} = \left\{ \begin{array}{cc} \delta _{\alpha }\sum \nolimits _{m=0}^{n} \lambda _{\alpha }(m) \left( Y_{r}^{n+1-m}(s)-Y_{r}^{n-m}(s) \right) +{\mathcal {O}}\left( {\Delta t}^{2-\alpha }\right) , \quad 0< \alpha <1,~n\ge 0,\\ \frac{Y_{r}^{n+1}(s)-Y_{r}^{n}(s)}{\Delta t}+{\mathcal {O}}\left( \Delta t \right) ,\qquad \alpha =1, ~n\ge 0, \end{array} \right. \end{aligned}$$

where $r=1,2$, $\delta _{\alpha }=\left( \Delta t\right) ^{-\alpha }/\Gamma (2-\alpha ),~ \lambda _{\alpha }(m)=\left( m+1 \right) ^{1-\alpha } - \left( m\right) ^{1-\alpha }$.

With the aid of the above relation and waiving the error term, Eqs. (1.1) and (1.2) in semi-discrete implicit form become

$$\begin{aligned}&\delta _{\alpha }\sum _{m=0}^{n} \lambda _{\alpha }(m) \left[ Y_{1}^{n+1-m}(s)-Y_{1}^{n-m}(s) \right] - \frac{\partial ^{2} Y^{n+1}_{1}(s)}{\partial s^{2}} - \varepsilon Y^{n+1}_{1}(s)\frac{\partial Y^{n+1}_{1}(s)}{\partial s} \nonumber \\&\quad =-\varepsilon _{1}\left[ Y^{n}_{1}(s)\frac{\partial Y^{n}_{2}(s)}{\partial s} + Y^{n}_{2}(s)\frac{\partial Y^{n}_{1}(s)}{\partial s} \right] + Z^{n+1}_{1}(s) , \end{aligned}$$

(2.1)

$$\begin{aligned}&\delta _{\alpha }\sum _{m=0}^{n} \lambda _{\alpha }(m) \left[ Y_{2}^{n+1-m}(s)-Y_{2}^{n-m}(s) \right] - \frac{\partial ^{2} Y^{n+1}_{2}(s)}{\partial s^{2}} - \varepsilon Y^{n+1}_{2}(s) \frac{\partial Y^{n+1}_{2}(s)}{\partial s} \nonumber \\&\quad = -\varepsilon _{2}\left[ Y^{n}_{1}(s) \frac{\partial Y^{n}_{2}(s)}{\partial s} + Y^{n}_{2}\frac{\partial Y^{n}_{1}(s)}{\partial s} \right] + Z^{n+1}_{2}(s). \end{aligned}$$

(2.2)

Linearizing the nonlinear terms in the above equations as follows:

$$\begin{aligned} Y^{n+1}_{r}(s)\frac{\partial Y^{n+1}_{r}(s)}{\partial s} = Y_{r}^{n}(s) \frac{\partial Y^{n+1}_{r}(s)}{\partial s} + Y_{r}^{n+1}(s) \frac{\partial Y^{n}_{r}(s)}{\partial s} - Y^{n}_{r}(s) \frac{\partial Y^{n}_{r}(s)}{\partial s} ,\quad (r=1,2) \end{aligned}$$

and then using in Eqs. (2.1) and (2.2), we get

$$\begin{aligned}&\delta _{\alpha }Y_{1}^{n+1}(s) - \frac{\partial ^{2} Y^{n+1}_{1}(s)}{\partial s^{2}} -\varepsilon \left[ Y_{1}^{n}(s) \frac{\partial Y^{n+1}_{1}(s)}{\partial s} + Y^{n+1}_{1}(s) \frac{\partial Y^{n}_{1}(s)}{\partial s} \right] \nonumber \\&\quad = \delta _{\alpha }Y^{n}_{1}(s) - \varepsilon Y^{n}_{1}(s)\frac{\partial Y^{n}_{1}(s)}{\partial s} \nonumber \\&\qquad - \varepsilon _{1}\left\{ Y^{n}_{1}(s)\frac{\partial Y^{n}_{2}(s)}{\partial s} + Y^{n}_{2}(s)\frac{\partial Y^{n}_{1}(s)}{\partial s} \right\} - {\mathcal {B}}_{1}^{n}(s)+ Z^{n+1}_{1}(s), \end{aligned}$$

(2.3)

$$\begin{aligned}&\delta _{\alpha } Y_{2}^{n+1}(s)- \frac{\partial ^{2} Y^{n+1}_{2}(s)}{\partial s^{2}} - \varepsilon \left[ Y_{2}^{n}(s) \frac{\partial Y^{n+1}_{2}(s)}{\partial s} + Y_{2}^{n+1}(s) \frac{\partial Y^{n}_{2}(s)}{\partial s} \right] \nonumber \\&\quad = \delta _{\alpha }Y_{2}^{n}(s) - \varepsilon Y^{n}_{2}(s)\frac{\partial Y^{n}_{2}(s)}{\partial s} \nonumber \\&\qquad - \varepsilon _{2} \left\{ Y^{n}_{1}(s) \frac{\partial Y^{n}_{2}(s)}{\partial s} + Y^{n}_{2}(s) \frac{\partial Y^{n}_{1}(s)}{\partial s} \right\} -{\mathcal {B}}_{2}^{n}(s)+ Z^{n+1}_{2}(s), \end{aligned}$$

(2.4)

where ${\mathcal {B}}_{r}^{n}(s)=\delta _{\alpha }\sum _{m=1}^{n} \lambda _{\alpha }(m) \left[ Y_{r}^{n+1-m}(s) - Y_{r}^{n-m}(s) \right]$ and ${\mathcal {B}}_{r}^{n}(s)=0$, whenever $n=0,~ (r=1,2)$. It is remarked that Eqs. (2.3) and (2.4) are the time-discrete version of Eqs. (1.1) and (1.2).

Now, we approximate the spatial part using meshfree shape functions. According to the point interpolation method (PIM), let $Y_{r}(s),~(r=1,2)$ be smooth functions approximated at the point s as:

$$\begin{aligned} Y_{1}\left( s \right)= & {} \sum _{j=1}^{M} \mu _{j} f \left( \left\| s-s_{j} \right\| \right) + \mu _{M+1}\nonumber \\= & {} \sum _{j=1}^{M} \mu _{i} f_{j}(s)+ \mu _{M+1}, \end{aligned}$$

(2.5)

and

$$\begin{aligned} Y_{2}\left( s \right) =\sum _{j=1}^{M} \nu _{j} g \left( \left\| s-s_{j} \right\| \right) + \nu _{M+1} =\sum _{j=1}^{M} \nu _{j} g_{j}(s)+ \nu _{M+1}. \end{aligned}$$

(2.6)

The matrix–vector form of the above equations is:

$$\begin{aligned} \mathbf{Y}_{1} = \mathbf{f} \Gamma _{1} \quad \Rightarrow \quad \Gamma _{1} = \mathbf{f}^{-1} \mathbf{Y}_{1} , \\ \mathbf{Y}_{2} = \mathbf{g} \Gamma _{1} \quad \Rightarrow \quad \Gamma _{2} = \mathbf{g}^{-1} \mathbf{Y}_{2} , \end{aligned}$$

where $r=1,2$, $\mathbf{Y}_{r}=[Y_{r,1},\ldots ,Y_{r,M},0]^{\texttt {T}}$, $Y_{r,j}=Y_{r}(s_{j})$, $\Gamma _{1}=[\mu _{1},\ldots ,\mu _{M+1}]^{\texttt {T}},$ $\Gamma _{2}=[\nu _{1},\ldots ,\nu _{M+1}]^{\texttt {T}}$ are vectors of expansion coefficients, $f_{j}(s), g_{j}(s)$ are given RBFs with $\left\| \cdot \right\|$ as Euclidean norm. Distinct collocation points always result in non-singularity of $\mathbf{f}$ and $\mathbf{g}$ (Micchelli 1986). For the matrices $\mathbf{f}$ and $\mathbf{g}$, the entries are

$$\begin{aligned} \mathbf{f}=\begin{bmatrix} \{f_{ij}\}_{1 \le i,j \le M}&\quad \mathbf{0} \\ \mathbf{0}^{\texttt {T}}&\quad 1 \\ \end{bmatrix}, \quad \mathbf{g}=\begin{bmatrix} \{g_{ij}\}_{1 \le i,j \le M}&\quad \mathbf{0} \\ \mathbf{0}^{\texttt {T}}&\quad 1 \\ \end{bmatrix}. \end{aligned}$$

where $\mathbf{0}^{\texttt {T}}=[0,\ldots ,0]_{M \times 1}$. So we can write Eqs. (2.5) and (2.6) in the form:

$$\begin{aligned} Y_{1}\left( s \right) = \Phi \mathbf{Y_{1}} = \sum _{j=1}^{M} {\vartheta }_{j} \left( s \right) Y_{1,j}, \quad Y_{2}\left( s \right) = \Psi \mathbf{Y_{2}} = \sum _{j=1}^{M} \psi _{j} \left( s \right) Y_{2,j}. \end{aligned}$$

(2.7)

The shape functions ${\vartheta }_{j},~\psi _{j}$ possess Kronecker delta function property

$$\begin{aligned} \vartheta _{j}(s_{i})=\delta ^{{\vartheta }}_{ij}=\left\{ \begin{array}{cc} 1 , \qquad i = j,\\ \\ 0, \qquad i \ne j, \end{array} \right. \quad \text{ and } \quad \psi _{j}(s_{i})=\delta ^{\psi }_{ij}=\left\{ \begin{array}{cc} 1 , \qquad i = j,\\ \\ 0, \qquad i \ne j. \end{array} \right. \end{aligned}$$

(2.8)

The shape functions also satisfy the following property:

$$\begin{aligned} \sum _{j=1}^{M} {\vartheta }_{j}(s)=1, \quad \text{ and } \quad \sum _{j=1}^{M} \psi _{j}(s)=1, \end{aligned}$$

where it is not necessary that $0 \le {\vartheta }_{j}(s), \psi _{j}(s) \le 1$ (Liu and Gu 2005).

Similarly, the spatial derivatives at point s are evaluated as:

$$\begin{aligned} \frac{\partial ^{l} Y_{1}(s)}{\partial s^{l}}= & {} \sum _{j=1}^{M} \frac{\partial ^{l} {\vartheta }_{j} \left( s \right) }{\partial s^{l}} Y_{1,j} = \sum _{j=1}^{M} \Phi ^{(l)}_{j}(s) Y_{1,j} , \qquad \nonumber \\ \frac{\partial ^{l} Y_{2}(s)}{\partial s^{l}}= & {} \sum _{j=1}^{M} \frac{\partial ^{l} \psi _{j} \left( s \right) }{\partial s^{l}} Y_{1,j} = \sum _{j=1}^{M} \Psi ^{(l)}_{i}(s) Y_{2,j} , \end{aligned}$$

(2.9)

where $\Phi ^{(l)}(s), ~ \Psi ^{(l)}(s)$ are the explicit differentiation matrices of lth order derivative.

Incorporating Eqs. (2.5)–(2.9) into Eqs. (2.3) and (2.4) and after simplifications, there comes

$$\begin{aligned}&\sum _{j=1}^{M} \left[ \delta _{\alpha }{\vartheta }_{j}(s) -\Phi ^{(2)}_{j}(s) - \varepsilon \left\{ a_{1}^{n}(s) \Phi ^{(1)}_{j}(s) + b_{1}^{n}(s) {\vartheta }_{j}(s) \right\} \right] Y_{1,j}^{n+1} = {\mathcal {H}}_{1}^{n+1}(s) \nonumber \\&\quad + \sum _{j=1}^{M} \left[ \delta _{\alpha } {\vartheta }_{j}(s) - \varepsilon b_{1}^{n}(s) {\vartheta }_{j}(s) - \varepsilon _{1} \left\{ b_{2}^{n}(s) {\vartheta }_{j}(s) + a_{2}^{n}(s) \Phi ^{(1)}_{j}(s) \right\} \right] Y_{1,j}^{n}, \end{aligned}$$

(2.10)

$$\begin{aligned}&\sum _{j=1}^{M} \left[ \delta _{\alpha } \psi _{j}(s) -\Psi ^{(2)}_{j}(s)- \varepsilon \left\{ a_{2}^{n}(s) \Psi ^{(1)}_{j}(s)+ b_{2}^{n}(s) \psi _{j}(s) \right\} \right] Y_{2,j}^{n+1}= {\mathcal {H}}_{2}^{n+1}(s) \nonumber \\&\quad + \sum _{j=1}^{M} \left[ \delta _{\alpha }\psi _{j}(s) - \varepsilon b_{2}^{n}(s) \psi _{j}(s) - \varepsilon _{2} \left\{ b_{1}^{n}(s) \psi _{j}(s) + a_{1}^{n}(s) \Psi ^{(1)}_{j}(s) \right\} \right] Y_{2,j}^{n}. \end{aligned}$$

(2.11)

where

$$\begin{aligned} {\mathcal {H}}_{r}^{n+1}(s) = Z^{n+1}_{r}(s) - {\mathcal {B}}_{r}^{n}(s), \quad a_{r}^{n}(s) = Y_{r}^{n}(s), \quad b_{r}^{n}(s) = \frac{\partial Y^{n}_{r}(s)}{\partial s}, \quad (r=1,2). \end{aligned}$$

Now, collocate Eqs. (2.10) and (2.11) at M collocation points $\{{s}_{i} = \gamma _{1} + (i-1) h \}_{i=1}^{M}$ such that $s_{1} = \gamma _{1}$ and $s_{M} = \gamma _{2}$ and h is the distance between two mesh points. Utilizing boundary conditions together with Eq. (2.7), we have

$$\begin{aligned} \mathbf{A } \mathbf{P }^{n+1}=\mathbf{B } \mathbf{P }^{n}+\mathbf{Q }^{n+1}, \quad \text{ and } \quad \mathbf{C } \mathbf{S }^{n+1}=\mathbf{D } \mathbf{S }^{n}+\mathbf{R }^{n+1}, \end{aligned}$$

(2.12)

where $\mathbf{P }^{n}=[Y_{1}^{n}(s_{1}), \ldots ,Y_{1}^{n}(s_{M})]^{\texttt {T}},~ \mathbf{S }^{n}=[Y_{2}^{n}(s_{1}), \ldots ,Y_{2}^{n}(s_{M})]^{\texttt {T}}$. Entries of the matrices $\mathbf{A}, \mathbf{B}, \mathbf{C}, \mathbf{D}$ for all $j \ge 1$ are listed as:

$$\begin{aligned} \mathbf{A }_{ij}= & {} \left\{ \begin{array}{cc} \left[ \delta _{\alpha } -\varepsilon b_{1}^{n}(s_{i})\right] * \delta ^{{\vartheta }}_{ij} - \Phi ^{(2)}_{ij} - \varepsilon \left\{ a_{1}^{n}(s_{i}) * \Phi ^{(1)}_{ij} \right\} ,&{} \quad i=2, \ldots ,M-1 \\ \\ \delta ^{{\vartheta }}_{ij}, \qquad \quad &{} i=1,M \end{array} \right. , \\ \mathbf{B }_{ij}= & {} \left\{ \begin{array}{cc} \left[ \delta _{\alpha } - \varepsilon b_{1}^{n}(s_{i}) - \varepsilon _{1} b_{2}^{n}(s_{i}) \right] * \delta ^{{\vartheta }}_{ij} - \varepsilon _{1} \left\{ a_{2}^{n}(s_{i}) * \Phi ^{(1)}_{ij} \right\} , \quad &{} i=2, \ldots ,M-1\\ \\ 0, &{}i=1,M \end{array} \right. , \\ \mathbf{C }_{ij}= & {} \left\{ \begin{array}{cc} \left[ \delta _{\alpha } -\varepsilon b_{2}^{n}(s_{i}) \right] * \delta ^{\psi }_{ij} - \Psi ^{(2)}_{ij} - \varepsilon \left\{ a_{2}^{n}(s_{i}) * \Psi ^{(1)}_{ij} \right\} , &{} i=2, \ldots ,M-1 \\ \\ \delta ^{\psi }_{ij}, &{} i=1, M \end{array} \right. , \\ \mathbf{D }_{ij}= & {} \left\{ \begin{array}{cc} \left[ \delta _{\alpha } - \varepsilon b_{2}^{n}(s_{i}) - \varepsilon _{2} b_{1}^{n}(s_{i}) \right] * \delta ^{\psi }_{ij} - \varepsilon _{2} \left\{ a_{1}^{n}(s_{i}) * \Psi ^{(1)}_{ij} \right\} , \quad &{} i=2, \ldots ,M-1\\ \\ 0, &{} i=1,M \end{array} \right. , \end{aligned}$$

where $*$ denotes element-wise multiplication of vector and matrix and

$$\begin{aligned} \mathbf{Q }^{n+1}=\left\{ \begin{array}{cc} {\mathcal {H}}_{1}^{n+1}(s_{i}), \quad &{}i=2, \ldots ,M-1\\ \\ G_{1}^{n+1}, &{} i=1, M \end{array} \right. , \\ \mathbf{R }^{n+1}=\left\{ \begin{array}{cc} {\mathcal {H}}_{2}^{n+1}(s_{i}), \quad &{}i=2, \ldots ,M-1\\ \\ G_{2}^{n+1}, &{} i=1, M. \end{array} \right. . \end{aligned}$$

Here,

$$\begin{aligned} G_{1}^{n+1}=[\chi _{1}(t_{n+1}),0,\ldots ,0,\chi _{2}(t_{n+1})]^{\texttt {T}}, \quad G_{2}^{n+1}=[\chi _{3}(t_{n+1}),0,\ldots ,0,\chi _{4}(t_{n+1})]^{\texttt {T}}. \end{aligned}$$

Equation (2.12) is an iterative process that advances the solution from time $t=t_{n}$ to the next time $t=t_{n+1}$. The iteration is started via the initial solution

$$\begin{aligned} \mathbf{P}^{0}=\left[ \phi _{1}(s_{i}) \}_{i=1}^{M} \right] ^{\texttt {T}}, \quad \mathbf{S}^{0}=\left[ \phi _{2}(s_{i}) \}_{i=1}^{M} \right] ^{\texttt {T}}. \end{aligned}$$

3 Stability analysis

To analyze stability of the proposed method, assume that $\mathbf{A}^{-1}$ and $\mathbf{C}^{-1}$ exist. Now, consider for $n \ge 0$ the equation

$$\begin{aligned} \mathbf{P}^{n+1}=\mathbf{A}^{-1}{} \mathbf{B} \mathbf{P}^{n} + \mathbf{A}^{-1}\mathbf{Q}^{n+1} \quad \text{ and } \quad \mathbf{S}^{n+1}=\mathbf{C}^{-1}{} \mathbf{D} \mathbf{S}^{n} + \mathbf{C}^{-1}{} \mathbf{R}^{n+1}. \end{aligned}$$

(3.1)

Define $\mathbf{e }$ as error vector of difference between exact and numerical solution. Then accordingly,

$$\begin{aligned} \mathbf{e }^{n+1}_{\mathbf{P}}=\mathbf{U }\mathbf{e }_{\mathbf{P}}^{n}, \quad \mathbf{e }^{n+1}_{\mathbf{S}}=\mathbf{V }\mathbf{e }_{\mathbf{S}}^{n}, \end{aligned}$$

(3.2)

where $\mathbf{e}^{n+1}_\mathbf{P}$ and $\mathbf{e}^{n+1}_\mathbf{S}$ are error vectors corresponding to vectors $\mathbf{P}$ and $\mathbf{S}$. It follows from Eq. (3.2) that the method produces convergent solution if for matrices $\mathbf{U}=\mathbf{A}^{-1}{} \mathbf{B}$ and $\mathbf{V}=\mathbf{C}^{-1}{} \mathbf{D}$, one has the stability criterion

$$\begin{aligned} \left\| \mathbf{U } \right\| \le 1 \quad \text{ and } \quad \left\| \mathbf{V } \right\| \le 1. \end{aligned}$$

These matrices are called amplification matrices and $\left\| \mathbf{U} \right\| =\rho (\mathbf{U}), ~\left\| \mathbf{V} \right\| =\rho (\mathbf{V})$ in case when these matrices are normal. However, the inequalities $\rho (\mathbf{U })\le \left\| \mathbf{U } \right\|$ and $\rho (\mathbf{V })\le \left\| \mathbf{V } \right\|$ always hold true, where $\rho$ denotes spectral radius of a matrix. The elements of these matrices mainly depend on the ratio:

$$\begin{aligned} \frac{h^{k}}{\Delta t}, \end{aligned}$$

where k is the order of highest spatial derivative in a given PDE. Thus to keep this ratio constant, for h to be small enough, one must have $\Delta t \rightarrow 0$. Hence, for given values of $h~ (\text {or}~ M)$ and $\Delta t$, we shall computationally establish the stability criterion of the proposed method in case of parameter base RBFs. It will be shown in Sect. 5 that there always exists an interval of shape parameters in which stable and accurate computation can be achieved, and where the solution converges.

4 Convergence analysis

In this section, we analyze the convergence of the proposed method. To achieve our goal, we use the idea of Mardani et al. (2018).

First, recall that in time discretization formula (first equation in Sect. 2) the truncation error is of ${\mathcal {O}}(\Delta t^{2-\alpha })$. For error estimations in functions and their derivatives using RBFs, let ${\mathbb {D}}^{k}$ be multi-indexed differential operator defined by

$$\begin{aligned} {\mathbb {D}}^{k}= \frac{\partial ^{\left| k\right| }}{({\partial s_{1}})^{k_{1}}\dots ({\partial s_{q}})^{k_{q}}}, \quad | k|=k_{1}+ k_{2}+\cdots +k_{q},~ q\in {\mathbb {N}}. \end{aligned}$$

Assume ${\mathcal {N}}_{\varphi }\left( \Omega \right)$ to be the native space of RBFs and $Y \in {\mathcal {N}}_{\varphi }\left( \Omega \right)$. Also, let $\ell \in {\mathbb {N}}$ and $|k| \le \ell ,$ then according to Fasshauer (2007), we have

$$\begin{aligned} \left| {\mathbb {D}}^{k}Y^{*}(s)- {\mathbb {D}}^{k}Y(s) \right| \le {\mathcal {C}} h^{\ell -\left| k \right| } \left| Y^{*}(s) \right| _{{\mathcal {N}}_{\varphi }\left( \Omega \right) }, \quad k \in {\mathbb {N}}\cup \left\{ 0\right\} , \end{aligned}$$

where $Y^{*}$ is exact and Y is an approximate function, and ${\mathcal {C}}$ is a constant depending on $\ell$. Similarly, for $\varphi \in C^{2k}(\Omega \times \Omega ),$ the following holds: (Fasshauer 2007)

$$\begin{aligned} |Y^{*}(s)-{\mathcal {I}}_{Y}(s)| \le {\mathcal {C}}_1 h^{k} \sqrt{{\mathcal {C}}_{\varphi } (s)} ||Y^{*}(s)||_{{\mathcal {N}}_{\varphi }\left( \Omega \right) }, \end{aligned}$$

where ${\mathcal {I}}_{Y}(s)$ is interpolating function, and $h \le h_{0}$ and ${\mathcal {C}}_1,~ h_{0}$ are positive constants independent of $s,Y,\varphi$. Here, ${\mathcal {C}}_{\varphi }(s)$ is a function that depends on ${\mathbb {D}}^{k}$ and h . For instance, if $\varphi (s)=s$ and $\varphi (s)=s^{2}\log {s}$, the approximation order is ${\mathcal {O}}(h)$ and ${\mathcal {O}}(h^{2}),$ respectively. Based on the above discussion, we can say that the proposed scheme is affected by temporal and spatial approximation errors of ${\mathcal {O}}(\Delta t^{2-\alpha })$ and ${\mathcal {O}}(h^{\wp }),$ respectively.

Now without loss of generality, let us assume that the numerical scheme (3.1) is $\wp ^{th}$ order accurate in space. Then for exact solution vectors $\mathbf{P}^{*}, \mathbf{S}^{*}$, we have for $n \ge 0$

$$\begin{aligned} (\mathbf{P}^{*})^{n+1}=\mathbf{A}^{-1}{} \mathbf{B}(\mathbf{P}^{*})^{n} + \mathbf{A}^{-1}{} \mathbf{Q}^{n+1} + {\mathcal {O}}\left( {\Delta t}^{2-\alpha } \right) + {\mathcal {O}}\left( h^{\wp }\right) , \end{aligned}$$

and

$$\begin{aligned} (\mathbf{S}^{*})^{n+1}=\mathbf{C}^{-1}{} \mathbf{D}(\mathbf{S}^{*})^{n} + \mathbf{C}^{-1}{} \mathbf{R}^{n+1} + {\mathcal {O}}\left( {\Delta t}^{2-\alpha } \right) + {\mathcal {O}}\left( h^{\wp }\right) , \end{aligned}$$

provided $h, \Delta t \rightarrow 0$.

For error vectors $\mathbf{e}_{\mathbf{P}},~ \mathbf{e}_{\mathbf{S}}$ we can write

$$\begin{aligned} \mathbf{e}^{n+1}_{\mathbf{P}} =\mathbf{U} \mathbf{e}_{\mathbf{P}}^{n} + {\mathcal {O}}\left( {\Delta t}^{2-\alpha } +h^{\wp }\right) ,\\ \mathbf{e}^{n+1}_{\mathbf{S}} =\mathbf{V} \mathbf{e}_{\mathbf{S}}^{n} + {\mathcal {O}}\left( {\Delta t}^{2-\alpha } +h^{\wp }\right) . \end{aligned}$$

Therefore, the proposed scheme (3.1) is convergent if it satisfies Lax–Richtmyer criterion

$$\begin{aligned} \Vert \mathbf{U}\Vert \le 1, \quad \Vert \mathbf{V}\Vert \le 1. \end{aligned}$$

If we assume that the initial conditions and solutions of problem (1.1) and (1.2) are of enough smoothness then for $n \ge 0,$

$$\begin{aligned} \left\| \mathbf{e }^{n+1}_{\mathbf{P}} \right\| \le \left\| \mathbf{U }\right\| \left\| \mathbf{e }_{\mathbf{P}}^{n}\right\| +{\mathcal {C}}^{*} \left( {\Delta t}^{2-\alpha }+ h^{\wp }\right) , \quad h, \Delta t \rightarrow 0, \end{aligned}$$

and

$$\begin{aligned} \left\| \mathbf{e }^{n+1}_{\mathbf{S}} \right\| \le \left\| \mathbf{V }\right\| \left\| \mathbf{e }_{\mathbf{S}}^{n}\right\| +{\mathcal {C}}_{*} \left( {\Delta t}^{2-\alpha }+ h^{\wp }\right) , \quad h, \Delta t \rightarrow 0, \end{aligned}$$

where ${\mathcal {C}}^{*}$ and ${\mathcal {C}}_{*}$ are positive generic constants.

Now as $\mathbf{e }^{0}=0$ and $\mathbf{e }^{n}=0$ at boundaries, application of mathematical induction yields

$$\begin{aligned} \left\| \mathbf{e }^{n+1}_{\mathbf{P}} \right\| \le \left( 1+ \left\| \mathbf{U }\right\| +\cdots +\left\| \mathbf{U }\right\| ^{n-1} \right) {\mathcal {C}}^{*} \left( {\Delta t}^{2-\alpha }+ h^{\wp }\right) ,\\ \left\| \mathbf{e }^{n+1}_{\mathbf{S}} \right\| \le \left( 1+ \left\| \mathbf{V }\right\| +\cdots +\left\| \mathbf{V }\right\| ^{n-1} \right) {\mathcal {C}}_{*} \left( {\Delta t}^{2-\alpha }+ h^{\wp }\right) . \end{aligned}$$

Implying that

$$\begin{aligned} \left\| \mathbf{e }^{n+1}_{\mathbf{P}} \right\| \le n {\mathcal {C}}^{*} \left( {\Delta t}^{2-\alpha }+ h^{\wp }\right) , \quad \text{ and } \quad \left\| \mathbf{e }^{n+1}_{\mathbf{S}} \right\| \le n {\mathcal {C}}_{*} \left( {\Delta t}^{2-\alpha }+ h^{\wp }\right) , \quad \forall n \ge 0. \end{aligned}$$

This proves the convergence of the proposed method.

5 Computational results

Here, the method implementation for the viscous Burgers’ equations considered in Sect. 1 is demonstrated. The approximation quality and efficiency of the method are measured in terms of discrete error norms:

$$\begin{aligned} {E}_{2}{:}{=}\left\| Y_{r}^{*}-Y_{r} \right\| _{2} = \sqrt{h \sum _{i=1}^{M}\left( Y_{r}^{*}-Y_{r} \right) ^{2}},\quad {E}_{\infty }{:}{=}\left\| Y_{r}^{*}-Y_{r}\right\| _{\infty } =\max _{1\le i\le M} \left| Y_{r}^{*}- Y_{r} \right| \end{aligned}$$

and

$$\begin{aligned} {E}_{\text {rms}}=\sqrt{\left( 1/M \right) \sum _{l=1}^{M}\left( Y_{r}^{*}- Y_{r} \right) ^{2}}. \end{aligned}$$

Here, $Y_{r}^{*},Y_{r} ~(r=1,2)$ denote the exact and computed solutions, respectively.

In this work, the following RBFs are used:

• 1. Multi quadric (MQ):

  $$\begin{aligned} f_{ij}=\sqrt{\xi _{ij}^2+\kappa _{1}^{2}}, \quad g_{ij}=\sqrt{\xi _{ij}^2+\kappa _{2}^{2}}. \end{aligned}$$

• 2. Inverse quadric (IQ):

  $$\begin{aligned} f_{ij} = \left( \xi _{ij}^2+\kappa _{1}^{2} \right) ^{-1}, \quad g_{ij} = \left( \xi _{ij}^2+\kappa _{2}^{2} \right) ^{-1}. \end{aligned}$$

• 3. Gaussian (Gs):

  $$\begin{aligned} f_{ij} = \exp \left( -\kappa _{1}( \xi _{ij}^{2}) \right) , \quad g_{ij} = \exp \left( -\kappa _{2}( \xi _{ij}^{2}) \right) , \end{aligned}$$

where $\{ \xi _{ij}=\left\| s_{i}-s_{j} \right\| \}_{i,j=1}^{M}$ and $\kappa _{1,2} \in {\mathbb {R}}^{+}$ are shape parameters. The accuracy and numerical stability of the discussed method mainly depend on this parameter (Liu and Gu 2005). Thus for approximation quality and numerical stability of the method, it is sufficient to find values of $\kappa$’s for which the method remains stable and produces a convergent solution. To do so, we let

$$\begin{aligned} \kappa _{r}=c_{r} \times h, \quad (r=1,2), \end{aligned}$$

where $c_{1,2}$’s are positive real numbers.

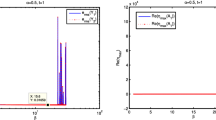
In Figs.  1 and  2, the stability condition of the proposed method is shown for MQ and IQ RBFs by taking $h=0.1,~ \Delta t=0.01,~ M=10,~ \alpha =0.5$ against $c_{1}$ and $c_{2}$. From the displayed figures, it is clear that the present method produces convergent solution as long as the spectral radius is less than unity. One thing from these figures can be deduced that over the stability intervals, all the error curves drop down to a minimum where the best value of $c_{i}$s occur. After that the curves start to rise and show constant behavior. Also, error curves start fluctuating when the stability criterion is violated. Moreover MQ has a smaller stability interval in contrast to IQ RBF in both cases. The spectral radius is less than unity for $1< c_{1,2} < 20$ in case of MQ and $1< c_{1,2} < 25$ in case of IQ RBF.

Computer simulations are performed in the spatial interval [0, 1] and time interval $[0,t_{\max }]$ for all test examples unless mentioned otherwise.

Problem 1 Consider the time-fractional Burgers’ equations (1.1), (1.2) with $\varepsilon =2$ and $\varepsilon _{1}=\varepsilon _{2}=1$. The exact solution is

$$\begin{aligned} Y_{r}(s,t)=\sin (s){\mathcal {M}}_{\alpha ,1}\left( -t^{\alpha } \right) , \quad (r=1,2), \end{aligned}$$

where ${\mathcal {M}}_{a,b}\left( \cdot \right)$ is the generalized Mittag–Leffler function defined as:

$$\begin{aligned} {\mathcal {M}}_{a,b}\left( z\right) = \sum _{k=0}^{\infty }\frac{z^{k}}{\Gamma \left( ka + b \right) }, \quad {\mathcal {M}}_{1,1}\left( z\right) = \exp (z), \quad \forall z \in {\mathbb {C}}, \ a,b \in {\mathbb {R}}. \end{aligned}$$

(5.1)

The initial conditions are $Y_{r}(s,0)=\sin (s) ~ (r=1,2)$, whereas the boundary conditions are extracted from the exact solution. By setting $M = 10,~ \Delta t = 0.01,$ the values of shape parameters are obtained as MQ: $c_{1,2}=15.6$ and IQ: $c_{1,2}=10$ for $\alpha =0.2,0.5,0.7,0.9$. The proposed method is examined up to $t_{\max }=2$ and the obtained results are recorded in Table 1 at various time levels. As the problem is symmetric and so is the solution, the error norms are the same for both the solution vectors $Y_{1},Y_{2}$ and hence tabulated once. By examining Table 1, one can see that MQ and IQ RBFs produce almost the same accurate results. For different values of nodal points M and step-size $\Delta t,$ the computed maximum error norms are summarized in Table 2 when $\alpha =0.5$. This table shows that high accuracy is attainable by increasing M and decreasing $\Delta t$ values indicating convergence of the technique. Moreover, for $\alpha =0.7$ at $t_{\max }=1$, Table 3 shows error rates (E.R.) in time computed via the formula:

$$\begin{aligned} \text{ E.R. }=\frac{E_{\infty }(\Delta t_{i})}{E_{\infty }(\Delta t_{i+1})}, \end{aligned}$$

where $E_{\infty }(\Delta t_{i})$ is the maximum observed error at time-step $\Delta t_{i}$. The stability of the proposed method is demonstrated for $\alpha =0.5$ and depicted in Fig. 1 for MQ and IQ RBFs for given $M=10$ and $\Delta t=0.01$. Next, a large spatial domain [0, 10] is taken to check the efficiency of the method and computer simulation is performed up to $t_{\max }=10$. The outcomes are displayed in Table 4 depicting the performance of the method. Various error norms for $\alpha =0.9$ using MQ and IQ RBFs with $c_{1,2}=10$, $M=100,~ \Delta t=0.01$ are reported there. It is observed that even for large time, accuracy is well maintained as earlier observed and both RBFs produced error norms of the same magnitude.

Table 1 Error norms at indicated times and RBFs for various $\alpha$s corresponding to Problem 1

Table 2 Maximum error norms for different values of M and $\Delta t$ at $t_{\max }=1$ corresponding to Problem 1

Table 3 Error norms and error rates in Problem 1 for different values of $\Delta t$ at $t_{\max }=1,~ M=10$

Fig. 1

Spectral radii and error norms corresponding to Problem 1 when $M=10, \Delta t= 0.01,~ \alpha =0.5$ using IQ and MQ RBFs

Table 4 Error norms at indicated times and RBFs for $\alpha =0.9$ and $s \in [0,10]$ in Problem 1

Problem 2 Consider the time-fractional Burgers’ equations (1.1) and (1.2) with $\varepsilon =2$ and $\varepsilon _{1}=\varepsilon _{2}=1$. The exact solution is

$$\begin{aligned} Y_{r}(s,t)=\cos (s){\mathcal {M}}_{\alpha ,1}\left( -t^{\alpha } \right) , \quad (r=1,2). \end{aligned}$$

where ${\mathcal {M}}_{a,b}\left( \cdot \right)$ is the Mintag–Leffler function. The initial conditions are $Y_{r}(s,0)=\cos (s) ~ (r=1,2)$, whereas the boundary conditions are taken from the exact solution. By setting $M = 10,~ \Delta t = 0.01,$ the values of $c_{1,2}$s are obtained as MQ: $c_{1,2}=15.6$ and IQ: $c_{1,2}=10$ for $\alpha =0.2,0.5,0.7,0.9$. The proposed method is examined when $t_{\max }=2$ and error norms are recorded in Table 5 at various time levels. Again as the problem is symmetric and so is the solution, the error norms are same for both the solution vectors $Y_{1},Y_{2}$ and hence tabulated once. By examining Table 5, once again MQ and IQ RBFs give almost the same accurate results. For $\alpha =0.5$ in Table 6, maximum error norms are reported by varying the number of nodal points M and time-step size $\Delta t$. Again as previously observed, good accuracy is attainable with the decrement in $\Delta t$ and increment in M showing that the technique is convergent. Similarly, Table 7 shows E.R. along with $E_{\infty }$ and $E_{\text {rms}}$ error norms when $\alpha =0.7$. The stability of the method is demonstrated for $\alpha =0.5$ and presented in Fig. 2 for IQ and MQ RBFs. To validate the effectiveness of the proposed method, once again computation is done in space interval [0, 10]. Simulation is carried out up to $t_{\max }=10$ using MQ and IQ RBFs. The obtained results are shown in Table 8 for $\alpha =0.7, \Delta t=0.01, M=100$. From this table, it is clear that for large time, accuracy is maintained as observed earlier.

Table 5 Error norms at indicated times and RBFs for various $\alpha$s corresponding to Problem 2

Table 6 Maximum error norms for different values of M and $\Delta t$ when $t=1$ corresponding to Problem 2

Table 7 Error norms and error rates in Problem 2 for different values of $\Delta t$ at $t=1,~ M=10$

Table 8 Error norms at indicated times and RBFs for $\alpha =0.7$ and $s \in [0,10]$ in Problem 2

Fig. 2

Spectral radii and error norms corresponding to Problem 2 when $M=10, \Delta t =0.01,~ \alpha =0.5$ using IQ and MQ RBFs

Problem 3 Now consider the non-symmetric time-fractional Burgers’ equations as:

$$\begin{aligned} \frac{\partial ^{\alpha } Y_{1}}{\partial t^{\alpha }}+\frac{\partial ^{2} Y_{1}}{\partial s^{2}} -2 Y_{1}\frac{\partial Y_{1}}{\partial s} - \frac{\partial \left( Y_{1}Y_{2}\right) }{\partial s} =Z_{1}(s,t),\\ \frac{\partial ^{\alpha } Y_{2}}{\partial t^{\alpha }}-\frac{\partial ^{2} Y_{2}}{\partial s^{2}} +2 Y_{2}\frac{\partial Y_{2}}{\partial s}+ \frac{\partial \left( Y_{1}Y_{2}\right) }{\partial s} =Z_{2}(s,t), \end{aligned}$$

where

$$\begin{aligned} Z_{r}(s,t) = (-1)^{r+1} t^{1-\alpha } {\mathcal {M}}_{1,2-\alpha }(t)\sin (s) + (-1)^{r} \exp (t) \sin (s), \quad (r=1,2). \end{aligned}$$

The initial conditions are

$$\begin{aligned} Y_{r}(s,0) = (-1)^{r+1} \sin (s), \quad (r=1,2), \end{aligned}$$

whereas the boundary conditions are set according to the exact solution $Y_{r}(s,t) = (-1)^{r+1} \sin (s) \exp (t),~ (r=1,2)$. This problem is solved for $\alpha =0.2,0.6$ using IQ: $c_{1,2}=2.01$ and Gs: $c_{1,2}=389$ RBFs with $\Delta t =0.05$ and $M=10$. It is noted that the error norms are the same for both the components and thus summarized once in Table 9. At different time levels for $(s,t) \in [0,1] \times [0,1],$ the table shows reasonable accuracy. Table 10 presents variation of maximum error norms obtained while varying $M \in \{10,20,25\}$ and $\Delta t \in \{0.1,0.05,0.01\}$ at $t=0.5$ using MQ RBF. From the table, it is clear that the proposed method is convergent. Figure 3 shows the absolute errors and solution profiles when $\alpha = 0.2,0.6$. The obtained results indicate reasonable accuracy achieved by the proposed method.

Table 9 Error norms at indicated times and RBFs for various $\alpha$s corresponding to Problem 3

Table 10 Maximum error norms for different values of M and $\Delta t$ at $t=0.5$ corresponding to Problem 3

Fig. 3

Space-time solution profiles and absolute errors corresponding to Problem 3

Table 11 Comparison of reaction dominated case at indicated nodes using MQ RBF corresponding to Problem 4

Table 12 Comparison of diffusion dominated case at indicated nodes using MQ RBF corresponding to Problem 4

Table 13 Error norms in Problem 4 using MQ, IQ and Gs RBFs at different time levels for $\alpha =0.9$

Problem 4 Now, we consider the following coupled time-fractional PDEs (Mittal and Jiwari 2016):

$$\begin{aligned} \frac{\partial ^{\alpha } Y_{1}}{\partial t^{\alpha }} -\varepsilon \frac{\partial ^{2} Y_{1}}{\partial s^{2}} + \varepsilon _{1} Y_{1} - Y_{2} = Z_{1}(s,t),\\ \frac{\partial ^{\alpha } Y_{2}}{\partial t^{\alpha }} -\varepsilon \frac{\partial ^{2} Y_{2}}{\partial s^{2}} + \varepsilon _{2} Y_{2} = Z_{2}(s,t), \end{aligned}$$

where $Z_{r}(s,t),~ (r=1,2)$ are adjusted so that the equations satisfy the solution given by:

$$\begin{aligned} Y_{1}(s,t)= & {} \left[ \exp (-(\varepsilon +\varepsilon _{1})t) + \exp (-(\varepsilon +\varepsilon _{2})t) \right] \cos (s), \\ Y_{2}(s,t)= & {} (\varepsilon _{1}-\varepsilon _{2}) \exp (-(\varepsilon +\varepsilon _{2})t) \cos (s). \end{aligned}$$

The initial and boundary conditions are extracted from the exact solution. With the help of the proposed method, this problem is solved for two sets of parameters: $\varepsilon =0.001, \varepsilon _{1}=0.1, \varepsilon _{2}=0.01$ (reaction dominated case) and $\varepsilon =1, \varepsilon _{1}=0.1, \varepsilon _{2}=0.01$ (diffusion dominated case), when $\alpha =1$ and $M=20,~ \Delta t = 0.01,0.001$. In Tables 11 and 12, the computed solutions are matched with the exact solution as well as with those reported in Mittal and Jiwari (2016). For comparison purpose, we have set $(s,t) \in [0,\pi /2] \times [0,0.1]$. From these tables, one can clearly see that the current approach produces more accurate solutions than (Mittal and Jiwari 2016) with less number of nodal points and time steps. Moreover, in Table 13, error norms are reported for the reaction and diffusion dominated cases at $t_{\max }=0.1$ when $\alpha =0.9$ and $s \in [0,\pi ]$. For convergence of the method, we present variation of maximum error norms achieved via varying $M \in \{10,20,25\}$ and $\Delta t \in \{0.05,0.01,0.001\}$ at $t=0.1$ using MQ RBF in Table 14. Solution behavior is pictured in Fig. 4 at $t_{\max }=0.1$ for the reaction and diffusion domination when $\alpha =0.9$.

Fig. 4

Solution profiles for $\alpha =0.9$ corresponding to Problem 4

Table 14 Maximum error norms for different values of M and $\Delta t$ at $t=0.1$ corresponding to Problem 4 via MQ RBF

Problem 5 Finally, we consider the time-fractional Burgers’ equations (1.1) and (1.2) with $\varepsilon =20$ and $\varepsilon _{1}=\varepsilon _{2}=1$. The initial conditions are

$$\begin{aligned} Y_{1}(s,0)=\left\{ \begin{array}{cc} \sin (2 \pi s), &{} 0 \le s \le 0.5, \\ \\ 0, &{} 0.5< s \le 1, \end{array} \right.&Y_{2}(s,0)=\left\{ \begin{array}{cc} 0,&{} 0 \le s \le 0.5, \\ \\ -\sin (2 \pi s), &{} 0.5 < s \le 1, \end{array} \right. \end{aligned}$$

whereas the boundary conditions are set to zero. Computer simulation is run up to $t_{\max }=0.1$ for $\alpha =0.6,0.9,1$ by setting $M=500$ and $\Delta t=0.025$. Since the exact solution in not known, the maximum error is calculated using the formula (Bhatt and Khaliq 2016):

$$\begin{aligned} \max | Y_{1}(\Delta t)- Y_{1}(\Delta t /2) |, \end{aligned}$$

by varying $\Delta t$. The obtained results are recorded in Table 15 for $\alpha =1$ in comparison with those of Bhatt and Khaliq (2016) at $t_{\max }=0.1$. From the table, one can easily notice that the current approach is better than Krogstad-P22, while less accurate than ETDRK4-P13. The spectral radii are also provided in Table 15 showing the method’s stability for all the given time step sizes. Table 16 presents the variation of maximum error norms at $t=0.1$ and $\alpha =1$ obtained via varying $M \in \{5,10,20,40,80,160\}$ using $\Delta t =0.025$. The maximum error in space is computed using

$$\begin{aligned} \max | Y_{r}(M)- Y_{r}(2M) |, \quad r=1,2. \end{aligned}$$

The tabulated data show that increasing M gives convergence toward a true solution. Finally, Fig. 5 gives the solution behavior at various time levels for $\alpha =0.6$ and $\alpha =0.9$, when $M=40,~ \Delta t=0.025/32$.

Table 15 Maximum error norm in Problem 5 using MQ RBF for $\alpha =1$ and $Y_{1}$

Table 16 Maximum error norm in Problem 5 using MQ RBF for $\alpha =1$ at $t=0.1$

6 Conclusion

In this article, the application of meshfree spectral interpolation method for the numerical solutions of a family of time-fractional viscous Burgers’ equations has been successfully demonstrated. Numerically computed solutions have been matched with exact solutions as well as to earlier works, showing a good agreement. For various $\alpha$s, the obtained solutions’ accuracy is highly satisfactory. Also, the stability of the proposed method fully justified the shape parameter-dependent RBFs. The reported results show the potential applicability of the proposed algorithm for obtaining accurate solutions of various potential time-dependent PDEs and FPDEs arising in engineering and applied sciences.

Fig. 5

Solution profiles correspond to Problem 5