Abstract
The constructions of entanglement-assisted quantum codes have been studied intensively by researchers. Nevertheless, it is hard to determine the number of shared pairs required for constructing entanglement-assisted quantum codes from linear codes. In this paper, by making use of the notion of decomposition for defining sets of constacyclic codes, we construct several new families of entanglement-assisted quantum MDS codes from constacyclic codes, some of which are of minimum distances greater than \(q+1\). Moreover, we tabulate their parameters to illustrate what we find in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Theoretical advantages of quantum mechanics to classical mechanics led scholars to study quantum computation and communication, which caused quantum bits (qubits) to be studied in place of classical bits. However, one principal difficulty for qubits was decoherence which overthrows the information in a superposition of qubits (Shor 1995). Shor realized that this key difficulty could be coped by introducing the first quantum code that encodes one qubit to a superposition of nine qubits and corrects at most one quantum error (Shor 1995). This pioneer paper of Shor encouraged researchers to develop quantum error correcting codes (QECCs). Called CSS construction, the first systematic construction for QECCs was explored by Calderbank et al. and Steane, independently in Calderbank and Shor (1996) and Steane (1996), respectively. According to CSS construction, one can construct a QECC from binary linear codes which are nested. Later, Gottesman developed a stabilizer formalism for QECCs that defines a QECC to be a subspace of \({C^{{2^{ \otimes n}}}}\) fixed by a commutative subgroup of Pauli matrix group on binary qubits, where \({C}^{{2^{ \otimes n}}}\) is an n-fold tensor product of the two-dimensional complex vector space \(C^2\) (Gottesman 1997). Calderbank et al. (1998) turned constructing QECCs into finding self-orthogonal additive codes over the finite field of four elements with respect to trace inner product. As a generalization of the paper (Calderbank et al. 1998), Ketkar et al. (2006) defined Pauli matrices for highly states over \(F_q\) and gave a way for constructing nonbinary quantum stabilizer codes from self-orthogonal additive codes over \(F_{q^2}\) with respect to trace-alternating form, in particular, self-orthogonal linear codes over \(F_{q^2}\) with respect to Hermitian inner product. Inspired by Ketkar et al. (2006), many scholars have focused on construction of new nonbinary stabilizer quantum codes (Aly et al. 2007; Chen et al. 2015; Grassl and Rötteler 2015; He et al. 2016; Hu et al. 2015; Jin et al. 2017; Kai and Zhu 2013; Kai et al. 2014; Liqin et al. 2016; Liu et al. 2017; Yuan et al. 2017; Zhang and Chen 2014; Zhang and Ge 2015).
Brun et al. (2006) developed a new systematic method for constructing QECCs. According to the construction given by Brun et al. (2006), the requirement of self-orthogonality for linear codes over \(F_{q^2}\) was no longer needed, which allows us to quantize all linear codes over \(F_{q^2}\). The QECCs obtained via the construction presented by Brun et al. (2006) are called entanglement-assisted quantum error correcting codes (EAQECCs). An EAQECC of length n and minimum distance d over \(F_q\) is denoted by  , and this EAQECC encodes k qubits to n-channel qubits via c pairs of maximally entanglement states and corrects up to \(\lfloor {\frac{{d - 1}}{2}} \rfloor \) errors. An
, and this EAQECC encodes k qubits to n-channel qubits via c pairs of maximally entanglement states and corrects up to \(\lfloor {\frac{{d - 1}}{2}} \rfloor \) errors. An  EAQECC with \(n-k=c\) is called a maximal entanglement EAQECC. An
EAQECC with \(n-k=c\) is called a maximal entanglement EAQECC. An  EAQECC is called an entanglement-assisted quantum MDS code (EAQMDSC) if its parameters attain the entanglement-assisted singleton bound \(k \le n - 2 ( {d - 1} ) + c\). For more details for EAQECCs, we refer the readers to (Brun et al. 2006, 2014; Lai and Brun 2013; Wilde and Brun 2008). There have been many studies on the constructions for EAQECCs which improve the parameters of existing ones (Chen et al. 2017; Fan et al. 2016; Guenda et al. 2018; Li et al. 2011; Lu et al. 2018; Lv et al. 2015; Qian and Zhang 2015, 2017). Fan et al. (2016) constructed several classes of EAQMDSCs from classical MDS codes with one or more shared entangled states. Guenda et al. (2018) proved that the number of shared pairs required is associated with the hull of linear codes and, using this connection, obtained methods for constructing EAQECCs with desired amount of entanglement. Qian and Zhang (2015) constructed
EAQECC is called an entanglement-assisted quantum MDS code (EAQMDSC) if its parameters attain the entanglement-assisted singleton bound \(k \le n - 2 ( {d - 1} ) + c\). For more details for EAQECCs, we refer the readers to (Brun et al. 2006, 2014; Lai and Brun 2013; Wilde and Brun 2008). There have been many studies on the constructions for EAQECCs which improve the parameters of existing ones (Chen et al. 2017; Fan et al. 2016; Guenda et al. 2018; Li et al. 2011; Lu et al. 2018; Lv et al. 2015; Qian and Zhang 2015, 2017). Fan et al. (2016) constructed several classes of EAQMDSCs from classical MDS codes with one or more shared entangled states. Guenda et al. (2018) proved that the number of shared pairs required is associated with the hull of linear codes and, using this connection, obtained methods for constructing EAQECCs with desired amount of entanglement. Qian and Zhang (2015) constructed  EAQECCs from arbitrary [ n, k, d ] linear codes. Brun et al. (2006) also proved that there exists an
EAQECCs from arbitrary [ n, k, d ] linear codes. Brun et al. (2006) also proved that there exists an  EAQECC if there exits an \({[ {n,k,d} ]_q}\) linear code C with \(c = \mathrm{{rank}} ( {H{H^\dag }} )\), where H is the parity check matrix of the code C and \(H^\dag \) is the conjugate transpose of the matrix H. While this construction enables us to quantize all linear codes over \(F_{q^2}\), determining the parameter c, which is the number of entanglement states required, is an open problem. Li et al. (2011) proposed a solution to this problem by making use of a decompose notion for the defining sets of cyclic codes and constructed EAQECCs from cyclic codes. Then, Chen et al. (2017) extended this decompose notion for the defining sets of cyclic codes to negacyclic codes over \(F_{q^2}\) and obtained a few families of EAQMDSCs with minimum distances greater than \(q+1\). They also constructed two classes of maximal entanglement EAQECCs. Motivated from these studies, in this paper, we consider a decomposition of defining sets of constacyclic codes over \(F_{q^2}\) to determine the number of shared pairs required and, by taking advantage of this decomposition, we construct a few new families of EAQMDSs.
EAQECC if there exits an \({[ {n,k,d} ]_q}\) linear code C with \(c = \mathrm{{rank}} ( {H{H^\dag }} )\), where H is the parity check matrix of the code C and \(H^\dag \) is the conjugate transpose of the matrix H. While this construction enables us to quantize all linear codes over \(F_{q^2}\), determining the parameter c, which is the number of entanglement states required, is an open problem. Li et al. (2011) proposed a solution to this problem by making use of a decompose notion for the defining sets of cyclic codes and constructed EAQECCs from cyclic codes. Then, Chen et al. (2017) extended this decompose notion for the defining sets of cyclic codes to negacyclic codes over \(F_{q^2}\) and obtained a few families of EAQMDSCs with minimum distances greater than \(q+1\). They also constructed two classes of maximal entanglement EAQECCs. Motivated from these studies, in this paper, we consider a decomposition of defining sets of constacyclic codes over \(F_{q^2}\) to determine the number of shared pairs required and, by taking advantage of this decomposition, we construct a few new families of EAQMDSs.
EAQMDSCs constructed in this paper are as follows:
-
1.
For odd prime power \(q \equiv 3 ( {\bmod 4} )\),
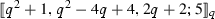 and
and 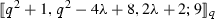 , where \(q + 1 \le \lambda \le 2q - 2\).
, where \(q + 1 \le \lambda \le 2q - 2\). -
2.
For odd prime power \(q \equiv 3 ( {\bmod 4} )\),
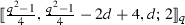 , where \(\frac{{q + 9}}{4} \le d \le q\).
, where \(\frac{{q + 9}}{4} \le d \le q\). -
3.
For odd prime power \(q \equiv 3 ( {\bmod 4} )\),
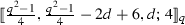 , where \(\frac{{3q + 7}}{4} \le d \le \frac{{5q + 1}}{4}\).
, where \(\frac{{3q + 7}}{4} \le d \le \frac{{5q + 1}}{4}\).
The contents of this paper are organized as follows: In Sect. 2, we present the fundamentals needed for following sections. In Sect. 3, we construct four new families of EAQMDSCs from constacyclic codes by making use of a decomposition for defining sets of constacyclic codes over \(F_{q^2}\). Moreover, by tabulating the parameters of some of EAQMDSCs that we derive, we illustrate the findings in this paper. In Sect. 4, we conclude the paper.
2 Preliminaries
Let \(F_{q^2}\) be a finite field of \(q^2\) elements. A k-dimensional subspace of the vector space \(F_{q^2}^n\) is a linear code of length n over \(F_{q^2}\) and this linear code is denoted by \({[ {n,k} ]_{q^2}}\). An \({[ {n,k} ]_{q^2}}\) linear code C is an \({[ {n,k,d} ]_{q^2}}\) linear code if C detects \(d-1\) errors but not d errors, where d is called the minimum distance of the code C. The Hermitian inner product \({\langle {x,y} \rangle _h}\) of the vectors \(x = ( {{x_1},{x_2}, \ldots ,{x_n}} )\) and \(y = ( {{y_1},{y_2}, \ldots ,{y_n}} )\) in \(F_{q^2}^n\) is \({\langle {x,y} \rangle _h} = \sum \nolimits _{i = 1}^n {{x_i}y_i^q} \). The Hermitian dual \({C^{{ \bot _h}}}\) of a linear code C over \(F_{q^2}\) of length n is the set of vectors in \(F_{q^2}^n\) which are perpendicular to all vectors in C with respect to the Hermitian inner product. A parity check matrix H of an \({[ {n,k} ]_{q^2}}\) linear code C with respect to Hermitian inner product is an \(( n - k ) \times n\) matrix whose rows constitute a basis for \({C^{{ \bot _h}}}\). Conjugate of a vector \(x = ( {{x_1},{x_2}, \ldots ,{x_n}} )\) in \(F_{q^2}^n\) is \({x^\dag } = ( {x_1^q,x_2^q, \ldots ,x_n^q} )\) and conjugate transpose of an \(m \times n\) matrix \(H = ( {{x_{i,j}}} )\) with entries in \(F_{q^2}\) is an \(n \times m\) matrix \({H^\dag } = ( {x_{j,i}^q} )\).
Let \(\alpha \) be a nonzero element in \(F_{q^2}\) with multiplicative order r. A linear code C over \(F_{q^2}\) of length n is called an \(\alpha \)-constacyclic code if \(\mu ( c ) \in C\) for all \(c \in C\), where \(\mu :F_{{q^2}}^n \rightarrow F_{{q^2}}^n\), \(\mu ( {( {{c_1},{c_2}, \ldots ,{c_n}} )} ) = ( {\alpha {c_n},{c_1}, \ldots ,{c_{n - 1}}} )\). In the case that \(\alpha =-1\), an \(\alpha \)-constacyclic code is called a negacyclic code. It is a well-known fact that an \(\alpha \)-constacyclic code C in \(F_{q^2}^n\) can be viewed as an ideal in the quotient ring \(\frac{{{F_{{q^2}}} [ x ]}}{{ \langle {{x^n} - \alpha } \rangle }}\) and so \(C = \langle {g ( x )} \rangle \) for some g(x) dividing \({x^n} - \alpha \). Let \(\left( {n,q} \right) = 1\). All roots of \({x^n} - \alpha \) over \(F_{q^2}\) are \(\gamma \), \(\gamma ^{1+r} \),..., \(\gamma ^{1+(n-1)r} \), where \(\gamma \) is an rnth primitive root of unity in some extension field of \(F_{q^2}\) and \({\gamma ^n} = \alpha \). Set \({O_{r,n}} = \{ {1,1 + r, \ldots ,1 + ( {n - 1} )r} \}\). The \(q^2\)-cyclotomic coset modulo rn containing i is the set \({C_i} = \{ {i{q^{2j}}\bmod rn:j \in N} \}\). The defining set \(Z \subseteq {O_{r,n}}\) of an \(\alpha \)-constacyclic code \(C = \langle {g ( x )} \rangle \) over \(F_{q^2}\) is the set \(Z = \{ {i \in {O_{r,n}}:g ( {{\gamma ^i}} ) = 0} \}\). The following is a lower bound for \(\alpha \)-constacyclic codes:
Theorem 1
(BCH bound for constacyclic codes) (Krishna and Sarwate 1990; Aydin et al. 2001) Let \( ( {n,q} ) = 1\). Let \(\gamma \) be an rnth primitive root of unity, such that \({\gamma ^n} = \alpha \), where \(\alpha \) is a nonzero element in \( F_{{q^2}} \) with multiplicative order r. Then, the minimum distance of an \(\alpha \)-constacyclic code of length n over \(F_{{q^2}}\) with the defining set including the set \( \{ {1 + rj,\,l \le j \le l + d - 2} \}\) is at least d.
It is well known that the Hermitian dual of an \(\alpha \)-constacyclic code over \(F_{q^2}\) is an \(\alpha ^{-q}\)-constacyclic code. Kai et al. (2014) give a necessary and sufficient condition for constacyclic codes over \(F_{q^2}\) to contain their Hermitian duals.
Lemma 1
(Kai et al. 2014) Let C be a constacyclic code of length n over \(F_{q^2}\) with defining set Z, where \(( {n,q} ) = 1\). Then, \({C^{{ \bot _h}}}\) is included by C if and only if \(Z \cap - qZ = \emptyset \).
Let c be a nonnegative integer. Via c pairs of maximally entanglement states, an  EAQECC encodes k information qubits into n qubits, and can correct up to \(\big \lfloor {\frac{{d - 1}}{2}} \big \rfloor \) errors which act on n qubits, where d is called minimum distance of the EA quantum code. From Wilde and Brun (2008), we have the following analog between linear codes over \(F_{q^2}\) and EAQECCs.
EAQECC encodes k information qubits into n qubits, and can correct up to \(\big \lfloor {\frac{{d - 1}}{2}} \big \rfloor \) errors which act on n qubits, where d is called minimum distance of the EA quantum code. From Wilde and Brun (2008), we have the following analog between linear codes over \(F_{q^2}\) and EAQECCs.
Theorem 2
(Wilde and Brun 2008) If there exists an \({ [ {n,k,d} ]_{{q^2}}}\) linear code with parity check matrix H, then there exists an EAQECC having parameters  , where \(c=\mathrm{{rank}} ( {H{H^\dag }} )\).
, where \(c=\mathrm{{rank}} ( {H{H^\dag }} )\).
Brun et al. (2006) establish a bound on the parameters of an  EAQECC.
EAQECC.
Proposition 1
(Brun et al. 2006) (Entanglement-Assisted (EA) Singleton bound) For an  EAQECC, \(k \le n - 2 ( {d - 1} ) + c\).
EAQECC, \(k \le n - 2 ( {d - 1} ) + c\).
An EAQECC satisfying EA singleton bound is called an EAQMDSC. For an  EAQECC, the number c of maximally entanglement states based on the linear codes is less than or equal to \(n-k\), and if \(c=n-k\), then this is called a maximal entanglement EAQECC.
EAQECC, the number c of maximally entanglement states based on the linear codes is less than or equal to \(n-k\), and if \(c=n-k\), then this is called a maximal entanglement EAQECC.
3 Entanglement-assisted quantum MDS codes derived from constacyclic codes
In Chen et al. (2017), by taking advantage of a decomposition of the defining sets of negacyclic codes, Jianzhang Chen et al. determine the number of entanglement states of EAQECCs obtained from negacyclic codes over \(F_{q^2}\). Then, this result is extended to constacyclic codes over \(F_{q^2}\) in Liu et al. (2018) and Lu et al. (2018).
For a constacyclic code C over \(F_{q^2}\) with defining set Z, define the sets \({Z_\beta } = \{ {i \in Z:-qi \in Z} \}\) and \({Z_\delta } = \{ {i \in Z:-qi \notin Z} \}\). Then, \(Z = {Z_\beta } \cup {Z_\delta }\), \({Z_\beta } \cap {Z_\delta } = \emptyset \) and \({Z_\beta } = Z \cap - qZ\). We call \(Z = {Z_\beta } \cup {Z_\delta }\) as a decomposition of Z. Note that constacyclic codes \(C_\beta \) and \(C_\delta \) with defining set \(Z_\beta \) or \(Z_\delta \), respectively, are codes over \(F_{q^2}\), since \(Z_\beta \) and \(Z_\delta \) are union of some \(q^2\)-cyclotomic cosets, and in this case, \(C = {C_\beta } \cap {C_\delta }\). Moreover, the definition of \(Z_\delta \) implies that \( - q{Z_\delta } \cap {Z_\delta } = \emptyset \), and by Lemma 1, \(C_\delta ^{{ \bot _h}} \subseteq {C_\delta }\). We have the following result from Liu et al. (2018) and Lu et al. (2018).
Proposition 2
(Liu et al. 2018; Lu et al. 2018) Let C be a constacyclic code over \(F_{q^2}\) with length n and defining set Z, where \(\left( {n,q} \right) = 1\), and let \(Z = {Z_\beta } \cup {Z_\delta }\) be a decomposition of Z. Then, the number c of entanglement states required for EAQECCs obtained from C is equal to \(| {{Z_\beta }} |\).
3.1 Entanglement-assisted quantum MDS codes of length \(n=q^2+1\)
In Chen et al. (2017), authors study the construction of EAQMDSCs of length \(q^2+1\) for odd prime power \(q \equiv 1\left( {\bmod 4} \right) \). However, the case \(q \equiv 3\left( {\bmod 4} \right) \) is not considered. In this section, using negacyclic codes over \(F_{q^2}\), we construct EAQMDSCs codes of length \(q^2+1\) for odd prime power q satisfying \(q \equiv 3\left( {\bmod 4} \right) \) and \(q > 3\).
Lemma 2
Let \(q>3\) be an odd prime power of the form \(q=4k+3\). Let \(n=q^2+1\) and \(s = {n / 2}\). For \(0 \le i \le \frac{{{q^2} - 1}}{4}\), all \(q^2\)-cyclotomic cosets modulo 2n containing \(s-2i\) are as follows:
-
1.
For all \(0 < i \le \frac{{{q^2} - 1}}{4}\), \({C_{s - 2i}} = \left\{ {s - 2i,s + 2i} \right\} \).
-
2.
\({C_s} = \left\{ s \right\} \).
Proof
Since \({o_{2n}}\left( {{q^2}} \right) = 2\), the size of \(q^2\)-cyclotomic coset modulo 2n is less than or equal to 2. For \(C_{s-2i}\), \(0 \le i \le \frac{{{q^2} - 1}}{4}\), it follows from \({q^2}\left( {1 + 2j} \right) \equiv 1 + 2\left( {\frac{{{q^2} - 1}}{2} - j} \right) \bmod 2n\) that \({q^2}\left( {s - 2i} \right) = {q^2}\left( {1 + 2\left( {\frac{{{q^2} - 1}}{4} - i} \right) } \right) \equiv 1 + 2\left( {\frac{{{q^2} - 1}}{4} + i} \right) = s + 2i\bmod 2n\) and so \({C_{s - 2i}} = \left\{ {s - 2i,s + 2i} \right\} \). Moreover, if \(i=0\), then \(C_s=\left\{ {s} \right\} \). \(\square \)
Lemma 3
Let \(q>3\) be an odd prime power of the form \(q=4k+3\). Let \(n=q^2+1\) and \(s = {n / 2}\). Then
-
1.
\( - q{C_s} = {C_s}\),
-
2.
\( - q{C_{s - 2\left( {q - 1} \right) }} = {C_{s - 2\left( {q + 1} \right) }}\),
-
3.
\( - qZ \cap Z = \emptyset \), where \(Z = \bigcup \nolimits _{i = 1}^\lambda {{C_{s - 2i}}} \), \(1 \le \lambda \le q - 1\),
-
4.
\( - q{C_{s - 2}} = {C_{s - 2q}}\).
Proof
-
1.
It follows from \(\left( {q + 1} \right) \frac{{{q^2} + 1}}{2} \equiv 0\bmod 2n\) that \( - q\frac{{{q^2} + 1}}{2} \equiv \frac{{{q^2} + 1}}{2}\bmod 2n\), and so, \( - q{C_s} = {C_s}\).
-
2.
Since \({q^2} \equiv - 1\bmod 2n\) and \( - qs \equiv s\bmod 2n\), \( - q\left( {s - 2\left( {q - 1} \right) } \right) \equiv s - 2\left( {q + 1} \right) \bmod 2n\). This implies that \(- q{C_{s - 2\left( {q - 1} \right) }} = {C_{s - 2\left( {q + 1} \right) }}\).
-
3.
It is enough to prove that \(- qZ \cap Z = \emptyset \) for \(Z = \bigcup \nolimits _{i = 1}^{q-1} {{C_{s - 2i}}} \). By Lemma 2, \(Z = \left\{ {s - 2\left( {q - 1} \right) ,s - 2\left( {q - 2} \right) , \ldots ,s - 2,s + 2, \ldots ,s + 2\left( {q - 2} \right) ,s + 2\left( {q - 1} \right) } \right\} \). Suppose that \( - qZ \cap Z \ne \emptyset \). Then, there exists \(s \pm 2i\), \(s \pm 2j\) for some \(1 \le i,j \le q - 1\), such that \( - q\left( {s \pm 2i} \right) \equiv s \pm 2j\bmod 2n\). This implies that \( \pm qi \pm j \equiv 0\bmod n\). However, since \(q + 1 \le qi + j \le {q^2} - 1 < n\) and \(1 \le qi - j < n - q\), there does not exist \(1 \le i,j \le q - 1\) satisfying the congruence \( \pm qi \pm j \equiv 0\bmod n\). This is a contradiction.
-
4.
It follows directly from \( - qs \equiv s\bmod 2n\) and \({C_{s - 2q}} = \left\{ {s - 2q,s + 2q} \right\} \).
\(\square \)
Let \(Z = {Z_1} \cup \left( {\bigcup \nolimits _{i = 2}^{q - 1} {{C_{s - 2i}}} } \right) \), where \({Z_1} = {C_s} \cup {C_{s - 2}} \cup {C_{s - 2q}}\). Then, by Lemma 3, it follows that \( - q{Z_1} = {Z_1}\) and \(( { - q\bigcup \nolimits _{i = 2}^{q - 1} {{C_{s - 2i}}} } ) \cap ( {\bigcup \nolimits _{i = 2}^{q - 1} {{C_{s - 2i}}} }) = \emptyset \). In this case, \(\left| { - qZ \cap Z} \right| = 5\). Take C as a negacyclic code of length \(q^2+1\) over \(F_{q^2}\) with the defining set Z. Then, C is a \({\left[ {{q^2} + 1,{q^2} - 2q,2q + 2} \right] _{{q^2}}}\) negacyclic code. Applying Theorem 2 to the negacyclic code C and using Proposition 2, we have the following:
Theorem 3
Let \(q>3\) be an odd prime power with \(q \equiv 3\left( {\bmod 4} \right) \). Then, there exists EAQMDSC with parameters  .
.
Proof
By the above argument, we have EAQECC with desired parameters. Since these parameters attain EA singleton bound, this is EAQMDSC. \(\square \)
We list parameters of some EAQMDSCs obtained via Theorem 3 in Table 1.
In addition to the EAQMDSCs obtained above, we have the following class of EAQMDSCs of length \(q^2+1\) when \(q \equiv 3\left( {\bmod 4} \right) \).
Theorem 4
Let \(q>3\) be an odd prime power with \(q \equiv 3\left( {\bmod 4} \right) \). Then, there exist EAQMDSCs with parameters  , where \(q + 1 \le \lambda \le 2q - 2\).
, where \(q + 1 \le \lambda \le 2q - 2\).
Proof
For each \(q+1 \le \lambda \le 2q - 2\), define \({Z_\lambda } = \bigcup \nolimits _{i = 0}^\lambda {{C_{s - 2i}}} \) and \(Z' = ( {\bigcup \nolimits _{i = 0}^1 {{C_{s - 2i}}} } ) \cup ( {\bigcup \nolimits _{j = q - 1}^{q + 1} {{C_{s - 2j}}} } )\). For \(\lambda = q+1\), \({Z_{q + 1}} = Z' \cup ( {\bigcup \nolimits _{i = 2}^{q - 2} {{C_{s - 2i}}} })\). Then, by Lemma 3, \(\left| {{Z_{q + 1}} \cap - q{Z_{q + 1}}} \right| = 9\). For \(q+2 \le \lambda \le 2q - 2\), we get \({Z_\lambda } = Z' \cup ( {\bigcup \nolimits _{i = 2}^{q - 2} {{C_{s - 2i}}} } ) \cup ( {\bigcup \nolimits _{j = q + 2}^\lambda {{C_{s - 2j}}} } )\). Since \( - qZ' = Z' \) by Lemma 3 (1), (2), and (4), it follows that \( - qZ_\lambda = Z' \cup ( { - q\bigcup \nolimits _{i = 2}^{q - 2} {{C_{s - 2i}}} }) \cup ( { - q\bigcup \nolimits _{j = q + 2}^\lambda {{C_{s - 2j}}} } )\). Since \(Z' \subseteq - q{Z_\lambda } \cap {Z_\lambda }\), \(| { - q{Z_\lambda } \cap {Z_\lambda }} | \ge 9\). To get the result \( | { - q{Z_\lambda } \cap {Z_\lambda }} | = 9\), we need to prove the following:
By Lemma 3 (3), the equality (1) holds. Since
if and only if
it is enough to prove (2) instead of proving both (2) and (3). Suppose that \(( { - q\bigcup \nolimits _{i = 2}^{q - 2} {{C_{s - 2i}}} } ) \cap \left( {\bigcup \nolimits _{j = q + 2}^\lambda {{C_{s - 2j}}} } \right) \ne \emptyset \). Then, there exist four cases for some integers \(2 \le i \le q - 2\) and \(q + 2 \le j \le \lambda \):
The case \( - q\left( {s - 2i} \right) \equiv s - 2j\bmod 2n\): it follows that \(qi + j \equiv 0\bmod n\). However, this contradicts with \(0< 3q + 2 \le qi + j \le {q^2} - 2 < n\).
The case \( - q\left( {s - 2i} \right) \equiv s + 2j\bmod 2n\): this implies that \(qi - j \equiv 0\bmod n\). Since \(0< 2 \le qi - j \le {q^2} - 3q - 2 < n\), this is a contradiction.
The proofs of the cases \( - q\left( {s + 2i} \right) \equiv s - 2j\bmod 2n\) and \( - q\left( {s + 2i} \right) \equiv s + 2j\bmod 2n\) are similar to the proofs of the above cases.
For (4), suppose that \(\left( { - q\bigcup \nolimits _{i = q + 2}^\lambda {{C_{s - 2i}}} } \right) \cap \left( {\bigcup \nolimits _{i = q + 2}^\lambda {{C_{s - 2i}}} } \right) \ne \emptyset \). Then, for some integers \(q + 2 \le i,j \le \lambda \), there are four cases.
The case \( - q\left( {s - 2i} \right) \equiv s - 2j\bmod 2n\): this congruence is equivalent to \(qi + j \equiv 0\bmod n\). However, this is a contradiction, since \(n< q^2+3q+2 \le qi + j \le 2q^2-2 < 2n\).
The case \( - q\left( {s - 2i} \right) \equiv s + 2j\bmod 2n\): then, \(qi - j \equiv 0\bmod n\), which contradicts with \(n< q^2+2 \le qi - j \le 2q^2-3q-2 < 2n\).
The proofs of the cases \( - q\left( {s + 2i} \right) \equiv s - 2j\bmod 2n\) and \( - q\left( {s + 2i} \right) \equiv s + 2j\bmod 2n\) are similar to the proofs of the cases \( - q\left( {s - 2i} \right) \equiv s + 2j\bmod 2n\) and \( - q\left( {s - 2i} \right) \equiv s - 2j\bmod 2n\), respectively.
Now, for each \(q+1 \le \lambda \le 2q - 2\), let \(C_{\lambda }\) be a negacyclic code of length \(q^2+1\) over \(F_{q^2}\) with the defining set \(Z_{\lambda }\). Then, \(C_{\lambda }\) is a \({\left[ {{q^2} + 1,{q^2} - 2\lambda ,2\lambda + 2} \right] _{{q^2}}}\) negacyclic code. Since \(\left| { - q{Z_\lambda } \cap {Z_\lambda }} \right| = 9\), by Theorem 2 and Proposition 2, for each \(q+1 \le \lambda \le 2q - 2\), we get EAQECC having desired parameters. Since EA singleton bound is attained, these EAQECCs are MDS. \(\square \)
We list parameters of some EAQECCs obtained via Theorem 4 in Table 2.
3.2 Entanglement-assisted quantum MDS codes of length \(\frac{{{q^2} - 1}}{4}\)
Let \(q=4m+3\) be an odd prime power with \(m\ge 1\) and \(n=\frac{{{q^2} - 1}}{4}\). Let \(\alpha \) be a \((r=4)\)th primitive root of unity over \(F_{q^2}\). Using \(\alpha \)-constacyclic codes over \(F_{q^2}\) of length \(\frac{{{q^2} - 1}}{4}\), we are going to construct EAQMDSCs of length \(\frac{{{q^2} - 1}}{4}\). We have from Zhang and Chen (2014) that each \(q^2\)-cyclotomic coset modulo rn has exactly one element; that is, \({C_{1 + 4j}} = \left\{ {1 + 4j} \right\} \), \(0 \le j \le n - 1\), since \({q^2} \equiv 1\bmod rn\).
We also have the following from Zhang and Chen (2014) with the notation \({C_{1 - 4j}} = {C_{1 + 4\left( {n - j} \right) }}\).
Lemma 4
(Zhang and Chen 2014) Let \(n=\frac{{{q^2} - 1}}{4}\) and \(r=4\), where \(q>3\) is an odd prime power of the form \(q=4m+3\). If \(Z = \bigcup \nolimits _{j = - \frac{{q - 3}}{4}}^{\frac{{q - 3}}{2}} {{C_{1 + 4j}}} \), then \( - q{Z} \cap {Z} = \emptyset \).
Since \(1 + 4\left( {n - \left( \frac{{q + 1}}{4} \right) } \right) = 4n - q \equiv - q\bmod rn\), we have the following:
Lemma 5
Let \(q=4m+3\) and \(m \ge 1\) be an odd prime power. Let \(n=\frac{{{q^2} - 1}}{4}\) and \(r=4\). For \(q^2\)-cyclotomic cosets \({C_{1}}\) and \({C_{ - \frac{{q + 1}}{4}}}\) modulo rn, we have \( - q{C_1} = {C_{ - \frac{{q + 1}}{4}}}\).
Theorem 5
Let q be an odd prime power of the form \(4m+3\), \(m \ge 1\). Then, for each integer \(\frac{{q + 9}}{4} \le d \le q\), there exists an EAQMDSC having the parameters  .
.
Proof
For each \(0 \le \lambda \le \frac{{q - 3}}{4}\) and \(0 \le \delta \le \frac{{q - 3}}{2}\), define the sets \({Z_{\lambda ,\delta }} = \bigcup \nolimits _{j = - \frac{{q + 1}}{4} - \lambda }^{\delta } {{C_{1 + 4j}}} \), \({Z_\lambda } = \bigcup \nolimits _{j = - \frac{{q + 1}}{4} - \lambda }^{ - \frac{{q + 1}}{4}} {{C_{1 + 4j}}} \) and \({Z_\delta } = \bigcup \nolimits _{j = - \frac{{q - 3}}{4}}^{ \delta } {{C_{1 + 4j}}} \). We are going to prove that \(\left| {{Z_{\lambda ,\delta }} \cap - q{Z_{\lambda ,\delta }}} \right| = 2\). Since \({Z_{\lambda ,\delta }} = {Z_\lambda } \cup {Z_\delta }\), we get
Since \({C_1} \subseteq -q{Z_\lambda } \cap {Z_\delta } \) and \({C_{ - \frac{{q + 1}}{4}}} \subseteq {Z_\lambda } \cap - q{Z_\delta }\), to get the result \(\left| {{Z_{\lambda ,\delta }} \cap - q{Z_{\lambda ,\delta }}} \right| = 2\), we are going to prove the following:
It follows from Lemma 4 that equality (7) holds. For (8), suppose that \({Z_\lambda } \cap - q{Z_\lambda } \ne \emptyset \). Then, there exist some integers \( - \frac{{q + 1}}{4} - \lambda \le i,j \le - \frac{{q + 1}}{4}\), such that \( - q\left( {1 + 4i} \right) \equiv 1 + 4j\bmod rn\). This implies that \(\frac{{q + 1}}{4} + qi + j \equiv 0\bmod n\). It follows from \( - \frac{{q - 1}}{2} \le - \frac{{q + 1}}{4} - \lambda \le i,j \le - \frac{{q + 1}}{4}\) that \( - \frac{{{q^2} - 1}}{2} + \frac{{q + 1}}{4} \le \frac{{q + 1}}{4} + qi + j \le - \frac{{{{\left( {q + 1} \right) }^2}}}{4} + \frac{{q + 1}}{4}\). This contradicts with \(\frac{{q + 1}}{4} + qi + j \equiv 0\bmod n\), since \( - 2n< - \frac{{{q^2} - 1}}{2} + \frac{{q + 1}}{4} \le \frac{{q + 1}}{4} + qi + j \le - \frac{{{{\left( {q + 1} \right) }^2}}}{4} + \frac{{q + 1}}{4} < - n\).
To prove the equality (9), for \( - \frac{{q - 3}}{4} \le j \le \delta \) we count the integer(s) \( - \frac{{q + 1}}{4} - \lambda \le i \le - \frac{{q + 1}}{4}\) satisfying \( - q\left( {1 + 4i} \right) \equiv 1 + 4j\bmod rn\) or, equivalently, \(\frac{{q + 1}}{4} + qi + j \equiv 0\bmod n\). It follows from \( - \frac{{q - 1}}{2} \le - \frac{{q + 1}}{4} - \lambda \le i \le - \frac{{q + 1}}{4}\) and \( - \frac{{q - 3}}{4} \le j \le \delta \le \frac{{q - 3}}{2}\) that \(\frac{{ - {q^2} + q + 2}}{2} \le \frac{{q + 1}}{4} + qi + j \le \frac{{ - {q^2} + 2q - 5}}{4}\). Since \( - 2n< \frac{{ - {q^2} + q + 2}}{2} \le \frac{{q + 1}}{4} + qi + j \le \frac{{ - {q^2} + 2q - 5}}{4} < 0\), the only possible value of \(\frac{{q + 1}}{4} + qi + j\) is \(-n\). The equality \(\frac{{q + 1}}{4} + qi + j = - n\) implies that \(j \equiv 0\bmod q\). Since \( - \frac{{q - 3}}{4} \le j \le \delta \le \frac{{q - 3}}{2}\), j must be 0, and so, i must be \( - \frac{{q + 1}}{4}\). This shows that \(-q{Z_\lambda } \cap {Z_\delta } = {C_1}\). Therefore, the equality (9) holds. Then, since \({Z_\lambda } \cap - q{Z_\delta } = - q\left( { - q{Z_\lambda } \cap {Z_\delta }} \right) = - q{C_1} = {C_{ - \frac{{q + 1}}{4}}}\), the equality (10) holds.
Now, for each \(0 \le \lambda \le \frac{{q - 3}}{4}\) and \(0 \le \delta \le \frac{{q - 3}}{2}\), let \(C_{\lambda ,\delta }\) be an \(\alpha \)-constacyclic code of length \(\frac{q^2-1}{4}\) over \(F_{q^2}\) with the defining set \(Z_{\lambda ,\delta }\). Then, \(C_{\lambda ,\delta }\) is an \(\alpha \)-constacyclic code with parameters \({\left[ {\frac{{{q^2} - 1}}{4},\frac{{{q^2} - 1}}{4} - d + 1,d} \right] _{{q^2}}}\), where \(d = \frac{{q + 9}}{4} + \lambda + \delta \). In this case, since \(\left| { - q{Z_{\lambda ,\delta } } \cap {Z_{\lambda ,\delta } }} \right| = 2\), by Theorem 2 and Proposition 2, for each \(\frac{{q + 9}}{4} \le d \le q\), we get an EAQECC having the parameters  . Since EA singleton bound is attained, EAQECCs that are constructed are MDS.
. Since EA singleton bound is attained, EAQECCs that are constructed are MDS.
\(\square \)
We list parameters of some EAQMDSCs obtained via Theorem 5 in Table 3.
Since \( - q\left( {1 + r\frac{{q - 3}}{4}} \right) \equiv 1 + r\frac{{q - 1}}{2}\bmod rn\), we have the following:
Lemma 6
Let \(q=4m+3\), \(m \ge 1\) be an odd prime power. Let \(n=\frac{{{q^2} - 1}}{4}\) and \(r=4\). For \(q^2\)-cyclotomic cosets \({C_{\frac{{q - 3}}{4}}}\) and \({C_{ \frac{{q - 1}}{2}}}\) modulo rn, we have \( - q{C_{\frac{{q - 3}}{4}}} = {C_{ \frac{{q - 1}}{2}}}\).
We derive another class of EAQMDSCs with length \(n=\frac{{{q^2} - 1}}{4}\), where the number of entanglement states required is \(c=4\).
Theorem 6
Let q be an odd prime power of the form \(4m+3\), \(m \ge 1\). Then, for each integer \(\frac{{3q + 7}}{4} \le d \le \frac{{5q + 1}}{4}\), there exists an EAQMDSC having the parameters  .
.
Proof
For each \(0 \le \lambda ,\delta \le \frac{{q - 3}}{4}\), define the sets \({Z_{\lambda ,\delta }} = \bigcup \nolimits _{j = - \frac{{q + 1}}{4} - \lambda }^{\frac{{q - 1}}{2} + \delta } {{C_{1 + 4j}}} \), \({Z_\lambda } = \bigcup \nolimits _{j = - \frac{{q + 1}}{4} - \lambda }^{-\frac{{q + 1}}{4}} {{C_{1 + 4j}}} \), and \({Z_\delta } = \bigcup \nolimits _{j = - \frac{{q - 3}}{4}}^{\frac{{q - 1}}{2} + \delta } {{C_{1 + 4j}}} \). We are going to prove that \(\left| {{Z_{\lambda ,\delta }} \cap - q{Z_{\lambda ,\delta }}} \right| = 4\). Since \({Z_{\lambda ,\delta }} = {Z_\lambda } \cup {Z_\delta }\), we get
To prove that \(\left| {{Z_{\lambda ,\delta }} \cap - q{Z_{\lambda ,\delta }}} \right| = 4\), it is enough to prove the following:
The equality (8) implies that the equality (11) holds. For (12), we count the integer(s) \( - \frac{{q - 3}}{4} \le j \le \frac{{q - 1}}{2} + \delta \), such that \( - q\left( {1 + 4i} \right) \equiv 1 + 4j\bmod rn\) or, equivalently, \(\frac{{q + 1}}{4} + qi + j \equiv 0\bmod n\), where \( - \frac{{q + 1}}{4} - \lambda \le i \le -\frac{{q + 1}}{4}\). It follows from \( - \frac{{q - 1}}{2} \le - \frac{{q + 1}}{4} - \lambda \le i \le -\frac{{q + 1}}{4}\) and \( - \frac{{q - 3}}{4} \le j \le \frac{{q - 1}}{2} + \delta \le \frac{{3q - 5}}{4}\) that \( - 2n< - \frac{{{q^2} - q - 2}}{2} \le \frac{{q + 1}}{4} + qi + j \le -\frac{{{q^2} - 3q +4}}{4} < 0\). This implies that the only possible value of \(\frac{{q + 1}}{4} + qi + j\) is \(-n\). If \(\frac{{q + 1}}{4} + qi + j=-n\), then \(j \equiv 0 \bmod q\). Since \( - \frac{{q - 3}}{4} \le j \le \frac{{3q - 5}}{4}\), j must be 0, and so, the equality (12) holds. Since \({Z_\lambda } \cap - q{Z_\delta } = - q\left( { - q{Z_\lambda } \cap {Z_\delta }} \right) = - q{C_1} = {C_{ - \frac{{q + 1}}{4}}}\), the equality (13) holds.
To prove the equality (14), for \( - \frac{{q - 3}}{4} \le i \le \frac{{q - 1}}{2} + \delta \) we count the integer(s) \( - \frac{{q - 3}}{4} \le j \le \frac{{q - 1}}{2} + \delta \) satisfying \( - q\left( {1 + 4i} \right) \equiv 1 + 4j\bmod rn\) or, equivalently, \(\frac{{q + 1}}{4} + qi + j \equiv 0\bmod n\). It follows from \( - \frac{{q - 3}}{4} \le i,j \le \frac{{q - 1}}{2} + \delta \le \frac{{3q - 5}}{4}\) that \( - n< - \frac{{{q^2} - 3q - 4}}{4} \le \frac{{q + 1}}{4} + qi + j \le \frac{{3{q^2} - q - 4}}{4} < 3n\). This implies that the possible values of \(\frac{{q + 1}}{4} + qi + j\) are 0, n, and 2n.
The case \(\frac{{q + 1}}{4} + qi + j=0\): Then, \(4j+1 \equiv 0 \bmod q\). Since \( - q< -q+4 \le 4j + 1 \le 3q - 4 < 3q\), \(4j+1\) can be 0, q or 2q. These cases are impossible, since j is an integer and \(q \equiv 3 \bmod 4\). Hence, there is no solution in this case.
The case \(\frac{{q + 1}}{4} + qi + j=n\): Then, \(4j+2 \equiv 0 \bmod q\). Since \( - q< -q+5 \le 4j + 2 \le 3q - 3 < 3q\), \(4j+2\) can be 0, q and 2q. The only possibility is \(4j+2=2q\). If \(4j+2=2q\), then \(j = \frac{{q - 1}}{2}\) and \(i = \frac{{q - 3}}{4}\).
The case \(\frac{{q + 1}}{4} + qi + j=2n\): Then, \(4j+3 \equiv 0 \bmod q\). Since \( - q< -q+6 \le 4j + 3 \le 3q - 2 < 3q\), \(4j+3\) can be 0, q, or 2q. The only possibility is \(4j+3=q\). If \(4j+3=q\), then \(j = \frac{{q - 3}}{4}\) and \(i = \frac{{q - 1}}{2}\).
All cases of \(\frac{{q + 1}}{4} + qi + j\) imply that \( - q{Z_\delta } \cap {Z_\delta } = {C_{ \frac{{q - 3}}{4}}} \cup {C_{ \frac{{q - 1}}{2}}} \). Hence, the equality (14) holds. Since the equalities (11), (12), (13), and (14) hold, we conclude that \(\left| {{Z_{\lambda ,\delta }} \cap - q{Z_{\lambda ,\delta }}} \right| = 4\).
Now, for each \(0 \le \lambda ,\delta \le \frac{{q - 3}}{4}\), let \(C_{\lambda ,\delta }\) be an \(\alpha \)-constacyclic code of length \(\frac{q^2-1}{4}\) over \(F_{q^2}\) with the defining set \(Z_{\lambda ,\delta }\). Then, \(C_{\lambda ,\delta }\) is an \(\alpha \)-constacyclic code with parameters \({\left[ {\frac{{{q^2} - 1}}{4},\frac{{{q^2} - 1}}{4} - d + 1,d} \right] _{{q^2}}}\), where \(d = \frac{{3q + 7}}{4} + \lambda + \delta \). In this case, since \(\left| { - q{Z_{\lambda ,\delta } } \cap {Z_{\lambda ,\delta } }} \right| = 4\), by Theorem 2 and Proposition 2, for each \(\frac{{3q + 7}}{4} \le d \le \frac{{5q + 1}}{4}\), we get an EAQECC having the parameters  . Since EA singleton bound is attained, EAQECCs that are constructed are MDS. \(\square \)
. Since EA singleton bound is attained, EAQECCs that are constructed are MDS. \(\square \)
We list parameters of some EAQMDSCs obtained via Theorem 6 in Table 4.
4 Conclusion
We derive four new families of EAQMDSCs from constacyclic codes over \(F_{q^2}\) for lengths \(q^2+1\) and \(\frac{q^2-1}{4}\). The EAQMDSCs with length \({q^2+1}\) are of minimum distance more greater than \(q+1\). When compared to quantum MDS codes existing in the literature, the EAQMDSCs with length \(\frac{q^2-1}{4}\) have large minimum distances. For instance, while  ,
,  , and
, and  quantum codes are obtained via the construction in Zhang and Chen (2014), for same length and dimensions, we get
quantum codes are obtained via the construction in Zhang and Chen (2014), for same length and dimensions, we get  ,
,  , and
, and  EAQMDSCs of larger minimum distance via Theorem 5. We present Table 5 to indicate this comparison.
EAQMDSCs of larger minimum distance via Theorem 5. We present Table 5 to indicate this comparison.
Recently, Lu et al. (2018) derived EAQMDSCs with length \(\frac{q^2-1}{at}\), where \(q=atm+1\), a is even or a is odd and t is even. We remark that this class of EAQMDSCs does not include our construction of EAQMDSCs with length \(\frac{q^2-1}{4}\) since \(q \equiv 3\left( {\bmod 4} \right) \) for our construction, but \(q=4m+1\) for the construction given in Lu et al. (2018).
Chen et al. (2017) constructed EAQMDSc with \(c=4\) and length \(\lambda \left( q+1 \right) \), where \(\lambda \ge 3\) is an odd integer dividing \(q-1\). Since \(q \equiv 3\left( {\bmod 4} \right) \) in our construction given in Theorem 6, their construction does not include ours. Moreover, they also constructed a class of EAQMDSCs of length \(q^2+1\) for odd prime power \(q \equiv 1\left( {\bmod 4} \right) \). However, the construction given in Theorems 3 and 4 is different from their construction, since \(q \equiv 3\left( {\bmod 4} \right) \) for our construction.
Liu et al. (2018) derived two classes of EAQMDSCs with the parameters  , \(\frac{{3\left( {q + 1} \right) }}{4} \le d \le q\) and
, \(\frac{{3\left( {q + 1} \right) }}{4} \le d \le q\) and  , \(q + 1 \le d \le \frac{{5q + 1}}{4}\). However, our constructions in Theorems 5 and 6 give us larger classes than ones in Theorem 10 of Liu et al. (2018) since \(\frac{{q + 9}}{4} \le \frac{{3 ( {q + 1} )}}{4}\) and \(\frac{{3q + 7}}{4} \le q + 1\). For instance, letting \(q=11\), we get EAQMDSCs having the parameters
, \(q + 1 \le d \le \frac{{5q + 1}}{4}\). However, our constructions in Theorems 5 and 6 give us larger classes than ones in Theorem 10 of Liu et al. (2018) since \(\frac{{q + 9}}{4} \le \frac{{3 ( {q + 1} )}}{4}\) and \(\frac{{3q + 7}}{4} \le q + 1\). For instance, letting \(q=11\), we get EAQMDSCs having the parameters  , \(5 \le d \le 11\) and
, \(5 \le d \le 11\) and  , \(10 \le d \le 14\), while EAQMDSCs with parameters
, \(10 \le d \le 14\), while EAQMDSCs with parameters  , \(9 \le d \le 11\) and
, \(9 \le d \le 11\) and  , \(12 \le d \le 14\) are obtained via the construction in Liu et al. (2018). We give Table 6 to indicate this comparison.
, \(12 \le d \le 14\) are obtained via the construction in Liu et al. (2018). We give Table 6 to indicate this comparison.
For future studies, the construction of EAQECCs which are both maximal entanglement and MDS with respect to entanglement-assisted singleton bound is an open and attractive problem. While Guenda et al. (2018) obtained such EAQECCs from linear complementary dual (LCD) codes and Reed–Solomon codes based on the hull of classical linear codes, this problem is not solved completely.
References
Aly SA, Klappenecker A, Sarvepalli PK (2007) On quantum and classical BCH codes. IEEE Trans Inf Theory 53(3):1183–1188
Aydin N, Siap I, Ray-Chaudhuri DK (2001) The structure of 1-generator quasi-twisted codes and new linear codes. Des Codes Cryptogr 24(3):313–326
Brun TA, Devetak I, Hsieh MH (2006) Correcting quantum errors with entanglement. Science 314(5798):436–439
Brun TA, Devetak I, Hsieh MH (2014) Catalytic quantum error correction. IEEE Trans Inf Theory 60(6):3073–3089
Calderbank AR, Shor PW (1996) Good quantum error-correcting codes exist. Phys Rev A 54(2):1098–1105
Calderbank AR, Rains EM, Shor PW, Sloane NJA (1998) Quantum error correction via codes over \(GF (4)\). IEEE Trans Inf Theory 44:1369–1387
Chen B, Ling S, Zhang G (2015) Application of constacyclic codes to quantum MDS codes. IEEE Trans Inf Theory 61(3):1474–1484
Chen J, Huang Y, Feng C, Chen R (2017) Entanglement-assisted quantum MDS codes constructed from negacyclic codes. Quantum Inf Process 16(12):303
Fan J, Chen H, Xu J (2016) Constructions of \(q\)-ary entanglement-assisted quantum MDS codes with minimum distance greater than \(q+1\). Quantum Inf Comput 16(5–6):0423–0434
Gottesman D (1997) Stabilizer codes and quantum error correction. Caltech Ph.D. Thesis. arXiv:quant-ph/9705052
Grassl M, Rötteler M (2015) Quantum MDS codes over small fields. In: Proceedings of the international symposium on information theory (ISIT), pp 1104–1108
Guenda K, Jitman S, Gulliver TA (2018) Constructions of good entanglement-assisted quantum error correcting codes. Des Codes Cryptogr 86(1):121–136
He X, Xu L, Chen H (2016) New \(q\)-ary quantum MDS codes with distances bigger than \(q/2\). Quantum Inf Process 15(7):2745–2758
Hu X, Zhang G, Chen B (2015) Constructions of new nonbinary quantum codes. Int J Theor Phys 54(1):92–99
Jin L, Kan H, Wen J (2017) Quantum MDS codes with relatively large minimum distance from Hermitian self-orthogonal codes. Des Codes Cryptogr 84(3):463–471
Kai X, Zhu S (2013) New quantum MDS codes from negacyclic codes. IEEE Trans Inf Theory 59(2):1193–1197
Kai X, Zhu S, Li P (2014) Constacyclic codes and some new quantum MDS codes. IEEE Trans Inf Theory 60(4):2080–2086
Ketkar A, Klappenecker A, Kumar S, Sarvepalli PK (2006) Nonbinary stabilizer codes over finite fields. IEEE Trans Inf Theory 52(11):4892–4914
Krishna A, Sarwate Dilip V (1990) Pseudocyclic maximum-distance-separable codes. IEEE Trans Inf Theory 36(4):880–884
Lai CY, Brun TA (2013) Entanglement increases the error-correcting ability of quantum error-correcting codes. Phys Rev A 88(1):012320
Li RH, Zuo F, Liu Y (2011) A study of skew symmetric \(q^2\)-cyclotomic coset and its application. J Air Force Eng Univ (Nat Sci Ed) 12(1):87–89
Liqin H, Qin Y, Zhu X (2016) New quantum MDS code from constacyclic codes. Chin Ann Math Ser B 37(6):891–898
Liu Y, Li R, Lv L, Ma Y (2017) A class of constacyclic BCH codes and new quantum codes. Quantum Inf Process. https://doi.org/10.1007/s11128-017-1533-y
Liu Y, Li R, Lv L, Ma Y (2018) Application of constacyclic codes to entanglement-assisted quantum maximum distance separable codes. Quantum Inf Process 17(8):210
Lu L, Li R, Guo L, Ma Y, Liu Y (2018) Entanglement-assisted quantum MDS codes from negacyclic codes. Quantum Inf Process. https://doi.org/10.1007/s11128-018-1838-5
Lu L, Ma W, Li R, Ma Y, Liu Y, Cao M (2018) Entanglement-assisted quantum MDS codes from constacyclic codes with large minimum distance. Finite Fields Appl 53:309–325
Lv L, Li R, Fu Q, Li X (2015) Maximal entanglement entanglement-assisted quantum codes from quaternary BCH codes. In: Advanced information technology, electronic and automation control conference (IAEAC) IEEE, pp 709–713
Qian J, Zhang L (2015) Entanglement-assisted quantum codes from arbitrary binary linear codes. Des Codes Cryptogr 77(1):193–202
Qian J, Zhang L (2017) On MDS linear complementary dual codes and entanglement-assisted quantum codes. Des Codes Cryptogr. https://doi.org/10.1007/s10623-017-0413-x
Shor PW (1995) Scheme for reducing decoherence in quantum memory. Phys Rev A 52(4):2493–2496
Steane A (1996) Multiple-particle interference and quantum error correction. Proc R Soc Lond Ser A Math Phys Eng Sci 452(1954):2551–2577
Wilde MM, Brun TA (2008) Optimal entanglement formulas for entanglement-assisted quantum coding. Phys Rev A 77(6):064302
Yuan J, Zhu S, Kai X, Li P (2017) On the construction of quantum constacyclic codes. Des Codes Cryptogr 85(1):179–190
Zhang G, Chen B (2014) New quantum MDS codes. Int J Quantum Inf 12(4):1450019
Zhang T, Ge G (2015) Some new classes of quantum MDS codes from constacyclic codes. IEEE Trans Inf Theory 61(9):5224–5228
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Thomas Aaron Gulliver.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Sarı, M., Kolotoğlu, E. An application of constacyclic codes to entanglement-assisted quantum MDS codes. Comp. Appl. Math. 38, 75 (2019). https://doi.org/10.1007/s40314-019-0837-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-019-0837-1



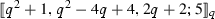 and
and 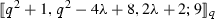 , where
, where 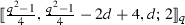 , where
, where 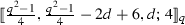 , where
, where