High-Accuracy Numerical Methods and Convergence Analysis for Schrödinger Equation with Incommensurate Potentials

Abstract

Numerical solving the Schrödinger equation with incommensurate potentials presents a great challenge since its solutions could be space-filling quasiperiodic structures without translational symmetry nor decay. In this paper, we propose two high-accuracy numerical methods to solve the time-dependent quasiperiodic Schrödinger equation. Concretely, we discretize the spatial variables by the quasiperiodic spectral method and the projection method, and the time variable by the second-order operator splitting method. The corresponding convergence analysis is also presented and shows that the proposed methods both have spectral convergence rates in space and second order accuracy in time, respectively. Meanwhile, we analyse the computational complexity of these numerical algorithms. One- and two-dimensional numerical results verify these convergence conclusions, and demonstrate that the projection method is more efficient.

1 Introduction

In this paper, we consider the time-dependent quasiperiodic Schrödinger equation (TQSE)

$$\begin{aligned} i\frac{\partial u(\varvec{x},t)}{\partial t} =-\varDelta u(\varvec{x},t)+V(\varvec{x})u(\varvec{x},t)+f(\varvec{x},t),~~(\varvec{x},t)\in \mathbb {R}^d\times [0,T], \end{aligned}$$

(1)

where $\varDelta =\partial ^{2}_{x_1}+\cdots +\partial ^{2}_{x_d}$ is the Laplacian operator, $V(\varvec{x})$ is the incommensurate potential, such as a one-dimensional quasiperodic function $V(x)=\cos x+\cos \sqrt{5} x$ is a standard incommensurate potential. $f(\varvec{x},t)$ is an external field function and $u(\varvec{x},t)$ is quasiperiodic in $\varvec{x}$. The initial value $u(\varvec{x}, 0)=u_0(\varvec{x})$ is given.

The Schrödinger equation is a fundamental equation in quantum mechanics. The study of the Schrödinger equation with periodic/random potentials or given boundary conditions has reached a relatively mature stage [1,2,3]. When the potential V is quasiperiodic function which contains at least two rationally independent frequencies, it is related to irrational numbers. What is surprising is that we can observe more abundant and fascinating phenomena in the (nonlinear) quasiperiodic Schrödinger equations (QSEs) and quasiperiodic Schrödinger operators, such as superconductivity, Hall conductivity, Anderson localization, localization-delocalization transition [4,5,6,7,8,9,10]. The quasiperiodic Schrödinger systems have also attracted much attention in the mathematical community. However, the solution of quasiperiodic Schrödinger system may lack translation, and the existence of irrational numbers may cause the small divisor problem. These result in many challenges in analyzing and numerical computing these quasiperiodic systems. For the discrete quasiperiodic Schrödinger operator, the so-call almost Mathieu operator, relatively many results have been obtained [11,12,13,14], including its spectrum of 1D case being a Cantor set [11]. For the continuous and multidimensional cases, the study of spectral theory is more challenging, and only a few recent research results [15]. Recently, there have been some preliminary results on the existence and construction of quasiperiodic solutions of QSE [16,17,18,19,20].

Numerically solving the QSE is still a great challenge since their solutions could be quasiperiodic, related to irrational numbers, without translational symmetry and nor decay. There are several numerical methods to address these quasiperiodic systems. The periodic approximation method (PAM) has been used to obtain an approximate periodic solution within a finite domain [9]. Besides, the PAM is also used to solve and analyze the eigenvalues of Schrödinger operators [21, 22]. However, the PAM is often unsatisfactory in terms of algorithm accuracy and convergence rate, see [23] for details. Recently, several accurate numerical methods, quasiperiodic spectral method (QSM), projection method (PM), and finite points recovery method, have been proposed to solve quasiperiodic systems [24,25,26]. The corresponding approximation analysis for QSM and PM has been given in [27]. The PM has been also applied to quasiperiodic Schrödinger equations [7], and eigenvalues problem [28]. Extensive studies have demonstrated that the PM can achieve high accuracy in computing various quasiperiodic systems [29,30,31,32]. However, the corresponding numerical analysis is lacking. These theoretical results and applications illuminate our problems.

The purpose of this work is to study how to efficiently solve the spatially quasiperiodic solutions of higher-dimensional quasiperiodic Schrödinger equation to high accuracy, and to establish the corresponding convergence analysis. Concretely, we apply QSM and PM to solve the quasiperiodic solution of TQSE (1) and analyze their computational complexity. Meanwhile, the rigorous error analysis shows that both algorithms have spectral convergence rates. One- and two-dimensional numerical examples are given to verify the effectiveness of the proposed algorithms. Furthermore, we can obtain quasiperiodic solutions and show that the PM is an efficient and high-precision algorithm for solving TQSE.

The rest of the paper is organized as follows. Section 2 proposes two methods, the PM and the QSM, coupled with the second-order operator splitting scheme, to solve TQSE (1). We also give their numerical implementation and computational complexity analysis. Section 3 introduces quasiperiodic spaces and gives the convergence analysis of the proposed methods. Section 4 presents numerical results to further validate the theoretical analysis. Finally, the conclusion of this paper is given in Sect. 5.

2 Numerical Methods

Throughout, we make use of the following notations. Let $\Omega _L=[-L,L]^d \subset \mathbb {R}^d$ and $\vert \Omega _L\vert =(2L)^d$. For any vector $\varvec{x}\in \mathbb {R}^d$, we define $\Vert \varvec{x}\Vert ^2=\sum _{j=1}^{d}\vert x_j\vert ^2$ and $\vert \varvec{x}\vert =\sum _{j=1}^{d}\vert x_j\vert$. For any multi-index $\mu =(\mu _1,\cdots ,\mu _d)\in \mathbb {N}^d$ and $\varvec{x}\in \mathbb {R}^d$, let $\partial ^\mu _{\varvec{x}}=\partial ^{\mu _1}_{x_1}\cdots \partial ^{\mu _d}_{x_d}$. We present the definition of the quasiperiodic function.

Definition 1

A matrix $\varvec{P}\in \mathbb {R}^{d\times n}$ is the projection matrix, if it belongs to the set $\mathbb {P}^{d\times n}:=\{\varvec{P}=(\varvec{p}_1,\cdots ,\varvec{p}_n)\in \mathbb {R}^{d\times n}: \varvec{p}_1,\cdots ,\varvec{p}_n ~\text{ are } \mathbb {Q}\text{-linearly } \text{ independent }\}.$

Definition 2

A d-dimensional function $u(\varvec{x})$ is quasiperiodic if there exists an n-dimensional periodic function $u_p$ and a projection matrix $\varvec{P}\in \mathbb {P}^{d\times n}$, such that $u(\varvec{x})=u_p(\varvec{P}^T \varvec{x})$ for all $\varvec{x}\in \mathbb {R}^d$.

In particular, when $n=d$ and $\varvec{p}_1,~\varvec{p}_2,\cdots ,\varvec{p}_d$ form a basis of $\mathbb {R}^d$, $u(\varvec{x})$ is periodic. For convenience, we refer to $u_p$ in Definition 2 as the parent function of u. The continuous Fourier-Bohr transformation of $u(\varvec{x})$ is

$$\begin{aligned} \hat{u}_{\varvec{\lambda }}= \lim _{L\rightarrow \infty } \frac{1}{\vert \Omega _L\vert } \int _{\Omega _L} u(\varvec{x})e^{-i\varvec{\lambda }\cdot \varvec{x}}\,d\varvec{x}:= {\mathchoice{{-\hspace{-10.55542pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}} u(\varvec{x})e^{-i\varvec{\lambda }\cdot \varvec{x}}\,d\varvec{x}, \end{aligned}$$

(2)

where $\varvec{\lambda }\in \mathbb {R}^d$. The Fourier series associated to $u(\varvec{x})$ is

$$\begin{aligned} u(\varvec{x})\sim \sum _{j=1}^{\infty } \hat{u}_{\varvec{\lambda }_j} e^{i\varvec{\lambda }_j\cdot \varvec{x}}, \end{aligned}$$

(3)

where $\varvec{\lambda }_j\in \sigma (u)=\{\varvec{\lambda }: \varvec{\lambda }= \varvec{P}\varvec{k},~\varvec{k}\in \mathbb {Z}^n \}$ are Fourier exponents, $\hat{u}_{\varvec{\lambda }_j}$ computed by (2) are Fourier coefficients. If the Fourier series (3) is absolutely convergent, it is also uniformly convergent. Therefore, when $\sum _{j=1}^{\infty } \vert \hat{u}_{\varvec{\lambda }_j}\vert <+\infty$, we have

$$\begin{aligned} u(\varvec{x})=\sum _{j=1}^{\infty } \hat{u}_{\varvec{\lambda }_j} e^{i\varvec{\lambda }_j\cdot \varvec{x}}. \end{aligned}$$

Moreover, the Parseval equality

$$\begin{aligned} \sum _{j=1}^{\infty }\vert \hat{u}_{\varvec{\lambda }_j}\vert ^2 = {\mathchoice{{-\hspace{-10.55542pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}} \vert u(\varvec{x})\vert ^2\,d\varvec{x} \end{aligned}$$

(4)

is true.

For simplicity, we consider the homogeneous TQSE, i.e., $f=0$, in the following analysis. For inhomogeneous $f\ne 0$, the presented analysis below can be easily extended. Denote the operator $A=-\varDelta$ and for a given quasiperiodic potential

$$\begin{aligned} V(\varvec{x})=\sum _{\varvec{\lambda }\in \sigma (V)}\hat{V}_{\varvec{\lambda }}e^{i\varvec{\lambda }\cdot \varvec{x}}, \end{aligned}$$

(5)

TQSE (1) becomes

$$\begin{aligned} \frac{\partial u}{\partial t}=-iA u-iVu. \end{aligned}$$

(6)

The formal solution of (6) is

$$\begin{aligned} u(\varvec{x},t)=e^{-it(A+V)}u_0=\mathcal {T}u_0,~~(\varvec{x},t)\in \mathbb {R}^d\times [0,T]. \end{aligned}$$

Next, we employ QSM and PM to discretize TQSE (6) in space direction, and the second-order operator splitting (OS2) method in time direction.

2.1 Spatial Discretization

We first introduce the QSM and the PM, respectively. For a positive integer $N\in \mathbb {N}_0=\mathbb {N}\setminus \{0\}$ and the given projection matrix $\varvec{P}\in \mathbb {P}^{d\times n}$ of the quasiperiodic function u, denote

$$\begin{aligned} \varvec{K}_N^n=\{\varvec{k}=(k_j)_{j=1}^n \in \mathbb {Z}^n: \, -N \le k_j < N \}, \end{aligned}$$

and

$$\begin{aligned} \sigma _{N}(u)=\{\varvec{\lambda }= \varvec{P}\varvec{k}: \varvec{k}\in \varvec{K}_N^n \}. \end{aligned}$$

The order of set $\sigma _{N}(u)$ is $\# (\sigma _{N}(u))=(2N)^n:=D$.

2.1.1 QSM Method

The QSM approximates the quasiperiodic function $u(\varvec{x})$ by the truncation operator $\mathcal {P}_N$, i.e.,

$$\begin{aligned} u(\varvec{x})\approx \mathcal {P}_N u(\varvec{x}) =\sum _{\varvec{\lambda }_j \in \sigma _N(u) } \hat{u}_{\varvec{\lambda }_j} e^{i \varvec{\lambda }_j\cdot \varvec{x}},~~\varvec{x}\in \mathbb {R}^d, \end{aligned}$$

where $\hat{u}_{\varvec{\lambda }_j}$ is obtained by the continuous Fourier-Bohr transformation of $u(\varvec{x})$. The function approximation theory of QSM can be found in [27].

2.1.2 PM Method

An alternative way is PM, seizing the fact that the quasiperiodic system is defined on the irrational manifold of higher-dimensional torus. Concretely, the PM efficiently computes the Fourier coefficient of the periodic parent function on a higher-dimensional torus in a pseudo-spectral manner. Then, the quasiperiodic structure can be obtained by projecting the high-dimensional periodic structure onto a corresponding irrational manifold. Let $\mathbb {T}^n=(\mathbb {R}/2\pi \mathbb {Z})^n$ be the n-dimensional torus. To discretize $\mathbb {T}^n$, we consider a fundamental domain $[0,2\pi )^n$ and assume that the discrete node along each dimension is the same, i.e., $N\in \mathbb {N}_0$. Then $[0,2\pi )^n$ is discretized by grid points $\varvec{y}_{\varvec{j}} =(y_{1,j_1}, y_{2,j_2},\dots , y_{n,j_n})$, where $y_{1,j_1}=j_1 h$, $y_{2,j_2}=j_2 h, \dots , y_{n,j_n}=j_n h$, $0\le j_1,j_2,\dots , j_n < 2N$, with the spatial discretization size $h=\pi /N$. The discrete n-dimensional torus $\mathbb {T}^n_N$ can be obtained by periodic extending these grid points $\varvec{y}_{\varvec{j}}$. The grid periodic function space defined on $\mathbb {T}^n_N$ is

$$\begin{aligned} \mathcal {G}_N := \{U: \mathbb {T}^n_N \mapsto \mathbb {C}: ~ U~ \text{ is }~ \mathbb {T}^n_N \text{-periodic } \}. \end{aligned}$$

Given any periodic grid functions $U_1, U_2\in \mathcal {G}_N$, the $\ell ^2$-inner product is

$$\begin{aligned} \langle U_1, U_2 \rangle _N = \frac{1}{(2 N)^n}\sum _{\varvec{y}_{\varvec{j}}\in \mathbb {T}^n_N} U_1(\varvec{y}_{\varvec{j}})\overline{U}_2(\varvec{y}_{\varvec{j}}). \end{aligned}$$

(7)

For $\varvec{k}, \varvec{\ell }\in \mathbb {Z}^n$, we have the discretize orthogonality

$$\begin{aligned} \langle e^{i\varvec{k}\cdot \varvec{y}_{\varvec{j}} }, e^{i\varvec{\ell }\cdot \varvec{y}_{\varvec{j}} } \rangle _N = {\left\{ \begin{array}{ll} 1,~~\varvec{k}=\varvec{\ell }+ 2N\varvec{m},~\varvec{m}\in \mathbb {Z}^n,\\ 0,~~\text{ otherwise }. \end{array}\right. } \end{aligned}$$

(8)

The discrete Fourier coefficient of $U\in \mathcal {G}_N$ is

$$\begin{aligned} \tilde{U}_{\varvec{k}} = \langle U, e^{i \varvec{k}\cdot \varvec{y}_{\varvec{j}}} \rangle _N,~~~ \varvec{k}\in \varvec{K}_N^n. \end{aligned}$$

(9)

The PM designates $\tilde{U}_{\varvec{k}}$ as the Fourier-Bohr coefficient $\tilde{u}_{\varvec{\lambda }}$, $\varvec{\lambda }=\varvec{P}\varvec{k}$. Then the discrete Fourier-Bohr expansion of $u(\varvec{x})$ is

$$\begin{aligned} u(\varvec{x}_{\varvec{j}})=\sum _{\varvec{\lambda }\in \sigma _N(u)} \tilde{u}_{\varvec{\lambda }}e^{i\varvec{\lambda }\cdot \varvec{x}_{\varvec{j}}}, \end{aligned}$$

where collocation points $\varvec{x}_{\varvec{j}}\in \mathbb {Q}_N=\{\varvec{x}_{\varvec{j}}=\varvec{P}\varvec{y}_{\varvec{j}}$, $\varvec{y}_{\varvec{j}}\in \mathbb {T}^n_N\}$. The trigonometric interpolation of u is

$$\begin{aligned} I_N u(\varvec{x})=\sum _{\varvec{\lambda }\in \sigma _N(u)} \tilde{u}_{\varvec{\lambda }}e^{i\varvec{\lambda }\cdot \varvec{x}}. \end{aligned}$$

(10)

Consequently, let $I_N u(\varvec{x}_j) \approx u(\varvec{x}_j)$. Recently, it is proved that the PM has spectral accuracy based on function approximation theory[27].

2.2 Second-Order Operator Splitting (OS2) Method

The OS2 scheme is one of the most popular numerical methods of solving Schrödinger equations [33, 34]. The basic idea of OS2 method is splitting TQSE (6) into two subproblems

$$\begin{aligned} \frac{\partial u}{\partial t}=-iA u,~~ \frac{\partial u}{\partial t}=-iVu. \end{aligned}$$

(11)

For the time grid points $0 = t_0< t_1<\cdots < t_M = T$, where $t_m=m\tau$, $m=0,1,\dots , M$, and the time step size $\tau =T/M$, the OS2 method numerically approximates the solution by the recurrence relation

$$\begin{aligned} u^{m}=e^{-\frac{i}{2}\tau A} e^{-i\tau V} e^{-\frac{i}{2}\tau A}u^{m-1} =\mathcal {S}^m u^0\approx u(\cdot , t_m),~~ 1\le m\le M, \end{aligned}$$

(12)

where $\mathcal {S}=e^{-\frac{i}{2}\tau A} e^{-i\tau V} e^{-\frac{i}{2}\tau A}$ and $u^0=u(\cdot ,0)$.

2.3 Numerical Implementation

In numerical implementation, the semi-discrete subproblems of (11) can be solved by QSM and PM, in terms of QSM-OS2 and PM-OS2, respectively. The detailed implementation to solve TQSE (6) and computational complexity analysis are shown below.

2.3.1 QSM-OS2 Method

From $t_m$ to $t_{m+1}$, the QSM-OS2 involves three steps.

$\bullet$ QSM-OS2-Step 1. For $t\in [t_m, t_m+\tau /2]$, consider the ordinary differential equation

$$\begin{aligned} \frac{\partial u}{\partial t}=-iA u, \end{aligned}$$

(13)

with initial value $u(\cdot , t_m)$. Therefore, we have

$$\begin{aligned} u(\varvec{x}, t_m+\frac{\tau }{2})&\approx \phi (\varvec{x}, t_m) =e^{-\frac{i}{2}\tau \check{A}_N} u(\varvec{x}, t_m) \\&=e^{-\frac{i}{2}\tau A}\mathcal {P}_N u(\varvec{x}, t_m) =\sum _{\varvec{\lambda }\in \sigma _N(u)} \hat{u}_{\varvec{\lambda }}(t_m)e^{-\frac{i}{2}\tau \Vert \varvec{\lambda }\Vert ^2}e^{i\varvec{\lambda }\cdot \varvec{x}}. \end{aligned}$$

Denote $\hat{\phi }_{\varvec{\lambda }}(t_m)= \hat{u}_{\varvec{\lambda }}(t_m)e^{-\frac{i}{2}\tau \Vert \varvec{\lambda }\Vert ^2}$.

$\bullet$ QSM-OS2-Step 2. For $t\in [t_m, t_{m+1}]$, consider the ordinary differential equation

$$\begin{aligned} \frac{\partial u}{\partial t}=-iV u, \end{aligned}$$

with initial value $\phi (\varvec{x}, t_m)$. From the definition of V in (5), we have

$$\begin{aligned} \psi (\varvec{x}, t_m)=\phi (\varvec{x}, t_{m+1}) =e^{-i\tau \check{V}_N} \phi (\varvec{x}, t_m) =e^{-i\tau V}\mathcal {P}_N \phi (\varvec{x}, t_m), \end{aligned}$$

where Fourier coefficient vector $\hat{\Psi }(t_m)=(\hat{\psi }_{\varvec{\lambda }_1}(t_m),\hat{\psi }_{\varvec{\lambda }_2}(t_m),\cdots , \hat{\psi }_{\varvec{\lambda }_D}(t_m))$ satisfies

$$\begin{aligned} \hat{\Psi }(t_m)=e^{-i\tau \mathcal {V}}\hat{\Phi }(t_m) \end{aligned}$$

(14)

with

$$\begin{aligned} \mathcal {V}=\begin{pmatrix} \hat{V}_{\varvec{\lambda }_1-\varvec{\lambda }_1} & \hat{V}_{\varvec{\lambda }_1-\varvec{\lambda }_2} & \cdots & \hat{V}_{\varvec{\lambda }_1-\varvec{\lambda }_D}\\ \hat{V}_{\varvec{\lambda }_2-\varvec{\lambda }_1} & \hat{V}_{\varvec{\lambda }_2-\varvec{\lambda }_2} & \cdots & \hat{V}_{\varvec{\lambda }_2-\varvec{\lambda }_D}\\ \vdots & \vdots & & \vdots \\ \hat{V}_{\varvec{\lambda }_D-\varvec{\lambda }_1} & \hat{V}_{\varvec{\lambda }_D-\varvec{\lambda }_2} & \cdots & \hat{V}_{\varvec{\lambda }_D-\varvec{\lambda }_D} \end{pmatrix}, \end{aligned}$$

and $\hat{\Phi }(t_m)=(\hat{\phi }_{\varvec{\lambda }_1}(t_m),\hat{\phi }_{\varvec{\lambda }_2}(t_m),\cdots , \hat{\phi }_{\varvec{\lambda }_D}(t_m))$. Note that $\hat{V}_{\varvec{\lambda }_j-\varvec{\lambda }_{\ell }}$ means the Fourier coefficient of V on the Fourier exponent $\varvec{\lambda }=\varvec{\lambda }_j-\varvec{\lambda }_{\ell }$.

$\bullet$ QSM-OS2-Step 3. For $t\in [t_m, t_m+\tau /2]$, we still consider (13) but with initial value $\psi (\varvec{x}, t_m)$, and have

$$\begin{aligned} u(\varvec{x},t_{m+1})\approx e^{-\frac{i}{2}\tau \check{A}_N} \psi (\varvec{x}, t_m). \end{aligned}$$

Consequently, the fully discrete scheme of QSM-OS2 can be written as

$$\begin{aligned} u_N^{m+1}=e^{-\frac{i}{2}\tau \check{A}_N} e^{-i\tau \check{V}_N} e^{-\frac{i}{2}\tau \check{A}_N}u_N^{m} =\check{\mathcal {S}}^{m+1}_Nu^0\approx u(\cdot , t_{m+1}),~~ 0\le m\le M-1, \end{aligned}$$

(15)

where

$$\begin{aligned} \check{\mathcal {S}}_N=e^{-\frac{i}{2}\tau \check{A}_N} e^{-i\tau \check{V}_N} e^{-\frac{i}{2}\tau \check{A}_N} =e^{-\frac{i}{2}\tau A}\mathcal {P}_N e^{-i\tau V}\mathcal {P}_N e^{-\frac{i}{2}\tau A} \mathcal {P}_N. \end{aligned}$$

Note that the idenitity $\mathcal {P}_Ne^{-\frac{i}{2}\tau A}\mathcal {P}_Nu=e^{-\frac{i}{2}\tau A}\mathcal {P}_Nu$ holds.

2.3.2 PM-OS2 Method

From $t_m$ to $t_{m+1}$, the PM-OS2 contains three steps.

$\bullet$ PM-OS2-Step 1. For $t\in [t_m, t_m+\tau /2]$, similar to QSM-OS2-Step 1, we have

$$\begin{aligned} u(\varvec{x},t_m+\tau /2) \approx \phi (\varvec{x},t_m)= e^{-\frac{i}{2}\tau A_N} u(\varvec{x}, t_m) =\sum _{\varvec{\lambda }\in \sigma _N(u)} \tilde{u}_{\varvec{\lambda }}(t_m)e^{-\frac{i}{2}\tau \Vert \varvec{\lambda }\Vert ^2}e^{i\varvec{\lambda }\cdot \varvec{x}}. \end{aligned}$$

Then, denote $\tilde{\phi }_{\varvec{k}}(t_m)=\tilde{u}_{\varvec{\lambda }}(t_m)e^{-\frac{i}{2}\tau \Vert \varvec{\lambda }\Vert ^2}$ with $\varvec{\lambda }=\varvec{P}\varvec{k}$.

$\bullet$ PM-OS2-Step 2. Applying the fast Fourier transform (FFT) yields

$$\begin{aligned} I_N\phi _p(\varvec{y}_j,t_m)=\sum _{\varvec{k}\in K^n_N} \tilde{\phi }_{\varvec{k}}(t_m)e^{i\varvec{k}\cdot \varvec{y}_j}, \end{aligned}$$

where the grid points $\varvec{y}_j\in \mathbb {T}^n_N$. For $t\in [t_m, t_{m+1}]$, we have

$$\begin{aligned} \psi _p(\varvec{y},t_{m})=e^{-i\tau V_p} I_N \phi _p(\varvec{y}, t_m), \end{aligned}$$

where $V_p$ is the parent function of V. Using FFT again, we have $\tilde{\psi }_{\varvec{\lambda }}(t_m)=\langle \psi _p(\varvec{y}_j,t_{m}), e^{i \varvec{k}\cdot \varvec{y}_j} \rangle _N$ with $\varvec{\lambda }=\varvec{P}\varvec{k}$. Consequently, we can obtain

$$\begin{aligned} \psi (\varvec{x},t_{m}) =e^{-i\tau V_N}\phi (\varvec{x}, t_m) =e^{-i\tau V} I_N \phi (\varvec{x}, t_m). \end{aligned}$$

$\bullet$ PM-OS2-Step 3. For $t\in [t_m, t_m+\tau /2]$, similar to PM-OS2-Step 1, we have

$$\begin{aligned} u(\varvec{x},t_{m+1})\approx u_N^{m+1}=e^{-\frac{i}{2}\tau A_N} \psi (\varvec{x}, t_m) =\sum _{\varvec{\lambda }\in \sigma _N(\psi )} \tilde{\psi }_{\varvec{\lambda }}(t_m) e^{-\frac{i}{2}\tau \Vert \varvec{\lambda }\Vert ^2} e^{i\varvec{\lambda }\cdot \varvec{x}}. \end{aligned}$$

Therefore, we can write the fully discrete scheme of PM-OS2 as

$$\begin{aligned} u_N^{m+1}=e^{-\frac{i}{2}\tau A_N} e^{-i\tau V_N} e^{-\frac{i}{2}\tau A_N}u_N^m =\mathcal {S}^{m+1}_Nu^0\approx u(\cdot , t_{m+1}),~~ 0\le m\le M-1, \end{aligned}$$

(16)

where

$$\begin{aligned} \mathcal {S}_N=e^{-\frac{i}{2}\tau A_N} e^{-i\tau V_N} e^{-\frac{i}{2}\tau A_N} =e^{-\frac{i}{2}\tau A}I_N e^{-i\tau V}I_N e^{-\frac{i}{2}\tau A} I_N. \end{aligned}$$

Remark 1

From the implementation, it is apparent that the PM can use the n-dimensional FFT to obtain Fourier coefficients but the QSM could not.

2.3.3 Computational Complexity Analysis

Here we analyze the computational complexity of each time step for QSM-OS2 and PM-OS2, respectively. In the implementation of QSM-OS2-Step 1 and 3, the QSM requires D multiplication operators to solve (13). In QSM-OS2-Step 2, we compute the finite terms of the Taylor expansion for $e^{-i\tau \mathcal {V}}$, i.e.,

$$\begin{aligned} e^{-i\tau \mathcal {V}}\approx \sum _{j=0}^{k}\frac{(-i\tau \mathcal {V})^j}{j!}. \end{aligned}$$

(17)

Therefore, there require $2(k-1)D^3+D^2$ operators to compute (17) and $2D^2-D$ operators to compute (14). The computational complexity of QSM-OS2 in solving TQSE (6) is $O(D^3)$.

In the implementation of PM-OS2, there require D multiplication operators in PM-OS2-Step 1 and 3. However, in PM-OS2-Step 2, the availability of FFT allows us to compute the convolutions economically in physical space as dot product, only requiring $O(D \log D)$ operators. Therefore, the computational complexity of PM-OS2 in solving TQSE (6) is $O(D \log D)$.

3 Theoretical Analysis

In this section, we present the convergence analysis of QSM-OS2 and PM-OS2.

3.1 Preliminaries

In this subsection, we will introduce some Hilbert spaces on $\mathbb {T}^n$ and quasiperiodic spaces on $\mathbb {R}^d$.

• $L^2(\mathbb {T}^n)$space: $L^2(\mathbb {T}^n)=\Big \{U(\varvec{y}): \frac{1}{|\mathbb {T}^n|}\int _{\mathbb {T}^n}\vert U\vert ^2\,d\varvec{y}< +\infty \Big \},$ equipped with inner product

  $$\begin{aligned} (U_1, U_2)_{L^2(\mathbb {T}^n)}=\frac{1}{|\mathbb {T}^n|}\int _{\mathbb {T}^n}U_1\overline{U}_2\,d\varvec{y}. \end{aligned}$$

• $H^\alpha (\mathbb {T}^n)$space: for any integer $\alpha \ge 0$, the $\alpha$-derivative Hilbert space on $\mathbb {T}^n$ is

  $$\begin{aligned} H^\alpha (\mathbb {T}^n)=\{U\in L^2(\mathbb {T}^n): \Vert U\Vert _{\alpha }< +\infty \}, \end{aligned}$$

  where $\Vert U \Vert _\alpha =\Big (\sum _{\varvec{k}\in \mathbb {Z}^n}(1+\vert \varvec{k}\vert ^{2})^{\alpha } \vert \hat{U}_{\varvec{k}}\vert ^2 \Big )^{1/2},~\hat{U}_{\varvec{k}}=(U,e^{i\varvec{k}\cdot \varvec{y}})_{L^2(\mathbb {T}^n)}.$ The semi-norm of $H^\alpha (\mathbb {T}^n)$ can be defined as $\vert U \vert _\alpha =\Big (\sum _{\varvec{k}\in \mathbb {Z}^n}\vert \varvec{k}\vert ^{2\alpha } \vert \hat{U}_{\varvec{k}}\vert ^2 \Big )^{1/2}.$

• $X_{\alpha }$space: for any $U\in L^2(\mathbb {T}^n)$ and $\alpha \in \mathbb {R}$, the Fourier series expansion is

  $$\begin{aligned} U(\varvec{y})=\sum _{\varvec{k}\in \mathbb {Z}^n} \hat{U}_{\varvec{k}}e^{i\varvec{k}\cdot \varvec{y}}, \end{aligned}$$

  the linear operator $(-\varDelta )^\alpha$ is given by

  $$\begin{aligned} (-\varDelta )^\alpha U =\sum _{\varvec{k}\in \mathbb {Z}^n} \Vert \varvec{k}\Vert ^{2\alpha } \hat{U}_{\varvec{k}} e^{i\varvec{k}\cdot \varvec{y}}, \end{aligned}$$

  and

  $$\begin{aligned} X_{\alpha }= \Big \{U(\varvec{y})=\sum _{\varvec{k}\in \mathbb {Z}^n} \hat{U}_{\varvec{k}}e^{i\varvec{k}\cdot \varvec{y}}\in L^2(\mathbb {T}^n): \Vert (-\varDelta )^\alpha U \Vert ^2 =\sum _{\varvec{k}\in \mathbb {Z}^n} \vert \hat{U}_{\varvec{k}}\vert ^2\cdot \Vert \varvec{k}\Vert ^{4\alpha } <\infty \Big \}. \end{aligned}$$

  The set $X_{\alpha }$ forms a Hilbert space with inner product

  $$\begin{aligned} (U,W)_{X_{\alpha }}=(U,W)_{L^2(\mathbb {T}^n)} +((-\varDelta )^\alpha U,(-\varDelta )^\alpha W)_{L^2(\mathbb {T}^n)}, \end{aligned}$$

  and

  $$\begin{aligned} \Vert U\Vert ^2_{X_{\alpha }}=\sum _{\varvec{k}\in \mathbb {Z}^n} (1+\Vert \varvec{k}\Vert ^{4\alpha }) \vert \hat{U}_{\varvec{k}} \vert ^2. \end{aligned}$$

  When $\alpha =0$, $\Vert U\Vert _{X_0}=\Vert U \Vert _0=\Vert U\Vert$.

• $\text{ QP }(\mathbb {R}^d)$ space: let $\text{ QP }(\mathbb {R}^d)$ be the space of all d-dimensional quasiperiodic functions.

• $L^q_{QP}(\mathbb {R}^d)$space: for any fixed $q\in [1,\infty )$, denote

  $$\begin{aligned} L^q_{QP}(\mathbb {R}^d)=\Big \{v(\varvec{x})\in \text{ QP }(\mathbb {R}^d):~\Vert v \Vert ^q_{q} = {\mathchoice{{-\hspace{-10.55542pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}} \vert v(\varvec{x}) \vert ^q\,d\varvec{x}< \infty \Big \}, \end{aligned}$$

  and

  $$\begin{aligned} L^{\infty }_{QP}(\mathbb {R}^d)=\{v(\varvec{x})\in \text{ QP }(\mathbb {R}^d):~\Vert v \Vert _{\infty }=\sup _{\varvec{x}\in \mathbb {R}^d}\vert v(\varvec{x}) \vert < \infty \}, \end{aligned}$$

  the inner product $(\cdot , \cdot )_{L_{QP}^2(\mathbb {R}^d)}$

  $$\begin{aligned} (v, w)_{L^2_{QP}(\mathbb {R}^d)}= {\mathchoice{{-\hspace{-10.55542pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}} v(\varvec{x})\bar{w}(\varvec{x})\,d\varvec{x}. \end{aligned}$$

  By the Parseval identity (4), we have

  $$\begin{aligned} \Vert v \Vert _{L^2_{QP}(\mathbb {R}^d)}^2=\sum _{\varvec{\lambda }\in \sigma (v)} \vert \hat{v}_{\varvec{\lambda }} \vert ^2. \end{aligned}$$

• $\mathcal {C}^{\alpha }_{QP}(\mathbb {R}^d)$space: the space $\mathcal {C}^{\alpha }_{QP}(\mathbb {R}^d)$ consists of quasiperiodic functions with continuous derivatives up to order $\alpha$ on $\mathbb {R}^d$. The $\mathcal {C}^{\alpha }_{QP}$-norm of $v\in \mathcal {C}^{\alpha }_{QP}(\mathbb {R}^d)$ is defined by

  $$\begin{aligned} \Vert v \Vert _{\mathcal {C}^{\alpha }_{QP}} =\sum _{\vert \varvec{m}\vert \le \alpha } \sup _{\varvec{x}\in \mathbb {R}^d} \vert \partial _{\varvec{x}}^{\varvec{m}}v \vert . \end{aligned}$$

• $H^{\alpha }_{QP}(\mathbb {R}^d)$space: for any $\alpha \in \mathbb {N}_0$, the space $H^{\alpha }_{QP}(\mathbb {R}^d)$ comprises all quasiperiodic functions with partial derivatives order $\alpha \ge 1$. For $v,w\in H^{\alpha }_{QP}(\mathbb {R}^d)$, the inner product $(\cdot , \cdot )_{H^{\alpha }_{QP}(\mathbb {R}^d)}$ is

  $$\begin{aligned} (v, w)_{H^{\alpha }_{QP}(\mathbb {R}^d)}=(v, w)_{L^2_{QP}(\mathbb {R}^d)}+ \sum _{\vert \varvec{m}\vert =\alpha }(\partial ^{\varvec{m}}_{\varvec{x}} v, \partial ^{\varvec{m}}_{\varvec{x}} w)_{L^2_{QP}(\mathbb {R}^d)}. \end{aligned}$$

  The corresponding norm is

  $$\begin{aligned} \Vert v \Vert _{H^{\alpha }_{QP}(\mathbb {R}^d)}^2=\sum _{\varvec{\lambda }\in \sigma (v)}(1+\vert \varvec{\lambda }\vert ^2)^{\alpha }\vert \hat{v}_{\varvec{\lambda }} \vert ^2. \end{aligned}$$

  In particular, for $\alpha =0$, $H^0_{QP}(\mathbb {R}^d)=L^2_{QP}(\mathbb {R}^d)$. To simplify notation, we denote $(\cdot , \cdot )=(\cdot , \cdot )_{L^2_{QP}(\mathbb {R}^d)}$ and $(\cdot , \cdot )_{\alpha }=(\cdot , \cdot )_{H^{\alpha }_{QP}(\mathbb {R}^d)}$. The embedding theorem of $H^{\alpha }_{QP}(\mathbb {R}^d)$ can be found in [35].

A recent study has revealed an important relationship between quasiperiodic function and its parent function, see Lemma 1.

Lemma 1

([27]) Consider a d-dimensional quasiperiodic function $v(\varvec{x})=v_p(\varvec{P}^{T}\varvec{x})$ where $v_p(\varvec{y})$ is its parent function and $\varvec{P}\in \mathbb {P}^{d\times n}$. Let the quasiperiodic Fourier coefficient $\hat{v}_{\varvec{\lambda }}=(v, e^{i\varvec{\lambda }\cdot \varvec{x}})$ and the periodic Fourier coefficient $\hat{v}_p(\varvec{k})=(v_p, e^{i\varvec{k}\cdot \varvec{y}})_{L^2(\mathbb {T}^n)}$. Then, we have

$$\begin{aligned} \hat{v}_{\varvec{\lambda }}= \hat{v}_p(\varvec{k}), \end{aligned}$$

where $\varvec{\lambda }=\varvec{P}\varvec{k}$, $\varvec{k}\in \mathbb {Z}^n$.

Based on Lemma 1, we prove the norm inequality between quasiperiodic function and its parent function.

Theorem 1

For any $v\in \text{ QP }(\mathbb {R}^d)$, and $v_p$ is the corresponding n-dimensional parent function. Assume that $\alpha \ge s/2> n/4$ and $v_p\in X_{\alpha }$. Then, the bound

$$\begin{aligned} \Vert v\Vert _{L_{QP}^{\infty }(\mathbb {R}^d)}\le C\, \Vert v_p\Vert _{s} \le C\, \Vert v_p\Vert _{X_{\alpha }} \end{aligned}$$

(18)

is valid and the following estimate

$$\begin{aligned} \Vert wv \Vert _{L_{QP}^2(\mathbb {R}^d)} \le C \, \Vert w \Vert _{L_{QP}^2(\mathbb {R}^d)} \cdot \Vert v_p\Vert _{X_\alpha }, ~~w\in L_{QP}^{2}(\mathbb {R}^d),~~v_p\in X_{\alpha } \end{aligned}$$

holds where C is a constant.

Proof

Applying Lemma 1 and Cauchy-Schwarz inequality, we have

$$\begin{aligned} \sum _{j=1}^{\infty }\vert \hat{v}_{\varvec{\lambda }_j}\vert&=\sum _{j=1}^{\infty }\Big [\vert \hat{v}_p(\varvec{k}_j)\vert \, (1+\vert \varvec{k}_j\vert ^2)^{s/2}\, (1+\vert \varvec{k}_j\vert ^2)^{-s/2} \Big ]\\&\le \sum _{j=1}^{\infty }\Big [\vert \hat{v}_p(\varvec{k}_j)\vert ^2\, (1+\vert \varvec{k}_j\vert ^2)^{s}\Big ]\,\sum _{j=1}^{\infty } (1+\vert \varvec{k}_j\vert ^2)^{-s}\\&=C\Vert v_p\Vert _s. \end{aligned}$$

The last estimate holds since $s> n/2$ implies the series $\sum _{j=1}^{\infty } (1+\vert \varvec{k}_j\vert ^2)^{-s}$ converges.

When the Fourier series of v is absolutely convergent, then it uniformly convergent to the quasiperiodic function v (Theorem 1.20 in [36]), such that $\Vert v\Vert _{L_{QP}^{\infty }(\mathbb {R}^d)}\le \sum _{j=1}^{\infty }\vert \hat{v}_{\varvec{\lambda }_j}\vert$. Therefore, we have $\Vert v\Vert _{L_{QP}^{\infty }(\mathbb {R}^d)}\le C\, \Vert v_p\Vert _{s}$, where C is a positive constant. Using the definition of $\Vert \cdot \Vert _{s}$ and $\Vert \cdot \Vert _{X_\alpha }$, we can obtain

$$\begin{aligned} \Vert v_p\Vert _{s} \le C\,\Vert v_p\Vert _{X_{2s}}, \end{aligned}$$

and for $0\le \alpha _1\le \alpha _2$,

$$\begin{aligned} \Vert v_p\Vert _{X_{\alpha _1}} \le \Vert v_p\Vert _{X_{\alpha _2}}. \end{aligned}$$

Combining $\alpha \ge s/2$, it follows that $\Vert v_p\Vert _{s}\le C\,\Vert v_p\Vert _{X_{\alpha }}$. Therefore, the inequality (18) holds. Further, for any $w\in L_{QP}^{2}(\mathbb {R}^d)$, we can obtain

$$\begin{aligned} \Vert vw \Vert _{L_{QP}^2(\mathbb {R}^d)} \le \Vert w\Vert _{L_{QP}^2(\mathbb {R}^d)} \cdot \Vert v \Vert _{L_{QP}^{\infty }(\mathbb {R}^d)} \le C\, \Vert w\Vert _{L_{QP}^2(\mathbb {R}^d)} \cdot \Vert v_p \Vert _{X_\alpha }. \end{aligned}$$

3.2 Convergence Analysis

This subsection presents the convergence analysis of full discretization scheme (16).

3.2.1 Main Theorem

Let $u^j_p$ denote the parent function of $u^j$, where $u^j$ is the approximate solution at $t=t_j$ exactly satisfying the scheme (12). Below, we give the main theorem of the error analysis of PM-OS2.

Theorem 2

Let $u(\cdot ,t_m)$ and $u^m_N$ be the solutions of problems (6) and (16) at $t_m$, respectively. Then under the conditions

(i) The potential V is a $\mathcal {C}^1$-smooth function and $\Vert V_p\Vert _{X_\alpha }\le C_V$, $\alpha \ge s/2> n/4$;

(ii) The parent function $u^j_p\in H^{\alpha }(\mathbb {T}^n)$ and there exists a constant $C_p$ such that $\Vert u^j_p\Vert _{\alpha }<C_p$, $0\le j\le m$;

the global error bound of PM-OS2 (16) is

$$\begin{aligned} \Vert u^m_N- u(\cdot ,t_m)\Vert _{L_{QP}^2(\mathbb {R}^d)}\le C(\tau ^2 + N^{-\alpha }). \end{aligned}$$

The constant $C>0$ depends on the bounds $C_V$, $\sup \{\Vert u(\cdot , t) \Vert _{L_{QP}^2(\mathbb {R}^d)}: 0\le t \le T \}$.

Before proving the main conclusion, we present some required results, see Sect. 3.2.2. The detailed proof of Theorem 2 is given in Sect. 3.2.3.

3.2.2 Some Results

Lemma 2

The operator A defined in (6) is self-adjoint in the inner product $L^2_{QP}$.

Proof

When $v,w\in \text{ QP }(\mathbb {R}^d)$ and are differentiable, applying the Green identity, we have

$$\begin{aligned} (Av, w)-(v, Aw)&=-(\varDelta v, w)+(v, \varDelta w)\\&=- {\mathchoice{{-\hspace{-10.55542pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}} \varDelta v\cdot w\,d\varvec{x}+ {\mathchoice{{-\hspace{-10.55542pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}{{-\hspace{-8.88885pt}\int }}} v\cdot \varDelta w\,d\varvec{x}\\&=-\lim _{L\rightarrow \infty } \frac{1}{\vert \Omega _L\vert } \int _{\partial \Omega _L} \frac{\partial v}{\partial \varvec{n}}\cdot w\,dS +\lim _{L\rightarrow \infty } \frac{1}{\vert \Omega _L\vert } \int _{\partial \Omega _L} v\cdot \frac{\partial w}{\partial \varvec{n}}\,dS, \end{aligned}$$

where $\varvec{n}$ is the outward normal of $\partial \Omega _L$. Since the quasiperiodic functions v, w are bounded, i.e., $\sup _{\varvec{x}\in \mathbb {R}^d} \{v(\varvec{x}), w(\varvec{x})\}\le C<\infty$, it follows that

$$\begin{aligned} \Big \vert \lim _{L\rightarrow \infty } \frac{1}{\vert \Omega _L\vert } \int _{\partial \Omega _L} \frac{\partial v}{\partial \varvec{n}}\cdot w\,dS \Big \vert \le \lim _{L\rightarrow \infty } \frac{C^22d(2L)^{d-1}}{(2L)^d}=0,~~ \Big \vert \lim _{L\rightarrow \infty } \frac{1}{\vert \Omega _L\vert } \int _{\partial \Omega _L} v \cdot \frac{\partial w}{\partial \varvec{n}}\,dS \Big \vert =0. \end{aligned}$$

Therefore, $(-\varDelta v,w)=(v,-\varDelta w)$ is true. The proof of this theorem is completed.

We recall some basic definitions that occur in the following.

Definition 3

The operator B is unitary if $BB^*=B^*B=\mathcal {I}$, where $\mathcal {I}$ is the identity operator and $B^*$ is adjoint operator of B.

Definition 4

A one-parametric family $\Psi (t), t\in \mathbb {R}$, of linear operators on a Banach space X is a group of operators on X if $\Psi (0)=\mathcal {I}$ and $\Psi (t+s)=\Psi (t)\Psi (s), s\in \mathbb {R}$. Moreover, $\Psi (t)$ is $C_0$-group if $\lim \limits _{t\rightarrow 0} \Psi (t) x=x,$ for all $x\in X$.

Lemma 3

(Stone Theorem [37]) Let H be a Hilbert space, and $\Psi (t)$ be a one-parameter family of linear operators on H for $t\in \mathbb {R}$.

(i) If $\Psi (t)$ is $C_0$-group of unitary operators on H, then there exists a unique self-adjoint operator A such that $\Psi (t)=e^{-itA}$, where $-iA$ is the generator.

(ii) Conversely, let A be a self-adjoint operator on H. Then $\Psi (t)=e^{-itA}$ is a $C_0$-group of unitary operator with the generator $-iA$.

Lemma 2 and Lemma 3 demonstrate $\Vert e^{-itA}\Vert _{L_{QP}^2(\mathbb {R}^d)}=1$. Next, we will give an error bound of OS2 method (12) for TQSE (6). For operators A and B, we denote the commutators $[A,B]=AB-BA$ and $[A,[A,B]]=A^2B-2ABA+BA^2$.

Lemma 4

(Theorem 2.1, [2]) Suppose that the operators $\Phi$ and $\Psi$ are self-adjoint on the space $L^2_{QP}(\mathbb {R}^d)$.

(1) Under the following conditions

(i) $\Psi$ is bounded, i.e., $\Vert \Psi v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le \beta \Vert v\Vert _{L_{QP}^2(\mathbb {R}^d)}$, where $\beta$ is a constant and $v\in L^2_{QP}(\mathbb {R}^d)$.

(ii) Commutator bound $\Vert [\Phi , \Psi ] v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le c_1 \Vert v\Vert _{H^1_{QP}}, ~\forall ~v\in H^1_{QP}(\mathbb {R}^d).$

We have

$$\begin{aligned} \Vert e^{-\frac{i}{2}\tau \Psi } e^{-i\tau \Phi } e^{-\frac{i}{2}\tau \Psi }v -e^{-i\tau (\Phi +\Psi )}v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C_1 \tau ^2 \Vert v\Vert _{L_{QP}^2(\mathbb {R}^d)}, \end{aligned}$$

where $C_1$ depends only on $c_1$ and $\beta$.

(2) Under the conditions in (1) and additionally

(iii) Commutator bound $\Vert [\Phi , [\Phi , \Psi ] ] v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le c_2 \Vert v\Vert _{L_{QP}^2(\mathbb {R}^d)}, ~\forall ~v\in L^2_{QP}(\mathbb {R}^d).$

We have

$$\begin{aligned} \Vert e^{-\frac{i}{2}\tau \Psi } e^{-i\tau \Phi } e^{-\frac{i}{2}\tau \Psi }v -e^{-i\tau (\Phi +\Psi )}v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C_2 \tau ^3 \Vert v\Vert _{L_{QP}^2(\mathbb {R}^d)}, \end{aligned}$$

where $C_2$ depends only on $c_1$, $c_2$ and $\beta$.

Theorem 3

For a quasiperiodic function V, the following conclusions are valid.

(i) If $V\in \mathcal {C}^2_{QP}(\mathbb {R}^d)$, then $\Vert \mathcal {S}v-\mathcal {T}v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C \tau ^2 \Vert v \Vert _{L_{QP}^2(\mathbb {R}^d)}$.

(ii) If $V\in \mathcal {C}^1_{QP}(\mathbb {R}^d)$, then $\Vert \mathcal {S}v-\mathcal {T}v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C \tau ^3 \Vert v \Vert _{L_{QP}^2(\mathbb {R}^d)}$.

Proof

According to Lemma 2, the operator $A=-\varDelta$ is self-adjoint in the sense of $L^2_{QP}$-norm. Next, we verify that the operators A and V satisfy commutator bounds. From the equation

$$\begin{aligned} \varDelta (\phi \psi )=(\varDelta \phi ) \psi +2(\nabla \phi ) (\nabla \psi )+ \phi (\varDelta \psi ), \end{aligned}$$

we have

$$\begin{aligned} \Vert [\varDelta , V]\phi \Vert _{L_{QP}^2(\mathbb {R}^d)} \le \Vert (\varDelta V)\phi \Vert _{L_{QP}^2(\mathbb {R}^d)} +2\Vert (\nabla V)\cdot (\nabla \phi )\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C(\Vert V\Vert _{\mathcal {C}_{QP}^2}, \Vert \phi \Vert _{1}), \end{aligned}$$

and

$$\begin{aligned} \Vert [V, [V, \varDelta ]]\phi \Vert _{L_{QP}^2(\mathbb {R}^d)} =\Vert 2 (\nabla V)(\nabla V)\phi \Vert _{L_{QP}^2(\mathbb {R}^d)} \le C(\Vert V\Vert _{\mathcal {C}_{QP}^1}, \Vert \phi \Vert ). \end{aligned}$$

Combining with the conclusions in Lemma 4, this theorem is easy to prove.

To prove the difference between $\mathcal {S}_N$ and $I_N\mathcal {S}$, we first introduce the following lemmas.

Lemma 5

It holds

$$\begin{aligned} \Vert (I_N e^{-\frac{i}{2}\tau A}-e^{-\frac{i}{2}\tau A}I_N )v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le \int ^\tau _{0} \Vert [A, I_N-\mathcal {I}] e^{-\frac{i}{2}t A} v \Vert _{L_{QP}^2(\mathbb {R}^d)} \, dt. \end{aligned}$$

Proof

Consider the following two initial value problems

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{d}{d\tau }u(\tau ) =-\dfrac{i}{2}Au(\tau ),\\ u(0)=v, \end{array}\right. } ~\text{ and }~~~~ {\left\{ \begin{array}{ll} \dfrac{d}{d\tau }w(\tau ) =-\dfrac{i}{2}Aw(\tau ),\\ w(0)=I_Nv. \end{array}\right. } \end{aligned}$$

For the initial value problem

$$\begin{aligned} \frac{d}{d\tau }(w-I_Nu)(\tau ) =-\frac{i}{2}Aw(\tau )-I_N(-\frac{i}{2}A)u(\tau ), \end{aligned}$$

(19)

with initial value $(w-I_Nu)(0)=0$, we have

$$\begin{aligned} (w-I_Nu)(\tau )=e^{-\frac{i}{2}\tau A}I_N v-I_N e^{-\frac{i}{2}\tau A}v. \end{aligned}$$

We rewrite (19) as

$$\begin{aligned} \frac{d}{d\tau }(w-I_Nu)(\tau ) =-\frac{i}{2}A(w-I_Nu)(\tau )-\frac{i}{2}AI_Nu(\tau )-I_N(-\frac{i}{2}A)u(\tau ). \end{aligned}$$

Applying the linear variation-of-constants formula, we obtain

$$\begin{aligned} (w-I_Nu)(\tau )&=e^{-\frac{i}{2}A\tau }(w-I_Nu)(0) +\int ^{\tau }_{0}e^{-\frac{i}{2}A(t-\tau )}[-\frac{i}{2}A,I_N] e^{-\frac{i}{2}t A} v\,dt \nonumber \\&=\int ^{\tau }_{0}e^{-\frac{i}{2}A(t-\tau )}[-\frac{i}{2}A, I_N-\mathcal {I}] e^{-\frac{i}{2} t A} v\,dt. \end{aligned}$$

(20)

For any $v\in L^2_{QP}(\mathbb {R}^d)$, applying Lemma 3, it follows that

$$\begin{aligned} \Vert e^{-\frac{i}{2}\tau A} v\Vert _{L_{QP}^2(\mathbb {R}^d)} =\Vert v\Vert _{L_{QP}^2(\mathbb {R}^d)}, \end{aligned}$$

(21)

then $(e^{-\frac{i}{2}\tau A})_{\tau \in \mathbb {R}}$ on $L_{QP}^{2}(\mathbb {R}^d)$ is a unitary group. Combining with the formula (20), this completes the proof.

Lemma 6

Assume that there exists a constant $C_V>0$ such that $\Vert V_p\Vert _{X_\alpha }\le C_V$. Then we have

$$\begin{aligned} \Vert I_N e^{-i\tau V} v\Vert _{L_{QP}^2(\mathbb {R}^d)} \le e^{CC_V\tau } \Vert I_N v\Vert _{L_{QP}^2(\mathbb {R}^d)},~~v\in L_{QP}^2(\mathbb {R}^d), \end{aligned}$$

where $\tau \in [0,T]$ and C is a constant.

Proof

Consider the problem

$$\begin{aligned} I_N \frac{d}{d\tau }u(\tau )=I_N(-iV)u(\tau ),~~\tau \in [0,T], \end{aligned}$$

(22)

with initial value $I_Nu(0)=I_Nv$. We can obtain

$$\begin{aligned} I_Nu(\tau )=I_N e^{-i\tau V} v. \end{aligned}$$

For any $v_1\in L_{QP}^\infty (\mathbb {Q}_N),~v_2\in L_{QP}^2(\mathbb {R}^d)$, assume that $v_{p_1}\in X_{\alpha }$ is the parent function of $v_1$. Using Theorem 1, we have

$$\begin{aligned} \Vert I_N (v_1v_2) \Vert _{L_{QP}^2(\mathbb {R}^d)} \le \Vert v_1 \Vert _{L_{QP}^{\infty }(\mathbb {Q}_N)}\Vert I_N v_2\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C\,\Vert v_{p_1} \Vert _{X_{\alpha }}\Vert I_N v_2\Vert _{L_{QP}^2(\mathbb {R}^d)}. \end{aligned}$$

Integrating (22) from 0 to $\tau$ yields

$$\begin{aligned} \Vert I_Nu\Vert _{L_{QP}^2(\mathbb {R}^d)}&\le \Vert I_N v \Vert _{L_{QP}^2(\mathbb {R}^d)} +\int ^\tau _{0} \Vert I_NVu(t)\Vert _{L_{QP}^2(\mathbb {R}^d)}\,dt\le \Vert I_Nv \Vert _{L_{QP}^2(\mathbb {R}^d)} +C\Vert V_p \Vert _{X_{\alpha }}\int ^\tau _{0} \Vert I_Nu\Vert _{L_{QP}^2(\mathbb {R}^d)}\,dt\\&\le \Vert I_N v \Vert _{L_{QP}^2(\mathbb {R}^d)} +CC_V\int ^\tau _{0} \Vert I_Nu\Vert _{L_{QP}^2(\mathbb {R}^d)}\,dt. \end{aligned}$$

Then we can prove the theorem by applying the Gronwall inequality.

The error analysis of PM in the sense of $L^2_{QP}$-norm is as follows.

Lemma 7

([27]) Suppose that $u(\varvec{x})\in \text{ QP }(\mathbb {R}^d)$ and its parent function $u_p(\varvec{y})\in H^{\alpha }(\mathbb {T}^n)$ with $\alpha > n/2$. There exists a constant C, independent of $u_p$ and N, such that

$$\begin{aligned} \Vert I_N u-u\Vert _{L_{QP}^2(\mathbb {R}^d)} \le CN^{-\alpha }\vert u_p \vert _\alpha . \end{aligned}$$

Now, we analyze the difference between $\mathcal {S}_N$ and $I_N\mathcal {S}$. Let $u_p$, $v_p$ and $w_p$ be the parent functions of quasiperiodic functions u, v and w, respectively.

Theorem 4

For $u\in \text{ QP }(\mathbb {R}^d)$, $v =\mathcal {S}u$ and $w= e^{-\frac{i}{2}\tau A}u$. Assume that $\Vert V_p \Vert _{X_\alpha } \le C_V$ and $u_p,~v_p,~w_p\in H^{\alpha }(\mathbb {T}^n)$ with $\alpha \ge s/2> n/4$. Then we have

$$\begin{aligned} \Vert \mathcal {S}_N(u)-I_N\mathcal {S}(u)\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C\tau N^{-\alpha } (\vert v_p\vert _\alpha +\vert w_p\vert _\alpha ), \end{aligned}$$

where C is a constant.

Proof

Since

$$\begin{aligned} I_N\mathcal {S}(u)-\mathcal {S}_N(u)&=I_N e^{-\frac{i}{2}\tau A} e^{-i\tau V} e^{-\frac{i}{2}\tau A}u -e^{-\frac{i}{2}\tau A}I_N e^{-i\tau V}I_N e^{-\frac{i}{2}\tau A} I_Nu\\&=I_N e^{-\frac{i}{2}\tau A} e^{-i\tau V} e^{-\frac{i}{2}\tau A}u- e^{-\frac{i}{2}\tau A} I_N e^{-i\tau V} e^{-\frac{i}{2}\tau A}u\\&~~+e^{-\frac{i}{2}\tau A} I_N e^{-i\tau V} e^{-\frac{i}{2}\tau A}u- e^{-\frac{i}{2}\tau A} I_N e^{-i\tau V} I_N e^{-\frac{i}{2}\tau A}u\\&~~+e^{-\frac{i}{2}\tau A} I_N e^{-i\tau V} I_N e^{-\frac{i}{2}\tau A}u -e^{-\frac{i}{2}\tau A}I_N e^{-i\tau V}I_N e^{-\frac{i}{2}\tau A} I_Nu\\&=Z_1+Z_2+Z_3. \end{aligned}$$

Then we estimate the bounds of $\Vert Z_1 \Vert _{L_{QP}^2(\mathbb {R}^d)}$, $\Vert Z_2 \Vert _{L_{QP}^2(\mathbb {R}^d)}$ and $\Vert Z_3 \Vert _{L_{QP}^2(\mathbb {R}^d)}$, respectively.

(i) For $Z_1$ and using Lemma 5, we have

$$\begin{aligned} \Vert Z_1 \Vert _{L_{QP}^2(\mathbb {R}^d)}&=\Vert (I_N e^{-\frac{i}{2}\tau A}-e^{-\frac{i}{2}\tau A} I_N) e^{-i\tau V} e^{-\frac{i}{2}\tau A}u\Vert _{L_{QP}^2(\mathbb {R}^d)} \\&\le \int ^\tau _{0} \Vert [A (I_N-\mathcal {I})- (I_N-\mathcal {I})A] e^{-\frac{i}{2} t A}e^{-i t V} e^{-\frac{i}{2} t A}u \Vert _{L_{QP}^2(\mathbb {R}^d)}\,dt \\&=\int ^\tau _{0} \Vert [A (I_N-\mathcal {I})- (I_N-\mathcal {I})A]v \Vert _{L_{QP}^2(\mathbb {R}^d)}\,dt \end{aligned}$$

where $v=\mathcal {S}u$. Since $\vert v_p \vert _\alpha < +\infty$, applying Lemma 7, it follows that

$$\begin{aligned} \Vert Z_1 \Vert _{L_{QP}^2(\mathbb {R}^d)}\le C \tau N^{-\alpha } \vert v_p \vert _\alpha . \end{aligned}$$

(ii) For $Z_2$, using (21) and Lemma 6, we have

$$\begin{aligned} \Vert Z_2 \Vert _{L_{QP}^2(\mathbb {R}^d)}&=\Vert e^{-\frac{i}{2}\tau A} I_N e^{-i\tau V}( e^{-\frac{i}{2}\tau A}u -I_N e^{-\frac{i}{2}\tau A} u)\Vert _{L_{QP}^2(\mathbb {R}^d)}\\&= \Vert I_N e^{-i\tau V} (e^{-\frac{i}{2}\tau A}u -I_N e^{-\frac{i}{2}\tau A} u)\Vert _{L_{QP}^2(\mathbb {R}^d)}\\&\le e^{CC_V\tau } \Vert I_N (e^{-\frac{i}{2}\tau A}u -I_N e^{-\frac{i}{2}\tau A} u)\Vert _{L_{QP}^2(\mathbb {R}^d)}=0. \end{aligned}$$

(iii) For $Z_3$, using (21), Lemma 5 and Lemma 6, we have

$$\begin{aligned} \Vert Z_3 \Vert _{L_{QP}^2(\mathbb {R}^d)}&=\Vert e^{-\frac{i}{2}\tau A} I_N e^{-i\tau V} (I_N e^{-\frac{i}{2}\tau A}u - I_N e^{-\frac{i}{2}\tau A}I_N u) \Vert _{L_{QP}^2(\mathbb {R}^d)}\\&\le e^{CC_V\tau }\Vert I_N (I_N e^{-\frac{i}{2}\tau A}u - I_N e^{-\frac{i}{2}\tau A}I_N u) \Vert _{L_{QP}^2(\mathbb {R}^d)}\\&=e^{CC_V\tau }\Vert (I_N e^{-\frac{i}{2}\tau A} -e^{-\frac{i}{2}\tau A}I_N) u \Vert _{L_{QP}^2(\mathbb {R}^d)}\\&\le e^{CC_V\tau } \int ^\tau _{0} \Vert [A, I_N-\mathcal {I}] e^{-\frac{i}{2} t A} u \Vert _{L_{QP}^2(\mathbb {R}^d)}\, dt \\&\le C \tau N^{-\alpha } \vert w_p \vert _\alpha . \end{aligned}$$

3.2.3 The Proof of Theorem 2

Using the triangle inequality, we have

$$\begin{aligned} \Vert u^m_N- u(\cdot ,t_m)\Vert _{L_{QP}^2(\mathbb {R}^d)}\le \Vert u^m_N- u^m\Vert _{L_{QP}^2(\mathbb {R}^d)}+ \Vert u^m- u(\cdot , t_m)\Vert _{L_{QP}^2(\mathbb {R}^d)}, \end{aligned}$$

where $u^m$ is the splitting solution of the scheme (12) at $t=t_m$ with $u^0=u_0$. We now apply the Lady Windermere’s fan to represent the global errors as follows

$$\begin{aligned}&u^m- u(\cdot , t_m)=\mathcal {S}^m u_0-\mathcal {T}^m u_0=\sum ^{m-1}_{j=0} \mathcal {S}^{m-j-1}(\mathcal {S}-\mathcal {T})\mathcal {T}^{j}u_0,\\&u^m_N- u^m=\mathcal {S}_N^m u_0-\mathcal {S}^m u_0=(I_N-\mathcal {I})u^m+\sum ^{m}_{j=1} \mathcal {S}_N^{m-j}(\mathcal {S}_N(u^{j-1})-I_N\mathcal {S}(u^{j-1})). \end{aligned}$$

Applying Theorem 3, we have

$$\begin{aligned} \Vert u^m- u(\cdot , t_m)\Vert _{L_{QP}^2(\mathbb {R}^d)}&=\Big \Vert \sum ^{m-1}_{j=0} \mathcal {S}^{m-j-1}(\mathcal {S}-\mathcal {T})\mathcal {T}^{j}u_0\Big \Vert _{L_{QP}^2(\mathbb {R}^d)}\\&\le \sum ^{m-1}_{j=0}\Vert \mathcal {S}-\mathcal {T}\Vert _{L_{QP}^2(\mathbb {R}^d)} \cdot \Vert \mathcal {T}^{j}u_0 \Vert _{L_{QP}^2(\mathbb {R}^d)}\\&\le C\tau ^2 \sup _{0\le t\le T}\Vert u(\cdot ,t) \Vert _{L_{QP}^2(\mathbb {R}^d)}. \end{aligned}$$

Considering the regularity of the solution, then

$$\begin{aligned} \Vert u^m_N- u^m \Vert _{L_{QP}^2(\mathbb {R}^d)}&\le \Vert (I_N-\mathcal {I})u^m\Vert _{L_{QP}^2(\mathbb {R}^d)} + \Big \Vert \sum ^{m}_{j=1} \mathcal {S}_N^{m-j}(\mathcal {S}_N(u^{j-1})-I_N\mathcal {S}(u^{j-1})) \Big \Vert _{L_{QP}^2(\mathbb {R}^d)} \\&\le CN^{-\alpha } \vert u_p^m\vert _{\alpha } + \sum ^{m}_{j=1} e^{CC_V(m-j)\tau } \Vert \mathcal {S}_N(u^{j-1})-I_N\mathcal {S}(u^{j-1})\Vert _{L_{QP}^2(\mathbb {R}^d)}\\&\le CN^{-\alpha } \vert u_p^m\vert _{\alpha } + C m\tau N^{-\alpha }\max _{0\le j\le m-1} \vert u_p^{j}\vert _{\alpha }\\&\le CN^{-\alpha } \max _{0\le j\le m} \vert u_p^{j}\vert _{\alpha }. \end{aligned}$$

Therefore, the desired result can be directly obtained from the above two estimates. The proof of Theorem 2 is complete.

The above analysis framework of the PM-OS2 is also applicable to the QSM-OS2, showing spectral convergence rate in space and second-order accuracy in time. Besides, since QSM is essentially a generalization of Fourier spectral method, we can offer another way to analyze QSM. Concretely, similar to the analytical framework of Fourier spectral method to solve the Schrödinger equation with periodic potentials [2], we give the error analysis of QSM-OS2 based on the embedding theorem of quasiperiodic function space, see Appendix 1 for details.

4 Numerical Results

In this section, we provide some numerical experiments to verify the accuracy and performance of QSM-OS2 and PM-OS2 for solving TQSE (1). In the following numerical results, we only show the quasiperiodic structure in the finite domain. It also should be emphasized that the developed methods have obtained a global quasiperiodic solution over $\mathbb {R}^d$. All algorithms are implemented using MSVC++ 14.29 on Visual Studio Community 2019. The software of FFTW 3.3.5 is used to compute FFT [38]. All computations are performed on a workstation with an Intel Core 2.30GHz CPU, 16GB RAM. Let CPU(s) denote the computational time in seconds. For QSM-OS2, let $k=5$ in (17).

Our numerical examples focus on verifying the accuracy in space direction and the error order in time direction. We use $L_{QP}^2$-norm to measure the numerical error

$$\begin{aligned} \text{ Err}^\tau _{h}=\Vert u^M_N- u(\cdot ,T)\Vert _{L_{QP}^2(\mathbb {R}^d)}, \end{aligned}$$

where $\tau$ is the time step size and h is the mesh size of the n-dimensional torus. The error order in time direction is calculated by

$$\begin{aligned} \text{ Ord }=\frac{\ln (\text{ Err}^{\tau _1}_{h}/\text{Err}^{\tau _2}_{h})}{\ln (\tau _{1}/\tau _{2})}. \end{aligned}$$

In the following one- and two-dimensional numerical experiments, we can obtain the corresponding reference solution $u(\varvec{x},T)$ on $\mathbb {R}^d$ by using PM-OS2, but show partial morphology of solution in the finite region.

4.1 One-Dimensional Case

Consider one dimensional TQSE (1) with the incommensurate potential

$$\begin{aligned} V(x)=2(\cos x+\cos \sqrt{3}x), \end{aligned}$$

and initial value

$$\begin{aligned} u_0(x)=\sum _{\lambda \in \sigma (u_0)}\hat{u}_{\lambda }e^{i\lambda x}, \end{aligned}$$

where $\hat{u}_{\lambda }=e^{-(\vert m_1\vert +\vert m_2\vert )}$ and $\sigma (u_0)=\{\lambda = m_1+m_2\sqrt{3}: m_1,m_2\in \mathbb {Z}, -32\le m_1,m_2\le 31\}$.

As a result, the final time T can be arbitrarily chosen. For simplicity, we choose $T=0.001$. The reference solution on $\mathbb {R}$ is obtained by using PM-OS2 with the time step size $\tau =1\times 10^{-8}$ and the mesh size of the two-dimensional torus $h=\pi /128$ in each space direction. Figure 1 only shows the distribution of the probability density function $\vert u(x,T) \vert ^2$ in $x\in [0,240\pi )$ and corresponding diffraction pattern of the reference solution, respectively. In the right plot of Fig. 1, we can see that the dots of different colors are constantly alternating and the distribution Fourier exponent has rotational symmetry but no translational symmetry.

Fig. 1

The reference solution of one-dimensional TQSE. Left: Probability density distribution $\vert u(x,T) \vert ^2$ in $x\in [0,240\pi )$. Right: Distribution of Fourier exponents $\mathbf \lambda$ when $\vert \hat{u}_\mathbf{\lambda }\vert >8.620\text{ e- }02$. We arrange the values of $\vert \hat{u}_\mathbf{\lambda }\vert$ from largest to smallest, then red, purple and blue dots represent the order of $\vert \hat{u}_\mathbf{\lambda }\vert$ at the corresponding Fourier exponents from the largest to the smallest, respectively

We first show the convergence rate when solving TQSE using PM and QSM in space direction. Set the time step size $\tau =1\times 10^{-6}$, Table 1 shows numerical error $\text{ Err}^\tau _{h}$ and the required CPU time of PM-OS2 and QSM-OS2, respectively. We find that $\text{ Err}^\tau _{h}$ fast decays as N increases due to the smoothness of wave function u(x, t). Meanwhile, the CPU time of PM is less than that of QSM since PM can use 2D FFT. Figure 2 further details CPU time of both methods as N increases.

Table 1 Numerical error $\text{ Err}^\tau _{h}$ and CPU time of PM-OS2 and QSM-OS2 for different N and $\tau =1\times 10^{-6}$

Fig. 2

CPU time between PM-OS2 and QSM-OS2 against N

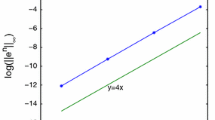
Next, we verify the error order of applying OS2 method to solve TQSE in time direction. Meanwhile, we choose $h=\pi /128$ to make the approximation error in space direction that does not affect the error in time direction. From the numerical results shown in Table 1, PM-OS2 and QSM-OS2 have the same convergence rate in space direction, while the PM-OS2 is more efficient in CPU time. Therefore, the time error of both methods is the same and we only present the temporal error of PM-OS2, see Table 2.

Table 2 Temporal error test of PM-OS2 with $h=\pi /128$

4.2 Two-Dimensional Cases

In this subsection, we further demonstrate that the PM is a high-precision and efficient algorithm to solve TQSE through the two-dimensional example. Consider the potential function

$$\begin{aligned} V(\varvec{x})=\sum _{j=1}^{5} e^{i (\varvec{P}_1\varvec{k}_j)\cdot \varvec{x}}-e^{i (\varvec{P}_1\varvec{k}_6)\cdot \varvec{x}}, ~~\varvec{x}\in \mathbb {R}^2, \end{aligned}$$

where

$$\begin{aligned} (\varvec{k}_1, \varvec{k}_2, \varvec{k}_3,\varvec{k}_4,\varvec{k}_5,\varvec{k}_6)= \begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0\\ 1 & -1& 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & -1\\ 0 & 0 & 0 & 1 & 0 & 0 \end{pmatrix}, \end{aligned}$$

and the corresponding projection matrix

$$\begin{aligned} \varvec{P}_1 = \begin{pmatrix} 1 & \cos (\pi /4) & 0 & -\cos (\pi /4) \\ 0 & \sin (\pi /4) & 1 & \sin (\pi /4) \end{pmatrix}. \end{aligned}$$

Therefore, this quasiperiodic system can be embedded into a four-dimensional parent system. Let the initial value

$$\begin{aligned} u_0(\varvec{x})=\sum _{\varvec{\lambda }\in \sigma _1(u_0)}e^{-(\vert k_1\vert +\vert k_2\vert +\vert k_3\vert +\vert k_4\vert )} e^{i\varvec{\lambda }\cdot \varvec{x}},~~\varvec{\lambda }= \varvec{P}_1\varvec{k}, \end{aligned}$$

where $\sigma _1(u_0)=\{\varvec{\lambda }= \varvec{P}_1\varvec{k}: k_1, k_2, k_3, k_4\in \mathbb {Z}, -16\le k_1, k_2, k_3,k_4\le 15\}.$

The reference solution on $\mathbb {R}^2$ is given by PM-OS2 under $\tau =1\times 10^{-7}$ and the mesh size of the four-dimensional torus $h=\pi /64$ in each space direction. Let $T=0.001$, in Fig. 3, we only present the distribution of the probability density function $\vert u(\varvec{x},T) \vert ^2$ and the corresponding diffraction pattern of the reference solution when $\varvec{x}\in [0,80\pi )^2$, respectively. The structure shown in Fig. 3 is a typical octagonal quasicrystal. The reciprocal space, shown on the right plot of Fig. 3, indicates octagonal rotational symmetry.

Fig. 3

The reference solution of two-dimensional TQSE. Left: Probability density distribution $\vert u(\varvec{x},T) \vert ^2$ in $\varvec{x}\in [0,80\pi )^2$. Right: Distribution of Fourier exponents $\varvec{\lambda }$ when $\vert \hat{u}_{\varvec{\lambda }} \vert >23.970$. By arranging the values of $\vert \hat{u}_{\varvec{\lambda }}\vert$ from largest to smallest, red, purple and blue dots represent the distribution of Fourier exponents corresponding to the first, first nine and first twenty-five values of $\vert \hat{u}_{\varvec{\lambda }}\vert$, respectively

Table 3 shows the numerical error $\text{ Err}^\tau _{h}$ and CPU time of PM-OS2. Obviously, the PM-OS2 has spectral convergence rate. When the fine mesh size $h=\pi /16$, the numerical error in space does not affect the error in time direction. Table 4 verifies that the PM-OS2 has second-order error accuracy in time direction with $h=\pi /16$.

Table 3 Numerical error $\text{ Err}^\tau _{h}$ and CPU time of PM-OS2 for different N

Table 4 Temporal error test of PM-OS2 with $h=\pi /16$

Furthermore, by changing the projection matrix and the initial value, we can obtain different quasicrystal. Let projection matrix be

$$\begin{aligned} \varvec{P}_2 = \begin{pmatrix} 1 & \cos (\pi /6) & \cos (\pi /3) & 0\\ 0 & \sin (\pi /6) & \sin (\pi /3) & 1 \end{pmatrix}, \end{aligned}$$

and initial value be

$$\begin{aligned} u_0(\varvec{x})=\sum _{\varvec{\lambda }\in \sigma _2(u_0)}e^{-\Vert \varvec{\lambda }\Vert ^2} e^{i\varvec{\lambda }\cdot \varvec{x}}, \end{aligned}$$

where $\sigma _2(u_0)=\{\varvec{\lambda }= \varvec{P}_2\varvec{k}: k_1, k_2, k_3, k_4\in \mathbb {Z}, -8\le k_1, k_2, k_3, k_4\le 7\}$, we can obtian the dodecagonal quasicrystal as shown in Fig. 4 under the time step size $\tau =1\times 10^{-7}$ and the mesh size $h=\pi /32$ of the four-dimensional torus.

Fig. 4

The reference solution of two-dimensional TQSE. Left: Probability density distribution $\vert u(\varvec{x},T) \vert ^2$, $\varvec{x}\in [0,120\pi )^2$. Right: Distribution of Fourier exponents $\varvec{\lambda }$ when $\vert \hat{u}_{\varvec{\lambda }} \vert >0.044$. We arrange the values of $\vert \hat{u}_{\varvec{\lambda }}\vert$ from largest to smallest, then red, purple and blue dots represent the distribution of Fourier exponents corresponding to the first, first thirteen and first thirty-seven values of $\vert \hat{u}_{\varvec{\lambda }}\vert$, respectively

5 Conclusions

In this paper, two high-accuracy numerical methods, the QSM-OS2 and PM-OS2, have been developed to solve arbitrary dimensional TQSE (1) and to obtain global quasiperiodic solutions. A rigorous convergence analysis shows that QSM-OS2 and PM-OS2 have spectral convergence rates in space when the potential function has enough regularity and second-order accuracy in time. Meanwhile, the computational complexity analysis demonstrates that the PM-OS2 is more efficient than the QSM-OS2. One- and two-dimensional numerical experiments have verified the theoretical results. For the nonlinear QSEs, it needs to explore the in-depth relationship between quasiperiodic functions and periodic parent functions. We will discuss the nonlinear cases in the future work.

A Another Way to Analyze QSM-OS2

The QSM is an extension of Fourier spectral method. Based on the embedding theorem of the quasiperiodic function given below, we can give the convergence analysis of QSM-OS2. Firstly, we give the following embedding theorem. Similar to the definition of $X_{\alpha }$ on a torus $\mathbb {T}^n$, we define the quasiperiodic function space $\mathcal {X}_{\alpha }$ on $\mathbb {R}^d$

$$\begin{aligned} \mathcal {X}_{\alpha }= \Big \{f(\varvec{x})=\sum _{\varvec{\lambda }\in \sigma (f)} \hat{f}_{\varvec{\lambda }}e^{i\varvec{\lambda }\cdot \varvec{x}}\in L_{QP}^2(\mathbb {R}^d): \Vert (-\varDelta )^\alpha f \Vert ^2 =\sum _{\varvec{\lambda }\in \sigma (f)} \vert \hat{f}_{\varvec{\lambda }}\vert ^2\cdot \Vert \varvec{\lambda }\Vert ^{4\alpha } <\infty \Big \}. \end{aligned}$$

Theorem 5

For any $f\in \text{ QP }(\mathbb {R}^d)$. Assume that $\alpha \ge s/2$ and

$$\begin{aligned} \sum ^{\infty }_{j=1} (1+\vert \varvec{\lambda }_j \vert ^2)^{-s} <+\infty . \end{aligned}$$

Then, the bound

$$\begin{aligned} \Vert f\Vert _{L_{QP}^{\infty }(\mathbb {R}^d)}\le C\, \Vert f\Vert _{s} \le C\, \Vert f\Vert _{\mathcal {X}_{\alpha }} \end{aligned}$$

is valid and the following estimate

$$\begin{aligned} \Vert w f \Vert _{L_{QP}^2(\mathbb {R}^d)}\le C \, \Vert w \Vert _{L_{QP}^2(\mathbb {R}^d)}\cdot \Vert f\Vert _{\mathcal {X}_\alpha }, ~~w\in L_{QP}^{2}(\mathbb {R}^d),~~f\in \mathcal {X}_{\alpha } \end{aligned}$$

holds where C is a constant.

Proof

By the Hölder inequality, we have

$$\begin{aligned} \sum ^{p}_{j=1}\vert \hat{f}_{\varvec{\lambda }_j}\vert&=\sum ^{p}_{j=1}\vert \hat{f}_{\varvec{\lambda }_j}\vert \cdot (1+\vert \varvec{\lambda }_j \vert ^2)^{s/2} \cdot (1+\vert \varvec{\lambda }_j \vert ^2)^{-s/2}\\&\le \Big ( \sum ^{p}_{j=1}\vert \hat{f}_{\varvec{\lambda }_j}\vert ^{2} (1+\vert \varvec{\lambda }_j \vert ^2)^{s} \Big )^{\frac{1}{2}} \cdot \Big (\sum ^{p}_{j=1} (1+\vert \varvec{\lambda }_j \vert ^2)^{-s}\Big )^{\frac{1}{2}}. \end{aligned}$$

Set $p\rightarrow \infty$, it follows that

$$\begin{aligned} \sum ^{\infty }_{j=1}\vert \hat{f}_{\varvec{\lambda }_j}\vert&\le \Big ( \sum ^{\infty }_{j=1}\vert \hat{f}_{\varvec{\lambda }_j}\vert ^{2} (1+\vert \varvec{\lambda }_j \vert ^2)^{s} \Big )^{\frac{1}{2}} \cdot \Big ( \sum ^{\infty }_{j=1} (1+\vert \varvec{\lambda }_j \vert ^2)^{-s}\Big )^{\frac{1}{2}}\\&=\Vert f \Vert _{H^s_{QP}(\mathbb {R}^d)} \cdot \Big ( \sum ^{\infty }_{j=1} (1+\vert \varvec{\lambda }_j \vert ^2)^{-s}\Big )^{\frac{1}{2}}. \end{aligned}$$

For $f\in H^s_{QP}(\mathbb {R}^d)$, then $f\in L^1_{QP}(\mathbb {R}^d)$ and the Bohr-Fourier series of f is absolutely convergence. This means that it converges uniformly to f. Consequently,

$$\begin{aligned} \Vert f\Vert _{L_{QP}^{\infty }(\mathbb {R}^d)} \le \sum ^{\infty }_{j=1}\vert \hat{f}_{\varvec{\lambda }_j}\vert \le C \Vert f \Vert _{H^s_{QP}(\mathbb {R}^d)}, \end{aligned}$$

where C is a constant. Similar to the proof of Theorem 1, this theorem is proved.

The error analysis of QSM without the help of parent functions is given below, see [27] for details.

Theorem 6

([27]) Suppose that $f\in H^{\alpha }_{QP}(\mathbb {R}^d)$ and the nonzero minimum singular value $\sigma _{\min }(\varvec{P})$ of the projection matrix $\varvec{P}$ satisfies $\sigma _{\min }(\varvec{P})>\theta >0$. Then, there exists a constant $C(\theta )$, independent of f and N, such that

$$\begin{aligned} \Vert \mathcal {P}_N f-f\Vert _{L_{QP}^2(\mathbb {R}^d)} \le C(\theta ) N^{-\alpha }\vert f \vert _\alpha . \end{aligned}$$

Jahnke et al. have proved the convergence analysis by applying OS2 method in time and the Fourier pseudo-spectral method in space to solve the Schrödinger equation with periodic potentials [2]. Therefore, based on Theorems 5 and 6, similar to the analysis in [2], we can obtain the error analysis of QSM-OS2.

Theorem 7

Let $u(\cdot ,t_m)$ and $u^m_N$ be the solutions of problems (6) and (15) at $t_m$, respectively. Then under the conditions

(i) The potential V is a $\mathcal {C}^1$-smooth function and $\Vert V\Vert _{\mathcal {X}_\alpha }\le C$, $\alpha \ge s/2$;

(ii) The quasiperiodic function $u^j\in H_{QP}^{\alpha }(\mathbb {R}^d)$ and there exists a constant $C_q$ such that $\Vert u^j\Vert _{\alpha }<C_q$, $0\le j\le m$;

the global error bound of QSM-OS2 (15) is

$$\begin{aligned} \Vert u^m_N- u(\cdot ,t_m)\Vert _{L_{QP}^2(\mathbb {R}^d)}\le C(\tau ^2 + N^{-\alpha }). \end{aligned}$$

The constant $C>0$ depends on $C_V$, $\sup \{\Vert u(\cdot , t) \Vert _{L_{QP}^2(\mathbb {R}^d)}: 0\le t \le T \}$.