1 Introduction

Fractional calculus is introduced to fill the existing gap for describing different phenomena in real life. After introducing fractional calculus, many problems in physics, chemistry, biology, and engineering are modeled as fractional differential equations (Dabiri and Butcher 2017), fractional partial differential equations (Moghaddam and Machado 2017), or fractional integral equations. For example Bagley–Torvik equation (Youssri 2017), Nizhnik–Novikov–Veselov equations (Osman 2017), evolution equations (Abdel-Gawad and Osman 2013), and fractional diffusion equation (Yang et al. 2016). There are numerous methods for solving these equations like homotopy perturbation method (Pandey et al. 2009), Adomian decomposition method (Li and Wang 2009), wavelet method (Lepik 2009), Lucas polynomial sequence approach (Abd-Elhameed and Youssri 2017a), orthonormal Chebyshev polynomial method (Abd-Elhameed and Youssri 2017b), and many other methods which are not mentioned them, here.

Since 1960, by increasing computational power, some random factors are inserted to deterministic integral equations and are created stochastic integral equations such as stochastic integral equations (Mohammadi 2015) or stochastic integro-differential equations (Dareiotis and Leahy 2016; Mei et al. 2016). In more cases, the analytical solutions of these equations are not exist or finding their analytic solution is very difficult. Thus, presenting an accurate numerical method is an essential requirement in numerical analysis. Numerical solution of stochastic integral equations because of the randomness has its own difficulties. In recent years, mathematicians studied numerous methods to obtain the numerical solution of stochastic differential equations (Higham 2001; Tocino and Ardanuy 2002; Dehghan and Shirzadi 2015; Kamrani 2015; Gong and Rui 2015; Mao 2015; Zhou and Hu 2016) or stochastic integral equations (Mirzaee and Samadyar 2017a, b; Mirzaee et al. 2017, 2018; Mirzaee and Samadyar 2018a, b, c). The reader should know the concept of independence, expected values, variance, and fundamental definition of stochastic process which are necessary to read papers in this field.

According to the above explanations, two-dimensional stochastic fractional integral equations are used to model various problems occur in different sciences (Denisov et al. 2009). In many cases, these equations can not be solved analytically. Therefore, presenting an accurate and efficient numerical method is an essential requirement in numerical analysis. In this paper, numerical solution of 2DSFIEs via two-dimensional hat basis functions are investigated. In general, 2DSFIEs have the following form:

$$\begin{aligned} f(x,y)=&\,g(x,y)+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1}k_1(x,y,s,t)f(s,t)\mathrm{d}t\mathrm{d}s\nonumber \\&+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1}k_2(x,y,s,t)f(s,t)\mathrm{d}B(t)\mathrm{d}B(s), \end{aligned}$$
(1)

where \((x,y)\in D=([0,T]\times [0,T])\) and \(r=(r_1,r_2)\in (0,\infty )\times (0,\infty )\). In addition, g(x, y), \(k_1(x,y,s,t)\) and \(k_2(x,y,s,t)\) are the known and continuous functions and f(x, y) is unknown function which should be approximated. Moreover, \(\Gamma \) denotes Gamma function and B(t) is Brownian motion process which satisfies the following properties:

  • \(B(t)-B(s)\) for \(t>s\) is independent of the past. That means for \(0<u<v<s<t<T\), the increments \(B(t)-B(s)\) and \(B(v)-B(u)\) are independent.

  • The increment \(B(t)-B(s)\) for \(t>s\) has Normal distribution with mean zero and variance \(t-s\).

  • B(t) for \(t\ge 0\) are continuous functions of t.

In this paper, we use hat basis functions to get numerical solution of 2DSFIEs. Different advantages with the proposed numerical method are listed as follows:

\(\checkmark \) :

Using these functions, equation under consideration is converted to a system of algebraic equations which can be easily solved.

\(\checkmark \) :

The proposed scheme is convergent and the rate of convergence is \(O(h^2)\).

\(\checkmark \) :

The unknown coefficients of the approximation of the function with these basis are easily calculated without any integration. Therefore, the computational cost of the proposed numerical method is low.

\(\checkmark \) :

Because of the simplicity of hat functions, this method is a powerful mathematical tool to solve various kinds of equations with little additional works.

Using a linear mapping, any closed interval [0, T] can be converted to closed interval [0, 1]. Therefore, we let \(T=1\) in Sects. 5 and 6.

2 Fundamental concepts

2.1 Fractional calculus

There are many definitions for fractional integrals and fractional derivatives. For example the Riemann–Liouville, Caputo, Weil, Hadamard, Riesz, Grunwald–Letnikov and Erdelyi–Kober. Among them, Riemann–Liouville definition usually is used for fractional integrals, whereas the Caputo definition is frequently applied for fractional derivatives (Podlubny 1999; Kilbas et al. 2006).

Definition 1

The definition of Riemann–Liouville fractional integral operator \(I^{r_1}\) of order \(r_1>0\) on \(L^1[a,b]\) is as follows Asgari and Ezzati (2017):

$$\begin{aligned} (I^{r_1} f)(x)=\frac{1}{\Gamma (r_1)}\int _0^x(x-y)^{r_1-1}f(y)\mathrm{d}y. \end{aligned}$$
(2)

The most important properties of operator \(I^{r_1}\) are listed in the following:

  1. 1.

    \((I^0f)(x)=f(x)\),

  2. 2.

    \((I^{r_1}I^{r_2}f)(x)=(I^{r_1+r_2}f)(x)\),

  3. 3.

    \((I^{r_1}I^{r_2}f)(x)=(I^{r_2}I^{r_1}f)(x)\).

Definition 2

Let \(r=(r_1,r_2)\in (0,\infty )\times (0,\infty )\) and \(f(x,y)\in L^1(D)\). The definition of left-side mixed Riemann–Liouville fractional integral f of order r is as follows Vityuk and Golushkov (2004):

$$\begin{aligned} (I^rf)(x,y)=\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1}f(s,t)\mathrm{d}t\mathrm{d}s. \end{aligned}$$
(3)

2.2 Hat functions and their properties

In this section, we define one-dimensional (1D) and two-dimensional (2D) hat basis functions and use them to construct a new efficient method for solving 2DSFIEs, numerically.

2.2.1 1D-hat basis functions

1D-hat basis functions usually are defined on the interval [0, 1]. In the following definition, we present the more general case and extend the interval [0, 1] to the interval [0, T]. The interval [0, T] is divided to n subintervals of equal lengths h where \(h=\frac{T}{n}\).

Definition 3

The family of first \((n+1)\) 1D-hat basis functions on the interval [0, T] are defined as follows Babolian et al. (2009):

$$\begin{aligned} \phi _0(x) = {\left\{ \begin{array}{ll} \frac{h-x}{h}, &{} 0\le x\le h, \\ 0,&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

For \(i=1,2,\ldots ,n-1\),

$$\begin{aligned} \phi _i(x) = {\left\{ \begin{array}{ll} \frac{x-(i-1)h}{h}, &{} (i-1)h\le x< ih, \\ \frac{(i+1)h-x}{h}, &{} ih\le x< (i+1)h, \\ 0,&{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \phi _n(x) = {\left\{ \begin{array}{ll} \frac{x-(T-h)}{h}, &{} T-h\le x\le T, \\ 0,&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

An arbitrary function f(x) can be approximated using 1D-hat basis functions as follows:

$$\begin{aligned} f(x)\simeq f_n(x)=\sum _{i=0}^n f_i\phi _i(x)=F^T\Phi (x)=\Phi ^T(x)F, \end{aligned}$$
(4)

where

$$\begin{aligned}&F=[f_0,f_1,\ldots ,f_n]^T, \end{aligned}$$
(5)
$$\begin{aligned}&\Phi (x)=[\phi _0(x),\phi _1(x),\ldots ,\phi _n(x)]^T. \end{aligned}$$
(6)

The most important reason for using 1D-hat basis functions to approximate function f(x) is that the entries of vector F in Eq. (5) can be computed as follows:

$$\begin{aligned} f_i=f(ih),\quad i=0,1,2,\ldots ,n. \end{aligned}$$
(7)

In addition, an arbitrary function k(x, y) cab be expanded using 1D-hat basis functions as follows:

$$\begin{aligned} k(x,y)\simeq k_n(x,y)=\Phi ^T(x)K\Phi (y)=\Phi ^T(y)K^T\Phi (x), \end{aligned}$$
(8)

where \(K=[k_{ij}]\) is the \((n+1)\times (n+1)\) coefficients matrix which

$$\begin{aligned} k_{ij}=k(ih,jh),\quad i,j=0,1,\ldots ,n. \end{aligned}$$
(9)

2.2.2 2D-hat basis functions

Definition 4

2D-hat basis functions are defined on the interval \([0,T]\times [0,T]\) as follows:

$$\begin{aligned} \phi _{ij}(x,y)=\phi _i(x)\phi _j(y),\quad i,j=0,1,\ldots ,n, \end{aligned}$$
(10)

where \(\phi _i(x)\) and \(\phi _j(y)\) are 1D-hat basis functions.

A bivariate function f(x, y) can be expanded using 2D-hat basis functions as follows:

$$\begin{aligned} f(x,y)\simeq f_n(x,y)=\sum _{i=0}^n\sum _{j=0}^n f_{ij}\phi _{ij}(x,y)=F^T\Phi (x,y)=\Phi ^T(x,y)F, \end{aligned}$$
(11)

where

$$\begin{aligned} F=\bigl [f_{00},f_{01},\ldots ,f_{0n},f_{10},f_{11},\ldots ,f_{1n},\ldots ,f_{n0},f_{n1},\ldots ,f_{nn}\bigl ]^T, \end{aligned}$$
(12)

and

$$\begin{aligned} \Phi (x,y)&=\Phi (x)\otimes \Phi (y)\nonumber \\&=\bigl [\phi _{00}(x,y),\ldots ,\phi _{0n}(x,y),\ldots ,\phi _{n0}(x,y),\ldots , \phi _{nn}(x,y)\bigl ]^T, \end{aligned}$$
(13)

and \(\otimes \) denote Kronecker product.

The entries of vector F in Eq. (12) can be computed as follows:

$$\begin{aligned} f_{ij}=f(ih,jh),\quad i,j=0,1,\ldots ,n. \end{aligned}$$
(14)

In addition, every function with four variables k(x, y, s, t) can be expanded using 2D-hat basis functions as follows:

$$\begin{aligned} k(x,y,s,t)\simeq k_n(x,y,s,t)=\Phi ^T(x,y)K\Phi (s,t)=\Phi ^T(s,t)K^T\Phi (x,y), \end{aligned}$$
(15)

where K is coefficients matrix of order \((n+1)^2\times (n+1)^2\).

From 2D-hat basis functions elementary properties, we conclude

$$\begin{aligned} \Phi (x,y)\Phi ^T(x,y)F=\tilde{F}\Phi (x,y), \end{aligned}$$
(16)

where F is a column vector of order \((n+1)^2\) and \(\tilde{F}=diag(F)\).

Moreover, for every matrix A of order \((n+1)^2\times (n+1)^2\), we get

$$\begin{aligned} \Phi ^T(x,y)A\Phi (x,y)=\Phi ^T(x,y)\tilde{A}=\tilde{A}^T\Phi (x,y), \end{aligned}$$
(17)

where \(\tilde{A}\) is a column vector of order \((n+1)^2\) and the elements of \(\tilde{A}\) are diagonal entries of matrix A.

3 Operational matrix of fractional order

In this section, we derive fractional-order operational matrix and fractional-order stochastic operational matrix of integration for hat basis function.

3.1 Fractional-order operational matrix of integration

We utilize fractional operational matrix in confronting with fractional differential equations and fractional integral equations.

If the following relation be satisfied, then matrix \(P^{r_1}\) is named fractional-order operational matrix:

$$\begin{aligned} (I^{r_1}\Phi )(x)=\frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\Phi (s)ds \simeq P^{r_1} \Phi (x). \end{aligned}$$
(18)

Theorem 1

The fractional-order hat basis functions operational matrix of integration \(P^{r_1}\) is a matrix of order \((n+1)\times (n+1)\) which can be computed as follows Tripathi et al. (2013):

$$\begin{aligned} P^{r_1}=\frac{h^{r_1}}{\Gamma (r_1+2)}\begin{pmatrix} 0&{}\quad \zeta _1&{}\quad \zeta _2 &{}\quad \zeta _3 &{}\quad \ldots &{}\quad \zeta _n\\ 0&{}\quad 1&{}\quad \xi _1 &{}\quad \xi _2 &{}\quad \ldots &{}\quad \xi _{n-1}\\ 0&{}\quad 0&{}\quad 1&{}\quad \xi _1 &{}\quad \ldots &{}\quad \xi _{n-2}\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad \ldots &{}\quad \xi _{n-3}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\vdots \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \ldots &{}\quad 1 \end{pmatrix}, \end{aligned}$$
(19)

where

$$\begin{aligned}&\zeta _j=j^{r_1}(r_1-j+1)+(j-1)^{r_1+1},\quad j=1,2,\ldots ,n,\\&\xi _j=(j+1)^{r_1+1}-2j^{r_1+1}+(j-1)^{r_1+1},\quad j=1,2,\ldots ,n-1. \end{aligned}$$

Using Eqs. (13) and (18), we get

$$\begin{aligned} (I^r\Phi )(x,y)&=\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1}\Phi (s,t)\mathrm{d}t\mathrm{d}s\nonumber \\&=\Bigl (\frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\Phi (s)\mathrm{d}s\Bigl )\,\otimes \, \Bigl (\frac{1}{\Gamma (r_2)}\int _0^y (y-t)^{r_2-1}\Phi (t)\mathrm{d}t\Bigl )\nonumber \\&=(P^{r_1}\Phi (x))\otimes (P^{r_2}\Phi (y))=(P^{r_1}\otimes P^{r_2})(\Phi (x)\otimes \Phi (y))\nonumber \\&=\mathbf P ^r\Phi (x,y), \end{aligned}$$
(20)

where \(\mathbf P ^r=P^{r_1}\otimes P^{r_2}\).

3.2 Fractional-order stochastic operational matrix of integration

Theorem 2

Matrix \(P_s^{r_1}\) is called fractional-order stochastic operational matrix, if the following relation be satisfied:

$$\begin{aligned} \frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\Phi (s)\mathrm{d}B(s) \simeq P_s^{r_1} \Phi (x), \end{aligned}$$
(21)

where \(P_s^{r_1}\) is given by

$$\begin{aligned} P_s^{r_1}=\frac{1}{h\Gamma (r_1)}\begin{pmatrix} 0&{}\quad \alpha _1 &{}\quad \alpha _2 &{}\quad \alpha _3 &{}\quad \ldots &{}\quad \alpha _{n-1}&{}\quad \alpha _n\\ 0&{}\quad \beta _{1,1}&{}\quad \beta _{1,2} &{}\quad \beta _{1,3} &{}\quad \ldots &{}\quad \beta _{1,n-1}&{}\quad \beta _{1,n}\\ 0&{}\quad 0&{}\quad \beta _{2,2}&{}\quad \beta _{2,3}&{}\quad \ldots &{}\quad \beta _{2,n-1}&{}\quad \beta _{2,n}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \ldots &{}\quad \beta _{n-1,n-1}&{}\quad \beta _{n-1,n}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \ldots &{}\quad 0&{}\quad \eta _{n,n} \end{pmatrix}, \end{aligned}$$
(22)

where

$$\begin{aligned} \alpha _j&=\int _0^h(r_1-1)(jh-s)^{r_1-2}(h-s)B(s)\mathrm{d}s\\&\quad +\int _0^h(jh-s)^{r_1-1}B(s)\mathrm{d}s, \quad j=1,2,\ldots ,n,\\ \beta _{i,i}&=\int _{(i-1)h}^{ih}(r_1-1)(ih-s)^{r_1-2}(s-(i-1)h)B(s)\mathrm{d}s\\&\quad -\int _{(i-1)h}^{ih}(ih-s)^{r_1-1}B(s)\mathrm{d}s, \quad i=1,2,\ldots ,n-1,\\ \beta _{i,j}&=\int _{(i-1)h}^{ih}(r_1-1)(jh-s)^{r_1-2}(s-(i-1)h)B(s)\mathrm{d}s\\&\quad +\int _{ih}^{(i+1)h}(r_1-1)(jh-s)^{r_1-2}((i+1)h-s)B(s)\mathrm{d}s\nonumber \\&\quad -\int _{(i-1)h}^{ih}(jh-s)^{r_1-1}B(s)\mathrm{d}s+\int _{ih}^{(i+1)h}(jh-s)^{r_1-1}B(s)\mathrm{d}s,\quad \\&\quad i=1,2,\ldots ,n-1, \quad j=i+1,\ldots ,n,\\ \eta _{n,n}&=\int _{T-h}^T (r_1-1)(T-s)^{r_1-2}(s-(T-h))B(s)\mathrm{d}s-\int _{T-h}^T(T-y)^{r_1-1}B(s)\mathrm{d}s. \end{aligned}$$

Proof

Using part by part integration formula, we have

$$\begin{aligned} \frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\phi _i(s)\mathrm{d}B(s)&=\frac{1}{\Gamma (r_1)}\int _0^x(r_1-1)(x-s)^{r_1-2}\phi _i(s)B(s)\mathrm{d}s\nonumber \\&\quad -\frac{1}{\Gamma (r_1)}\int _0^x(x-s)^{r_1-1}\phi _i'(s)B(s)\mathrm{d}s. \end{aligned}$$
(23)

Remark

Additional explanation to get Eq. (23) is as follows:

$$\begin{aligned}&u=(x-s)^{r_1-1}\phi _i(s), \quad \Longrightarrow du=-(r_1-1)(x-s)^{r_1-2}\phi _i(s)\mathrm{d}s+(x-s)^{r_1-1}\phi _i'(s)\mathrm{d}s,\\&dv=\mathrm{d}B(s),\quad \Longrightarrow v=B(s). \end{aligned}$$

Therefore

$$\begin{aligned}&\int _0^x (x-s)^{r_1-1}\phi _i(s)\mathrm{d}B(s)\nonumber \\&\quad =(x-s)^{r_1-1}\phi _i(s)B(s)\Bigl |_{s=0}^{s=x}+\int _0^x(r_1-1)(x-s)^{r_1-2}\phi _i(s)B(s)\mathrm{d}s\nonumber \\&\qquad -\int _0^x(x-s)^{r_1-1}\phi _i'(s)B(s)\mathrm{d}s. \end{aligned}$$
(24)

Since \(B(0)=0\), so the first term in Eq. (24) is zero. By multiplying Eq. (24) in \(\frac{1}{\Gamma (r_1)}\), we get Eq. (23).

In addition, we can expand \(\frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\phi _i(s)\mathrm{d}B(s)\), using hat basis functions as follows:

$$\begin{aligned} \frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\phi _i(s)\mathrm{d}B(s)\simeq \sum _{j=0}^n a_{ij}\phi _j(x), \end{aligned}$$
(25)

where

$$\begin{aligned} a_{ij}&=\frac{1}{\Gamma (r_1)}\int _0^{jh} (jh-s)^{r_1-1}\phi _i(s)\mathrm{d}B(s)\nonumber \\&=\frac{1}{\Gamma (r_1)}\int _0^{jh}(r_1-1)(jh-s)^{r_1-2}\phi _i(s)B(s)\mathrm{d}s\nonumber \\&\quad -\frac{1}{\Gamma (r_1)}\int _0^{jh}(jh-s)^{r_1-1}\phi _i'(s)B(s)\mathrm{d}s. \end{aligned}$$
(26)

Using definition of 1D-hat basis function and Eq. (26), we get

$$\begin{aligned} a_{0j}= {\left\{ \begin{array}{ll} 0, &{} j=0,\\ \frac{1}{h\Gamma (r_1)}\int _0^h(r_1-1)(jh-s)^{r_1-2}(h-s)B(s)\mathrm{d}s+\frac{1}{h\Gamma (r_1)}\int _0^h(jh-s)^{r_1-1}B(s)\mathrm{d}s,&{} j=1,2,\ldots ,n. \end{array}\right. } \end{aligned}$$

For \(i=1,2,\ldots ,n-1,\) we get

$$\begin{aligned}&a_{ij}= {\left\{ \begin{array}{ll} 0,\quad j=1,2,\ldots ,i-1,\\ \displaystyle \frac{1}{h\Gamma (r_1)}\int _{(i-1)h}^{ih}(r_1-1)(ih-s)^{r_1-2}(s-(i-1)h)B(s)\mathrm{d}s- \displaystyle \frac{1}{h\Gamma (r_1)}\int _{(i-1)h}^{ih}(ih-s)^{r_1-1}B(s)\mathrm{d}s, \quad j=i,\\ \begin{aligned} &{}\frac{1}{h\Gamma (r_1)}\int _{(i-1)h}^{ih}(r_1-1)(jh-s)^{r_1-2}(s-(i-1)h)B(s)\mathrm{d}s\\ &{}+ \frac{1}{h\Gamma (r_1)}\int _{ih}^{(i+1)h}(r_1-1)(jh-s)^{r_1-2}((i+1)h-s)B(s)\mathrm{d}s\\ &{}-\frac{1}{h\Gamma (r_1)}\int _{(i-1)h}^{ih}(jh-s)^{r_1-1}B(s)\mathrm{d}s+ \frac{1}{h\Gamma (r_1)}\int _{ih}^{(i+1)h}(jh-s)^{r_1-1}B(s)\mathrm{d}s, \quad j=i+1,\ldots ,n. \end{aligned} \end{array}\right. } \end{aligned}$$

Finally, for \(i=n\), we have

$$\begin{aligned} a_{nj}={\left\{ \begin{array}{ll} 0, &{} j=0,1,\ldots ,n-1,\\ \frac{1}{h\Gamma (r_1)}\int _{T-h}^T (r_1-1)(T-s)^{r_1-2}(s-(T-h))B(s) \mathrm{d}s-\frac{1}{h\Gamma (r_1)}\int _{T-h}^T(T-y)^{r_1-1}B(s)\mathrm{d}s, &{} j=n. \end{array}\right. } \end{aligned}$$

This complete the proof. \(\square \)

Using Eqs. (13) and (21), we have

$$\begin{aligned}&\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1} \Phi (s,t)\mathrm{d}B(t)\mathrm{d}B(s)\nonumber \\&\quad =\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1} (\Phi (s)\otimes \Phi (t))\mathrm{d}B(t)\mathrm{d}B(s)\nonumber \\&\quad =\Bigl (\frac{1}{\Gamma (r_1)}\int _0^x (x-s)^{r_1-1}\Phi (s)\mathrm{d}B(s) \Bigl )\,\otimes \,\Bigl (\frac{1}{\Gamma (r_2)}\int _0^y (y-t)^{r_2-1}\Phi (t)\mathrm{d}B(t) \Bigl )\nonumber \\&\quad =(P_s^{r_1}\Phi (x))\,\otimes \,(P_s^{r_2}\Phi (y))=(P_s^{r_1}\otimes P_s^{r_2})(\Phi (x)\otimes \Phi (y))\nonumber \\&\quad =\mathbf P _s^r\Phi (x,y), \end{aligned}$$
(27)

where \(\mathbf P _s^r=P_s^{r_1}\otimes P_s^{r_2}\).

4 The proposed algorithm to solve 2DSFIEs

This section is devoted to find numerical solution of 2DSFIEs. We present a numerical method that, using the matrices provided in the previous section, transforms the original Eq. (1) to a linear system of algebraic equations. The numerical solution of Eq. (1) is obtained by solving this linear system.

We approximate the functions f(x, y), g(x, y), and \(k_i(x,y,s,t), i=1,2,\) in terms of 2D-hat basis functions as follows:

$$\begin{aligned}&f(x,y) \simeq f_n(x,y)= F^T\Phi (x,y)=\Phi ^T(x,y)F, \nonumber \\&g(x,y) \simeq g_n(x,y)=G^T\Phi (x,y)=\Phi ^T(x,y)G,\nonumber \\&k_i(x,y,s,t) \simeq k_{in}(x,y,s,t)=\Phi ^T(x,y)K_i\Phi (s,t)=\Phi ^T(s,t)K_i^T\Phi (x,y),\quad i=1,2, \end{aligned}$$
(28)

where G and \(K_i, i=1,2,\) are known \((n+1)^2\times 1\) column vector and known \((n+1)^2\times (n+1)^2\) matrices, respectively, whereas F is unknown \((n+1)^2\times 1\) column vector which should be determined.

The result of substituting of Eq. (28) into Eq. (1) is

$$\begin{aligned} \Phi ^T(x,y)F \simeq&\,\Phi ^T(x,y)G+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1} \nonumber \\&\times \Phi ^T(x,y)K_1\Phi (s,t)\Phi ^T(s,t)F\mathrm{d}t\mathrm{d}s\nonumber \\&+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1} \nonumber \\&\times \Phi ^T(x,y)K_2\Phi (s,t)\Phi ^T(s,t)F\mathrm{d}B(t)\mathrm{d}B(s). \end{aligned}$$
(29)

Now, using Eq. (16) concludes

$$\begin{aligned} \Phi ^T(x,y)F \simeq \,\,&\,\Phi ^T(x,y)G+\frac{\Phi ^T(x,y)K_1\tilde{F}}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1} \Phi (s,t)\mathrm{d}t\mathrm{d}s\nonumber \\&+\frac{\Phi ^T(x,y)K_2\tilde{F}}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1} \Phi (s,t)\mathrm{d}B(t)\mathrm{d}B(s). \end{aligned}$$
(30)

Now, using 2D-fractional-order operational matrix together with 2D-fractional-order stochastic operational matrix of integration computed in Eqs. (20) and (27), we get

$$\begin{aligned} \Phi ^T(x,y)F \simeq \Phi ^T(x,y)G+\Phi ^T(x,y)K_1\tilde{F}{} \mathbf P ^r\Phi (x,y)+\Phi ^T(x,y)K_2\tilde{F}{} \mathbf P _s^r\Phi (x,y). \end{aligned}$$

Let \(R_1=K_1\tilde{F}{} \mathbf P ^r\) and \(R_2=K_2\tilde{F}{} \mathbf P _s^r\) and apply Eq. (17). Thus, we have

$$\begin{aligned} \Phi ^T(x,y)F \simeq \Phi ^T(x,y)G+\Phi ^T(x,y)\tilde{R}_1+\Phi ^T(x,y)\tilde{R}_2, \end{aligned}$$

or

$$\begin{aligned} F \simeq G+\tilde{R}_1+\tilde{R}_2. \end{aligned}$$
(31)

Equation (31) is a very simple system with \((n+1)^2\) linear equations and \((n+1)^2\) unknown variables. We can solve this system using an appropriate iterative method such as Jacobi method or Gauss–Seidel method. After solving this system, the numerical solution of Eq. (1) is computed from Eq. (28) as

$$\begin{aligned} f(x,y)\simeq F^T\Phi (x,y). \end{aligned}$$

5 Error analysis

This section is devoted to get the rate of convergence of the suggested method for solving 2DSFIEs. We prove that the rate of convergence is \(O(h^2)\). We define

$$\begin{aligned} \Vert f(x,y)\Vert =\sup _{(x,y)\in D}|f(x,y)|, \end{aligned}$$

where \(D=[0,1]\times [0,1]\).

Theorem 3

Let \(g(x,y)\in C^2(D)\) and \(g_n(x,y)\) be the expansion of g(x, y) using 2D-hat basis functions. Mirzaee and Hadadiyan established that

$$\begin{aligned} \Vert g(x,y)-g_n(x,y)\Vert \simeq O(h^2). \end{aligned}$$

Proof

See Mirzaee and Hadadiyan (2016). \(\square \)

Theorem 4

Assume that \(k(x,y,s,t)\in C^2(D\times D)\) and \(k_n(x,y,s,t)\) be approximation of k(x, y, s, t) using 2D-hat basis functions. Mirzaee and Hadadiyan proved that

$$\begin{aligned} \Vert k(x,y,s,t)-k_n(x,y,s,t)\Vert \simeq O(h^2). \end{aligned}$$

Proof

See Mirzaee and Hadadiyan (2016). \(\square \)

Theorem 5

Suppose that f(x, y) is the exact solution of Eq. (1) and \(f_n(x,y)\) be the approximate solution of Eq. (1) using proposed algorithm. Moreover, suppose that the following assumptions are satisfied:

  1. (i)

    \(\Vert f(x,y)\Vert \le \mathcal {N}, \quad (x,y)\in D\),

  2. (ii)

    \(\Vert k_i(x,y,s,t)\Vert \le \mathcal {L}_i, \quad i=1,2,\quad (x,y,s,t)\in D\times D,\)

  3. (iii)

    \(1-\frac{1}{\Gamma (r_1)\Gamma (r_2)} \bigl (\mathcal {L}_1+C_1h^2+\mathcal {M}^2\mathcal {L}_2+\mathcal {M}^2C_2h^2\bigl )>0,\)

where \(\mathcal {M}=\sup \{B(x);\ 0\le x\le 1\}\) and the constants N, \(L_1\), \(L_2\), \(C_1\), and \(C_2\) are generic constants. Then, we have

$$\begin{aligned} \Vert f(x,y)-f_n(x,y)\Vert \simeq O(h^2). \end{aligned}$$
(32)

Proof

Let \(g_n(x,y)\) and \(k_{in}(x,y,s,t), i=1,2,\) be the approximate functions of g(x, y) and \(k_i(x,y,s,t),\), respectively. Therefore, we have

$$\begin{aligned} f_n(x,y)=\,&\,g_n(x,y)+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1}k_{1n}(x,y,s,t)f_n(s,t)\mathrm{d}t\mathrm{d}s\nonumber \\&+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1}k_{2n}(x,y,s,t)f_n(s,t)\mathrm{d}B(t)\mathrm{d}B(s). \end{aligned}$$
(33)

From Eqs. (1) and (33), we can write

$$\begin{aligned} f(x,y)-f_n(x,y)=\,&\,g(x,y)-g_n(x,y)+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1}\nonumber \\ {}&\quad \times \bigl (k_1(x,y,s,t)f(s,t)-k_{1n}(x,y,s,t)f_n(s,t)\bigl )\mathrm{d}t\mathrm{d}s \nonumber \\&\quad +\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y(x-s)^{r_1-1}(y-t)^{r_2-1} \nonumber \\ {}&\quad \times \bigl (k_2(x,y,s,t)f(s,t)-k_{2n}(x,y,s,t)f_n(s,t)\bigl ) \mathrm{d}B(t)\mathrm{d}B(s). \end{aligned}$$
(34)

Thus

$$\begin{aligned} |f(x,y)-f_n(x,y)|&\le |g(x,y)-g_n(x,y)|+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y |x-s|^{r_1-1}|y-t|^{r_2-1}\nonumber \\ {}&\quad \bigl |k_1(x,y,s,t)f(s,t)-k_{1n}(x,y,s,t)f_n(s,t)\bigl |\mathrm{d}t\mathrm{d}s \nonumber \\&\quad +\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y|x-s|^{r_1-1}|y-t|^{r_2-1} \nonumber \\ {}&\quad \bigl |k_2(x,y,s,t)f(s,t)-k_{2n}(x,y,s,t)f_n(s,t)\bigl | \mathrm{d}B(t)\mathrm{d}B(s). \end{aligned}$$
(35)

Since \(|x-s|<1\) and \(|y-t|<1\), so

$$\begin{aligned} |f(x,y)-f_n(x,y)|&\le |g(x,y)-g_n(x,y)|\nonumber \\&\quad +\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y \bigl |k_1(x,y,s,t)f(s,t) \nonumber \\ {}&\quad -k_{1n}(x,y,s,t)f_n(s,t)\bigl |\mathrm{d}t\mathrm{d}s \nonumber \\&\quad +\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y\bigl |k_2(x,y,s,t)f(s,t)\nonumber \\ {}&\quad -k_{2n}(x,y,s,t)f_n(s,t)\bigl | \mathrm{d}B(t)\mathrm{d}B(s)\\&\le \Vert g(x,y)-g_n(x,y)\Vert +\frac{xy}{\Gamma (r_1)\Gamma (r_2)}\Vert k_1(x,y,s,t)f(s,t)\nonumber \\ {}&\quad -k_{1n}(x,y,s,t)f_n(s,t)\Vert \nonumber \\&\quad +\frac{B(x)B(y)}{\Gamma (r_1)\Gamma (r_2)}\Vert k_2(x,y,s,t)f(s,t)-k_{2n}(x,y,s,t)f_n(s,t)\Vert . \end{aligned}$$

We define \(\mathcal {M}=\sup \{B(x);\ 0\le x\le 1\}.\) Since \(x<1, y<1\) and using this definition, we get

$$\begin{aligned} \Vert f(x,y)-f_n(x,y)\Vert&\le \Vert g(x,y)-g_n(x,y)\Vert +\frac{1}{\Gamma (r_1)\Gamma (r_2)}\Vert k_1(x,y,s,t)f(s,t)\nonumber \\&\quad -k_{1n}(x,y,s,t)f_n(s,t)\Vert \nonumber \\&\quad +\frac{\mathcal {M}^2}{\Gamma (r_1)\Gamma (r_2)}\Vert k_2(x,y,s,t)f(s,t)-k_{2n}(x,y,s,t)f_n(s,t)\Vert . \end{aligned}$$
(36)

From assumptions (i) and (ii) and Theorem 4, we conclude that

$$\begin{aligned}&\Vert k_i(x,y,s,t)f(s,t)-k_{in}(x,y,s,t)f_n(s,t)\Vert \nonumber \\&\quad \le \Vert k_i(x,y,s,t)\Vert \Vert f(x,y)-f_n(x,y)\Vert \nonumber \\&\qquad +\Vert k_i(x,y,s,t)-k_{in}(x,y,s,t)\Vert \Bigl (\Vert f(x,y)-f_n(x,y)\Vert +\Vert f(x,y)\Vert \Bigl )\nonumber \\&\quad \le \mathcal {L}_i\Vert f(x,y)-f_n(x,y)\Vert +C_ih^2\Vert f(x,y)-f_n(x,y)\Vert +C_i\mathcal {N}h^2,\quad i=1,2. \end{aligned}$$
(37)

From Eqs. (36) and (37) and using Theorem 3 and assumption (iii), we get

$$\begin{aligned} \Vert f(x,y)-f_n(x,y)\Vert \le \frac{Ch^2+\frac{1}{\Gamma (r_1)\Gamma (r_2)}(C_1\mathcal {N}h^2+C_2\mathcal {M}^2\mathcal {N}h^2)}{1-\frac{1}{\Gamma (r_1)\Gamma (r_2)}(\mathcal {L}_1+C_1h^2+\mathcal {M}^2\mathcal {L}_2+\mathcal {M}^2C_2h^2)}. \end{aligned}$$
(38)

From Eq. (38), we conclude \(\Vert f(x,y)-f_n(x,y)\Vert \simeq O(h^2).\) \(\square \)

6 Numerical examples

In this section, some numerical examples have been solved using proposed method explained in the previous section to demonstrate the accuracy and efficiency of this method. The values of exact solution, approximate solution, and absolute error at the some selected points is reported in tables. To clarify accuracy and efficiency of the present method, the values of absolute error are computes as follows:

$$\begin{aligned} e(x,y)=\bigl |f(x,y)-f_n(x,y)\bigl |,\quad (x,y)\in D, \end{aligned}$$

where f(x, y) and \(f_n(x,y)\) are the exact solution and approximate solution of 2DSFIEs, respectively. All of the computational reported in tables have been obtained by running some computer programs written in MATLAB software. In addition, the “pinv” command is used to solve the generated linear system of algebraic equations.

Example 1

Let us consider the following 2DSFIEs:

$$\begin{aligned} f(x,y)=\,&\,g(x,y)+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1}xf(s,t)\mathrm{d}t\mathrm{d}s\\&+\frac{1}{\Gamma (r_1)\Gamma (r_2)}\int _0^x\int _0^y (x-s)^{r_1-1}(y-t)^{r_2-1}xyf(s,t)\mathrm{d}B(t)\mathrm{d}B(s), \end{aligned}$$

with the exact solution \(f(x,y)=1\).

We solve this example for two cases \(r_1=\frac{7}{2}, r_2=\frac{5}{2}\) and \(r_1=\frac{9}{2}, r_2=\frac{7}{2}\). For case \(r_1=\frac{7}{2}, r_2=\frac{5}{2}\), we have

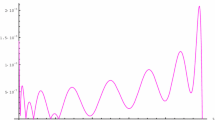
$$\begin{aligned} g(x,y)&=1-\frac{1}{\Gamma \Bigl (\frac{7}{2}\Bigr ) \Gamma \Bigl (\frac{5}{2}\Bigr )} \Bigl (\frac{4}{45}x^\frac{9}{2}y^\frac{5}{2}\Bigl )\\&\quad -\frac{1}{\Gamma \left( \frac{7}{2}\right) \Gamma \Bigl (\frac{5}{2}\Bigr )} \left( \frac{5}{2}\int _0^xx(x-s)^\frac{3}{2}B(s)\mathrm{d}s\right) \left( \frac{3}{2}\int _0^yy(y-t)^\frac{1}{2}B(t)\mathrm{d}t\right) . \end{aligned}$$

In this case, the values of approximate solution and absolute error obtained from present method for \(n=2,3\) is reported in Table 1. In addition, absolute error for \(n=2\) and \(n=3\) are plotted in Figs. 1 and 2, respectively.

For case \(r_1=\frac{9}{2}, r_2=\frac{7}{2}\), we have

$$\begin{aligned} g(x,y)&=1-\frac{1}{\Gamma (\frac{9}{2})\Gamma (\frac{7}{2})}\Bigl (\frac{4}{77}x^\frac{11}{2}y^\frac{7}{2}\Bigl )\\&\quad -\frac{1}{\Gamma (\frac{9}{2})\Gamma (\frac{7}{2})}\Bigl (\frac{7}{2}\int _0^xx(x-s)^\frac{5}{2}B(s)\mathrm{d}s\Bigl )\Bigl (\frac{5}{2}\int _0^yy(y-t)^\frac{3}{2}B(t)\mathrm{d}t\Bigl ). \end{aligned}$$

In this case, the values of approximate solution and absolute error obtained from present method for \(n=2,3\) are reported in Table 2. In addition, absolute error for \(n=2\) and \(n=3\) are plotted in Figs. 3 and 4, respectively.

Table 1 Numerical results of Example 1 in the case \(r_1=\frac{7}{2}\) and \( r_2=\frac{5}{2}\)
Full size table
Fig. 1
figure 1

Absolute error of Example 1 for \(n=2\)

Full size image
Fig. 2
figure 2

Absolute error of Example 1 for \(n=3\)

Full size image
Table 2 Numerical results of Example 1 in the case \(r_1=\frac{9}{2}\) and \( r_2=\frac{7}{2}\)
Full size table
Fig. 3
figure 3

Absolute error of Example 1 for \(n=2\)

Full size image
Fig. 4
figure 4

Absolute error of Example 1 for \(n=3\)

Full size image

Example 2

Let us consider the following 2DSFIEs:

$$\begin{aligned} f(x,y)=&\,g(x,y)+\frac{1}{\Gamma \left( \frac{7}{2}\right) \Gamma \left( \frac{5}{2}\right) }\int _0^x\int _0^y (x-s)^{\frac{5}{2}}(y-t)^{\frac{3}{2}}(x+y)f(s,t)\mathrm{d}t\mathrm{d}s\\&+\frac{1}{\Gamma \left( \frac{7}{2}\right) \Gamma \left( \frac{5}{2}\right) }\int _0^x\int _0^y (x-s)^{\frac{5}{2}}(y-t)^{\frac{3}{2}}yf(s,t)\mathrm{d}B(t)\mathrm{d}B(s), \end{aligned}$$

where

$$\begin{aligned} g(x,y)=\,&\,xy -\frac{1}{\Gamma \Bigl (\frac{7}{2}\Bigr )\Gamma \Bigl (\frac{5}{2}\Bigr )}(x+y) \Bigl (\frac{2}{9}x^\frac{9}{2}\Bigr )\Bigl (\frac{2}{7}y^\frac{7}{2}\Bigr )\\&-\frac{1}{\Gamma \Bigl (\frac{7}{2}\Bigr )\Gamma \Bigl (\frac{5}{2}\Bigr )}\Bigl (\int _0^x \Bigl (\frac{5}{2}s(x-s)^\frac{3}{2}-(x-s)^\frac{5}{2}\Bigr )B(s)\mathrm{d}s\Bigl )\\&\Bigl (\int _0^y\Bigl (\frac{3}{2}yt(y-t)^\frac{1}{2}-y(y-t)^\frac{3}{2}\Bigr )B(t)\mathrm{d}t\Bigl ), \end{aligned}$$

with the exact solution \(f(x,y)=xy\).

The values of approximate solution and absolute error achieved from present method for \(n=2,3\) are reported in Table 3. Also, absolute error for \(n = 2\) and \(n = 3\) are plotted in Figs. 5 and 6, respectively. Moreover, computational time of these examples are compared in the Table 4.

Table 3 Numerical results of Example 2
Full size table
Fig. 5
figure 5

Absolute error of Example 2 for \(n=2\)

Full size image
Fig. 6
figure 6

Absolute error of Example 2 for \(n=3\)

Full size image
Table 4 Comparison of computational time for given examples
Full size table

7 Conclusion

In this article, 2D-hat basis functions have been applied to provide an efficient numerical approach to solve 2DSFIEs. For this goal, first, we calculate operational matrix and stochastic operational matrix of fractional order, and then, using these matrices, the solution of considered problem is converted to the solution of linear system of algebraic equations. Some results concerning the convergence and error analysis associated with the present method are discussed and we establish the rate of convergence of this approach for solving 2DSFIEs is \(O(h^2)\). Finally, some numerical examples are solved using proposed method to confirm applicability of this technique. The numerical results reported in the tables verify that the suggested algorithm is very accurate (Table 4).