High-order adaptive finite-volume schemes in the context of multiresolution analysis for dyadic grids

Abstract

This paper considers the design of adaptive finite-volume discretizations for conservation laws. The methodology comes from the context of multiresolution representation of functions, which is based on cell averages on a hierarchy of nested grids. The refinement process is performed by the partition of each cell at a certain level into two equal child cells at the next refined level by a hyperplane perpendicular to one of the coordinate axes, which varies cyclically from level to level. The resulting dyadic grids allow the organization of the multiscale information by the same binary-tree data structure for domains in any dimension. Cell averages of neighbouring stencil cells, chosen on the subdivision direction axis, are used to approximate the cell average of the child cells in terms of a classical A. Harten prediction formula for 1D discretizations. The difference between successive refinement levels is encoded as the prediction errors (wavelet coefficients) in one of the child cells. Adaptivity is obtained by interrupting the refinement at the cells where the wavelet coefficients are sufficiently small. The efficiency of the adaptive method is analysed in applications to typical test problems in one and two space dimensions for second- and third-order schemes for the space discretization (WENO) and time integration (explicit Runge–Kutta). The results show that the adaptive solutions fit the reference finite-volume solution on the finest regular grid, and memory and CPU requirements can be considerably reduced, thanks to the efficient self-adaptive grid refinement.

1 Introduction

Adaptive techniques require a memory-efficient data structure to give fast access to the stored data. An efficient way to store the reduced data is to use a tree data structure, where grid adaptivity is related with an incomplete tree and where the refinement may be interrupted at intermediate scale levels.

Our purpose is to present a high-order adaptive finite-volume multiresolution (FV/MR) scheme for $d$-dimensional nonlinear hyperbolic conservation laws which is a combination of a finite-volume (FV) discretization and multiresolution analysis for cell averages in dyadic grids, using binary data structure. This technique can lead to significant memory savings and accelerate considerably the simulation with respect to the discretization on the finest uniform mesh, without contaminating its accuracy. In Castro et al. (2012), preliminary results are published for standard second-order accurate discretization method applied to linear transport equations. The new contributions of the present manuscript are the usage of higher-order schemes, requiring larger stencils, and the application to typical nonlinear problems.

A dyadic grid is a hierarchy of meshes where a cell at a certain level is partitioned into two equal children at the next refined level by a hyperplane perpendicular to one of the coordinate axes, which varies cyclically from level to level. Cell averages of neighbouring cells, chosen on the subdivision direction axis, are used to approximate the cell average of the child cells in terms of a classical A. Harten prediction formula for 1D discretizations. The difference between successive refinement levels is encoded as the prediction errors (wavelet coefficients) in one of the child cells. Adaptivity is obtained by interrupting the refinement at the cells where the wavelet coefficients are sufficiently small. Consequently, instead of using the cell-average representation on the uniform fine grid, the MR scheme computes the numerical solution represented by its cell averages on an adaptive sparse grid, which is formed by the cells whose wavelet coefficients are significant and above a given threshold.

One important aspect of multiresolution representations in dyadic grids is that we can use the same binary-tree data structure for domains of any dimension. The tree structure allows us to succinctly represent the data and efficiently navigate through it. Dyadic grids also provide a more gradual refinement as compared to the traditional $2^d$ refinements [dividing a cell into $2^d$ children at each level, e.g. quad-trees (2D) or oct-trees (3D)] that are commonly used for multiresolution analyses.

Using traditional $2^d$ refinements, FV/MR schemes have been successfully applied to conservation laws (Cohen et al. 2003; Kaibara and Gomes 2003; Müller 2003; Roussel et al. 2003; Roussel and Schneider 2005; Domingues et al. 2008, 2009; Bürger et al. 2010). For comprehensive studies on adaptive FV/MR techniques, we refer to the books of Cohen (1998) and Müller (2003) and also to the review papers: Schneider and Vasilyev (2010) and Domingues et al. (2011).

The remaining text is organized as follows. Section 2 is dedicated to describe multiresolution representations for cell averages based on dyadic grids. One example for image compression shows the efficiency of dyadic grids in 2D as compared to quad grids. In Sect. 3 we describe the adaptive MR finite-volume scheme, giving a description of the algorithm. For the reference scheme in uniform grid, we use second- and third-order finite-volume schemes. We present the results of the adaptive FV/MR scheme on two-dimensional dyadic grids applied to a test problem for Burgers to be compared with the reference finite-volume solution on the finest regular grid in terms of CPU time and memory requirements.

2 MR analyses for cell averages on $d$-dimensional dyadic grids

A general framework for the construction of multiresolution representations of data is presented in Hartten (1996) and Abgrall (1996). It requires a hierarchy of meshes and inter-level transformations (restriction and prediction operators). Traditionally, $2^d$-schemes (which divides a cell into $2^d$ children at each level) are used. In the present context, we consider an hierarchy of dyadic grids $\mathcal {G}=\{G^\ell \}$ for a box region $R\subset \mathbb {R}^d$ [see Cardoso et al. (2006) or Castro et al. (2012) for more details]. Experiments indicate that the gradual dyadic subdivision scheme is more space- and computation-efficient than the well-known, especially in higher dimensions.

2.1 Dyadic grids

The hierarchy starts with a box-like domain $R\subset \mathbb {R}^d$ as the rootcell. A point $x=(x_0,\ldots , x_{d-1})$ is in $R$ if and only if $a_i<x_i< b_i$, for all $i$, for certain bounds $a_0, \ldots , a_{d-1}$, and $b_0, \ldots , b_{d-1}$.

• 1. At each level $\ell \ge 0$ of the hierarchy, $G^\ell =\{c_\alpha ^\ell , \alpha \in \mathcal {K}(\ell )\}$ form a partition: $\overline{R}=\cup _{\alpha \in \mathcal {K}(\ell )}\overline{c}_{\alpha }^\ell$, the cells having pairwise disjoint interiors. The cells have the form $c_\alpha ^\ell =c_{\alpha _0}^{\ell _0}\times \cdots \times c_{\alpha _{d-1}}^{\ell _{d-1}}:=\prod _{i=0}^{d-1}c_{\alpha _i}^{\ell _i}$, where $c_{\alpha _i}^{\ell _i}$ correspond to one-dimensional cells on the $(\overrightarrow{0x_i})$ axis, with $\ell =\sum _{i=0}^{d-1}\ell _i$.

• 2. The dyadic bisection goes from cells $c_{\alpha }^\ell$ at level $\ell$ to two child cells $c_{\alpha _L}^{\ell +1}, c_{\alpha _H}^{\ell +1}$ at level $\ell +1$, such that $|c_{\alpha _L}^{\ell +1}|=|c_{\alpha _H}^{\ell +1}|=\frac{1}{2}|c_{\alpha }^\ell |$, and $\overline{c}_{\alpha }^\ell = \overline{c}_{\alpha _L}^\ell \cup \overline{c}_{\alpha _H}^\ell$.

• 3. In each level $\ell$, the dyadic bisection is performed in a cyclic fashion, by a hyperplane orthogonal to the coordinate axis $(\overrightarrow{0x_n})$, with $n=\ell \hbox {mod} d$. That is, starting at $\ell =0$ with the root cell $R$, the first bisection is by a hyperplane orthogonal to axis $(\overrightarrow{0x_0})$, next by a hyperplane orthogonal to axis $(\overrightarrow{0x_1})$ and so on. Figure 1 illustrates the first eight subdivision steps of a three-dimensional grid.

Fig. 1

The first eight subdivision steps of a three-dimensional dyadic grid

2.2 Discretization by cell averages, restriction and prediction operators

The discretization of an integrable function $u$ at resolution $\ell$ is defined by the cell-average values

$$\begin{aligned} u_\alpha ^\ell = \frac{1}{\vert c_\alpha ^\ell \vert }\int \limits _{c_\alpha ^\ell }u \; \mathrm {d}\mu . \end{aligned}$$

Note that $u^\ell _\alpha$ can be computed from the averages $u^{\ell +1}_{\alpha _L}$ and $u^{\ell +1}_{\alpha _H}$ of the two child cells

$$\begin{aligned} u_{\alpha }^\ell = \frac{1}{2}(u^{\ell +1}_{\alpha _H}+u^{\ell +1}_{\alpha _L}). \end{aligned}$$

(1)

Formula (1) can be viewed as a restriction operator $P_{\ell +1}^{\ell }$, that yields the coarser discretization $u^\ell$ from the finer one $u^{\ell +1}$.

For MR analysis we also require a prediction operation $P_{\ell }^{\ell +1}$ that yields a finer approximation $\tilde{u}^{\ell +1}$ from the coarser approximation $u^{\ell }$. For conservation, $P_{\ell +1}^{\ell } P_{\ell }^{\ell +1}$ should be the identity operator.

For the prediction of the cell average at a child cell $c_{\alpha _H}^{\ell +1}$, information is required from neighbouring cells on the direction $n=(\ell \mod d)$. Denote by $c^\ell _{\alpha \pm j}$, $1\le j\le s$ the $2s$ closer cells $c_{\alpha \pm j}^\ell =\left( \prod _{i=0,i\ne n}^{d-1}c_{\alpha _i}^{\ell _i}\right) \times c_{\alpha _n \pm j}^{\ell _n}$. We shall consider prediction formulae of the form

$$\begin{aligned} \tilde{u}_{\alpha _H}^{\ell +1} =\left( P_\ell ^{\ell +1} u^\ell \right) _{\alpha _H} = u_\alpha ^\ell + \sum _{j=1}^{s} \lambda _j \left[ u_{\alpha +j}^\ell - u_{\alpha -j}^\ell \right] . \end{aligned}$$

(2)

Similarly, for the left child cell $c_{\alpha _L}^{\ell +1}$, we consider

$$\begin{aligned} \tilde{u}_{\alpha _L}^{\ell +1} = \left( P_\ell ^{\ell +1} u^\ell \right) _{\alpha _L} = u_\alpha ^\ell - \sum _{j=1}^{s} \lambda _j \left[ u_{\alpha +j}^\ell - u_{\alpha -j}^\ell \right] . \end{aligned}$$

(3)

It is clear that conservation holds for any choice of the coefficients $\lambda _j$. We assume that the coefficients $\lambda _j$ are the ones used in the cell-average predictions given in Harten (1996), which are exact for one-dimensional polynomials of degree $p\le 2s$. Under this condition, it can be seen that the prediction (2–3) applied to $d$-dimensional dyadic grids is also exact for any $d$-dimensional polynomials of degree $\le 2s$ in each coordinate. In fact, taking $u(x)=\prod _{i = 0}^{d-1}x_i^{p_i}, 0\le p_i \le 2s$, and considering that $c_{\alpha _H}^{\ell +1}=\prod _{i=0, i\ne n}^{d-1}c_{\alpha _i}^{\ell _i} \times c^{\ell _{n}+1}_{\alpha _{nH}}$, from (2) we get

$$\begin{aligned} \tilde{u}^{\ell +1}_{\alpha _H}&= \displaystyle \frac{1}{|c^\ell _{\alpha }|}\prod _{i=0,i\ne n}^{d-1}\,\,\,\int \limits _{c_{\alpha _i}^{\ell }}x_i^{p_i}\mathrm{d}x_i\left[ \,\,\,\int \limits _{c^{\ell }_{\alpha _n}}x_n^{p_n}\mathrm{d}x_n+ \sum _{j=1}^{s} \lambda _j\left( \,\,\,\int \limits _{c^{\ell }_{\alpha _n+j}}x_n^{p_n}\mathrm{d}x_n - \displaystyle \int \limits _{c^{\ell }_{\alpha _n-j}}x_n^{p_n}\mathrm{d}x_n\right) \right] \nonumber \\&= \displaystyle \frac{2}{|c^\ell _{\alpha }|}\prod _{i=0,i\ne n}^{d-1}\,\,\,\int \limits _{c_{\alpha _i}^{\ell }}x_i^{p_i}\mathrm{d}x_i\int \limits _{c^{\ell +1}_{\alpha _nR}}x_n^{p_n}\mathrm{d}x_n,\\ \end{aligned}$$

which coincides to the exact value $u^{\ell +1}_{\alpha _H}$.

For the applications of this paper we shall use the prediction that is exact for polynomials of degree less or equal to 2 and 4. Namely, with $s=1$, $\lambda _1=\frac{1}{8}$, and with $s=2$, $\lambda _1=\frac{22}{128}$, and $\lambda _2=-\frac{3}{128}$.

2.3 Detail coefficients

For MR analyses, the important quantities are the details, or wavelet coefficients, that express the new information between successive levels. Namely, for the present context, one considers the differences between the actual cell averages $u_\alpha ^{\ell +1}$ and the predicted values $\tilde{u}_\alpha ^{\ell +1}$, extrapolated from the cell averages at level $\ell$. The detail $d_\alpha ^\ell$ associated to the cell $c_\alpha$ is then defined as the prediction error for one of its children. For instance,

$$\begin{aligned} d_\alpha ^\ell = u_{\alpha _H}^{\ell +1} - \tilde{u}^{\ell +1}_{\alpha _H}. \end{aligned}$$

As prediction errors, $d_\alpha ^\ell$ vanishes for polynomials of degree $\le 2s$.

Observe that the average values of both children of $c_\alpha$ can be computed from the average $u^\ell$ and the detail $d_\alpha ^\ell$, namely

$$\begin{aligned} u_{\alpha _H}^{\ell +1}&= \tilde{u}^{\ell +1}_{\alpha _H} + d_\alpha ^\ell , \\ u_{\alpha _L}^{\ell +1}&= 2 u_\alpha ^\ell - u_{\alpha _H}^{\ell +1}. \end{aligned}$$

These formulae define a bijection $u^{\ell +1}\leftrightarrow (d^\ell ,u^\ell )$. In general, if $u^L$ denotes the cell averages of $u$ to a specified highest resolution level $L$, we obtain the direct (decomposition) and inverse (reconstruction) multiresolution transformations

$$\begin{aligned} u^L \leftrightarrow (u^0;d^0,d^1,\dots , d^{L-1}), \end{aligned}$$

where $u^0$ is the vector whose single element is the average of $u$ in the root cell $R$.

2.4 Functional MR context

As in traditional MR analyses, it is proved in Castro (2011) that the MR algorithms defined in the previous sections are related to multilevel functional spaces decompositions

$$\begin{aligned} U^{\ell +1} = U^\ell \oplus W^\ell \end{aligned}$$

which are associated with representations of the form

$$\begin{aligned} \sum _{\alpha \in \mathcal {K}(\ell +1)} u^{\ell +1}_\alpha \phi _\alpha ^{\ell +1}(x) = \sum _{\alpha \in \mathcal {K}(\ell )} u^{\ell }_\alpha \phi _\alpha ^{\ell }(x) + \sum _{\alpha \in \mathcal {K}(\ell )} d_\alpha ^\ell \psi _\alpha ^{\ell }(x). \end{aligned}$$

For each cell $c_\alpha ^\ell = \prod _{i=0}^{d-1}c_{\alpha _i}^{\ell _i}$, the scaling function

$$\begin{aligned} \phi _\alpha ^\ell (x) = \prod _{i=0}^{d-1}\phi _{\alpha _i}^{\ell _i}(x_i), \end{aligned}$$

is defined in terms of the basic Harten’s scaling functions associated to one-dimensional cells $c_{\alpha _i}^{\ell _i}$. Similarly, the wavelets are

$$\begin{aligned} \psi _\alpha ^\ell (x) = \psi _{\alpha _n}^{\ell _n}(x_n)\prod _{i=0,i\ne n}^{d-1} \phi _{\alpha _i}^{\ell _i}(x_i),\\ \end{aligned}$$

where $\psi _{\alpha _n}^{\ell _n}(x_n)$ is the one-dimensional Harten’s wavelet associated to the cell $c_{\alpha _n}^{\ell _n}$.

2.5 Adaptive MR representation

The wavelet coefficients $d_\alpha ^\ell$, as prediction errors, can be used as indicators of local regularity of the function $u$. Precisely, let $S_\alpha$ be a region containing the stencil centred on cell $c_\alpha ^\ell$ used to compute the prediction $\tilde{u}_{\alpha _H}^{\ell +1}$. Suppose that $u$ has continuity to some order $r\le 2s$ in $S_\alpha$, where $2s$ is the degree of polynomial exactness for the prediction operator.

Using the classical theory of local approximation by polynomials, the magnitude of the details $d_\alpha ^{\ell }$ can be bounded as

$$\begin{aligned} \vert d_\alpha ^\ell \vert \le C 2^{-r\ell } \vert u \vert _{C^r(S_\alpha )}, \end{aligned}$$

where $C$ is a constant independent of $\ell$ (Cohen 1998). Therefore, $|d_\alpha ^\ell |$ is expected to be small in regions where $u$ is smooth and large in regions of sharp variation.

As in general adaptive MR applications, the main idea is to use the wavelet coefficients in a multiresolution representation of cell averages to construct adaptive grids by stopping the dyadic bisection in regions where the analysed function is smooth, indicated by the cells where $|d_\alpha ^\ell |$ are bellow a prescribed tolerance $\epsilon _\ell$. Usually, the threshold strategy has the level-dependent form

$$\begin{aligned} \epsilon _\ell = 2^{(\ell -L)}\epsilon , \end{aligned}$$

(4)

where $\epsilon > 0$ is previously specified. Experience shows that, in many problems, such adaptive representations reduce significantly the required storage, with control of the accuracy. The crucial property for that is the $\ell ^1$-stability

$$\begin{aligned} \Vert \tilde{u}^L - u^L \Vert _{\ell ^1} = \sum _{\alpha \in \mathcal {K}(L)}|u_\alpha ^L-\tilde{u}_\alpha ^L| \le C \sum _{\ell =0}^{L-1}\epsilon _\ell , \end{aligned}$$

which is expected to hold, independently of $L$. This property is valid for the MR schemes considered here as a consequence of the underlying prediction formulae, which are based on stable one-dimensional refinement schemes. Therefore, we can control the information loss of the pruning algorithm by choosing $\epsilon$ properly.

2.6 Example: image compression

Consider the $512\times 512$ pixels grey-scale image from Lichtenstein’s Castle (Fig. 2) with pixel values between 0 (black) and 255 (white).

Fig. 2

Lichtenstein’s Castle, $512 \times 512$ pixels grey-scale image

Figure 3 shows two adaptive dyadic MR representations of that image using the prediction operator with $s=1$. Figure 4 shows the $\ell ^1$ relative error of the reconstructed thresholded images, as a function of compression ratio = $\frac{N-N_\epsilon }{N}\times 100$, where $N_\epsilon$ is the cells in the adaptive grid, and $N$ is the total cells in the full grid at level $L$. On the left plot, we compare three threshold strategies: $eps$ refers to a constant threshold $\epsilon _\ell =\epsilon$, $eps1$ corresponds to the formula (4), where the threshold is halved in every bisection, and $eps2$ means that it is halved after two bisections. Observe that for $eps1$ and $eps2$ the compromise error $\times$ compression is similar. However, the constant threshold affects significantly the error for high compression values, showing the importance of decreasing the threshold at coarse levels of resolution. On the right side, the plots compare the performance of the MR schemes in dyadic grids and quad grids. For a given accuracy level, the compression with dyadic grids for this example is about $2~\%$ higher than with quad grid. We also mention that the dyadic-grid structure saves $10~\%$ in memory space when compared with quad-tree.

Fig. 3

Adaptive dyadic grids (left) and the recovered images (right) of the MR representation of Fig. 2, using $\epsilon =5$ (top) and $\epsilon =20$ (bottom)

Fig. 4

Reconstruction error versus compression ratio using MR in dyadic grids for $s=1$, with different threshold strategies (left), and comparison with MR in quad grids (right)

3 Adaptive FV/MR scheme for PDE

Several authors have used the quad-grid subdivision in adaptive multiresolution finite-volume schemes for the integration of conservation laws (Müller 2003; Cohen et al. 2003; Roussel et al. 2003; Domingues et al. 2008, 2009). For completeness, in this section we summarize the main steps required for the implementation of FV/MR schemes based on dyadic grids, as presented in Castro et al. (2012). We first describe a reference finite-volume scheme based on uniform grids in any dimension, which we then modify for an adaptive multiresolution representation using dyadic grids.

3.1 Reference finite-volume discretization

We consider the problem of integrating the generic conservation law

$$\begin{aligned} \frac{\partial v}{\partial t} = - \nabla \cdot f(v), \end{aligned}$$

(5)

where $v$ is an unknown real function of $x\in R\subseteq \mathbb {R}^d$ and $t\in [0,\infty )$, with appropriate initial and boundary conditions; and $f$ is a given function from $\mathbb {R}$ to $\mathbb {R}^d$.

We use the finite-volume method, with a uniform dyadic grid $G^L$ over $R$. The function $v$ is approximated the cell averages $u=u^L=(u_\alpha )$, where

$$\begin{aligned} u_\alpha (t)\approx \bar{v}_\alpha (t) = \frac{1}{\vert c_\alpha ^L\vert }\int \limits _{c_\alpha ^L} v(x,t) \mathrm {d}x. \end{aligned}$$

Equation (5) then reduces to a system of ordinary differential equations

$$\begin{aligned} \frac{\partial u}{\partial t} = \bar{\mathcal {D}}(u), \end{aligned}$$

(6)

where $\bar{\mathcal {D}}_\alpha (u)$ is the numerical flux

$$\begin{aligned} \bar{\mathcal {D}}_\alpha (u) \approx \mathcal {D}_\alpha (v)=-\frac{1}{\vert c_\alpha ^L\vert } \int \limits _{\partial c_\alpha ^L} f(v)\cdot \sigma _\alpha \mathrm {d}s, \end{aligned}$$

(7)

where $\sigma _\alpha$ denotes the outer normal vector to $c_\alpha ^L$.

For the applications of this paper, the numerical flux is represented in the form

$$\begin{aligned} \bar{\mathcal {D}}_\alpha = -\frac{1}{\Delta x_0} \left( \bar{F}^0_{\alpha +\frac{1}{2}} - \bar{F}^0_{\alpha -\frac{1}{2}}\right) -\frac{1}{\Delta x_1}\left( \bar{F}^1_{\alpha +\frac{1}{2}} - \bar{F}^1_{\alpha -\frac{1}{2}}\right) . \end{aligned}$$

where $\bar{F}^i_{\alpha \pm \frac{1}{2}}$ are the numerical fluxes throughout the boundary of cell $c_\alpha$ parallel to the $i$-axes, as indicated in Fig. 5. We shall consider WENO-type numerical fluxes [see Liu et al. (1994)], defined in terms of linear convex combinations of polynomial reconstructions of degree $r-1$ approximating $v(x,t)$ on $c_\alpha$, which require cell-average information of $2r-1$ centred stencil cells in each $i$ direction. For the present applications WENO2 ($r=2$) and WENO3 ($r=3$) are applied.

Fig. 5

Numerical fluxes through the boundaries of cell $c_\alpha$

For the time integration, we consider a sequence of uniform discrete instants $t^n=n\Delta t$, where $\Delta t$ denotes the time step, and denote by $u^n$ the approximation of $u$ at $t^n$. Depending on the choice of the numerical flux WENO2 or WENO3, the ODE system (6) is integrated, respectively, by the second-order (RK2) Runge–Kutta formulae or by applying the third-order accurate TVD Runge–Kutta scheme (Shu and Osher 1988).

3.2 Adaptive MR scheme

The purpose of an adaptive grid refinement technique for partial differential equations (PDE) is to save computational resources while preserving the accuracy of the solution with respect to the uniform discretization in the finest scale level. Grid adaptation means that refined grids are used only where they are required, such as in regions where the solution exhibits localized strong features.

In the adaptive MR version of the finite-volume method, the numerical solution $u_\mathrm{MR}^n$ is the set of cell averages in an adaptive grid $G^n$. The grid $G^n$ is associated to a non-uniform data tree structure, where the refinement stops before the maximum level of resolution is reached. To get $u_\mathrm{MR}^{n+1}$ from $u_\mathrm{MR}^n$ we need three steps: refinement, evolution and thresholding.

Refinement This step is necessary because the grid $G^n$, that is adequate to represent the solution at time $n$, may not be adequate for time $n+1$. We assume that the time step $\Delta t$ is small enough so that at most one extra level of refinement is sufficient. Therefore, in this step we construct a refined grid $G^{n+}$ by splitting each leaf cell $c_\alpha ^\ell$ of $G^n$, such that $\ell < L$, by a hyperplane orthogonal to axis $i=\ell \hbox {mod} d$. The cell averages $u^{n+}$ of the current solution in the leaf cells of $G^{n+}$ are obtained by applying the prediction operator to the current approximation $u^n_\mathrm{MR}$. We denote the refinement operator by $\mathbf {R}$, and write $G^{n+}=\mathbf {R}G^n$ and $u^{n+} = \mathbf {R}u^n_\mathrm{MR}$.

Evolution The discrete evolution operator computes the numerical solution $\tilde{u}^{n+1}$ at time $t^{n+1}$, over the grid $G^{n+}$, from the refined solution $u^{n+}$ at time $t^n$. First, for each leaf cell $c_\alpha ^\ell$ of $G^{n+}$, we estimate the flux across each of its $2d$ facets as follows. Let $c_\beta ^\ell$ be the cell of the multigrid $\mathcal {G}=\cup _{0\le \ell \le L}G^\ell$ that is adjacent to $c_\alpha ^\ell$ on the same level $\ell$. Then:

• If some $c_\beta ^\ell$ is a leaf cell of $G^{n+}$, the flux across the shared facet is computed as in the uniform grid.

• Otherwise, if $c_\beta ^\ell$ is not in $G^{n+}$, we locate the leaf $c_\gamma ^\kappa$ of $G^{n+}$ (with $\kappa < \ell$) that contains $c_\beta ^\ell$, then use the prediction operator repeatedly to obtain the cell average for $c_\beta ^\ell$, and proceed as in the previous case.

• Otherwise, if $c_\beta ^\ell$ is present in $G^{n+}$ but is not a leaf, the desired flux is obtained by adding the appropriate fluxes from all leaf cells that descend from $c_\beta ^\ell$ and are adjacent to $c_\alpha ^\ell$.

Once we have the fluxes across all facets of $c_\alpha ^\ell$, we obtain $\tilde{u}^{n+1}$ by applying the Runge–Kutta scheme. We denote the evolution operator by $\mathbf {E}_\mathrm{MR}$, and write $\tilde{u}^{n+1} = \mathbf {E}_\mathrm{MR} u^{n+}$.

Thresholding In this last step, to get the solution $u^{n+1}_{MR}$ from $\tilde{u}^{n+1}$, we use the restriction operator to refresh the cell averages of non-leaf nodes of the tree, and prune any leaf cells that make a negligible contribution to the representation of $u^{n+1}_\mathrm{MR}$, as described in Sect. 2.5. We denote this operator by $\mathbf {T}(\epsilon )$, and write $u^{n+1}_\mathrm{MR} = \mathbf {T}(\epsilon )\tilde{u}^{n+1}$.

Therefore, the inner loop of the integrator can be written as

$$\begin{aligned} u^{n+1}_\mathrm{MR} = \mathbf {T}(\epsilon )\, \mathbf {E}_\mathrm{MR}\, \mathbf {R}\, u^n_\mathrm{MR}. \end{aligned}$$

3.3 Outline of the algorithm

The integration algorithm can be summarized as follows. It depends on six main parameters—the dimension $d$, the root cell $R$, the total integration time $T$, the CFL factor $\sigma = \Delta t/\Delta x$, the maximum resolution level $L$, and pruning threshold $\epsilon$—as well as on the flux function $f$ and the initial state $v^0(x) = v(x,0)$.

• Compute the maximum width $W$ of the domain $R$ along any axis, the minimum cell size $\Delta x = W/2^L$, the number of iterations $N = \lceil T/(\sigma \Delta x)\rceil$, and the time step $\Delta t = T/N$.

• Create a uniform data tree structure with depth $L$. Store in each cell the average of the initial state $v^0$. Prune nodes from this tree which have details below the threshold parameter $\epsilon$, as described in Sect. 2.5.

• For $n$ from $0$ to $N-1$, do:

  • Split each leaf cell of the grid which is not at the maximum level $L$. Estimate the cell averages at those cells using the prediction operator.

  • Evaluate the numerical flux in each leaf cell, as detailed in Sect. 3.

  • Apply the Runge–Kutta scheme in each leaf cell, to estimate the cell average at time $n+1$.

  • Update the cell average of each internal node, from the finest to coarsest level, by the restriction operator (averaging the values of its two children).

  • Prune nodes from this tree which have details below the threshold parameter, as described in Sect. 2.5.

In the current implementation, the tree is generally traversed recursively, in depth-first mode (Knuth 1997). Namely, the children of each cell are considered in some order, and the entire sub-tree that descends from each child is processed before any cell that descends from the next child. During this traversal, however, the implementation maintains a pack of tree nodes that have the same level as the current tree node and whose cells surround the cell of that node.

More precisely, the pack $P$ is a $d$-dimensional array of node pointers, with some odd number $m$ of elements along each axis. The array is stored as a vector with $M = m^d$ elements, which we will denote by $P[0]$ through $P[M-1]$. The central element $P[(M-1)/2]$ of this array corresponds to the current node $t$ of the traversal. The remaining elements of $P$ correspond to cells that surround the cell $c$ of $t$ in the same level $\ell$ of the infinite multiscale grid, so that the union of those cells is a $d$-dimensional box centred on $c$.

Each element $P[i]$ thus represents some cell, denoted by $P[i].{\textit{cell}}$, and contains a pointer $P[i].{\textit{node}}$ to the node of the tree that represents that cell. The pointer is null if that node does not exist in the tree. Each element $P[i]$ of the pack also contains a vector of values $P[i].{\textit{val}}$ of the state variables for the corresponding cell $P[i].{\textit{cell}}$, even if the corresponding pointer $P[i].{\textit{node}}$ is null.

When the traversal algorithm moves from the current node $t$ to some child node $t'$, it builds a pack $P'$ for the latter. Each cell of $P'[j].{\textit{cell}}$ of $P'$ is a child of some cell $P[i].{\textit{cell}}$ in $P$, so every pointer $P'[j].{\textit{node}}$ is the corresponding child pointer of the node $P[i].{\textit{node}}$; or null, if $P[i].{\textit{node}}$ is null. In any case, the value vector $P'[j].{\textit{val}}$ is computed from $P[i].{\textit{val}}$ and its neighbours by the interpolation formula, plus the detail data stored in node $P'[j].{\textit{node}}$ if that node exits.

The pack size $m$ must be large enough to allow the computation of every cell of $P'$ from the values stored in the parent pack $P$. For the second-order schema used in the previous paper (Castro et al. 2012), $m=5$ is sufficient. For the third-order schema used here, we must use $m=9$.

4 Illustrative examples

In this section, we apply the adaptive multiresolution scheme based on dyadic grids to solve some typical test problems, with periodic boundary conditions. The basic FV schemes (denoted by FV2 and FV3) are the combination WENO2 + RK2 or WENO3 + RK3, as described in Sect. 3.1. In all the cases, $\textit{CFL}=0.5$.

The adopted threshold strategy uses the level-dependent form given in Eq. (4). The errors are evaluated at the final instant $T=0.5$ by interpolating the adaptive solution up to finest uniform level and by comparing it with respect to the exact solution (in the 1D advection case) or to the corresponding reference FV solutions (2D test case for Burgers equation). The compression is defined as the percentage of cells not used in the adaptive grid at $T$, with respect to the uniform finest grid, and the CPU gain is the ratio of CPU times spent to evolve the solution by the reference FV scheme and by the FV/MR scheme.

Fig. 6

1D advection equation. Adaptive schemes FV2/MR with $s=1$ and FV3/MR with $s=1,2$: plots of $\epsilon$ versus accuracy (left side), compression (midle side), and CPU gain (right side)

Advection equation in 1D Let us consider the advection equation

$$\begin{aligned} v_t+ v_{x_0}= 0,&x_0 \in R=(-1,1), \end{aligned}$$

subjected to periodic boundary condition and smooth initial condition $v(x_0,0)=\exp (-100x_0^2)$. In Fig. 6, the errors refer to the exact solution $v(x_0,0.5)=v_0(x_0-0.5)$ at the finest uniform grid with spacing $\Delta _{x_0}=2^{-12}$. The $L^1$ errors for reference FV2 and FV3 schemes are $3.7998\times 10^{-6}$ and $2.92969\times 10^{-9}$, respectively.

The plots in Fig. 6 illustrate the effects of increasing the order of the reference FV scheme and/or of the prediction operator by comparing accuracy, compression, CPU gain for the schemes FV2/MR with lower-order prediction operator (for $s=1$), and FV3/MR for $s=1$ or $s=2$, as functions of the threshold parameter $\epsilon$.

We observe in the plots of the top-left side that there is a range of $\epsilon$, where the threshold errors dominate, and consequently, the three schemes produce similar accuracy. Decreasing $\epsilon$, the accuracy improves when the higher-order scheme FV3/MR is used. However, when the lower-order prediction scheme ($s=1$) is applied, the adaptive scheme FV3/MR is not able to get the accuracy of the reference FV3 scheme, which is reached by the FV3/MR scheme when the prediction for $s=2$ is used. Concerning compression rate, the behaviour is determined by the prediction operator, as indicated in the plots of the top-right side. Independently of the order of the reference finite-volume scheme, both FV2/MR and FV3/MR using the prediction operator for $s=1$ show quite similar compression rates. However, for the FV3/MR scheme using the prediction operator for $s=2$, the compression is significantly superior. From the plots on the bottom side, it is also evident the good effect on the gain in the CPU time when a higher-order scheme FV3/MR with $s=2$ is used.

Table 1 2D Burgers Equation: data for FV3/MR solutions in function of threshold parameter

Fig. 7

Burgers equation. Adaptive schemes FV2/MR with $s=1$ and FV3/MR with $s=2$: plots of $\epsilon$ versus compression and CPU gain (top side), and error (bottom side)

Fig. 8

2D Burgers’s equation: FV2/MR (left side) and FV3/MR (right side) solutions with $\epsilon =10^{-6}$, at $T=0.5$. Isolines (top side), varying from $0.1$ to $0.6$ with step $0.1$, and the corresponding adaptive grids (bottom side)

Burgers’s Equation Consider now the equation

$$\begin{aligned} v_t+\left( f(v) \right) _{x_0}+\left( f(v) \right) _{x_1} = 0,&(x_0,x_{1})\in R= (-1,1)\times (-1,1), \end{aligned}$$

with $f(v)=\frac{1}{2} u^2$, subjected to periodic boundary condition and initial condition:

$$\begin{aligned} v_0(x_0,x_1)&=\exp \left( -100(x_0^2+x_1^2)\right) \!,\quad (x_0,x_1)\in R. \end{aligned}$$

For this test case the finest uniform grid corresponds to $\Delta _{x_0}=\Delta _{x_1}=2^{-10}$, and the results are for FV2/MR (with $s=1$) and FV3/MR (with $s=2$).

Table 1 shows FV3/MR data for compression, reconstruction error and CPU gain with respect to the FV3 scheme on the finest regular grid. In Fig. 7, these data are plotted to be compared with the corresponding ones produced by the lower-order scheme FV2/MR. As for the 1D advection test case, it is also evident the good effect on the compression and CPU gain when a higher-order scheme FV3/MR with $s=2$ is used. Since now the errors are computed with respect to the corresponding FV solution on the finest uniform grid, the results show that they are only controlled by the threshold parameter $\epsilon$.

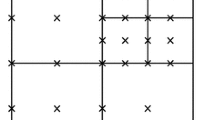
In Fig. 8 the isolines of the solutions for the schemes FV2/MR (left side) and FV3/MR with $\epsilon =10^{-6}$ are plotted, with the curves varying from $0.1$ to $0.6$, with step $0.1$. The corresponding adaptive grids, presented on the bottom side, illustrate the ability of the adaptive schemes in automatically fitting the refinement to the numerical solution features.

5 Final remarks

This paper deals with adaptive multiresolution finite-volume schemes FV/MR for hyperbolic conservation laws. Special attention is drawn onto the data structure. Here dyadic tree structures are advocated, which provide a more gradual refinement as compared to the traditional quad-trees (2D) or oct-trees (3D) that are commonly used for multiresolution analysis, leading to adaptive binary-tree representations in any dimension. The efficiency of the method is illustrated by the application to typical scalar test problems showing significant savings in data storage and CPU time when compared with the reference scheme in uniform grid at the finest scale level, with accuracy controlled by the truncation threshold. The effect of increasing the order of the basic FV scheme is also analysed by considering the combinations FV2 $=$ WENO2 $+$ RK2 and FV3 $=$ WENO3 $+$ RK3. Adaptive flux computations introduce some overhead on the evolution of each cell average, which increases with costly larger stencils required by the higher-order scheme FV3. However, this drawback is compensated on the adaptive FV3/MR by higher compression rates and better accuracy. For the current implementation of the adaptive FV/MR method, a depth-first traversal method is adopted by keeping for each leaf cell a pack of tree nodes corresponding to some cells surrounding it. However, it may occur that some missing cell averages of these packs are re-computed many times, since a cell may occur in the packs of many different nodes. In the future, we propose to improve this implementation using a breadth-first (that is, level by level) traversal (Knuth 1997). Then, for each level $\ell$ one would process all the level-$\ell$ cells of the finite mesh together, “dilated” by $(m-1)/2$ cells all around; in that way, each cell value would be interpolated only once.