Approximate series solution of singular boundary value problems with derivative dependence using Green’s function technique

Abstract

In this work, we propose an effective approach for solving singular boundary-value problems with derivative dependence. The present approach is based on a modification of the Adomian decomposition method (ADM) which combines with Green’s function. In fact, it depends on constructing Green’s function before establishing the recursive scheme for the solution components. In contrast to the existing recursive schemes based on ADM, the proposed method avoids solving a sequence of transcendental equations for the undetermined coefficients. The approximations of the solution are obtained in the form of series with easily computable components. Additionally, the convergence analysis and error estimation of the proposed method is discussed under quite general conditions. Moreover, the numerical examples are included to demonstrate the accuracy, applicability, and generality of the proposed scheme. The numerical results reveal that the proposed method is very effective and simple.

1 Introduction

Two-point singular boundary value problems for ordinary differential equations arise very frequently in many branches of applied mathematics and physics such as gas dynamics, chemical reactions, nuclear physics, atomic structures, atomic calculations, electrical potential theory, study of positive radial solutions of nonlinear elliptic equations and physiological studies. Therefore, it has been studied extensively in recent years. However, such nonlinear singular boundary value problems cannot be solved analytically in general. So these must be tackled by various numerical or approximate methods. However, the numerical treatment of the singular boundary value problems has always been far from trivial due to the singularity.

The aim of this paper is to propose an effective recursive scheme for solving nonlinear derivative-dependent singular boundary value problems (SBVPs). This scheme is based on Adomian decomposition method (ADM) and the Green’s function technique. We consider the SBVPs with derivative dependence (Bobisud 1990; Verma and Pandey 2011)

$$\begin{aligned} \left. \begin{array}{ll} (p(x)u^{\prime }(x))^{\prime }=q(x)f(x,u(x),p(x)u^{\prime }(x)),\ x\in (0,1],\\ u(0)=\alpha _1, \beta _1u(1)+\gamma _1 u^{\prime }(1)=\eta _1, \end{array} \right\} \end{aligned}$$

(1.1)

where $\alpha _1,\beta _1>0,\gamma _1$ and $\eta _1$ are any finite real constants. The condition $p(0)=0$ says that the Eq. (1.1) is singular and if $q(x)$ is allowed to be discontinuous at $x=0$ then the Eq. (1.1) is called doubly singular (Bobisud 1990). Throughout the paper the following conditions are assumed on $p(x),q(x)$ and $f(x,u(x),p(x)u^{\prime }(x))$

$({\hbox {E}}_{1})$ :

$p(x)\in C[0,1]\cap C^{1}(0,1]$ with $p(x)>0$ in $(0,1]$ and $\in L^1(0,1].$

$({\hbox {E}}_{2})$ :

$q(x)>0$ in $(0,1],\,q(x)\in L^1(0,1]$ and $q(x)$ is not identically zero.

$({\hbox {E}}_{3})$ :

Assume $f(x,u,pu^{\prime })$ is continuous on $D_1=\{{(0,1]\times (0,\infty )\times \mathbb{R }}$} and is not identically zero.

$({\hbox {E}}_{4})$ :

The nonlinear function $f(x,u,pu^{\prime })$ is locally Lipschitz continuous such that

$$\begin{aligned} |f(x,u,pu^{\prime })-f(x,v,pv^{\prime })|\le L_1|u-v|+L_2|p(u^{\prime }-v^{\prime })|, \end{aligned}$$

(1.2)

where $L_1$ and $L_2$ are Lipschitz constants.

There has been much interest devoted in the study of singular two point boundary value problems, Bobisud (1990), Verma and Pandey (2011), Wazwaz et al. (2013), Singh and Kumar (2013b), Chawla and Katti (1982), Inc and Evans (2003), Kumar and Aziz (2006), Ebaid (2011), Khuri and Sayfy (2010), Kumar and Singh (2010), Singh et al. (2012), Ravi Kanth and Aruna (2010), Wazwaz and Rach (2011), Cen (2007), Öztürk and Gülsu (2013) and many of the references therein. The main difficulty of (1.1) is that the singularity behavior occurs at $x=0.$Bobisud (1990) and Verma and Pandey (2011) discussed the existence and uniqueness of solution of the problem (1.1). Recently, a great deal of numerical methods have been used to solve the particular case of (1.1). For example, the cubic spline, B-spline and finite difference methods were carried out in Chawla and Katti (1982), Kanth and Bhattacharya (2006), Çağlar et al. (2009) and Kumar and Aziz (2006). Although, these numerical methods have many advantages, but an immense amount of computational work is involved that combines some root-finding techniques to obtain accurate numerical solution especially for nonlinear problems.

Furthermore, some newly developed numerical-approximate methods have also been applied to handle (1.1). Such as, the ADM and modified Adomian decomposition method (MADM) were employed in Khuri and Sayfy (2010), Kumar and Singh (2010), Inc and Evans (2003), Ebaid (2011). The homotopy analysis method (HAM) was introduced inDanish et al. (2012). It is well known that solving (1.1) by using ADM or MADM is always a computationally involved task as it requires the computation of undetermined coefficients in a sequence of nonlinear algebraic or more difficult transcendental equations which increases the computational work (for details see Kumar and Singh 2010; Khuri and Sayfy 2010; Danish et al. 2012; Bataineh et al. 2009). Moreover, the undetermined coefficients may not be uniquely determined in some cases. This may be the major disadvantage of these methods for solving nonlinear two-point BVPs. Furthermore, the variational iteration method (VIM) and its modified versions have been employed in Wazwaz and Rach (2011) and Ravi Kanth and Aruna (2010). Wazwaz and Rach (2011) showed that VIM gives good approximations only when the problem is linear or weakly nonlinear with nonlinearity of the form $u^{n}, uu^{\prime }\ldots$ etc. However, the VIM suffers when the nonlinearity is of the form $e^{u}, \ln (u), \sin u, \sinh u\ldots$ etc. This may be one of the major drawbacks of VIM for solving difficult nonlinear problems.

In this paper, we present a modification of the ADM which combines with Green’s function to overcome the difficulties occurring in the ADM or MADM for solving nonlinear SBVPs (1.1). In fact, we propose an efficient recursive scheme which does not require any computation of undetermined coefficients, that is, without solving a sequence of growingly higher order polynomials or difficult transcendental equations for obtaining undetermined coefficients (Kumar and Singh 2010; Khuri and Sayfy 2010; Inc and Evans 2003; Wazwaz and Rach 2011). The main advantage of proposed method is that it provides a direct recursive scheme for solving the SBVP. Moreover, the convergence analysis and error estimation of the proposed method is discussed. In addition, the numerical examples are included to demonstrate the accuracy of the proposed method.

1.1 Review of ADM

In this subsection, we shall briefly describe ADM for nonlinear second order differential equation of the form (1.1).

It is well-known that ADM allows us to solve both nonlinear IVPs and BVPs without unphysical restrictive assumptions such as linearization, discretization, perturbation and guessing the initial term or a set of basis function. In recent years, many authors Singh and Kumar (2013a, b), Wu et al. (2009), Duan and Rach (2011), Singh et al. (2012, 2013), Ebaid (2011), Wazwaz and Rach (2011), Khuri and Sayfy (2010), Kumar and Singh (2010), Benabidallah and Cherruault (2004), Inc and Evans (2003), Adomian (1994), Adomian and Rach (1983), Wazwaz (2001), Al-Khaled and Allan (2005), El-Kalla (2012), El-Sayed et al. (2013) and Duan et al. (2013) have shown interest in the study of ADM for different scientific models. According to the ADM, the operator form of (1.1) can be written as

$$\begin{aligned} \mathcal{L }u(x)=Ru(x)+Nu(x),\quad x\in (0,1], \end{aligned}$$

(1.3)

where $\mathcal{L }=\frac{\mathrm{d}^2}{\mathrm{d}x^2}$ is linear second-order differential operator, $R u(x)=-\frac{p^{\prime }(x)}{p(x)}u^{\prime }(x)$ is remainder operator and $Nu(x)=\frac{q(x)}{p(x)}f(x,u(x),p(x)u^{\prime }(x))$ represents the nonlinear function. The inverse operator of $\mathcal{L }$ is defined as

$$\begin{aligned} \mathcal{L }^{-1}[\cdot ]=\int \limits _{0}^{x} \int \limits _{0}^{x}[\cdot ]\,\hbox {d}x\,\hbox {d}x. \end{aligned}$$

(1.4)

Operating the inverse operator $\mathcal{L }^{-1}[\cdot ]$ on both sides of (1.3) and using the boundary condition $u(0)=\alpha _1$ we obtain

$$\begin{aligned} u(x)=\alpha _1+c x+\mathcal{L }^{-1}[Ru(x)+Nu(x)], \end{aligned}$$

(1.5)

where $c=u^{\prime }(0)\ne 0$ is unknown constant, and it will be determined later using boundary conditions at $x=1.$

The solution $u(x)$ and the nonlinear function $Nu(x)$ are decomposed by infinite series

$$\begin{aligned} u(x)=\sum _{n=0}^{\infty }u_n(x),\quad Nu(x)=\sum _{n=0}^{\infty }A_n, \end{aligned}$$

(1.6)

where $A_n$ are Adomian’s polynomials that can be constructed for various classes of nonlinear functions with the formula given by Adomian and Rach (1983)

$$\begin{aligned} A_n=\frac{1}{n!}\frac{\mathrm{d}^n}{\mathrm{d} \lambda ^n}\left[ N\left( \sum _{k=0}^{\infty } u_k\lambda ^k \right) \right] _{\lambda =0},\quad n=0,1,2,\ldots \end{aligned}$$

(1.7)

Substituting the series (1.6) into (1.5), we obtain

$$\begin{aligned} \sum _{n=0}^{\infty }u_n(x)=\alpha _1+c x+\mathcal{L }^{-1}\left[ R\sum _{n=0}^{\infty }u_n(x) +\sum _{n=0}^{\infty }A_n\right] . \end{aligned}$$

(1.8)

Upon comparing both sides of (1.8), the ADM admits the following recursive scheme

$$\begin{aligned} \left. \begin{array}{ll} u_0(x,c)=\alpha _1+c x,\\ u_{j}(x,c)= \mathcal{L }^{-1} [Ru_{j-1}+A_{j-1}],\quad j\ge 1, \end{array} \right\} \end{aligned}$$

(1.9)

that will lead to the complete determination of components $u_j(x,c), j=0,1,2,\ldots ,$ of the solution $u.$ Hence the $n$-term truncated approximate series solution can be obtained as

$$\begin{aligned} \phi _n(x,c)=\sum _{j=0}^{n} u_j(x,c). \end{aligned}$$

(1.10)

One can note that the approximate solution $\phi _n(x, c)$ depends on the unknown constant $c.$ This constant $c$ will be determined approximately by imposing the boundary condition at $x=1$ on $\phi _n(x,c),$ which leads to a sequence of transcendental equations $\phi _n(1,c)=0, n=1,2,3,\ldots .$

Recently, in Wazwaz (2001), Inc and Evans (2003), Benabidallah and Cherruault (2004), Khuri and Sayfy (2010) and Kumar and Singh (2010) authors applied ADM for solving nonlinear two-point BVPs. However, solving such BVPs using ADM is always a computationally involved task because it requires the computation of undetermined coefficients in a sequence of difficult transcendental equations that increases the computational work. For example, consider

$$\begin{aligned} u^{\prime \prime }(x)= -\mathrm{e}^{u(x)},\quad u(0)=0,\quad u(1)=0, \end{aligned}$$

(1.11)

According to the ADM (1.9), the (1.11) can be transformed into the recursive scheme as

$$\begin{aligned} u_0(x,c)=cx,\quad u_{j}(x,c)=-\mathcal{L }^{-1}[A_{j-1}],\quad j\ge 1. \end{aligned}$$

(1.12)

Using the formula (1.7), the Adomian’s polynomials for $f(u)=\mathrm{e}^u$ about $u_0=cx$ are

$$\begin{aligned} A_0=\mathrm{e}^{cx},\quad A_1=u_1 c \mathrm{e}^{cx},\quad A_2=u_2 c \mathrm{e}^{cx}+\frac{1}{2} u_1^2 c^{2}\mathrm{e}^{cx}, \ldots \end{aligned}$$

(1.13)

Using (1.12) and (1.13), we obtain the components as

$$\begin{aligned} u_0(x, c)&= c x,\\ u_1(x, c)&= \frac{1}{c^2}-\frac{\mathrm{e}^{c x} }{c^2}+\frac{x }{c},\\ u_2(x, c)&= -\frac{5 }{4 c^4}+\frac{\mathrm{e}^{c x}}{c^4}+\frac{\mathrm{e}^{2 c x}}{4 c^4}-\frac{x }{2 c^3}-\frac{\mathrm{e}^{c x}x}{c^3},\\ u_3(x, c)&= \frac{11}{6 c^6}-\frac{5 \mathrm{e}^{c x}}{4 c^6}-\frac{\mathrm{e}^{2 c x}}{2 c^6}-\frac{\mathrm{e}^{3 c x}}{12 c^6}+\frac{x}{2 c^5}+\frac{3 \mathrm{e}^{c x} x}{2 c^5}+\frac{\mathrm{e}^{2 c x} x}{2 c^5}-\frac{\mathrm{e}^{c x} x^2}{2 c^4},\\ \vdots \end{aligned}$$

Consequently, the $n$-term truncated series solution is obtained

$$\begin{aligned} \phi _n(x,c)=\sum _{j=0}^{n} u_j(x,c). \end{aligned}$$

(1.14)

By imposing the boundary condition at $x=1$ on $\phi _n(x,c),$ which leads to a sequence of transcendental equations $\phi _n(1,c)=0, n=1,2,3,\ldots$

$$\begin{aligned} \left. \begin{array}{ll} \phi _1(1,c)&{}\equiv c +\left( \frac{1}{c^2}-\frac{\mathrm{e}^{c } }{c^2}+\frac{1}{c}\right) =0 \\ \phi _2(1,c)&{}\equiv c +\left( \frac{1}{c^2}-\frac{\mathrm{e}^{c } }{c^2}+\frac{ 1}{c}\right) + \left( -\frac{5}{4 c^4}+\frac{\mathrm{e}^{c } }{c^4}+\frac{\mathrm{e}^{2 c } }{4 c^4}-\frac{ 1}{2 c^3}-\frac{\mathrm{e}^{c }}{c^3}\right) =0 \\ \phi _3(1, c)&{}\equiv c +\left( \frac{1}{c^2}-\frac{\mathrm{e}^{c } }{c^2}+\frac{ 1}{c}\right) + \left( -\frac{5}{4 c^4}+\frac{\mathrm{e}^{c } }{c^4}+\frac{\mathrm{e}^{2 c } }{4 c^4}-\frac{ 1}{2 c^3}-\frac{\mathrm{e}^{c }}{c^3}\right) \\ &{}\quad +\left( \frac{11 }{6 c^6}-\frac{5 \mathrm{e}^{c } }{4 c^6}-\frac{\mathrm{e}^{2 c }}{2 c^6}-\frac{\mathrm{e}^{3 c }}{12 c^6}+\frac{ 1}{2 c^5}+\frac{3 \mathrm{e}^{c } }{2 c^5}+\frac{\mathrm{e}^{2 c } }{2 c^5}-\frac{\mathrm{e}^{c }}{2 c^4}\right) =0\\ \vdots \end{array} \right\} \end{aligned}$$

(1.15)

In order to obtain unknown constant $c,$ we need some root finding techniques and these techniques require additional computational work. However, solving a sequence of transcendental equations (1.15) for $c$ is difficult task in general. Moreover, in some cases the undetermined coefficient $c$ may not be uniquely determined. This may be the major drawback of ADM for solving nonlinear boundary value problems. In order to avoid solving such types of a sequence of transcendental equations for unknown constant $c,$ in next section we shall propose a new recursive scheme which does not involve any undetermined coefficient to be determined.

2 ADM with Green’s function technique

In this section, we propose an efficient recursive scheme which is based on the Green’s function technique and ADM for solving nonlinear derivative-dependent singular two point boundary value problems of the form (1.1). To this end, we first consider the following homogeneous SBVP:

$$\begin{aligned} \left. \begin{array}{ll} (p(x)v(x))^{\prime }=0,\quad x\in (0,1],\\ v(0)=\alpha _1,\quad \beta _1 v(1)+\gamma _1 v^{\prime }(1)=\eta _1. \end{array} \right\} \end{aligned}$$

(2.1)

Note that the unique solution of (2.1) is given by

$$\begin{aligned} v(x)=\alpha _1+\frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x), \end{aligned}$$

(2.2)

where $h(x)=\int \nolimits _{0}^{x}\frac{\mathrm{d}s}{p(s)},\,\mu =\beta _1h(1)+\gamma _1 h^{\prime }(1),\,h(1)=\int \nolimits _{0}^{1}\frac{\mathrm{d}s}{p(s)}$ and $h^{\prime }(1)=\frac{1}{p(1)}.$

In order to construct the Green’s function, we now consider the linear SBVP as

$$\begin{aligned} \left. \begin{array}{ll} (p(x)u^{\prime }(x))^{\prime }=q(x)F(x),\quad x\in (0,1],\\ u(0)=0,\quad \beta _1 u(1)+\gamma _1 u^{\prime }(1)=0. \end{array} \right\} \end{aligned}$$

(2.3)

Integrating the Eq. (2.3) twice first from $x$ to 1 and then from 0 to $x,$ changing the order of integration, and applying the boundary conditions, we obtain

$$\begin{aligned} u(x)&= -\frac{1}{\mu }\int \limits _{0}^{1}\beta _1h(x) h(\xi )q(\xi )F(\xi )\,\hbox {d}\xi +\int \limits _{0}^{x}h(\xi )q(\xi )F(\xi )\,\hbox {d}\xi +\int \limits _{x}^{1}h(x) q(\xi )F(\xi )\,\hbox {d}\xi ,\\ u(x)&= -\frac{1}{\mu }\int \limits _{0}^{x}\beta _1h(x) h(\xi )q(\xi )F(\xi )\,\hbox {d}\xi -\frac{1}{\mu }\int \limits _{x}^{1}\beta _1h(x) h(\xi )q(\xi )F(\xi )\,\hbox {d}\xi \\&+\int \limits _{0}^{x}h(\xi )q(\xi )F(\xi )\,\hbox {d}\xi +\int \limits _{x}^{1}h(x) q(\xi )F(\xi )\,\hbox {d}\xi ,\\ u(x)&= \int \limits _{0}^{x} h(\xi )\left( 1-\frac{\beta _1h(x)}{\mu }\right) q(\xi )F(\xi )\,\hbox {d}\xi +\int \limits _{x}^{1} h(x)\left( 1-\frac{\beta _1h(\xi )}{\mu }\right) q(\xi )F(\xi )\,\hbox {d}\xi ,\\ u(x)&= \int \limits _{0}^{1}G(x,\xi ) q(\xi )F(\xi )\,\hbox {d}\xi , \end{aligned}$$

where the Green’s function of the problem (2.3) is given by

$$\begin{aligned} G(x,\xi )=\left\{ \begin{array}{ll} h(x)\left( 1-\frac{\beta _1h(\xi )}{\mu }\right) , &{}\quad 0\le x \le \xi \le 1,\\ h(\xi )\left( 1-\frac{\beta _1h(x)}{\mu }\right) , &{}\quad 0\le \xi \le x\le 1. \end{array} \right. \end{aligned}$$

(2.4)

It is easy to check that the function $G(x,\xi )$ satisfies all the properties of Green’s function.

Making use of (2.2) and (2.4), we transform original SBVP (1.1) into the integral equation as

$$\begin{aligned} u(x)=\alpha _1+\frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x)+\int \limits _{0}^{1} G(x,\xi )q(\xi ) f(\xi ,u(\xi ),p(\xi )u^{\prime }(\xi ))\,\hbox {d}\xi . \end{aligned}$$

(2.5)

It should be noted that the (2.5) does not involve any undetermined coefficients to be determined.

We now decompose the solution $u(x)$ by a series as follows

$$\begin{aligned} u(x)=\sum _{n=0}^{\infty }u_n(x), \end{aligned}$$

(2.6)

and the nonlinear function $f(x,u(x),p(x)u^{\prime }(x))$ by a series as

$$\begin{aligned} f(x,u(x),p(x)u^{\prime }(x))=\sum _{n=0}^{\infty } A_n, \end{aligned}$$

(2.7)

where $A_n$ are Adomian’s polynomials (Adomian and Rach 1983). Recently, in Duan (2010a, b) Duan developed several new efficient algorithms for rapid computer-generation of the one-variable and the multi-variable Adomian polynomials. El-Kalla (2012) deduced another programmable formula for Adomian polynomials

$$\begin{aligned} A_n=f(x,\chi _n,p\chi _n^{\prime })-\sum _{j=0}^{n-1} A_j, \end{aligned}$$

(2.8)

where $\chi _n=\sum _{j=0}^{n} u_j$ is partial sum of the series solution $\sum _{j=0}^{\infty }u_j.$

Substituting the series (2.6) and (2.7) into (2.5), we obtain

$$\begin{aligned} \sum _{n=0}^{\infty }u_n(x)=\alpha _1+ \frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x)+\int \limits _{0}^{1} G(x,\xi )q(\xi ) \sum _{n=0}^{\infty } A_n\,\hbox {d}\xi . \end{aligned}$$

(2.9)

Comparing both sides of (2.9), we obtain a new recursive scheme as

$$\begin{aligned} \left. \begin{array}{ll} u_0(x)=\alpha _1,\\ u_{1}(x)=\frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x)+\int \limits _{0}^{1} G(x,\xi )q(\xi ) A_0\,\hbox {d}\xi ,\\ u_{j}(x)=\int \limits _{0}^{1} G(x,\xi ) q(\xi ) A_{j-1}\,\hbox {d}\xi ,\quad j\ge 2. \end{array} \right\} \end{aligned}$$

(2.10)

Using the recursive scheme (2.10), we can determine the solution components $u_j(x)$ and hence, the $n$-term truncated series solution can be obtained as

$$\begin{aligned} \chi _n=\sum _{j=0}^{n} u_j(x). \end{aligned}$$

(2.11)

Unlike ADM or MADM, the proposed recursive scheme (2.10) does not involve any undetermined coefficients to be determined. In other words, it avoids solving the sequence of transcendental equations for the undetermined coefficients.

3 Convergence analysis

In this section, we shall discuss the convergence analysis and the error estimation of the proposed scheme (2.10). To do this, let $\mathbb X = C[0,1]\bigcap C^1(0,1]$ be a Banach space with the norm

$$\begin{aligned} \Vert u\Vert =\max \{\Vert u\Vert _0, \Vert u\Vert _1\},\quad u\in \mathbb X , \end{aligned}$$

(3.1)

where, $\Vert u\Vert _0=\max _{ x\in [0,1]} |u(x)|$ and $\Vert u\Vert _1=\max _{ x\in [0,1]} |p(x)u'(x)|.$ It is well known that $\mathbb X$ is Banach space with norm (3.1) (see Bobisud 1990). The operator equation form of (2.5) is given by

$$\begin{aligned} u={\mathcal{N }}(u), \end{aligned}$$

(3.2)

where ${\mathcal{N }}:\mathbb X \rightarrow \mathbb X$ is a nonlinear operator given by

$$\begin{aligned} \mathcal{N }(u)=\alpha _1+\frac{1}{\mu } (\eta _1-\alpha _1\beta _1)h(x)+\int \limits _{0}^{1} G(x,\xi )q(\xi ) f(\xi ,u(\xi ),p(\xi )u'(\xi ))\,\hbox {d}\xi . \end{aligned}$$

(3.3)

We next discuss the existence of the unique solution of the Eq. (3.2). To do this, we first prove the following lemma.

Lemma 3.1

Let the assumptions $({\hbox {E}}_1)$ and $({\hbox {E}}_2)$ hold, then

• (i) $M_1:=\max _{ x\in [0,1]}\int \nolimits _{0}^{1} |G(x,\xi )q(\xi )\,\hbox {d}\xi |<\infty ,$

• (ii) $M_2:=\max _{ x\in [0,1]} \int \nolimits _{0}^{1} |p(x)G_x(x,\xi ) q(\xi )\,\hbox {d}\xi |<\infty ,$    where $G_x(x,\xi )=\frac{\partial G(x,\xi )}{\partial x}.$

Proof

(i) The maximum value of Green’s function (2.4) is given by

$$\begin{aligned} C_1=\max _{x,\xi \in [0,1]} |G(x,\xi )| =\frac{\mu }{4\beta _1}. \end{aligned}$$

(3.4)

Using the assumption $(E_2)$ and (3.4), we obtain

$$\begin{aligned} \int \limits _{0}^{1}| G(x,\xi )q(\xi )\,\hbox {d}\xi |\le \max _{ x,\xi \in [0,1]}|G(x,\xi )| \int \limits _{0}^{1} |q(\xi )|\,\hbox {d}\xi = C_1 \int \limits _{0}^{1} |q(\xi )|\,\hbox {d}\xi <\infty . \end{aligned}$$

Hence, $M_1:=\max _{ x \in [0,1]}\int \nolimits _{0}^{1}| G(x,\xi )q(\xi )\,\hbox {d}\xi |<\infty .$

(ii) From (2.4), we see that

$$\begin{aligned} p(x) G_{x}(x,\xi )=\left\{ \begin{array}{ll} 1-\frac{\beta _1h(\xi )}{\mu }, &{}\quad 0\le x \le \xi \le 1, \\ \frac{-\beta _1 h(\xi )}{\mu }, &{}\quad 0\le \xi \le x\le 1. \end{array} \right. \end{aligned}$$

(3.5)

Hence, we obtain $C_2=\max _{ x,\xi \in [0,1]}|p(x) G_x(x,\xi )|<\infty .$

Again using $({\hbox {E}}_2),$ we have

$$\begin{aligned} \int \limits _{0}^{1}| p(x)G_{x}(x,\xi )q(\xi )\,\hbox {d}\xi |\le \max _{ x,\xi \in [0,1]}|p(x)G_x(x,\xi )|\int \limits _{0}^{1}| q(\xi )|\,\hbox {d}\xi \!=\! C_2 \int \limits _{0}^{1} |q(\xi )|\,\hbox {d}\xi <\infty .\nonumber \\ \end{aligned}$$

(3.6)

Hence it follows that $M_2:=\max _{ x \in [0,1]}\int \nolimits _{0}^{1}|p(x)G_{x}(x,\xi )q(\xi )\,\hbox {d}\xi |< \infty .\,\square$

Theorem 3.1

Let $\mathbb X$ be Banach space with norm given by (3.1). Also, assume that the nonlinear function $f(x,u,pu')$ satisfies the Lipschitz condition $({\hbox {E}}_4).$ Let $M=\max \{M_1,M_2\}$ and $L=\max \{L_1,L_2\},$ where the constants $M_1$ and $M_2$ given as in Lemma 3.1 and $L_1$ and $L_2$ are Lipschitz constants. If $\delta =2 LM<1,$ then the equation (3.2) has a unique solution in $\mathbb X .$

Proof

Using the Lemma 3.1 and the Lipschitz continuity of $f,$ we have for any $u,\,v\in \mathbb X ,$

$$\begin{aligned} \Vert \mathcal{N }u-\mathcal{N }v\Vert _0&= \max _{ x \in [0,1]} \left| \int \limits _{0}^{1} G(x,\xi )q(\xi )\left[ f(\xi ,u,pu')- f(\xi ,v,pv')\right] \,\hbox {d}\xi \right| ,\\&\le \max _{ x \in [0,1]} \int \limits _{0}^{1} |G(x,\xi )q(\xi )\,\hbox {d}\xi |\left| f(\xi ,u,pu')- f(\xi ,v,pv')\right| ,\\&\le M_1 \max _{ x \in [0,1]}[L_1|u-v|+L_2|p(u'-v')|],\\&\le 2LM_1 \max \{\Vert u-v\Vert _0, \Vert u-v\Vert _1\}=2LM_1 \Vert u-v\Vert , \end{aligned}$$

where $L=\max \{L_1,L_2\}.$ Thus we have

$$\begin{aligned} \Vert \mathcal{N }u-\mathcal{N }v\Vert _0\le 2 LM_1 \Vert u-v\Vert . \end{aligned}$$

(3.7)

Similarly, we have

$$\begin{aligned} \Vert \mathcal{N }u-\mathcal{N }v\Vert _1&= \max _{ x \in [0,1]} \left| \int \limits _{0}^{1} p(x)G_x(x,\xi )q(\xi )[ f(\xi ,u,pu')- f(\xi ,v,pv')]\,\hbox {d}\xi \right| ,\\&\le \max _{ x \in [0,1]} \int \limits _{0}^{1} |p(x)G_x(x,\xi )q(\xi ) \,\hbox {d}\xi | | f(\xi ,u,pu')- f(\xi ,v,pv')|,\\&\le M_2 \max _{ x \in [0,1]}\{L_1|u-v|+L_2|p(u'-v')|\},\\&\le 2LM_2 \max \{\Vert u-v\Vert _0, \Vert u-v\Vert _1\}=\le 2L M_2 \Vert u-v\Vert . \end{aligned}$$

Hence

$$\begin{aligned} \Vert \mathcal{N }u-\mathcal{N }v\Vert _1\le 2L M_2 \Vert u-v\Vert . \end{aligned}$$

(3.8)

Combining the estimates (3.7) and (3.8), we obtain

$$\begin{aligned} \Vert \mathcal{N }u-\mathcal{N }v\Vert&= \max \{ \Vert \mathcal{N }u-\mathcal{N }v\Vert _0, \Vert \mathcal{N }u-\mathcal{N }v\Vert _1\},\nonumber \\&\le \max \{ 2LM_1 \Vert u-v\Vert , 2LM_2 \Vert u-v\Vert \},\nonumber \\&= \delta \Vert u-v\Vert , \end{aligned}$$

(3.9)

where $\delta =2 LM$ and $M=\max \{M_1,M_2\}.$ If $\delta <1,$ then $\mathcal{N }:\mathbb X \rightarrow \mathbb X$ is contraction mapping and hence by the Banach contraction mapping theorem, the Eq. (3.2) has a unique solution in $\mathbb X .\,\square$

Now let $\{\chi _n=\sum \nolimits _{j=0}^{n} u_j\}$ be a sequence of partial sums of the series solution $\sum \nolimits _{j=0}^{\infty }u_j.$

Using (2.10) and (2.11), we have

$$\begin{aligned} \chi _n&= u_0+\sum _{j=1}^{n} u_j =\alpha _1+\frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x)+\sum _{j=1}^{n} \left[ \int \limits _{0}^{1} G(x,\xi ) q(\xi ) A_{j-1}\,\hbox {d}\xi \right] ,\nonumber \\&= \alpha _1+\frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x)+ \int \limits _{0}^{1} G(x,\xi ) q(\xi ) \sum _{j=0}^{n-1} A_j\,\hbox {d}\xi . \end{aligned}$$

(3.10)

Using (2.8) in (3.10), it follows that

$$\begin{aligned} \chi _{n}=\alpha _1+\frac{1}{\mu }(\eta _1-\alpha _1\beta _1)h(x)+ \int \limits _{0}^{1} G(x,\xi ) q(\xi ) f(x,\chi _{n-1},p\chi _{n-1}')\,\hbox {d}\xi . \end{aligned}$$

(3.11)

which is equivalent to the following operator equation

$$\begin{aligned} \chi _{n}=\mathcal{N }(\chi _{n-1}),\quad n=1,2,\ldots . \end{aligned}$$

(3.12)

In following theorem, we give the convergence of the sequence $\chi _n$ to the exact solution $u$ of (3.2).

Theorem 3.2

Let $\mathcal{N }(u)$ be the nonlinear operator defined by (3.3) is contractive that is $\Vert \mathcal{N }(u)-\mathcal{N }(v)\Vert \le \delta \Vert u-v\Vert ,$ for all $u, v\in \mathbb X$ with $0<\delta <1.$ If $\Vert u_1\Vert <\infty ,$ then the sequence $\chi _n$ defined by (2.11) converges to the exact solution $u$ of (3.2).

Proof

Using the relation (3.12) and the estimate (3.9), we have

$$\begin{aligned} \Vert \chi _{m+1}-\chi _{m}\Vert =\Vert \mathcal{N }(\chi _{m}) -\mathcal{N }(\chi _{m-1})\Vert \le \delta \Vert \chi _{m}-\chi _{m-1}\Vert . \end{aligned}$$

Thus we have

$$\begin{aligned} \Vert \chi _{m+1}-\chi _{m}\Vert \le \delta \Vert \chi _{m}-\chi _{m-1}\Vert \le \delta ^{2} \Vert \chi _{m-1}-\chi _{m-2}\Vert , \le \cdots \le \delta ^{m} \Vert \chi _{1}-\chi _{0}\Vert . \end{aligned}$$

For all $n,m\in \mathbb N ,$ with $n>m,$ consider

$$\begin{aligned} \Vert \chi _{n}-\chi _{m}\Vert&= \Vert (\chi _n-\chi _{n-1}) +(\chi _{n-1}-\chi _{n-2})+\cdots +(\chi _{m+1}-\chi _{m})\Vert ,\\&\le \Vert \chi _n-\chi _{n-1}\Vert +\Vert \chi _{n-1}-\chi _{n-2}\Vert +\cdots +\Vert \chi _{m+1}-\chi _{m}\Vert ,\\&\le [\delta ^{n-1} + \delta ^{n-2} +\cdots + \delta ^{m}]\Vert \chi _{1}-\chi _{0}\Vert ,\\&= \delta ^{m}[ 1+\delta + \delta ^{2} +\cdots + \delta ^{n-m-1} ]\Vert \chi _{1}-\chi _{0}\Vert ,\\&= \delta ^{m}\left( \frac{1-\delta ^{n-m}}{1-\delta }\right) \Vert u_1\Vert . \end{aligned}$$

Since $0< \delta <1$ so, $(1-\delta ^{n-m})<1,$ and $\Vert u_1\Vert <\infty ,$ it follows that

$$\begin{aligned} \Vert \chi _{n}-\chi _{m}\Vert \le \frac{\delta ^{m}}{1-\delta }\Vert u_1\Vert , \end{aligned}$$

(3.13)

which converges to zero, that is, $\Vert \chi _{n}-\chi _{m}\Vert \rightarrow 0,$ as $m\rightarrow \infty .$ This implies that there exits a $\chi$ such that $\lim _{n\rightarrow \infty } \chi _{n}=\chi .$ Since, we have $u=\sum \nolimits _{n=0}^{\infty }u_n=\lim _{n\rightarrow \infty } \chi _{n},$ that is, $u=\chi$ which is exact solution of (3.2). $\square$

In the following theorem we obtain the error bounds for the approximate solution $\chi _n.$

Theorem 3.3

Let $u(x)$ be the exact solution of (3.2). Let $\chi _{m}$ be the sequence of approximate series solution defined by (3.2). Then there holds

$$\begin{aligned} \max _{ x\in [0,1]}\left| u(x)-\sum _{j=0}^{m} u_j(x)\right| \le \frac{\delta ^{m} }{(1-\delta )}\max _{ x\in [0,1]}|u_1|. \end{aligned}$$

Proof

Using the estimate (3.13), for $n\ge m,~n,m\in \mathbb{N },$ we have

$$\begin{aligned} \Vert \chi _{n}-\chi _{m}\Vert \le \frac{\delta ^{m}}{1-\delta }\Vert u_1\Vert . \end{aligned}$$

Since $\lim _{n\rightarrow \infty } \chi _{n}=u,$ fixing $m$ and letting $n\rightarrow \infty ,$ we obtain

$$\begin{aligned} \Vert u-\chi _{m}\Vert \le \frac{\delta ^{m}}{1-\delta }\max _{ x\in [0,1]}|u_1|. \end{aligned}$$

(3.14)

Hence, we have

$$\begin{aligned} \max _{ x\in [0,1]}\left| u(x)-\sum _{j=0}^{m} u_j(x)\right| \le \frac{\delta ^{m} }{(1-\delta )}\max _{ x\in [0,1]}|u_1|. \end{aligned}$$

$\square$

4 Numerical illustrations

In this section, the proposed recursive scheme (2.10) is applied to solve SBVP of form (1.1). In order to check the efficiency of proposed scheme (2.10), we shall consider one linear and two strongly nonlinear singular problems.

Example 4.1

We first consider linear SBVPs with derivative dependence

$$\begin{aligned} \left. \begin{array}{rllll} (x^{\alpha }u')'&{}=x^{\alpha +\beta -2} (\beta x u'+\beta (\alpha +\beta -1)u),\quad x\in (0,1],\\ u(0)&{}=1,\ u(1)=e, \end{array} \right\} \end{aligned}$$

(4.1)

with the exact solution $u(x)=\mathrm{e}^{x^\beta },\,0\le \alpha <1$ and $\beta >0$ are any real constants.

According to proposed scheme (2.10), the (4.1) can be converted into following recursive scheme

$$\begin{aligned} \left. \begin{array}{ll} u_0=1,\\ u_{1}=(e-1)x^{1-\alpha }+\int \nolimits _{0}^{1}G(x,\xi ) \xi ^{\alpha +\beta -2} A_0\,\hbox {d}\xi ,\\ u_{j}=\int \nolimits _{0}^{1}G(x,\xi ) \xi ^{\alpha +\beta -2} A_{j-1} \,\hbox {d}\xi ,\quad j\ge 2.\\ \end{array} \right\} \end{aligned}$$

(4.2)

where,

$$\begin{aligned} A_j=(\beta xu'_j+\beta (\alpha +\beta -1)u_j). \end{aligned}$$

(4.3)

For the demonstration purpose, we pick some specific values of $\alpha$ and $\beta .$

For $\alpha =0.5,\,\beta =1,$ using (4.2) and (4.3), we obtain the components $u_n$ as:

$$\begin{aligned} u_0&= 1,\\ u_1&= 0.718282 x^{0.5}+x,\\ u_2&= -0.978855 x^{0.5}+0.478855 x^{1.5}+0.5 x^{2},\\ u_3&= 0.294361 x^{0.5}-0.65257 x^{1.5}+0.191542 x^{2.5}+0.166667 x^{3},\\ u_4&= -0.0316058 x^{0.5}+0.196241 x^{1.5}-0.261028 x^{2.5}+0.0547262 x^{3.5}+0.0416667 x^{4},\\ \vdots&\end{aligned}$$

For $\alpha =0.5,\,\beta =2.5,$ using (4.2), the components $u_n$ are obtained as:

$$\begin{aligned} u_0&= 1,\\ u_1&= 0.718282 x^{0.5}+ x^{2.5},\\ u_2&= -1.09857 x^{0.5}+0.598568 x^{3}+0.5 x^{5},\\ u_3&= 0.47673 x^{0.5}-0.915473 x^{3}+0.272076 x^{5.5}+0.166667 x^{7.5},\\ u_4&= -0.107842 x^{0.5}+0.397275 x^{3}-0.416124 x^{5.5}+0.0850239 x^{8}+0.0416667 x^{10},\\ \vdots&\end{aligned}$$

Note that all above components are computed by computer algebra system, such as ‘MATHEMATICA’. Now, we define absolute error function as $E_n(x)=|\chi _n(x)-u(x)|, n=1,2,\ldots$ and the maximum absolute errors as

$$\begin{aligned} E^{n}=\max _{x\in (0,1]}E_n(x) \end{aligned}$$

(4.4)

where $u(x)$ is exact solution and $\chi _n(x)$ is $n$-term approximate series solution. In order test efficiency and accuracy of the proposed recursive scheme (2.10), we exhibit the maximum absolute error estimate for various values of $\alpha$ and $\beta$ in Tables 1 and 2. From these numerical results, it is observed that as the number of iterations increases the maximum absolute error decreases. Furthermore, the comparison between our approximate series solutions $\chi _2, \chi _3$ and the exact solution is plotted in Fig. 1, it is shown that our three terms approximate solution $\chi _3$ is coincides with the exact solution.

Table 1 Maximum absolute error estimate for Example 4.1, when $\beta =1$

Table 2 Maximum absolute error estimate for Example 4.1, when $\beta =2.5$

Fig. 1

Comparison of the approximate series $\chi _2, \chi _3$ and the exact $u$ solutions of Example 4.1, when a $\alpha =0.5$ and $\beta =1$ b $\alpha =0.5$ and $\beta =2.5$

Example 4.2

Consider the nonlinear SBVPs with derivative dependence

$$\begin{aligned} \left. \begin{array}{ll} (x^{\alpha }u')'= x^{\alpha -1}(-x u'\mathrm{e}^{u}-\alpha \mathrm{e}^{u}),\quad x\in (0,1],\\ u(0)=\ln \left( \frac{1}{2}\right) ,\quad u(1)=\ln \left( \frac{1}{3}\right) , \end{array} \right\} \end{aligned}$$

(4.5)

and the exact solution is $u(x)=\ln \left( \frac{1}{2+x}\right) ,$ where $0\le \alpha <1.$

According to proposed scheme (2.10), where $p(x)=x^{\alpha },\, q(x)=x^{\alpha -1},\,\alpha _1=\ln \left( \frac{1}{2}\right) ,$ $\beta _1=1,\,\gamma _1=0$ and $\eta _1=\ln \left( \frac{1}{3}\right) ,$ we have the recursive scheme:

$$\begin{aligned} \left. \begin{array}{ll} u_0=\ln \left( \frac{1}{2}\right) ,\\ u_1=\left[ \ln \left( \frac{1}{3}\right) - \ln \left( \frac{1}{2}\right) \right] x^{1-\alpha }+ \int \limits _{0}^{1}G(x,\xi ) \xi ^{\alpha -1} A_0\,\hbox {d}\xi ,\\ u_{j}=\int \limits _{0}^{1} G(x,\xi )\xi ^{\alpha -1} A_{j-1} \,\hbox {d}\xi ,\quad j\ge 2. \end{array} \right\} \end{aligned}$$

(4.6)

Using the formula (1.7), the Adomian’s polynomials for $f=-(x \mathrm{e}^{u} u'+\mathrm{e}^{u}\alpha )$ about $u_0=\ln \left( \frac{1}{2}\right)$ are calculated as:

$$\begin{aligned} \left. \begin{array}{l} A_0=-\mathrm{e}^{u_0}(x u'_0+\alpha ), \\ A_1=-\mathrm{e}^{u_0}(x u'_1+u_1\alpha ),\\ A_2=-\mathrm{e}^{u_0}\left( x (u'_2+u_1 u'_1)+\left( u_2+\frac{u_1^2}{2} \right) \alpha \right) ,\\ A_3=-\mathrm{e}^{u_0}\left( x \left( u'_3+u'_2u_1+u'_1 \left( \frac{u_1^2}{2}+u_2\right) \right) + \left( u_3+u_1 u_2+\frac{u_1^3}{6}\right) \alpha \right) ,\\ \vdots \end{array} \right\} \end{aligned}$$

(4.7)

For $\alpha =0.5,$ using (4.6) and (4.7), we obtain the successive solution components $u_n$ as:

$$\begin{aligned} u_0&= -0.693147,\\ u_1&= 0.0945349x^{0.5}-0.5x,\\ u_2&= -0.0934884 x^{0.5}-0.0315116 x^{1.5}+0.125 x^{2},\\ u_3&= -0.00413483 x^{0.5}\!+\!0.0311628 x^{1.5}\!-\!0.00111711 x^{2}\!+\!0.0157558 x^{2.5}-0.0416667 x^{3},\\ u_4&= 0.00321966 x^{0.5}\!+\!0.00137828 x^{1.5}\!+\!0.00220948 x^{2}\!-\!0.0156096 x^{2.5}\!+\!0.00105504 x^{3}\\&-0.00787791 x^{3.5}+0.015625 x^{4},\\ \vdots&\end{aligned}$$

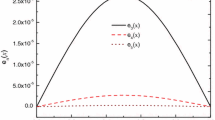
In similar manner as we did in last example Table 3 shows the maximum absolute error estimate for various values of $\alpha .$ From these results, one can observe that as the number of iterations increases, the maximum absolute error decreases. Furthermore, we plot the approximate series solutions $\chi _1, \chi _3$ with the exact solution in Fig. 2. It is clear from the figure that only three term approximate series solution $\chi _3$ is almost identical to the exact solution $u(x).$

Fig. 2

Comparison of the approximate series $\chi _1, \chi _3$ and the exact $u$ solutions of Example 4.2, when a $\alpha =0.5$ and $\beta =1$

Table 3 Maximum absolute error estimate for Example 4.2

Example 4.3

Consider the nonlinear SBVP

$$\begin{aligned} \left. \begin{array}{ll} (x^{\alpha }u')'= - x^{\alpha +\beta -2}(\beta x\mathrm{e}^{u}u'+\beta (\alpha +\beta -1)\mathrm{e}^{u}),\quad x\in (0,1],\\ u(0)=\ln \left( \frac{1}{4}\right) ,\quad u(1)=\ln \left( \frac{1}{5}\right) , \end{array} \right\} \end{aligned}$$

(4.8)

with exact solution $u(x)=\ln \left( \frac{1}{4+x^{\beta }}\right) .$

According to proposed scheme (2.10), where $p(x)=x^{\alpha },\, q(x)=x^{\alpha +\beta -2},\,\alpha _1=\ln \left( \frac{1}{4}\right) ,~\beta _1=1,~\gamma _1=0,$ and $\eta _1=\ln \left( \frac{1}{5}\right) ,$ we obtain:

$$\begin{aligned} \left. \begin{array}{ll} u_0=\ln \left( \frac{1}{4}\right) ,\\ u_{1}=\left[ \ln \left( \frac{1}{5}\right) -\ln \left( \frac{1}{4}\right) \right] x^{1-\alpha }+\int \nolimits _{0}^{1}G(x,\xi ) \xi ^{\alpha +\beta -2} A_0\,\hbox {d}\xi ,\\ u_{j}=\int \nolimits _{0}^{1}G(x,\xi ) \xi ^{\alpha +\beta -2} A_{j-1} \,\hbox {d}\xi ,\quad j\ge 2. \end{array} \right\} \end{aligned}$$

(4.9)

Using the formula (1.7) the Adomian’s polynomials for $f=- (\beta x\mathrm{e}^{u}u'+\beta (\alpha +\beta -1)\mathrm{e}^{u})$ about $u_0$ are obtained as:

$$\begin{aligned} \left. \begin{array}{l} A_0=-\beta \mathrm{e}^{u_0}(x u'_0+(\alpha +\beta -1)) \\ A_1=-\beta \mathrm{e}^{u_0}(x u'_1+u_1(\alpha +\beta -1)),\\ A_2=-\beta \mathrm{e}^{u_0}\left( x (u'_2+u_1 u'_1)+( u_2+\frac{u_1^2}{2})(\alpha -\beta +1)\right) ,\\ A_3=-\beta \mathrm{e}^{u_0}\left( x \left( u'_3+u'_2u_1+u'_1\left( \frac{u_1^2}{2}+u_2\right) \right) +\left( u_3+u_1 u_2 +\frac{u_1^3}{6}\right) (\alpha +\beta -1) \right) ,\\ \vdots \end{array} \right\} \nonumber \\ \end{aligned}$$

(4.10)

As we did before we pick some specific values of $\alpha$ and $\beta .$

For $\alpha =0.5,\,\beta =1,$ using (4.9) and (4.10), we obtain the components $u_n$ as

$$\begin{aligned} u_0&= -1.38629436,\\ u_1&= 0.0268564x^{0.5}-0.25 x,\\ u_2&= -0.0267739x^{0.5}-0.00447607 x^{1.5}+0.03125 x^{2},\\ u_3&= -0.0003279x^{0.5}\!+\!0.0044623x^{1.5}\!-\!0.000045079x^{2}\!+\!0.00111902x^{2.5}\!-\!0.0052083x^{3},\\ u_4&= 0.00025327x^{0.5}\!+\!0.0000546545 x^{1.5}\!+\!0.0000898816 x^{2}\!-\!0.0011159 x^{2.5}\\&+0.0000212874 x^{3}-0.0002797x^{3.5}+0.000976563 x^{4},\\ \vdots&\end{aligned}$$

For $\alpha =0.5,\,\beta =3.5,$ using (4.9) and (4.10), we have components $u_n$ as follows:

$$\begin{aligned} u_0&= -1.38629436,\\ u_1&= 0.+0.0268564 x^{0.5}-0.25 x^{3.5},\\ u_2&= -0.0253752 x^{0.5}-0.00587485 x^{4}+0.03125 x^{7},\\ u_3&= -0.00174107 x^{0.5}+0.00555081x^{4}\!-\!0.000070123x^{4.5}\!+\!0.00146871x^{7.5}\\&-0.00520833x^{10.5},\\ u_4&= 0.000230726 x^{0.5}+0.000380859 x^{4}+0.000132511 x^{4.5}-5.6497931825\times 10^{-7} x^{5}\\&-0.0013877 x^{7.5}+0.0000347878 x^{8}-0.000367178 x^{11}+0.000976563 x^{14},\\ \vdots&\end{aligned}$$

In similar fashion, Tables 4 and 5 show the maximum absolute error for different values of $\alpha$ and $\beta .$ It is obvious from these results that the error decreases as one increases the terms in approximate solution. In addition, by plotting approximate solutions $\chi _2, \chi _3$ and the exact solution in Fig. 3, we have shown that only few terms are required for acceptable solution.

Fig. 3

Comparison of the approximate series $\chi _2, \chi _3$ and the exact $u$ solutions of Example 4.3, when a $\alpha =0.5$ and $\beta =1$ b $\alpha =0.5$ and $\beta =3.5$

Table 4 Maximum absolute error estimate for Example 4.3, when $\beta =1$

Table 5 Maximum absolute error estimate for Example 4.3, when $\beta =3.5$

Remark

It can be seen from the numerical results of all three examples discussed in this section that only three terms are sufficient for obtaining good approximations to the exact solution.

5 Conclusion

In this article, we have verified the proposed recursive scheme by solving one linear and two nonlinear singular two-point boundary value problems. The accuracy of the numerical results shows that the proposed method is suitable for solving such problems. Unlike ADM or MADM, the proposed method does not involve any undetermined coefficients to be determined. In fact, the proposed method provides a direct recursive scheme for obtaining the approximations of the exact solution.