Sensorless Nonlinear Control of Wind Energy Systems with Doubly Fed Induction Generator

Abstract

The problem of controlling doubly fed induction generators (DFIG) associated with wind turbines is addressed. The control objective is twofold: maximum power point tracking and reactive power regulation in the DFIG. Unlike previous works, we seek the achievement of this control objective without resorting to physical sensors of mechanical variables (e.g., wind turbine velocity and DFIG rotor speed). Interestingly, wind velocity is also not assumed to be accessible to measurements. The control problem is dealt with using an output feedback controller designed on the basis of the nonlinear state-space representation of the controlled system. The controller is constituted of a high-gain nonlinear state observer and a nonlinear sliding state feedback mode. Using tools from Lyapunov’s stability, it is formally shown that the closed-loop control system, expressed in terms of the state estimation errors and the output-reference tracking errors, enjoys a semi-global practical stability. Accordingly, it is possible to tune the controller design parameters so that it meets its objectives with an arbitrarily high accuracy, whatever the initial conditions are. These theoretical results are confirmed by simulations involving wide range variation of the wind speed.

1 Introduction

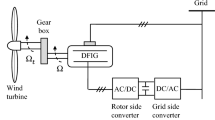
Among all renewable energy sources, wind energy is the most growing worldwide in the field of electricity generation. Typically, the conversion of wind energy into electricity is performed using wind turbines with electric AC or DC machines operating in generator mode. Among all existing machines, DFIG machines stand as the most promising. In this paper, the DFIG-based system of Fig. 1 is considered. The rotor is connected to the power grid through an AC-DC-AC converter, while the stator is directly connected to the network. Accordingly, the power flowing through the converter is only a fraction of the total wind turbine power. This entails a smaller size, lower losses and lower cost, compared to the case of a full-scale power converter placed on the stator (El Fadili et al. 2013).

Fig. 1

Wind turbine system architecture considered

Fig. 2

The shape of the aerodynamic power according to the rotor speed for various values of wind speed. Highlighting MPP

It is well known that the optimal DFIG rotor speed is a function of the wind speed value (Fig. 2). It turns out that the achievement of maximum wind energy extraction in the presence of varying wind speed conditions necessitates a varying DFIG rotor speed operation mode (Patnaik and Dash 2015). Specifically, the turbine rotor velocity must be controlled so that its power-speed working point is constantly maintained near the optimal position (Fig. 2). This control objective is commonly referred to as maximum power point tracking (MPPT), and its achievement guarantees an optimal aerodynamic efficiency. Also, Fig. 2 shows that the MPPT requirement can only be met by controlling the rotor speed $\Omega$ (which is substantially proportional to the turbine speed, due to the gearbox coupling both axes). It turns out that the true values of wind velocity, aerodynamic torque and rotor speed are needed in control systems meeting the MPPT objective.

The point is that mechanical sensors entail several accuracy and/or robustness issues. Furthermore, the implementation and maintenance of these sensors are quite costly. Therefore, it is of great interest to develop sensorless controllers meeting the MPPT requirement for wind turbines associated with AC machines.

Several previous studies have dealt with the MPPT requirement for various wind turbine AC aero-generators. In Sarrias-Mena et al. (2014), the case of squirrel cage induction aero-generator has been considered and MPPT has been achieved using sliding mode control and backstepping control, respectively. But, both proposed controllers were not sensorless. In Rocha (2011), Kerrouchea et al. (2013), Dida and Benattous (2015), linear, neuro-fuzzy and hysteresis controllers have been proposed for the achievement of MPPT objectives. The control design has been performed on the basis of approximate models, typically transfer functions of the DFIG wind turbine system. As the nonlinearity system is not explicitly and fully accounted for in the control design, the control performances entail intrinsic limitations, especially in the presence of wide range variations of wind velocity. Furthermore, the proposed controllers are generally not backed by a formal stability analysis and their performances cannot be accurately quantified.

The problem of designing sensorless controllers for AC aero-generators based on the nonlinear model system has recently been studied in (e.g., El Fadili et al. 2013). The aero-generator is an induction machine, and the control objective includes MPPT and reactive power control. The sensorless feature was achieved using an output feedback controller combining a backstepping nonlinear controller and an interconnected Kalman-like state observer. The controller is formally shown to meet its objective, but the analysis relies on two restrictive assumptions, namely all control system signals are supposed to be a priori bounded and the state vector estimates are assumed to be persistently exciting. The first assumption is resorted to in order to enforce the separation principle, while the second is made to enforce the observer exponential convergence. Similarly, in Akel et al. (2014) a sensorless controller is performed for DFIG wind turbine system. The regulator design analysis considers that all state system signals are a priori bounded.

In the present paper, the problem of sensorless control of aero-generators is considered for DFIG machines. In addition to the MPPT requirement, we seek the achievement of a tight regulation of the DFIG reactive power. To meet these objectives, we propose an output feedback controller combining a state feedback controller with a state observer providing online estimates of wind velocity, aerodynamic torque and rotor speed. The feedback state controller is a sliding mode type, while the observer is a high-gain structure. The controller and the observer are simultaneously analyzed to emphasize sufficient conditions for the closed-loop control system. In particular, the separation principle and the observer exponential convergence are not enforced through restrictive assumptions. Using tools from Lyapunov’s stability, it is formally shown that the closed-loop control system expressed in terms of the state estimation errors and the output-reference tracking errors, enjoys a semi-global practical stability. Accordingly, it is possible to tune the controller design parameters so that it meets its objectives with an arbitrarily high accuracy, whatever the initial conditions are. These theoretical results are confirmed by simulations with a wide range variation of the wind speed.

In practice, the wind turbine system is sensitive to disturbances, which could affect the electrical grid. Indeed, for the studied structure, the rotor current can have a hard transitional regime during the occurrence of these disturbances. To avoid these problems, the crowbar system can be used. The latter increases the apparent rotor resistance in order to face the current peaks that may appear during an electric network default (Maurício et al. 2010). In this context, it is interesting to check the robustness of the wind system control law with respect to defects that may affect the electrical grid.

This paper is organized as follows: The modeling of the wind turbine DFIG system is presented in Sect. 2; a state observer structure is considered and analyzed in Sect. 3; the whole sensorless output feedback controller is designed and analyzed in Sect. 4; the control performances are illustrated by the simulation in Sect. 5.

2 Wind Turbine Model

In this section, we present the wind turbine model for the MPPT control with the rotor speed regulation. Figure 1 shows the overall architecture of the wind energy conversion system considered. The involved notations are described in Table 1.

2.1 Turbine Model

The available aerodynamic wind power is given by Kerrouchea et al. (2013):

$$\begin{aligned} P_a =T_a {\varOmega } =\frac{1}{2}\rho \pi R^{2}C_P \left( {\lambda ,\beta } \right) v^{3} \end{aligned}$$

(1)

where $\beta$ is the pitch angle and $\lambda$ is tip speed ratio given by:

$$\begin{aligned} \lambda =\frac{R.{\varOmega } }{K_{gb} v} \end{aligned}$$

(2)

In this work, we give interest to the wind turbine control in zone II (moderate wind speed). In this region, the wind turbine is controlled at variable speed to track the maximum power point. Furthermore, in this zone, the pitch angle is kept constant equals zero (Rocha 2011).

Table 1 Notations and symbols

2.2 DFIG Control Model

State-space model: The model considered for DFIG is a state model widely used in the literature (Zamanifar et al. 2014). It is developed in a rotating reference frame (d-q) and oriented according to the stator flux direction ($\varphi _{\mathrm{sd}} =\varphi _{s} ;\varphi _{\mathrm{sq}} =0)$. The state-space model is given by:

$$\begin{aligned}&\left[ \begin{array}{c} \dot{z}_1\\ \dot{z}_2\\ \dot{z}_3\\ \dot{z}_4\\ \dot{z}_5 \end{array} \right] = \left[ \begin{array}{cc} -\frac{a}{\sigma }&{}{}0\\ 0&{}{}-\frac{a}{\sigma }\\ 0&{}{}0\\ \frac{1}{\sigma L_r}&{}{}0\\ 0&{}{} \frac{1}{\sigma L_r} \end{array} \right] u+ \left[ \begin{array}{c} \frac{1}{\sigma L_s}V_{\mathrm {sd}}-\frac{R_s}{\sigma L_s}z_1+\frac{a R_r}{\sigma }z_4\\ \frac{1}{\sigma L_s}V_{\mathrm {sq}}-\frac{R_s}{\sigma L_s}z_2+\frac{a R_r}{\sigma }z_5\\ 0\\ -\frac{a}{\sigma }V_{\mathrm {sd}}-\frac{R_r}{\sigma L_r}z_4+\frac{a R_s}{\sigma }z_1\\ -\frac{a}{\sigma }V_{\mathrm {sq}}-\frac{R_r}{\sigma L_r}z_5+\frac{a R_s}{\sigma }z_2 \end{array} \right] \nonumber \\&\qquad +\left[ \begin{array}{c} \frac{M_{\mathrm {sr}}}{\sigma L_{s}}pz_3z_5+\frac{1}{\sigma }(1-aM_{\mathrm {sr}})\omega _sz_2+\frac{1}{\sigma }aM_{\mathrm {sr}}pz_3z_2\\ -\frac{M_{\mathrm {sr}}}{\sigma L_{s}}pz_3z_4-\frac{1}{\sigma }(1-aM_{\mathrm {sr}})\omega _sz_1-\frac{1}{\sigma }aM_{\mathrm {sr}}pz_3z_1\\ -\frac{f}{J}z_3 +m(z_5z_1-z_4z_2)-\frac{T_a}{J}\\ -\frac{M_{\mathrm {sr}}}{\sigma L_{r}}pz_3z_2-\frac{1}{\sigma }(aM_{\mathrm {sr}}-1)\omega _sz_5-\frac{1}{\sigma }pz_3z_5\\ \frac{M_{\mathrm {sr}}}{\sigma L_{r}}pz_3z_1+\frac{1}{\sigma }(aM_{\mathrm {sr}}-1) \omega _sz_4+\frac{1}{\sigma }pz_3z_4 \end{array} \right] \nonumber \\ \end{aligned}$$

(3)

where the state-space vector and the control vector considered are, respectively:

$$\begin{aligned} Z= & {} \left[ {z_1\ z_2\ z_3\ z_4\ z_5 } \right] ^{T}=[i_{\mathrm{sd}}\ i_{\mathrm{sq}}\ \Omega ~i_{\mathrm{rd}}\ i_{\mathrm{rq}} ]^{T}\end{aligned}$$

(4)

$$\begin{aligned} u= & {} [V_{\mathrm{rd}}\ V_{\mathrm{rq}} ]^{T} \end{aligned}$$

(5)

where ($V_{\mathrm{sd}} =0;V_{\mathrm{sq}} =V_s )$ and the model parameters are:

$$\begin{aligned} a=\frac{M_{\mathrm{sr}} }{L_r L_s };\, \sigma =1-\frac{M_{\mathrm{sr}} ^{2}}{L_r L_s };\, \quad m=-\frac{pM_{\mathrm{sr}} }{J};\, \beta =\frac{1-\sigma }{\sigma M_{\mathrm{sr}} }\nonumber \\ \end{aligned}$$

(6)

Flux equations: In the oriented $d-q$ reference frame, stator and rotor flux equations are given by Zamanifar et al. (2014):

$$\begin{aligned} \varphi _{\mathrm{rd}}= & {} L_r i_{\mathrm{rd}} +M_{\mathrm{sr}} i_{\mathrm{sd}}\end{aligned}$$

(7)

$$\begin{aligned} \varphi _{\mathrm{rq}}= & {} L_r i_{\mathrm{rq}} +M_{\mathrm{sr}} i_{\mathrm{sq}}\end{aligned}$$

(8)

$$\begin{aligned} \varphi _{\mathrm{sd}}= & {} L_s i_{\mathrm{sd}} +M_{\mathrm{sr}} i_{\mathrm{rd}} =\frac{V_s }{\omega _s }\end{aligned}$$

(9)

$$\begin{aligned} \varphi _{\mathrm{sq}}= & {} L_s i_{\mathrm{sq}} +M_{\mathrm{sr}} i_{\mathrm{rq}} =0 \end{aligned}$$

(10)

Reactive power expression: The reactive power expression is given by Rocha (2011):

$$\begin{aligned} Q=V_s i_{\mathrm{sd}} =\frac{V_s^2 }{\omega _s L_s }-\frac{V_s M_{\mathrm{sr}} }{L_s }i_{\mathrm{rd}} \end{aligned}$$

(11)

3 Observer Design and Wind Speed Computation

The MPPT control strategy requires knowledge of the wind speed, rotor speed and aerodynamic torque (Sarrias-Mena et al. 2014). As mentioned before, the use of physical sensors raises several practical problems. In this section, based on the DFIG turbine model (1)–(11) a new observer is designed for the aerodynamic torque and wind turbine speed. The estimation of these two variables is then used for wind speed computation.

3.1 DFIG High-Gain Observer

The developed observer is based on a DFIG reduced model, constructed from the global model given by (3). The considered reduced state vector x is constituted by the stator current components $(i_{\mathrm{sd}} i_{\mathrm{sq}} )$, the rotor speed $\left( {\varOmega } \right)$ and the aerodynamic torque ($T_a )$. The latter will be considered constant or slowly varying.

Using (3), the reduced DFIG model is in the form:

$$\begin{aligned} \dot{x}= & {} A(s)x+G(u,s,x)\end{aligned}$$

(12)

$$\begin{aligned} y= & {} C_y x \end{aligned}$$

(13)

where

$$\begin{aligned}&\hbox {--}\quad x\hbox { is the reduced state-space vector defined by:}\nonumber \\&\quad \, x=\left[ x_{1}\ x_{2}\ x_{3}\ x_{4} \right] ^{T}= \left[ i_{\mathrm{sd}}\ i_{\mathrm{sq}}\ {\varOmega }\ T_a \right] ^{T}\end{aligned}$$

(14)

$$\begin{aligned}&\hbox {--}\quad y\hbox { is the output vector }y=[i_{\mathrm{sd}}\ i_{\mathrm{sq}} ]^{T}\end{aligned}$$

(15)

$$\begin{aligned}&\hbox {--}\quad C_y\hbox { is the output matrix }C_y =\left[ \begin{array}{cccc} 1&{} 0&{} 0&{} 0 \\ 0&{} 1&{} 0&{} 0 \end{array}\right] \end{aligned}$$

(16)

$$\begin{aligned}&\hbox {--}\quad \hbox {s includes all variables considered}\nonumber \\&\quad \hbox { as measurable quantities: } s=[V_{\mathrm{sd}}\ V_{\mathrm{sq}}\ i_{\mathrm{rd}}\ i_{\mathrm{rq}}\ \varphi _{\mathrm{rd}}\ \varphi _{\mathrm{rq}} ]^{T}\nonumber \\\end{aligned}$$

(17)

$$\begin{aligned}&A\left( s \right) \nonumber \\&\quad = \left[ \begin{array}{cc} {0_2 }&{} {F_1 \left( s \right) } \\ {0_2 }&{} {0_2 } \\ \end{array} \right] \hbox { where } F_1 \left( s \right) =\left[ \begin{array}{cc} {\beta \varphi _{\mathrm{rq}} }&{} {\varphi _{\mathrm{rd}} } \\ {-\beta \varphi _{\mathrm{rd}} }&{} {\varphi _{\mathrm{rq}} } \\ \end{array} \right] \end{aligned}$$

(18)

$$\begin{aligned}&G\left( {u,s,x} \right) \nonumber \\&\quad =\left[ \begin{array}{c} \frac{1}{\sigma L_s }V_{\mathrm{sd}} -\frac{a}{\sigma }V_{\mathrm{rd}} -\frac{R_s }{\sigma L_s }x_{1} +\frac{aR_r }{\sigma }i_{\mathrm{rd}} +\frac{1}{\sigma }\left( {1-aM_{\mathrm{sr}} } \right) \omega _s i_{\mathrm{rq}} -x_4 \varphi _{\mathrm{rd}} \\ \frac{1}{\sigma L_s }V_{\mathrm{sq}} -\frac{a}{\sigma }V_{\mathrm{rq}} -\frac{R_s }{\sigma L_s }x_{2} +\frac{aR_r }{\sigma }i_{\mathrm{rq}} +\frac{1}{\sigma }\left( {1-aM_{\mathrm{sr}} } \right) \omega _s i_{\mathrm{rd}} -x_4 \varphi _{\mathrm{rq}} \\ -\frac{f}{J}x_3 +m\left( {i_{\mathrm{rq}} x_{1} -i_{\mathrm{rd}} x_{2} } \right) -\frac{x_4 }{J} \\ 0 \end{array} \right] \nonumber \\ \end{aligned}$$

(19)

Remark 1

In (17), rotor flux components (7)–(8) are considered as measurable quantities since they are directly dependent on the stator and rotor DFIG currents (available for the measurement). $\square$

The proposed high-gain observer is formulated as follows (Boizot et al. 2010):

$$\begin{aligned} {\dot{\hat{x}}} =A\left( s\right) \hat{x} +\hat{G} \left( {u,s,y} \right) +M\left( {y,s} \right) C_y \tilde{x} \end{aligned}$$

(20)

where

$$\begin{aligned}&\hat{G} \left( {u,s,y} \right) \nonumber \\&\quad =\left[ \begin{array}{c} \frac{1}{\sigma L_s }V_{\mathrm{sd}} -\frac{a}{\sigma }V_{\mathrm{rd}} -\frac{R_s }{\sigma L_s }x_{1} +\frac{aR_r }{\sigma }i_{\mathrm{rd}} +\frac{1}{\sigma }\left( {1-aM_{\mathrm{sr}} } \right) \omega _s i_{\mathrm{rq}} \\ \frac{1}{\sigma L_s }V_{\mathrm{sq}} -\frac{a}{\sigma }V_{\mathrm{rq}} -\frac{R_s }{\sigma L_s }x_{2} +\frac{aR_r }{\sigma }i_{\mathrm{rq}} +\frac{1}{\sigma }\left( {1-aM_{\mathrm{sr}} } \right) \omega _s i_{\mathrm{rd}} \\ m\left( {i_{\mathrm{rq}} x_{1} -i_{\mathrm{rd}} x_{2} } \right) \\ 0 \end{array} \right] \nonumber \\ \end{aligned}$$

(21)

The aim of the observer analysis is to perform a suitable choice of the observer gain $M\left( {y,s} \right)$. This is the subject of the next theorem where the following notations are used:

$$\begin{aligned}&\Delta _{\theta } = \left[ \begin{array}{cccc} 1&{} 0&{} 0&{} 0 \\ 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} {\frac{1}{\theta }}&{} 0 \\ 0&{} 0&{} 0&{} {\frac{1}{\theta }} \\ \end{array} \right] ; K=\left[ \begin{array}{cc} {K_1 }&{} 0 \\ 0&{} {K_1 } \\ {K_2 }&{} 0 \\ 0&{} {K_2 } \\ \end{array} \right] ;\nonumber \\&\Gamma \left( \hbox {s} \right) = \left[ \begin{array}{cc} {I_2 }&{} {O_2 } \\ {O_2 }&{} {F_1 \left( s \right) } \end{array} \right] \end{aligned}$$

(22)

$$\begin{aligned}&\bar{A} =\left[ \begin{array}{cc} O_2&{} I_2 \\ O_2&{} O_2 \\ \end{array} \right] ;\nonumber \\&C_1 \left( s \right) =C_y \Gamma ^{-1}\left( \hbox {s} \right) \Delta _{\theta } ^{-1} ; \,\, \bar{\bar{\hbox {A}}} =\left( {\bar{A} -KC_1 \left( s \right) } \right) \end{aligned}$$

(23)

where $\theta ,K_1 K_2$ are positive real observer design parameters.

3.2 Observer Analysis

The observer is developed to estimate mechanical variables (wind turbine speed and aerodynamic torque) from the measurement of the electrical state. To this end, let us introduce the following estimation error:

$$\begin{aligned} \tilde{x}=x-\hat{x} \end{aligned}$$

(24)

Using (12) and (20), time derivative for the estimation error is given by:

$$\begin{aligned} \dot{\tilde{x}} = \left( {A-M\left( {y,s} \right) C_y } \right) \tilde{x}+\partial \left( {x_4 ,x_3 ,s} \right) \end{aligned}$$

(25)

The second part of Eq. (25) can be expressed as:

$$\begin{aligned} \partial \left( {x_4 ,x_3 ,s} \right) = \left[ \begin{array}{cccc} {-x_4 \varphi _{\mathrm{rd}} }&{-x_4 \varphi _{\mathrm{rq}} }&{\left( {\frac{-x_4 }{J}-\frac{f}{J}x_3 } \right) }&0 \end{array} \right] ^{T} \end{aligned}$$

(26)

As suggested in Maurício et al. (2010), let us introduce the following modified observer error:

$$\begin{aligned} \hbox {e}_{\mathrm{o}} = \Gamma \left( \hbox {s}\right) \Delta _{\theta } \tilde{x} \end{aligned}$$

(27)

then it follows by introducing (27) in (25) that:

$$\begin{aligned} {\dot{\mathrm{e}}}_{\mathrm{o}}= & {} \dot{\Gamma } \left( \mathrm{s}\right) \Gamma ^{-1} \left( \mathrm{s}\right) {e_o} + {{\Gamma }}\left( {\mathrm {s}} \right) {{{\Delta }}_\theta } \left( {A - M\left( {y,s} \right) {C_y}} \right) \nonumber \\&{{\Delta }}_\theta ^{ - 1}{{{\Gamma }}^{ - 1}} \left( s \right) {e_o} + \Gamma \left( \mathrm{s}\right) \Delta _{\theta } \partial (\left( x_4,x_3,s \right) \end{aligned}$$

(28)

Note that the inversion of matrices $\Gamma \left( \hbox {s} \right)$ and $\Delta _{\theta }$ will be discussed in remark 2.

Fig. 3

Solid line: General shape of Dotted line: Evolution of the right side of equation (31), versus $\lambda$

To analyze the stability of the error system (28), consider the Lyapunov candidate function (Slotine and Li 1991) defined by:

$$\begin{aligned} \hbox {V}_{\mathrm{o}} =e_o^T Pe_o \end{aligned}$$

(29)

where P is a symmetric positive definite matrix satisfying the following equation:

$$\begin{aligned} \bar{\bar{\hbox {A}}}^{T}P+P \bar{\bar{\hbox {A}}} =-P \end{aligned}$$

(30)

As suggested in Ouadi et al. (2005), the observer gain is chosen as:

$$\begin{aligned} M\left( {y,s} \right) =\Gamma ^{-1}\left( \hbox {s} \right) \Delta _{\theta } ^{-1} K \end{aligned}$$

(31)

By substituting (31) in (28), with notation (23), one has:

$$\begin{aligned} \dot{\mathrm{e}}_{\mathrm{o}} = \dot{\Gamma } \left( \mathrm{s} \right) {{{\Gamma }}^{ - 1}}\left( s \right) {e_o} + {{\theta }} {\bar{\bar{\mathrm {A}}}} {e_o} + {{\Gamma }}\left( {\mathrm {s}} \right) {{{\Delta }}_\theta }\partial \left( {{x_4},{x_3},s} \right) \end{aligned}$$

(32)

Then, using (32) and (30), time derivative of Lyapunov candidate function (29) is given by:

$$\begin{aligned} \dot{\mathrm{V}}_{\mathrm{o}}= & {} - \theta V_o + 2e_o^TP \dot{\Gamma } \left( \mathrm{s}\right) \Gamma ^{-1}\left( s \right) e_o\nonumber \\&+\, 2 e_o^TP \Gamma \left( \mathrm{s} \right) \Delta _{\theta } \partial \left( x_4,x_3,s\right) \end{aligned}$$

(33)

At this stage, the observer stability analysis cannot be achieved separately from the controller synthesis. Equation (33) will be exploited further for the stability analysis of the closed loop involving the observer, the DFIG model and the control law.

Remark 2

• Equation (28) shows that $\Delta _{\theta }$ must be invertible. Indeed, the diagonal form of $\Delta _{\theta }$ proves that it is invertible since the design parameter $\theta$ is chosen different from zero $\square$

• Similarly, by using (22) and (18) the inverse of the matrix $\Gamma \left( \hbox {s} \right)$ is given by:

  $$\begin{aligned} \Gamma \left( \hbox {s} \right) ^{-1}=\left[ \begin{array}{cc} {I_2 }&{} {O_2 } \\ {O_2 }&{} {F_1 \left( s \right) ^{-1}} \end{array} \right] \end{aligned}$$

  (34)

  with $F_1 \left( s \right) ^{-1}=\frac{1}{\beta \varphi _r^2 }\left[ \begin{array}{cc} {\varphi _{\mathrm{rq}} }&{} {-\varphi _{\mathrm{rd}} } \\ {\beta \varphi _{\mathrm{rd}} }&{} {\beta \varphi _{\mathrm{rq}} } \\ \end{array} \right]$

  $$\begin{aligned} \hbox {where }\phi _r^2 =\varphi _{\mathrm{rd}} ^{2}+\varphi _{\mathrm{rq}} ^{2} \end{aligned}$$

  (35)

  Due to the practical considerations (magnetic saturation on the one hand and remnant flux on the other), the rotor flux amplitude satisfies the inequality: $\varphi _{\mathrm{min}}^2<\phi _r^2 <\varphi _{\mathrm{max}}^2$. This shows that $\phi _r$ is proved different from zero. Therefore, $\Gamma \left( \hbox {s} \right)$ is invertible. Let us denote by $L_{\Gamma ^{-1}}$ the upper bound for $\Vert \Gamma ^{-1}\left( s \right) \Vert$. $\square$

• With the notations defined in (22) and by introducing (34) in (31), the gain observer can be developed as:

  $$\begin{aligned} M\left( {y,s} \right) =\left[ \begin{array}{c} K_1 I_2 \\ K_2 \theta F_1 \left( s \right) ^{-1} \end{array} \right] \square \nonumber \\ \end{aligned}$$

  (36)

3.3 Wind Speed Computation

The objective of this subsection is to determine the wind speed from the estimation of the aerodynamic torque and rotor speed. By using the turbine model (1)–(2), the estimation of the speed ratio $\hat{\lambda }$ is given by resolving the nonlinear equation:

$$\begin{aligned} C_P \left( \hat{\lambda } \right) =2\frac{\hat{T}_a \hat{\lambda }^{3}}{\rho \pi R^{5}\hat{{\varOmega }}^{2}} \end{aligned}$$

(37)

Recall that the general shape of $C_p$ versus $\lambda$ is represented in Fig. 3 (see, e.g., Yang et al. 2016).

Figure 3 shows that for a given value of $\hat{T}_a$ and $\hat{{\varOmega }}$, Eq. (37) presents a unique solution (there is a single intersection point). In the present study, the $C_{p}$ ($\lambda )$ curve has been a priori approximated by a polynomial interpolation. For the considered wind turbine, this curve was approximated by (see Liao et al. 2011):

$$\begin{aligned} C_p \left( \lambda \right)= & {} -2.86335.10^{-6}.\lambda ^{3}+7.704.10^{-5}\nonumber \\&.\lambda ^{2}+0.015234\lambda \end{aligned}$$

(38)

The online resolution of the polynomial equation (37) has been performed using digital tools of MATLAB/SIMULINK. Now, with the estimated speed ratio $\hat{\lambda }$, and by using (2), one can easily deduce the wind speed estimation according to:

$$\begin{aligned} \hat{v}=\frac{R.\hat{\Omega }}{\hat{\lambda }} \end{aligned}$$

(39)

Fig. 4

Control loops of the whole studied system

4 Controller Design

Recall that the control objective is twofold:

• (i) Tracking the maximum available wind power with a variable turbine speed control.

• (ii) Regulating the DFIG reactive power.

The speed reference is computed online from wind speed and aerodynamic torque estimated values (provided by the observer described previously). Furthermore, the new standard guidelines for producing electrical energy require a limiting production to 90 % of the available power. On the one hand, this ensures an energy reserve to cope with critical uses. On the other hand, the control law is developed by using the sliding mode technique (Utkin 1978). As shown in Fig. 4, the regulator includes estimated inputs. The general structure of the proposed controller is described in Fig. 4.

For designing the control law, some realistic assumptions are crucial:

A.1. :

The references signals $\Omega _{\mathrm{ref}}$ and $\hbox {Q}_{\mathrm{ref}}$ are considered, continuous, bounded and twice time differentiable; their first and second derivatives are also bounded.

A.2.:

The wind speed and its acceleration are considered bounded. Therefore, the turbine speed and its acceleration are also bounded ($\left| {x_3 } \right| \le {\varOmega } _{\mathrm{max}}$ and $\left| \dot{x}_3\right| \le \dot{{\varOmega }}_{\mathrm{max}})$.

A.3.:

Aerodynamic torque $T_a$ is considered bounded and slowly varying ($\left| {T_a } \right| \le \hbox {T}_{\mathrm{max}} )$.

4.1 Optimal Speed Reference Generator

As was previously mentioned, the authorized power to be extracted corresponds to 90 % of the maximum power available. For this purpose, the speed reference signal is chosen according to Fig. 2. This figure also shows that for a given wind speed there exists a unique optimal rotor speed reference for extracting the maximum mechanical power. In the present study, a graphical search of global maxima is privileged. Indeed, a sample of 20 relevant wind speed values $v_j \left( {j=1,\ldots ,20} \right)$ have been a priori selected and the corresponding global maxima $\left( {{\varOmega } _j^*,P_{aj}^*} \right)$ can be graphically determined as illustrated in Fig. 2. By doing so, a set of 20 points $\left( {{\varOmega } _{rj}^*,0.9*P_{aj}^*} \right) \left( {j=1,\ldots ,20} \right)$ has been constructed (see Fig. 2). Then, a nth-order polynomial function R(.), fitting in the least squares sense the set of $\left( {{\varOmega } _{rj}^*,0.9 *P_{aj}^*} \right)$ points, has been built. For the considered wind turbine, characterized by the numerical parameters of Table 3 and the shape of $C_P \left( \lambda \right)$ presented in (38), the degree $n=4$ turned out to be convenient for the considered data. The polynomial thus constructed is denoted:

$$\begin{aligned} R\left( v \right) =h_4 v^{4}+h_3 v^{3}+h_2 v^{2}+h_1 v+h_0 \end{aligned}$$

(40)

where the coefficients $h_j$ have the numerical values of Table 2. For the considered wind system, the shape of $R\left( v \right)$ is plotted in Fig. 5, which will be referred to as an optimal wind speed power (OWRS) characteristic.

Fig. 5

Optimal wind rotor speed (OWRS) characteristic

Table 2 Numerical values of coefficients in the polynomial $R\left( v \right)$

4.2 Rotor Speed and Reactive Power Controller Design Analysis

The sliding surface considered is defined by:

$$\begin{aligned} S=\left[ \begin{array}{c} {S_1 } \\ {S_2 } \\ \end{array} \right] =\left[ \begin{array}{c} {k_1 e_1 } \\ {k_2 e_2 } \\ \end{array} \right] \end{aligned}$$

(41)

where $e_1$ and $e_2$ are, respectively, the speed and reactive power tracking errors

$$\begin{aligned} e_1= & {} \hat{{\varOmega }} -{\varOmega } _{\mathrm{ref}} =\hat{x} _3 -{\varOmega } _{\mathrm{ref}}\end{aligned}$$

(42)

$$\begin{aligned} e_2= & {} Q-Q_{\mathrm{ref}} \end{aligned}$$

(43)

Table 3 Electrical machine parameters

By using (21), time derivative of (42) is given by:

$$\begin{aligned}&\dot{e}_1 = m\left( i_{\mathrm{rq}} x_{1} - i_{\mathrm{rd}}x_{2}\right) + c_2M\left( y,s\right) C_y\bar{x}-\dot{{\varOmega }}_{\mathrm{ref}}\end{aligned}$$

(44)

$$\begin{aligned}&\quad \hbox {where }c_2 =\left[ {0\ 0\ 1\ 0} \right] \end{aligned}$$

(45)

with (7)–(9), Eq. (44) becomes.

$$\begin{aligned} \dot{e}_1 = \frac{m}{L_s} \frac{V_s}{\omega _s}i_{\mathrm{rq}} - \dot{{\varOmega }}_{\mathrm{ref}} + c_2M\left( y,s\right) c_y\tilde{x} \end{aligned}$$

(46)

Similarly, by substituting (11) in (43), the reactive dynamic power error tracking is given by:

$$\begin{aligned} \dot{e}_2= & {} \dot{Q} - \dot{Q}_{\mathrm{ref}}\end{aligned}$$

(47)

$$\begin{aligned} \dot{e}_2= & {} - \frac{V_s M_{\mathrm{sr}}}{L_s} \left[ - \frac{a}{\sigma } V_{\mathrm{sd}} - \frac{R_r}{\sigma L_r} i_{\mathrm{rd}} + \frac{a R_s}{\sigma } x_{1} - \frac{M_{\mathrm{sr}}}{\sigma L_r} p x_3 x_{2} \right. \nonumber \\&\left. - \frac{1}{\sigma } \left( a M_{\mathrm{sr}} - 1 \right) \omega _s i_{\mathrm{rq}} \right. \nonumber \\&\left. - \frac{1}{\sigma }p x_3 i_{\mathrm{rq}} + \frac{1}{\sigma L_r} V_{\mathrm{rd}}\right] - \dot{Q}_{\mathrm{ref}} \end{aligned}$$

(48)

The control synthesis is now done in two steps.

First step: using (41), (46) and (48), the sliding surface dynamics will take the following form:

$$\begin{aligned} \dot{S}= & {} F + D\left[ \begin{array}{c} i_{\mathrm{rq}}\\ V_{\mathrm{rd}} \end{array} \right] + M_r\left( y,s\right) \tilde{x} + k_2\frac{a V_s M_{\mathrm{sr}}}{\sigma } p\left[ \begin{array}{c} 0\\ 1 \end{array}\right] x_3 x_{2} \nonumber \\&+\, k_2 \frac{V_s M_{\mathrm{sr}}}{\sigma L_s} p\left[ \begin{array}{c} 0\\ 1 \end{array} \right] x_3 i_{\mathrm{rq}} \end{aligned}$$

(49)

where $D=\left[ \begin{array}{cc} -k_1 \frac{m}{L_s }\frac{V_s }{\omega _s}&{} 0 \\ 0&{} {-k_2 \frac{aV_s }{\sigma }} \end{array} \right]$; $F=\left[ \begin{array}{c} {F_{10} } \\ {F_{20} } \\ \end{array} \right]$;

$$\begin{aligned} \hbox {and }M_r \left( {y,s} \right)= & {} \left[ \begin{array}{c} 1 \\ 0 \\ \end{array} \right] c_2 M\left( {y,s} \right) c_y\end{aligned}$$

(50)

$$\begin{aligned} \hbox {with } F_{10}= & {} -k_1 \dot{{\varOmega }}_{\mathrm{ref}}\end{aligned}$$

(51)

$$\begin{aligned} F_{20}= & {} -k_2 \frac{V_s M_{\mathrm{sr}} }{L_s }\nonumber \\&\left( -\frac{a}{\sigma }V_{\mathrm{sd}} -\frac{R_r }{\sigma L_r }i_{\mathrm{rd}} +\frac{aR_s }{\sigma }x_{1} -\frac{1}{\sigma }\right. \nonumber \\&\left. \left( {aM_{\mathrm{sr}} -1} \right) \omega _s i_{\mathrm{rq}} )\phantom {\frac{R_r }{\sigma L_r }}\right) -k_2 \dot{Q}_{\mathrm{ref}} \end{aligned}$$

(52)

Equation (49) shows that the sliding surface S can be controlled by the virtual vector input $\left[ \begin{array}{cc} {i_{\mathrm{rq}} }&{V_{\mathrm{rd}} } \end{array}\right] ^{T}$. In this first step, the objective is to determine the considered control vector to ensure the attractiveness and invariance of the surface $\hbox {S}=0$.

Let us consider for the tracking errors system (42)–(43) the Lyapunov candidate function (Slotine and Li 1991):

$$\begin{aligned} V_c =\frac{1}{2}S^{T}S \end{aligned}$$

(53)

Its time derivative is given by (using 49):

$$\begin{aligned} \dot{V}_c= & {} S^T\dot{S} = S^T\left[ F + D\left[ \begin{array}{c} i_{\mathrm{rq}}\\ V_{\mathrm{rd}} \end{array} \right] + M_r \left( y,s \right) \tilde{x}\right] \nonumber \\&+\,k_2\frac{{a{V_s}{M_{\mathrm{sr}}}}}{\sigma }p{S_2}{x_3}{x_{2}} + k_2\frac{{{V_s}{M_{\mathrm{sr}}}}}{{\sigma {L_s}}}p{S_2}{x_3}{i_{\mathrm{rq}}} \end{aligned}$$

(54)

By choosing the virtual vector control $\left[ \begin{array}{c} {i_{\mathrm{rq}} } \\ {V_{\mathrm{rd}} } \end{array} \right]$ such that:

$$\begin{aligned} \left[ \begin{array}{c} i_{\mathrm{rq}} \\ V_{\mathrm{rd}} \\ \end{array} \right]= & {} \left[ \begin{array}{c} {i_{eq} } \\ {V_{eq} } \end{array} \right] +\left[ \begin{array}{l} {i_e } \\ {V_e } \\ \end{array} \right] \nonumber \\= & {} -D^{-1}F-D^{-1}\left[ \begin{array}{c} {d_1 \hbox {sign}\left( {S_1 } \right) } \\ {d_2 \hbox {sign}\left( {S_2 } \right) } \\ \end{array} \right] \end{aligned}$$

(55)

where $d_1 ,d_2$ are positive design parameters.

The time derivative of the Lyapunov candidate function (53) becomes [using (54)–(55) and (9)]:

$$\begin{aligned} \dot{V}_c= & {} - S^T\left[ \begin{array}{c} {{d_1}\hbox {sign}\left( {{S_1}} \right) }\\ {{d_2}\hbox {sign}\left( {{S_2}} \right) } \end{array} \right] \nonumber \\&+\,S^T M_r\left( {y,s} \right) \tilde{x}+ {g_1}{x_3}{e_2}{i_{\mathrm{rq}}} \end{aligned}$$

(56)

$$\begin{aligned} \hbox {where }g_1= & {} k_2^{2} p\frac{V_s M_{\mathrm{sr}} }{\sigma L_s }\left( {1-aM_{\mathrm{sr}} } \right) \end{aligned}$$

(57)

Noting that, from (55) the d component of the rotor voltage vector control is given by:

$$\begin{aligned} V_{\mathrm{rd}} =\frac{\sigma }{k_2 aV_s }\left( {F_{20} +\left[ {d_2 \hbox {sign}\left( {S_2 } \right) } \right] } \right) \end{aligned}$$

(58)

Second step: the first step assumes that $i_{\mathrm{rq}}$ is the input control variable. Unfortunately, this is not the case in reality; we will then seek to reach asymptotically $i_{\mathrm{rq}}$ to its reference ($I_{\mathrm{rqref}} )$ by acting on the real control input $V_{\mathrm{rq}}$. For this, we define the rotor current tracking error $e_i$ by:

$$\begin{aligned} e_i =i_{\mathrm{rq}} -I_{\mathrm{rqref}} \end{aligned}$$

(59)

where the reference signal $I_{\mathrm{rqref}}$ is deduced from (55) as

$$\begin{aligned} I_{\mathrm{rqref}} =\frac{L_s \omega _s }{k_1 mV_s }\left( {F_{10} +d_1 signS_1 } \right) \end{aligned}$$

(60)

Then, by using the wind system model (1)–(6), the rotor current tracking error dynamic can be expressed as follows:

$$\begin{aligned} \dot{e}_i = \frac{1}{{\sigma {L_r}}}{V_{\mathrm{rq}}} + {g_2}\left( {y,s} \right) - \dot{I}_{\mathrm{rqref}} + {g_3} \left( s \right) {x_3} + {g_4}\left( s \right) {x_3}{e_{2}}\nonumber \\ \end{aligned}$$

(61)

where the measurable quantities $g_1 \left( {y,s} \right)$, $g_2 \left( s \right)$, $g_3 \left( s \right)$ and $\dot{I}_{\mathrm{rqref}}$ are given by:

$$\begin{aligned} g_2 \left( {y,s} \right)= & {} -\frac{a}{\sigma }V_{\mathrm{sq}} -\frac{R_r }{\sigma L_r }i_{\mathrm{rq}} +\frac{aR_s }{\sigma }x_{2}\nonumber \\&+\frac{1}{\sigma }\left( {aM_{\mathrm{sr}} -1} \right) \omega _s i_{\mathrm{rd}} \end{aligned}$$

(62)

$$\begin{aligned}&g_3 \left( s \right) =\frac{V_s a}{\omega _s \sigma }p+\left( {\frac{1}{\sigma }p-\frac{aM_{\mathrm{sr}} }{\sigma }} \right) \frac{V_s }{\omega _s M_{\mathrm{sr}} }+g_3 Q_{\mathrm{ref}}\end{aligned}$$

(63)

$$\begin{aligned}&g_4 =-\left( {\frac{1}{\sigma }p-\frac{aM_{\mathrm{sr}} }{\sigma }} \right) \frac{L_s }{V_s M_{\mathrm{sr}} }\end{aligned}$$

(64)

$$\begin{aligned}&\dot{I}_{\mathrm{rqref}} = - \frac{{{L_s}{\omega _s}}}{{m{V_s}}}{\ddot{\varOmega } _{\mathrm{ref}}} \end{aligned}$$

(65)

Then, consider the Lyapunov extended candidate function

$$\begin{aligned} V_{cT} =V_c +\frac{1}{2}e_i^2 \end{aligned}$$

(66)

Using (54), (61) and (66), time derivative of the Lyapunov candidate function $V_{cT}$ is given by:

$$\begin{aligned} \dot{V}_{cT}= & {} -d_1{S_1}\hbox {sign}\left( {{S_1}} \right) - {d_2}{S_2}\hbox {sign}\left( {{S_2}} \right) \nonumber \\&-\, {d_3}{e_i}\hbox {sign}\left( {{e_i}} \right) + {S^T}{M_r}\left( {y,s} \right) \tilde{x}\nonumber \\&+\, {g_1}{x_3}{e_2}{e_i} + {g_1}{x_3}{I_{\mathrm{rqref}}}{e_2} \nonumber \\&+\, {e_i}\left( {d_3}\hbox {sign}\left( {{e_i}} \right) + \frac{1}{{\sigma {L_r}}}{V_{\mathrm{rq}}} + {g_2} \left( {y,s} \right) \right. \nonumber \\&\left. -\, \dot{I}_{\mathrm{rqref}} + {g_3}\left( s \right) {x_3} + {g_4}{x_3}{e_{2}} \right) . \end{aligned}$$

(67)

Equation (67) suggests the choice of the control input $V_{\mathrm{rq}}$ as:

$$\begin{aligned} V_{\mathrm{rq}} =\sigma L_r \left( -d_3 \hbox {sign}\left( {e_i } \right) -g_2 \left( {y,s} \right) +\dot{I}_{\mathrm{rqref}} \right) \end{aligned}$$

(68)

By introducing (68) in (67), the time derivative of the extended Lyapunov candidate function $V_{cT}$ becomes:

$$\begin{aligned} \dot{V}_{cT}= & {} - d_1 S_1\hbox {sign}\left( {{S_1}} \right) - {d_2}{S_2}\hbox {sign}\left( {{S_2}} \right) - {d_3}{e_i}\hbox {sign}\left( {{e_i}} \right) \nonumber \\&+\,S^{T}M_r \left( {y,s} \right) \tilde{x} +g_3 \left( s \right) x_3 e_i +g_4 x_3 e_{2} e_i \nonumber \\&+\,g_1 x_3 e_2 e_i +g_1 x_3 I_{\mathrm{rqref}} e_2 \end{aligned}$$

(69)

Remark 3

With assumption A1, Eqs. (60) and (65) show that the reference signal $I_{\mathrm{rqref}}$ and its time derivative are bounded. Let us denote by $I_{rqref\_M}$ and $\dot{I}_{rqref\_M}$, respectively, the largest values of $I_{\mathrm{rqref}}$ and $\dot{I}_{\mathrm{rqref}}$.

Theorem 1

Consider the overall control system consisting of the wind turbine (1)–(11), the DFI Generator described by the model (12)–(19) subject to assumptions A1–A3, and the output feedback controller including:

• (i) The high-gain observer (20),(21) and (31).

• (ii) The optimal speed generator (40).

• (iii) The sliding mode regulator (58) and (68).

Let the design parameters ($K_1 ,K_2 ,\theta ,d_1 ,d_2 ,d_3 ,k_1 ,k_2 )$ satisfy the following conditions:

$$\begin{aligned}&\theta >2\frac{\lambda _{\mathrm{max}} }{\lambda _{\mathrm{min}} }L_{\Gamma ^{-1}} \alpha _{10} -\frac{2}{k_1^2 \lambda _{\mathrm{min}} }\left( {\frac{\alpha _{21} \lambda _{\mathrm{max}} }{\theta }+\frac{\alpha _{30} }{2\theta }} \right) ^{2}\end{aligned}$$

(70)

$$\begin{aligned}&d=min\left( {d_1 ,d_2 ,d_3 } \right) >\alpha _{40}\end{aligned}$$

(71)

$$\begin{aligned}&K_2 =\frac{1}{\theta ^{2}}\hbox { and }K_1 ,k_1 ,k_2 \hbox { are any real positive constants}.\nonumber \\ \end{aligned}$$

(72)

where $\left( {\lambda _{\mathrm{max}} ,\lambda _{\mathrm{min}} } \right)$ denote, respectively, the largest and smallest eigenvalues of P, and are defined in the appendix.

• (i) The errors system control/observation defined by (59), (42), (43) and (27) is locally stable. The attractiveness region can be made arbitrarily wide by letting the design parameters $\theta \hbox { and }d$ be sufficiently large.

• (ii) The larger the design parameter $\theta$ is, the smaller the norm of the control/observation error $\left[ {e_i ,e_1 ,e_2 ,e_o^T } \right] ^{T}$ is $\square$

Proof of Theorem 1

Let us consider the Lyapunov global candidate function:

$$\begin{aligned} V_{oc} =V_o +V_{cT} \end{aligned}$$

(73)

Using (33) and (69), the time derivative of Lyapunov candidate function (73) is given by:

$$\begin{aligned} \dot{V}_{oc}< & {} - \theta V_o - d_1\left| S_1 \right| - d_2\left| S_2 \right| - d_3\left| e_i \right| \nonumber \\&+\, \mathop {\underbrace{\Vert 2 e_o^TP\dot{\varGamma }\left( s \right) \varGamma ^{-1} \left( s \right) e_o\Vert }}\limits _{Term~1} \nonumber \\&+ \mathop {\underbrace{\Vert 2 e_o^TP\varGamma \left( s \right) \Delta _{\theta }\partial \left( x_4,x_3,s\right) \Vert }}\limits _{Term~2} + \mathop {\underbrace{\Vert S^TM_r\left( {y,s} \right) \tilde{x}\Vert }}\limits _{Term~3}\nonumber \\&+ \mathop {\underbrace{\Vert g_3\left( s \right) x_3 e_i + g_4 x_3 e_{2} e_i + g_1 x_3 e_2 e_i + g_1 I_{\mathrm{rqref}} x_3 e_2\Vert }}\limits _{Term~4}\nonumber \\ \end{aligned}$$

(74)

The development of the four disturbance terms is explicitly presented in the appendix. With the notations defined in the appendix (bounding terms 1,2,3,4), time derivative of the Lyapunov global candidate function (74) becomes:

$$\begin{aligned} \dot{V}_{oc}\le & {} - \theta V_o - d_1\left| S_1 \right| - d_2\left| S_2 \right| - d_3\left| e_i \right| + 2 \lambda _{\mathrm{max}}\nonumber \\&L_{\Gamma }^{-1} \Vert e_o^2\Vert \left( \alpha _{10} + \alpha _1 \Vert e_c\Vert \right) \nonumber \\&+\, 2\lambda _{\mathrm{max}} \left( \alpha _{20} \Vert e_o\Vert + \alpha _{21} \Vert e_c \Vert . \Vert e_o\Vert \right) \nonumber \\&+\, \alpha _{30} \Vert e_o\Vert \Vert e_c\Vert + \alpha _{40} \Vert e_c \Vert + \alpha _{41} \Vert e_c^2\Vert \end{aligned}$$

(75)

Referring to the appendix (Eqs. 94, 99, 105 and 111), (75) can be written as follows:

$$\begin{aligned} \dot{V}_{oc}\le & {} - \left( \theta - 2\frac{{{\lambda _{\mathrm{max}}}}}{{{\lambda _{\mathrm{min}}}}}{L_{{{{\Gamma }}^{ - 1}}}}{\alpha _{10}} + \frac{2}{{k_1^2{\lambda _{\mathrm{min}}}}}\right. \nonumber \\&\left. \left( {\frac{{{\alpha _{21}}{\lambda _{\mathrm{max}}}}}{\theta } + \frac{{{\alpha _{30}}}}{{2\theta }}} \right) ^2 \right) {V_o} \nonumber \\&+ \,2{\alpha _{20}}\frac{{{\lambda _{\mathrm{max}}}}}{{\sqrt{{\lambda _{\mathrm{min}}}} }}\sqrt{{V_o}} + {V_o}^2 - \left( {d - {\alpha _{40}}} \right) \sqrt{2} \sqrt{V_{cT}} \nonumber \\&+\, \left( 1 + \frac{{2{\alpha _{41}}}}{{{k_2}}} + \left( {\frac{{{\lambda _{\mathrm{max}}}}}{{{\lambda _{\mathrm{min}}}}}{\alpha _1}{L_{{{{\Gamma }}^{ - 1}}}}} \right) ^2 \right) V_{cT} \end{aligned}$$

(76)

Finally, by using (76), the time derivative of Lyapunov candidate function (73) can be written in more compact form as:

$$\begin{aligned} \dot{V}_{oc}\le & {} \mathop {\underbrace{ - {\beta _1}{V_o} + {\beta _2}\sqrt{{V_o}} + {V_o}^2}}\limits _{Term~A} - \mathop {\underbrace{{\beta _3}\sqrt{{V_{cT}}} + {\beta _4}{V_{cT}}}}\limits _{Term~B} \end{aligned}$$

(77)

where (using the notations defined in the appendix)

$$\begin{aligned} \beta _1= & {} \theta -2\frac{\lambda _{\mathrm{max}} }{\lambda _{\mathrm{min}} }L_{\Gamma ^{-1}} \alpha _{10} +\frac{2}{k_1^2 \lambda _{\mathrm{min}} }\nonumber \\&\left( {\frac{\alpha _{21} \lambda _{\mathrm{max}} }{\theta }+\frac{\alpha _{30} }{2\theta }} \right) ^{2}\end{aligned}$$

(78)

$$\begin{aligned} \beta _2= & {} 2\alpha _{20} \frac{\lambda _{\mathrm{max}} }{\sqrt{\lambda _{\mathrm{min}} }}\end{aligned}$$

(79)

$$\begin{aligned} \beta _3= & {} \left( {d-\alpha _{40} } \right) \sqrt{2}\end{aligned}$$

(80)

$$\begin{aligned} \beta _4= & {} 1+\frac{2\alpha _{41} }{k_2 }+\left( {\frac{\lambda _{\mathrm{max}} }{\lambda _{\mathrm{min}} }\alpha _1 L_{\Gamma ^{-1}} } \right) ^{2} \end{aligned}$$

(81)

$\square$

Remark 4

• If the design parameter $\theta$ is chosen in accordance with (70), the constant $\beta _1$ given by (78) becomes positive.

• Similarly, if the parameter d is chosen in accordance with (71), the constant $\beta _3$ given by (80) becomes positive.

• With Eq. (98), one can deduce that to reduce the term $\beta _2$ [in (77)], choose the design parameter $\theta$ large enough.

• Similarly, with Eq. (95) one can deduce that to reduce the term $\beta _4$ [in (77)], choose the design parameter $k_2$ which is large enough $\square$

To discuss the sign of $\dot{V}_{oc}$, let us consider Fig. 6 representing the general shape of different terms in (77), where :

$$\begin{aligned}&\sigma _0 \left( {V_o } \right) =\beta _2 \sqrt{V_o }+V_o ^{2}\end{aligned}$$

(82)

$$\begin{aligned}&\sigma _1 \left( {V_o } \right) =\beta _1 V_o\end{aligned}$$

(83)

$$\begin{aligned}&\sigma _2 \left( {V_{cT} } \right) =\beta _3 \sqrt{V_{cT} }\end{aligned}$$

(84)

$$\begin{aligned}&\sigma _3 \left( {V_{cT} } \right) =\beta _4 V_{cT} \end{aligned}$$

(85)

Fig. 6

a Term A of (77): Solid line: General shape of $\sigma _0 \left( {V_o } \right)$. Dotted line: Shape of $\sigma _1 \left( {V_o} \right)$. b Term B of (77): Solid line: General shape of $\sigma _2 \left( {V_{cT} } \right)$. Dotted line: Shape of $\sigma _3 \left( {V_{cT}} \right)$

Figure 6a shows that for high values of the observer design parameter $\theta$, there exist two solutions (noted, respectively, $V_{o1}$ and $V_{o2}$.) for the equation $\sigma _0 \left( {V_o } \right) =\sigma _1 \left( {V_o } \right)$. Figure 6a points that if the initial condition of Lyapunov candidate function $V_o$ lies in the interval $\left[ \begin{array}{cc} 0&{V_{o1} } \end{array} \right]$, term A of Eq. (77) converges (in steady state) to the interval $\left[ \begin{array}{cc} 0&{V_{o2} } \end{array} \right]$. Moreover, this figure shows that $V_{o1}$ is an increasing function of the parameter $\beta _1$. Therefore, by using (78) one deduces that $V_{o1}$ is an increasing function of the design parameter $\theta$. Similarly, Fig. 6b shows for a given value of the design parameter d, there exists a unique nonzero solution (noted by $V_{c1} )$ of the equation: $\sigma _2 \left( {V_{cT} } \right) =\sigma _3 \left( {V_{cT} } \right)$ ie: $V_{c1} =\left( {\frac{\beta _3 }{\beta _4 }} \right) ^{2}$ which clearly shows [using (80)–(81)] that $V_{c1}$ is an increasing function of the design parameter d.

Finally, the attractive region of Lyapunov candidate function $V_{oc}$ given by (72) is the smallest value between $V_{c1}$ and $V_{o1}$. This region can be made arbitrarily large by letting the design parameters $\theta \hbox { and }d$ be sufficiently large. This proves Part 1 of Theorem 1.

Fig. 7

The mean wind speed step variation

Fig. 8

Reactive power reference

On the other hand, if the initial condition of $V_{oc}$ lies in the attractive region, Fig. 6a and b shows that the term B converges in steady state to the origin, while the term A converges to the interval $\left[ \begin{array}{cc} 0&{V_{o2} } \end{array} \right]$. Figure 6a points that $V_{o2}$ is a decreasing function of the parameter $\beta _1$. Therefore, using (78), one can deduce that $V_{o2}$ is a decreasing function of the design parameter $\theta$. This completes the proof of Theorem 1.

Table 4 Controller and observer parameters

5 Simulation Results

The simulations are performed on MATLAB/SIMULINK environment. The DFIG and turbine parameters considered in this work are given in Table 3. The observer and the control law are implemented using Eqs. (20)–(21), (31), (58) and (68), respectively. The corresponding design parameters are given the following numerical values of Table 4, which proved to be convenient. In this respect, note that there is no systematic way, especially in nonlinear control, to make suitable choices for these values. Therefore, the usual practice consists of proceeding with trial-and-error approach.

By doing so, the numerical values of Table 4 are retained.

The whole simulated control system is illustrated in Fig. 4.

5.1 Simulation Protocol

The simulation protocol is designed in such a way to consider a large step variation of the mean wind speed (14–6 m/s: at time 8 s (Fig. 7)). A slight deformation was introduced to represent a faithful image of the actual shape of the wind speed. The DFIG reactive power reference signal considered is plotted in Fig. 8. It also corresponds to a large step variation ([4000–1000 VAR] at time 10 s).

The initial conditions of both actual and estimated values of rotor speed and aerodynamic torque are chosen sufficiently different, respectively [0 rad/s, 40 Nm/s] and [40 rad/s, 0 Nm/s].

5.2 Speed Reference Construction

Based on the wind profile described in Fig. 7, the optimal rotor speed reference [determined by using the MPPT curve (Fig. 5)] is plotted in Fig. 9. Note that the obtained reference signal presents also a wide variation [180–57 rad/s] at time 8 s.

Fig. 9

DFIG rotor speed optimal reference

5.3 Observer Validation

The high-gain observer is implemented using Eqs. (20), (21) and (31). The corresponding design parameters satisfy the conditions (70) and (72). They are given by the numerical values of Table 4.

Figures 10, 11 and 12 show the satisfactory performances of the proposed observer. In fact, they confirm, respectively, that the estimated rotor speed, estimated aerodynamic torque and the estimated wind speed track well their actual value.

Fig. 10

Observer performances. Solid line: Estimated rotor speed. Dotted line: its actual value

Fig. 11

Observer performances. Solid line: Estimated aerodynamic torque. Dotted line: its actual value

Fig. 12

Observer performances. Dotted line: Estimated wind speed. Solid line: its actual value

5.4 Controller Validation

The sliding mode controller is implemented using Eqs. (58), (68) and (40). The corresponding design parameters satisfy the condition (71). They are given by the numerical values of Table 4.

Figures 13, 14 and 15 show the satisfactory performances of the proposed sensorless controller. In fact, they attest, respectively, that the rotor speed, active and reactive power track well their reference signals.

Fig. 13

Controller performances. Dotted line: DFIG Rotor speed. Solid line: optimal rotor speed reference

Fig. 14

Controller performances. Dotted line: DFIG Reactive power. Solid line: its reference signal

Fig. 15

Controller performances. Dotted line: DFIG Active power. Solid line: optimal aerodynamic power

5.5 Robustness Tests

To evaluate the robustness of the proposed regulator, several tests were performed; indeed, these tests aim to check whether the controller’s performances are conserved even in the presence of the DFIG and the wind turbine parameters’ uncertainties or under grid fault. These tests are classified into three parts: robustness despite wind turbine parameters’ uncertainties, robustness despite DFIG parameters’ uncertainties and robustness despite the grid’s characteristics variation.

5.5.1 Robustness Under Wind Turbine Parameters Uncertainties

This test was carried out by considering a 10 % of uncertainty in the power coefficient $C_p$ defined in (1) and (38). The considered uncertainty is introduced at time 4 s.

Figures 16 and 17 show, respectively, the satisfactory robustness of the proposed sensorless controller. In fact, Fig. 16 attests that the estimated rotor speed and aerodynamic torque track well their actual value despite the introduction of uncertainty on the turbine parameters. Similarly, Fig. 17 shows that the rotor speed and reactive power track well their reference signals despite the introduction of uncertainty on the power coefficient $C_p$.

Fig. 16

Observer robustness under turbine parameter uncertainty. a Dotted line: estimated wind speed. Solid line: its actual value, b Solid line: estimated aerodynamic torque. Dotted line: its actual value

Fig. 17

Controller robustness under turbine parameter uncertainty. a Dotted line: DFIG Rotor speed. Solid line: optimal rotor speed reference, b Dotted line: DFIG Reactive power. Solid line: its reference signal

5.5.2 Robustness Under DFIG Parameters’ Uncertainties

This test was carried out by considering a 5 % of uncertainty in the values of rotor resistance ($\hbox {R}_{\mathrm{r}})$ and inductance ($\hbox {L}_{\mathrm{r}} )$. The considered uncertainties are introduced, respectively, at time 3 and 6 s. Practically, the rotor resistance uncertainty is due to skin effect phenomenon, while the inductance error value is introduced by the magnetic saturation problem.

Figures 18 and 19 show, respectively, the satisfactory robustness of the proposed sensorless controller. In fact, Fig. 18 attests that the estimated rotor speed and aerodynamic torque track well their actual value despite the introduction of uncertainty on the DFIG parameters. Similarly, Fig. 19 shows that the rotor speed and reactive power track well their reference signals despite the introduction of uncertainty on the values of $\hbox {R}_{\mathrm{r}}$ and $\hbox {L}_{\mathrm{r}}$.

Fig. 18

Observer robustness under DFIG parameter uncertainty. a Dotted line: estimated aerodynamic torque. Solid line: its actual value, b Solid line: estimated rotor speed. Dotted line: its actual value

Fig. 19

Controller robustness under DFIG parameter uncertainty. a Dotted line: DFIG Rotor speed. Solid line: optimal rotor speed reference, b Dotted line: Reactive power. Solid line: its reference

5.5.3 Robustness Under Grid Faults

Voltage dip was introduced to check the controller’s robustness under grid faults.

Indeed, Fig. 20 shows that the considered dip is introduced at time 4, 5 s. It corresponds to a voltage drop of about 90 % over the nominal value.

Figures 21 and 22 show, respectively, the satisfactory robustness of the proposed sensorless controller. In fact, Fig. 21 attests that the estimated rotor speed and aerodynamic torque track well their actual values despite the introduction of grid faults. Similarly, Fig. 22 shows that the rotor speed and reactive power track well their reference signals despite the introduction of a dip disturbance.

Fig. 20

The considered grid faults. The shape of $V_{sabc}$ (grid voltage phases)

Fig. 21

Observer robustness under grid faults. a Solid line: estimated rotor speed. Dotted line: its actual value, b Dotted line: estimated aerodynamic torque. Solid line: its actual value

Fig. 22

Controller robustness under grid faults. a Dotted line: DFIG rotor speed. Solid line: optimal rotor speed reference, b Dotted line: Reactive power. Solid line: its reference

Fig. 23

Experimental rig interfaces

Fig. 24

Algorithm for implementation of the proposed observer/controller

Remark 5

This note aims at describing the procedure for experimental validation of the proposed observer/controller. To this end, a list of the necessary equipments has been compiled to build an experimental test bench (Suwan et al. 2012). Basically the rig setup can be separated into seven subsystems (see Fig. 23):

(i) Drive train (DFIG, Squirrel cage asynchronous motor and their coupling): the DFIG will be driven by a standard ASM emulating the wind turbine main mover. The driving motor will be controlled by a commercial variable-frequency converter.

(ii) Measurement unit: it will provide the control system with real-time measured values (only electrical ones).

(iii) Transformer: to connect the test bench to power grid.

(iv) PWM Inverters: to link the DFIG rotor to the grid.

(v) Computer provided with MATLAB/SIMULINK and LabVIEW: the DSP program will be developed using MATLAB/SIMULINK. Also, the software LabVIEW will be used for data acquisition and visualization of the application. The data will be adapted with a signal conditioner and received through the data acquisition (DAQ).

(vi) Digital Signal Processor (DSP): it will mainly execute the control/observation program and will send the PWM signals to each IGBT.

(vii) Fault Ride Through (FRT) testing set up: it is an inductive voltage divider that will be used to produce voltage dips with defined depths and durations. The FRT capability of the DFIG can be tested to determine whether it meets certain grid code requirements

The algorithm of the controller program to be implemented is represented in Fig. 24.

6 Conclusion

This paper focused on an output feedback control of a wind power system involving a DFIG. The control objectives were the achievement of MPPT and DFIG reactive power control without resorting to any mechanical sensors. To meet these objectives, we proposed a regulator combining a state feedback controller (58, 68) with a state observer (20) providing online estimates of wind velocity, aerodynamic torque and rotor speed. The state feedback controller is a sliding mode type, while the observer is a high-gain structure. Interestingly, the controller and the observer were simultaneously analyzed to emphasize sufficient conditions for the closed-loop control system, which proved to be sufficient and convenient to reach the control objectives fixed upstream. Using tools from Lyapunov’s stability, it was formally shown that the closed-loop control system, expressed in terms of the state estimation errors and the output-reference tracking errors, enjoys a semi-global practical stability. These theoretical results were confirmed by simulations involving wide range variation of the wind speed. The robustness of the proposed regulator was also evaluated through several tests. Indeed, this allowed to verify that the proposed controller maintained its good performances despite the uncertainties on DFIG and wind turbine parameters or under grid faults.

Appendix: Development and Bounding of the Disturbance Terms in (74)

Bounding Term 1:

The first term of (74) satisfies the following inequality

$$\begin{aligned} \Vert 2 e_o ^TP\dot{\varGamma }\left( s \right) {\varGamma ^{ - 1}} \left( s \right) {e_o} \Vert \le 2 \lambda _{\mathrm{max}}\Vert \dot{\Gamma }\left( \mathrm{s}\right) \Vert \Vert \Gamma ^{-1}\left( s \right) \Vert \Vert e_o^2\Vert \nonumber \\ \end{aligned}$$

(86)

Then with assumptions A1–A3 and remark 2, using (93), inequality (86) can be rewritten as

$$\begin{aligned}&\Vert 2 e_o^TP\dot{\varGamma } \left( s \right) \varGamma ^{-1}\left( s \right) {e_o}\Vert \nonumber \\&\quad \le 2{\lambda _{\mathrm{max}}}{L_{\Gamma }^{-1}} \Vert e_o^2\Vert \left( \alpha _{10} + \alpha _{11}\left| e_i \right| + \alpha _{12}\left| e_2 \right| \right) \end{aligned}$$

(87)

where

$$\begin{aligned}&\bullet \quad \alpha _{10} =\left\| \left[ \begin{array}{cc} {0_2 }&{} {O_2 } \\ {O_2 }&{} \rho \\ \end{array} \right] \right\| \hbox { with } \rho =\left[ \begin{array}{cc} {\alpha \rho _{11} }&{} {\frac{\alpha }{\beta }\rho _{21} } \\ {-\alpha \rho _{21} }&{} {\frac{\alpha }{\beta }\rho _{11} } \\ \end{array} \right] \end{aligned}$$

(88)

$$\begin{aligned}&\left\{ \begin{array}{l} \rho _{11} = \left( {\frac{{{L_s}{\omega _s}}}{{m{V_s}}}{k_1}{{\ddot{\varOmega } }_{ref\_M}} + {g_{3\_M}}{{\varOmega } _{\mathrm{max}}}} \right) \\ \rho _{21} = - \frac{{{L_s}}}{{{V_s}{M_{\mathrm{sr}}}{k_2}}}{d_2}\hbox {sign}\left( {{S_2}} \right) \\ \quad \qquad - {{\varOmega } _{\mathrm{max}}} \left( {\frac{{a{M_{\mathrm{sr}}}}}{\sigma } + \frac{1}{\sigma }} \right) p I_{rqref\_M} - \frac{{{L_s}}}{{{V_s}{M_{\mathrm{sr}}}}}{\dot{Q}_{ref\_M}} \end{array} \right. \end{aligned}$$

(89)

$$\begin{aligned}&\hbox {with }g_{3\_M} \nonumber \\&\quad =\frac{V_s a}{\omega _s \sigma }p+\left( {\frac{1}{\sigma }p-\frac{aM_{\mathrm{sr}} }{\sigma }} \right) \nonumber \\&\qquad \frac{V_s }{\omega _s M_{\mathrm{sr}} }+g_4 Q_{ref\_M} \end{aligned}$$

(90)

and

$$\begin{aligned}&\bullet \quad \alpha _{11} \!=\!\left\| \begin{array}{cccc} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {-\alpha d_3 }&{} {-\frac{\alpha }{\beta }\left( {\frac{aM_{\mathrm{sr}} }{\sigma }+\frac{1}{\sigma }} \right) p{\varOmega } _{\mathrm{max}} } \\ 0&{} 0&{} {\alpha \left( {\frac{aM_{\mathrm{sr}} }{\sigma }+\frac{1}{\sigma }} \right) p{\varOmega } _{\mathrm{max}} }&{} {-\frac{\alpha }{\beta }d_3 } \end{array}\right\| \nonumber \\ \end{aligned}$$

(91)

$$\begin{aligned}&\bullet \quad \alpha _{12} \!=\!\left\| \begin{array}{cccc} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {\alpha \left[ {g_4 {\varOmega } _{\mathrm{max}} } \right] }&{} 0 \\ 0&{} 0&{} 0&{} {\frac{\alpha }{\beta }\left[ {g_4 {\varOmega } _{\mathrm{max}} } \right] } \\ \end{array}\right\| \end{aligned}$$

(92)

$$\begin{aligned}&\hbox {and }\alpha =\frac{M_{\mathrm{sr}} }{\sigma L_s }p\left( {1-aM_{\mathrm{sr}} } \right) \end{aligned}$$

(93)

Using (29), (66), and using Young’s inequality, (87) can be written as follows:

$$\begin{aligned} Term1\le & {} \left( \frac{\lambda _{\mathrm{max}} }{\lambda _{\mathrm{min}} }L_{\Gamma ^{-1}} \alpha _1 \right) ^{2}V_{cT} \nonumber \\&+\,2\frac{\lambda _{\mathrm{max}} }{\lambda _{\mathrm{min}} }L_{\Gamma ^{-1}} \alpha _{10} V_o +V_o \end{aligned}$$

(94)

With

$$\begin{aligned} \alpha _1 =\sqrt{2}\,\hbox {sup}\left( {\alpha _{11} ,\frac{\alpha _{12} }{k_2 }} \right) \end{aligned}$$

(95)

Bounding Term 2:

From (22) and (26), one has:

$$\begin{aligned}&\Vert \Gamma \left( \hbox {s} \right) \Delta _{\theta } \partial \left( {x_4 ,x_3 ,s} \right) \Vert \nonumber \\&\quad \le {\left\| \begin{array}{c} {T_a \varphi _{\mathrm{max}} } \\ {T_a \varphi _{\mathrm{max}} } \\ {\frac{\gamma _{31} }{\theta }+\frac{\gamma _{32} }{\theta }e_1 } \\ {\frac{\gamma _{31} }{\theta }+\frac{\gamma _{32} }{\theta }e_1 } \\ \end{array}\right\| }\end{aligned}$$

(96)

$$\begin{aligned} \hbox {with }\gamma _{31}= & {} \beta \varphi _{\mathrm{max}} \left( {\frac{T_a }{J}+\frac{f}{J}{\varOmega } _{ref\_M} } \right) ,\nonumber \\ \gamma _{32}= & {} \beta \varphi _{\mathrm{max}} \frac{f}{J}\end{aligned}$$

(97)

$$\begin{aligned} \bullet \quad \alpha _{20}= & {} T_{Max} \varphi _{\mathrm{max}} +\left| {\frac{\gamma _{31} }{\theta }} \right| ,\nonumber \\ \alpha _{21}= & {} \gamma _{32} \end{aligned}$$

(98)

Using (29), (66), and using Young’s inequality, inequality (96) can be written in the following form:

$$\begin{aligned} Term2\le & {} 4\frac{\lambda _{\mathrm{max}} }{\sqrt{\lambda _{\mathrm{min}} }}\alpha _{20} \sqrt{V_o }\nonumber \\&+\,\left( {2\frac{\lambda _{\mathrm{max}} }{\sqrt{\lambda _{\mathrm{min}} }}\frac{\sqrt{2}\alpha _{21} }{\theta k_1 }} \right) ^{2}V_o +V_{cT} \end{aligned}$$

(99)

Bounding Term 3:

Using (31) and (36)

$$\begin{aligned}&S^{T}M_r \left( y \right) \tilde{x} \nonumber \\&\quad =S_1 \frac{\theta K_2 }{\beta \varphi _{\mathrm{max}}^2 }\varphi _{\mathrm{rq}} \tilde{x} _1 \nonumber \\&\qquad -S_1 \frac{\theta K_2 }{\beta \varphi _{\mathrm{max}}^2 }\varphi _{\mathrm{rd}} \tilde{x} _2 \end{aligned}$$

(100)

introducing (27) in (100), one has:

$$\begin{aligned}&S^{T}M_r \left( y \right) \tilde{x} \nonumber \\&\quad =k_1 \frac{\theta K_2 }{\beta \varphi _{\mathrm{max}}^2 }\varphi _{\mathrm{rq}} N_1 \varDelta _{\theta } ^{-1} \varGamma \left( s \right) ^{-1}e_o e_1 \nonumber \\&\qquad -k_1 \frac{\theta K_2 }{\beta \varphi _{\mathrm{max}}^2 }\varphi _{\mathrm{rd}} N_2 \varDelta _{\theta } ^{-1} \varGamma \left( s \right) ^{-1}e_o e_1\end{aligned}$$

(101)

$$\begin{aligned}&\hbox {where }N_1 =\left[ \begin{array}{cccc} 1&{} 0&{} 0&{} 0 \\ \end{array} \right] ; \hbox {N}_2 =\left[ \begin{array}{cccc} 0&{} 1&{} 0&{} 0 \\ \end{array} \right] \end{aligned}$$

(102)

On the other hand, using Eqs. (22) and (34)–(35) one has:

$$\begin{aligned} N_1 \Delta _{\theta }^{-1} \Gamma \left( \hbox {s} \right) ^{-1}= & {} \left[ \begin{array}{cccc} 1&{} 0&{} 0&{} 0 \\ \end{array} \right] \end{aligned}$$

(103)

$$\begin{aligned} N_2 \Delta _{\theta }^{-1} \Gamma \left( \hbox {s} \right) ^{-1}= & {} \left[ \begin{array}{cccc} 0&{} 1&{} 0&{} 0 \\ \end{array} \right] \end{aligned}$$

(104)

To avoid that the observer gain $\theta$ boosts this disturbing term, one can choose the observer design parameter $K_2 =\frac{1}{\theta ^{2}}$

Then term 3 becomes:

$$\begin{aligned} Term\,\,3\le \alpha _{30} \Vert e_o\Vert \left| {e_1 } \right| \le \left( {\frac{\alpha _{30} }{2\theta \sqrt{\lambda _{\mathrm{min}} }}\frac{\sqrt{2}}{k_1 }} \right) ^{2}V_o +V_{cT}\nonumber \\ \end{aligned}$$

(105)

with

$$\begin{aligned} \bullet \quad \alpha _{30} =2\,\,Sup\left( {\frac{k_1 }{\beta \varphi _{\mathrm{max}}^2 }\varphi _{\mathrm{max}} \Vert N_1\Vert ,\frac{k_1 }{\beta \varphi _{\mathrm{max}}^2 }\varphi _{\mathrm{max}} \Vert N_2\Vert } \right) \nonumber \\ \end{aligned}$$

(106)

Bounding Term 4:

Using remark 3, (57) and (63)–(64), the four terms of inequality (74) will be discussed separately.

$$\begin{aligned}&\left| {g_3 \left( s \right) x_3 e_i } \right| \le g_{3\_M} {\varOmega } _{\mathrm{max}} \left| {e_i } \right| \end{aligned}$$

(107)

$$\begin{aligned}&\left| {g_4 x_3 e_{2} e_i } \right| \le g_4 {\varOmega } _{\mathrm{max}} \left| {e_i } \right| \left| {e_2 } \right| \end{aligned}$$

(108)

$$\begin{aligned}&\left| {g_1 x_3 e_{2} e_i } \right| \le g_1 {\varOmega } _{\mathrm{max}} \left| {e_i } \right| \left| {e_2 } \right| \end{aligned}$$

(109)

$$\begin{aligned}&\left| {g_1 I_{\mathrm{rqref}} x_3 e_2 } \right| \le g_1 I_{rqref\_M} {\varOmega } _{\mathrm{max}} \left| {e_i } \right| \end{aligned}$$

(110)

Using (29), (66), inequalities (107–110) can take the form:

$$\begin{aligned} Term\,\,4\le \sqrt{2}\alpha _{40} \sqrt{V_{cT} }+\frac{2\alpha _{41} }{k_2 }V_{cT} \end{aligned}$$

(111)

where

$$\begin{aligned}&\bullet \quad \alpha _{40} =Sup\left( {g_{3\_M} \Omega _{\mathrm{max}} ,g_1 I_{rqref\_M} {\varOmega } _{\mathrm{max}} } \right) \end{aligned}$$

(112)

$$\begin{aligned}&\bullet \quad \alpha _{41} =Sup\left( {g_4 {\varOmega } _{\mathrm{max}} ,g_1 \Omega _{\mathrm{max}} } \right) \end{aligned}$$

(113)