1 Introduction

Magnetic levitation systems have practical significance in many engineering applications such as high-speed maglev passenger trains, frictionless bearings, levitation of wind tunnel models, vibration isolation of sensitive machinery and levitation of molten metal in induction furnaces. The maglev systems are usually open-loop unstable and are modeled by highly nonlinear differential equations which present difficulties in controlling these systems. Therefore, it is an important task to construct high-performance feedback controllers for regulating the position of the levitated object.

In recent years, many techniques have been reported in the literature for controlling magnetic levitation systems. The feedback linearization technique has been used to design controllers for magnetic levitation systems (Barie and Chiasson 1996; Hajjaji and Ouladsine 2001; Trumper et al. 1997). Other types of nonlinear control approaches have been proposed (see, e.g., Green and Craig 1998; Huang et al. 2000; Yang and Tateishi 1998; Zhao and Thornton 1992). Robust control methods have also been applied to control magnetic levitation systems Fujita et al. (1990), Fujita et al. (1995). Control laws based on phase space Zhao et al. (1999), linear controller design El Rifai and Youcef-Toumi (1998), the gain scheduling approach Kim and Kim (1994) and natural network techniques Lairi and Bloch (1999) have also been used to control magnetic levitation systems.

Sliding mode control (SMC) Hung et al. (1993), Yong et al. (1999), Zinober (1994) is a powerful nonlinear control method that is well known for its robustness. Sliding mode control gets attention owing to its ability to eliminate uncertainties and external disturbances. The SMC design consists of two parts, the continuous equivalent control and discontinuous switching control. To satisfy the reachability conditions the switching gain should be larger than the upper bounds of the model uncertainty and disturbance.

Recently, terminal sliding mode control (TSMC) has been developed Tang (1998), Wu et al. (1998). Compared with linear hyperplane-based sliding modes, terminal sliding mode offers some superior properties such as fast, finite-time convergence. The TSMC is particularly useful for high-precision control as it speeds up the convergence rate near an equilibrium point. ASMC and AFTSMC have been successfully applied to many practical control systems (see. e.g, Wu et al. 1998; Man et al. 1999; Keleher and Stonier 2001; Feng et al. 2001; Keleher and Stonier 2001; Li et al. 2013; Yu and Man 2002). Adaptive terminal sliding mode control (ATSMC) is proposed in Man et al. (1999), Keleher and Stonier (2001), Feng et al. (2001), Keleher and Stonier (2001) to control a rigid robot manipulator. This control method relaxes the need of the known upper bound of parameter uncertainties and disturbance. Later, Yu and Man (2002), Almutairi and Zribi (2006) presented the fast terminal sliding mode control (FTSMC). Using FTSMC scheme, the system state variables can converge fast to the equilibrium point in finite time Wu et al. (1998). Evidently, it is of theoretical importance to design the FTSMC. Tao and Taur (2004) developed a new adaptive fuzzy terminal sliding mode controller for linear systems with mismatched time varying uncertainties. Adaptive nonsigular FTSMC has been used in Li et al. (2013) for application to electromechanical actuator. However, the AFTSMC law has not been developed for a magnetic levitation system.

The main contributions of this paper are that new ASMC and AFTSMC laws for a magnetic levitation system are designed to achieve a fast convergence rate and high accuracy of results. To the best knowledge of the authors, AFTSMC has not previously been used to develop a controller for a magnetic levitation system. In the controller designs, we assume that the disturbance d is taken into account [(see Eq. (5)]. A rigorous Lyapunov function is used to ensure the finite-time stability of the closed-loop system. Moreover, the proposed control methods have adaptive laws which can estimate the upper bound of a disturbance.

The paper is organized as follows. In Sect. 2, the model of the magnetic levitation system is presented. Section 3 presents a sliding mode controller design for the magnetic levitation system. Section 4 proposes an adaptive sliding mode control (ASMC) algorithm to solve the same control problem as in Sect. 3. The sliding manifold is chosen and the sliding control law is studied and a proof of finite-time convergence is given by using the Lyapunov stability theory. Section 5 gives the design of AFTSMC. The finite time reachability to the designed state is also ensured by the Lyapunov stability theory. In Sect. 6, numerical simulations on a magnetic levitation system are presented to demonstrate the usefulness of the proposed controllers. In Sect. 7, we present conclusions.

2 Model of the Magnetic Levitation System

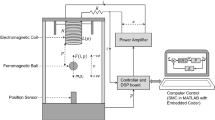
The model of a magnetic levitation system considered in this paper consists of a ferromagnetic ball suspended in a voltage-controlled magnetic field. Only the vertical motion is considered. The objective is to keep the ball at a reference level. The dynamic model of the system can be written as Barie and Chiasson (1996), AL-Muthairi and Zribi (2004)

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}t}= & {} v, \quad Ri + \frac{\mathrm{d}(L(p)i)}{\mathrm{d}t} = e, \nonumber \\ m \frac{\mathrm{d}v}{\mathrm{d}t}= & {} mg_\mathrm{c}-C\left( \frac{i}{p}\right) ^2 , \end{aligned}$$
(1)

where p is the ball’s position, v represents the ball’s velocity, i is the current in the coil of the electromagnet, e denotes the applied voltage, R denotes the coil’s resistance, L represent the coil’s inductance, \(g_\mathrm{c}\) is the gravitational constant, C denotes the magnetic force constant and m is the mass of the levitated ball.

The inductance L is considered as a nonlinear function of the ball’s position p. The approximation

$$\begin{aligned} L(p) =L_1+\frac{2C}{p} \end{aligned}$$
(2)

will be used, where \(L_1\) is a parameter of the system. Let us define \(x_1 = p,\ x_2 = v,\ x_3 = i,\ u =e,\) and let \(x = ( x_1 \quad x_2 \quad x_3)^T\) be the state vector. Thus, the state-space model of the magnetic levitation system is expressed as AL-Muthairi and Zribi (2004)

$$\begin{aligned} \dot{x}_1= & {} x_2,\nonumber \\ \dot{x}_2= & {} g_\mathrm{c}-\frac{C}{m} \left( \frac{x_3}{x_1}\right) ^2,\\ \dot{x}_3= & {} -\frac{R}{L} x_3 +\frac{2C}{L}\left( \frac{x_2 x_3}{{x_1}^2}\right) + \frac{1}{L} u. \nonumber \end{aligned}$$
(3)

The objective of the proposed control schemes is to drive the states \(x_1 ,\ x_2\) and \(x_3\) to their desired constant values \(x_{1d} ,\ x_{2d}\) and \(x_{3d},\) respectively.

Let \(z_1=x_1-x_{1d}, \) \(z_2=x_2-x_{2d}\) and \(z_3=g_\mathrm{c}-\frac{C}{m}\left( \frac{x_3}{x_1}\right) ^2\), where \( x_{1d} ,\ x_{2d}, \) and \(x_{3d}\) are the desired position, velocity and current. Here, we assume that \(x_{2d}=0, x_{3d}=\sqrt{g_\mathrm{c}m/C}x_{1d}\) and the disturbance d is taken into account.

Therefore, the time derivatives of \(z_1, z_3\) and \(z_3\) can be obtained as

$$\begin{aligned} \dot{z_1}&= \dot{x}_1 - \dot{x}_{1d} = z_2\\ \dot{z_2}&= \dot{x}_2-\dot{x}_{2d} = z_3 \end{aligned}$$

and

$$\begin{aligned} \dot{z}_3&= -\frac{2C}{m}\left( \frac{x_3}{x_1}\right) \left( \frac{x_1\dot{x}_3-x_3\dot{x}_1}{x_1^2}\right) +d = -\frac{2C}{m} \frac{x_3}{x^{3}_1}\\&\quad \times \left( -\frac{R}{L}x_1 x_3 +\,\frac{2C}{L}\left( \frac{x_2x_3}{x^2_1}\right) +\frac{1}{L}x_1u - x_3x_2\right) +d\\&=\frac{2CRx_3^2}{mLx_1^2}-\frac{4C^2x_2x_3^2}{mLx_1^4}-\frac{2Cx_3}{mLx_1^2}u+\frac{2Cx_3^2x_2}{mx_1^3}+d\\&=\frac{-2}{Lx_1}\left( \frac{Cx_3}{mx_1}\right) u+2\left( \frac{C}{m}\left( \frac{x_3}{x_1}\right) ^2\right) \\&\quad \times \left[ \frac{R}{L}-\frac{2Cx_2}{Lx_1^2} +\frac{x_2}{x_1}\right] +d\\&=\frac{-2}{L(z_1+x_{1d})}\sqrt{\frac{c}{m}(g_\mathrm{c}-z_3)}u+2(g_\mathrm{c}-z_3)\\&\quad \times \left[ \left( 1-\frac{2C}{L(z_1+x_{1d})}\right) \frac{z_2}{z_1+x_{1d}}+\frac{R}{L}\right] +d\\&=f(z)+g(z)u+d, \end{aligned}$$

where f(z) and g(z) are given by

$$\begin{aligned}&f(z) = 2(g_\mathrm{c} - z_3)\left( 1- \frac{2C}{L(z_1 + x_{1d})}\right) \frac{z_2}{(z_1+x_{1d})} + \frac{R}{L},\nonumber \\&g(z) = \frac{-2}{L(z_1+x_{1d})} \sqrt{\frac{C}{m}(g_\mathrm{c} -z_3)}. \end{aligned}$$
(4)

Now, suppose that the disturbance d is added into the system. We consider the following nonlinear change of coordinates AL-Muthairi and Zribi (2004)

$$\begin{aligned} \dot{z_1}= & {} z_2, \nonumber \\ \dot{z_2}= & {} z_3,\\ \dot{z_3}= & {} f(z)+g(z)u+d, \nonumber \end{aligned}$$
(5)

Note that f(z) and g(z) correspond in the original coordinate to the following functions.

$$\begin{aligned} f_1(x)&= \frac{2C}{m}\frac{x_3^2}{x_1^2}\left( \left( 1-\frac{2C}{Lx_1}\right) \frac{x_2}{x_1}+\frac{R}{L}\right) \nonumber \\&= \frac{2C}{m}\left( \left( 1-\frac{2C}{Lx_1}\right) \frac{x_2x_3^2}{x_1^3}+\frac{R}{L}\frac{x_3^2}{x_1^2}\right) \\ g_1(x)&= -\frac{2Cx_3}{Lmx_1^2} \end{aligned}$$

where \(f_1(x)=f(z)\) and \(g_1(x)=g(z)\). Let the output of the system be defined as

$$\begin{aligned} y = z_1 = x_1 -x_{1d}. \end{aligned}$$
(6)

Note that the equilibrium point for the system (5) is \(z_1=z_2=z_3=0\).

The transformation is normally required to change the equilibrium point from \(x_d\) to the origin. The stability property of the transformed system is the same with the original system. This is the standard step to analysis the stability of a nonlinear system by using the Lyapunov stability theory.

The design of SMC schemes for the magnetic levitation system will be studied in the next sections.

We now present a basic lemma that we will use in the following sections.

Lemma 1

(Bhat and Berstein 2000) Consider the system

$$\begin{aligned} \dot{x}=F(x),\quad F(0)=0, \quad x \in R^n, \quad x(0)=x_0, \end{aligned}$$
(7)

where \(F:D \rightarrow R^n\) is continuous on an open neighborhood D of the origin \(x=0\). Suppose that there is a continuous function \(V(x) : D \rightarrow R\) defined on a neighborhood \(U \subset D\) of the origin such that the following conditions hold:

  1. 1.

    V(x) is positive definite on \(D \subset R^n ; \)

  2. 2.

    there exist real numbers \(k>0\) and \(\lambda \in (0,1)\), such that

$$\begin{aligned} \dot{V} (x) + k V^{\lambda } (x) \le 0 , \quad x \in U / \{0\}. \end{aligned}$$
(8)

Then, system (7) is locally finite-time stable. The settling time, depending on the initial state \(x(0) = x_0 \), satisfies

$$\begin{aligned} T(x_0) \le \frac{V(x_0)^{1-\lambda }}{k(1-\lambda )} \end{aligned}$$
(9)

for all \(x_0\) in some open neighborhood of the origin. If \( D=R^n \) and V(x) is also unbounded, system (7) is globally finite-time stable.

3 Design of a Sliding Mode Control

The design of a SMC scheme for the magnetic levitation system is presented in this section. The first step in designing an SMC scheme for the system is to design the sliding surface. Let the sliding surface s be

$$\begin{aligned} s= z_3+\lambda _1 z_2+\lambda _2 z_1 , \end{aligned}$$
(10)

where \(\lambda _1\) and \(\lambda _2\) are positive constants. The sliding mode controller is designed as

$$\begin{aligned} u =-\frac{1}{g(z)}(f(z)+\lambda _1 z_3+ \lambda _2 z_2+w\, \hbox {sign(s)} ), \end{aligned}$$
(11)

where sign\((\cdot )\) denotes the signum function and w is a positive constant.

For the original system (3), the sliding surface (10) and the controller (11), may be written as

$$\begin{aligned}&s=g_\mathrm{c}-\frac{C}{m}\left( \frac{x_3}{x_1}\right) ^2+\lambda _1x_2+\lambda _2x_1, \end{aligned}$$
(12)
$$\begin{aligned} u&=-\frac{1}{g_1(x)}\nonumber \\&\quad \times \left( f_1(x)+\lambda _1\left( g_\mathrm{c}- \frac{C}{m}\left( \frac{x_3}{x_1}\right) ^2\right) + \lambda _2 x_2+w \hbox {sign(s)} \right) , \end{aligned}$$
(13)

Assumption 2

The disturbance d in (5) is unknown but bounded, i.e., \(|d| \le D\) where D is a positive constant.

Theorem 3

If Assumption 2 is valid, then the system (5) converges to the origin in finite time under the feedback law (11) with the sliding surface (10).

Proof

Consider the following Lyapunov function

$$\begin{aligned} V_1=\frac{1}{2} s^2. \end{aligned}$$
(14)

By applying (5), (10) and (11), we get

$$\begin{aligned} \dot{V_1}= & {} s \dot{s}\nonumber \\= & {} s(\dot{z_3}+\lambda _1 \dot{z_2}+\lambda _2\dot{z_1}) \nonumber \\= & {} s(f(z)+g(z)u+d+\lambda _1 z_3+\lambda _2z_3+\lambda _2 z_2). \end{aligned}$$
(15)

Substituting (11) into (15), we obtain

$$\begin{aligned} \dot{V}_1= & {} s \left( f(z)+g(z)\left( -\frac{1}{g(z)}(f(z)+ \lambda _1 z_3+ \lambda _2 z_2\right. \right. \nonumber \\&\left. \left. +\,w \hbox {sign(s)}+d )\right) +\lambda _1 z_3+\lambda _2 z_3+\lambda _2 z_2 \right) \nonumber \\= & {} -s (w\,\hbox {sign(s)}-d)\nonumber \\= & {} -w|s| + d\,s\nonumber \\\le & {} -w|s| + D\, |s|\nonumber \\= & {} -(w-D)|s|. \end{aligned}$$
(16)

Letting \(\gamma = w-D\) and selecting \(w>D\), we obtain that \(\dot{V}_1\) is negative definite. Using (14), one has \(|s|=\sqrt{2V_1}\) and it follows that

$$\begin{aligned} \dot{V_1} \quad \le -\sqrt{2} \gamma V_1^{\frac{1}{2}} . \end{aligned}$$
(17)

By Lemma 1, the sliding surface \(s=0\) is achieved in finite time. Then the system trajectories move toward the sliding surface (10) to the origin in finite time. \(\square \)

4 Design of an Adaptive Sliding Mode Control

To relax the requirement of an upper bound on the uncertainties or disturbance, we design an adaptive SMC law for the system (5).

The proposed adaptive sliding mode controller is designed as

$$\begin{aligned} u =-\frac{1}{g(z)}(f(z)+\lambda _1 z_3+ \lambda _2 z_2+\hat{\varOmega }\, \hbox {sign(s)}), \end{aligned}$$
(18)

where \(\hat{\varOmega }\) is an adjustable gain and s is the sliding surface defined in (10).

For the original system (3), the controller (18) may be written as

$$\begin{aligned} u&=-\frac{1}{g_1(x)}\left( f_1(x)+\lambda _1 \left( g_\mathrm{c}-\frac{C}{m}\left( \frac{x_3}{x_1}\right) ^2\right) \right. \nonumber \\&\left. +\,\lambda _2 x_2+\hat{\varOmega } \hbox {sign(s)}\right) , \end{aligned}$$
(19)

Let the adaptive law be given as

$$\begin{aligned} \dot{\hat{\varOmega }} = \frac{1}{\alpha } |s|, \end{aligned}$$
(20)

where \(\hat{\varOmega }\) is the estimated value of \(\bar{\varOmega }\), and \(\alpha > 0\) is denoted as an adaptive gain. The compensated control with adaptive algorithm is designed as follows

$$\begin{aligned} v_s=-\hat{\varOmega }(t)\hbox {sign(s)}, \end{aligned}$$
(21)

and the estimation error is defined as

$$\begin{aligned} \tilde{\varOmega }(t) = \hat{\varOmega }(t)-\bar{\varOmega }. \end{aligned}$$
(22)

The adaptation speed of \(\hat{\varOmega }(t)\) can be tuned by \(\alpha \). Choosing a suitable adaptation gain \(\alpha \) can also effectively avoid a high level of control activity in the reaching phase. In the following, the validity of the compensated control is confirmed by using Lyapunov theory.

Theorem 4

Consider the sliding variable dynamics (10) and the control law (18) with the adaptive law (20); then, the gain \(\hat{\varOmega }(t)\) has an upper bound; that is, there exists a positive constant \(\varOmega _d\) so that

$$\begin{aligned} \hat{\varOmega }(t) \le \varOmega _d, \quad \forall t > 0. \end{aligned}$$
(23)

Proof

Choose a Lyapunov function cadidate as

$$\begin{aligned} V_2=\frac{1}{2}s^2+\frac{1}{2} \alpha \tilde{\varOmega }^2 . \end{aligned}$$
(24)

By taking the time derivative of \(V_2\) , one obtains

$$\begin{aligned} \dot{V_2}= & {} s\dot{s}+\alpha \tilde{\varOmega } \dot{\tilde{\varOmega }} \nonumber \\= & {} s(f(z)+g(z)u+d+\lambda _1 z_3+\lambda _2 z_2)+\alpha (\hat{\varOmega }-\bar{\varOmega })\frac{1}{\alpha }|s| \nonumber \\= & {} s\left( f(z)+g(z)\left( -\frac{1}{g(z)}(f(z)+\lambda _1 z_3+ \lambda _2 z_2\,+\right. \right. \nonumber \\&\left. \left. \hat{\varOmega } \hbox {sign(s)} \right) +d +\lambda _1 z_3+\lambda _2 z_2 \right) +\alpha (\hat{\varOmega }-\bar{\varOmega })\frac{1}{\alpha }|s|\nonumber \\= & {} -s\hat{\varOmega } \hbox {sign(s)}+s d + (\hat{\varOmega }-\bar{\varOmega }) |s|\nonumber \\\le & {} -\hat{\varOmega }|s| +sd+\hat{\varOmega }|s|-\bar{\varOmega }|s|\nonumber \\\le & {} |s||d|-\bar{\varOmega }|s| \quad \nonumber \\= & {} |s|(|d|-\bar{\varOmega }) \quad \le \quad 0. \end{aligned}$$
(25)

Using Lyapunov stability theory, the estimated gain \(\hat{\varOmega }\) is bounded, that is, there exists a positive constant \(\varOmega _d\) such that \(\hat{\varOmega } \le \varOmega _d\), \(\forall t > 0\) . This completes the proof. \(\square \)

Theorem 5

The system (5) converges to the origin in finite time under the feedback law (18) with the adaptive law (20) and the sliding surface (10) .

Proof

Consider the following Lyapunov function

$$\begin{aligned} V_3=\frac{1}{2}s^2+\frac{1}{2} \alpha _1 {(\hat{\varOmega }-\varOmega _d)}^2. \end{aligned}$$
(26)

By taking the time derivative of \(V_3\), one obtains

$$\begin{aligned} \dot{V_3}= & {} s\dot{s}+\alpha _1(\hat{\varOmega }-\varOmega _d)\dot{\hat{\varOmega }} \nonumber \\= & {} s(f(z)+g(z)u+d+\lambda _1 z_3+\lambda _2 z_2)\nonumber \\&+\,\alpha _1(\hat{\varOmega }-\varOmega _d)\frac{1}{\alpha }|s|. \end{aligned}$$
(27)

Substituting (18) into (27), one has

$$\begin{aligned} \dot{V}_3= & {} s(f(z)+g(z)\left( -\frac{1}{g(z)}\big (f(z)+\lambda _1 z_3+ \lambda _2 z_2 +\hat{\varOmega } \hbox {sign(s)}\big )\right) \nonumber \\&\left. +\,d+\lambda _1 z_3+\lambda _2 z_2\right) +\alpha _1(\hat{\varOmega }-\varOmega _d)\frac{1}{\alpha }|s|\nonumber \\= & {} s(-\hat{\varOmega }\hbox {sign(s)}+d+\frac{\alpha _1}{\alpha }|s|(\hat{\varOmega }-\varOmega _d) \nonumber \\\le & {} -|s|\hat{\varOmega }+|s|\bar{\varOmega }+\frac{\alpha _1}{\alpha }|s|(\hat{\varOmega }-\varOmega _d)\nonumber \\= & {} -\sqrt{2}(\hat{\varOmega }-\bar{\varOmega })\frac{|s|}{\sqrt{2}}+\sqrt{2}\frac{\alpha _1}{\alpha }|s |\frac{(\hat{\varOmega }-\varOmega _d)}{\sqrt{2}} \nonumber \\\le & {} -\sqrt{2}(\hat{\varOmega }-\bar{\varOmega })\frac{|s|}{\sqrt{2}}-\sqrt{2}\frac{\alpha _1}{\alpha }|s|\frac{|\hat{\varOmega }-\varOmega _d|}{\sqrt{2}} , \end{aligned}$$
(28)

Let \(\beta _1=\hat{\varOmega }-\bar{\varOmega }\) and \( \beta _2=\displaystyle \frac{\sqrt{\alpha _1}}{\alpha }|s|\). Therefore, (28) becomes

$$\begin{aligned} \dot{V_3}\le & {} -\min (\sqrt{2}\beta _1,\sqrt{2}\beta _2)\left( \frac{|s|}{\sqrt{2}}+\sqrt{\alpha _1}\frac{|\hat{\varOmega }-\varOmega _d|}{\sqrt{2}}\right) \nonumber \\\le & {} -\min (\sqrt{2}\beta _1,\sqrt{2}\beta _2)\sqrt{(\frac{|s|}{\sqrt{2}})^2+(\sqrt{\alpha _1}\frac{|\hat{\varOmega }-\varOmega _d|}{\sqrt{2}})^2} \nonumber \\= & {} - \beta V_3^{\frac{1}{2}}, \end{aligned}$$
(29)

where \(\beta = \min (\sqrt{2}\beta _1,\sqrt{2}\beta _2)\). Therefore, by Lemma 1, the sliding surface \(s=0\) is achieved in finite time.

5 Design of an Adaptive Fast Terminal Sliding Mode Control

In this section, we design a fast terminal sliding mode control which does not require upper bounds on the uncertainties or disturbance (5).

Let the new sliding surface be Wu et al. (2014)

$$\begin{aligned} \sigma = \dot{S}+k_1 S^{\frac{a}{b}}+k_2 S, \end{aligned}$$
(30)

where a, b are positive odd numbers with \(b > a\) and

$$\begin{aligned} S=z_2+\lambda _1 z_1+\lambda _2 \int z_1 \mathrm{d}t. \end{aligned}$$
(31)

The proposed adaptive fast terminal sliding mode control is

$$\begin{aligned} u= & {} - \frac{1}{g(z)}\left[ f(z)+\lambda _1 z_3+\lambda _2 z_2 +k_1 \frac{a}{b} S^{\frac{a}{b}-1} \dot{S}+k_2 \dot{S}\right. \nonumber \\&\left. +\,\hat{\mu } \sigma + \hat{\lambda } \mathrm {sign}({\upsigma })\right] , \end{aligned}$$
(32)

where \(\hat{\mu }\) and \(\hat{\lambda }\) are adjustable gain constants and s is the sliding surface design in (30). For the original system (3), system (31) and the controller (32) may be written as

$$\begin{aligned} S&=x_2+\lambda _1( x_1+x_{1d})+\lambda _2 \int ( x_1+x_{1d}) \mathrm{d}t,\end{aligned}$$
(33)
$$\begin{aligned} u&= - \frac{1}{g_1(x)}\left[ f_1(x)+\lambda _1 \left( g_c-\frac{C}{m}\left( \frac{x_3}{x_1}\right) ^2\right) \right. \nonumber \\&\left. \quad +\,\lambda _2 x_2 +k_1 \frac{a}{b} S^{\frac{a}{b}-1} \dot{S}+k_2 \dot{S}+\hat{\mu } \sigma + \hat{\lambda } \mathrm {sign}({\upsigma }) \right] . \end{aligned}$$
(34)

In most cases of control design, controller gains remain constant, and they have been selected by using the conservative approach. But, in an uncertain environment, upper bounds are not known very precisely. Thus, the constant gain approach may apply excessive gain which may be a reason for chattering in control input.

Therefore, we consider adaptive laws \(\hat{\mu }(t)\) and \(\hat{\lambda }(t)\) defined as follows:

$$\begin{aligned} \dot{\hat{\mu }}= \left\{ \begin{array}{ll} \displaystyle \frac{1}{\rho }\sigma ^2, &{}\quad \hbox {if}\quad |\sigma | \ge \Delta \\ \Delta , &{}\quad \hbox {if}\quad |\sigma | <\Delta \\ \end{array}\right. \end{aligned}$$
(35)
$$\begin{aligned} \dot{\hat{\lambda }}= \left\{ \begin{array}{ll} \displaystyle \frac{1}{\eta } |\sigma |, &{}\quad \hbox {if}\quad |\sigma | \ge \Delta \\ \Delta , &{}\quad \hbox {if}\quad |\sigma | <\Delta \\ \end{array}\right. \end{aligned}$$
(36)

and where the estimation error is defined as

$$\begin{aligned} \bar{\mu }(t) =\hat{\mu }(t) -\mu \end{aligned}$$
(37)
$$\begin{aligned} \bar{\lambda }(t) =\hat{\lambda }(t) -\lambda . \end{aligned}$$
(38)

Here \( \hat{\mu }\) and \(\hat{\lambda }\) are the estimates of \(\mu \) and \(\lambda \), respectively, \(\rho \) and \(\eta \) are the adaptation parameters used to control the adaptation speed and \(\Delta \) is a design constant used to avoid unbounded growth of the adaptive gain.

Theorem 6

Consider the sliding surface (30) and the control law (32) with adaptive gains (35) and (36); then, the gains \(\hat{\mu }(t)\) and \(\hat{\lambda }(t)\) have upper bounds; that is, there exist positive constants \(\mu \) and \(\lambda \) such that

$$\begin{aligned} \hat{\mu }(t) \le \mu ,\quad \forall \ t > 0. \end{aligned}$$
(39)
$$\begin{aligned} \hat{\lambda }(t) \le \lambda ,\quad \forall \ t > 0. \end{aligned}$$
(40)

Proof

Choose a Lyapunov function candidate as

$$\begin{aligned} V_4=\frac{1}{2} \sigma ^2 +\frac{1}{2} \rho \bar{\mu }^2 +\frac{1}{2} \eta \bar{\lambda }^2 \end{aligned}$$
(41)

By taking the time derivative of \(V_4\), one obtains

$$\begin{aligned} \dot{V_4}= & {} \sigma \dot{\sigma }+\rho \bar{\mu }\dot{\hat{\mu }} + \eta \bar{\lambda }\dot{\hat{\lambda }}\nonumber \\= & {} \sigma \left( f(z)+g(z)u+d+\lambda _1z_3+\lambda _2 z_2 +k_1\frac{a}{b} S^{\frac{a}{b}-1}\dot{S}\right. \nonumber \\&\quad \left. +\,k_2\dot{\sigma }+\hat{\mu } \sigma \right) +\rho \bar{\mu }\frac{1}{\rho }s^2 + \eta \bar{\lambda }\frac{1}{\eta }|s|\nonumber \\= & {} \sigma \left( f(z)+g(z)\left( - \frac{1}{g(z)}\left[ f(z)+\lambda _1 z_3+\lambda _2 z_2 \right. \right. \right. \nonumber \\&\left. + \left. \left. k_1 \frac{a}{b} S^{\frac{a}{b}-1} \dot{S}+k_2 \dot{S} +\hat{\mu } \sigma + \hat{\lambda } \mathrm {sign(\sigma )}\right] \right) +d+\lambda _1z_3\right. \nonumber \\&\left. +\,\lambda _2 z_2 +k_1\frac{a}{b} S^{\frac{a}{b}-1}\dot{S}+k_2\dot{\sigma }+\hat{\mu } \sigma \right) \nonumber \\&+\,\rho \bar{\mu }\frac{1}{\rho }s^2 + \eta \bar{\lambda }\frac{1}{\eta }|s|\nonumber \\\le & {} -\,\hat{\mu }\sigma ^2-\hat{\lambda }|\sigma |+\bar{\mu }\sigma ^2+\bar{\lambda }|\sigma |+d |\sigma |\nonumber \\= & {} -\,\hat{\mu }\sigma ^2-\hat{\lambda }|\sigma |+(\hat{\mu }-\mu )\sigma ^2+(\hat{\lambda }-\lambda )|\sigma |+d |\sigma |. \nonumber \end{aligned}$$

Since \(\mu > 0\) and \(\lambda > 0\), the above equation can be rewritten as

$$\begin{aligned} \dot{V}_4 =-\mu \sigma ^2 -\lambda |\sigma | +d |\sigma |=-\mu \sigma ^2 -|\sigma |(\lambda -d) \le 0.\nonumber \\ \end{aligned}$$
(42)

\(\square \)

Clearly \(\dot{V_4} < 0 \) when \(\sigma \ne 0\) and \(\lambda > d\). Using Lyapunov stability theory, the estimated gain \(\hat{\mu }\) and \(\hat{\lambda }\) are bounded; that is, there exists a positive constant \(\mu \) and \(\lambda \) such that \(\hat{\mu } \le \mu \) and \(\hat{\lambda } \le \lambda ,\forall t > 0\). This completes the proof.

Theorem 7

The system (5) converges to the origin in finite time under the feedback law (32) and adaptive gains defined in (35), (36) and the sliding surface (30).

Proof

Consider the Lyapunov function

$$\begin{aligned} V_5=\frac{1}{2} \sigma ^2 +\frac{1}{2} \omega _1 \bar{\mu }^2 +\frac{1}{2}\omega _2 \bar{\lambda }^2, \end{aligned}$$
(43)

where \(\bar{\mu }=\hat{\mu }(t) - \mu \) and \(\bar{\lambda }=\hat{\lambda }(t) - \lambda \) represent the adaptation errors, \(\alpha _1 > 0 , \alpha _2>0\) and \(\omega _1, \omega _2\) are positive constants.

Now, finding the first time derivative of the Lyapunov function, one obtains

$$\begin{aligned} \dot{V_5}= \sigma \dot{\sigma }+\omega _1 \bar{\mu }\dot{\hat{\mu }}+\omega _2 \bar{\lambda }\dot{\hat{\lambda }} \end{aligned}$$
(44)

By applying (5) ,(10), (32), (39) and (40), we get

$$\begin{aligned} \dot{V_5}- & {} \sigma \Big (f(z)+g(z)u+d+\lambda _1z_3+\lambda _2 z_2 +k_1\frac{a}{b} S^{\frac{a}{b}-1}\dot{S}+k_2\dot{S}\Big ) \nonumber \\&\quad +\,\frac{\omega _1}{\rho }\sigma ^2 (\hat{\mu }-\mu )+\frac{\omega _2}{\eta }|\sigma | (\hat{\lambda }-\lambda )\nonumber \\= & {} \sigma \left( f(z)+g(z)\left( - \frac{1}{g(z)}\left[ f(z)+\lambda _1 z_3+\lambda _2 z_2 +k_1 \frac{a}{b} S^{\frac{a}{b}-1} \dot{S}\right. \right. \right. \nonumber \\&\quad \left. \left. +\,k_2 \dot{S} + \hat{\lambda } \mathrm {sign(\sigma )} \right] \right) +d+\lambda _1z_3+\lambda _2 z_2 +k_1\frac{a}{b} S^{\frac{a}{b}-1}\dot{S}\nonumber \\&\left. +\,\,k_2\dot{S} +\frac{\omega _1}{\rho }\sigma ^2 (\hat{\mu }-\mu )+\frac{\omega _2}{\eta }|\sigma | (\hat{\lambda }-\lambda )\right) \nonumber \\= & {} -\,\hat{\mu }\sigma ^2-\hat{\lambda }\sigma \mathrm {sign(\sigma )}+\sigma d+\frac{\omega _1}{\rho }\sigma ^2 (\hat{\mu }-\mu )+\frac{\omega _2}{\eta }|\sigma | (\hat{\lambda }-\lambda ))\nonumber \\\le & {} -\,\hat{\mu }\sigma ^2-\hat{\lambda }|\sigma |+|\sigma | d+\frac{\omega _1}{\rho }\sigma ^2 (\hat{\mu }-\mu )+\frac{\omega _2}{\eta }|\sigma | (\hat{\lambda }-\lambda ) \end{aligned}$$
(45)
Table 1 Control parameters and initial conditions
Full size table

With \(\mu >0\), we add \(\mu \sigma ^2\) to the right hand side of (45). Now, we obtain

$$\begin{aligned} \dot{V_5}\le & {} \frac{\omega _1}{\rho }\sigma ^2 (\hat{\mu }-\mu )+\frac{\omega _2}{\eta }|\sigma | (\hat{\lambda }-\lambda ) -\lambda |\sigma |+\lambda |\sigma | +\mu \sigma ^2 \nonumber \\&-\,\hat{\mu }\sigma ^2-\hat{\lambda }|\sigma |+|\sigma | d \nonumber \\= & {} \frac{\omega _1}{\rho }\sigma ^2 (\hat{\mu }-\mu )+\frac{\omega _2}{\eta }|\sigma |(\hat{\lambda }-\lambda )-|\sigma |(\hat{\lambda }-\lambda )\nonumber \\&-\,\sigma ^2(\hat{\mu }-\mu )-|\sigma |\lambda +|\sigma | d\nonumber \\\le & {} -( \lambda -d) |\sigma |+ \bar{\mu }(\frac{\omega _1}{\rho }\sigma ^2-\sigma ^2)+\bar{\lambda }(\frac{\omega _2}{\eta } |\sigma |-|\sigma |)\nonumber \end{aligned}$$

Using Theorem 6, we have \(\bar{\mu }<0\) and \(\bar{\lambda }<0\) and it follows that

$$\begin{aligned} \dot{V_5}\le & {} -( \lambda -d) |\sigma | - |\bar{\mu }|(\frac{\omega _1}{\rho }\sigma ^2-\sigma ^2)-|\bar{\lambda }|(\frac{\omega _2}{\eta } |s|-|s|)\nonumber \\\le & {} -|\sigma |\zeta _1 - |\bar{\mu }|\zeta _2-|\bar{\lambda }|\zeta _3\nonumber \\\le & {} -\sqrt{2}\frac{|\sigma |}{\sqrt{2}}\zeta _1 - \sqrt{2 \omega _1}|\bar{\mu }|\frac{\zeta _2}{\sqrt{2 \omega _1}}-\sqrt{2 \omega _2}|\bar{\lambda }|\frac{\zeta _3}{\sqrt{2 \omega _2}},\nonumber \\ \end{aligned}$$
(46)

where \(\zeta _1=\lambda -d\), \(\zeta _2 =\displaystyle \frac{\omega _1}{\rho }\sigma ^2-\sigma ^2\) and \(\zeta _3 =\displaystyle \frac{\omega _2}{\eta } |\sigma |-|\sigma |\). Therefore, (46) becomes

$$\begin{aligned} \dot{V_5}\le & {} -\min \left( \sqrt{2}\zeta _1, \sqrt{\frac{2}{\omega _1}}\zeta _2, \sqrt{\frac{2}{\omega _2}}\zeta _3)(\frac{|\sigma |}{\sqrt{2}}+\sqrt{\frac{\omega _1}{2}}|\bar{\mu }|\right. \nonumber \\&\left. +\sqrt{\frac{\omega _2}{2}}|\bar{\lambda }|\right) \le -\zeta V_5^{\frac{1}{2}} \end{aligned}$$
(47)

where \(\zeta =\min \left( \sqrt{2}\zeta _1, \sqrt{\frac{2}{\omega _1}}\zeta _2, \sqrt{\frac{2}{\omega _2}}\zeta _3\right) >0 \), for \(\displaystyle \frac{1}{\omega _1} <\displaystyle \frac{1}{\rho }\) and \(\displaystyle \frac{1}{\omega _2} < \displaystyle \frac{1}{\eta }\). Therefore, by using Lemma 1, we have proved that \(\sigma (t)=0\) is achieved in finite time.

Fig. 1
figure 1

Time histories of positions

Full size image

6 Simulation Result

The parameters of the magnetic levitation system are taken from AL-Muthairi and Zribi (2004). The coil’s resistance \(R=28.7 \,\Omega \), the inductance \(L_1=0.65\,\)H, the gravitational constant \(g_\mathrm{c}=9.81\) m s\(^{-2}\), the magnetic force constant \(C=1.410\times 10^{-4}\) and the mass of the ball \(m=11.87\) g. Numerical simulations are performed to compare the ASMC (18) and AFTSMC (32) with the dynamic sliding mode (DSM) control presented in AL-Muthairi and Zribi (2004).The method in AL-Muthairi and Zribi (2004) seems to work well of the magnetic levitation system, so we choose this method to compare the performance with our proposed control laws. In the simulations, the disturbance d in (5) is set as \(d = 0.2\mathrm{sin}(0.2t)\) V. The control parameters and initial conditions for all controllers are given in Table 1.

Fig. 2
figure 2

Time histories of velocities

Full size image
Fig. 3
figure 3

Time histories of sliding surface

Full size image
Fig. 4
figure 4

Time histories of control responses

Full size image

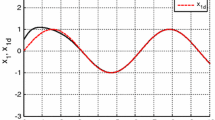
As shown in Fig. 1, for AFTSMC the trajectory of position converges to the desired position (\(x_{1d}=0.009\) m.) in finite time, while for ASMC and DSMC, position states are forced to the desired position with lower accuracy. Similarly, from Fig. 2 we can see that the trajectory of velocity obtained by AFTSMC converges to zero with higher accuracy than either ASMC or DSMC. Figure 3 shows that AFTSMC gives fast convergence to the sliding surface in finite time. For DSMC, the sliding surface \(s=0\) is achieved but more slowly and with a large error. ASMC gives a lower accuracy of the sliding state and reaches it more slowly than AFTSMC. As shown in Fig. 4 the control response obtained by AFTSMC is smooth and properly reaches zero. In view of this simulation, AFTSMC gives better results when compared with ASMC and DSMC.

7 Conclusion

New AFTSM and ASM controllers have been developed for the control of a magnetic levitation system. It is found that the combination of an adaptive control method and FTSMC gives good tracking results and achieves fast convergence to the sliding surface. Using Lyapunov stability theory, we have proved that the new controllers drive the states of a magnetic levitation system to desired values in finite time. Numerical simulations have been presented to demonstrate the effectiveness of the proposed control methods.