A Coupled Model to Multistage Transmission Expansion Planning

Abstract

This paper proposes a new approach to solving the multistage transmission line expansion planning problem. The proposed formulation incorporates decisions about where and when reinforcements should be placed to fit the desired demand. To accomplish that a expansion decision variable (ED) is incorporated into an integer, coupled and extended DC optimum power flow (I-COPF). The proposed I-COPF problem can be solved by using any commercial software for integer programming, but to reduce the computational complexity of this integer problem, a new heuristic method is presented. So, the integer problem is broken by adopting two steps: (i) the I-COPF is transformed into a continuous problem (C-COPF) by using a ED as continuous variable. This step provides a set of ED and the Lagrange multipliers for all planning period. The step (ii) uses the response provided by (i) to determine the optimal reinforcement set. These two steps are solved interactively during the planning horizon. To demonstrate the effectiveness of the proposed methodology, the results of three systems will be compared with a numerical-based approach provided by a commercial software and other academic researches.

1 Introduction

The static transmission system expansion planning (S-TSEP) consists of determining, among all possibilities, whatever set of reinforcements is able to attend a given demand considering all technical criteria with minimum investment cost. In this type of analysis, each studied reinforcement set presents constraints such as reactive and active power flows, multiareas power interchange and voltage limitations. These characteristics make S-TSEP a very complex process that deals with continuous and integer variables, which is classified as a nonlinear mixed-integer programming. The S-TSEP defines only the optimal locations and type of investments.

Combinatorial methods are able to deal with several variables producing interesting results; however, the computational time still remains an issue. Moreover, although nonlinear optimization methods have shown high computational efficiency, they are not suitable to deal with high-scale discrete systems.

There are four major groups of algorithms that have been proposed in the literature to solve mixed-integer programming with electrical power applications. They are based on: (i) nonlinear programming (Wu et al. 1994; ii) combinatorial (Gil and Da Silva 2001; Binato et al. 2001; iii) heuristic (deOliveira et al. 2005; Bustamante-Cedeño and Arora 2009; da Silva et al. 2008); and (iv) evolutionary methods (Leite da Silva et al. 2011; de la Torre et al. 2008).

If the chronological placement is taken into account, the problem will be even more complex and it will become a multistage transmission system expansion planning (Ms-TSEP). The mathematical model for this optimization problem is NP-hard, and the convergence time suits a polynomial function in which parameters are the number of years considered in the planning horizon and the number of reinforcements. This means that Ms-TSEP is a large-scale combinatorial problem and the number of options associated with local minimum solutions increases exponentially along with the size of the input parameters.

References (Leite da Silva et al. 2011) and (da Rocha and Saraiva 2011) studied multistage expansion planning using meta-heuristics. Reference (da Rocha and João Tomé Saraiva 2012) shows the application of evolutionary particle swarm optimization to deal with multiperiod planning as well as (da Rocha and João Tomé Saraiva 2013). Reference (Hinojosa et al. 2013) proposed a constructive heuristic model based on a local controlled random search to mitigate the complexity of the multistage problem.

Analysing nonlinear programming, they produce results in very short computational time, but they are not able to directly solve mixed-integer programming. For that, it is necessary to treat discrete variables as continuous ones and, at the end of the optimization process, round them off to their nearest discrete values (Liu et al. 2002). However, this strategy does not provide good results, so the constructive heuristic algorithms have been used to increase the quality of solutions as shown in references (deOliveira et al. 2005) and (Hinojosa et al. 2013).

Finally, evolutionary and combinatorial-search approaches are commonly used to solve mixed-integer programming models, but as stated before, the problem is NP-hard and these methods respond to the Ms-TSEP in polynomial time, indicating that they all suffer from the dimension of large-scale applications.

To solve the Ms-TSEP, this paper presents a new approach that treats the temporal reinforcements decision by a coupled DC optimal power flow that comprises all periods of the planning horizon. In addition, for reducing the computational effort, this work presents an constructive algorithm composed of a continuous and an integer steps that are linked by an iterative process using appropriate sensitivity indexes to decide where and when the reinforcements should be placed. Therefore, the main contributions of this paper are a new coupled model for the multistage expansion planning associated with a suitable constructive heuristic algorithm to solve this NP-hard problem. The proposed methodology is applied to a tutorial case and other two well-known test systems.

2 Proposed Formulation

Traditionally, the S-TSEP is modelled using the linear DC power flow formulation technique, in which the voltage and stability constraints are represented via active power flow limits. In this approach, the active power flow $(f_{ij})$ in a given line $i-j$ is expressed by (1):

$$\begin{aligned} f_{ij} = \gamma _{ij} \cdot \theta _{ij} \end{aligned}$$

(1)

where $\gamma _{ij}$ is the susceptance of branch $i-j$ and $\theta _{ij}$ is the angular difference between busbars $i-j$. The decision to include or not a candidate transmission line to be constructed requires the modification of equation (1) leading to (2) as shown in reference (deOliveira et al. 2005):

$$\begin{aligned} fC_{ij} = \mathrm{ED}_{ij} \cdot \left( \gamma _{ij} \cdot \theta _{ij} \right) \end{aligned}$$

(2)

where $fC_{ij}$ represents the active power flow in candidate branch $i-j$ and $(\mathrm{ED}_{ij})$ is an integer variable (1 or 0) which represents the decision of constructing or not the transmission line $i-j$.

The proposed extend DC power flow equations include the year when the transmission line will be built as well as the active power losses, as shown in Eq. (3):

$$\begin{aligned} fC_{ij}^{y} = \mathrm{ED}_{ij}^{y} \cdot f_{ij}^{y} \end{aligned}$$

(3)

where:

$$\begin{aligned} f_{ij}^{y} = \left( \gamma _{ij} \cdot \theta _{ij}^{y} + \dfrac{1}{2} \cdot g_{ij} \cdot \left( \theta _{ij}^{y}\right) ^2 \right) \end{aligned}$$

The parameter $g_{ij}$ is the conductance of line $i-j$ and $y$ represents each year in the transmission planning horizon. In this formulation, the variable $\mathrm{ED}_{ij}^{y}$ is an integer (1 or 0) that couples the decisions among the years of the planning period. For an already existing transmission line, the active power flow is given only by $(f^{y}_{ij})$.

The integer, coupled and extended DC optimum power flow (I-COPF) problem for the multistage transmission planning can be formulated using Eq. (3) as follow:

$$\begin{aligned}&\mathrm{Min} \sum _{y=0}^{ny} \left( \sum _{n=1}^{ng} Gc_{n}^{y} \cdot \mathrm{PG}_{n}^{y} + \sum _{(i,j) \in C} Ic_{ij}^{y} \cdot \mathrm{ED}_{ij}^{y}\right) \end{aligned}$$

(4a)

$$\begin{aligned}&\textit{Subject to:} \nonumber \\&\quad y=0:\mathrm{PG}_{i}^{0} - \sum _{j \in \Omega _{E_i}} fE_{ij}^{0} - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{0} \cdot f_{ij}^{0} = D^0_i \end{aligned}$$

(4b)

$$\begin{aligned}&y=1:\mathrm{PG}_{i}^{1} - \sum _{j \in \Omega _{E_i}} fE_{ij}^{1} - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{0} \cdot f_{ij}^{1} \nonumber \\&\qquad \qquad - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{1} \cdot f_{ij}^{1} = D^1_i \end{aligned}$$

(4c)

$$\begin{aligned}&y=2:\mathrm{PG}_{i}^{2} - \sum _{j \in \Omega _{E_i}} fE_{ij}^{2} - \sum _{j \in \Omega _{C_i}} ED_{ij}^{0} \cdot f_{ij}^{2} \nonumber \\&\quad \quad - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{1} \cdot f_{ij}^{2} - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{2} \cdot f_{ij}^{2}= D^2_i \end{aligned}$$

(4d)

$$\begin{aligned}&y=ny:\mathrm{PG}_{i}^{ny} - \sum _{j \in \Omega _{E_i}} fE_{ij}^{ny} - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{0} \cdot f_{ij}^{ny} - \nonumber \\&\quad \quad - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{1} \cdot f_{ij}^{ny} ... - \sum _{j \in \Omega _{C_i}} \mathrm{ED}_{ij}^{ny} \cdot f_{ij}^{ny} = D^{ny}_i \end{aligned}$$

(4e)

$$\begin{aligned}&i=1, 2, 3,\ldots , nb \nonumber \\&|f_{ij}|\le \overline{f}_{ij}, \forall (i,j) \in {\mathbb {E}}, {\mathbb {C}} \end{aligned}$$

(4f)

$$\begin{aligned}&\underline{\mathrm{PG}}_{i}^{y} \le \mathrm{PG}_{i}^{y} \le \overline{\mathrm{PG}}_{i}^{y} \end{aligned}$$

(4g)

$$\begin{aligned}&\mathrm{ED}_{ij}^{y} \in \mathbf I | \mathrm{ED}_{ij}^{y} = [0, 1], \forall (i,j) \in {\mathbb {C}} \end{aligned}$$

(4h)

$$\begin{aligned}&Ic_{ij}^{y}=\frac{Ic_{ij}^{0}}{(1+r)^{y-y_0}},\forall (i,j) \in {\mathbb {C}} \end{aligned}$$

(4i)

where:

${\mathbb {E}}$ :

set of existing branches of the network;

${\mathbb {C}}$ :

set of transmission lines that are candidates to expansion;

$Ic_{ij}^{y}$ :

investment cost of the transmission line $i-j$ at year $y$ (US$);

$Ic_{ij}^{0}$ :

unit investment cost for the reinforcements in branch $i-j$ (US$);

$r$ :

discount rate. In this paper, the cost is reduced in $10\%$ per year as adopted in reference (Leite da Silva et al. 2011);

$y-y_0$ :

numerical difference between the year stage y and the first base year $y_0$;

$n_g$ :

number of active power generations in the system;

$n_b$ :

number of busbars in the system;

$ny$ :

last year of the transmission planning;

${PG}_{i}^y$ :

active power generation at busbar $i$ at year $y$ (MW);

${Gc}_{i}^y$ :

generation cost of unit $i$ at year $y$ (US$/MWh-year);

$\underline{PG}^y_i$ :

inferior limit of $PG_i$ at year $y$;

$\overline{PG}^y_i$ :

superior limit of $PG_i$ at year $y$;

$D^{ny}_i$ :

demand at bus i at year y. In this paper $D^{ny}_i$ increases linearly per year;

$fE_{ij}^{y}$ :

active power flow for the existing line $i-j$ at year $y$;

$fC_{ij}^{y}$ :

active power flow for the candidate line $i-j$ at year $y$;

$\overline{f}_{ij}$ :

active power flow limit of existing or candidate transmission line $i-j$;

$\Omega _{E_i}$ :

set of existing transmission lines connected with bus $i$;

$\Omega _{C_i}$ :

set of candidate transmission lines connected with bus $i$;

The first term of the objective function (4a) represents operational costs of the generation plants, and the second term represents the investment costs in power system transmission line for all years of the planning horizon. Equations from (4b) to (4e) correspond to the extended expressions of the DC power flow. In the proposed model, all the transmission lines that are candidates to expansion are included in the network structure during the I-COPF solution process. These equations are coupled by the expansion decision variable $(\mathrm{ED}_{ij}^{y})$. This formulation comprises all years of planning in a unique I-COPF problem.

The constraints (4f) are related to the active power flow limits of both the existing and candidates transmission lines. The expression (4g) represents the lower and upper limits of the active power generation variables. The constraints (4h) represent the integer expansion variables. Equation (4i) represents the annualized investment cost of the candidate transmission lines.

The proposed multistage transmission planning increases the computational complexity by enlarging the network orders necessary to represent all the expansion period in an unique I-COPF problem. For example, suppose a two-bar system shown in Fig.  (1) composed by one existing line and one candidate line for expansion in year 0 or year 1 or year 2 to suit a load that increases every year of the planning. In this case, there are three expansion decision variables $(\mathrm{ED}_{ij}^{0}, \mathrm{ED}_{ij}^{1} \text{ and } \mathrm{ED}_{ij}^{2})$ to represent this candidate line in the I-COPF problem. In general, there are $(ny)$ expansion decision variables $(\mathrm{ED}_{ij}^{y})$ for each candidate transmission line.

Fig. 1

Two-bar system

Equations. (4b), (4c) and (4d) represent the coupled expansion network associated with the two-bar system shown in Fig.  (1). It can be observed that the decision to build or not to build the line in year 0 $(\mathrm{ED}_{ij}^{0}=1 \hbox {or} 0)$ is engaged in the subsequent years 1 and 2 through Eqs. (4c) and (4d), respectively. Then, $(ED_{ij}^{1})$ is engaged in the year 2 through equation (4d) and so on. Thus, the solution of unique I-COPF problem brings the lower cost of investment in a long-term vision.

Additionally, I-COPF is also a nonlinear and mixed-integer optimization problem. Any appropriate toolbox from existing optimization packages could be used to solve the proposed approach. However, these toolboxes are highly time-consuming for this class of problem and, therefore, not suitable to solve large systems. On the other hand, this paper proposes a specialized multistage transmission planning algorithm (Ms-TPA) to increase computational efficiency.

3 The Proposed Ms-TPA Design

This section describes a specialized algorithm based on continuous and discrete steps to determine, iteratively, the optimal reinforcements during the planning horizon. This heuristic algorithm adopts a search process close to work (deOliveira et al. 2005) and (de Oliveira et al. 2014) that also use sensitivity indexes associated with a step-by-step process to mitigate the integer variables. The advantage of these algorithms is that they have found high-quality solutions spending low computational effort. These solutions can even be used as initial generation into a meta-heuristic process, as shown in (de Mendonça et al. 2014).

The integer formulation (4h) is converted to continuous one by using the ED variables ranging from 0 to 1, resulting in a continuous coupled optimal power flow (C-COPF) instead of I-COPF. As consequence, the NP-hard optimization problem and computational time explosion are eliminated in C-COPF problem. Then, C-COPF can be solved many times with low computational effort.

It can be emphasized that C-COPF can be solved by using many optimization packages. In this paper, the continuous coupled optimal power flow is solved by using nonlinear continuous optimization toolbox from LINGO package (Copyright $\copyright$ LINDO SYSTEMS INC.).

Although the continuous results cannot be used directly in a expansion decision, these information can be just used to indicate the direction of the optimum solution. The main information provided from C-COPF solution is related to the presence or not of a reinforcement in a given year. The value of $(\mathrm{ED}_{ij}^{y})$ will select the most attractive reinforcements considering all years of the planning horizon. Therefore, the $ED_{ij}^{y}$ could be considered as a sensitivity index used to indicate good transmission investments. Equation (5) shows this index evaluation.

$$\begin{aligned} ID1_{ij}^y = \mathrm{ED}_{ij}^y, \forall (i,j) \in {\mathbb {C}} \end{aligned}$$

(5)

Another index to enhance the best choice for possible reinforcements uses the sensitivities related to the Lagrangian multipliers (LM). The LM are given by the solution of C-COPF and provide the marginal costs of a constraint regarding the objective function. In this case, the LM represent the sensitivity of the objective function to active power flow in the branches and it can be used to indicate interesting places to reinforce the system. Thus, the second index presented in Eq. (6) evaluates the sensitivity, normalized by the financial costs, of constructing the transmission line.

$$\begin{aligned} ID2_{ij}^y = \frac{\lambda _i^y - \lambda _j^y}{Ic_{ij}^y} \end{aligned}$$

(6)

where $\lambda _{i}^y$ and $\lambda _{j}^y$ are the Lagrange multipliers associated with the extended DC power flow constraint for buses $i$ and $j$ (line $i-j$), respectively, for year $y$.

It is important to emphasize that both indexes incorporate the impact in the long-term decisions because they are calculated using a coupled problem. This feature of these indexes results in an efficient search process.

The flowchart of the proposed Ms-TPA is shown in Fig.  (2). The following comments help to explain the proposed algorithm:

Fig. 2

Flowchart of multistage transmission planning algorithm (Ms-TPA)

• Step-1: The algorithm sets the candidate transmission lines ${\mathbb {C}}$ to be constructed from a user-defined data file. In addition, ${\mathbb {RE}}^{y}$ represents a set of reinforcements at each year of the planning horizon that starts empty.

• Step-2: In this step, the continuous coupled optimal power flow (C-COPF) is solved by using a nonlinear continuous optimization toolbox. The results for all years are: $\mathrm{ED}_{ij}^y$ for all (i,j) in ${\mathbb {C}}$ and $\lambda _{i}^y$ for all buses of the system. The sensitivity indexes are computed by Eqs. (5) and (6).

• Step-3: Using the values of $\mathrm{ED}_{ij}^y$, it is possible to determine at which year the reinforcements should be available. For example, consider that all $\mathrm{ED}_{ij}^0$ and $\mathrm{ED}_{ij}^1$ are equal to zero. Then, years $y=0$ and $y=1$ do not require reinforcements due to the fact that the existing transmission lines are able to operate the system. On the other hand, if at least one $\mathrm{ED}_{ij}^1$ is greater than zero, year $y\!=\!1$ will need reinforcements thus $y_f$ will be equal to 1.

• Step-4: This step analyses the year $y_f$ that needs reinforcements. For that, it constructs a dynamic ordered list for year $y_{f}\,({\mathbb {DOL}}^{y_f})$ based on both sensitivity indexes $ID1_{ij}^{y_f}$ and $ID2_{ij}^{y_f}$. The two greatest elements of each index indicate the transmission line candidates to compose the list $({\mathbb {DOL}}^{y_f})$. Then, the elements of ${\mathbb {DOL}}^{y_f}$ are sorted in ascending order regarding the investment costs $Ic_{ij}^{0}$ of its respective transmission line. If two or more elements of ${\mathbb {DOL}}^{y_f}$ have the same cost, the decision is accounted by the descending order of ED. In addition, in this step the number of $C-COPF$ simulations is initialized equal to 0 $(N^{yf}=0)$.

• Step-5: The first element of ${\mathbb {DOL}}^{y_f}$ represents the lowest investment, and it is always chosen to be tested as an option. This is done by making the corresponding $\mathrm{ED}_{ij}^{y_f}$ equal to one in the $C-COPF$ formulation. Considering, for example, ${\mathbb {DOL}}^{y_f}=\{TL_1, TL_5, TL_2, TL_9\}$ leads to $\mathrm{ED}_{LT_1}^{y_f}=1$.

• Step-6: Solve $C-COPF$ considering the choice of reinforcement suggested in the previous step and increments $N^{y_f}$. Because first element of ${\mathbb {DOL}}^{y_f}$ was done equal to one, this step provides a new values of $\mathrm{ED}_{ij}^y$, $ID1_{ij}^y$ and $ID2_{ij}^y$ for all years. Two cases may occur as described in the next step.

• Step-7: Case (i), if all values of $ED_{ij}^{y_f}$ (at year $y_f$) become zero or one, it means that the suggested reinforcements are enough for the year $y_f$. So these reinforcements will be stored in ${\mathbb {RE}}^{y_f}$ through Step-9, and the first element of ${\mathbb {DOL}}^{y_f}$ remains equal to one for the rest of the process as well as the existing transmission line. The next year will be analysed until the last year $(n_y)$ is achieved as checked in Step-10. If $y_f$ is equal to $n_y$, the Step-11 will indicate the final transmission expansion planning and the process will end.

• Step-7: Case (ii), in this case at least one $\mathrm{ED}_{ij}^{y_f}$ is greater than zero and less than one, which means that the reinforcement proposed in the Step-5 is not enough for the year $y_f$. Then, a new reinforcement option should be investigated for year $y_f$. This is done in Step-8 described next.

• Step-8: This step is responsible for increasing the ${\mathbb {DOL}}^{y_f}$ to improve the investment options. For this purpose, it uses the values of $\mathrm{ED}_{ij}^{y_f}$, $ID1_{ij}^{y_f}$ and $ID2_{ij}^{y_f}$ that have just been calculated in Step-6 in order to choose four new candidate to reinforce the previous transmission line investment that was not enough as described in Step-7 case (ii). From this point, the algorithm goes to Step-5 again.

It should be emphasized that dynamic ordered list $({\mathbb {DOL}}^{y_f})$ can change during the evaluation of each year $y_f$ by adding others transmission lines options and ranking new best reinforcement to be tested. Therefore, the algorithm always searches for the less expensive reinforcement that attends operational constrains. This process of updating the ${\mathbb {DOL}}^{y_f}$ and the successive tests prevent the algorithm from being trapped in a sub-optimal solution. This is the most important contribution of the proposed methodology.

4 Results

The proposed Ms-TPA was applied to three test systems. The first one, the six-bus system (Leite da Silva et al. 2011), was also used as a tutorial case where all steps of the algorithm were duly demonstrated and the results were compared with reference (Leite da Silva et al. 2011). The other case studies, which are well- known Garver system and the equivalent networks of the South Brazilian systems, represents a real large expansion planning scenario. In all test systems, the generation capacity increases at the same rate as demand. All simulations were obtained using a PC core I7 with 2.93  GHz.

4.1 Six-Bus System

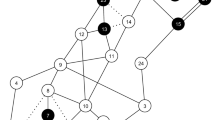
Figure 3 shows the diagram of the six-bus system where the dashed lines are candidates for the multistage expansion planning problem. This system presents three generations and three load buses connected by 11 double-transmission circuits in the base network. Three candidate transmission lines per path can be constructed during the planning period of 8 years starting at year 0.

Fig. 3

Six-bus system diagram

Table 1 shows, for each busbar, the corresponding demand at the last year, i.e. year 8 $(D^{8})$, and the generation limits $(\overline{\mathrm{PG}}^8_i)$ for the same year. The demand and the generator limits have a linear increase of 25 % per year. These values of the demand and generator limits come from reference (Leite da Silva et al. 2011). In addition, Table 2 shows the main data set of line $({\mathbb {C}})$ candidates to the multistage expansion planning.

Table 1 Main data for six-bus system

Table 2 Six-bus candidates transmission lines

The process begins in Step-1; after all data were set, the Ms-TPA goes to Step-2 to run the C-COPF problem. This simulation results in a continuous ED’s values for all candidates for all planning horizon. Table 3 shows the ED’s values for the six lines which had at least one ED greater than zero. The other five candidates, not showed in the table, have presented ED’s equal to zero for all years of the planning horizon.

Table 3 ED’s from C-COPF solutions (Step-2)

The first information that comes from C-COPF solution is related to the values of ED’s. It can be seen from Table 3 that all ED’s values are null at years 0 and 1, meaning that the existing transmission lines are enough for operation in these periods. However, from year 2 there are many nonzero values for ED’s, indicating that multistage expansion planning must be started in the year 2. From Table 3, year two needs 2 % of reinforcement at lines 1–4 and 1–5, year 3 needs 41 % of reinforcement at lines 1–4, 61 % at lines 1–5 and 17 % at lines 3–6 and so on.

Although continuous ED’s values are not acceptable, they bring important information to obtain sensitive indexes related to the decision to build or not a given candidate line. In addition, continuous ED’s values indicate when the reinforcement will start. In this case, it will start at year 2. So $y_f$ is initially set to 2 at Step-3.

Another information that come from the C-COPF are the Lagrange multipliers (LM) related to long-term investment cost. Table 4 shows the values of these coefficients for year 2, and they will also assemble the set of possible reinforcements for year 2 by using the two highest values of sensitivity indexes $ID1_{ij}^2$ and $ID2_{ij}^2$, calculated from Eqs.  (5) and (6), respectively.

Table 4 LM from C-COPF solutions (Step-2)

Table 5 shows $ID1_{ij}^2$ and $ID2_{ij}^2$ values where it can be observed that both indexes indicate lines 1–4 and 1–5 as reinforcements. As stated in Step-4, the dynamic ordered list for $y_f$ equal to 2 should be ${\mathbb {DOL}}^2 = \{1-5, 1-4\}$, because lines 1–5 have lower cost than lines 1–4, as shown in Table 2.

Table 5 $y_f=2$ and $\mathrm{lines}_{ij}$

Step-5 choose the first element of ${\mathbb {DOL}}^{2}\,(Line_{1-5})$ to be tested as possible reinforcement by setting $\mathrm{ED}_{1-5}^{2}=1$ in the C-COPF formulation that will be run in Step-6. Table 6 shows the ED’s values for the simulation of C-COPF in Step-6 considering the construction of the lines 1–5 at year 2. It can be observed that all ED’s values became zero for year 2, indicating that the option to build the lines 1–5 was enough for a proper system operation at this year. Therefore, this reinforcement was stored in $({\mathbb {RE}}^2)$ in Step 9. An important observation is that $\mathrm{ED}_{1-5}^{2}=1$ does not change for the rest of the simulation because the lines 1–5 have became equivalent to an existing line from year 2.

Table 6 ED’s from C-COPF solutions (Step-6)

As the planning is not over because there are many ED’s values between zero and one, the algorithm must return to Step-3 to identify the next year that needs reinforcements. In this case, from the C-COPF previously performed at Step-6, there are two ED’s values greater than zero at year 3, as shown in Table 6, indicating that a reinforcement is necessary, so $y_f$ should be equal to 3.

Similarly, Table 7 shows the sensitivity indexes for year 3 calculated from the results of C-COPF. It can be seen that for index 1 lines 1–4 and 3–6 present the two highest values, while index 2 indicated lines 1–4 and 4–5. Therefore, the dynamic ordered list for year 3 is ${\mathbb {DOL}}^3=\{4-5,1-4,3-6\}$, based on the line costs of Table 2.

Table 7 Indexes for $y_f=3$ and ${\hbox {lines}}_{ij}$

For this ${\mathbb {DOL}}^3$ set, Step-6 is performed again to solve C-COPF aiming to analyse the lines 4–5 as a possible reinforcement for year 3. As stated before, this is done considering $\mathrm{ED}_{4-5}^{3}=1$ in a C-COPF. As shown in Table 8, the lines 4–5 do not meet all constraints at year 3 and another reinforcement must be found to be joined with lines 4–5. The new sensitivity indexes were then calculated again. From the new index $ID1_{ij}^3$, lines 1–4 and 3–6 are selected to compose the reinforcement for lines 4–5 and the index $ID2_{ij}^3$ indicates lines 1–4 and 2–3.

Table 8 Main ED’s from C-COPF Solutions

So at Step-8, ${\mathbb {DOL}}^3$ replaces lines 4–5 by all pairs of reinforcements composed by lines 4–5 and the lines indicated by new indexes $ID1_{ij}^3$ and $ID2_{ij}^3$, resulting in new ${\mathbb {DOL}}^3=\{(1-4),(3-6),(4-5/2-3),(4-5/1-4),(4-5/3-6)\}$. These pairs are placed at the end of ${\mathbb {DOL}}^3$ because they have a higher cost than a single transmission line options. Then, the first element of ${\mathbb {DOL}}^3$ is now the lines 1–4 and the proposed algorithm starts to test these lines in Step-6. In this case, $\mathrm{ED}_{4-5}^{3}$ goes back to range from zero to one and $\mathrm{ED}_{1-4}^{3}=1$ in a C-COPF.

After running the C-COPF problem (Step-6) again, it is verified that transmission lines 1–4 are enough to meet the operational constraints at year 3 because others ED’s in year 3 are equal to zero. Thus, $\mathrm{ED}_{1-4}^{3}$ remains equal to one for the rest of the simulation and ${\mathbb {RE}}^3=\{1-4\}$. So the algorithm goes on. This example has shown the dynamism of ${\mathbb {DOL}}^3$ avoiding sub-optimal investment.

The next year that needs reinforcements is the year number 4 as shown in Table 9. For that, Table 10 shows the indexes results where the selected possible reinforcements are ${\mathbb {DOL}}^4=\{1-5,3-5,3-6\}$. In this case, all the three possible reinforcements have required new reinforcements. After running C-COPF to evaluate these options, the ${\mathbb {DOL}}^4$ list became $\{(1-5,3-6),(3-5,2-4),(3-6,1-4)...\}$. Thus, the first element of ${\mathbb {DOL}}^4$ (pair of lines 1–5 and 3–6) was tested in Step-6, and no more requirements were necessary to operate the system properly. Therefore, ${\mathbb {RE}}^4=\{(1-5, 3-6)\}$.

Table 9 Main ED’s from year 2 to year 4

Table 10 Indexes for $y_f=4$ and $\mathrm{Lines}_{ij}$

The analysis of years 5, 6, 7 and 8 by using the proposed algorithm completes the expansion planning during the period of 8 years. The multistage transmission planning found by the proposed approach is the same presented in reference (Leite da Silva et al. 2011). Table 11 shows the timeline when each selected line must be constructed. The last column of this table shows the number of the C-COPF runs to find the best investment for each year. Year 6 spent 20 runs of C-COPF because three lines were necessary for increasing ${\mathbb {DOL}}^6$. Despite year 8 receiving only two reinforcements, it spent 26 C-COPF runs because these two reinforcement are more expensive than others and they required the test of many groups composed for three cheaper lines.

Table 11 Final multistage expansion planning

While reference (Leite da Silva et al. 2011) spent about 23 min, the proposed Ms-TPA has spent about 6 min to solve this transmission expansion planning, indicating that the Ms-TPA is suitable to analyse large-scale systems.

Two other simulations were performed with the proposed algorithm, but using only one index for forming the ${\mathbb {DOL}}$. In the first simulation, it has considered only the index $ID1_{ij}^y$, resulting in a multistage expansion planning equal to 191.16 million US$. For the index $ID2_{ij}^y$, the cost was US$ 234.92 million. Although these two expansion plans were more expensive than the previous one shown in Table 11, they represent good planning options for the planner assessment.

To check the best results obtained using Ms-TPA, another simulation was carried out using the nonlinear integer optimization toolbox (NLI) from LINGO package (Copyright $\copyright$ LINDO SYSTEMS INC.) to solve directly the proposed I-COPF. However, the information that years 0 and 1 have no reinforcements and the maximum number of reinforcements is 3 for each year is added as constraints of the proposed I-COPF. These additional constraints made the NLI algorithm able to solve I-COPF by reducing the CPU time. After 18 min, the NLI converged to exactly the same results presented in Table 11.

4.2 Garver System

This is a well-known system proposed in (Garver 1970) which has been commonly used in many works that address the problem of transmission expansion planning. This system is formed by six busbars, six existing circuits on base topology and 15 candidate transmission line paths where three parallel transmission lines per path are allowed. The Ms-TPA is tested considering the losses in the circuits as well as the redispatch of the generating units.

Initially, the proposed methodology was used to simulate the S-TSEP by considering only the last year of the planning (year 10). For this simulation, the problem was solved three times, once for each index and again for both indexes simultaneously. The results for these simulations are shown in Table 12. It should be emphasized that the best solution is the same that was obtained from reference (deOliveira et al. 2005).

Table 12 Planning at year 10 for Garver system

For the multistage transmission system expansion planning (Ms-TSEP) studies, the proposed methodology Ms-TPA was applied to the Garver system considering 10 years of horizon planning starting at year 0. Both load and generation increase linearly from year 0. The demand at year 0 was considered equal to 10 % of the values corresponding to year 10. For the generation capacity, it was adopted 25 %.

Under these conditions, Table 13 shows the Ms-TSEP results where it can be observed that the best planning was obtained by using only the index $ID2_{ij}^y$, Plan-2. In other words, these results show more than one long-term investment option. For example, the Plan-2 performs the postponement of building lines 03–05 in year 6. Although it could be the best solution, the planner may adopt another scenario due to uncertainties or constrains not considered in the initial settings. This feature allows extending the financial and budget analysis.

Table 13 Results for multistage Garver system

To check the performance of Ms-TPA, it should be emphasized that also the best planning has been obtained by using the NLI from LINGO to solve the proposed problem I-COPF for Garver system.

4.3 South Brazilian System

The equivalent South Brazilian system comprises the most important busbars and branches of the respective real system. In the base network, it presents 46 busbars and 62 transmission lines. Standard data of this system for static expansion problem can be found at reference (Romero and Monticelli 1994).

To test the proposed Ms-TPA, the multistage expansion problem for this case study considers a 10-year planning horizon where each path can receive up to three transmission line reinforcements during the planning period. The total demand is 6880.0 MW in the tenth year ($D^{10}$), and at year 0, ($D^{0}$) is equal to 35 % of ($D^{10}$) varying linearly from $D^{0}$ to $D^{10}$. The total generation is 10,545.0 MW in the tenth year ($\overline{\mathrm{PG}}^{10}_i$), and in year 0, ($\overline{\mathrm{PG}}^0_i$) is made equal 35 % of ($\overline{\mathrm{PG}}^{10}_i$) varying linearly from $\overline{\mathrm{PG}}^0_i$ to $\overline{\mathrm{PG}}^{10}_i$. Under these considerations, two cases were simulated:

Case 1, without transmission losses by setting all $g_{ij}$ equal zero in equation (3). For this simulation, the set of candidates ${\mathbb {C}} = \{13-20; 20-23; 20-21; 42-43; 46-06; 05-06\}$ and $Ic_{ij}^{0} = \{7120.0; 6268.0; 8178.0; 8178.0; 16005.0; 8178.0\}$ times $10^3\,\mathrm{US}{\$}$ were adopted. The set ${\mathbb {C}}$ was obtained in reference (Romero and Monticelli 1994) for static planning at year 10, where generation rescheduling was allowed.

Case 2, with transmission losses by setting $g_{ij}$ to the respective value given in (Romero and Monticelli 1994). For this simulation, the set of candidate lines used in case 1 is not able to meet the load without load shedding at busbars ${\mathbb {BLS}}= \{04; 20; 24\}$. So the new set of candidates for case 2 is composed by ${\mathbb {C}}$ and the candidates connected to ${\mathbb {BLS}}$ is equal to $\{04-02; 04-05; 04-09; 04-11; 20-18; 24-25; 24-33; 24-34\}$. The transmission investment cost associated with these new candidates is {5965.0; 4046.0; 6217.0; 14,247.0; 12,732.0; 8178.0; 9399.0; 10,611.0} times $10^3 US{\$}$, respectively. Thus, the number of candidate increased to 14 lines.

Table 14 shows the results for these cases by using both indexes at the same time. The first column indicates the year the reinforcement lines were added. As expected, the inclusion of losses has resulted in a major investment cost to reinforce the system by anticipating the operation of some transmission lines as well as by demanding the construction of more expensive lines 18–20 instead of lines 13–20 as seen at year 10. These aspects show the importance to consider the active transmission line power losses to evaluate the planning in a more realistic way. However, the largest set of candidates lines and the fact that transmission losses introduces nonlinear equations lead the C-COPF formulation difficult to be solved, requiring more computational time. While case 1 spent 4 min running a total of 16 C-COPF, case 2 has spent 34 minutes of CPU time running a total of 14 C-COPF.

Table 14 Results for case 1 and case 2

Other simulations were carried out by using NLI from LINGO to directly solve the proposed I-COPF. These simulations have considered the same candidates transmission lines and adding information from previous results of Ms-TPA as follows: (1) the planning begins at year 1, and (2) the maximum number of expansion transmission lines to be constructed in each year is equal to the number given by Table 14. These constraints are enough to make the NLI algorithm able to solve I-COPF by reducing the CPU effort to a suitable computational time.

For case 1, NLI spent 12 hours of simulation and 28 hours for case 2. However, for both cases the results are the same as shown in Table 14. As expected, the inclusion of nonlinearities imposed by transmission losses and the larger set of candidates lines have led the NLI to spend more computational time to solve the problem.

5 Conclusion

This paper has presented a new technique for multistage transmission system expansion planning considering the coupled time investment. From the results obtained, the following aspects can be emphasized:

The multistage optimal power flow (I-COPF) proposed in this work has allowed the treatment of the nonlinearities and integer variables introduced by the transmission active losses and coupled expansion planning variable. In addition, the I-COPF problem can be solved for a small systems using an integer optimization package.

The complexity of the combinatorial search of I-COPF is avoided by using a continuous expansion variable to mitigate integer variable resulting in a continuous and nonlinear coupled (C-COPF) formulation that can be fast solved by using any continuous and nonlinear optimizations packages.

The C-COPF problem provides fast convergence and quality indexes represented by the continuous variable and Lagrange multipliers that are used to indicate good reinforcements during the step-by-step process.

Both the transmission losses and the high number of candidate lines make the proposed Ms-TPA more complex. However, the multistage expansion problem can still be solved in a reasonable computational time for planning matters.

The Ms-TPA proposed in this paper is very efficient to handle a large system together with extensive horizon planning spending low computational effort. This is an important contribution of this paper because these characteristics are not obtained in other methods presented in the literature.